Սահմանում
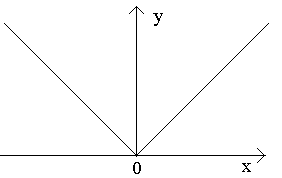
Թող «y=f(x)» ֆունկցիան սահմանվի «ainR» կետը պարունակող ինչ-որ միջակայքում: «ա» կետը կոչվում է տեղական առավելագույն կետ«f» ֆունկցիաները, եթե կա «epsilon» - «a» կետի հարևանություն, որը այս հարևանության ցանկացած «x!=a»-ի համար՝ «f(x) Եթե «f(x)>f(a)» անհավասարությունը բավարարված է, ապա կոչվում է «a». տեղական նվազագույն միավոր«f» ֆունկցիաները: Տեղական առավելագույն և տեղական նվազագույն կետերը կոչվում են կետեր տեղական ծայրահեղություն. Թեորեմ 5.1 (Ֆերմատ) Եթե «a» կետը «y=f(x)» ֆունկցիայի տեղական ծայրահեղ կետն է, և «f» ֆունկցիան այս կետում ունի ածանցյալ, ապա «f^»(a)=0»: Ֆիզիկական իմաստ. վերադարձով միաչափ շարժումով առավելագույն հեռացման կետում պետք է կանգառ լինի: Երկրաչափական նշանակություն. տեղական ծայրամասային կետում շոշափողը հորիզոնական է: Մեկնաբանություն. Ֆերմայի թեորեմից հետևում է, որ եթե ֆունկցիան «a» կետում ունի ծայրահեղություն, ապա այս պահին ֆունկցիայի ածանցյալը կամ զրո է, կամ գոյություն չունի: Օրինակ, «y=|x|» ֆունկցիան ունի նվազագույն «x=0» կետում, իսկ ածանցյալն այս կետում գոյություն չունի (տես օրինակ 4.2): Կկանչվեն այն կետերը, որոնցում ֆունկցիան սահմանված է, իսկ ածանցյալը հավասար է զրոյի կամ գոյություն չունի քննադատական.
Այսպիսով, եթե ֆունկցիան ունի ծայրահեղ կետեր, ապա դրանք գտնվում են կրիտիկական կետերի մեջ (կրիտիկական կետերը «կասկածելի» են ծայրահեղության համար): Կրիտիկական կետում էքստրեմումի առկայությունն ապահովող պայմանները ձևակերպելու համար մեզ անհրաժեշտ է հետևյալ հայեցակարգը. Հիշենք, որ ընդմիջում ասելով հասկանում ենք թվային ուղղի միջակայքը (վերջավոր կամ անվերջ), կիսատ միջակայքը կամ հատվածը։ Սահմանում Թող «y=f(x)» ֆունկցիան սահմանվի «I» միջակայքում: 1) «y=f(x)» ֆունկցիա ավելանում է 2) «y=f(x)» ֆունկցիա նվազում է«I»-ին, եթե որևէ «x,yinI»-ի համար՝ «x Եթե ֆունկցիան մեծանում կամ նվազում է «I»-ով, ապա ֆունկցիան կոչվում է միապաղաղ«I» միջակայքում: Միապաղաղության պայմաններ. Թող «y=f(x)» ֆունկցիան սահմանվի «I» միջակայքում՝ «a», «b» վերջնակետերով, «a, b)»-ի վրա տարբերվող և վերջնակետերում շարունակական, եթե դրանք պատկանում են «I»-ին: . Հետո 1) եթե `f^"(x)>0` `(a, b)`-ով, ապա ֆունկցիան մեծանում է `I`-ով; 2) եթե `f^"(x)<0` на `(a, b)`, то функция убывает на `I`. Ծայրահեղ պայմաններ. Թող «y=f(x)» ֆունկցիան սահմանվի «(ab)» միջակայքում, շարունակական «x_0» կետում (a, b)» և տարբերվող «(a,x_0) uu (x_0,b) վրա: «. Հետո 1) եթե `f^"(x)>0` դեպի "(a;x_0)" և "f^"(x)<0` на `(x_0;b)`, то `x_0` - точка локального максимума функции `f`; 2) եթե `f^"(x)<0` на `(a;x_0)` и `f^"(x)>0` դեպի «(x_0;b)», ապա «x_0»-ը «f» ֆունկցիայի տեղական նվազագույն կետն է: Օրինակ 5.1 Ուսումնասիրեք «y=x^3-3x» ֆունկցիան սահմանման տիրույթում միապաղաղության և ծայրահեղության համար: Այս ֆունկցիան սահմանված է «R»-ի վրա և տարբերվում է յուրաքանչյուր կետում (տե՛ս թեորեմ 4.2-ի հետևանքը), և «y^"=3(x^2-1)»: Քանի որ «y^"<0` при `x in(-1,1)`; `y^">0` «x in(-oo,-1)uu(1,+oo)»-ի համար, այնուհետև ֆունկցիան մեծանում է «(-oo,-1]» և «`» ճառագայթների վրա: «x» ծայրահեղության պայմանով: =-1` - տեղական առավելագույնի կետը, իսկ «x=1» -ը տեղական նվազագույնի կետն է, քանի որ «y^»=0» միայն «x=1» և «x=-1» կետերում է: ապա Ֆերմայի թեորեմի համաձայն ֆունկցիան չունի այլ ծայրամասային կետեր: Դիտարկենք խնդիրների մի կարևոր դաս, որոնք օգտագործում են ածանցյալ հասկացությունը՝ հատվածի վրա ֆունկցիայի ամենամեծ և ամենափոքր արժեքները գտնելու խնդիրը: Օրինակ 5.2 Գտե՛ք «y=x^3-3x» ֆունկցիայի ամենամեծ և ամենափոքր արժեքը հատվածի վրա՝ ա) «[-2;0]»; բ) «»: ա) Օրինակ 5.1-ից հետևում է, որ ֆունկցիան մեծանում է «(-oo,-1]»-ով և նվազում է «[-1,1]»-ով: Այսպիսով, «y(-1)>=y(x)» բոլոր « x in[-2;0]` և `y_"max"=y(-1)=2` - ֆունկցիայի ամենամեծ արժեքը «[-2;0]» հատվածում ամենափոքր արժեքը գտնելու համար անհրաժեշտ է. Ֆունկցիայի արժեքները համեմատելու համար հատվածների ծայրերում, քանի որ `y(-2)=-2` և `y(0)=0`, ապա `y_"max"=-2` ամենափոքր արժեքն է: «[-2;0]» հատվածի ֆունկցիայի: բ) Քանի որ ճառագայթի վրա կա ``, ուրեմն` y_"naim"=y(1)=-2`, `y_"naib"=y(3)=18`: Մեկնաբանություն Նկատի ունեցեք, որ ինտերվալի վրա շարունակական ֆունկցիան միշտ ունի ամենամեծ և ամենափոքր արժեքները: Օրինակ 5.3 Գտե՛ք «[-4;3]» հատվածի `y=x^3-12|x+1|` ֆունկցիայի ամենամեծ և ամենափոքր արժեքը: Նշենք, որ ֆունկցիան շարունակական է ամբողջ թվային տողի վրա։ Նշենք `f_1(x)=x^3+12(x+1)`, `f_2(x)=x^3-12(x+1)`: Այնուհետև `y=f_1(x)` -4-ում<=x<=-1` и `y=f_2(x)` при `-1<=x<=3`. Находим `f_1^"(x)=3x^2+12`, `f_2^"(x)=3x^2-12`. Уравнение `f_1^"(x)=0` не имеет действительных корней, а уравнение `f_2^"(x)=0` имеет два действительных корня `x_1=-2`, `x_2=2`, из которых интервалу `(-1;3)` принадлежит только точка `x_2`. В точке `x=-1` функция определена, но не имеет производной (можно, например, провести рассуждения, аналогичные рассуждениям примера 4.2). Итак, имеется две критические точки: `x=-1` и `x=2`. Производная `y^"(x)=f_1^"(x)>0` դեպի «(-4,-1)», «y^"(x)=f_2^"(x)<0` на `(-1;2)` и `y^"(x)=f_2^"(x)>0` դեպի «(2;3)»: Գրենք բոլոր ուսումնասիրությունները աղյուսակում. `y_"naib"=-1`; `y_"name"=-100`: ՖՈՒՆԿՑԻԱՆԵՐԻ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ ՇԱՐՈՒՆԱԿԱԿԱՆ ՀԱՐՑԱԶՐՈՒՅՑՈՒՄ Դիտարկենք ֆունկցիաների մի քանի հատկություն՝ շարունակական ընդմիջումով։ Մենք ներկայացնում ենք այս հատկությունները առանց ապացույցների: Գործառույթ y = f(x)կանչեց շարունակական հատվածի վրա [ա, բ], եթե այն շարունակական է այս հատվածի բոլոր ներքին կետերում և նրա ծայրերում, այսինքն. կետերում աԵվ բ, շարունակական է համապատասխանաբար աջ և ձախ կողմում։ Թեորեմ 1.Շարունակական ֆունկցիա [ինտերվալի վրա ա, բ], այս հատվածի առնվազն մի կետում վերցնում է ամենամեծ արժեքը և առնվազն մի կետում ամենափոքրը: Թեորեմն ասում է, որ եթե ֆունկցիան y = f(x)շարունակական է միջակայքում [ ա, բ], ապա կա առնվազն մեկ կետ x 1 Î
[ ա, բ] այնպիսին, որ ֆունկցիայի արժեքը f(x)այս պահին կլինի ամենամեծը իր բոլոր արժեքներից այս հատվածում. f(x 1) ≥ f(x). Նմանապես, կա նման կետ x 2, որտեղ ֆունկցիայի արժեքը կլինի հատվածի բոլոր արժեքներից ամենափոքրը. f(x 1) ≤ f(x). Հասկանալի է, որ կարող են լինել մի քանի այդպիսի կետեր, օրինակ, նկարը ցույց է տալիս, որ ֆունկցիան f(x)երկու կետում վերցնում է ամենափոքր արժեքը x 2Եվ x 2 ". Մեկնաբանություն. Թեորեմի պնդումը կարող է սխալ դառնալ, եթե հաշվի առնենք ֆունկցիայի արժեքը միջակայքում ( ա, բ) Իսկապես, եթե դիտարկենք ֆունկցիան y = xվրա (0, 2), այնուհետև այն շարունակական է այս միջակայքում, բայց չի հասնում դրանում ոչ ամենամեծ, ոչ ամենափոքր արժեքներին. այն հասնում է այդ արժեքներին միջակայքի ծայրերում, բայց ծայրերը չեն պատկանում: մեր տիրույթին: Բացի այդ, թեորեմը դադարում է ճշմարիտ լինել ընդհատվող ֆունկցիաների համար։ Օրինակ բերեք։ Հետևանք.Եթե ֆունկցիան f(x)շարունակական է [ ա, բ], ապա այն սահմանափակված է այս հատվածում: Թեորեմ 2.Թողեք գործառույթը y = f(x)շարունակական է միջակայքում [ ա, բ] և այս հատվածի ծայրերում վերցնում է տարբեր նշանների արժեքներ, ապա հատվածի ներսում կա առնվազն մեկ կետ x = C, որտեղ ֆունկցիան անցնում է զրոյի. f(C)= 0, որտեղ ա< C< b Այս թեորեմն ունի պարզ երկրաչափական նշանակություն՝ եթե շարունակական ֆունկցիայի գրաֆիկի կետերը y = f(x)հատվածի ծայրերին համապատասխան [ ա, բ] պառկել առանցքի հակառակ կողմերում Եզ, ապա այս գրաֆիկը հատում է առանցքը հատվածի առնվազն մեկ կետում Եզ. Անդադար գործառույթները կարող են չունենալ այս հատկությունը: Այս թեորեմն ընդունում է հետևյալ ընդհանրացումը. Թեորեմ 3 (միջանկյալ արժեքի թեորեմ).Թողեք գործառույթը y = f(x)շարունակական է միջակայքում [ ա, բ] Եվ f(a) = A, f(b) = B. Հետո ցանկացած թվի համար Գ, կնքված միջեւ ԱԵվ Բ, այս հատվածի ներսում կա այսպիսի կետ ԳÎ [ ա, բ], Ինչ f(c) = C. Այս թեորեմը երկրաչափորեն ակնհայտ է. Դիտարկենք ֆունկցիայի գրաֆիկը y = f(x). Թող f(a) = A, f(b) = B. Հետո ցանկացած ուղիղ գիծ y = C, Որտեղ Գ- միջև եղած ցանկացած թիվ ԱԵվ Բ, կհատի ֆունկցիայի գրաֆիկը առնվազն մի կետում։ Այդ արժեքը կլինի հատման կետի աբսցիսան x = C, որը f(c) = C. Այսպիսով, շարունակական ֆունկցիան, շարժվելով մի արժեքից մյուսը, անպայման անցնում է բոլոր միջանկյալ արժեքներով։ Մասնավորապես: Հետևանք.Եթե ֆունկցիան y = f(x)շարունակական է որոշակի միջակայքում և ընդունում է ամենամեծ և ամենափոքր արժեքները, այնուհետև այս միջակայքում առնվազն մեկ անգամ վերցնում է իր ամենափոքր և ամենամեծ արժեքների միջև պարունակվող ցանկացած արժեք: ԱԾԱԾԱՆՑ ԵՎ ՆՐԱ ԿԻՐԱՌՈՒՄՆԵՐԸ. ածանցյալի սահմանումը Եկեք որոշ գործառույթ ունենանք y=f(x),սահմանվում է որոշակի ընդմիջումով: Յուրաքանչյուր փաստարկի արժեքի համար xայս միջակայքից ֆունկցիան y=f(x)որոշակի նշանակություն ունի. Դիտարկենք երկու արգումենտ արժեք՝ սկզբնական x 0 և նոր x. Տարբերություն x–x 0 կոչվում է մեծացնելով x արգումենտըկետում x 0 և նշվում է Δx. Այսպիսով, Δx = x – x 0 (արգումենտի աճը կարող է լինել դրական կամ բացասական): Այս հավասարությունից բխում է, որ x=x 0 +Δx, այսինքն. փոփոխականի սկզբնական արժեքը որոշակի աճ է ստացել: Ապա, եթե կետում x 0 ֆունկցիայի արժեքը եղել է f(x 0 ),
հետո նոր կետում xֆունկցիան կվերցնի արժեքը f(x) = f(x 0 +Δx). Տարբերություն y–y 0 = f(x) – f(x 0 )
կանչեց ֆունկցիայի ավելացում y = f(x)կետում x 0 և նշվում է խորհրդանիշով Δy. Այսպիսով, Սովորաբար փաստարկի սկզբնական արժեքը x 0-ը համարվում է ֆիքսված, իսկ նոր արժեքը x- փոփոխական: Հետո y 0 = f(x 0 )
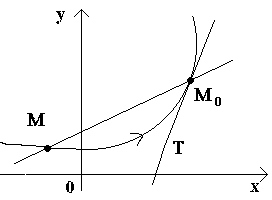
ստացվում է մշտական, և y = f(x)- փոփոխական: Ավելացումներ ΔyԵվ Δxկլինեն նաև փոփոխականներ և (1) բանաձևը ցույց է տալիս, որ Դիփոփոխականի ֆունկցիա է Δx. Ստեղծենք ֆունկցիայի աճի հարաբերակցությունը փաստարկի ավելացմանը Եկեք գտնենք այս հարաբերակցության սահմանը ժամը Δx→0. Եթե այս սահմանը գոյություն ունի, ապա այն կոչվում է այս ֆունկցիայի ածանցյալ f(x)կետում x 0 և նշանակում զ "(x 0): Այսպիսով, Ածանցյալայս գործառույթը y = f(x)կետում x 0-ը կոչվում է Δ ֆունկցիայի աճի հարաբերակցության սահման yարգումենտի ավելացման Δ x, երբ վերջինս կամայականորեն ձգտում է զրոյի։ Նկատի ունեցեք, որ նույն ֆունկցիայի համար ածանցյալը տարբեր կետերում xկարող է ընդունել տարբեր արժեքներ, այսինքն. ածանցյալը կարելի է դիտարկել որպես փաստարկի ֆունկցիա x. Այս գործառույթը նշանակված է զ "(x) Ածանցյալը նշվում է նշաններով զ "(x), y«, . Ածանցյալի հատուկ արժեքը ժամը x = aնշվում է զ "(ա) կամ y "| x=a. Ֆունկցիայի ածանցյալը գտնելու գործողություն f(x)կոչվում է այս ֆունկցիայի տարբերակում։ Ածանցյալը ըստ սահմանման ուղղակիորեն գտնելու համար կարող եք օգտագործել հետևյալը. հիմնական կանոնը: Օրինակներ. ածանցյալի մեխանիկական զգացում Ֆիզիկայից հայտնի է, որ միատեսակ շարժման օրենքն ունի ձև s = v t, Որտեղ ս- ճանապարհն անցել է ժամանակի պահը տ, v- միատեսակ շարժման արագություն. Այնուամենայնիվ, քանի որ Բնության մեջ տեղի ունեցող շարժումների մեծ մասը անհավասար է, այնուհետև ընդհանուր առմամբ արագությունը և, հետևաբար, հեռավորությունը սկախված կլինի ժամանակից տ, այսինքն. կլինի ժամանակի ֆունկցիա։ Այսպիսով, թող նյութական կետը օրենքի համաձայն շարժվի ուղիղ գծով մեկ ուղղությամբ s=s(t). Եկեք նշենք ժամանակի որոշակի կետ տ 0 . Այս պահին կետն անցել է ճանապարհը s=s(t 0 ).
Եկեք որոշենք արագությունը vնյութական կետը տվյալ պահին տ 0 . Դա անելու համար եկեք դիտարկենք ժամանակի մեկ այլ կետ տ 0 +
Δ տ. Այն համապատասխանում է անցած ճանապարհին s =s(t 0 +
Δ տ) Այնուհետև որոշակի ժամանակահատվածում Δ տկետը անցել է Δs ճանապարհը =s(t 0 +
Δ տ)–s(t). Դիտարկենք վերաբերմունքը. Այն կոչվում է միջին արագություն Δ ժամանակային միջակայքում տ. Միջին արագությունը չի կարող ճշգրիտ բնութագրել տվյալ պահին կետի շարժման արագությունը տ 0 (քանի որ շարժումը անհավասար է): Որպեսզի ավելի ճշգրիտ արտահայտեք այս իրական արագությունը՝ օգտագործելով միջին արագությունը, դուք պետք է ավելի կարճ ժամանակ անցկացնեք Δ տ. Այսպիսով, շարժման արագությունը ժամանակի տվյալ պահին տ 0 (ակնթարթային արագություն) միջին արագության սահմանն է միջակայքում տ 0 դեպի տ 0 +Δ տ, երբ Դ տ→0: դրանք. անհավասար արագությունսա ժամանակի նկատմամբ անցած տարածության ածանցյալն է: ածանցյալի երկրաչափական նշանակությունը Նախ ներկայացնենք տվյալ կետում կորի շոշափողի սահմանումը: Եկեք դրա վրա ունենանք կոր և ֆիքսված կետ Մ 0(տես նկարը): Մայս կորը և գծիր հատված M 0 M. Եթե կետը Մսկսում է շարժվել կորի երկայնքով, իսկ կետը Մ 0մնում է անշարժ, ապա սեկանտը փոխում է իր դիրքը։ Եթե կետի անսահմանափակ մոտավորությամբ Մկորի երկայնքով մինչև մի կետ Մ 0ցանկացած կողմում սեկանտը հակված է զբաղեցնելու որոշակի ուղիղ գծի դիրք Մ 0 Տ, ապա ուղիղ Մ 0 Տկոչվում է տվյալ կետում կորի շոշափողը Մ 0. Դա., շոշափողդեպի կորը տվյալ կետում Մ 0կոչվում է սեկանտի սահմանային դիրք M 0 Mերբ կետ Մձգվում է կորի երկայնքով մինչև մի կետ Մ 0. Այժմ դիտարկենք շարունակական ֆունկցիան y=f(x)և այս ֆունկցիային համապատասխանող կորը։ Որոշակի արժեքով X 0 ֆունկցիան արժեք է ընդունում y 0 =f(x0):Այս արժեքները x 0 և y 0-ը կորի վրա համապատասխանում է մի կետի M 0 (x 0; y 0):Եկեք փաստարկենք x 0ավելացում Δ X. Փաստարկի նոր արժեքը համապատասխանում է ֆունկցիայի ավելացված արժեքին y 0 +Δ y=f(x 0 –Δ x). Մենք հասկանում ենք կետը M (x 0+Δ x; y 0+Δ y).Եկեք սեկանտ նկարենք M 0 Mիսկ φ-ով նշել առանցքի դրական ուղղությամբ հատվածով գոյացած անկյունը Եզ. Եկեք հարաբերություն ստեղծենք և նկատենք, որ . Եթե հիմա Դ x→0, ապա Δ ֆունկցիայի շարունակականության շնորհիվ ժամը→0 և հետևաբար կետը Մ, շարժվելով կորի երկայնքով, մոտենում է կետին առանց սահմանի Մ 0. Հետո սեկանտը M 0 Mհակված կլինի կետում կորի շոշափողի դիրքը վերցնել Մ 0, և φ→α անկյունը Δ-ում x→0, որտեղ α-ն նշանակում է շոշափողի և առանցքի դրական ուղղության անկյունը Եզ. Քանի որ tan φ ֆունկցիան շարունակաբար կախված է φ-ից φ≠π/2-ի համար, ապա φ→α tan φ → tan α-ի համար և, հետևաբար, շոշափողի թեքությունը կլինի. դրանք. f "(x)= tg α . Այսպիսով, երկրաչափական y" (x 0)ներկայացնում է տվյալ ֆունկցիայի գրաֆիկին շոշափողի թեքությունը տվյալ կետում x 0, այսինքն. տրված փաստարկի արժեքի համար x, ածանցյալը հավասար է ֆունկցիայի գրաֆիկին շոշափողով գոյացած անկյան շոշափմանը. f(x)համապատասխան կետում M 0 (x; y)դրական առանցքի ուղղությամբ Եզ. Օրինակ։Գտեք կորի վրա շոշափողի թեքությունը y = x 2 կետում Մ(-1; 1). Մենք արդեն տեսել ենք, որ ( x 2)" = 2X. Բայց կորի շոշափողի անկյունային գործակիցը tan α = է y«| x=-1 = – 2. ՖՈՒՆԿՑԻԱՆԵՐԻ ՏԱՐԲԵՐԱԿԱՆՈՒԹՅՈՒՆԸ. ՏԱՐԲԵՐԱԿԱՆ ՖՈՒՆԿՑԻԱՅԻ ՇԱՐՈՒՆԱԿԱԿԱՆՈՒԹՅՈՒՆԸ Գործառույթ y=f(x)կանչեց տարբերակելիինչ-որ պահի x 0, եթե այն ունի որոշակի ածանցյալ այս կետում, այսինքն. եթե հարաբերությունների սահմանը գոյություն ունի և վերջավոր է: Եթե ֆունկցիան տարբերելի է որոշակի հատվածի յուրաքանչյուր կետում [ Ա; բ] կամ ընդմիջում ( Ա; բ), հետո ասում են, որ նա տարբերակելիհատվածի վրա [ Ա; բ] կամ, համապատասխանաբար, միջակայքում ( Ա; բ). Վավերական է հետևյալ թեորեմը, որը կապ է հաստատել տարբերվող և շարունակական ֆունկցիաների միջև. Թեորեմ.Եթե ֆունկցիան y=f(x)ինչ-որ պահի տարբերվող x 0, ապա այս պահին այն շարունակական է։ Այսպիսով, ֆունկցիայի տարբերակելիությունից հետևում է նրա շարունակականությունը։ Ապացույց. Եթե որտեղ α-ն անվերջ փոքր մեծություն է, այսինքն. մի մեծություն, որը հակված է զրոյի որպես Δ x→0. Բայց հետո Δ y=զ "(x 0)
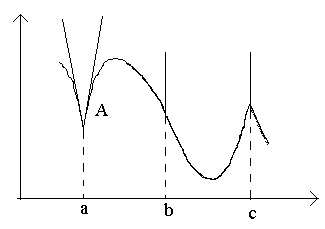
Δ x+αΔ x=> Δ y→0 ժամը Δ x→0, այսինքն. f(x) – f(x 0)→0 ժամը x→x 0, ինչը նշանակում է, որ ֆունկցիան f(x)շարունակական մի կետում x 0 . Ք.Ե.Դ. Այսպիսով, ֆունկցիան չի կարող ածանցյալ ունենալ ընդհատման կետերում։ Հակառակը ճիշտ չէ. կան շարունակական ֆունկցիաներ, որոնք որոշ կետերում տարբերվող չեն (այսինքն՝ այս կետերում չունեն ածանցյալ)։ Դիտարկենք նկարի կետերը ա, բ, գ. Կետում աժամը Δ x→0 հարաբերակցությունը սահման չունի (քանի որ միակողմանի սահմանները տարբեր են Δ-ի համար x→0–0 և Δ x→0+0): Կետում Ագրաֆիկ չկա սահմանված շոշափող, բայց կան երկու տարբեր միակողմանի շոշափողներ՝ թեքություններով Դեպի 1 և Դեպի 2. Այս տեսակի կետը կոչվում է անկյունային կետ: Կետում բժամը Δ x→0 հարաբերակցությունը անսահման մեծ քանակի հաստատուն նշան է: Ֆունկցիան ունի անսահման ածանցյալ։ Այս պահին գրաֆիկն ունի ուղղահայաց շոշափող: Կետի տեսակ – ուղղահայաց շոշափողի «թեքման կետ»: Կետում գմիակողմանի ածանցյալները տարբեր նշանների անսահման մեծ քանակություն են: Այս պահին գրաֆիկն ունի երկու միավորված ուղղահայաց շոշափողներ: Տեսակ – «վերադարձի կետ» ուղղահայաց շոշափողով – անկյունային կետի հատուկ դեպք: Սահմանում 4. Ֆունկցիան կոչվում է շարունակական հատվածի վրա, եթե այն շարունակական է այս հատվածի յուրաքանչյուր կետում (a կետում այն շարունակական է աջից, այսինքն, իսկ b կետում՝ ձախից, այսինքն.): Բոլոր հիմնական տարրական գործառույթները շարունակական են իրենց սահմանման տիրույթում: Անընդհատ շարունակական ֆունկցիաների հատկությունները. ֆունկցիայի շարունակականության կետի հատված Այն կետերը, որոնցում շարունակականության պայմանը չի բավարարվում, կոչվում են այս ֆունկցիայի ընդմիջման կետեր: Եթե ֆունկցիայի անջատման կետ է, ապա 1, 2 սահմանումներում նշված ֆունկցիայի շարունակականության երեք պայմաններից առնվազն մեկը բավարարված չէ, այն է՝ 1) Ֆունկցիան սահմանվում է կետի հարևանությամբ, բայց չի սահմանվում բուն կետում: Այսպիսով, օրինակ 2-ում դիտարկված ֆունկցիան ա) կետում ունի դադար, քանի որ այն այս կետում սահմանված չէ: 2) Ֆունկցիան սահմանված է մի կետում և դրա շրջակայքում, կան միակողմանի սահմաններ և, բայց դրանք միմյանց հավասար չեն. Օրինակ, օրինակ 2 բ) ֆունկցիան սահմանվում է մի կետում և նրա մոտակայքում, բայց քանի որ ա. 3) Ֆունկցիան սահմանված է կետում և դրա շրջակայքում, կան միակողմանի սահմաններ և դրանք հավասար են միմյանց, բայց ոչ հավասար են կետում գտնվող ֆունկցիայի արժեքին. Օրինակ՝ ֆունկցիա։ Ահա ընդմիջման կետը. այս պահին ֆունկցիան սահմանվում է, կան միակողմանի սահմաններ և միմյանց հավասար, բայց, այսինքն. Ֆունկցիայի ընդմիջման կետերը դասակարգվում են հետևյալ կերպ. Սահմանում 5. Կետը կոչվում է առաջին տեսակի ֆունկցիայի ընդհատման կետ, եթե այս կետում կան վերջավոր սահմաններ և, բայց դրանք իրար հավասար չեն. Մեծությունը կոչվում է ֆունկցիայի թռիչք կետում։ Սահմանում 6. Կետը կոչվում է ֆունկցիայի շարժական ընդհատման կետ, եթե այս կետում կան վերջավոր սահմաններ, և դրանք հավասար են միմյանց. Սահմանում 7. Կետը կոչվում է երկրորդ տեսակի ֆունկցիայի անջատման կետ, եթե այս պահին միակողմանի սահմաններից (կամ) գոնե մեկը գոյություն չունի կամ հավասար է անվերջությանը։ Օրինակ 3. Գտե՛ք հետևյալ ֆունկցիաների ընդմիջման կետերը և որոշե՛ք դրանց տեսակը՝ ա) բ. Լուծում. ա) Ֆունկցիան սահմանված և շարունակական է ընդմիջումներով, և քանի որ այս ինտերվալներից յուրաքանչյուրի վրա այն սահմանվում է շարունակական տարրական ֆունկցիաներով: Հետևաբար, տվյալ ֆունկցիայի ընդմիջման կետերը կարող են լինել միայն այն կետերը, որոնց դեպքում ֆունկցիան փոխում է իր վերլուծական առաջադրանքը, այսինքն. միավորներ և Գտնենք ֆունկցիայի միակողմանի սահմանները կետում. Քանի որ միակողմանի սահմանները գոյություն ունեն և վերջավոր են, բայց միմյանց հավասար չեն, կետը առաջին տեսակի անդադար կետ է: Ֆունկցիոնալ թռիչք. Այն կետի համար, որը մենք գտնում ենք. Սեգմենտի վրա ֆունկցիայի շարունակականությունը: Մի կետում ֆունկցիայի շարունակականության հետ մեկտեղ դիտարկվում է նրա շարունակականությունը տարբեր ընդմիջումներով: F (x) ֆունկցիան կոչվում է շարունակական (a, b) միջակայքում, եթե այն շարունակական է այս միջակայքի յուրաքանչյուր կետում: F (x) ֆունկցիան ասում են, որ շարունակական է [a, b] միջակայքում, եթե այն շարունակական է (a, b) միջակայքում, աջ շարունակական է a կետում, և թողնում է շարունակական՝ b կետում: Ֆունկցիան կոչվում է շարունակական հատվածի վրա, եթե այն շարունակական է միջակայքում, շարունակական աջ կողմում կետում, այն է իսկ ձախ կողմում շարունակական կետում, այն է ։ Մեկնաբանություն.Գործառույթը, որը շարունակական է [a, b] հատվածի վրա կարող է լինել ընդհատվող a և b կետերում (նկ. 1): [a, b] միջակայքում շարունակական ֆունկցիաների բազմությունը նշանակվում է C[a, b] նշանով։ Հիմնական թեորեմներ ինտերվալի վրա շարունակական ֆունկցիաների մասին: Թեորեմ 1(շարունակական ֆունկցիայի սահմանի վրա): Եթե f (x) ֆունկցիան շարունակական է [a, b] միջակայքում, ապա այն սահմանափակված է այս միջակայքում, այսինքն. կա C > 0 այնպիսի թիվ, որ «x O [a, b] անհավասարությունը | f (x)| ≤ C է: M-ի ամենամեծ արժեքը նշվում է max x նշանով O [a, b] f (x), իսկ m-ի ամենափոքր արժեքը min x խորհրդանիշն է O [a, b] f(x). Ստորև բերված նկարները ցույց են տալիս, թե որտեղ կարող է ֆունկցիան հասնել իր ամենափոքր և ամենամեծ արժեքին: Ձախ նկարում ամենափոքր և ամենամեծ արժեքները ամրագրված են ֆունկցիայի տեղական նվազագույնի և առավելագույնի կետերում: Ճիշտ նկարում - հատվածի ծայրերում: Եթե ֆունկցիան y = զ(x)
շարունակական է միջակայքում [ ա, բ] , ապա այն հասնում է այս հատվածին առնվազն
Եվ բարձրագույն արժեքներ
. Սա, ինչպես արդեն նշվեց, կարող է տեղի ունենալ կամ ներսում ծայրահեղ կետեր, կամ հատվածի ծայրերում։ Հետեւաբար, գտնել առնվազն
Եվ ֆունկցիայի ամենամեծ արժեքները
, շարունակական միջակայքում [ ա, բ], դուք պետք է հաշվարկեք դրա արժեքները բոլորովին կրիտիկական կետերև հատվածի ծայրերում, այնուհետև ընտրել դրանցից ամենափոքրն ու ամենամեծը: Թող, օրինակ, դուք ուզում եք որոշել ֆունկցիայի ամենամեծ արժեքը զ(x) հատվածում [ ա, բ] . Դա անելու համար դուք պետք է գտնեք նրա բոլոր կրիտիկական կետերը, որոնք գտնվում են [ ա, բ]
. Կրիտիկական կետ
կոչվում է այն կետը, որտեղ սահմանված գործառույթը, և նրան ածանցյալկա՛մ հավասար է զրոյի, կա՛մ գոյություն չունի։ Այնուհետև դուք պետք է հաշվարկեք ֆունկցիայի արժեքները կրիտիկական կետերում: Եվ վերջապես, պետք է համեմատել ֆունկցիայի արժեքները կրիտիկական կետերում և հատվածի ծայրերում ( զ(ա) Եվ զ(բ)): Այս թվերից ամենամեծը կլինի սեգմենտի վրա ֆունկցիայի ամենամեծ արժեքը
[ա, բ]
. Գտնելու խնդիրներ ֆունկցիայի ամենափոքր արժեքները
. Օրինակ 1. Գտեք ֆունկցիայի ամենափոքր և ամենամեծ արժեքները Լուծում. Գտե՛ք այս ֆունկցիայի ածանցյալը: Հավասարեցնենք ածանցյալը զրոյի () և ստացենք երկու կրիտիկական կետ՝ և . Տվյալ հատվածի վրա ֆունկցիայի ամենափոքր և ամենամեծ արժեքները գտնելու համար բավական է հաշվել դրա արժեքները հատվածի ծայրերում և կետում, քանի որ կետը չի պատկանում [-1, հատվածին, 2]։ Այս ֆունկցիայի արժեքներն են՝ , , . Դրանից բխում է, որ ֆունկցիայի ամենափոքր արժեքը(ներքևի գծապատկերում նշված է կարմիրով), հավասար է -7-ի, ձեռք է բերվում հատվածի աջ վերջում՝ կետում, և մեծագույն(կարմիր է նաև գրաֆիկի վրա), հավասար է 9, - կրիտիկական կետում: Եթե ֆունկցիան որոշակի ինտերվալում շարունակական է, և այդ ինտերվալը հատված չէ (այլ, օրինակ, ինտերվալ է. ինտերվալի և հատվածի տարբերությունը. միջակայքի սահմանային կետերը ներառված չեն ինտերվալի մեջ, բայց հատվածի սահմանային կետերը ներառված են հատվածում), այնուհետև ֆունկցիայի արժեքների թվում չի կարող լինել ամենափոքրը և ամենամեծը: Այսպիսով, օրինակ, ստորև նկարում ներկայացված ֆունկցիան շարունակական է ]-∞, +∞[-ում և չունի ամենամեծ արժեքը: Այնուամենայնիվ, ցանկացած ինտերվալի համար (փակ, բաց կամ անսահման) ճշմարիտ է շարունակական ֆունկցիաների հետևյալ հատկությունը. Հաշվարկների ընթացքում ինքնաստուգման համար կարող եք օգտագործել առցանց ածանցյալ հաշվիչ . Օրինակ 4. Գտեք ֆունկցիայի ամենափոքր և ամենամեծ արժեքները հատվածի վրա [-1, 3]
. Լուծում. Մենք գտնում ենք այս ֆունկցիայի ածանցյալը որպես գործակիցի ածանցյալ. Մենք ածանցյալը հավասարեցնում ենք զրոյի, ինչը մեզ տալիս է մեկ կրիտիկական կետ. Պատկանում է [-1, 3] հատվածին։ Տվյալ հատվածի վրա ֆունկցիայի ամենափոքր և ամենամեծ արժեքները գտնելու համար մենք գտնում ենք դրա արժեքները հատվածի ծայրերում և գտնված կրիտիկական կետում. Եկեք համեմատենք այս արժեքները: Եզրակացություն՝ հավասար է -5/13, կետում և ամենաբարձր արժեքըկետում հավասար է 1-ի: Կան ուսուցիչներ, ովքեր ֆունկցիայի ամենափոքր և ամենամեծ արժեքները գտնելու թեմայով ուսանողներին չեն տալիս լուծելու օրինակներ, որոնք ավելի բարդ են, քան նոր քննարկվածները, այսինքն՝ այնպիսիք, որոնցում ֆունկցիան բազմանդամ է կամ բազմանդամ։ կոտորակ, որի համարիչն ու հայտարարը բազմանդամներ են։ Բայց մենք չենք սահմանափակվի նման օրինակներով, քանի որ ուսուցիչների մեջ կան այնպիսիք, ովքեր սիրում են ստիպել ուսանողներին մտածել ամբողջությամբ (ածանցյալների աղյուսակ): Հետևաբար, կօգտագործվեն լոգարիթմը և եռանկյունաչափական ֆունկցիան: Օրինակ 8. Գտեք ֆունկցիայի ամենափոքր և ամենամեծ արժեքները հատվածի վրա
. Լուծում. Մենք գտնում ենք այս ֆունկցիայի ածանցյալը որպես արտադրանքի ածանցյալ : Ածանցյալը հավասարեցնում ենք զրոյի, որը տալիս է մեկ կրիտիկական կետ. Այն պատկանում է հատվածին։ Տվյալ հատվածի վրա ֆունկցիայի ամենափոքր և ամենամեծ արժեքները գտնելու համար մենք գտնում ենք դրա արժեքները հատվածի ծայրերում և գտնված կրիտիկական կետում. Բոլոր գործողությունների արդյունքը. ֆունկցիան հասնում է իր նվազագույն արժեքին, հավասար է 0-ի, կետում և կետում և ամենաբարձր արժեքը, հավասար ե², կետում: Հաշվարկների ընթացքում ինքնաստուգման համար կարող եք օգտագործել առցանց ածանցյալ հաշվիչ . Օրինակ 9. Գտեք ֆունկցիայի ամենափոքր և ամենամեծ արժեքները Լուծում. Գտեք այս ֆունկցիայի ածանցյալը. Մենք ածանցյալը հավասարեցնում ենք զրոյի. Միակ կրիտիկական կետը պատկանում է հատվածին. Տվյալ հատվածի վրա ֆունկցիայի ամենափոքր և ամենամեծ արժեքները գտնելու համար մենք գտնում ենք դրա արժեքները հատվածի ծայրերում և գտնված կրիտիկական կետում. Եզրակացություն: ֆունկցիան հասնում է իր նվազագույն արժեքին, հավասար է , կետում և ամենաբարձր արժեքը, հավասար , կետում : Կիրառական էքստրեմալ խնդիրների դեպքում ֆունկցիայի ամենափոքր (առավելագույն) արժեքները գտնելը, որպես կանոն, հանգում է նվազագույնի (առավելագույնը) գտնելուն: Բայց ավելի մեծ գործնական հետաքրքրություն են ներկայացնում ոչ թե նվազագույնները կամ առավելագույնները, այլ փաստարկի այն արժեքները, որոնցով դրանք ձեռք են բերվել: Կիրառական խնդիրները լուծելիս առաջանում է լրացուցիչ դժվարություն՝ ֆունկցիաների կազմում, որոնք նկարագրում են դիտարկվող երեւույթը կամ գործընթացը։ Օրինակ 10. 4 հատ տարողությամբ տանկը, որն ունի քառակուսի հիմքով զուգահեռականի ձև և վերևում բաց, պետք է թիթեղապատվի։ Ինչ չափի պետք է լինի բաքը, որպեսզի այն ծածկվի նվազագույն քանակությամբ նյութով: Լուծում. Թող x- հիմքի կողմը, հ- տանկի բարձրությունը, Ս- դրա մակերեսը առանց ծածկույթի, Վ- դրա ծավալը. Տանկի մակերեսը արտահայտվում է բանաձևով, այսինքն. երկու փոփոխականի ֆունկցիա է։ Արտահայտել Սորպես մեկ փոփոխականի ֆունկցիա՝ մենք օգտագործում ենք այն փաստը, որ որտեղից . Գտնված արտահայտության փոխարինում հբանաձևի մեջ Ս: Եկեք քննենք այս ֆունկցիան մինչև վերջ: Այն սահմանվում և տարբերվում է ամենուր ]0, +∞[ և Ածանցյալը հավասարեցնում ենք զրոյի () և գտնում կրիտիկական կետը։ Բացի այդ, երբ ածանցյալը գոյություն չունի, բայց այս արժեքը ներառված չէ սահմանման տիրույթում և, հետևաբար, չի կարող լինել ծայրահեղ կետ: Այսպիսով, սա միակ կրիտիկական կետն է։ Եկեք ստուգենք այն ծայրահեղության առկայության համար, օգտագործելով երկրորդ բավարար նշանը: Գտնենք երկրորդ ածանցյալը։ Երբ երկրորդ ածանցյալը մեծ է զրոյից (). Սա նշանակում է, որ երբ գործառույթը հասնում է նվազագույնի Հաշվարկների ընթացքում ինքնաստուգման համար կարող եք օգտագործել


Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 )
.
(1)
![]()
![]()
![]() ,
,

![]()
![]() , Դա
, Դա![]() ,
,
![]()
Ֆունկցիայի ընդմիջման կետերը և դրանց դասակարգումը


![]()
![]()



Թեորեմ 2(Weierstrasse). Եթե f (x) ֆունկցիան շարունակական է [a, b] միջակայքում, ապա այն հասնում է իր ամենամեծ արժեքին M և ամենափոքր արժեքին m այս միջակայքում, այսինքն. կան α, β O [a, b] այնպիսի կետեր, որ m = f (α) ≤ f (x) ≤ f (β) = M բոլոր x O-ի համար [a, b] (նկ. 2):
Թեորեմ 3(զրոյի գոյության մասին)։ Եթե f (x) ֆունկցիան շարունակական է [a, b] միջակայքում և վերցնում է տարբեր նշանների ոչ զրոյական արժեքներ հատվածի ծայրերում, ապա (a, b) միջակայքում կա առնվազն մեկ կետ. ξ, որի դեպքում f (ξ) = 0:
Թեորեմի երկրաչափական իմաստն այն է, որ ֆունկցիայի գրաֆիկը, որը բավարարում է թեորեմի պայմանները, անպայման հատում է առանցքը. ԵԶ(նկ. 3): 
կոչվում է բիսեկցիայի (դիխոտոմիա) մեթոդ կամ բիսեկցիոն մեթոդ։
f(x) = 0, (1)
Թեորեմ 4(Բոլցանո–Կոշի)։ Եթե f (x) ֆունկցիան շարունակական է [a, b] միջակայքում, ապա այն վերցնում է (a, b) բոլոր միջանկյալ արժեքները f (a) և f (b) միջև:
Շարունակական հակադարձ ֆունկցիայի առկայությունը
Թող y = f (x) ֆունկցիան լինի խիստ միատոն և շարունակական [a, b] միջակայքում: Այնուհետև [α, β] (α = f (a), β = f (b)) միջակայքում գոյություն ունի x = g (y) հակադարձ ֆունկցիա, որը նույնպես խիստ միատոն է և շարունակական (α, β) ինտերվալի վրա: ) 
Մենք միասին փնտրում ենք ֆունկցիայի ամենափոքր և ամենամեծ արժեքները
![]() հատվածի վրա [-1, 2]
.
հատվածի վրա [-1, 2]
.

 .
.
Մենք շարունակում ենք միասին փնտրել ֆունկցիայի ամենափոքր և ամենամեծ արժեքները


![]() հատվածի վրա .
հատվածի վրա .

![]() .
.![]() . Քանի որ այս նվազագույնը այս ֆունկցիայի միակ ծայրահեղությունն է, դա նրա ամենափոքր արժեքն է. Այսպիսով, տանկի հիմքի կողմը պետք է լինի 2 մ, իսկ բարձրությունը՝ .
. Քանի որ այս նվազագույնը այս ֆունկցիայի միակ ծայրահեղությունն է, դա նրա ամենափոքր արժեքն է. Այսպիսով, տանկի հիմքի կողմը պետք է լինի 2 մ, իսկ բարձրությունը՝ .