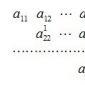Հավասարումների լուծում Վիետայի թեորեմի օրինակներով։ Վիետայի թեորեմը, հակադարձ Վիետայի բանաձևը և օրինակներ՝ կեղծիքների լուծումներով

Ֆրանսուա Վիետ (1540-1603) - մաթեմատիկոս, հայտնի Վիետի բանաձևերի ստեղծող

Վիետայի թեորեմահամար անհրաժեշտ արագ լուծումքառակուսի հավասարումներ (պարզ բառերով):

Ավելի մանրամասն, ապա Վիետայի թեորեմը տրվածի արմատների գումարն է քառակուսային հավասարումհավասար է երկրորդ գործակցին, որը վերցված է հակառակ նշանով, իսկ արտադրյալը հավասար է ազատ անդամին։ Ցանկացած կրճատված քառակուսի հավասարում, որն ունի արմատներ, ունի այս հատկությունը:

Օգտագործելով Վիետայի թեորեմը, դուք հեշտությամբ կարող եք լուծել քառակուսի հավասարումներ ընտրությամբ, ուստի եկեք «շնորհակալություն» ասենք սուրը ձեռքին այս մաթեմատիկոսին մեր երջանիկ 7-րդ դասարանի համար:

Վիետայի թեորեմի ապացույց

Թեորեմն ապացուցելու համար կարող եք օգտագործել արմատային հայտնի բանաձևեր, որոնց շնորհիվ կկազմենք քառակուսի հավասարման արմատների գումարը և արտադրյալը։ Միայն սրանից հետո կարող ենք համոզվել, որ դրանք հավասար են և, համապատասխանաբար, .

Ենթադրենք, մենք ունենք հավասարում. Այս հավասարումն ունի հետևյալ արմատները՝ և . Եկեք ապացուցենք, որ.

Համաձայն քառակուսի հավասարման արմատների բանաձևերի.

1. Գտի՛ր արմատների գումարը.

Եկեք նայենք այս հավասարմանը, թե ինչպես ենք ստացել այն ճիշտ այսպես.

= .

Քայլ 1. Կոտորակները նվազեցնելով ընդհանուր հայտարարի, ստացվում է.

= = .

Քայլ 2. Մենք ունենք մի կոտորակ, որտեղ մենք պետք է բացենք փակագծերը.

Կոտորակը փոքրացնում ենք 2-ով և ստանում.

Մենք ապացուցել ենք քառակուսի հավասարման արմատների գումարի կապը՝ օգտագործելով Վիետայի թեորեմը:

2. Գտե՛ք արմատների արտադրյալը.

= = = = = .

Եկեք ապացուցենք այս հավասարումը.

Քայլ 1. Կոտորակները բազմապատկելու կանոն կա, ըստ որի մենք բազմապատկում ենք այս հավասարումը.

Հիմա հիշենք սահմանումը քառակուսի արմատև հաշվի առեք.

= .

Քայլ 3. Հիշենք քառակուսի հավասարման դիսկրիմինանտը. Հետևաբար, D-ի փոխարեն (տարբերիչ) փոխարինում ենք վերջին կոտորակում, այնուհետև ստացվում է.

= .

Քայլ 4. Մենք բացում ենք փակագծերը և համանման տերմինները կրճատում ենք կոտորակի վրա.

Քայլ 5. Մենք կրճատում ենք «4a»-ն և ստանում:

Այսպիսով, մենք ապացուցեցինք արմատների արտադրյալի կապը Վիետայի թեորեմի միջոցով:

ԿԱՐԵՎՈՐ!Եթե ​​դիսկրիմինանտը զրո է, ապա քառակուսի հավասարումն ունի միայն մեկ արմատ:

Թեորեմը հակասում է Վիետայի թեորեմին

Ըստ թեորեմի՝ թեորեմի հակադարձՎիետա, մենք կարող ենք ստուգել, ​​թե արդյոք մեր հավասարումը ճիշտ է լուծված: Թեորեմն ինքնին հասկանալու համար հարկավոր է այն ավելի մանրամասն դիտարկել:

Եթե ​​թվերն այսպիսին են.

Եվ, ապա դրանք քառակուսի հավասարման արմատներն են:

Վիետայի հակադարձ թեորեմի ապացույց

Քայլ 1.Նրա գործակիցների արտահայտությունները փոխարինենք հավասարման մեջ.

Քայլ 2.Փոխակերպենք հավասարման ձախ կողմը.

Քայլ 3. Եկեք գտնենք հավասարման արմատները, և դրա համար օգտագործում ենք այն հատկությունը, որ արտադրյալը հավասար է զրոյի.

Կամ . որտեղից է այն գալիս. կամ .

Վիետայի թեորեմի օգտագործմամբ լուծումներով օրինակներ

Օրինակ 1

Զորավարժություններ

Գտե՛ք քառակուսի հավասարման արմատների քառակուսիների գումարը, արտադրյալը և գումարը՝ առանց հավասարման արմատները գտնելու:

Լուծում

Քայլ 1. Հիշենք խտրականության բանաձեւը. Մենք մեր թվերը փոխարինում ենք տառերով: Այսինքն, , – սա փոխարինում է , և . Սա ենթադրում է.

Պարզվում է:

Title="Մատուցված է QuickLaTeX.com-ի կողմից" height="13" width="170" style="vertical-align: -1px;">. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма , а произведение . !}

Արմատների քառակուսիների գումարն արտահայտենք դրանց գումարի և արտադրյալի միջոցով.

Պատասխանել

7; 12; 25.

Օրինակ 2

Զորավարժություններ

Լուծե՛ք հավասարումը. Այնուամենայնիվ, մի օգտագործեք քառակուսի հավասարումների բանաձևեր:

Լուծում

Այս հավասարումն ունի արմատներ, որոնց դիսկրիմինանտը (D) մեծ է զրոյից։ Ըստ Վիետայի թեորեմի՝ այս հավասարման արմատների գումարը հավասար է 4-ի, իսկ արտադրյալը՝ 5։ Նախ որոշում ենք թվի բաժանարարները, որոնց գումարը հավասար է 4-ի։ Սրանք թվերն են։ 5» և «-1»: Նրանց արտադրյալը հավասար է 5-ի, իսկ գումարը՝ 4։ Սա նշանակում է, որ Վիետայի թեորեմին հակառակ թեորեմի համաձայն՝ դրանք այս հավասարման արմատներն են։

Պատասխանել

ԵՎ Օրինակ 4

Զորավարժություններ

Գրի՛ր հավասարում, որտեղ յուրաքանչյուր արմատ հավասարության համապատասխան արմատից երկու անգամ մեծ է.

Լուծում

Վիետայի թեորեմի համաձայն՝ այս հավասարման արմատների գումարը հավասար է 12-ի, իսկ արտադրյալը՝ 7։ Սա նշանակում է, որ երկու արմատները դրական են։

Նոր հավասարման արմատների գումարը հավասար կլինի.

Եվ աշխատանքը.

Վիետայի թեորեմին հակառակ թեորեմով նոր հավասարումն ունի հետևյալ ձևը.

Պատասխանել

Ստացվում է հավասարում, որի յուրաքանչյուր արմատը երկու անգամ ավելի մեծ է.

Այսպիսով, մենք նայեցինք, թե ինչպես լուծել հավասարումը Վիետայի թեորեմի միջոցով: Շատ հարմար է օգտագործել այս թեորեմը, եթե լուծում եք խնդիրներ, որոնք ներառում են քառակուսի հավասարումների արմատների նշանները: Այսինքն, եթե բանաձևի ազատ անդամը դրական թիվ է, և եթե քառակուսի հավասարումն ունի իրական արմատներ, ապա երկուսն էլ կարող են լինել կամ բացասական կամ դրական։

Իսկ եթե ազատ անդամը բացասական թիվ է, և եթե քառակուսի հավասարումը իրական արմատներ ունի, ապա երկու նշաններն էլ տարբեր կլինեն։ Այսինքն, եթե մի արմատը դրական է, ապա մյուս արմատը կլինի միայն բացասական:

Օգտակար աղբյուրներ.

1. Դորոֆեև Գ.Վ., Սուվորովա Ս.Բ., Բունիմովիչ Է.Ա. Հանրահաշիվ 8-րդ դասարան. Մոսկվա «Լուսավորություն», 2016 – 318 էջ.
2. Ռուբին Ա.Գ., Չուլկով Պ.Վ. – դասագիրք Հանրահաշիվ 8-րդ դասարան. Մոսկվա «Բալաս», 2015 – 237 էջ.
3. Նիկոլսկի Ս. Մ., Պոտոպավ Մ. Կ., Ռեշետնիկով Ն. Ն., Շևկին Ա. Վ. – Հանրահաշիվ 8-րդ դասարան. Մոսկվայի «Լուսավորություն», 2014 – 300 թ.

Վիետայի թեորեմը, հակադարձ Վիետայի բանաձևը և կեղծիքների լուծումներով օրինակներԹարմացվել է՝ 22 նոյեմբերի, 2019 կողմից՝ Գիտական ​​հոդվածներ.Ru

Վիետայի թեորեմի ձևակերպումը և ապացուցումը քառակուսի հավասարումների համար. Վիետայի հակադարձ թեորեմը. Վիետայի թեորեմը խորանարդ հավասարումների և կամայական կարգի հավասարումների համար։

Բովանդակություն

Տես նաեւ: Քառակուսային հավասարման արմատները

Քառակուսային հավասարումներ

Վիետայի թեորեմա

Եկեք և նշանակենք կրճատված քառակուսի հավասարման արմատները
(1) .
Այնուհետև արմատների գումարը հավասար է հակառակ նշանով վերցված գործակցի: Արմատների արտադրյալը հավասար է ազատ տերմինին.
;
.

Մի քանի արմատների մասին նշում

Եթե ​​(1) հավասարման դիսկրիմինանտը զրո է, ապա այս հավասարումն ունի մեկ արմատ: Բայց, ծանր ձևակերպումներից խուսափելու համար, ընդհանուր առմամբ ընդունված է, որ այս դեպքում հավասարումը (1) ունի երկու բազմակի կամ հավասար արմատներ.
.

Ապացույց մեկը

Գտնենք (1) հավասարման արմատները։ Դա անելու համար կիրառեք քառակուսի հավասարման արմատների բանաձևը.
;
;
.

Գտե՛ք արմատների գումարը.
.

Ապրանքը գտնելու համար կիրառեք բանաձևը.
.
Հետո

.

Թեորեմն ապացուցված է.

Ապացույց երկու

Եթե ​​թվերը քառակուսի (1) հավասարման արմատներն են, ապա
.
Բացելով փակագծերը.

.
Այսպիսով, հավասարումը (1) կունենա հետևյալ ձևը.
.
Համեմատելով (1)-ի հետ՝ մենք գտնում ենք.
;
.

Թեորեմն ապացուցված է.

Վիետայի հակադարձ թեորեմը

Թող լինեն կամայական թվեր։ Այնուհետև և են քառակուսի հավասարման արմատները
,
Որտեղ
(2) ;
(3) .

Վիետայի հակադարձ թեորեմի ապացույց

Դիտարկենք քառակուսի հավասարումը
(1) .
Մենք պետք է ապացուցենք, որ եթե և , ապա և-ն (1) հավասարման արմատներն են:

(2) և (3)-ը փոխարինենք (1)-ով.
.
Մենք խմբավորում ենք հավասարման ձախ կողմում գտնվող տերմինները.
;
;
(4) .

Եկեք փոխարինենք (4):
;
.

Եկեք փոխարինենք (4):
;
.
Հավասարումը պահպանվում է. Այսինքն՝ թիվը (1) հավասարման արմատն է։

Թեորեմն ապացուցված է.

Վիետայի թեորեմը ամբողջական քառակուսի հավասարման համար

Այժմ դիտարկենք ամբողջական քառակուսի հավասարումը
(5) ,
որտեղ և կան որոշ թվեր: Ավելին.

Եկեք (5) հավասարումը բաժանենք հետևյալի.
.
Այսինքն՝ ստացանք տրված հավասարումը
,
Որտեղ; .

Այնուհետև Վիետայի թեորեմը ամբողջական քառակուսի հավասարման համար ունի հետևյալ ձևը.

Եկեք և նշանակենք ամբողջական քառակուսի հավասարման արմատները
.
Այնուհետև արմատների գումարը և արտադրյալը որոշվում են բանաձևերով.
;
.

Վիետայի թեորեմը խորանարդ հավասարման համար

Նման կերպ մենք կարող ենք կապեր հաստատել խորանարդ հավասարման արմատների միջև: Դիտարկենք խորանարդ հավասարումը
(6) ,
որտեղ , , , որոշ թվեր են: Ավելին.
Եկեք այս հավասարումը բաժանենք հետևյալի.
(7) ,
Որտեղ , , .
Թող , , լինեն (7) (և հավասարման (6)) հավասարման արմատները։ Հետո

.

Համեմատելով (7) հավասարման հետ՝ մենք գտնում ենք.
;
;
.

Վիետայի թեորեմը n-րդ աստիճանի հավասարման համար

Նույն կերպ կարող եք կապեր գտնել արմատների միջև , , ... , , հավասարման համար n-րդ աստիճան
.

Վիետայի թեորեմը համար n-րդ հավասարումներըաստիճանն ունի հետևյալ ձևը.
;
;
;

.

Այս բանաձևերը ստանալու համար մենք հավասարումը գրում ենք հետևյալ կերպ.
.
Այնուհետև մենք հավասարեցնում ենք , , , ...-ի գործակիցները և համեմատում ազատ անդամը։

Հղումներ:
Ի.Ն. Բրոնշտեյն, Կ.Ա. Սեմենդյաև, Մաթեմատիկայի ձեռնարկ ինժեներների և քոլեջի ուսանողների համար, «Լան», 2009 թ.
ՍՄ. Նիկոլսկին, Մ.Կ. Պոտապով և ուրիշներ, Հանրահաշիվ: Դասագիրք 8-րդ դասարանի համար ուսումնական հաստատություններ, Մոսկվա, Կրթություն, 2006 թ.

Տես նաեւ:

Ութերորդ դասարանում աշակերտներին ծանոթանում են քառակուսի հավասարումների և դրանց լուծման եղանակների հետ: Միևնույն ժամանակ, ինչպես ցույց է տալիս փորձը, ուսանողների մեծ մասը ամբողջական քառակուսի հավասարումներ լուծելիս օգտագործում է միայն մեկ մեթոդ՝ քառակուսի հավասարման արմատների բանաձևը: Ուսանողների համար, ովքեր ունեն լավ մտավոր թվաբանական հմտություններ, այս մեթոդը ակնհայտորեն իռացիոնալ է: Աշակերտները հաճախ ստիպված են լինում լուծել քառակուսի հավասարումներ նույնիսկ ավագ դպրոցում, և այնտեղ պարզապես ափսոս է ժամանակ ծախսել դիսկրիմինանտը հաշվարկելու վրա։ Իմ կարծիքով քառակուսի հավասարումներ ուսումնասիրելիս պետք է ավելի շատ ժամանակ և ուշադրություն դարձնել Վիետայի թեորեմի կիրառմանը (ըստ Ա.Գ. Մորդկովիչի հանրահաշիվ-8 ծրագրի՝ «Վիետայի թեորեմ. Քառակուսի քայքայումը» թեմայի ուսումնասիրության համար նախատեսված է ընդամենը երկու ժամ. եռանդամը գծային գործոնների մեջ»):

Հանրահաշվի դասագրքերի մեծ մասում այս թեորեմը ձևակերպված է կրճատված քառակուսի հավասարման համար և ասում է. եթե հավասարումն ունի արմատներ և , ապա հավասարությունները , , բավարարվում են դրանց համար։Այնուհետև ձևակերպվում է Վիետայի թեորեմին հակասող հայտարարություն, և առաջարկվում են մի շարք օրինակներ այս թեմայի կիրառման համար:

Վերցնենք կոնկրետ օրինակներև հետագծեք լուծման տրամաբանությունը՝ օգտագործելով Վիետայի թեորեմը:

Օրինակ 1. Լուծե՛ք հավասարումը.

Ենթադրենք այս հավասարումն ունի արմատներ, այն է՝ և . Այնուհետև, Վիետայի թեորեմի համաձայն, հավասարությունները պետք է միաժամանակ պահպանվեն.

Խնդրում ենք նկատի ունենալ, որ արմատների արտադրյալը դրական թիվ է: Սա նշանակում է, որ հավասարման արմատները նույն նշանի են։ Եվ քանի որ արմատների գումարը նույնպես դրական թիվ է, եզրակացնում ենք, որ հավասարման երկու արմատներն էլ դրական են։ Կրկին վերադառնանք արմատների արտադրանքին։ Ենթադրենք, որ հավասարման արմատները դրական ամբողջ թվեր են։ Այնուհետև ճիշտ առաջին հավասարությունը կարելի է ձեռք բերել միայն երկու եղանակով (մինչև գործոնների հերթականությունը). կամ . Առաջարկվող թվերի զույգերի համար ստուգենք Վիետայի թեորեմի երկրորդ դրույթի իրագործելիությունը. . Այսպիսով, 2 և 3 թվերը բավարարում են երկու հավասարումներն էլ, հետևաբար հանդիսանում են տվյալ հավասարման արմատները։

Պատասխան՝ 2; 3.

Վիետայի թեորեմի միջոցով վերը նշված քառակուսի հավասարումը լուծելիս առանձնացնենք դատողության հիմնական փուլերը.

գրի՛ր Վիետայի թեորեմի պնդումը

(*)

• որոշել հավասարման արմատների նշանները (եթե արտադրյալը և արմատների գումարը դրական են, ապա երկու արմատներն էլ դրական թվեր են։ Եթե արմատների արտադրյալը դրական թիվ է, իսկ արմատների գումարը բացասական է, ապա երկու արմատներն էլ բացասական թվեր են։Եթե արմատների արտադրյալը բացասական թիվ է, ապա արմատներն ունեն տարբեր նշաններ. Ընդ որում, եթե արմատների գումարը դրական է, ապա ավելի մեծ մոդուլով արմատը դրական թիվ է, իսկ եթե արմատների գումարը զրոյից փոքր է, ապա ավելի մեծ մոդուլով արմատը բացասական թիվ է);
• ընտրել ամբողջ թվերի զույգեր, որոնց արտադրյալը տալիս է ճիշտ առաջին հավասարությունը (*);
• Գտնված թվերի զույգերից ընտրեք այն զույգը, որը (*) նշումով երկրորդ հավասարության մեջ փոխարինելու դեպքում ճիշտ հավասարություն կտա.
• Ձեր պատասխանում նշե՛ք հավասարման հայտնաբերված արմատները:

Բերենք ևս մի քանի օրինակ։

Օրինակ 2. Լուծե՛ք հավասարումը .

Լուծում.

Թող և լինեն տրված հավասարման արմատները: Այնուհետև Վիետայի թեորեմով մենք նշում ենք, որ արտադրյալը դրական է, իսկ գումարը բացասական թիվ է: Սա նշանակում է, որ երկու արմատներն էլ բացասական թվեր են։ Մենք ընտրում ենք գործակիցների զույգեր, որոնք տալիս են 10 (-1 և -10; -2 և -5) արտադրյալ: Երկրորդ զույգ թվերը գումարվում են մինչև -7: Սա նշանակում է, որ -2 և -5 թվերը այս հավասարման արմատներն են։

Պատասխան. -2; -5.

Օրինակ 3. Լուծե՛ք հավասարումը .

Լուծում.

Թող և լինեն տրված հավասարման արմատները: Այնուհետև Վիետայի թեորեմով մենք նշում ենք, որ արտադրանքը բացասական է: Սա նշանակում է, որ արմատները տարբեր նշանների են։ Արմատների գումարը նույնպես բացասական թիվ է։ Սա նշանակում է, որ ամենամեծ մոդուլով արմատը բացասական է։ Մենք ընտրում ենք գործակիցների զույգեր, որոնք արտադրյալին տալիս են -10 (1 և -10; 2 և -5): Թվերի երկրորդ զույգը գումարում է -3: Սա նշանակում է, որ 2 և -5 թվերն այս հավասարման արմատներն են։

Պատասխան. 2; -5.

Նկատի ունեցեք, որ Վիետայի թեորեմը, սկզբունքորեն, կարող է ձևակերպվել ամբողջական քառակուսային հավասարման համար. եթե քառակուսի հավասարում ունի արմատներ և, ապա հավասարությունները, , բավարարվում են նրանց համար։Այնուամենայնիվ, այս թեորեմի կիրառումը բավականին խնդրահարույց է, քանի որ ամբողջական քառակուսային հավասարման մեջ արմատներից առնվազն մեկը (եթե իհարկե այդպիսիք կան) կոտորակային թիվ է: Իսկ կոտորակների ընտրության հետ աշխատելը երկար է և դժվար: Բայց դեռ ելք կա.

Դիտարկենք ամբողջական քառակուսի հավասարումը . Հավասարման երկու կողմերը բազմապատկեք առաջին գործակցով Աև ձևով գրի՛ր հավասարումը . Եկեք ներմուծենք նոր փոփոխական և ստանանք կրճատված քառակուսի հավասարումը, որի արմատները և (եթե առկա են) կարելի է գտնել Վիետայի թեորեմի միջոցով։ Այնուհետև սկզբնական հավասարման արմատները կլինեն . Խնդրում ենք նկատի ունենալ, որ օժանդակ կրճատված հավասարումը ստեղծելը շատ պարզ է. երկրորդ գործակիցը պահպանվում է, իսկ երրորդ գործակիցը հավասար է արտադրյալին. ակ. Որոշակի հմտությամբ սովորողները անմիջապես ստեղծում են օժանդակ հավասարում, Վիետայի թեորեմով գտնում են դրա արմատները և նշում տրված ամբողջական հավասարման արմատները: Բերենք օրինակներ.

Օրինակ 4. Լուծե՛ք հավասարումը .

Եկեք ստեղծենք օժանդակ հավասարում և օգտագործելով Վիետայի թեորեմը մենք կգտնենք դրա արմատները։ Սա նշանակում է, որ սկզբնական հավասարման արմատները .

Պատասխան. .

Օրինակ 5. Լուծե՛ք հավասարումը .

Օժանդակ հավասարումն ունի ձև. Վիետայի թեորեմի համաձայն, դրա արմատներն են. Գտնելով սկզբնական հավասարման արմատները .

Պատասխան. .

Եվ ևս մեկ դեպք, երբ Վիետայի թեորեմի կիրառումը թույլ է տալիս բանավոր կերպով գտնել ամբողջական քառակուսի հավասարման արմատները: Դա ապացուցելը դժվար չէ 1 թիվը հավասարման արմատն է , եթե և միայն եթե. Հավասարման երկրորդ արմատը գտնում ենք Վիետայի թեորեմով և հավասար է . Եվս մեկ հայտարարություն. այնպես, որ –1 թիվը հավասարման արմատն է անհրաժեշտ և բավարար է. Այնուհետև Վիետայի թեորեմի համաձայն հավասարման երկրորդ արմատը հավասար է. Նմանատիպ հայտարարություններ կարող են ձևակերպվել կրճատված քառակուսի հավասարման համար:

Օրինակ 6. Լուծե՛ք հավասարումը.

Նշենք, որ հավասարման գործակիցների գումարը զրո է։ Այսպիսով, հավասարման արմատները .

Պատասխան. .

Օրինակ 7. Լուծե՛ք հավասարումը.

Այս հավասարման գործակիցները բավարարում են հատկությունը (իրոք, 1-(-999)+(-1000)=0): Այսպիսով, հավասարման արմատները .

Պատասխան. ..

Վիետայի թեորեմի կիրառման օրինակներ

Առաջադրանք 1. Տրված քառակուսի հավասարումը լուծե՛ք Վիետայի թեորեմի միջոցով։

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Առաջադրանք 2. Լուծե՛ք ամբողջական քառակուսային հավասարումը` անցնելով օժանդակ կրճատված քառակուսային հավասարմանը:

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Առաջադրանք 3. Լուծե՛ք քառակուսի հավասարում` օգտագործելով հատկությունը:

Քառակուսային հավասարման արմատների և գործակիցների միջև, բացի արմատային բանաձևերից, կան նաև այլ օգտակար հարաբերություններ, որոնք տրված են. Վիետայի թեորեմա. Այս հոդվածում մենք կտանք Վիետայի թեորեմի ձևակերպումը և ապացույցը քառակուսի հավասարման համար: Այնուհետև մենք դիտարկում ենք թեորեմը Վիետայի թեորեմի հակառակը: Դրանից հետո մենք կվերլուծենք առավել բնորոշ օրինակների լուծումները։ Ի վերջո, մենք գրում ենք Վիետայի բանաձևերը, որոնք սահմանում են իրական արմատների միջև կապը հանրահաշվական հավասարում n աստիճանը և դրա գործակիցները:

Էջի նավարկություն.

Վիետայի թեորեմ, ձևակերպում, ապացույց

a·x 2 +b·x+c=0 ձևի քառակուսի հավասարման արմատների բանաձևերից, որտեղ D=b 2 −4·a·c հետևում են հետևյալ հարաբերությունները՝ x 1 +x 2 =−. b/a, x 1 ·x 2 = c/a . Այս արդյունքները հաստատված են Վիետայի թեորեմա:

Թեորեմ.

Եթե x 1-ը և x 2-ը a x 2 +b x+c=0 քառակուսի հավասարման արմատներն են, ապա արմատների գումարը հավասար է b և a գործակիցների հարաբերությանը, վերցված հակառակ նշանով և արտադրյալի. արմատները հավասար են c և a գործակիցների հարաբերությանը, այսինքն՝ .

Ապացույց.

Վիետայի թեորեմի ապացուցումը կիրականացնենք հետևյալ սխեմայով. հայտնի արմատական ​​բանաձևերով կազմում ենք քառակուսի հավասարման արմատների գումարը և արտադրյալը, այնուհետև ստացված արտահայտությունները փոխակերպում ենք և համոզվում, որ դրանք հավասար են −b/-ի։ a և c/a, համապատասխանաբար:

Սկսենք արմատների գումարից և կազմենք այն։ Այժմ մենք կոտորակները բերում ենք ընդհանուր հայտարարի, ունենք . Ստացված կոտորակի համարիչում, որից հետո՝. Վերջապես, 2-ից հետո մենք ստանում ենք. Սա ապացուցում է Վիետայի թեորեմի առաջին կապը քառակուսի հավասարման արմատների գումարի համար։ Անցնենք երկրորդին։

Կազմում ենք քառակուսի հավասարման արմատների արտադրյալը՝ . Կոտորակների բազմապատկման կանոնի համաձայն. վերջին կտորկարելի է գրել որպես. Այժմ մենք բազմապատկում ենք փակագիծը համարիչի վրա, բայց ավելի արագ է այս արտադրյալը փլուզել քառակուսի տարբերության բանաձև, Ուրեմն . Հետո, հիշելով, կատարում ենք հաջորդ անցումը։ Եվ քանի որ քառակուսի հավասարման դիսկրիմինանտը համապատասխանում է D=b 2 −4·a·c բանաձևին, ապա վերջին կոտորակում D-ի փոխարեն կարող ենք փոխարինել b 2 −4·a·c, ստանում ենք. Փակագծերը բացելուց և համանման տերմիններ բերելուց հետո հասնում ենք կոտորակին, որի կրճատումը 4·a-ով տալիս է. Սա ապացուցում է Վիետայի թեորեմի երկրորդ կապը արմատների արտադրյալի համար։

Եթե ​​բաց թողնենք բացատրությունները, Վիետայի թեորեմի ապացույցը կստանա լակոնիկ ձև.
,
.

Մնում է միայն նշել, որ եթե դիսկրիմինանտը հավասար է զրոյի, ապա քառակուսի հավասարումն ունի մեկ արմատ: Այնուամենայնիվ, եթե ենթադրենք, որ այս դեպքում հավասարումը ունի երկու նույնական արմատներ, ապա Վիետայի թեորեմի հավասարությունները նույնպես գործում են: Իսկապես, երբ D=0 քառակուսի հավասարման արմատը հավասար է , ապա և , և քանի որ D=0, այսինքն՝ b 2 −4·a·c=0, որտեղից b 2 =4·a·c, ապա. .

Գործնականում Վիետայի թեորեմն ամենից հաճախ օգտագործվում է x 2 +p·x+q=0 ձևի կրճատված քառակուսի հավասարման (առաջատար գործակիցով a հավասար է 1-ի) առնչությամբ: Երբեմն այն ձևակերպվում է հենց այս տիպի քառակուսի հավասարումների համար, ինչը չի սահմանափակում ընդհանրությունը, քանի որ ցանկացած քառակուսի հավասարում կարող է փոխարինվել համարժեք հավասարմամբ՝ երկու կողմերը բաժանելով ոչ զրոյական թվի a: Տանք Վիետայի թեորեմի համապատասխան ձևակերպումը.

Թեորեմ.

Կրճատված քառակուսային հավասարման արմատների գումարը x 2 +p x+q=0 հավասար է հակառակ նշանով վերցված x-ի գործակցին, իսկ արմատների արտադրյալը հավասար է ազատ անդամին, այսինքն՝ x 1. +x 2 =−p, x 1 x 2 = q.

Թեորեմը հակասում է Վիետայի թեորեմին

Վիետայի թեորեմի երկրորդ ձևակերպումը, որը տրված է նախորդ պարբերությունում, ցույց է տալիս, որ եթե x 1 և x 2 կրճատված քառակուսի հավասարման արմատներն են x 2 +p x+q=0, ապա x 1 +x 2 =−p հարաբերությունները. , x 1 x 2 =ք. Մյուս կողմից, x 1 +x 2 =−p, x 1 x 2 =q գրավոր հարաբերություններից հետևում է, որ x 1 և x 2 x 2 +p x+q=0 քառակուսի հավասարման արմատներն են։ Այլ կերպ ասած, Վիետայի թեորեմի հակառակը ճիշտ է: Ձևակերպենք թեորեմի տեսքով և ապացուցենք։

Թեորեմ.

Եթե ​​x 1 և x 2 թվերն այնպիսին են, որ x 1 +x 2 =−p և x 1 · x 2 =q, ապա x 1 և x 2 կրճատված քառակուսային հավասարման արմատներն են x 2 +p · x+q. =0.

Ապացույց.

x 2 +p·x+q=0 հավասարման մեջ p և q գործակիցները x 1 և x 2-ի միջոցով իրենց արտահայտություններով փոխարինելուց հետո այն վերածվում է համարժեք հավասարման։

Ստացված հավասարման մեջ փոխարինենք x 1 թիվը x-ի փոխարեն, և մենք կունենանք հավասարություն x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 =0, որը ցանկացած x 1-ի և x 2-ի համար ներկայացնում է ճիշտ թվային հավասարություն 0=0, քանի որ x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 = x 1 2 -x 1 2 -x 2 ·x 1 +x 1 ·x 2 =0. Հետևաբար, x 1-ը հավասարման արմատն է x 2 −(x 1 +x 2) x+x 1 x 2 =0, ինչը նշանակում է, որ x 1-ը x 2 +p·x+q=0 համարժեք հավասարման արմատն է։

Եթե ​​հավասարման մեջ x 2 −(x 1 +x 2) x+x 1 x 2 =0 x-ի փոխարեն x 2 թիվը փոխարինում ենք, ստանում ենք հավասարություն x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. Սա իսկական հավասարություն է, քանի որ x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Հետևաբար, x 2-ը նույնպես հավասարման արմատ է x 2 −(x 1 +x 2) x+x 1 x 2 =0, և հետևաբար x 2 +p·x+q=0 հավասարումները։

Սա ավարտում է Վիետայի թեորեմին հակադրվող թեորեմի ապացույցը:

Վիետայի թեորեմի օգտագործման օրինակներ

Ժամանակն է խոսել Վիետայի թեորեմի և դրա հակադարձ թեորեմի գործնական կիրառման մասին։ Այս բաժնում մենք կվերլուծենք մի քանի առավել բնորոշ օրինակների լուծումները:

Սկսենք Վիետայի թեորեմի հետ հակադարձ թեորեմը կիրառելով։ Այն հարմար է օգտագործել՝ ստուգելու համար, թե արդյոք տրված երկու թվերը տրված քառակուսի հավասարման արմատներ են: Այս դեպքում հաշվարկվում է դրանց գումարն ու տարբերությունը, որից հետո ստուգվում է հարաբերությունների վավերականությունը։ Եթե ​​այս երկու հարաբերություններն էլ բավարարված են, ապա Վիետայի թեորեմին հակասող թեորեմի ուժով եզրակացվում է, որ այս թվերը հավասարման արմատներն են։ Եթե ​​հարաբերություններից գոնե մեկը բավարարված չէ, ապա այս թվերը քառակուսի հավասարման արմատները չեն։ Այս մոտեցումը կարող է օգտագործվել քառակուսի հավասարումներ լուծելիս՝ հայտնաբերված արմատները ստուգելու համար:

Օրինակ.

1) x 1 =−5, x 2 =3, թե 2) կամ 3) թվերի զույգերից ո՞րն է 4 x 2 −16 x+9=0 քառակուսի հավասարման զույգ արմատներ։

Լուծում.

Տրված քառակուսային հավասարման 4 x 2 −16 x+9=0 գործակիցներն են a=4, b=−16, c=9։ Վիետայի թեորեմի համաձայն՝ քառակուսի հավասարման արմատների գումարը պետք է հավասար լինի −b/a, այսինքն՝ 16/4=4, իսկ արմատների արտադրյալը՝ c/a, այսինքն՝ 9։ /4.

Հիմա եկեք հաշվարկենք տրված երեք զույգերից յուրաքանչյուրի թվերի գումարն ու արտադրյալը և համեմատենք դրանք հենց նոր ստացված արժեքների հետ։

Առաջին դեպքում ունենք x 1 +x 2 =−5+3=−2։ Ստացված արժեքը տարբերվում է 4-ից, ուստի հետագա ստուգում չի կարող իրականացվել, սակայն օգտագործելով Վիետայի թեորեմի հակադարձ թեորեմը, կարելի է անմիջապես եզրակացնել, որ թվերի առաջին զույգը տվյալ քառակուսի հավասարման զույգ արմատներ չէ:

Անցնենք երկրորդ դեպքին. Այստեղ, այսինքն, առաջին պայմանը կատարվում է. Մենք ստուգում ենք երկրորդ պայմանը՝ ստացված արժեքը տարբերվում է 9/4-ից։ Հետևաբար, թվերի երկրորդ զույգը քառակուսի հավասարման զույգ արմատներ չէ։

Մնացել է մի վերջին դեպք. Այստեղ և. Երկու պայմաններն էլ բավարարված են, ուստի այս x 1 և x 2 թվերը տրված քառակուսի հավասարման արմատներն են:

Պատասխան.

Վիետայի թեորեմի հակադարձ տարբերակը գործնականում կարող է օգտագործվել քառակուսի հավասարման արմատները գտնելու համար։ Սովորաբար ընտրվում են տվյալ քառակուսի հավասարումների ամբողջ թվային արմատներ ամբողջ թվային գործակիցներով, քանի որ այլ դեպքերում դա բավականին դժվար է անել։ Այս դեպքում նրանք օգտագործում են այն փաստը, որ եթե երկու թվերի գումարը հավասար է մինուս նշանով վերցված քառակուսի հավասարման երկրորդ գործակցին, և այդ թվերի արտադրյալը հավասար է ազատ անդամին, ապա այդ թվերը այս քառակուսի հավասարման արմատները: Սա հասկանանք օրինակով.

Վերցնենք քառակուսի հավասարումը x 2 −5 x+6=0: Որպեսզի x 1 և x 2 թվերը լինեն այս հավասարման արմատները, պետք է բավարարվեն երկու հավասարումներ՝ x 1 + x 2 =5 և x 1 · x 2 =6: Մնում է միայն ընտրել այդպիսի թվեր։ Այս դեպքում դա անելը բավականին պարզ է. այսպիսի թվեր են 2-ը և 3-ը, քանի որ 2+3=5 և 2·3=6: Այսպիսով, 2-ը և 3-ը այս քառակուսի հավասարման արմատներն են:

Վիետայի թեորեմին հակադարձ թեորեմը հատկապես հարմար է օգտագործել տրված քառակուսի հավասարման երկրորդ արմատը գտնելու համար, երբ արմատներից մեկն արդեն հայտնի է կամ ակնհայտ։ Այս դեպքում երկրորդ արմատը կարելի է գտնել հարաբերություններից որևէ մեկից։

Օրինակ՝ վերցնենք քառակուսի հավասարումը 512 x 2 −509 x −3=0։ Այստեղ հեշտ է տեսնել, որ միասնությունը հավասարման արմատն է, քանի որ այս քառակուսի հավասարման գործակիցների գումարը հավասար է զրոյի։ Այսպիսով, x 1 = 1: Երկրորդ արմատը x 2 կարելի է գտնել, օրինակ, x 1 ·x 2 =c/a հարաբերությունից: Ունենք 1 x 2 =−3/512, որից x 2 =−3/512։ Այսպես մենք որոշեցինք քառակուսի հավասարման երկու արմատները՝ 1 և −3/512:

Հասկանալի է, որ արմատների ընտրությունը նպատակահարմար է միայն ամենապարզ դեպքերում։ Այլ դեպքերում, արմատներ գտնելու համար կարող եք օգտագործել քառակուսի հավասարման արմատների բանաձևերը դիսկրիմինանտի միջոցով:

Մեկ այլ գործնական օգտագործումԹեորեմը, ընդհակառակը Վիետայի թեորեմի, բաղկացած է քառակուսի հավասարումներ կազմելուց, որոնք տրված են x 1 և x 2 արմատներին: Դրա համար բավական է հաշվարկել արմատների գումարը, որը տալիս է x-ի գործակիցը տրված քառակուսի հավասարման հակառակ նշանով, և արմատների արտադրյալը, որը տալիս է ազատ անդամը։

Օրինակ.

Գրի՛ր քառակուսի հավասարում, որի արմատները −11 և 23 են։

Լուծում.

Նշանակենք x 1 =−11 և x 2 =23։ Հաշվում ենք այս թվերի գումարը և արտադրյալը՝ x 1 +x 2 =12 և x 1 ·x 2 =−253: Հետևաբար, նշված թվերը −12 երկրորդ գործակցով և −253 ազատ անդամով կրճատված քառակուսի հավասարման արմատներն են։ Այսինքն՝ x 2 −12·x−253=0 պահանջվող հավասարումն է։

Պատասխան.

x 2 −12·x−253=0 .

Վիետայի թեորեմը շատ հաճախ օգտագործվում է քառակուսի հավասարումների արմատների նշանների հետ կապված խնդիրներ լուծելիս։ Ինչպե՞ս է Վիետայի թեորեմը կապված կրճատված քառակուսի հավասարման արմատների նշանների հետ x 2 +p·x+q=0: Ահա երկու համապատասխան հայտարարություն.

• Եթե ​​q հատվողը դրական թիվ է, և եթե քառակուսային հավասարումն ունի իրական արմատներ, ապա երկուսն էլ դրական են, կամ երկուսն էլ բացասական:
• Եթե ​​q ազատ անդամը բացասական թիվ է, և եթե քառակուսի հավասարումն ունի իրական արմատներ, ապա դրանց նշանները տարբեր են, այլ կերպ ասած՝ մի արմատը դրական է, մյուսը՝ բացասական։

Այս պնդումները բխում են x 1 · x 2 =q բանաձեւից, ինչպես նաեւ տարբեր նշաններով դրական, բացասական թվերը եւ թվերը բազմապատկելու կանոններից։ Դիտարկենք դրանց կիրառման օրինակները:

Օրինակ.

R դա դրական է: Օգտագործելով տարբերակիչ բանաձևը՝ գտնում ենք D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, r 2 +8 արտահայտության արժեքը։ դրական է ցանկացած իրական r-ի համար, հետևաբար D>0 ցանկացած իրական r-ի համար: Հետևաբար, սկզբնական քառակուսի հավասարումը ունի երկու արմատ r պարամետրի ցանկացած իրական արժեքի համար:

Հիմա եկեք պարզենք, թե երբ արմատները տարբեր նշաններ ունեն: Եթե ​​արմատների նշանները տարբեր են, ապա դրանց արտադրյալը բացասական է, իսկ Վիետայի թեորեմի համաձայն՝ կրճատված քառակուսի հավասարման արմատների արտադրյալը հավասար է ազատ անդամին։ Հետևաբար, մեզ հետաքրքրում են r-ի այն արժեքները, որոնց համար r−1 ազատ տերմինը բացասական է: Այսպիսով, մեզ հետաքրքրող r-ի արժեքները գտնելու համար մեզ անհրաժեշտ է լուծել գծային անհավասարությունը r−1<0 , откуда находим r<1 .

Պատասխան.

ժամը r<1 .

Վիետա բանաձեւեր

Վերևում մենք խոսեցինք Վիետայի թեորեմի մասին քառակուսի հավասարման համար և վերլուծեցինք դրա հաստատված հարաբերությունները: Բայց կան բանաձևեր, որոնք կապում են ոչ միայն քառակուսի հավասարումների, այլև խորանարդ հավասարումների, չորրորդ աստիճանի հավասարումների իրական արմատներն ու գործակիցները և ընդհանրապես. հանրահաշվական հավասարումներաստիճան n. Նրանք կոչվում են Վիետայի բանաձեւերը.

Եկեք գրենք Վիետայի բանաձևը ձևի n աստիճանի հանրահաշվական հավասարման համար և կենթադրենք, որ այն ունի n իրական արմատ x 1, x 2, ..., x n (դրանց թվում կարող են լինել համընկնողներ).

Վիետայի բանաձևերը կարելի է ձեռք բերել թեորեմ բազմանդամի գծային գործակիցների տարրալուծման մասին, ինչպես նաև հավասար բազմանդամների սահմանումը նրանց բոլոր համապատասխան գործակիցների հավասարության միջոցով։ Այսպիսով, բազմանդամը և նրա ընդլայնումը ձևի գծային գործակիցների մեջ հավասար են: Բացելով փակագծերը վերջին արտադրյալում և հավասարեցնելով համապատասխան գործակիցները՝ ստանում ենք Վիետայի բանաձևերը։

Մասնավորապես, n=2-ի համար մենք ունենք քառակուսի հավասարման արդեն ծանոթ Վիետա բանաձևերը:

Խորանարդային հավասարման համար Վիետայի բանաձևերն ունեն ձևը

Մնում է միայն նշել, որ Վիետայի բանաձևերի ձախ կողմում կան այսպես կոչված տարրական. սիմետրիկ բազմանդամներ.

Մատենագիտություն.

• Հանրահաշիվ:դասագիրք 8-րդ դասարանի համար. հանրակրթական հաստատություններ / [Յու. Ն. Մակարիչև, Ն. Գ. Մինդյուկ, Կ. Ի. Նեշկով, Ս. Բ. Սուվորովա]; խմբագրել է Ս.Ա.Տելյակովսկի. - 16-րդ հրատ. - Մ.: Կրթություն, 2008. - 271 էջ. : հիվանդ. - ISBN 978-5-09-019243-9 ։
• Մորդկովիչ Ա.Գ.Հանրահաշիվ. 8-րդ դասարան. 2 ժամում Մաս 1. Դասագիրք հանրակրթական հաստատությունների ուսանողների համար / Ա. Գ. Մորդկովիչ. - 11-րդ հրատ., ջնջված։ - M.: Mnemosyne, 2009. - 215 p.: հիվանդ. ISBN 978-5-346-01155-2 ։
• Հանրահաշիվև մաթեմատիկական վերլուծության սկիզբը: 10-րդ դասարան՝ դասագիրք. հանրակրթության համար հաստատություններ՝ հիմնական և պրոֆիլ: մակարդակներ / [Յու. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; խմբագրել է A. B. Ժիժչենկո. - 3-րդ հրատ. - Մ.: Կրթություն, 2010.- 368 էջ. : հիվանդ. - ISBN 978-5-09-022771-1։

Վիետայի թեորեմը հաճախ օգտագործվում է արդեն իսկ գտնված արմատները ստուգելու համար։ Եթե ​​գտել եք արմատները, կարող եք օգտագործել \(\սկիզբ(դեպքեր)x_1+x_2=-p \\x_1 \cdot x_2=q\end(դեպքեր)\) բանաձևերը՝ \(p-ի արժեքները հաշվարկելու համար: \) և \(ք\ ). Իսկ եթե դրանք նույնն են, ինչ սկզբնական հավասարման մեջ, ապա արմատները ճիշտ են գտնվել։

Օրինակ՝ եկեք, օգտագործելով , լուծենք \(x^2+x-56=0\) հավասարումը և ստանանք արմատները՝ \(x_1=7\), \(x_2=-8\): Եկեք ստուգենք՝ արդյոք սխալվել ենք լուծման գործընթացում։ Մեր դեպքում՝ \(p=1\), և \(q=-56\): Վիետայի թեորեմով մենք ունենք.

\(\սկիզբ(դեպքեր)x_1+x_2=-p \\x_1 \cdot x_2=q\վերջ(դեպքեր)\) \(\ձախ աջ սլաքը\) \(\սկիզբ(դեպքեր)7+(-8)=-1 \\7\cdot(-8)=-56\վերջ (դեպքեր)\) \(\Ձախ աջ սլաքը\) \(\սկիզբ(դեպքեր)-1=-1\\-56=-56\վերջ (դեպքեր)\ )

Երկու պնդումներն էլ միացան, ինչը նշանակում է, որ մենք ճիշտ լուծեցինք հավասարումը:

Այս ստուգումը կարող է իրականացվել բանավոր: Դա կտևի 5 վայրկյան և կփրկի ձեզ հիմար սխալներից։

Վիետայի հակադարձ թեորեմը

Եթե ​​\(\սկիզբ(դեպքեր)x_1+x_2=-p \\x_1 \cdot x_2=q\end(դեպքեր)\), ապա \(x_1\) և \(x_2\) քառակուսի հավասարման արմատներն են \ (x^ 2+px+q=0\):

Կամ պարզ ձևով. եթե ունեք \(x^2+px+q=0\) ձևի հավասարում, ապա լուծել համակարգը \(\սկիզբ(դեպքեր)x_1+x_2=-p \\x_1 \cdot x_2=q\ end(cases)\) դուք կգտնեք դրա արմատները:

Այս թեորեմի շնորհիվ դուք կարող եք արագ գտնել քառակուսի հավասարման արմատները, հատկապես, եթե այդ արմատները . Այս հմտությունը կարևոր է, քանի որ այն խնայում է շատ ժամանակ:

Օրինակ . Լուծե՛ք \(x^2-5x+6=0\) հավասարումը։

Լուծում Օգտագործելով Վիետայի հակադարձ թեորեմը՝ մենք գտնում ենք, որ արմատները բավարարում են հետևյալ պայմանները.
Նայեք \(x_1 \cdot x_2=6\) համակարգի երկրորդ հավասարմանը: Ի՞նչ երկուսի կարելի է բաժանել \(6\) թիվը: \(2\) և \(3\), \(6\) և \(1\) կամ \(-2\) և \(-3\), և \(-6\) և \(-) վրա 1 \). Համակարգի առաջին հավասարումը ձեզ կասի, թե որ զույգն ընտրել՝ \(x_1+x_2=5\): \(2\) և \(3\) նման են, քանի որ \(2+3=5\):
Պատասխանել : \(x_1=2\), \(x_2=3\):

Օրինակներ . Օգտագործելով Վիետայի թեորեմի հակադարձը, գտե՛ք քառակուսի հավասարման արմատները.
ա) \(x^2-15x+14=0\); բ) \(x^2+3x-4=0\); գ) \(x^2+9x+20=0\); դ) \(x^2-88x+780=0\):

Լուծում :
ա) \(x^2-15x+14=0\) – ինչ գործոնների է քայքայվում \(14\)-ը: \(2\) և \(7\), \(-2\) և \(-7\), \(-1\) և \(-14\), \(1\) և \(14\): ) Ի՞նչ զույգ թվերի գումարվում է \(15\): Պատասխան՝ \(1\) և \(14\):

բ) \(x^2+3x-4=0\) – ինչ գործոնների է քայքայվում \(-4\): \(-2\) և \(2\), \(4\) և \(-1\), \(1\) և \(-4\): Ի՞նչ զույգ թվեր են գումարվում \(-3\): Պատասխան՝ \(1\) և \(-4\):

գ) \(x^2+9x+20=0\) – ինչ գործոնների է քայքայվում \(20\): \(4\) և \(5\), \(-4\) և \(-5\), \(2\) և \(10\), \(-2\) և \(-10\ ), \(-20\) և \(-1\), \(20\) և \(1\): Ի՞նչ զույգ թվեր են գումարվում \(-9\): Պատասխան՝ \(-4\) և \(-5\):

դ) \(x^2-88x+780=0\) – ինչ գործոնների է քայքայվում \(780\): \(390\) և \(2\): Արդյո՞ք դրանք կավելանան մինչև \(88\): Ոչ Ի՞նչ այլ բազմապատկիչներ ունի \(780\)-ը: \(78\) և \(10\): Արդյո՞ք դրանք կավելանան մինչև \(88\): Այո՛։ Պատասխան՝ \(78\) և \(10\):

Պետք չէ ընդլայնել վերջին տերմինը բոլոր հնարավոր գործոնների մեջ (ինչպես վերջին օրինակում): Դուք կարող եք անմիջապես ստուգել, ​​թե արդյոք դրանց գումարը տալիս է \(-p\):

Կարևոր.Վիետայի թեորեմը և հակադարձ թեորեմն աշխատում են միայն , այսինքն՝ մեկի հետ, որի համար \(x^2\) գործակիցը հավասար է մեկի։ Եթե ​​ի սկզբանե մեզ տրված էր չկրճատված հավասարում, ապա այն կարող ենք կրճատել՝ պարզապես բաժանելով \(x^2\-ի դիմացի գործակցին):

Օրինակ, թող տրվի \(2x^2-4x-6=0\) հավասարումը և ուզում ենք օգտագործել Վիետայի թեորեմներից մեկը։ Բայց մենք չենք կարող, քանի որ \(x^2\)-ի գործակիցը հավասար է \(2\-ի): Եկեք ազատվենք դրանից՝ ամբողջ հավասարումը բաժանելով \(2\-ի):

\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)

Պատրաստ. Այժմ դուք կարող եք օգտագործել երկու թեորեմները:

Հաճախակի տրվող հարցերի պատասխաններ

Հարց: Օգտագործելով Վիետայի թեորեմը, դուք կարող եք լուծել ցանկացած.
Պատասխան. Ցավոք, ոչ. Եթե ​​հավասարումը չի պարունակում ամբողջ թվեր կամ հավասարումն ընդհանրապես արմատներ չունի, ապա Վիետայի թեորեմը չի օգնի։ Այս դեպքում դուք պետք է օգտագործեք խտրական . Բարեբախտաբար, դպրոցական մաթեմատիկայի հավասարումների 80%-ն ունեն ամբողջական լուծումներ: