Երկու կետերի միջև հեռավորությունը առցանց: Գտեք երկու կետերի միջև հեռավորությունը

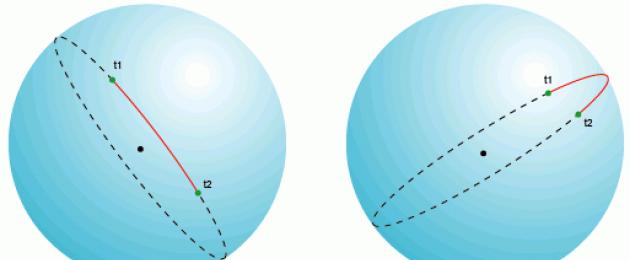
Երկրի մակերևույթի վրա կետերի միջև հեռավորությունները հաշվարկելը տարրական է. մենք կքննարկենք կետերի միջև հեռավորությունը և սկզբնական ազիմուտը առանց պրոյեկցիոն փոխակերպումների: Նախ, եկեք հասկանանք տերմինաբանությունը:

Ներածություն

Շրջանի աղեղի մեծ երկարություն– գնդի մակերևույթի վրա գտնվող ցանկացած երկու կետերի միջև ամենակարճ հեռավորությունը, որը չափվում է այս երկու կետերը միացնող գծի երկայնքով (այդպիսի գիծը կոչվում է օրթոդրոմիա) և անցնում է ոլորտի կամ պտտման այլ մակերևույթի երկայնքով։ Գնդային երկրաչափությունը տարբերվում է սովորական Էվկլիդեսյան երկրաչափությունից, և հեռավորության հավասարումները նույնպես տարբեր ձև են ստանում: Էվկլիդեսյան երկրաչափության մեջ երկու կետերի միջև ամենակարճ հեռավորությունը ուղիղ գիծ է։ Գնդի վրա ուղիղ գծեր չկան։ Ոլորտի վրա գտնվող այս գծերը մեծ շրջանակների մի մասն են՝ շրջանակներ, որոնց կենտրոնները համընկնում են ոլորտի կենտրոնի հետ: Սկզբնական ազիմուտ- ազիմուտ, որը վերցնելով A կետից շարժվելիս, հետևելով մեծ շրջանին մինչև B կետը ամենակարճ հեռավորության վրա, վերջնակետը կլինի B կետը: Մեծ շրջանագծի գծով A կետից B կետ շարժվելիս ազիմուտը ներկայիս դիրքն է վերջնակետ B-ն անընդհատ փոխվում է: Սկզբնական ազիմուտը տարբերվում է հաստատունից, որին հետևելով ընթացիկ կետից մինչև վերջնական կետ ազիմուտը չի փոխվում, բայց հետևած երթուղին երկու կետերի միջև ամենակարճ հեռավորությունը չէ:

Գնդի մակերևույթի ցանկացած երկու կետերի միջով, եթե դրանք ուղղակիորեն հակադիր չեն միմյանց (այսինքն՝ հակապոդներ չեն), կարելի է գծել եզակի մեծ շրջան։ Երկու կետը մեծ շրջանը բաժանում է երկու կամարի։ Կարճ աղեղի երկարությունը երկու կետերի միջև ամենակարճ հեռավորությունն է: Անսահման թվով մեծ շրջանակներ կարելի է գծել երկու հակապոդալ կետերի միջև, սակայն նրանց միջև հեռավորությունը կլինի նույնը ցանկացած շրջանագծի վրա և հավասար է շրջանագծի շրջագծի կեսին, կամ π*R, որտեղ R-ը ոլորտի շառավիղն է։

Հարթության վրա (ուղղանկյուն կոորդինատային համակարգում) մեծ շրջանակները և դրանց բեկորները, ինչպես նշվեց վերևում, ներկայացնում են աղեղներ բոլոր ելուստներում, բացառությամբ գնոմոնիկից, որտեղ մեծ շրջանակները ուղիղ գծեր են: Գործնականում դա նշանակում է, որ ինքնաթիռները և այլ օդային տրանսպորտը վառելիք խնայելու համար միշտ օգտագործում են կետերի միջև նվազագույն հեռավորության երթուղին, այսինքն՝ թռիչքն իրականացվում է շրջանագծի մեծ հեռավորության վրա, ինքնաթիռում այն ​​կարծես աղեղ է:

Երկրի ձևը կարելի է նկարագրել որպես գունդ, ուստի մեծ շրջանի հեռավորության հավասարումները կարևոր են Երկրի մակերևույթի կետերի միջև ամենակարճ հեռավորությունը հաշվարկելու համար և հաճախ օգտագործվում են նավիգացիայի մեջ: Այս մեթոդով հեռավորության հաշվարկն ավելի արդյունավետ և շատ դեպքերում ավելի ճշգրիտ է, քան նախագծված կոորդինատների համար (ուղղանկյուն կոորդինատային համակարգերում), քանի որ, նախ, այն թարգմանություն չի պահանջում: աշխարհագրական կոորդինատներըՎ ուղղանկյուն համակարգկոորդինատները (իրականացնում են պրոյեկցիոն փոխակերպումներ) և, երկրորդ, շատ կանխատեսումներ, եթե սխալ ընտրված են, կարող են հանգեցնել երկարության զգալի աղավաղումների՝ պայմանավորված պրոյեկցիոն աղավաղումների բնութագրերով: Հայտնի է, որ դա ոչ թե գնդիկ է, այլ էլիպսոիդ, որն ավելի ճշգրիտ է նկարագրում Երկրի ձևը, այնուամենայնիվ, այս հոդվածում քննարկվում է հեռավորությունների հաշվարկը հատուկ գնդի վրա, օգտագործվում է 6,372,795 մետր շառավղով գունդ , ինչը կարող է հանգեցնել 0,5% կարգի հեռավորությունների հաշվարկման սխալի:

Բանաձևեր

Մեծ շրջանի գնդաձև հեռավորությունը հաշվարկելու երեք եղանակ կա. 1. Գնդային կոսինուսների թեորեմՓոքր հեռավորությունների և հաշվարկի փոքր խորության դեպքում (տասնորդական տեղերի թիվը) բանաձևի օգտագործումը կարող է հանգեցնել զգալի կլորացման սխալների։ φ1, λ1; φ2, λ2 - երկու կետի լայնություն և երկայնություն ռադիաններով Δλ - կոորդինատների տարբերություն երկայնության Δδ - անկյունային տարբերություն Δδ = arccos (sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) Անկյունային հեռավորությունը մետրիկի փոխարկելու համար անհրաժեշտ է. բազմապատկենք անկյունային տարբերությունը Երկրի շառավղով (6372795 մետր), վերջնական հեռավորության միավորները հավասար կլինեն այն միավորներին, որոնցում արտահայտված է շառավիղը (տվյալ դեպքում՝ մետր): 2. Haversine բանաձեւըՕգտագործվում է կարճ հեռավորությունների հետ կապված խնդիրներից խուսափելու համար: 3. Փոփոխություն անտիպոդների համարՆախորդ բանաձևը նույնպես ենթակա է հակապոդալ կետերի խնդրին, այն լուծելու համար օգտագործվում է հետևյալ փոփոխությունը.

Իմ իրականացումը PHP-ում

// Երկրի շառավիղը սահմանում ("EARTH_RADIUS", 6372795); /* * Երկու կետերի միջև հեռավորությունը * $φA, $λA - լայնություն, 1-ին կետի երկայնություն, * $φB, $λB - լայնություն, 2-րդ կետի երկայնություն * Գրված է http://gis-lab.info/ հիման վրա։ qa/great-circles.html * Միխայիլ Կոբզարև< >* */ ֆունկցիան հաշվարկել Հեռավորությունը ($φA, $λA, $φB, $λB) ( // կոորդինատները փոխարկել ռադիանի $lat1 = $φA * M_PI / 180; $lat2 = $φB * M_PI / 180; $long1 = $λA * M_PI / 180 $ λB * M_PI / 180 // լայնությունների և երկայնությունների սինուսներ $cl1 = $sl2 = $; long1 $ cdelta = cos ($ sdelta = sin ($cl2 * $sdelta, 2) + pow ($cl1 * $sl2 - $ cl2 * $ cdelta, 2)); $x = $sl1 * $cl2 * $cdelta = atan2 ($y, $x = $ad * EARTH_RADIUS): $lat1; = 77,1539; $ երկար1 = -139,398; $lat2 = -77,1804; $ երկար2 = -139,55; echo հաշվարկել TheDistance ($lat1, $long1, $lat2, $long2) . «մետր»; // Վերադարձ «17166029 մետր»

Հոդվածը վերցված է կայքից

Բարեւ Ձեզ,

PHP օգտագործված:

Հարգանքներով՝ Ալեքսանդր։

Բարեւ Ձեզ,

Արդեն բավական ժամանակ է, ինչ ես պայքարում եմ մի խնդրի հետ. ես փորձում եմ հաշվարկել երկու կամայական կետերի միջև հեռավորությունը, որոնք գտնվում են միմյանցից 30-ից 1500 մետր հեռավորության վրա:

PHP օգտագործված:

$cx=31.319738; //x առաջին կետի կոորդինատը
$cy=60.901638; //y առաջին կետի կոորդինատը

$x=31,333312; //x երկրորդ կետի կոորդինատը
$y=60.933981; //y երկրորդ կետի կոորդինատը

$mx=abs($cx-$x); //հաշվիր x-ի տարբերությունը (ուղղանկյուն եռանկյունու առաջին ոտքը), abs(x) ֆունկցիան - վերադարձնում է x x թվի մոդուլը
$my=abs ($cy-$y); //հաշվիր խաղացողների տարբերությունը (աջ եռանկյունու երկրորդ ոտքը)

$dist=sqrt(pow($mx,2)+pow($my,2)); //Ստացեք մետրոյի հեռավորությունը (հիպոթենուսի երկարությունը ըստ կանոնի, հիպոթենուզը հավասար է ոտքերի քառակուսիների գումարի արմատին)

Եթե ​​պարզ չէ, թույլ տվեք բացատրել. ես պատկերացնում եմ, որ երկու կետերի միջև հեռավորությունը ուղղանկյուն եռանկյան հիպոթենուսն է: Այնուհետև երկու կետերից յուրաքանչյուրի X-երի տարբերությունը կլինի ոտքից մեկը, իսկ մյուս ոտքը կլինի նույն երկու կետերի Y-ների տարբերությունը: Այնուհետև, հաշվարկելով X-երի և Y-երի միջև եղած տարբերությունները, կարող եք օգտագործել հիպոթենուսի երկարությունը (այսինքն՝ երկու կետերի միջև հեռավորությունը) հաշվարկելու բանաձևը:

Ես գիտեմ, որ այս կանոնը լավ է աշխատում դեկարտյան կոորդինատների համակարգի համար, այնուամենայնիվ, այն պետք է քիչ թե շատ աշխատի երկարատև կոորդինատների միջոցով, քանի որ երկու կետերի միջև չափված հեռավորությունը աննշան է (30-ից մինչև 1500 մետր):

Այնուամենայնիվ, այս ալգորիթմի համաձայն հեռավորությունը սխալ է հաշվարկված (օրինակ, այս ալգորիթմի կողմից հաշվարկված հեռավորությունը 1-ը գերազանցում է 2-ը ընդամենը 13%-ով, մինչդեռ իրականում 1-ին հեռավորությունը հավասար է 1450 մետրի, իսկ հեռավորությունը 2-ը հավասար է 970 մետրի. իրականում տարբերությունը հասնում է գրեթե 50%-ի):

Եթե ​​որևէ մեկը կարող է օգնել, ես շատ շնորհակալ կլինեմ:

Հարգանքներով՝ Ալեքսանդր։

","contentType":"text/html"),"proposedBody":("աղբյուր":"

Բարեւ Ձեզ,

Արդեն բավական ժամանակ է, ինչ ես պայքարում եմ մի խնդրի հետ. ես փորձում եմ հաշվարկել երկու կամայական կետերի միջև հեռավորությունը, որոնք գտնվում են միմյանցից 30-ից 1500 մետր հեռավորության վրա:

PHP օգտագործված:

$cx=31.319738; //x առաջին կետի կոորդինատը
$cy=60.901638; //y առաջին կետի կոորդինատը

$x=31,333312; //x երկրորդ կետի կոորդինատը
$y=60.933981; //y երկրորդ կետի կոորդինատը

$mx=abs($cx-$x); //հաշվիր x-ի տարբերությունը (ուղղանկյուն եռանկյունու առաջին ոտքը), abs(x) ֆունկցիան - վերադարձնում է x x թվի մոդուլը
$my=abs ($cy-$y); //հաշվիր խաղացողների տարբերությունը (աջ եռանկյունու երկրորդ ոտքը)

$dist=sqrt(pow($mx,2)+pow($my,2)); //Ստացեք մետրոյի հեռավորությունը (հիպոթենուսի երկարությունը ըստ կանոնի, հիպոթենուզը հավասար է ոտքերի քառակուսիների գումարի արմատին)

Եթե ​​պարզ չէ, թույլ տվեք բացատրել. ես պատկերացնում եմ, որ երկու կետերի միջև հեռավորությունը ուղղանկյուն եռանկյան հիպոթենուսն է: Այնուհետև երկու կետերից յուրաքանչյուրի X-երի տարբերությունը կլինի ոտքից մեկը, իսկ մյուս ոտքը կլինի նույն երկու կետերի Y-ների տարբերությունը: Այնուհետև, հաշվարկելով X-երի և Y-երի միջև եղած տարբերությունները, կարող եք օգտագործել հիպոթենուսի երկարությունը (այսինքն՝ երկու կետերի միջև հեռավորությունը) հաշվարկելու բանաձևը:

Ես գիտեմ, որ այս կանոնը լավ է աշխատում դեկարտյան կոորդինատների համակարգի համար, այնուամենայնիվ, այն պետք է քիչ թե շատ աշխատի երկարատև կոորդինատների միջոցով, քանի որ երկու կետերի միջև չափված հեռավորությունը աննշան է (30-ից մինչև 1500 մետր):

Այնուամենայնիվ, այս ալգորիթմի համաձայն հեռավորությունը սխալ է հաշվարկված (օրինակ, այս ալգորիթմի կողմից հաշվարկված հեռավորությունը 1-ը գերազանցում է 2-ը ընդամենը 13%-ով, մինչդեռ իրականում 1-ին հեռավորությունը հավասար է 1450 մետրի, իսկ հեռավորությունը 2-ը հավասար է 970 մետրի. իրականում տարբերությունը հասնում է գրեթե 50%-ի):

Եթե ​​որևէ մեկը կարող է օգնել, ես շատ շնորհակալ կլինեմ:

Հարգանքներով՝ Ալեքսանդր։

Բարեւ Ձեզ,

Արդեն բավական ժամանակ է, ինչ ես պայքարում եմ մի խնդրի հետ. ես փորձում եմ հաշվարկել երկու կամայական կետերի միջև հեռավորությունը, որոնք գտնվում են միմյանցից 30-ից 1500 մետր հեռավորության վրա:

PHP օգտագործված:

$cx=31.319738; //x առաջին կետի կոորդինատը
$cy=60.901638; //y առաջին կետի կոորդինատը

$x=31,333312; //x երկրորդ կետի կոորդինատը
$y=60.933981; //y երկրորդ կետի կոորդինատը

$mx=abs($cx-$x); //հաշվիր x-ի տարբերությունը (ուղղանկյուն եռանկյունու առաջին ոտքը), abs(x) ֆունկցիան - վերադարձնում է x x թվի մոդուլը
$my=abs ($cy-$y); //հաշվիր խաղացողների տարբերությունը (աջ եռանկյունու երկրորդ ոտքը)

$dist=sqrt(pow($mx,2)+pow($my,2)); //Ստացեք մետրոյի հեռավորությունը (հիպոթենուսի երկարությունը ըստ կանոնի, հիպոթենուզը հավասար է ոտքերի քառակուսիների գումարի արմատին)

Եթե ​​պարզ չէ, թույլ տվեք բացատրել. ես պատկերացնում եմ, որ երկու կետերի միջև հեռավորությունը ուղղանկյուն եռանկյան հիպոթենուսն է: Այնուհետև երկու կետերից յուրաքանչյուրի X-երի տարբերությունը կլինի ոտքից մեկը, իսկ մյուս ոտքը կլինի նույն երկու կետերի Y-ների տարբերությունը: Այնուհետև, հաշվարկելով X-երի և Y-երի միջև եղած տարբերությունները, կարող եք օգտագործել հիպոթենուսի երկարությունը (այսինքն՝ երկու կետերի միջև հեռավորությունը) հաշվարկելու բանաձևը:

Ես գիտեմ, որ այս կանոնը լավ է աշխատում դեկարտյան կոորդինատների համակարգի համար, այնուամենայնիվ, այն պետք է քիչ թե շատ աշխատի երկարատև կոորդինատների միջոցով, քանի որ երկու կետերի միջև չափված հեռավորությունը աննշան է (30-ից մինչև 1500 մետր):

Այնուամենայնիվ, այս ալգորիթմի համաձայն հեռավորությունը սխալ է հաշվարկված (օրինակ, այս ալգորիթմի կողմից հաշվարկված հեռավորությունը 1-ը գերազանցում է 2-ը ընդամենը 13%-ով, մինչդեռ իրականում 1-ին հեռավորությունը հավասար է 1450 մետրի, իսկ հեռավորությունը 2-ը հավասար է 970 մետրի. իրականում տարբերությունը հասնում է գրեթե 50%-ի):

Եթե ​​որևէ մեկը կարող է օգնել, ես շատ շնորհակալ կլինեմ:

Հարգանքներով՝ Ալեքսանդր։

","contentType":"text/html"),"authorId":"108613929","slug":"15001","canEdit":false,"canComment":false,"isBanned":false,"canPublish" :false,"viewType":"հին","isDraft":false,"isOnModeration":false,"isSubscriber":false,"commentsCount":14,"modificationDate":"Չորք, 27 հունիսի 2012թ. 20:07:00 GMT +0000 (համակարգված համընդհանուր ժամանակ)","showPreview":true,"approvedPreview":("աղբյուր":"

Բարեւ Ձեզ,

Արդեն բավական ժամանակ է, ինչ ես պայքարում եմ մի խնդրի հետ. ես փորձում եմ հաշվարկել երկու կամայական կետերի միջև հեռավորությունը, որոնք գտնվում են միմյանցից 30-ից 1500 մետր հեռավորության վրա:

PHP օգտագործված:

$cx=31.319738; //x առաջին կետի կոորդինատը
$cy=60.901638; //y առաջին կետի կոորդինատը

$x=31,333312; //x երկրորդ կետի կոորդինատը
$y=60.933981; //y երկրորդ կետի կոորդինատը

$mx=abs($cx-$x); //հաշվիր x-ի տարբերությունը (ուղղանկյուն եռանկյունու առաջին ոտքը), abs(x) ֆունկցիան - վերադարձնում է x x թվի մոդուլը
$my=abs ($cy-$y); //հաշվիր խաղացողների տարբերությունը (աջ եռանկյունու երկրորդ ոտքը)

$dist=sqrt(pow($mx,2)+pow($my,2)); //Ստացեք մետրոյի հեռավորությունը (հիպոթենուսի երկարությունը ըստ կանոնի, հիպոթենուզը հավասար է ոտքերի քառակուսիների գումարի արմատին)

Եթե ​​պարզ չէ, թույլ տվեք բացատրել. ես պատկերացնում եմ, որ երկու կետերի միջև հեռավորությունը ուղղանկյուն եռանկյան հիպոթենուսն է: Այնուհետև երկու կետերից յուրաքանչյուրի X-երի տարբերությունը կլինի ոտքից մեկը, իսկ մյուս ոտքը կլինի նույն երկու կետերի Y-ների տարբերությունը: Այնուհետև, հաշվարկելով X-երի և Y-երի միջև եղած տարբերությունները, կարող եք օգտագործել հիպոթենուսի երկարությունը (այսինքն՝ երկու կետերի միջև հեռավորությունը) հաշվարկելու բանաձևը:

Ես գիտեմ, որ այս կանոնը լավ է աշխատում դեկարտյան կոորդինատների համակարգի համար, այնուամենայնիվ, այն պետք է քիչ թե շատ աշխատի երկարատև կոորդինատների միջոցով, քանի որ երկու կետերի միջև չափված հեռավորությունը աննշան է (30-ից մինչև 1500 մետր):

Այնուամենայնիվ, այս ալգորիթմի համաձայն հեռավորությունը սխալ է հաշվարկված (օրինակ, այս ալգորիթմի կողմից հաշվարկված հեռավորությունը 1-ը գերազանցում է 2-ը ընդամենը 13%-ով, մինչդեռ իրականում 1-ին հեռավորությունը հավասար է 1450 մետրի, իսկ հեռավորությունը 2-ը հավասար է 970 մետրի. իրականում տարբերությունը հասնում է գրեթե 50%-ի):

Եթե ​​որևէ մեկը կարող է օգնել, ես շատ շնորհակալ կլինեմ:

Հարգանքներով՝ Ալեքսանդր։

","html":"Բարև,","contentType":"text/html"),"proposedPreview":("աղբյուր":"

Բարեւ Ձեզ,

Արդեն բավական ժամանակ է, ինչ ես պայքարում եմ մի խնդրի հետ. ես փորձում եմ հաշվարկել երկու կամայական կետերի միջև հեռավորությունը, որոնք գտնվում են միմյանցից 30-ից 1500 մետր հեռավորության վրա:

PHP օգտագործված:

$cx=31.319738; //x առաջին կետի կոորդինատը
$cy=60.901638; //y առաջին կետի կոորդինատը

$x=31,333312; //x երկրորդ կետի կոորդինատը
$y=60.933981; //y երկրորդ կետի կոորդինատը

$mx=abs($cx-$x); //հաշվիր x-ի տարբերությունը (ուղղանկյուն եռանկյունու առաջին ոտքը), abs(x) ֆունկցիան - վերադարձնում է x x թվի մոդուլը
$my=abs ($cy-$y); //հաշվիր խաղացողների տարբերությունը (աջ եռանկյունու երկրորդ ոտքը)

$dist=sqrt(pow($mx,2)+pow($my,2)); //Ստացեք մետրոյի հեռավորությունը (հիպոթենուսի երկարությունը ըստ կանոնի, հիպոթենուզը հավասար է ոտքերի քառակուսիների գումարի արմատին)

Եթե ​​պարզ չէ, թույլ տվեք բացատրել. ես պատկերացնում եմ, որ երկու կետերի միջև հեռավորությունը ուղղանկյուն եռանկյան հիպոթենուսն է: Այնուհետև երկու կետերից յուրաքանչյուրի X-երի տարբերությունը կլինի ոտքից մեկը, իսկ մյուս ոտքը կլինի նույն երկու կետերի Y-ների տարբերությունը: Այնուհետև, հաշվարկելով X-երի և Y-երի միջև եղած տարբերությունները, կարող եք օգտագործել հիպոթենուսի երկարությունը (այսինքն՝ երկու կետերի միջև հեռավորությունը) հաշվարկելու բանաձևը:

Ես գիտեմ, որ այս կանոնը լավ է աշխատում դեկարտյան կոորդինատների համակարգի համար, այնուամենայնիվ, այն պետք է քիչ թե շատ աշխատի երկարատև կոորդինատների միջոցով, քանի որ երկու կետերի միջև չափված հեռավորությունը աննշան է (30-ից մինչև 1500 մետր):

Այնուամենայնիվ, այս ալգորիթմի համաձայն հեռավորությունը սխալ է հաշվարկված (օրինակ, այս ալգորիթմի կողմից հաշվարկված հեռավորությունը 1-ը գերազանցում է 2-ը ընդամենը 13%-ով, մինչդեռ իրականում 1-ին հեռավորությունը հավասար է 1450 մետրի, իսկ հեռավորությունը 2-ը հավասար է 970 մետրի. իրականում տարբերությունը հասնում է գրեթե 50%-ի):

Եթե ​​որևէ մեկը կարող է օգնել, ես շատ շնորհակալ կլինեմ:

Հարգանքներով՝ Ալեքսանդր։

","html":"Բարև,","contentType":"text/html"),"titleImage":null,"tags":[("displayName":"հեռավորության չափում","slug":"izmerenie- rasstoyaniy","categoryId":"10615601","url":"/blog/mapsapi??tag=izmerenie-rasstoyaniy"), ("displayName":"API 1.x","slug":"api-1 -x","categoryId":"150000131","url":"/blog/mapsapi??tag=api-1-x")],"isModerator":false,"publishCount":1,"commentsEnabled": true,"url":"/blog/mapsapi/15001","urlTemplate":"/blog/mapsapi/%slug%","fullBlogUrl":"https://yandex.ru/blog/mapsapi","addCommentUrl" ":"/blog/createComment/mapsapi/15001","updateCommentUrl":"/blog/updateComment/mapsapi/15001","addCommentWithCaptcha":"/blog/createWithCaptcha/mapsapi/150pi/150001"aptch" /api/captcha/new","putImageUrl":"/blog/image/put","urlBlog":"/blog/mapsapi","urlEditPost":"/blog/56a98d48b15b79e31e0d54c8/edit","urlSlug": / Օրագիր / Post / Greenateslug "," Urlpublishpost ":" / Blog / 56A98D48B15B79E31E0D54CC8 / Publish "," Urlunpublishpost ": B79E31E0D54C8 / Հեռացնել «», - Ուրդրոֆթ " :"/blog/mapsapi/15001/draft","urlDraftTemplate":"/blog/mapsapi/%slug%/draft","urlRemoveDraft":"/blog/56a98d48b15b79e31e0d54Draft8"/remogl" / api/suggest/mapsapi","urlAfterDelete":"/blog/mapsapi","isAuthor":false,"subscribeUrl":"/blog/api/subscribe/56a98d48b15b79e31e0d54c8","unsubscribe"/bloga": չեղարկել բաժանորդագրությունը /56a98d48b15b79e31e0d54c8","urlEditPostPage":"/blog/mapsapi/56a98d48b15b79e31e0d54c8/edit","urlF orTranslate:"/"Reslate"/blog/ Issue","urlUpdateTranslate" :" /blog/post/updateTranslate","urlLoadTranslate":"/blog/post/loadTranslate","urlTranslationStatus":"/blog/mapsapi/15001/translationInfo","urlRelatedArticles":"/blog/api/relatedArticles mapsapi/ 15001","author":("id":"108613929","uid":("value":"108613929","lite":false,"hosted":false),"aliases":() ," login":"mrdds","display_name":("name":"mrdds","avatar":("default":"0/0-0","դատարկ":true)),,"հասցե ":" [էլփոստը պաշտպանված է]","defaultAvatar":"0/0-0","imageSrc":"https://avatars.mds.yandex.net/get-yapic/0/0-0/islands-middle","isYandexStaff": false),"originalModificationDate":"2012-06-27T16:07:49.000Z","socialImage":("oriig":("fullPath":"https://avatars.mds.yandex.net/get-yablogs /47421/file_1456488726678/orig"))))))">

Դասախոսություն: Երկու կետերի միջև հեռավորության բանաձև; ոլորտի հավասարումը

Հեռավորությունը երկու կետերի միջև

Նախորդ հարցի գծի երկու կետերի միջև հեռավորությունը գտնելու համար օգտագործեցինք d = x 2 – x 1 բանաձևը:

Բայց ինչ վերաբերում է ինքնաթիռին, ամեն ինչ այլ է։ Բավական չէ պարզապես գտնել կոորդինատների տարբերությունը։ Կետերի միջև հեռավորությունը դրանց կոորդինատների միջոցով գտնելու համար օգտագործեք հետևյալ բանաձևը.

Օրինակ, եթե դուք ունեք երկու կետ որոշակի կոորդինատներով, ապա կարող եք գտնել նրանց միջև հեռավորությունը հետևյալ կերպ.

A (4;-1), B (-4;6):

AB = ((4 + 4) 2 + (-1 – 6) 2) 1/2 ≈ 10.6.

Այսինքն՝ հարթության վրա երկու կետերի միջև հեռավորությունը հաշվարկելու համար անհրաժեշտ է գտնել կոորդինատների տարբերությունների քառակուսիների գումարի արմատը։

Եթե ​​Ձեզ անհրաժեշտ է գտնել հարթության երկու կետերի միջև հեռավորությունը, ապա պետք է օգտագործեք նմանատիպ բանաձև՝ լրացուցիչ կոորդինատով.

Ոլորտի հավասարում

Տիեզերքում գունդ սահմանելու համար անհրաժեշտ է իմանալ դրա կենտրոնի կոորդինատները, ինչպես նաև շառավիղը, որպեսզի օգտագործեք հետևյալ բանաձևը.

Այս հավասարումը համապատասխանում է մի ոլորտի, որի կենտրոնը գտնվում է սկզբնակետում:

Եթե ​​առանցքների երկայնքով ոլորտի կենտրոնը տեղաշարժված է որոշակի թվով միավորներով, ապա պետք է օգտագործել հետևյալ բանաձևը.

Թող , (Նկար 2.3): Պահանջվում է գտնել:

Նկար 2.3. Երկու կետերի միջև հեռավորությունը.

Ուղղանկյունից ըստ Պյութագորասի թեորեմի ունենք

Այն է ,

Այս բանաձևը վավեր է կետերի ցանկացած տեղակայման և .

II. Այս առումով հատվածի բաժանում.

Թող ,. Պահանջվում է գտնել հատվածի վրա պառկած և տրված հարաբերակցությամբ այն բաժանելով (Նկար 2.4.):

Նկար 2.4. Այս առումով հատվածի բաժանում.

From the similarity ~, այսինքն որտեղից. Նմանապես։

Այսպիսով,

- հատվածի նկատմամբ բաժանման բանաձև:

Եթե, ապա

- հատվածի կեսի կոորդինատները:

Մեկնաբանություն.Ստացված բանաձևերը կարելի է ընդհանրացնել տարածական ուղղանկյուն դեկարտյան կոորդինատային համակարգի դեպքում։ Թող միավորները,. Հետո

- կետերի և կետերի միջև հեռավորությունը գտնելու բանաձևը.

Սեգմենտի առնչությամբ բաժանելու բանաձևը.

Բացի դեկարտյաններից ինքնաթիռում և տիեզերքում, դուք կարող եք կառուցել մեծ թիվայլ կոորդինատային համակարգեր, այսինքն՝ հարթության վրա կամ տարածության վրա կետի դիրքը բնութագրելու եղանակներ՝ օգտագործելով երկու կամ երեք թվային պարամետր (կոորդինատներ): Եկեք նայենք դրանցից մի քանիսին գոյություն ունեցող համակարգերկոորդինատները

Ինքնաթիռում հնարավոր է որոշել բևեռային կոորդինատային համակարգ , որն օգտագործվում է, մասնավորապես, պտտվող շարժումների ուսումնասիրության ժամանակ։

Նկար 2.5. Բևեռային կոորդինատային համակարգ.

Եկեք հարթության վրա ֆիքսենք մի կետ և դրանից դուրս եկող կիսագիծ, ինչպես նաև ընտրենք մասշտաբի միավոր (Նկար 2.5): Կետը կոչվում է բեւեռ , կես տող – բևեռային առանցք . Եկեք կամայական կետին վերագրենք երկու թիվ.

– բևեռային շառավիղ , հավասար է M կետից մինչև O բևեռ հեռավորությանը;

– բևեռային անկյուն , հավասար է բևեռային առանցքի և կիսագծի անկյան հետ։

Չափված ռադիաններով, արժեքների դրական ուղղությունը հաշվվում է ժամացույցի սլաքի հակառակ ուղղությամբ, սովորաբար ենթադրվում է:

Բևեռային շառավիղը համապատասխանում է բևեռին, դրա համար բևեռային անկյունը սահմանված չէ:

Գտնենք ուղղանկյուն և բևեռային կոորդինատների հարաբերությունները (Նկար 2.6):

Նկար 2.6. Ուղղանկյուն և բևեռային կոորդինատային համակարգերի կապը:

Ուղղանկյուն կոորդինատային համակարգի սկզբնաղբյուրը կհամարենք բևեռ, իսկ ճառագայթը՝ բևեռային առանցք: Թող - ուղղանկյուն դեկարտյան կոորդինատային համակարգում և - բևեռային կոորդինատային համակարգում: Գտնենք ուղղանկյուն և բևեռային կոորդինատների հարաբերությունները։

Ուղղանկյունից, իսկ ուղղանկյունից: Այսպիսով, բանաձեւերը

արտահայտել ուղղանկյուն կոորդինատներմատնանշում է իր բևեռային կոորդինատների միջով:

Հակադարձ կապն արտահայտվում է բանաձևերով

Մեկնաբանություն.Բևեռային անկյունը կարող է որոշվել նաև բանաձևից՝ նախապես որոշելով ուղղանկյուն կոորդինատներից, որոնց քառորդում է գտնվում կետը:

Օրինակ 1.Գտե՛ք կետի բևեռային կոորդինատները:

Լուծում.Մենք հաշվարկում ենք; Բևեռային անկյունը հայտնաբերվում է հետևյալ պայմաններից.

Հետևաբար, հետևաբար.

Օրինակ 2.Գտե՛ք կետի ուղղանկյուն կոորդինատները:

Լուծում.Մենք հաշվարկում ենք

Մենք ստանում ենք.

Եռաչափ տարածության մեջ, բացի ուղղանկյուն դեկարտյան կոորդինատային համակարգից, հաճախ օգտագործվում են գլանաձև և գնդաձև կոորդինատային համակարգեր։

Գլանային կոորդինատային համակարգհարթության բևեռային կոորդինատային համակարգ է, որին ավելացված է այս հարթությանը ուղղահայաց տարածական առանցք (Նկար 2.7): Ցանկացած կետի դիրքը բնութագրվում է երեք թվերով՝ նրա գլանաձև կոորդինատները. որը հավասար է կետից մինչև նշված հարթության հեռավորությանը:

Նկար 2.7. Գլանային կոորդինատային համակարգ

Ուղղանկյուն դեկարտյան կոորդինատային համակարգի և գլանաձևի միջև կապը հաստատելու համար մենք դրանք տեղադրում ենք միմյանց համեմատ, ինչպես նկար 2.8-ում (մենք հարթությունը տեղադրում ենք հարթության մեջ, և բևեռային առանցքը համընկնում է առանցքի, առանցքի դրական ուղղության հետ: տարածված է երկու կոորդինատային համակարգերում):

Թող լինեն կետի ուղղանկյուն կոորդինատները, լինեն այս կետի գլանաձև կոորդինատները և լինեն կետի պրոյեկցիան հարթության վրա: Հետո

կետի ուղղանկյուն և գլանաձև կոորդինատները միացնող բանաձևեր.

Նկար 2.8. Ուղղանկյուն դեկարտյան հարաբերակցությունը

և գլանաձև կոորդինատային համակարգեր

Մեկնաբանություն.Պտտման մարմինները դիտարկելիս հաճախ օգտագործվում են գլանաձև կոորդինատներ, որոնց առանցքը գտնվում է պտտման առանցքի երկայնքով:

Գնդային կոորդինատային համակարգկարող է կառուցվել հետևյալ կերպ. Եկեք ընտրենք բևեռային առանցքը հարթության մեջ: Կետի միջով գծում ենք հարթությանը ուղղահայաց ուղիղ գիծ (նորմալ)։ Այնուհետև տարածության ցանկացած կետ կարող է կապված լինել երեք իրական թվերի հետ, որտեղ հեռավորությունը կետից մինչև անկյունն է, առանցքի և հատվածի պրոյեկցիայի անկյունն է հարթության վրա, և անկյունն է նորմալի և հատվածի միջև: Ուշադրություն դարձրեք, որ , , .

Եթե ​​հարթությունը տեղադրենք հարթության մեջ և ընտրենք բևեռային առանցքը, որպեսզի համընկնի առանցքի դրական ուղղության հետ, և առանցքը ընտրենք որպես նորմալ (Նկար 2.9), ապա մենք ստանում ենք այս երկու կոորդինատային համակարգերը միացնող բանաձևեր:

Նկար 2.9. Գնդաձև և ուղղանկյուն դեկարտյան կապը

կոորդինատային համակարգեր

Սկալային մեծություններ,կամ սկալարները ամբողջությամբ բնութագրվում են իրենց թվային արժեքով ընտրված միավորների համակարգում: Վեկտորային մեծություններ կամ վեկտորները, բացի թվային արժեքից, ունեն նաև ուղղություն. Օրինակ, եթե ասենք, որ քամին փչում է 10 մ/վ արագությամբ, ապա կներկայացնենք քամու արագության սկալյար արժեքը, բայց եթե ասենք, որ հարավ-արևմտյան քամին փչում է 10 մ/վ արագությամբ, ապա այս դեպքում քամու արագությունն արդեն վեկտոր կլինի։

Վեկտորկոչվում է որոշակի երկարություն ունեցող ուղղորդված հատված, այսինքն. որոշակի երկարության հատված, որում սահմանափակող կետերից մեկը վերցվում է որպես սկիզբ, իսկ երկրորդը` վերջ: Մենք կնշանակենք վեկտորը կամ կամ (Նկար 2.10):

Վեկտորի երկարությունը նշվում է նշանով կամ և կոչվում է վեկտորի մոդուլ։ Այն վեկտորը, որի երկարությունը 1 է, կոչվում է միայնակ . Վեկտորը կոչվում է զրո , եթե դրա սկիզբն ու վերջը համընկնում են, և նշվում է θ կամ . Զրո վեկտորը չունի կոնկրետ ուղղություն և ունի զրոյի հավասար երկարություն։ Վեկտորները և գտնվում են նույն կամ զուգահեռ ուղիղների վրա կոչվում են համագիծ . Երկու վեկտորները կոչվում են հավասար , եթե դրանք համագիծ են, ունեն նույն երկարությունը և նույն ուղղությունը։ Բոլոր զրոյական վեկտորները համարվում են հավասար:

Երկու համագիծ վեկտոր, տարբերվում է զրոյից, ունենալով հավասար մոդուլներ, բայց հակառակ ուղղությամբ կոչվում են հակառակը . Հակառակ վեկտորը նշանակվում է , հակառակ վեկտորի համար:

Համարին գծային գործողություններ վեկտորների վրա ներառում են գումարման, վեկտորների հանման և վեկտորի բազմապատկման գործողությունները թվով, այսինքն. գործողություններ, որոնց արդյունքը վեկտոր է:

Սահմանենք վեկտորների վրա նշված գործողությունները: Թող երկու վեկտոր և տրվի: Վերցնենք կամայական O կետ և կառուցենք վեկտոր և գծենք վեկտորը A կետից: Այնուհետև կոչվում է վեկտորի առաջին անդամի սկիզբը երկրորդի վերջի հետ կապող վեկտորը գումարը այս վեկտորները նշանակվում են . Վեկտորների գումարը գտնելու դիտարկված կանոնը կոչվում է եռանկյունու կանոններ (Նկար 2.11):

Վեկտորների նույն գումարը կարելի է ստանալ այլ կերպ (Նկար 2.12): Եկեք գծենք վեկտորը և վեկտորը կետից: Այս վեկտորների վրա, ինչպես կողմերի վրա, կառուցենք զուգահեռագիծ: Վեկտորը, որը գագաթից գծված զուգահեռագծի անկյունագիծն է, կլինի գումարը։ Գումարը գտնելու այս կանոնը կոչվում է զուգահեռագծի կանոններ .

Ցանկացած վերջավոր թվով վեկտորների գումարը կարելի է ստանալ կոտրված գծի կանոնի միջոցով (Նկար 2.13): Կամայական կետից մենք գծում ենք վեկտոր, այնուհետև գծագրում ենք վեկտոր և այլն։ Առաջինի սկիզբը վերջինի վերջը կապող վեկտորը գումարն է

տվյալների վեկտորները, այսինքն. . Ակնհայտ է, որ եթե վեկտորի վերջին անդամի վերջը համընկնում է առաջինի սկզբի հետ, ապա վեկտորների գումարը հավասար է զրոյական վեկտորի:

Տարբերությամբ երկու վեկտոր և կոչվում է այնպիսի վեկտոր, որի գումարը հանված վեկտորի հետ տալիս է վեկտորը: Այստեղից Տարբերության վեկտոր կառուցելու կանոն(Նկար 2.14): Այն կետից մենք գծագրում ենք վեկտորը և վեկտորը: Տարբերությունն այն վեկտորն է, որը կապում է մինուենդ վեկտորի ծայրերը և ներքևի վեկտորը և ուղղորդվում ենթակետից դեպի մինուենդ վեկտոր:

Վեկտորի արտադրանքքանի որ իրական թիվը λ վեկտորն է, որը համագիծ է վեկտորին, ունի երկարություն և նույն ուղղությունը, ինչ վեկտորը, եթե , և հակառակ ուղղությունը վեկտորին, եթե .

Մտած է գծային գործողություններ ավելի վեկտորները ունեն հատկությունները :

10 . Հավելման փոխադարձություն.

20 . Ավելացման ասոցիատիվություն.

երեսուն. Չեզոք տարրի առկայությունը հավելումով.

4 0 . Հակառակ տարրի առկայությունը հավելումով.

50 . Վեկտորների գումարման համեմատ թվով բազմապատկման բաշխվածությունը.

6 0 . Վեկտորը երկու թվերի գումարով բազմապատկելու բաշխվածությունը.

7 0 . Ասոցիատիվ հատկություն՝ կապված վեկտորի բազմապատկման հետ թվերի արտադրյալով.

Թող տրվի վեկտորների համակարգ.

Այն արտահայտությունը, որտեղ λ i (i = 1,2,…, n) որոշ թվեր են, կոչվում է գծային համադրություն վեկտորների համակարգեր (2.1). Վեկտորների համակարգը (2.1) կոչվում է գծային կախված , եթե դրանց գծային համակցությունը հավասար է զրոյի, պայմանով, որ λ 1, λ 2, ..., λ n բոլոր թվերը հավասար չեն զրոյի։ Վեկտորների համակարգը (2.1) կոչվում է գծային անկախ , եթե նրանց գծային համակցությունը հավասար է զրոյի միայն այն դեպքում, եթե բոլոր թվերը λ i = 0 (). Մենք կարող ենք տալ վեկտորների գծային կախվածության մեկ այլ սահմանում. Վեկտորների համակարգը (2.1) կոչվում է գծային կախված , եթե այս համակարգի որևէ վեկտոր գծայինորեն արտահայտված է մյուսներով, հակառակ դեպքում՝ վեկտորների համակարգը (2.1) գծային անկախ .

Հարթության մեջ ընկած վեկտորների համար ճշմարիտ են հետևյալ պնդումները.

10 . Հարթության վրա գտնվող երեք վեկտորները գծային կախված են:

20 . Եթե ​​այս վեկտորների թիվը հարթության վրա երեքից ավելի է, ապա դրանք նույնպես գծային կախվածություն ունեն։

երեսուն. Որպեսզի հարթության վրա երկու վեկտորները գծային անկախ լինեն, անհրաժեշտ է և բավարար, որ դրանք լինեն ոչ գծային:

Այսպիսով, առավելագույն թիվը գծային է անկախ վեկտորներինքնաթիռում այն ​​հավասար է երկուսի։

Վեկտորները կոչվում են համակողմանի , եթե նրանք գտնվում են նույն հարթության վրա կամ զուգահեռ են նույն հարթությանը։ Հետևյալ պնդումները ճշմարիտ են տիեզերական վեկտորների համար.

10 . Տարածության յուրաքանչյուր չորս վեկտորը գծային կախված է:

20 . Եթե ​​տարածության մեջ այդ վեկտորների թիվը չորսից ավելի է, ապա դրանք նույնպես գծային կախվածություն ունեն։

երեսուն. Որպեսզի երեք վեկտորները լինեն գծային անկախ, անհրաժեշտ է և բավարար, որ դրանք լինեն ոչ համահավասար։

Այսպիսով, տարածության մեջ գծային անկախ վեկտորների առավելագույն թիվը երեքն է։

Գծային անկախ վեկտորների ցանկացած առավելագույն ենթահամակարգ, որի միջոցով արտահայտվում է այս համակարգի ցանկացած վեկտոր, կոչվում է. հիմք քննարկվողը վեկտորային համակարգեր . Հեշտ է եզրակացնել, որ հարթության վրա հիմքը կազմված է երկու ոչ համակողմանի վեկտորներից, իսկ հիմքը տարածության մեջ՝ երեք ոչ համահավասար վեկտորներից։ Հիմքի վեկտորների թիվը կոչվում է աստիճան վեկտորային համակարգեր. Վեկտորի ընդլայնման գործակիցները բազային վեկտորների կոչվում են վեկտորի կոորդինատները այս հիմքում։

Թող վեկտորները հիմք կազմեն և թող , ապա λ 1, λ 2, λ 3 թվերը հիմքում ընկած վեկտորի կոորդինատներն են Այս դեպքում կարելի է ցույց տալ, որ հիմքում վեկտորի տարրալուծումը եզակի է . Հիմքի հիմնական իմաստն այն է, որ վեկտորների վրա գծային գործողությունները դառնում են սովորական գծային գործողություններ թվերի վրա՝ այդ վեկտորների կոորդինատները: Օգտագործելով վեկտորների վրա գծային գործողությունների հատկությունները, կարող ենք ապացուցել հետևյալ թեորեմը.

Թեորեմ. Երբ գումարվում են երկու վեկտորներ, ավելացվում են դրանց համապատասխան կոորդինատները: Երբ վեկտորը բազմապատկվում է թվով, նրա բոլոր կոորդինատները բազմապատկվում են այդ թվով:

Այսպիսով, եթե և , ապա , որտեղ և որտեղ , λ-ն որոշակի թիվ է:

Որպես կանոն, հարթության բոլոր վեկտորների բազմությունը՝ կրճատված մինչև ընդհանուր սկզբնաղբյուր, ներմուծված գծային գործողություններով, նշվում է V 2-ով, իսկ տարածության բոլոր վեկտորների բազմությունը՝ կրճատված մինչև ընդհանուր սկզբնաղբյուր, նշվում է V 3-ով: V 2 և V 3 բազմությունները կոչվում են երկրաչափական վեկտորների տարածություններ.

Անկյուն վեկտորների միջևև կոչվում է ամենափոքր անկյունը (), որով վեկտորներից մեկը պետք է պտտվի մինչև այն համընկնի երկրորդի հետ՝ այս վեկտորները ընդհանուր սկզբնավորման բերելուց հետո։

Կետային արտադրանքերկու վեկտորը մի թիվ է, որը հավասար է այս վեկտորների մոդուլների և նրանց միջև անկյան կոսինուսի արտադրյալին: Վեկտորների սկալյար արտադրյալը և նշանակվում է կամ

Եթե ​​վեկտորների միջև անկյունը հավասար է , ապա

Երկրաչափական տեսանկյունից սկալյար արտադրանքվեկտորները հավասար են մի վեկտորի մոդուլի և մեկ այլ վեկտորի դրա վրա պրոյեկցիայի արտադրյալին: Հավասարությունից (2.2) հետևում է, որ

Այստեղից Երկու վեկտորների ուղղանկյունության պայման. երկու վեկտորԵվ ուղղանկյուն են, եթե և միայն այն դեպքում, եթե դրանց սկալյար արտադրյալը հավասար է զրոյի, այսինքն. .

Վեկտորների կետային արտադրյալը գծային գործողություն չէ, քանի որ դրա արդյունքը թիվ է, ոչ թե վեկտոր:

Սկալյար արտադրանքի հատկությունները.

1º. - փոխադարձություն.

2º. - բաշխվածություն.

3º. - ասոցիատիվությունը թվային գործոնի նկատմամբ:

4º. - սկալյար քառակուսու հատկություն:

4º սեփականությունից հետևում է սահմանմանը վեկտորի երկարությունը :

Թող հիմք տրվի V 3 տարածության մեջ, որտեղ վեկտորները միավոր վեկտորներ են (դրանք կոչվում են միավոր վեկտորներ), որոնցից յուրաքանչյուրի ուղղությունը համընկնում է դրական ուղղության հետ։ կոորդինատային առանցքներ Ox, Oy, Oz ուղղանկյուն դեկարտյան կոորդինատային համակարգ:

Եկեք ընդլայնենք V 3 տիեզերական վեկտորը ըստ այս հիմքի (Նկար 2.15).

Վեկտորները կոչվում են վեկտորային բաղադրիչներ կոորդինատային առանցքների երկայնքով կամ բաղադրիչներ, թվեր a x, a y, a z– վեկտորի ուղղանկյուն դեկարտյան կոորդինատները Ա. Վեկտորի ուղղությունը որոշվում է նրա կողմից կոորդինատային գծերով կազմված α, β, γ անկյուններով։ Այս անկյունների կոսինուսը կոչվում է ուղղության վեկտոր: Այնուհետև ուղղության կոսինուսները որոշվում են բանաձևերով.

Հեշտ է դա ցույց տալ

Եկեք արտահայտենք սկալյար արտադրյալը կոորդինատային տեսքով:

Թող այդպես լինի; թող դա լինի։ Բազմապատկելով այս վեկտորները որպես բազմանդամներ և հաշվի առնելով, որ մենք ստանում ենք արտահայտություն գտնելու համար կետային արտադրանք կոորդինատային ձևով:

դրանք. երկու վեկտորների սկալյար արտադրյալը հավասար է համանուն կոորդինատների զուգակցված արտադրյալների գումարին։

(2.6) և (2.4)-ից հետևում է գտնելու բանաձևը վեկտորի երկարությունը :

(2.6) և (2.7)-ից ստանում ենք որոշման բանաձև անկյունը վեկտորների միջև:

Վեկտորների եռապատիկը կոչվում է կարգավորված, եթե նշվում է, թե դրանցից որն է համարվում առաջինը, որը երկրորդը և որը երրորդը։

Պատվիրել է երեք վեկտոր կանչեց ճիշտ , եթե դրանք երրորդ վեկտորի վերջից ընդհանուր սկզբնաղբյուրի բերելուց հետո առաջինից երկրորդ վեկտորին ամենակարճ պտույտը կատարվում է ժամացույցի սլաքի ուղղությամբ։ Հակառակ դեպքում վեկտորների եռյակը կոչվում է ձախ . Օրինակ, Նկար 2.15-ում վեկտորները , , կազմում են վեկտորների աջ եռյակը, իսկ վեկտորները , , վեկտորների ձախ եռյակը:

Նմանապես ներկայացվում է եռաչափ տարածության մեջ աջ և ձախ կոորդինատային համակարգերի հայեցակարգը։

Վեկտորային արվեստի գործերվեկտոր առ վեկտոր վեկտոր է (այլ նշում), որը.

1) ունի երկարություն, որտեղ է անկյունը վեկտորների և ;

2) ուղղահայաց վեկտորներին և (), այսինքն. ուղղահայաց է այն հարթությանը, որում գտնվում են վեկտորները և ;

Ըստ սահմանման, մենք գտնում ենք կոորդինատային միավորի վեկտորների վեկտորային արտադրյալը, , :

Եթե ​​, , ապա վեկտորի և վեկտորի վեկտորի արտադրյալի կոորդինատները որոշվում են բանաձևով.

Սահմանումից հետևում է երկրաչափական իմաստվեկտորային արտադրանք Վեկտորային մոդուլ մակերեսին հավասարվեկտորների վրա կառուցված զուգահեռագիծ և .

Վեկտորային արտադրանքի հատկությունները.

4 0 . , եթե վեկտորները և են համագիծ, կամ այդ վեկտորներից մեկը զրո է:

Օրինակ 3.Զուգահեռագիծը կառուցված է վեկտորների վրա և , որտեղ , , . Հաշվեք այս զուգահեռագծի անկյունագծերի երկարությունը, անկյունագծերի և զուգահեռագծի մակերեսի միջև ընկած անկյունը:

Լուծում.Վեկտորների կառուցումը և ցույց է տրված Նկար 2.16-ում, այս վեկտորների վրա զուգահեռագծի կառուցումը ներկայացված է Նկար 2.17-ում:

Եկեք կատարենք այս խնդրի վերլուծական լուծումը։ Կառուցված զուգահեռագծի անկյունագծերը սահմանող վեկտորները արտահայտենք վեկտորների և , այնուհետև և . Մենք գտնում ենք,. Այնուհետև մենք գտնում ենք զուգահեռագծի անկյունագծերի երկարությունները՝ որպես կառուցված վեկտորների երկարություններ

Զուգահեռագծի անկյունագծերի միջև անկյունը նշանակվում է . Այնուհետև վեկտորների սկալյար արտադրյալի բանաձևից ունենք.

Հետևաբար, .

Օգտագործելով վեկտորի արտադրանքի հատկությունները, մենք հաշվարկում ենք զուգահեռագծի տարածքը.

Թող տրվեն երեք վեկտորներ և ,: Եկեք պատկերացնենք, որ վեկտորը բազմապատկվում է վեկտորականորեն, իսկ վեկտորը և ստացված վեկտորը սկալյար կերպով բազմապատկվում են վեկտորով, դրանով իսկ որոշելով թիվը: Այն կոչվում է վեկտոր-սկալար կամ խառը աշխատանք երեք վեկտոր, և. Նշվում է կամ.

Եկեք պարզենք խառը արտադրանքի երկրաչափական նշանակությունը (Նկար 2.18): Թող , , չլինի համահունչ: Եկեք այս վեկտորների վրա կառուցենք զուգահեռականություն, ինչպես եզրերի վրա: Խաչաձև արտադրյալը վեկտոր է, որի մոդուլը հավասար է զուգահեռագծի մակերեսին (զուգահեռագծի հիմքը), որը կառուցված է վեկտորների վրա և ուղղահայաց է զուգահեռագծի հարթությանը:

Կետային արտադրյալ (հավասար է վեկտորի մոդուլի և պրոեկցիայի արտադրյալին): Կառուցված զուգահեռականի բարձրությունը կազմում է բացարձակ արժեքայս կանխատեսումը. Հետևաբար, երեք վեկտորների խառը արտադրյալի բացարձակ արժեքը հավասար է վեկտորների վրա կառուցված զուգահեռականի ծավալին, և, այսինքն. .

Այստեղից էլ ծավալը եռանկյուն բուրգ, կառուցված վեկտորների վրա և , հաշվարկվում է բանաձևով .

Նկատենք ևս մի քանիսը խառը արտադրանքի հատկությունները վեկտորներ.

1 օ. Արտադրանքի նշանը դրական է, եթե վեկտորները , , և կազմում են հիմնականի համանուն համակարգ, իսկ հակառակ դեպքում՝ բացասական։

Իսկապես, սկալյար արտադրյալը դրական է, եթե և միջև անկյունը սուր է և բացասական, եթե անկյունը բութ է: Վեկտորների միջև սուր անկյան տակ և գտնվում են մի կողմում զուգահեռի հիմքի համեմատ, և, հետևաբար, վեկտորի վերջից պտույտը տեսանելի կլինի այնպես, ինչպես վեկտորի վերջից: , այսինքն. դրական ուղղությամբ (ժամացույցի սլաքի հակառակ ուղղությամբ):

Բութ անկյան տակ և՛ վեկտորները, և՛ վեկտորները գտնվում են տարբեր կողմերում՝ համեմատած զուգահեռագծի հիմքում ընկած զուգահեռագծի հարթության հետ, և, հետևաբար, վեկտորի վերջից պտույտը դեպի դեպի տեսանելի է բացասական ուղղությամբ ( ժամացույցի սլաքի ուղղությամբ):

2 o Խառը արտադրանքը չի փոխվում, երբ նրա գործոնները վերադասավորվում են շրջանաձև.

3 o Երբ որևէ երկու վեկտոր վերադասավորվում է, խառը արտադրյալը փոխում է միայն նշանը: Օրինակ, , ։ , . - անհայտ համակարգեր.

Համակարգ(3.1) կոչվում է միատարր , եթե բոլոր անդամներն ազատ են : Համակարգ (3.1) կոչվում է տարասեռ , եթե ազատ անդամներից գոնե մեկը։

Համակարգային լուծումկոչվում է թվերի բազմություն, երբ դրանք փոխարինելով համակարգի հավասարումների մեջ՝ համապատասխան անհայտների փոխարեն, համակարգի յուրաքանչյուր հավասարում վերածվում է ինքնության։ Այն համակարգը, որը լուծում չունի, կոչվում է անհամատեղելի, կամ հակասական . Համակարգը, որն ունի առնվազն մեկ լուծում, կոչվում է համատեղ .

Համատեղ համակարգը կոչվում է որոշակի , եթե այն ունի յուրահատուկ լուծում։ Եթե ​​հետևողական համակարգն ունի մեկից ավելի լուծումներ, ապա այն կոչվում է անորոշ . Միատարր համակարգը միշտ հետևողական է, քանի որ ունի, ըստ գոնե, զրոյական լուծում. Անհայտների արտահայտությունը, որից կարելի է ստանալ համակարգի որևէ կոնկրետ լուծում, կոչվում է ընդհանուր որոշում , և համակարգի ցանկացած կոնկրետ լուծում իրն է մասնավոր լուծում . Նույն անհայտներով երկու համակարգ համարժեք (համարժեք ), եթե դրանցից մեկի լուծումը մյուսի լուծումն է, կամ երկու համակարգերն էլ անհամապատասխան են:

Դիտարկենք համակարգերի լուծման մեթոդները գծային հավասարումներ.

Գծային հավասարումների համակարգերի լուծման հիմնական մեթոդներից է Գաուսի մեթոդ, կամ հաջորդական մեթոդ անհայտների բացառումը. Այս մեթոդի էությունը գծային հավասարումների համակարգը աստիճանաբար իջեցնելն է: Այս դեպքում պետք է կատարվեն հետևյալ հավասարումները. տարրական փոխակերպումներ :

1. Համակարգի հավասարումների վերադասավորում.

2. Մեկ հավասարման ավելացում:

3. Հավասարման երկու կողմերը զրոյից տարբեր թվով բազմապատկելը:

Արդյունքում համակարգը կունենա հետևյալ ձևը.

Շարունակելով այս գործընթացը՝ մենք վերացնում ենք անհայտը բոլոր հավասարումներից՝ սկսած երրորդից: Դա անելու համար երկրորդ հավասարումը բազմապատկեք թվերով և ավելացրեք համակարգի 3-րդ, ..., -րդ հավասարումը: Նմանապես կատարվում են Գաուսի մեթոդի հետևյալ քայլերը. Եթե ​​փոխակերպումների արդյունքում ստանում ենք նույնական հավասարում, ապա այն ջնջում ենք համակարգից։ Եթե ​​Գաուսի մեթոդի ինչ-որ քայլում ստացվում է ձևի հավասարում.

ապա դիտարկվող համակարգը անհամապատասխան է, և դրա հետագա լուծումը դադարում է։ Եթե ​​կատարելիս (3.2) ձևի հավասարումը չի հանդիպում տարրական փոխակերպումներ, ապա ոչ ավելի, քան - քայլերով համակարգը (3.1) կվերածվի փուլային ձևի.

Համակարգի որոշակի լուծում ստանալու համար անհրաժեշտ կլինի հատուկ արժեքներ վերագրել անվճար փոփոխականներին (3.4):

Նշենք, որ քանի որ Գաուսի մեթոդով բոլոր փոխակերպումները կատարվում են ժամը գործակիցների վրա անհայտ հավասարումներև ազատ տերմիններ, ապա գործնականում այս մեթոդը սովորաբար կիրառվում է անհայտների գործակիցներից և ազատ տերմինների սյունակից կազմված մատրիցին: Այս մատրիցը կոչվում է ընդլայնված: Օգտագործելով տարրական փոխակերպումներ, այս մատրիցը վերածվում է փուլային ձևի: Այնուհետև, օգտագործելով ստացված մատրիցը, համակարգը վերակառուցվում է և բոլոր նախորդ պատճառաբանությունները կիրառվում են դրա վրա:

Օրինակ 1.Լուծել համակարգը.

Լուծում.Մենք ստեղծում ենք ընդլայնված մատրիցա և նվազեցնում ենք այն աստիճանական ձևի.

~ *) ~ **) ~ ***)

*) - երկրորդ տողը բազմապատկվեց և երրորդ տողը հատվեց:

Հեռավորությունը կետից կետտվյալ սանդղակի վրա այս կետերը միացնող հատվածի երկարությունն է: Այսպիսով, երբ մենք խոսում ենքհեռավորությունը չափելու մասին, դուք պետք է իմանաք այն սանդղակը (երկարության միավորը), որով կիրականացվեն չափումները: Հետևաբար, կետից կետ հեռավորությունը գտնելու խնդիրը սովորաբար դիտարկվում է կամ կոորդինատային գծի վրա կամ ուղղանկյուն դեկարտյան կոորդինատային համակարգում հարթության վրա կամ եռաչափ տարածության մեջ։ Այլ կերպ ասած, ամենից հաճախ պետք է հաշվարկել կետերի միջև հեռավորությունը՝ օգտագործելով դրանց կոորդինատները:

Այս հոդվածում մենք նախ կհիշենք, թե ինչպես է որոշվում կոորդինատային գծի կետից կետ հեռավորությունը: Այնուհետև մենք ստանում ենք հարթության կամ տարածության երկու կետերի միջև հեռավորությունը ըստ տրված կոորդինատների հաշվելու բանաձևերը: Եզրափակելով, մենք մանրամասնորեն կքննարկենք բնորոշ օրինակների և խնդիրների լուծումները:

Էջի նավարկություն.

Կոորդինատային գծի երկու կետերի միջև հեռավորությունը:

Եկեք նախ սահմանենք նշումը. A կետից B կետ հեռավորությունը կնշենք որպես .

Այստեղից կարելի է եզրակացնել, որ հեռավորությունը կոորդինատով A կետից մինչև կոորդինատով B կետը հավասար է կոորդինատների տարբերության մոդուլին, այն է, կոորդինատային գծի կետերի ցանկացած տեղակայման համար:

Հեռավորությունը հարթության վրա կետից կետ, բանաձև.

Մենք ստանում ենք կետերի միջև հեռավորությունը հաշվարկելու բանաձև և տրված հարթության վրա ուղղանկյուն դեկարտյան կոորդինատային համակարգում:

Կախված A և B կետերի գտնվելու վայրից, հնարավոր են հետևյալ տարբերակները.

Եթե ​​A և B կետերը համընկնում են, ապա նրանց միջև հեռավորությունը զրո է:

Եթե ​​A և B կետերը գտնվում են աբսցիսայի առանցքին ուղղահայաց ուղիղ գծի վրա, ապա կետերը համընկնում են, և հեռավորությունը հավասար է հեռավորությանը: Նախորդ պարբերությունում պարզեցինք, որ կոորդինատային գծի երկու կետերի միջև հեռավորությունը հավասար է դրանց կոորդինատների տարբերության մոդուլին, հետևաբար. . Հետևաբար, .

Նմանապես, եթե A և B կետերը գտնվում են օրդինատների առանցքին ուղղահայաց ուղիղ գծի վրա, ապա A կետից մինչև B կետ հեռավորությունը հայտնաբերվում է որպես .

Այս դեպքում ABC եռանկյունը կառուցվածքով ուղղանկյուն է, և Եվ . Ըստ Պյութագորասի թեորեմմենք կարող ենք գրել հավասարությունը, որտեղից .

Եկեք ամփոփենք ստացված բոլոր արդյունքները. հարթության կետից մինչև հարթության կետ հեռավորությունը հայտնաբերվում է կետերի կոորդինատների միջոցով՝ օգտագործելով բանաձևը .

Կետերի միջև հեռավորությունը գտնելու արդյունքում ստացված բանաձևը կարող է օգտագործվել, երբ A և B կետերը համընկնում են կամ գտնվում են կոորդինատային առանցքներից մեկին ուղղահայաց ուղիղ գծի վրա: Իսկապես, եթե A-ն և B-ն համընկնում են, ապա . Եթե ​​A և B կետերը ընկած են Ox առանցքին ուղղահայաց ուղիղ գծի վրա, ապա. Եթե ​​A և B-ն ընկած են Oy առանցքին ուղղահայաց ուղիղ գծի վրա, ապա .

Տարածության կետերի միջև հեռավորությունը, բանաձևը:

Եկեք տիեզերքում ներկայացնենք Oxyz ուղղանկյուն կոորդինատային համակարգը: Ստացնենք կետից հեռավորությունը գտնելու բանաձևը դեպի կետ .

Ընդհանուր առմամբ, A և B կետերը չեն գտնվում կոորդինատային հարթություններից մեկին զուգահեռ հարթությունում: Եկեք գծենք A և B կետերի հարթությունները, որոնք ուղղահայաց են Ox, Oy և Oz կոորդինատային առանցքներին: Այս հարթությունների հատման կետերը կոորդինատային առանցքների հետ մեզ կտան A և B կետերի կանխատեսումներ այս առանցքների վրա: Մենք նշում ենք կանխատեսումները .

A և B կետերի միջև անհրաժեշտ հեռավորությունը անկյունագիծ է ուղղանկյուն զուգահեռականցույց է տրված նկարում: Ըստ կառուցման՝ այս զուգահեռականի չափերը հավասար են Եվ . Երկրաչափության ընթացքում ավագ դպրոցԱպացուցված է, որ խորանարդի անկյունագծի քառակուսին գումարին հավասարդրա երեք չափերի քառակուսիները, հետևաբար, . Այս հոդվածի առաջին բաժնի տեղեկատվության հիման վրա մենք կարող ենք գրել հետևյալ հավասարումները, հետևաբար.

որտեղի՞ց ենք վերցնում Տարածության կետերի միջև հեռավորությունը գտնելու բանաձևը .

Այս բանաձևը վավեր է նաև, եթե A և B կետերը

• համապատասխանեցնել;
• պատկանում է կոորդինատային առանցքներից մեկին կամ կոորդինատային առանցքներից մեկին զուգահեռ գծին.
• պատկանում են կոորդինատային հարթություններից մեկին կամ կոորդինատային հարթություններից մեկին զուգահեռ հարթության:

Գտնելով կետից կետ հեռավորությունը, օրինակներ և լուծումներ:

Այսպիսով, մենք ստացել ենք կոորդինատային գծի, հարթության և եռաչափ տարածության երկու կետերի միջև հեռավորությունը գտնելու բանաձևեր: Ժամանակն է դիտարկել բնորոշ օրինակների լուծումները:

Խնդիրների թիվը, որոնցում վերջին քայլը երկու կետերի միջև հեռավորությունն ըստ դրանց կոորդինատների գտնելն է, իսկապես հսկայական է: Նման օրինակների ամբողջական վերանայումը դուրս է այս հոդվածի շրջանակներից: Այստեղ մենք կսահմանափակվենք օրինակներով, որոնցում հայտնի են երկու կետերի կոորդինատները և անհրաժեշտ է հաշվարկել դրանց միջև եղած հեռավորությունը։