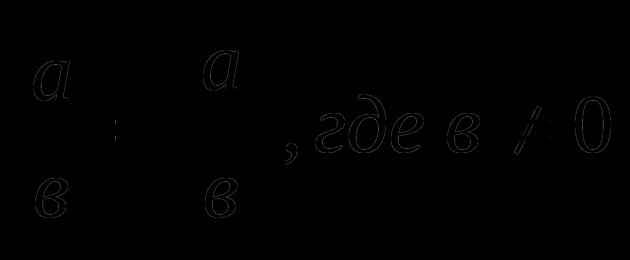Հրահանգներ
Եթե մոդուլը ներկայացված է որպես շարունակական ֆունկցիա, ապա դրա արգումենտի արժեքը կարող է լինել կամ դրական կամ բացասական՝ |x| = x, x ≥ 0; |x| = - x, x
Մոդուլը զրո է, իսկ ցանկացած դրական թվի մոդուլը . Եթե փաստարկը բացասական է, ապա փակագծերը բացելուց հետո նրա նշանը մինուսից փոխվում է գումարածի։ Ելնելով դրանից՝ հետևություն է արվում, որ հակադիրների մոդուլները հավասար են՝ |-x| = |x| = x.
Կոմպլեքս թվի մոդուլը գտնում ենք բանաձևով՝ |a| = √b ² + c ², և |a + b| ≤ |ա| + |բ|. Եթե արգումենտը որպես բազմապատկիչ պարունակում է դրական թիվ, ապա այն կարելի է հանել փակագծի նշանից, օրինակ՝ |4*b| = 4*|բ|.
Եթե արգումենտը ներկայացվում է կոմպլեքս թվով, ապա հաշվարկների հարմարության համար թույլատրվում է ուղղանկյուն փակագծերում փակցված արտահայտության տերմինների հերթականությունը՝ |2-3| = |3-2| = 3-2 = 1, քանի որ (2-3) զրոյից փոքր է:
Հզորության բարձրացված արգումենտը միաժամանակ գտնվում է նույն կարգի արմատի նշանի տակ. այն լուծվում է օգտագործելով՝ √a² = |a| = ± ա.
Եթե դուք ունեք խնդիր, որում նշված չէ մոդուլի փակագծերի ընդլայնման պայմանը, ապա դրանցից ազատվելու կարիք չկա, սա կլինի վերջնական արդյունքը: Իսկ եթե դրանք բացելու կարիք ունեք, ապա պետք է նշեք ± նշանը։ Օրինակ, դուք պետք է գտնեք √(2 * (4-b))² արտահայտության արժեքը: Նրա լուծումն ունի հետևյալ տեսքը՝ √(2 * (4-b))² = |2 * (4-b)| = 2 * |4-բ|. Քանի որ 4-բ արտահայտության նշանն անհայտ է, այն պետք է թողնել փակագծերում։ Եթե ավելացնեք լրացուցիչ պայման, օրինակ, |4-բ| >
Զրոյի մոդուլը հավասար է զրոյի, իսկ ցանկացած դրական թվի մոդուլն ինքն է։ Եթե փաստարկը բացասական է, ապա փակագծերը բացելուց հետո նրա նշանը մինուսից փոխվում է գումարածի։ Սրանից ելնելով եզրակացություն է արվում, որ հակադիր թվերի մոդուլները հավասար են՝ |-x| = |x| = x.
Կոմպլեքս թվի մոդուլը գտնում ենք բանաձևով՝ |a| = √b ² + c ², և |a + b| ≤ |ա| + |բ|. Եթե արգումենտը որպես գործոն պարունակում է դրական ամբողջ թիվ, ապա այն կարելի է հանել փակագծի նշանից, օրինակ՝ |4*b| = 4*|բ|.
Մոդուլը չի կարող բացասական լինել, ուստի ցանկացած բացասական թիվ վերածվում է դրականի՝ |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Եթե փաստարկը ներկայացվում է կոմպլեքս թվի տեսքով, ապա հաշվարկների հարմարության համար թույլատրվում է փոխել ուղղանկյուն փակագծերում փակցված արտահայտության տերմինների հերթականությունը՝ |2-3| = |3-2| = 3-2 = 1, քանի որ (2-3) զրոյից փոքր է:
Եթե դուք ունեք խնդիր, որում նշված չէ մոդուլի փակագծերի ընդլայնման պայմանը, ապա դրանցից ազատվելու կարիք չկա, սա կլինի վերջնական արդյունքը: Իսկ եթե դրանք բացելու կարիք ունեք, ապա պետք է նշեք ± նշանը։ Օրինակ, դուք պետք է գտնեք √(2 * (4-b))² արտահայտության արժեքը: Նրա լուծումն ունի հետևյալ տեսքը՝ √(2 * (4-b))² = |2 * (4-b)| = 2 * |4-բ|. Քանի որ 4-բ արտահայտության նշանն անհայտ է, այն պետք է թողնել փակագծերում։ Եթե ավելացնեք լրացուցիչ պայման, օրինակ, |4-բ| > 0, ապա արդյունքը կլինի 2 * |4-b| = 2 * (4 - բ): Անհայտ տարրը կարող է սահմանվել նաև որոշակի թվով, որը պետք է հաշվի առնել, քանի որ դա կազդի արտահայտության նշանի վրա։
MBOU միջնակարգ դպրոց թիվ 17, Իվանովո
« Հավասարումներ մոդուլով»
Մեթոդական մշակում
Կազմվել է
մաթեմատիկայի ուսուցիչ
Լեբեդևա Ն.Վ.20010 թ
Բացատրական նշում
Գլուխ 1. Ներածություն
Բաժին 2. Հիմնական հատկություններ Բաժին 3. Թվի մոդուլ հասկացության երկրաչափական մեկնաբանությունը Բաժին 4. y = |x| ֆունկցիայի գրաֆիկը Բաժին 5. ԿոնվենցիաներԳլուխ 2. Մոդուլ պարունակող հավասարումների լուծում
Բաժին 1. Ձևի հավասարումներ |F(x)| = m (ամենապարզ) Բաժին 2. F(|x|) = m ձևի հավասարումներ Բաժին 3. Ձևի հավասարումներ |F(x)| = G(x) Բաժին 4. Ձևի հավասարումներ |F(x)| = ± F(x) (ամենագեղեցիկ) Բաժին 5. |F(x)| ձևի հավասարումներ = |G(x)| Բաժին 6. Ոչ ստանդարտ հավասարումների լուծման օրինակներ Բաժին 7. Ձևի հավասարումներ |F(x)| + |G(x)| = 0 Բաժին 8. Ձևի հավասարումներ |a 1 x ± b 1 | ± |a 2 x ± 2-ում | ± …|a n x ± n-ում | = մ Բաժին 9. Մի քանի մոդուլներ պարունակող հավասարումներԳլուխ 3. Մոդուլով տարբեր հավասարումների լուծման օրինակներ:
Բաժին 1. Եռանկյունաչափական հավասարումներ Բաժին 2. Էքսպոնենցիալ հավասարումներ Բաժին 3. Լոգարիթմական հավասարումներ Բաժին 4. Իռացիոնալ հավասարումներ Բաժին 5. Ընդլայնված առաջադրանքներ Վարժությունների պատասխանները ՄատենագիտությունԲացատրական նշում.
Իրական թվի բացարձակ արժեքի (մոդուլի) հասկացությունը նրա էական բնութագրիչներից է։ Այս հայեցակարգը տարածված է ֆիզիկական, մաթեմատիկական և տեխնիկական գիտությունների տարբեր բաժիններում։ Ռուսաստանի Դաշնության ՊՆ ծրագրին համապատասխան միջնակարգ դպրոցներում մաթեմատիկայի դասընթացների դասավանդման պրակտիկայում բազմիցս հանդիպում է «թվի բացարձակ արժեք» հասկացությունը. 6-րդ դասարանում մոդուլի սահմանումը և ներկայացվում է դրա երկրաչափական նշանակությունը. 8-րդ դասարանում ձևավորվում է բացարձակ սխալ հասկացություն, դիտարկվում է մոդուլ պարունակող ամենապարզ հավասարումների և անհավասարությունների լուծումը, ուսումնասիրվում են թվաբանական քառակուսի արմատի հատկությունները. 11-րդ դասարանում հասկացությունը գտնվում է «Արմատ n-րդ աստիճան»:Դասավանդման փորձը ցույց է տալիս, որ ուսանողները հաճախ դժվարությունների են հանդիպում այս նյութի իմացություն պահանջող առաջադրանքները լուծելիս և հաճախ բաց են թողնում դրանք՝ չսկսելով դրանք ավարտին հասցնել: Նմանատիպ առաջադրանքներ են ներառված նաև 9-րդ և 11-րդ դասարանների քննական առաջադրանքների տեքստերում։ Բացի այդ, այն պահանջները, որոնք բուհերը դնում են դպրոցի շրջանավարտների նկատմամբ, տարբեր են, այն է՝ ավելի բարձր մակարդակով, քան դպրոցական ուսումնական պլանի պահանջները: Ժամանակակից հասարակության կյանքի համար շատ կարևոր է մտածողության մաթեմատիկական ոճի ձևավորումը, որը դրսևորվում է որոշակի մտավոր հմտություններով: Մոդուլների հետ խնդիրների լուծման գործընթացում պահանջվում է այնպիսի մեթոդներ օգտագործելու ունակություն, ինչպիսիք են ընդհանրացումը և ճշգրտումը, վերլուծությունը, դասակարգումը և համակարգումը և անալոգիան: Նման առաջադրանքների լուծումը թույլ է տալիս ստուգել ձեր գիտելիքները դպրոցական դասընթացի հիմնական բաժինների, տրամաբանական մտածողության մակարդակի և նախնական հետազոտական հմտությունների վերաբերյալ: Այս աշխատանքը նվիրված է բաժիններից մեկին՝ մոդուլ պարունակող հավասարումների լուծում։ Այն բաղկացած է երեք գլուխներից. Առաջին գլուխը ներկայացնում է հիմնական հասկացությունները և ամենակարևոր տեսական նկատառումները: Երկրորդ գլխում առաջարկվում են մոդուլ պարունակող ինը հիմնական տեսակի հավասարումներ, քննարկվում են դրանց լուծման մեթոդները և ուսումնասիրվում են բարդության տարբեր մակարդակների օրինակներ: Երրորդ գլխում ներկայացված են ավելի բարդ և ոչ ստանդարտ հավասարումներ (եռանկյունաչափական, էքսպոնենցիալ, լոգարիթմական և իռացիոնալ): Հավասարումների յուրաքանչյուր տեսակի համար կան ինքնուրույն լուծելու վարժություններ (պատասխանները և հրահանգները կցվում են): Այս աշխատանքի հիմնական նպատակն է ուսուցիչներին մեթոդական աջակցություն ցուցաբերել դասերին նախապատրաստվելու և ընտրովի դասընթացներ կազմակերպելու հարցում: Նյութը կարող է օգտագործվել նաև որպես ուսումնական նյութ ավագ դպրոցի աշակերտների համար: Աշխատանքում առաջարկվող առաջադրանքները հետաքրքիր են և միշտ չէ, որ հեշտ լուծելի են, ինչը հնարավորություն է տալիս ուսանողների կրթական մոտիվացիան ավելի գիտակցված դարձնել, ստուգել նրանց կարողությունները և բարձրացնել դպրոցների շրջանավարտների պատրաստության մակարդակը բուհ ընդունվելու համար: Առաջարկվող վարժությունների տարբերակված ընտրությունը ներառում է նյութի յուրացման վերարտադրողական մակարդակից անցում դեպի ստեղծագործական, ինչպես նաև հնարավորություն սովորեցնելու, թե ինչպես կիրառել ձեր գիտելիքները ոչ ստանդարտ խնդիրներ լուծելիս:Գլուխ 1. Ներածություն.
Բաժին 1. Բացարձակ արժեքի որոշում .
Սահմանում : Իրական թվի բացարձակ արժեքը (մոդուլը): ԱՈչ բացասական թիվը կոչվում է. Ակամ -Ա. Նշում: │ Ա │ Մուտքը հետևյալն է՝ «ա թվի մոդուլ» կամ «ա թվի բացարձակ արժեք».│ ա, եթե a > 0
│a│ = │ 0, եթե a = 0 (1)
│ - և, եթե աՕրինակներ. 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Ընդլայնել արտահայտման մոդուլը.
Բաժին 2. Հիմնական հատկություններ.
Դիտարկենք բացարձակ արժեքի հիմնական հատկությունները. Գույք թիվ 1: Հակառակ թվերն ունեն հավասար մոդուլներ, այսինքն. │а│=│- а│Եկեք ցույց տանք, որ հավասարությունը ճիշտ է։ Գրենք թվի սահմանումը - Ա : │- ա│= (2) Համեմատենք (1) և (2) բազմությունները։ Ակնհայտ է, որ թվերի բացարձակ արժեքների սահմանումները ԱԵվ - Ահամապատասխանեցնել։ Հետևաբար, │а│=│- а│Հետևյալ հատկությունները դիտարկելիս մենք կսահմանափակվենք դրանց ձևակերպմամբ, քանի որ դրանց ապացույցը բերված է Գույք թիվ 2: Վերջավոր թվով իրական թվերի գումարի բացարձակ արժեքը չի գերազանցում տերմինների բացարձակ արժեքների գումարը՝ │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Գույք թիվ 3: Երկու իրական թվերի տարբերության բացարձակ արժեքը չի գերազանցում դրանց բացարձակ արժեքների գումարը՝ │а - в│ ≤│а│+│в│ Գույք թիվ 4: Վերջավոր թվով իրական թվերի արտադրյալի բացարձակ արժեքը հավասար է գործոնների բացարձակ արժեքների արտադրյալին. │а·в│=│а│·│в│ Գույք թիվ 5: Իրական թվերի քանորդի բացարձակ արժեքը հավասար է դրանց բացարձակ արժեքների քանորդին.

Բաժին 3. Թվի մոդուլ հասկացության երկրաչափական մեկնաբանությունը:
Յուրաքանչյուր իրական թիվ կարող է կապված լինել թվային գծի մի կետի հետ, որը կլինի այս իրական թվի երկրաչափական պատկերը: Թվային տողի յուրաքանչյուր կետ համապատասխանում է սկզբնակետից իր հեռավորությանը, այսինքն. հատվածի երկարությունը սկզբից մինչև տվյալ կետ: Այս հեռավորությունը միշտ համարվում է ոչ բացասական արժեք։ Հետեւաբար, համապատասխան հատվածի երկարությունը կլինի տվյալ իրական թվի բացարձակ արժեքի երկրաչափական մեկնաբանությունը
Ներկայացված երկրաչափական նկարազարդումը հստակ հաստատում է թիվ 1 հատկությունը, այսինքն. Հակառակ թվերի մոդուլները հավասար են։ Այստեղից կարելի է հեշտությամբ հասկանալ հավասարության վավերականությունը՝ │х – а│= │а – x│: │х│= m հավասարման լուծումը, որտեղ m ≥ 0, այն է՝ x 1,2 = ± m, նույնպես ավելի ակնհայտ է դառնում: Օրինակներ. 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
 x 1.2 = 2; 4
x 1.2 = 2; 4 Բաժին 4. y = │х│ ֆունկցիայի գրաֆիկ
Այս ֆունկցիայի տիրույթը բոլոր իրական թվերն են։Բաժին 5. Կոնվենցիաներ.
Հետագայում, հավասարումների լուծման օրինակներ դիտարկելիս, կօգտագործվեն հետևյալ կոնվենցիաները. ( - համակարգի նշան [ - ամբողջության նշան Հավասարումների (անհավասարումների) համակարգը լուծելիս հայտնաբերվում է համակարգում ընդգրկված հավասարումների (անհավասարումների) լուծումների հատումը։ Հավասարումների բազմություն (անհավասարումներ) լուծելիս գտնվում է հավասարումների (անհավասարումների) բազմության մեջ ներառված լուծումների միությունը։Գլուխ 2. Մոդուլ պարունակող հավասարումների լուծում:
Այս գլխում մենք կանդրադառնանք մեկ կամ մի քանի մոդուլ պարունակող հավասարումների լուծման հանրահաշվական մեթոդներին:Բաժին 1. │F (x)│= m ձևի հավասարումներ
Այս տեսակի հավասարումը կոչվում է ամենապարզը: Այն լուծում ունի, եթե և միայն, եթե m ≥ 0: Ըստ մոդուլի սահմանման, սկզբնական հավասարումը համարժեք է երկու հավասարումների բազմությանը. │ Ֆ(x)│=մ
 Օրինակներ.
Օրինակներ.
№1. Լուծե՛ք հավասարումը` │7х - 2│= 9


 Պատասխան՝ x 1
= - 1; X 2
= 1
4
/
7
№2
Պատասխան՝ x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1

 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Պատասխան՝ արմատների գումարը 2 է.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Պատասխան՝ արմատների գումարը 2 է.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 նշանակում x 2 = m, m ≥ 0 x = 0 ; ±√5 մ 2 – 5 մ + 4 = 0 մ = 1; 4 – երկու արժեքներն էլ բավարարում են պայմանը m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Պատասխան՝ 7-րդ հավասարման արմատների թիվը։ Զորավարժություններ:
№1. Լուծե՛ք հավասարումը և նշե՛ք արմատների գումարը՝ │х - 5│= 3 №2 . Լուծե՛ք հավասարումը և նշե՛ք ավելի փոքր արմատը՝ │x 2 + x│= 0 №3 . Լուծե՛ք հավասարումը և նշե՛ք ավելի մեծ արմատը՝ │x 2 – 5x + 4│= 4 №4 .Լուծե՛ք հավասարումը և նշե՛ք ամբողջ արմատը՝ │2x 2 – 7x + 6│= 1 №5 .Լուծե՛ք հավասարումը և նշե՛ք արմատների թիվը՝ │x 4 – 13x 2 + 50│= 14.
Բաժին 2. F(│х│) = m ձևի հավասարումներ
Ձախ կողմում ֆունկցիայի փաստարկը գտնվում է մոդուլի նշանի տակ, իսկ աջ կողմը անկախ է փոփոխականից: Դիտարկենք այս տիպի հավասարումների լուծման երկու եղանակ: 1 ճանապարհ:Բացարձակ արժեքի սահմանմամբ սկզբնական հավասարումը համարժեք է երկու համակարգերի համակցությանը։ Որոնցից յուրաքանչյուրում պայման է դրված ենթամոդուլային արտահայտության վրա։ Ֆ(│х│) =մ Քանի որ F(│x│) ֆունկցիան հավասար է սահմանման ողջ տիրույթում, F(x) = m և F(- x) = m հավասարումների արմատները հակադիր թվերի զույգեր են: Ուստի բավական է լուծել համակարգերից մեկը (այսպես օրինակներ դիտարկելիս կտրվի մեկ համակարգի լուծումը)։ Մեթոդ 2:Նոր փոփոխականի ներդրման մեթոդի կիրառում. Այս դեպքում ներմուծվում է │x│= a նշանակումը, որտեղ a ≥ 0: Այս մեթոդը դիզայնով ավելի քիչ ծավալուն է:
Քանի որ F(│x│) ֆունկցիան հավասար է սահմանման ողջ տիրույթում, F(x) = m և F(- x) = m հավասարումների արմատները հակադիր թվերի զույգեր են: Ուստի բավական է լուծել համակարգերից մեկը (այսպես օրինակներ դիտարկելիս կտրվի մեկ համակարգի լուծումը)։ Մեթոդ 2:Նոր փոփոխականի ներդրման մեթոդի կիրառում. Այս դեպքում ներմուծվում է │x│= a նշանակումը, որտեղ a ≥ 0: Այս մեթոդը դիզայնով ավելի քիչ ծավալուն է: Օրինակներ. №1 . Լուծեք հավասարումը. 3x 2 – 4│x│= - 1 Եկեք օգտագործենք նոր փոփոխականի ներդրումը: Նշենք │x│= a, որտեղ a ≥ 0: Ստանում ենք 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 հավասարումը. Վերադառնալ սկզբնական փոփոխականին՝ │ x│=1 և │х│= 1/3: Յուրաքանչյուր հավասարում ունի երկու արմատ: Պատասխան՝ x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Լուծե՛ք հավասարումը. 5x 2 + 3│x│- 1 = 1/2 │x│ + 3x 2
 Եկեք գտնենք բնակչության առաջին համակարգի լուծումը՝ 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Նկատի ունեցեք, որ x 2-ը չի բավարարում. պայմանը x ≥ 0. Լուծում երկրորդ համակարգը կլինի x 1 արժեքին հակառակ թիվը: Պատասխան՝ x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Լուծե՛ք հավասարումը` x 4 – │х│= 0 Նշենք │х│= a, որտեղ a ≥ 0: Ստանում ենք a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 հավասարումը: a 2 = 1 Վերադառնալ սկզբնական փոփոխականին՝ │х│=0 և │х│= 1 x = 0; ± 1 Պատասխան՝ x 1
= 0; X 2
= 1; X 3
= - 1.
Եկեք գտնենք բնակչության առաջին համակարգի լուծումը՝ 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Նկատի ունեցեք, որ x 2-ը չի բավարարում. պայմանը x ≥ 0. Լուծում երկրորդ համակարգը կլինի x 1 արժեքին հակառակ թիվը: Պատասխան՝ x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Լուծե՛ք հավասարումը` x 4 – │х│= 0 Նշենք │х│= a, որտեղ a ≥ 0: Ստանում ենք a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 հավասարումը: a 2 = 1 Վերադառնալ սկզբնական փոփոխականին՝ │х│=0 և │х│= 1 x = 0; ± 1 Պատասխան՝ x 1
= 0; X 2
= 1; X 3
= - 1.
Զորավարժություններ: №6. Լուծեք հավասարումը. 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների քանակը՝ 3x 2 - 7│x│ + 2 = 0 №8 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ամբողջական լուծումներ՝ x 4 + │x│ - 2 = 0
Բաժին 3. │F(x)│ = G(x) ձևի հավասարումներ.
Այս տիպի հավասարման աջ կողմը կախված է փոփոխականից և, հետևաբար, ունի լուծում, եթե և միայն այն դեպքում, եթե աջ կողմը G(x) ≥ 0 ֆունկցիա է: Սկզբնական հավասարումը կարող է լուծվել երկու եղանակով: : 1 ճանապարհ:Ստանդարտ, որը հիմնված է մոդուլի բացահայտման վրա՝ հիմնված դրա սահմանման վրա և բաղկացած է համարժեք անցումից երկու համակարգերի համակցությանը: │ Ֆ(x)│ =Գ(X)
 Այս մեթոդը կարող է ռացիոնալ կերպով օգտագործվել G(x) ֆունկցիայի բարդ արտահայտության դեպքում, իսկ F(x) ֆունկցիայի համար ավելի քիչ բարդ արտահայտության դեպքում, քանի որ ենթադրվում է, որ F(x) ֆունկցիայի անհավասարությունները կլուծվեն: Մեթոդ 2:Բաղկացած է համարժեք համակարգի անցումից, որտեղ պայման է դրվում աջ կողմում: │ Ֆ(x)│=
Գ(x)
Այս մեթոդը կարող է ռացիոնալ կերպով օգտագործվել G(x) ֆունկցիայի բարդ արտահայտության դեպքում, իսկ F(x) ֆունկցիայի համար ավելի քիչ բարդ արտահայտության դեպքում, քանի որ ենթադրվում է, որ F(x) ֆունկցիայի անհավասարությունները կլուծվեն: Մեթոդ 2:Բաղկացած է համարժեք համակարգի անցումից, որտեղ պայման է դրվում աջ կողմում: │ Ֆ(x)│=
Գ(x)

 Այս մեթոդը ավելի հարմար է օգտագործել, եթե G(x) ֆունկցիայի արտահայտությունն ավելի քիչ բարդ է, քան F(x) ֆունկցիայի համար, քանի որ ենթադրվում է նաև G(x) ≥ 0 անհավասարության լուծումը մի քանի մոդուլներից, խորհուրդ է տրվում օգտագործել երկրորդ տարբերակը: Օրինակներ.
№1.
Լուծե՛ք հավասարումը` │x + 2│= 6 -2x
Այս մեթոդը ավելի հարմար է օգտագործել, եթե G(x) ֆունկցիայի արտահայտությունն ավելի քիչ բարդ է, քան F(x) ֆունկցիայի համար, քանի որ ենթադրվում է նաև G(x) ≥ 0 անհավասարության լուծումը մի քանի մոդուլներից, խորհուրդ է տրվում օգտագործել երկրորդ տարբերակը: Օրինակներ.
№1.
Լուծե՛ք հավասարումը` │x + 2│= 6 -2x  (1 ճանապարհ) Պատասխան՝ x = 1 1
/
3
№2.
(1 ճանապարհ) Պատասխան՝ x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 ճանապարհ) Պատասխան՝ Արմատների արտադրյալը 3 է։
(2 ճանապարհ) Պատասխան՝ Արմատների արտադրյալը 3 է։№3. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը.
│x - 6│= x 2 - 5x + 9

Պատասխան՝ արմատների գումարը 4 է։
Զորավարժություններ: №9. │x + 4│= - 3x №10. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք լուծումների քանակը՝│x 2 + x - 1│= 2x – 1 №11 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների արտադրյալը՝│x + 3│= x 2 + x – 6
Բաժին 4. │F(x)│= F(x) և │F(x)│= - F(x) ձևի հավասարումներ.
Այս տեսակի հավասարումները երբեմն անվանում են «ամենագեղեցիկ»։ Քանի որ հավասարումների աջ կողմը կախված է փոփոխականից, լուծումներ կան, եթե և միայն եթե աջ կողմը ոչ բացասական է: Հետևաբար, սկզբնական հավասարումները համարժեք են անհավասարություններին.│F(x)│= F(x) F(x) ≥ 0 և │F(x)│= - F(x) F(x) Օրինակներ. №1 . Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ավելի փոքր ամբողջական արմատը՝ │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 Պատասխան՝ x = 1№2. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք միջակայքի երկարությունը՝ │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Պատասխան՝ միջակայքի երկարությունը 6 է։№3 . Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամբողջ թվային լուծումների քանակը՝ │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Պատասխան՝ 4 ամբողջական լուծում։№4 . Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամենամեծ արմատը.
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1.2 =
x 2 – 5x + 5 = 0 D = 5 x 1.2 =  ≈ 1,4
≈ 1,4Պատասխան՝ x = 3:
Զորավարժություններ:
№12.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ամբողջ արմատը՝ │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք ամբողջ թվային լուծումների քանակը՝ │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Լուծեք հավասարումը ձեր պատասխանում, նշեք մի ամբողջ թիվ, որը հավասարման արմատը չէ. 
Բաժին 5. │F(x)│= │G(x)│ ձևի հավասարումներ.
Քանի որ հավասարման երկու կողմերն էլ ոչ բացասական են, լուծումը ներառում է երկու դեպք՝ ենթամոդուլային արտահայտությունները հավասար են կամ հակառակ նշանով: Հետևաբար, սկզբնական հավասարումը համարժեք է երկու հավասարումների համակցությանը՝ │ Ֆ(x)│= │ Գ(x)│ Օրինակներ.
№1.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ամբողջ արմատը՝ │x + 3│=│2x - 1│
Օրինակներ.
№1.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ամբողջ արմատը՝ │x + 3│=│2x - 1│  Պատասխան՝ ամբողջ արմատ x = 4:№2.
Լուծե՛ք հավասարումը. │
x – x 2 - 1│=│2x – 3 – x 2 │
Պատասխան՝ ամբողջ արմատ x = 4:№2.
Լուծե՛ք հավասարումը. │
x – x 2 - 1│=│2x – 3 – x 2 │  Պատասխան՝ x = 2:№3
.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների արտադրյալը.
Պատասխան՝ x = 2:№3
.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների արտադրյալը. 


 Արմատային հավասարումներ 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Պատասխան՝ արմատների արտադրյալը 0,25 է: Զորավարժություններ:
№15
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամբողջ լուծումը՝ │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝│5x - 3│=│7 - x│ №17
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը.
Արմատային հավասարումներ 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 Պատասխան՝ արմատների արտադրյալը 0,25 է: Զորավարժություններ:
№15
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամբողջ լուծումը՝ │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝│5x - 3│=│7 - x│ №17
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. 
Բաժին 6. Ոչ ստանդարտ հավասարումների լուծման օրինակներ
Այս բաժնում մենք կդիտարկենք ոչ ստանդարտ հավասարումների օրինակներ, որոնք լուծելիս արտահայտության բացարձակ արժեքը բացահայտվում է ըստ սահմանման: Օրինակներ.№1.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ x · │x│- 5x – 6 = 0  Պատասխան՝ արմատների գումարը 1 է №2.
.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝ x 2 - 4x ·
Պատասխան՝ արմատների գումարը 1 է №2.
.
Լուծե՛ք հավասարումը, պատասխանում նշե՛ք ավելի փոքր արմատը՝ x 2 - 4x ·  - 5 = 0
- 5 = 0  Պատասխան՝ ավելի փոքր արմատ x = - 5: №3.
Լուծե՛ք հավասարումը.
Պատասխան՝ ավելի փոքր արմատ x = - 5: №3.
Լուծե՛ք հավասարումը.  Պատասխան՝ x = -1: Զորավարժություններ:
№18.
Լուծե՛ք հավասարումը և նշե՛ք արմատների գումարը՝ x · │3x + 5│= 3x 2 + 4x + 3
Պատասխան՝ x = -1: Զորավարժություններ:
№18.
Լուծե՛ք հավասարումը և նշե՛ք արմատների գումարը՝ x · │3x + 5│= 3x 2 + 4x + 3
№19.
Լուծե՛ք հավասարումը x 2 – 3x = 
№20.
Լուծե՛ք հավասարումը. 
Բաժին 7. │F(x)│+│G(x)│=0 ձևի հավասարումներ.
Հեշտ է նկատել, որ այս տիպի հավասարման ձախ կողմում ոչ բացասական մեծությունների գումարն է։ Հետևաբար, սկզբնական հավասարումը լուծում ունի, եթե և միայն այն դեպքում, եթե երկու անդամները միաժամանակ հավասար են զրոյի: Հավասարումը համարժեք է հավասարումների համակարգին՝ │ Ֆ(x)│+│ Գ(x)│=0 Օրինակներ.
№1
. Լուծե՛ք հավասարումը.
Օրինակներ.
№1
. Լուծե՛ք հավասարումը.  Պատասխան՝ x = 2: №2.
Լուծե՛ք հավասարումը. Պատասխան՝ x = 1: Զորավարժություններ:
№21.
Լուծե՛ք հավասարումը. №22
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №23
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք լուծումների քանակը.
Պատասխան՝ x = 2: №2.
Լուծե՛ք հավասարումը. Պատասխան՝ x = 1: Զորավարժություններ:
№21.
Լուծե՛ք հավասարումը. №22
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №23
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք լուծումների քանակը. Բաժին 8. │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m ձևի հավասարումներ
Այս տեսակի հավասարումները լուծելու համար օգտագործվում է ինտերվալ մեթոդը: Եթե այն լուծենք մոդուլների հաջորդական ընդլայնմամբ, կստանանք nհամակարգերի հավաքածուներ, ինչը շատ դժվար է և անհարմար: Դիտարկենք ինտերվալ մեթոդի ալգորիթմը՝ 1). Գտեք փոփոխական արժեքներ X, որի համար յուրաքանչյուր մոդուլ հավասար է զրոյի (ենթամոդուլային արտահայտությունների զրո). 2). Նշեք գտնված արժեքները թվային տողի վրա, որը բաժանված է ինտերվալների (ինտերվալների քանակը համապատասխանաբար հավասար է n+1
) 3). Որոշեք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված յուրաքանչյուր միջակայքում (լուծում կատարելիս կարող եք օգտագործել թվային տող՝ նշելով դրա վրա նշանները) 4): Սկզբնական հավասարումը համարժեք է ագրեգատին n+1
համակարգեր, որոնցից յուրաքանչյուրում նշվում է փոփոխականի անդամակցությունը Xընդմիջումներից մեկը. Օրինակներ.
№1
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամենամեծ արմատը.
2). Նշեք գտնված արժեքները թվային տողի վրա, որը բաժանված է ինտերվալների (ինտերվալների քանակը համապատասխանաբար հավասար է n+1
) 3). Որոշեք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված յուրաքանչյուր միջակայքում (լուծում կատարելիս կարող եք օգտագործել թվային տող՝ նշելով դրա վրա նշանները) 4): Սկզբնական հավասարումը համարժեք է ագրեգատին n+1
համակարգեր, որոնցից յուրաքանչյուրում նշվում է փոփոխականի անդամակցությունը Xընդմիջումներից մեկը. Օրինակներ.
№1
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ամենամեծ արմատը.  1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 2; x = -3 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքերի վրա.
1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 2; x = -3 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքերի վրա. x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
 - լուծումներ չկան Հավասարումն ունի երկու արմատ: Պատասխան՝ ամենամեծ արմատը x = 2: №2.
Լուծե՛ք հավասարումը և ձեր պատասխանում տրամադրե՛ք ամբողջ արմատը.
- լուծումներ չկան Հավասարումն ունի երկու արմատ: Պատասխան՝ ամենամեծ արմատը x = 2: №2.
Լուծե՛ք հավասարումը և ձեր պատասխանում տրամադրե՛ք ամբողջ արմատը.  1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1,5; x = - 1 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված միջակայքերի վրա՝ x + 1 x + 1 x + 1 - + +
1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1,5; x = - 1 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե յուրաքանչյուր մոդուլ ինչ նշանով է բացահայտվում ստացված միջակայքերի վրա՝ x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 Վերջին համակարգը լուծումներ չունի, հետևաբար հավասարումն ունի երկու արմատ։ Հավասարումը լուծելիս պետք է ուշադրություն դարձնել երկրորդ մոդուլի դիմաց գտնվող «-» նշանին: Պատասխան՝ ամբողջ արմատ x = 7: №3.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 5; x = 1; x = - 2 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքում՝ x – 5 x – 5 x – 5 x – 5 - - - +
Վերջին համակարգը լուծումներ չունի, հետևաբար հավասարումն ունի երկու արմատ։ Հավասարումը լուծելիս պետք է ուշադրություն դարձնել երկրորդ մոդուլի դիմաց գտնվող «-» նշանին: Պատասխան՝ ամբողջ արմատ x = 7: №3.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 5; x = 1; x = - 2 2): Եկեք նշենք գտնված արժեքները թվային տողի վրա և որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլ ստացված միջակայքում՝ x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 Հավասարումն ունի երկու արմատ x = 0 և 2: Պատասխան՝ արմատների գումարը 2 է։ №4
.
Լուծե՛ք հավասարումը. 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1; x = 2; x = 3. 2): Եկեք որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլը ստացված միջակայքերի վրա։ 3).
Հավասարումն ունի երկու արմատ x = 0 և 2: Պատասխան՝ արմատների գումարը 2 է։ №4
.
Լուծե՛ք հավասարումը. 1). Եկեք գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 1; x = 2; x = 3. 2): Եկեք որոշենք, թե ինչ նշանով է բացահայտվում յուրաքանչյուր մոդուլը ստացված միջակայքերի վրա։ 3).  Համատեղենք առաջին երեք համակարգերի լուծումները։ Պատասխան՝ ; x = 5.
Համատեղենք առաջին երեք համակարգերի լուծումները։ Պատասխան՝ ; x = 5.Զորավարժություններ: №24. Լուծե՛ք հավասարումը.
 №25.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №26.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի փոքր արմատը. №27.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի մեծ արմատը.
№25.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների գումարը. №26.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի փոքր արմատը. №27.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք ավելի մեծ արմատը. Բաժին 9. Մի քանի մոդուլներ պարունակող հավասարումներ
Բազմաթիվ մոդուլներ պարունակող հավասարումները ենթադրում են բացարձակ արժեքների առկայություն ենթամոդուլային արտահայտություններում: Այս տեսակի հավասարումների լուծման հիմնական սկզբունքը մոդուլների հաջորդական բացահայտումն է՝ սկսած «արտաքինից»: Լուծման ժամանակ օգտագործվում են թիվ 1, թիվ 3 բաժիններում քննարկված տեխնիկան։Օրինակներ.
№1.
Լուծե՛ք հավասարումը.  Պատասխան՝ x = 1; - տասնմեկ: №2.
Լուծե՛ք հավասարումը.
Պատասխան՝ x = 1; - տասնմեկ: №2.
Լուծե՛ք հավասարումը.
Պատասխան՝ x = 0; 4; - 4. №3.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների արտադրյալը.  Պատասխան՝ արմատների արտադրյալը 8 է։ №4.
Լուծե՛ք հավասարումը.
Պատասխան՝ արմատների արտադրյալը 8 է։ №4.
Լուծե՛ք հավասարումը.  Նշենք բնակչության հավասարումները (1)
Եվ (2)
և դիզայնի հեշտության համար հաշվի առեք դրանցից յուրաքանչյուրի լուծումը առանձին: Քանի որ երկու հավասարումներն էլ պարունակում են մեկից ավելի մոդուլ, ավելի հարմար է համարժեք անցում կատարել համակարգերի հավաքածուներին: (1)
Նշենք բնակչության հավասարումները (1)
Եվ (2)
և դիզայնի հեշտության համար հաշվի առեք դրանցից յուրաքանչյուրի լուծումը առանձին: Քանի որ երկու հավասարումներն էլ պարունակում են մեկից ավելի մոդուլ, ավելի հարմար է համարժեք անցում կատարել համակարգերի հավաքածուներին: (1)

 (2)
(2)


 Պատասխան.
Պատասխան.
Զորավարժություններ:
№36.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ 5 │3x-5│ = 25 x №37.
Լուծե՛ք հավասարումը, եթե կա մեկից ավելի արմատ, ապա ձեր պատասխանում նշե՛ք արմատների գումարը՝ │x + 2│ x – 3x – 10 = 1 №38.
Լուծե՛ք հավասարումը. 3 │2x -4│ = 9 │x│ №39.
Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների թիվը՝ 2 │ sin x│ = √2 №40
. Լուծե՛ք հավասարումը և ձեր պատասխանում նշե՛ք արմատների թիվը.
Բաժին 3. Լոգարիթմական հավասարումներ.
Հետևյալ հավասարումները լուծելուց առաջ անհրաժեշտ է վերանայել լոգարիթմների հատկությունները և լոգարիթմական ֆունկցիան։ Օրինակներ. №1. Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների արտադրյալը՝ log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Դեպք 1. եթե x ≥ - 1, ապա log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – բավարարում է x ≥ - 1 2 պայմանը. եթե x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – բավարարում է x - 1 պայմանը
Պատասխան՝ արմատների արտադրյալը 15 է։
№2.
Լուծե՛ք հավասարումը, ձեր պատասխանում նշե՛ք արմատների գումարը՝ lg  Օ.Դ.Զ.
Օ.Դ.Զ. 



Պատասխան՝ արմատների գումարը 0,5 է։
№3.
Լուծե՛ք հավասարումը log 5  Օ.Դ.Զ.
Օ.Դ.Զ. 
 Պատասխան՝ x = 9: №4.
Լուծե՛ք հավասարումը` │2 + լոգ 0,2 x│+ 3 = │1 + լոգ 5 x│ O.D.Z. x > 0 Եկեք օգտագործենք մեկ այլ հիմք տեղափոխելու բանաձևը: │2 - մատյան 5 x│+ 3 = │1 + մատյան 5 x│
Պատասխան՝ x = 9: №4.
Լուծե՛ք հավասարումը` │2 + լոգ 0,2 x│+ 3 = │1 + լոգ 5 x│ O.D.Z. x > 0 Եկեք օգտագործենք մեկ այլ հիմք տեղափոխելու բանաձևը: │2 - մատյան 5 x│+ 3 = │1 + մատյան 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Գտնենք ենթամոդուլային արտահայտությունների զրոները՝ x = 25; x = Այս թվերը բաժանում են ընդունելի արժեքների տիրույթը երեք միջակայքի, ուստի հավասարումը համարժեք է երեք համակարգերի շարքին:  Պատասխան.
Պատասխան.
Մեկ այլ կարևոր փաստ. մոդուլը երբեք բացասական չէ. Ինչ թիվ էլ վերցնենք՝ լինի դա դրական, թե բացասական, նրա մոդուլը միշտ դրական է ստացվում (կամ ծայրահեղ դեպքերում՝ զրո): Ահա թե ինչու մոդուլը հաճախ անվանում են թվի բացարձակ արժեք։
Բացի այդ, եթե միավորենք մոդուլի սահմանումը դրական և բացասական թվերի համար, մենք ստանում ենք մոդուլի գլոբալ սահմանում բոլոր թվերի համար: Այսինքն՝ թվի մոդուլը հավասար է թվին, եթե թիվը դրական է (կամ զրո), կամ հավասար է հակառակ թվին, եթե թիվը բացասական է։ Դուք կարող եք սա գրել որպես բանաձև.
Կա նաև զրոյի մոդուլ, բայց այն միշտ հավասար է զրոյի։ Բացի այդ, զրոն միակ թիվն է, որը չունի հակադիր։
Այսպիսով, եթե դիտարկենք $y=\left| ֆունկցիան x \right|$ և փորձեք նկարել դրա գրաֆիկը, դուք կստանաք այսպիսի բան.
Մոդուլի գրաֆիկ և հավասարման լուծման օրինակ
Այս նկարից անմիջապես պարզ է դառնում, որ $\left| -m \աջ|=\ձախ| m \right|$, և մոդուլի գրաֆիկը երբեք չի ընկնում x առանցքից ցածր: Բայց սա դեռ ամենը չէ. կարմիր գիծը նշում է $y=a$ ուղիղ գիծը, որը դրական $a$-ի դեպքում մեզ տալիս է միանգամից երկու արմատ՝ $((x)_(1))$ և $((x) _(2)) $, բայց մենք ավելի ուշ կխոսենք:
Բացի զուտ հանրահաշվական սահմանումից, կա երկրաչափական սահմանում. Ենթադրենք, թվային տողի վրա կա երկու կետ՝ $((x)_(1))$ և $((x)_(2))$: Այս դեպքում $\left| արտահայտությունը ((x)_(1))-((x)_(2)) \right|$-ը պարզապես նշված կետերի միջև եղած հեռավորությունն է: Կամ, եթե նախընտրում եք, այս կետերը միացնող հատվածի երկարությունը.
 Մոդուլը թվային գծի կետերի միջև հեռավորությունն է
Մոդուլը թվային գծի կետերի միջև հեռավորությունն է Այս սահմանումը նաև ենթադրում է, որ մոդուլը միշտ ոչ բացասական է: Բայց բավականաչափ սահմանումներ և տեսություն՝ եկեք անցնենք իրական հավասարումների:
Հիմնական բանաձև
Լավ, մենք պարզեցինք սահմանումը: Բայց դա ավելի հեշտ չդարձրեց: Ինչպե՞ս լուծել այս մոդուլը պարունակող հավասարումները:
Հանգիստ, պարզապես հանգիստ: Սկսենք ամենապարզ բաներից։ Մտածեք այսպիսի մի բան.
\[\ձախ| x\աջ|=3\]
Այսպիսով, $x$-ի մոդուլը 3 է: Ինչի՞ կարող է հավասար լինել $x$-ը: Դե, դատելով սահմանումից, մենք բավականին գոհ ենք $x=3$-ից: Իրոք.
\[\ձախ| 3\աջ|=3\]
Այլ թվեր կա՞ն։ Կապը կարծես ակնարկում է, որ կա: Օրինակ, $x=-3$-ը նույնպես $\left| է -3 \աջ|=3$, այսինքն. պահանջվող հավասարությունը բավարարված է.
Այսպիսով, միգուցե եթե փնտրենք և մտածենք, ավելի շատ թվեր գտնե՞նք: Բայց եկեք խոստովանենք, որ այլևս թվեր չկան: Հավասարում $\ձախ| x \right|=3$-ն ունի ընդամենը երկու արմատ՝ $x=3$ և $x=-3$։
Հիմա մի փոքր բարդացնենք խնդիրը։ Թող $f\left(x \right)$ ֆունկցիան կախվի մոդուլի նշանի տակ՝ $x$ փոփոխականի փոխարեն, և դրեք կամայական $a$ թիվ աջ կողմում գտնվող եռակի փոխարեն։ Մենք ստանում ենք հավասարումը.
\[\ձախ| f\ ձախ (x \աջ) \աջ|=a\]
Այսպիսով, ինչպես կարող ենք լուծել սա: Հիշեցնեմ՝ $f\left(x \right)$-ը կամայական ֆունկցիա է, $a$-ը՝ ցանկացած թիվ։ Նրանք. Ընդհանրապես ինչ-որ բան: Օրինակ:
\[\ձախ| 2x+1 \աջ|=5\]
\[\ձախ| 10x-5 \աջ|=-65\]
Ուշադրություն դարձնենք երկրորդ հավասարմանը. Նրա մասին անմիջապես կարելի է ասել՝ նա արմատներ չունի։ Ինչո՞ւ։ Ամեն ինչ ճիշտ է, քանի որ դրա համար պահանջվում է, որ մոդուլը հավասար լինի բացասական թվի, ինչը երբեք չի լինում, քանի որ մենք արդեն գիտենք, որ մոդուլը միշտ դրական թիվ է, իսկ ծայրահեղ դեպքում՝ զրո։
Բայց առաջին հավասարման դեպքում ամեն ինչ ավելի զվարճալի է: Երկու տարբերակ կա՝ կա՛մ մոդուլի նշանի տակ կա դրական արտահայտություն, այնուհետև $\left| 2x+1 \right|=2x+1$, կամ այս արտահայտությունը դեռ բացասական է, իսկ հետո $\left| 2x+1 \աջ|=-\ձախ(2x+1 \աջ)=-2x-1$: Առաջին դեպքում մեր հավասարումը կվերագրվի հետևյալ կերպ.
\[\ձախ| 2x+1 \աջ|=5\Աջ սլաք 2x+1=5\]
Եվ հանկարծ պարզվում է, որ $2x+1$ ենթամոդուլային արտահայտությունն իսկապես դրական է՝ այն հավասար է 5 թվին։ մենք կարող ենք ապահով կերպով լուծել այս հավասարումը. արդյունքում ստացված արմատը կլինի պատասխանի մի մասը.
Նրանք, ովքեր հատկապես անվստահ են, կարող են փորձել փոխարինել գտած արմատը սկզբնական հավասարման մեջ և համոզվել, որ մոդուլի տակ իսկապես դրական թիվ կա:
Հիմա եկեք նայենք բացասական ենթամոդուլային արտահայտության դեպքին.
\[\ձախ\( \սկիզբ(հավասարեցնել)& \ձախ| 2x+1 \աջ|=5 \\& 2x+1 \lt 0 \\\վերջ (հավասարեցնել) \աջ.\Աջ սլաք -2x-1=5 \Աջ սլաք 2x+1=-5\]
Վա՜յ Կրկին ամեն ինչ պարզ է. մենք ենթադրեցինք, որ $2x+1 \lt 0$, և արդյունքում ստացանք $2x+1=-5$ - իսկապես, այս արտահայտությունը զրոյից փոքր է։ Մենք լուծում ենք ստացված հավասարումը, մինչդեռ արդեն հաստատ գիտենք, որ հայտնաբերված արմատը կհամապատասխանի մեզ.
Ընդհանուր առմամբ կրկին երկու պատասխան ստացանք՝ $x=2$ և $x=3$։ Այո, հաշվարկների քանակը մի փոքր ավելի մեծ է ստացվել, քան շատ պարզ հավասարման $\left| x \right|=3$, բայց սկզբունքորեն ոչինչ չի փոխվել: Այսպիսով, միգուցե կա ինչ-որ ունիվերսալ ալգորիթմ:
Այո, նման ալգորիթմ գոյություն ունի։ Եվ հիմա մենք կվերլուծենք այն:
Ազատվել մոդուլի նշանից
Եկեք մեզ տրվի $\left| հավասարումը f\left(x \right) \right|=a$, իսկ $a\ge 0$ (հակառակ դեպքում, ինչպես արդեն գիտենք, արմատներ չկան): Այնուհետև կարող եք ազատվել մոդուլի նշանից՝ օգտագործելով հետևյալ կանոնը.
\[\ձախ| f\ ձախ (x \աջ) \աջ|=a\Աջ սլաք f\ ձախ (x \աջ)=\pm a\]
Այսպիսով, մոդուլի հետ մեր հավասարումը բաժանվում է երկու մասի, բայց առանց մոդուլի: Ահա այսքանն է տեխնոլոգիան: Փորձենք լուծել մի քանի հավասարումներ։ Սկսենք սրանից
\[\ձախ| 5x+4 \աջ|=10\Աջ սլաք 5x+4=\pm 10\]
Եկեք քննարկենք առանձին, երբ աջ կողմում կա տասը գումարած, և առանձին, երբ կա մինուս: Մենք ունենք:
\[\սկիզբ (հավասարեցնել)& 5x+4=10\Աջ սլաք 5x=6\Աջ սլաք x=\frac(6)(5)=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2.8: \\\վերջ (հավասարեցնել)\]
Այսքանը: Ստացանք երկու արմատ՝ $x=1,2$ և $x=-2,8$։ Ամբողջ լուծումը տեւեց բառացիորեն երկու տող:
Լավ, հարց չկա, եկեք մի քիչ ավելի լուրջ բան նայենք.
\[\ձախ| 7-5x\աջ|=13\]
Կրկին բացում ենք մոդուլը պլյուս և մինուսով.
\[\սկիզբ (հավասարեցնել)& 7-5x=13\Աջ սլաք -5x=6\Աջ սլաք x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\վերջ (հավասարեցնել)\]
Կրկին մի քանի տող, և պատասխանը պատրաստ է: Ինչպես ասացի, մոդուլների մեջ բարդ բան չկա: Պարզապես պետք է հիշել մի քանի կանոն. Հետևաբար, մենք առաջ ենք շարժվում և սկսում իսկապես ավելի բարդ խնդիրներից:
Աջ կողմի փոփոխականի դեպք
Այժմ հաշվի առեք այս հավասարումը.
\[\ձախ| 3x-2 \աջ|=2x\]
Այս հավասարումը սկզբունքորեն տարբերվում է բոլոր նախորդներից: Ինչպե՞ս: Իսկ այն, որ հավասար նշանի աջ կողմում դրված է $2x$ արտահայտությունը, և մենք նախապես չենք կարող իմանալ՝ դա դրական է, թե բացասական։
Ի՞նչ անել այս դեպքում: Նախ, մենք պետք է մեկընդմիշտ դա հասկանանք եթե պարզվի, որ հավասարման աջ կողմը բացասական է, ապա հավասարումը արմատներ չի ունենա- մենք արդեն գիտենք, որ մոդուլը չի կարող հավասար լինել բացասական թվի:
Եվ երկրորդը, եթե աջ մասը դեռ դրական է (կամ հավասար է զրոյի), ապա կարող եք գործել ճիշտ այնպես, ինչպես նախկինում. պարզապես բացեք մոդուլը առանձին՝ գումարած նշանով և առանձին՝ մինուս նշանով։
Այսպիսով, մենք ձևակերպում ենք կանոն $f\left(x \right)$ և $g\left(x \right)$ կամայական ֆունկցիաների համար:
\[\ձախ| f\ ձախ (x \աջ) \աջ|=g\ ձախ (x \աջ)\ Աջ սլաք \ձախ\( \սկիզբ (հավասարեցնել)& f\ ձախ (x \աջ) =\pm g\ ձախ (x \աջ ), \\& g\ ձախ (x \աջ)\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]
Մեր հավասարման հետ կապված մենք ստանում ենք.
\[\ձախ| 3x-2 \աջ|=2x\Աջ սլաք \ձախ\( \սկիզբ(հավասարեցնել)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]
Դե, մենք ինչ-որ կերպ կհաղթահարենք $2x\ge 0$ պահանջը: Ի վերջո, մենք կարող ենք հիմարաբար փոխարինել այն արմատները, որոնք ստանում ենք առաջին հավասարումից և ստուգել, թե արդյոք անհավասարությունը պահպանվում է, թե ոչ:
Այսպիսով, եկեք լուծենք ինքնին հավասարումը.
\[\սկիզբ (հավասարեցնել)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\\վերջ (հավասարեցնել)\]
Դե, այս երկու արմատներից որն է բավարարում $2x\ge 0$ պահանջը: Այո երկուսն էլ! Հետևաբար, պատասխանը կլինի երկու թիվ՝ $x=(4)/(3)\;$ և $x=0$։ Սա է լուծումը:
Ես կասկածում եմ, որ ուսանողներից ոմանք արդեն սկսել են ձանձրանալ: Դե, եկեք նայենք նույնիսկ ավելի բարդ հավասարմանը.
\[\ձախ| ((x)^(3))-3((x)^(2))+x \աջ|=x-((x)^(3))\]
Թեև այն չար տեսք ունի, իրականում այն դեռևս նույն «մոդուլը հավասար է ֆունկցիայի» ձևի հավասարումն է.
\[\ձախ| f\ ձախ (x \աջ) \աջ|=g\ ձախ (x \աջ)\]
Եվ դա լուծվում է ճիշտ նույն կերպ.
\[\ձախ| ((x)^(3))-3((x)^(2))+x \աջ|=x-((x)^(3))\Աջ սլաք \ձախ\( \սկիզբ (հավասարեցնել)& ( (x)^(3))-3((x)^(2))+x=\pm \ձախ(x-((x)^(3)) \աջ), \\& x-((x) )^(3))\ge 0. \\\վերջ (հավասարեցնել) \աջ.\]
Անհավասարության հետ ավելի ուշ կզբաղվենք. այն ինչ-որ կերպ չափազանց չար է (իրականում պարզ է, բայց մենք չենք լուծի այն): Առայժմ ավելի լավ է գործ ունենալ ստացված հավասարումների հետ: Դիտարկենք առաջին դեպքը. սա այն դեպքում, երբ մոդուլը ընդլայնվում է գումարած նշանով.
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
Դե, անիմաստ է, որ դուք պետք է ամեն ինչ հավաքեք ձախից, բերեք նմանատիպերը և տեսնեք, թե ինչ է տեղի ունենում: Եվ սա տեղի է ունենում.
\[\սկիզբ(հավասարեցնել)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\վերջ (հավասարեցնել)\]
Փակագծերից հանում ենք $((x)^(2))$ ընդհանուր գործակիցը և ստանում շատ պարզ հավասարում.
\[((x)^(2))\ձախ(2x-3 \աջ)=0\Աջ սլաք \ձախ[ \սկիզբ(հավասարեցնել)& ((x)^(2))=0 \\& 2x-3 =0 \\\վերջ (հավասարեցնել) \աջ:\]
\[((x)_(1))=0;\քառակուսի ((x)_(2))=\frac(3)(2)=1.5.\]
Այստեղ մենք օգտվեցինք արտադրյալի կարևոր հատկությունից, հանուն որի գործոնավորեցինք սկզբնական բազմանդամը. արտադրյալը հավասար է զրոյի, երբ գործակիցներից գոնե մեկը հավասար է զրոյի։
Հիմա ճիշտ նույն կերպ վարվենք երկրորդ հավասարման հետ, որը ստացվում է մինուս նշանով ընդլայնելով մոդուլը.
\[\սկիզբ(հավասարեցնել)& ((x)^(3))-3((x)^(2))+x=-\ձախ(x-((x)^(3)) \աջ); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\ ձախ (-3x+2 \աջ)=0: \\\վերջ (հավասարեցնել)\]
Կրկին նույնը. արտադրյալը հավասար է զրոյի, երբ գործոններից գոնե մեկը հավասար է զրոյի: Մենք ունենք:
\[\ձախ[ \սկիզբ (հավասարեցնել)& x=0 \\& -3x+2=0 \\\վերջ (հավասարեցնել) \աջ:\]
Դե, ստացանք երեք արմատ՝ $x=0$, $x=1,5$ և $x=(2)/(3)\;$։ Դե, այս հավաքածուից ո՞րը կմտնի վերջնական պատասխանի մեջ: Դա անելու համար հիշեք, որ մենք ունենք լրացուցիչ սահմանափակում անհավասարության տեսքով.
Ինչպե՞ս հաշվի առնել այս պահանջը: Եկեք պարզապես փոխարինենք գտնված արմատները և ստուգենք, թե արդյոք անհավասարությունը պահպանվում է այս $x$-ի համար, թե ոչ: Մենք ունենք:
\[\սկիզբ(հավասարեցնել)& x=0\Աջ սլաք x-((x)^(3))=0-0=0\ge 0; \\& x=1.5\Աջ սլաք x-((x)^(3))=1.5-((1.5)^(3)) \lt 0; \\& x=\frac(2)(3)\Աջ սլաք x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\վերջ (հավասարեցնել)\]
Այսպիսով, $x=1,5$ արմատը մեզ չի համապատասխանում։ Եվ ի պատասխան կլինի միայն երկու արմատ.
\[((x)_(1))=0;\քառակուսի ((x)_(2))=\frac(2)(3).\]
Ինչպես տեսնում եք, նույնիսկ այս դեպքում ոչ մի բարդ բան չկար. մոդուլների հետ հավասարումները միշտ լուծվում են ալգորիթմի միջոցով: Պարզապես պետք է լավ հասկանալ բազմանդամներն ու անհավասարությունները: Հետևաբար, մենք անցնում ենք ավելի բարդ առաջադրանքների՝ արդեն կլինի ոչ թե մեկ, այլ երկու մոդուլ:
Հավասարումներ երկու մոդուլներով
Մինչ այժմ մենք ուսումնասիրել ենք միայն ամենապարզ հավասարումները՝ կար մեկ մոդուլ և մեկ այլ բան։ Այս «ուրիշ բանն» ուղարկեցինք անհավասարության մեկ այլ մաս՝ մոդուլից հեռու, որպեսզի վերջում ամեն ինչ կրճատվի $\left| ձևի հավասարման մեջ։ f\left(x \right) \right|=g\left(x \աջ)$ կամ նույնիսկ ավելի պարզ $\left| f\left(x \աջ) \աջ|=a$.
Բայց մանկապարտեզն ավարտվել է՝ ժամանակն է ավելի լուրջ բան մտածելու: Սկսենք հետևյալ հավասարումներից.
\[\ձախ| f\left(x \աջ) \աջ|=\ձախ| g\left(x \աջ) \աջ|\]
Սա «մոդուլը հավասար է մոդուլի» ձևի հավասարումն է։ Սկզբունքորեն կարևոր կետը այլ տերմինների և գործոնների բացակայությունն է. միայն մեկ մոդուլ ձախ կողմում, ևս մեկ մոդուլ աջում, և ոչ ավելին:
Ինչ-որ մեկը հիմա կմտածի, որ նման հավասարումներ ավելի դժվար է լուծել, քան այն, ինչ մինչ այժմ ուսումնասիրել ենք։ Բայց ոչ. այս հավասարումները նույնիսկ ավելի հեշտ են լուծել: Ահա բանաձևը.
\[\ձախ| f\left(x \աջ) \աջ|=\ձախ| g\ ձախ (x \աջ) \աջ |\ Աջ սլաք f\ ձախ (x \աջ) =\pm g\ ձախ (x \աջ)\]
Բոլորը! Մենք ուղղակի հավասարեցնում ենք ենթամոդուլային արտահայտությունները՝ դրանցից մեկի դիմաց գումարած կամ մինուս նշան դնելով։ Եվ հետո մենք լուծում ենք ստացված երկու հավասարումները, և արմատները պատրաստ են: Ոչ մի լրացուցիչ սահմանափակում, ոչ մի անհավասարություն և այլն: Ամեն ինչ շատ պարզ է.
Փորձենք լուծել այս խնդիրը.
\[\ձախ| 2x+3 \աջ|=\ձախ| 2x-7 \աջ|\]
Տարրական Ուոթսոն! Մոդուլների ընդլայնում.
\[\ձախ| 2x+3 \աջ|=\ձախ| 2x-7 \աջ|\Աջ սլաք 2x+3=\pm \ձախ(2x-7 \աջ)\]
Դիտարկենք յուրաքանչյուր դեպք առանձին.
\[\սկիզբ (հավասարեցնել)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\ձախ(2x-7 \աջ)\Աջ սլաք 2x+3=-2x+7: \\\վերջ (հավասարեցնել)\]
Առաջին հավասարումը արմատներ չունի։ Որովհետև ե՞րբ է $3=-7$: Ինչ արժեքներով $x$: «Ի՞նչ դժոխք է $x$-ը: Ձեզ քարկոծե՞լ են։ Այնտեղ ընդհանրապես $x$ չկա», - ասում եք դուք: Եվ դուք ճիշտ կլինեք: Մենք ստացել ենք հավասարություն, որը կախված չէ $x$ փոփոխականից, և միևնույն ժամանակ հավասարությունը ինքնին սխալ է։ Դրա համար էլ արմատներ չկան :)
Երկրորդ հավասարման դեպքում ամեն ինչ մի փոքր ավելի հետաքրքիր է, բայց նաև շատ, շատ պարզ.
Ինչպես տեսնում եք, ամեն ինչ լուծվեց բառացիորեն մի քանի տողում, մենք այլ բան չէինք սպասում գծային հավասարումից :)
Արդյունքում վերջնական պատասխանն է՝ $x=1$։
Այնպես, ինչպես? Դժվա՞ր: Իհարկե ոչ։ Փորձենք մեկ այլ բան.
\[\ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|\]
Կրկին մենք ունենք $\left| ձևի հավասարում f\left(x \աջ) \աջ|=\ձախ| g\left(x \աջ) \աջ|$. Հետևաբար, մենք անմիջապես վերագրում ենք այն՝ բացահայտելով մոդուլի նշանը.
\[((x)^(2))-3x+2=\pm \ձախ(x-1 \աջ)\]
Միգուցե ինչ-որ մեկը հիմա հարցնի. «Հեյ, ի՞նչ անհեթեթություն: Ինչո՞ւ է «պլյուս-մինուս»-ը հայտնվում աջ ձեռքի արտահայտության վրա, իսկ ձախում՝ ոչ»: Հանգստացեք, ես հիմա ամեն ինչ կբացատրեմ: Իսկապես, լավ իմաստով մենք պետք է վերագրեինք մեր հավասարումը հետևյալ կերպ.
Այնուհետև պետք է բացել փակագծերը, բոլոր տերմինները տեղափոխել հավասար նշանի մի կողմ (քանի որ հավասարումը, ակնհայտորեն, երկու դեպքում էլ քառակուսի է լինելու), ապա գտնել արմատները։ Բայց պետք է խոստովանեք. երբ «պլյուս-մինուս»-ը հայտնվում է երեք տերմինից առաջ (հատկապես, երբ այս տերմիններից մեկը քառակուսի արտահայտություն է), ինչ-որ կերպ ավելի բարդ է թվում, քան այն իրավիճակը, երբ «պլյուս-մինուս»-ը հայտնվում է ընդամենը երկու տերմինից առաջ:
Բայց ոչինչ չի խանգարում մեզ վերաշարադրել սկզբնական հավասարումը հետևյալ կերպ.
\[\ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|\Աջ սլաք \ձախ| ((x)^(2))-3x+2 \աջ|=\ձախ| x-1 \ճիշտ|\]
Ինչ է պատահել? Ոչ մի առանձնահատուկ բան. նրանք պարզապես փոխանակեցին ձախ և աջ կողմերը: Մի փոքրիկ բան, որն ի վերջո մի փոքր կհեշտացնի մեր կյանքը:)
Ընդհանուր առմամբ, մենք լուծում ենք այս հավասարումը, հաշվի առնելով տարբերակները գումարած և մինուսով.
\[\սկիզբ(հավասարեցնել)& ((x)^(2))-3x+2=x-1\Աջ սլաք ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\ձախ(x-1 \աջ)\Աջ սլաք ((x)^(2))-2x+1=0: \\\վերջ (հավասարեցնել)\]
Առաջին հավասարումն ունի $x=3$ և $x=1$ արմատներ։ Երկրորդը, ընդհանուր առմամբ, ճշգրիտ քառակուսի է.
\[((x)^(2))-2x+1=((\ձախ(x-1 \աջ))^(2))\]
Հետեւաբար, այն ունի միայն մեկ արմատ՝ $x=1$։ Բայց այս արմատը մենք արդեն ստացել ենք ավելի վաղ: Այսպիսով, վերջնական պատասխանի մեջ կմտնեն միայն երկու թվեր.
\[((x)_(1))=3;\քառակուսի ((x)_(2))=1.\]
Առաքելությունն ավարտված է: Կարելի է դարակից վերցնել կարկանդակ և ուտել։ Դրանք 2-ն են, քոնը միջինն է :)
Կարևոր նշում. Միանման արմատների առկայությունը մոդուլի ընդլայնման տարբեր տարբերակների համար նշանակում է, որ սկզբնական բազմանդամները ֆակտորիզացված են, և այդ գործոններից անպայման կլինի ընդհանուր մեկը: Իրոք.
\[\սկիզբ(հավասարեցնել)& \ձախ| x-1 \աջ|=\ձախ| ((x)^(2))-3x+2 \աջ|; \\& \ձախ| x-1 \աջ|=\ձախ| \ձախ(x-1 \աջ)\ձախ(x-2 \աջ) \աջ|. \\\վերջ (հավասարեցնել)\]
Մոդուլի հատկություններից մեկը՝ $\left| a\cdot b \աջ|=\ձախ| a \աջ|\cdot \ձախ| b \right|$ (այսինքն՝ արտադրյալի մոդուլը հավասար է մոդուլի արտադրյալին), ուստի սկզբնական հավասարումը կարող է վերաշարադրվել հետևյալ կերպ.
\[\ձախ| x-1 \աջ|=\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \ճիշտ|\]
Ինչպես տեսնում եք, մենք իսկապես ընդհանուր գործոն ունենք. Այժմ, եթե հավաքում եք բոլոր մոդուլները մի կողմից, կարող եք այս գործոնը հանել փակագծից.
\[\սկիզբ (հավասարեցնել)& \ձախ| x-1 \աջ|=\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \աջ|; \\& \ձախ| x-1 \աջ|-\ձախ| x-1 \աջ|\cdot \ձախ| x-2 \աջ|=0; \\& \ձախ| x-1 \աջ|\cdot \left(1-\left| x-2 \աջ| \աջ)=0. \\\վերջ (հավասարեցնել)\]
Դե, հիմա հիշեք, որ արտադրյալը հավասար է զրոյի, երբ գործոններից գոնե մեկը հավասար է զրոյի.
\[\ձախ[ \սկիզբ(հավասարեցնել)& \ձախ| x-1 \աջ|=0, \\& \ձախ| x-2 \աջ|=1. \\\վերջ (հավասարեցնել) \աջ:\]
Այսպիսով, սկզբնական հավասարումը երկու մոդուլով կրճատվել է երկու ամենապարզ հավասարումների, որոնց մասին մենք խոսեցինք դասի հենց սկզբում: Նման հավասարումները կարող են լուծվել բառացիորեն մի երկու տողով :)
Այս դիտողությունը կարող է անհարկի բարդ և գործնականում անկիրառելի թվալ: Այնուամենայնիվ, իրականում դուք կարող եք բախվել շատ ավելի բարդ խնդիրների, քան նրանք, որոնք մենք այսօր դիտարկում ենք: Դրանցում մոդուլները կարող են համակցվել բազմանդամների, թվաբանական արմատների, լոգարիթմների և այլնի հետ։ Եվ նման իրավիճակներում հավասարման ընդհանուր աստիճանն իջեցնելու ունակությունը՝ փակագծերից ինչ-որ բան հանելով, կարող է շատ, շատ օգտակար լինել:
Այժմ ես կցանկանայի վերլուծել մեկ այլ հավասարում, որն առաջին հայացքից կարող է խելահեղ թվալ։ Շատ ուսանողներ խրված են դրա վրա, նույնիսկ նրանք, ովքեր կարծում են, որ լավ են հասկանում մոդուլները:
Այնուամենայնիվ, այս հավասարումը նույնիսկ ավելի հեշտ է լուծել, քան այն, ինչ մենք նայեցինք ավելի վաղ: Եվ եթե հասկանաք, թե ինչու, դուք կստանաք ևս մեկ հնարք մոդուլներով հավասարումներ արագ լուծելու համար:
Այսպիսով, հավասարումը հետևյալն է.
\[\ձախ| x-((x)^(3)) \աջ|+\ձախ| ((x)^(2))+x-2 \աջ|=0\]
Ոչ, սա տառասխալ չէ. դա պլյուս է մոդուլների միջև: Եվ մենք պետք է գտնենք, թե $x$-ում երկու մոդուլների գումարը հավասար է զրոյի:
Ինչն է ամեն դեպքում խնդիրը: Բայց խնդիրն այն է, որ յուրաքանչյուր մոդուլ դրական թիվ է, կամ ծայրահեղ դեպքում՝ զրո։ Ի՞նչ կլինի, եթե գումարեք երկու դրական թիվ: Ակնհայտորեն կրկին դրական թիվ.
\[\սկիզբ (հավասարեցնել)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\վերջ (հավասարեցնել)\]
Վերջին տողը կարող է ձեզ պատկերացում տալ. միակ դեպքը, երբ մոդուլների գումարը զրոյական է, եթե յուրաքանչյուր մոդուլ զրո է.
\[\ձախ| x-((x)^(3)) \աջ|+\ձախ| ((x)^(2))+x-2 \աջ|=0\Աջ սլաք \ձախ\( \սկիզբ(հավասարեցնել)& \ձախ| x-((x)^(3)) \աջ|=0, \\& \ձախ|.
Իսկ ե՞րբ է մոդուլը հավասար զրոյի։ Միայն մեկ դեպքում, երբ ենթամոդուլային արտահայտությունը հավասար է զրոյի.
\[((x)^(2))+x-2=0\Աջ սլաք \ձախ(x+2 \աջ)\ձախ(x-1 \աջ)=0\Աջ սլաք \ձախ[ \սկիզբ (հավասարեցնել)& x=-2 \\& x=1 \\\վերջ (հավասարեցնել) \աջ.\]
Այսպիսով, մենք ունենք երեք կետ, որոնցում առաջին մոդուլը զրոյացված է. 0, 1 և −1; ինչպես նաև երկու կետեր, որոնցում երկրորդ մոդուլը զրոյականացվում է. −2 և 1: Այնուամենայնիվ, մեզ անհրաժեշտ է, որ երկու մոդուլները միաժամանակ զրոյացվեն, ուստի գտնված թվերից պետք է ընտրել դրանք, որոնք ներառված են. երկու հավաքածուները: Ակնհայտ է, որ կա միայն մեկ այդպիսի թիվ՝ $x=1$ - սա կլինի վերջնական պատասխանը։
Ճեղքման մեթոդ
Դե, մենք արդեն անդրադարձել ենք մի շարք խնդիրների և սովորել ենք շատ տեխնիկա: Կարծում եք՝ այսքանո՞վ է: Բայց ոչ! Այժմ մենք կանդրադառնանք վերջնական տեխնիկային, և միևնույն ժամանակ ամենակարևորին: Մենք կխոսենք մոդուլով հավասարումների բաժանման մասին։ Ինչի՞ մասին ենք նույնիսկ խոսելու։ Եկեք մի փոքր հետ գնանք և նայենք մի քանի պարզ հավասարման: Օրինակ սա.
\[\ձախ| 3x-5 \աջ|=5-3x\]
Սկզբունքորեն մենք արդեն գիտենք, թե ինչպես լուծել նման հավասարումը, քանի որ դա $\left| ձևի ստանդարտ կառուցում է։ f\left(x \right) \right|=g\left(x \աջ)$: Բայց եկեք փորձենք այս հավասարմանը նայել մի փոքր այլ տեսանկյունից: Ավելի ճիշտ, հաշվի առեք արտահայտությունը մոդուլի նշանի տակ: Հիշեցնեմ, որ ցանկացած թվի մոդուլը կարող է հավասար լինել հենց թվին, կամ կարող է հակառակ լինել այս թվին.
\[\ձախ| a \աջ|=\ձախ\( \սկիզբ (հավասարեցնել)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\վերջ (հավասարեցնել) \աջ.\]
Իրականում այս երկիմաստությունն է ամբողջ խնդիրը. քանի որ մոդուլի տակ թիվը փոխվում է (դա կախված է փոփոխականից), մեզ համար պարզ չէ՝ դա դրական է, թե բացասական։
Բայց ի՞նչ, եթե սկզբում պահանջեք, որ այս թիվը լինի դրական: Օրինակ, մենք պահանջում ենք, որ $3x-5 \gt 0$ - այս դեպքում մեզ երաշխավորված է դրական թիվ ստանալ մոդուլի նշանի տակ, և մենք կարող ենք ամբողջությամբ ազատվել հենց այս մոդուլից.
Այսպիսով, մեր հավասարումը կվերածվի գծայինի, որը հեշտությամբ կարելի է լուծել.
Ճիշտ է, այս բոլոր մտքերը իմաստ ունեն միայն $3x-5 \gt 0$ պայմանով - մենք ինքներս ենք ներկայացրել այս պահանջը՝ մոդուլը միանշանակ բացահայտելու համար։ Հետևաբար, գտնված $x=\frac(5)(3)$-ը փոխարինենք այս պայմանով և ստուգենք.
Ստացվում է, որ $x$-ի նշված արժեքի համար մեր պահանջը չի բավարարվում, քանի որ արտահայտությունը պարզվեց, որ հավասար է զրոյի, և մեզ անհրաժեշտ է, որ այն խիստ մեծ լինի զրոյից: Տխուր :(
Բայց դա լավ է! Ի վերջո, կա ևս մեկ տարբերակ $3x-5 \lt 0$։ Ավելին. կա նաև $3x-5=0$ դեպք, սա նույնպես պետք է դիտարկել, հակառակ դեպքում լուծումը թերի կլինի։ Այսպիսով, հաշվի առեք դեպքը $3x-5 \lt 0$:
Ակնհայտ է, որ մոդուլը կբացվի մինուս նշանով: Բայց հետո առաջանում է մի տարօրինակ իրավիճակ. սկզբնական հավասարման մեջ և՛ ձախ, և՛ աջ կողմում նույն արտահայտությունն է մնալու.
Հետաքրքիր է, $5-3x$ արտահայտությունը ինչ $x$-ով հավասար կլինի $5-3x$ արտահայտությանը: Նույնիսկ կապիտան Օբյոզենսը կխեղդի իր թուքը նման հավասարումներից, բայց մենք գիտենք, որ այս հավասարումը ինքնություն է, այսինքն. դա ճշմարիտ է փոփոխականի ցանկացած արժեքի համար:
Սա նշանակում է, որ ցանկացած $x$ կհամապատասխանի մեզ: Այնուամենայնիվ, մենք ունենք սահմանափակում.
Այլ կերպ ասած, պատասխանը կլինի ոչ թե մեկ թիվ, այլ ամբողջ ընդմիջում.
Վերջապես, մնում է ևս մեկ դեպք՝ $3x-5=0$: Այստեղ ամեն ինչ պարզ է. մոդուլի տակ կլինի զրո, և զրոյի մոդուլը նույնպես հավասար է զրոյի (սա ուղղակիորեն հետևում է սահմանումից).
Բայց հետո սկզբնական հավասարումը $\left| 3x-5 \right|=5-3x$-ը կվերագրվի հետևյալ կերպ.
Մենք արդեն ստացել ենք այս արմատը վերևում, երբ դիտարկեցինք $3x-5 \gt 0$-ի դեպքը: Ավելին, այս արմատը $3x-5=0$ հավասարման լուծումն է. սա այն սահմանափակումն է, որը մենք ինքներս ենք ներկայացրել մոդուլը վերականգնելու համար:)
Այսպիսով, բացի միջակայքից, մենք կբավարարվենք նաև այս միջակայքի ամենավերջում գտնվող թվով.
 Արմատների համակցում մոդուլային հավասարումների մեջ
Արմատների համակցում մոդուլային հավասարումների մեջ Ընդհանուր վերջնական պատասխան՝ $x\in \left(-\infty ;\frac(5)(3) \right]$ Շատ սովորական չէ նման խեղկատակություն տեսնել մոդուլով բավականին պարզ (ըստ էության գծային) հավասարման պատասխանում, Իսկապե՞ս, ընտելացիր. մոդուլի դժվարությունն այն է, որ նման հավասարումների պատասխանները կարող են լիովին անկանխատեսելի լինել:
Ուրիշ բան շատ ավելի կարևոր է. մենք հենց նոր վերլուծեցինք համընդհանուր ալգորիթմ մոդուլով հավասարումը լուծելու համար: Եվ այս ալգորիթմը բաղկացած է հետևյալ քայլերից.
- Հավասարման մեջ յուրաքանչյուր մոդուլ հավասարեցրու զրոյի: Մենք ստանում ենք մի քանի հավասարումներ.
- Լուծե՛ք այս բոլոր հավասարումները և նշե՛ք արմատները թվային տողի վրա։ Արդյունքում ուղիղ գիծը կբաժանվի մի քանի ընդմիջումների, որոնցից յուրաքանչյուրում բոլոր մոդուլները եզակիորեն բացահայտվում են.
- Լուծեք սկզբնական հավասարումը յուրաքանչյուր ընդմիջման համար և միավորեք ձեր պատասխանները:
Այսքանը: Մնում է միայն մեկ հարց՝ ի՞նչ անել 1-ին քայլով ստացված արմատների հետ։ Ենթադրենք՝ ունենք երկու արմատ՝ $x=1$ և $x=5$։ Նրանք թվային գիծը կբաժանեն 3 մասի.
 Թվային գիծը բաժանելով ընդմիջումների՝ օգտագործելով կետերը
Թվային գիծը բաժանելով ընդմիջումների՝ օգտագործելով կետերը Այսպիսով, որո՞նք են միջակայքերը: Պարզ է, որ դրանք երեքն են.
- Ամենա ձախը՝ $x \lt 1$ — միավորն ինքնին ներառված չէ միջակայքում;
- Կենտրոնական՝ $1\le x \lt 5$ - այստեղ մեկը ներառված է միջակայքում, բայց հինգը ներառված չէ;
- Ամենաաջինը. $x\ge 5$ - հինգը ներառված է միայն այստեղ:
Կարծում եմ, դուք արդեն հասկանում եք օրինաչափությունը: Յուրաքանչյուր ինտերվալ ներառում է ձախ ծայրը և չի ներառում աջը:
Առաջին հայացքից նման գրառումը կարող է թվալ անհարմար, անտրամաբանական և ընդհանրապես ինչ-որ խենթ: Բայց հավատացեք ինձ, մի փոքր պրակտիկայից հետո դուք կգտնեք, որ այս մոտեցումը ամենահուսալին է և չի խանգարում մոդուլների միանշանակ բացմանը: Ավելի լավ է օգտագործել նման սխեման, քան ամեն անգամ մտածել՝ ձախ/աջ ծայրը տվեք ընթացիկ ինտերվալին կամ «գցեք» այն հաջորդը:
Սա ավարտում է դասը: Ներբեռնեք խնդիրներ ինքնուրույն լուծելու համար, փորձեք, համեմատեք պատասխանների հետ - և կտեսնենք ձեզ հաջորդ դասին, որը նվիրված կլինի մոդուլներով անհավասարություններին:)
- հետ շփման մեջ 0
- Google+ 0
- լավ 0
- Ֆեյսբուք 0