Տատանումների հաճախականության որոշման բանաձևը. Հաճախականության ֆունկցիայի օրինակներ Excel-ում կրկնությունների հաճախականությունը հաշվարկելու համար

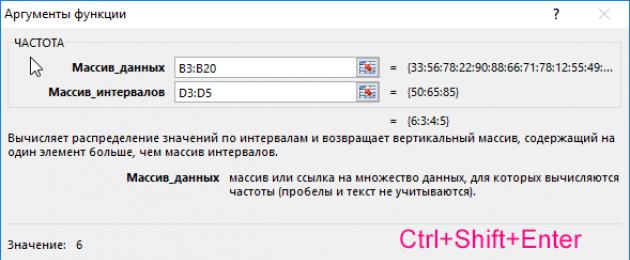
FREQUENCY ֆունկցիան օգտագործվում է տվյալ միջակայքում որոշակի արժեքների առաջացման քանակը որոշելու համար և տվյալները վերադարձնում է որպես արժեքների զանգված: Օգտագործելով FREQUENCY ֆունկցիան, մենք կսովորենք, թե ինչպես հաշվարկել հաճախականությունը Excel-ում:

Excel-ում FREQUENCY ֆունկցիայի օգտագործման օրինակ

Օրինակ 1. Համալսարանի խմբերից մեկի ուսանողները քննություն հանձնեցին ֆիզիկայից: Քննության որակը գնահատելիս կիրառվում է 100 միավորանոց համակարգ։ Վերջնական գնահատականը 5 բալանոց համակարգով որոշելու համար օգտագործվում են հետևյալ չափանիշները.

1. 0-ից մինչև 50 միավոր՝ քննությունը չի հանձնվում.
2. 51-ից մինչև 65 միավոր՝ 3 միավոր:
3. 66-ից մինչև 85 միավոր՝ 4 միավոր:
4. Ավելի քան 86 միավոր – 5 միավոր:

Վիճակագրության համար անհրաժեշտ է պարզել, թե քանի ուսանող է ստացել 5, 4, 3 միավոր և թե քանիսն են քննությունը չհանձնածները։

Եկեք տվյալները մուտքագրենք աղյուսակում.

Լուծելու համար ընտրեք 4 բջիջների տարածքներ և ներկայացրեք հետևյալ գործառույթը.

Փաստարկների նկարագրությունը.

• B3:B20 – ուսանողների գնահատականների վերաբերյալ տվյալների զանգված;
• D3:D5 – գնահատականների տվյալների զանգվածում առաջացման հաճախականությունը գտնելու չափանիշների զանգված:

Ընտրեք F3:F6 միջակայքը, նախ սեղմեք F2 ստեղնը, այնուհետև Ctrl+Shift+Enter ստեղների համակցությունը, որպեսզի զանգվածում կատարվի FREQUENCY ֆունկցիան։ Գանգուր փակագծերը () եզրերի երկայնքով բանաձևի բարում կծառայեն որպես հաստատում, որ ամեն ինչ ճիշտ է արվել: Սա նշանակում է, որ բանաձևը կատարվում է զանգվածով։ Արդյունքում մենք ստանում ենք.

Այսինքն՝ 6 ուսանող չի հանձնել քննությունը, 3, 4 և 5 գնահատականներ ստացել են համապատասխանաբար 3, 4 և 5 ուսանողներ։



Excel-ում FREQUENCY ֆունկցիայի միջոցով հավանականության որոշման օրինակ

Օրինակ 2. Հայտնի է, որ եթե կա միայն երկու հնարավոր սցենար, ապա առաջինի և երկրորդի հավանականությունը համապատասխանաբար 0,5 է։ Օրինակ, նետված մետաղադրամի համար «գլուխներ» կամ «պոչեր» ստանալու հավանականությունը ½ և ½ է (եթե անտեսենք մետաղադրամի եզրին ընկնելու հնարավորությունը): Նմանատիպ գնահատված հավանականության բաշխումը վերաբերում է հետևյալ RANDBETWEEN(1;2) ֆունկցիային, որը վերադարձնում է պատահական թիվ 1-ի և 2-ի միջև: Այս ֆունկցիայի օգտագործմամբ 20 հաշվարկ է եղել: Ստացված արդյունքների հիման վրա որոշե՛ք համապատասխանաբար 1 և 2 թվերի ի հայտ գալու փաստացի հավանականությունները։

Եկեք լրացնենք բնօրինակ աղյուսակը 1-ից 2-ի պատահական արժեքներով.

Աղբյուրի աղյուսակում պատահական արժեքները որոշելու համար օգտագործվել է հատուկ գործառույթ.

RANDBETWEEN (1,2)

Ստեղծված 1-ի և 2-ի թիվը որոշելու համար մենք օգտագործում ենք ֆունկցիան.

ՀԱՃԱԽԱԿԱՆՈՒԹՅՈՒՆ (A2:A21;1)

Փաստարկների նկարագրությունը.

• A2:A21 – արժեքների զանգված, որը ստեղծվում է ֆունկցիայի =RANDBETWEEN(1,2) արժեքներով;
• 1 – որոնման չափանիշ (FREQUENCY ֆունկցիան որոնում է արժեքներ 0-ից 1-ը ներառյալ և արժեքներ>1):

Արդյունքում մենք ստանում ենք.

Եկեք հաշվարկենք հավանականությունները՝ յուրաքանչյուր տեսակի իրադարձությունների թիվը բաժանելով դրանց ընդհանուր թվի վրա.

Իրադարձությունների քանակը հաշվելու համար օգտագործեք =COUNT($A$2:$A$21) ֆունկցիան: Կամ կարող եք պարզապես բաժանել 20 արժեքի վրա: Եթե պատահական արժեքներով իրադարձությունների քանակը և տիրույթի չափը նախապես հայտնի չեն, ապա COUNT-ի արգումենտներում կարող եք հղում կատարել ամբողջ սյունակին: ֆունկցիա՝ =COUNT(A:A): Սա ավտոմատ կերպով կհաշվի A սյունակի թվերի թիվը:

«1» և «2» գլորվելու հավանականությունը համապատասխանաբար 0,45 և 0,55 է: Համոզվեք, որ E2:E3 բջիջներին տվեք տոկոսային ձևաչափ՝ իրենց արժեքները որպես տոկոսներ ցուցադրելու համար՝ 45% և 55%:

Այժմ եկեք օգտագործենք ավելի բարդ բանաձև՝ առավելագույն կրկնության արագությունը հաշվարկելու համար.

!}

F2 և F3 բջիջների բանաձևերը տարբերվում են միայն մեկ թվով «ոչ հավասար» համեմատության օպերատորից հետո.<>1 և<>2.

Հետաքրքիր փաստ!Օգտագործելով այս բանաձևը, դուք հեշտությամբ կարող եք ստուգել, ​​թե ինչու խաղադրույքները կրկնապատկելու ռազմավարությունը չի գործում կազինո ռուլետկաում: Դրամախաղում խաղադրույքների կառավարման այս ռազմավարությունը կոչվում է նաև Martingale: Փաստն այն է, որ անընդմեջ պատահական կրկնությունների թիվը կարող է հասնել 18 անգամ կամ ավելի, այսինքն՝ տասնութ անգամ անընդմեջ կարմիր կամ սև: Օրինակ, եթե դուք կրկնապատկեք 2 դոլարի խաղադրույքը 18 անգամ, դա արդեն կես միլիոն դոլարի անկում է: Սա արդեն ձախողում է ռիսկերի պլանավորման ցանկացած տեխնիկայի համաձայն: Պետք է հաշվի առնել նաև, որ բացի «սևից» և «կարմիրից», երբեմն հայտնվում է նաև «զրո», որն ամբողջությամբ ոչնչացնում է բոլոր շանսերը։ Հետաքրքիր է նաև, որ ռուլետկա բոլոր թվերի գումարը 0-ից մինչև 36-ը 666 է։

Ինչպե՞ս հաշվել չկրկնվող արժեքները Excel-ում:

Օրինակ 3. Որոշեք թվային տվյալների զանգվածում եզակի երևույթների քանակը, այսինքն՝ չկրկնվող արժեքները:

Աղբյուրի աղյուսակ.

Եկեք որոշենք պահանջվող արժեքը բանաձևով.

!}

Այս դեպքում FREQUENCY ֆունկցիան ստուգում է տվյալների զանգվածի տարրերից յուրաքանչյուրի առկայությունը նույն տվյալների զանգվածում (երկու արգումենտները նույնն են): Օգտագործելով IF ֆունկցիան՝ սահմանվում է պայման, որն ունի հետևյալ նշանակությունը.

1. Եթե ​​ձեր փնտրած տարրը գտնվում է արժեքների միջակայքում, 1-ը կվերադարձվի դեպքերի իրական քանակի փոխարեն.
2. Եթե ​​ձեր փնտրած տարրը գոյություն չունի, 0 (զրո) կվերադարձվի:

Ստացված արժեքը (միավորների քանակը) ամփոփվում է:

Արդյունքում մենք ստանում ենք.

Այսինքն՝ նշված զանգվածը պարունակում է 8 եզակի արժեք։

FREQUENCY ֆունկցիան Excel-ում և դրա շարահյուսության առանձնահատկությունները

Այս ֆունկցիան ունի հետևյալ շարահյուսությունը.

Ֆունկցիայի փաստարկների նկարագրությունը (երկուսն էլ պարտադիր են).

• data_array - տվյալներ զանգվածի տեսքով կամ հղումներ մի շարք արժեքների, որոնց համար հաճախականությունները պետք է որոշվեն:
• interval_array - զանգվածի ձևաչափով տվյալները կամ հղումը արժեքների մի շարք չեն, որոնց մեջ խմբավորված են այս ֆունկցիայի առաջին արգումենտի արժեքները:

Ծանոթագրություններ 1:

1. Եթե ​​դատարկ զանգվածը կամ դատարկ արժեքների տիրույթի հղումը փոխանցվել է որպես range_array արգումենտ, FREQUENCY ֆունկցիայի արդյունքը կլինի տվյալների տիրույթում ներառված տարրերի թիվը, որոնք փոխանցվել են որպես առաջին արգումենտ:
2. FREQUENCY ֆունկցիան որպես սովորական Excel ֆունկցիա օգտագործելիս կվերադարձվի interval_array-ում առաջին երևույթին համապատասխանող մեկ արժեքը (այսինքն՝ առաջին պատահականության հաճախականության որոնման չափանիշը):
3. Այս ֆունկցիայի կողմից վերադարձված տարրերի զանգվածը պարունակում է մեկ տարր ավելի, քան interval_array-ում պարունակվող տարրերի թիվը։ Դա պայմանավորված է նրանով, որ FREQUENCY ֆունկցիան նաև հաշվարկում է այն արժեքների առաջացման քանակը, որոնց արժեքները գերազանցում են միջակայքերի վերին սահմանը: Օրինակ, տվյալների հավաքածուում 2,7, 10, 13, 18, 4, 33, 26, դուք պետք է գտնեք արժեքների առաջացման քանակը 1-ից 10, 11-ից 20, 21-ից 30 միջակայքերում, և 30-ից ավելի: Տարածքի զանգվածը պետք է պարունակի միայն դրանց սահմանային արժեքները, այսինքն՝ 10, 20 և 30: Ֆունկցիան կարող է գրվել հետևյալ ձևով՝ =FREQUENCY((2;7;10;13;18;4;33): ;26);(10;20;30)), և դրա կատարման արդյունքը կլինի չորս բջիջներից բաղկացած սյունակ, որը պարունակում է հետևյալ արժեքները՝ 4,2, 1, 1: Վերջին արժեքը համապատասխանում է դեպքերի թվին թվեր > 30 տվյալների զանգվածում: Այդպիսի թիվ իսկապես կա միայն մեկ՝ 33։
4. Եթե ​​տվյալների_զանգվածը պարունակում է բջիջներ, որոնք պարունակում են դատարկ արժեքներ կամ տեքստ, դրանք կբացակայվեն FREQUENCY ֆունկցիայի կողմից հաշվարկման գործընթացում:

Ծանոթագրություններ 2:

1. Ֆունկցիան կարող է օգտագործվել վիճակագրական վերլուծություն կատարելու համար, օրինակ՝ որոշելու հաճախորդների շրջանում ամենահայտնի ապրանքները:

ՀԱՃԱԽԱԿԱՆՈՒԹՅՈՒՆ (տվյալների_զանգված, միջակայքի_զանգված)

2. Այս ֆունկցիան պետք է օգտագործվի որպես զանգվածի բանաձև, քանի որ նրա վերադարձած տվյալները զանգվածի տեսքով են: Սովորական բանաձևերը կատարելու համար դրանք մուտքագրելուց հետո պետք է սեղմել Enter կոճակը: Այս դեպքում անհրաժեշտ է օգտագործել Ctrl+Shift+Enter ստեղնաշարի համադրությունը:

Կարևոր ֆիզիկական պարամետր, որն անհրաժեշտ է ակուստիկայի և ռադիոէլեկտրոնիկայի բազմաթիվ խնդիրների լուծման համար: Այն կարելի է հաշվարկել մի քանի եղանակով՝ կախված նրանից, թե ինչ պարամետրեր են նշված։ Դա անելը ամենահարմարն է, եթե գիտեք տարածման հաճախականությունը կամ ժամանակահատվածը և արագությունը:

Բանաձևեր

Հիմնական բանաձևը, որը պատասխանում է այն հարցին, թե ինչպես գտնել ալիքի երկարությունը հաճախականության միջոցով, ներկայացված է ստորև.

Այստեղ l-ն ալիքի երկարությունն է մետրերով, v-ն դրա տարածման արագությունն է մ/վ, u-ն՝ գծային հաճախականությունը հերցով։

Քանի որ հաճախականությունը կապված է հակադարձ հարաբերությունների ժամանակաշրջանի հետ, նախորդ արտահայտությունը կարող է տարբեր կերպ գրվել.

T-ն տատանումների ժամանակաշրջանն է վայրկյաններով:

Այս պարամետրը կարող է արտահայտվել ցիկլային հաճախականությամբ և փուլային արագությամբ.

l = 2 pi*v/w

Այս արտահայտության մեջ w-ը ցիկլային հաճախականությունն է՝ արտահայտված ռադիաններով վայրկյանում։

Երկարության միջով ալիքի հաճախականությունը, ինչպես երևում է նախորդ արտահայտությունից, հայտնաբերվում է հետևյալ կերպ.

Դիտարկենք էլեկտրամագնիսական ալիք, որը տարածվում է n-ով նյութում: Այնուհետև ալիքի հաճախականությունը երկարությամբ արտահայտվում է հետևյալ հարաբերությամբ.

Եթե ​​այն տարածվում է վակուումում, ապա n = 1, և արտահայտությունը ստանում է հետևյալ ձևը.

Վերջին բանաձևում ալիքի հաճախականությունը երկարությամբ արտահայտվում է՝ օգտագործելով c հաստատունը՝ լույսի արագությունը վակուումում, c=300000 կմ/վրկ։

Այս բաժինն ուսումնասիրելիս խնդրում ենք նկատի ունենալ, որ տատանումներտարբեր ֆիզիկական բնույթի նկարագրված են ընդհանուր մաթեմատիկական դիրքերից: Այստեղ անհրաժեշտ է հստակ հասկանալ այնպիսի հասկացություններ, ինչպիսիք են ներդաշնակ տատանումը, փուլը, փուլային տարբերությունը, ամպլիտուդը, հաճախականությունը, տատանումների ժամանակաշրջանը։

Պետք է նկատի ունենալ, որ ցանկացած իրական տատանողական համակարգում կա միջավայրի դիմադրություն, այսինքն. տատանումները կխոնավվեն։ Տատանումների մարումը բնութագրելու համար ներկայացվում են մարման գործակից և լոգարիթմական մարման նվազում:

Եթե ​​տատանումները տեղի են ունենում արտաքին, պարբերաբար փոփոխվող ուժի ազդեցությամբ, ապա այդպիսի տատանումները կոչվում են հարկադիր։ Դրանք չխոնավեցվելու են: Հարկադիր տատանումների ամպլիտուդը կախված է շարժիչ ուժի հաճախականությունից։ Քանի որ հարկադիր տատանումների հաճախականությունը մոտենում է բնական տատանումների հաճախականությանը, հարկադրված տատանումների ամպլիտուդը կտրուկ մեծանում է։ Այս երեւույթը կոչվում է ռեզոնանս։

Անցնելով էլեկտրամագնիսական ալիքների ուսումնասիրությանը, դուք պետք է հստակ հասկանաք դաէլեկտրամագնիսական ալիքտիեզերքում տարածվող էլեկտրամագնիսական դաշտ է։ Էլեկտրամագնիսական ալիքներ արձակող ամենապարզ համակարգը էլեկտրական դիպոլն է։ Եթե ​​դիպոլը ենթարկվում է ներդաշնակ տատանումների, ապա այն արձակում է միագույն ալիք։

Բանաձևերի աղյուսակ. տատանումներ և ալիքներ

Ֆիզիկական օրենքներ, բանաձևեր, փոփոխականներ	Տատանումների և ալիքների բանաձևեր
Հարմոնիկ թրթռման հավասարում. որտեղ x-ը տատանվող մեծության տեղաշարժն է (շեղումը) հավասարակշռության դիրքից. A - ամպլիտուդություն; ω - շրջանաձև (ցիկլային) հաճախականություն; α - նախնական փուլ; (ωt+α) - փուլ.
Ժամանակահատվածի և շրջանաձև հաճախականության միջև կապը.
Հաճախականությունը:
Շրջանաձև հաճախականության և հաճախականության միջև կապը.
Բնական տատանումների ժամանակաշրջաններ 1) զսպանակային ճոճանակ. որտեղ k-ն զսպանակի կոշտությունն է; 2) մաթեմատիկական ճոճանակ. որտեղ l-ը ճոճանակի երկարությունն է, g - ազատ անկման արագացում; 3) տատանողական միացում. որտեղ L-ը շղթայի ինդուկտիվությունն է, C-ն կոնդենսատորի հզորությունն է:
Բնական հաճախականություն.
Նույն հաճախականության և ուղղության տատանումների գումարում. 1) արդյունքում առաջացող տատանումների ամպլիտուդը որտեղ A 1 և A 2-ը թրթռման բաղադրիչների ամպլիտուդներն են, α 1 և α 2 - թրթռման բաղադրիչների սկզբնական փուլերը. 2) առաջացած տատանման սկզբնական փուլը
Խոնավ տատանումների հավասարումը. e = 2,71... - բնական լոգարիթմների հիմքը:
Խոնավ տատանումների լայնությունը. որտեղ A 0-ը ժամանակի սկզբնական պահին ամպլիտուդն է. β - թուլացման գործակից;
Թուլացման գործակիցը: տատանվող մարմին որտեղ r-ը միջավայրի դիմադրության գործակիցն է, մ - մարմնի քաշը; տատանողական միացում որտեղ R-ն ակտիվ դիմադրություն է, L-ն շղթայի ինդուկտիվությունն է:
Խոնավ տատանումների հաճախականությունը ω:
Թուլացած տատանումների ժամանակաշրջանը T:
Լոգարիթմական մարման նվազում.
χ լոգարիթմական նվազման և β թուլացման գործակցի միջև կապը.
Հարկադիր տատանումների առատություն որտեղ ω-ն հարկադիր տատանումների հաճախականությունն է, f o - շարժիչ ուժի կրճատված ամպլիտուդ, մեխանիկական թրթռումներով. էլեկտրամագնիսական թրթռումներով.

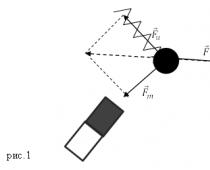
Այն ժամանակը, որի ընթացքում տեղի է ունենում էմֆ-ի մեկ ամբողջական փոփոխություն, այսինքն՝ տատանումների մեկ ցիկլ կամ շառավղով վեկտորի մեկ ամբողջական պտույտ, կոչվում է. փոփոխական հոսանքի տատանումների ժամանակաշրջան(նկար 1):

Նկար 1. Սինուսոիդային տատանումների ժամանակաշրջանը և ամպլիտուդը: Ժամանակահատվածը մեկ տատանման ժամանակն է. Ամպլիտուդությունը նրա ամենամեծ ակնթարթային արժեքն է:

Կետն արտահայտվում է վայրկյաններով և նշվում տառով Տ.

Օգտագործվում են նաև ժամանակաշրջանի չափման ավելի փոքր միավորներ՝ միլիվայրկյան (մս)՝ վայրկյանի հազարերորդականը և միկրովայրկյան (μs)՝ վայրկյանի մեկ միլիոներորդ մասը։

1 ms = 0.001 վ = 10 -3 վրկ.

1 μs = 0,001 ms = 0,000001 վրկ = 10 -6 վրկ.

1000 մկվ = 1 ms.

Էմֆ-ի ամբողջական փոփոխությունների թիվը կամ շառավղային վեկտորի պտույտների թիվը, այսինքն՝ մեկ վայրկյանում փոփոխական հոսանքի միջոցով կատարվող տատանումների ամբողջական ցիկլերի թիվը կոչվում է. AC տատանումների հաճախականությունը.

Հաճախականությունը նշվում է տառով զ և արտահայտվում է վայրկյանում ցիկլերով կամ հերցով։

Հազար հերցը կոչվում է կիլոհերց (կՀց), իսկ միլիոն հերցը՝ մեգահերց (ՄՀց): Գոյություն ունի նաև հազար մեգահերցին հավասար գիգահերց (ԳՀց):

1000 Հց = 10 3 Հց = 1 կՀց;

1000 000 Հց = 10 6 Հց = 1000 կՀց = 1 ՄՀց;

1000 000 000 Հց = 10 9 Հց = 1000 000 կՀց = 1000 ՄՀց = 1 ԳՀց;

Որքան արագ է փոխվում EMF-ը, այսինքն՝ որքան արագ է պտտվում շառավիղի վեկտորը, այնքան ավելի կարճ է տատանումների շրջանը, այնքան ավելի արագ է պտտվում շառավիղի վեկտորը, այնքան բարձր է հաճախականությունը: Այսպիսով, փոփոխական հոսանքի հաճախականությունը և ժամանակահատվածը միմյանց հակադարձ համեմատական ​​մեծություններ են: Որքան մեծ է դրանցից մեկը, այնքան փոքր է մյուսը:

Փոփոխական հոսանքի և լարման ժամանակաշրջանի և հաճախականության մաթեմատիկական կապն արտահայտվում է բանաձևերով

Օրինակ, եթե ընթացիկ հաճախականությունը 50 Հց է, ապա պարբերությունը հավասար կլինի.

T = 1 / f = 1/50 = 0,02 վրկ.

Եվ հակառակը, եթե հայտնի է, որ հոսանքի ժամանակաշրջանը 0,02 վրկ է, (T = 0,02 վրկ.), ապա հաճախականությունը հավասար կլինի.

f = 1/T=1/0.02 = 100/2 = 50 Հց

Լուսավորման և արդյունաբերական նպատակներով օգտագործվող փոփոխական հոսանքի հաճախականությունը ուղիղ 50 Հց է։

20-ից 20000 Հց հաճախականությունները կոչվում են աուդիո հաճախականություններ: Ռադիոկայանների ալեհավաքներում հոսանքները տատանվում են մինչև 1,500,000,000 Հց կամ, այլ կերպ ասած, մինչև 1500 ՄՀց կամ 1,5 ԳՀց հաճախականությամբ: Այս բարձր հաճախականությունները կոչվում են ռադիոհաճախականություններ կամ բարձր հաճախականության թրթռումներ։

Ի վերջո, ռադիոլոկացիոն կայանների, արբանյակային կապի կայանների և այլ հատուկ համակարգերի ալեհավաքների հոսանքները (օրինակ՝ GLANASS, GPS) տատանվում են մինչև 40000 ՄՀց (40 ԳՀց) և ավելի հաճախականությամբ:

AC հոսանքի ամպլիտուդ

Ամենամեծ արժեքը, որին emf-ը կամ հոսանքը հասնում է մեկ ժամանակահատվածում, կոչվում է emf կամ փոփոխական հոսանքի ամպլիտուդ. Հեշտ է նկատել, որ սանդղակի ամպլիտուդը հավասար է շառավղի վեկտորի երկարությանը։ Ընթացիկ, EMF և լարման ամպլիտուդները նշանակվում են համապատասխանաբար տառերով Ես, Էմը և Ումը (նկար 1):

Փոփոխական հոսանքի անկյունային (ցիկլային) հաճախականություն:

Շառավղի վեկտորի պտտման արագությունը, այսինքն՝ պտտման անկյան փոփոխությունը մեկ վայրկյանում, կոչվում է փոփոխական հոսանքի անկյունային (ցիկլային) հաճախականություն և նշվում է հունարեն տառով։ ? (օմեգա): Շառավղի վեկտորի պտտման անկյունը ցանկացած պահի իր սկզբնական դիրքի համեմատ սովորաբար չափվում է ոչ թե աստիճաններով, այլ հատուկ միավորներով՝ ռադիաններով։

Ռադիանը շրջանագծի աղեղի անկյունային արժեքն է, որի երկարությունը հավասար է այս շրջանագծի շառավղին (Նկար 2): Ամբողջ շրջանագիծը, որը կազմում է 360°, հավասար է 6,28 ռադիանի, այսինքն՝ 2-ի։

Նկար 2.

1 ռադ = 360°/2

Հետևաբար, շառավիղի վեկտորի վերջը մեկ ժամանակահատվածում ընդգրկում է 6,28 ռադիանի հավասար ճանապարհ (2): Քանի որ մեկ վայրկյանում շառավիղի վեկտորը կատարում է մի շարք պտույտներ, որոնք հավասար են փոփոխական հոսանքի հաճախականությանը զ, ապա մեկ վայրկյանում նրա ծայրը ծածկում է հավասար ճանապարհ 6.28 * զռադիան. Շառավիղի վեկտորի պտտման արագությունը բնութագրող այս արտահայտությունը կլինի փոփոխական հոսանքի անկյունային հաճախականությունը - ? .

? = 6.28*f = 2f

Շառավիղի վեկտորի պտտման անկյունը ցանկացած ակնթարթում սկզբնական դիրքի համեմատ կոչվում է AC փուլ. Փուլը բնութագրում է EMF-ի (կամ հոսանքի) մեծությունը տվյալ ակնթարթում կամ, ինչպես ասում են, EMF-ի ակնթարթային արժեքը, դրա ուղղությունը միացումում և դրա փոփոխության ուղղությունը. փուլը ցույց է տալիս, թե արդյոք emf-ը նվազում է, թե ավելանում:

Նկար 3.

Շառավիղի վեկտորի ամբողջական պտույտը 360° է: Շառավիղի վեկտորի նոր հեղափոխության սկզբում EMF-ը փոխվում է նույն կարգով, ինչ առաջին հեղափոխության ժամանակ: Հետևաբար, EMF-ի բոլոր փուլերը կկրկնվեն նույն հերթականությամբ: Օրինակ, EMF-ի փուլը, երբ շառավիղի վեկտորը պտտվում է 370° անկյան տակ, կլինի նույնը, ինչ 10°-ով պտտվող ժամանակ: Այս երկու դեպքերում էլ շառավիղի վեկտորը զբաղեցնում է նույն դիրքը, և, հետևաբար, emf-ի ակնթարթային արժեքները այս երկու դեպքերում էլ փուլային նույնը կլինեն:

Սահմանում

Հաճախականությունֆիզիկական պարամետր է, որն օգտագործվում է պարբերական գործընթացները բնութագրելու համար: Հաճախականությունը հավասար է ժամանակի միավորի վրա իրադարձությունների կրկնությունների կամ դեպքերի քանակին:

Ամենից հաճախ ֆիզիկայում հաճախականությունը նշվում է $\nu տառով, $ երբեմն հաճախականության այլ նշանակումներ են հանդիպում, օրինակ՝ $f$ կամ $F$։

Հաճախականությունը (ժամանակի հետ մեկտեղ) ամենաճիշտ չափված մեծությունն է։

Թրթռումների հաճախականության բանաձևը

Հաճախականությունը օգտագործվում է թրթռումները բնութագրելու համար: Այս դեպքում հաճախականությունը ֆիզիկական մեծություն է, որը փոխադարձ է $(T) տատանումների ժամանակաշրջանին:

\[\nu =\frac(1)(T)\ձախ(1\աջ):\]

Հաճախականությունը, այս դեպքում, ամբողջական տատանումների թիվն է ($N$), որը տեղի է ունենում ժամանակի մեկ միավորի համար.

\[\nu =\frac(N)(\Delta t)\ձախ(2\աջ),\]

որտեղ $\Delta t$-ն այն ժամանակն է, որի ընթացքում տեղի են ունենում $N$ տատանումներ:

Միավորների միջազգային համակարգում (SI) հաճախականության միավորը հերցն է կամ փոխադարձ վայրկյանները.

\[\ձախ[\nu \աջ]=ս^(-1)=Հց.\]

Հերցը պարբերական պրոցեսի հաճախականության չափման միավոր է, որի ժամանակ պրոցեսի մեկ ցիկլը տեղի է ունենում մեկ վայրկյանին հավասար ժամանակում։ Պարբերական պրոցեսի հաճախականությունը չափող միավորն իր անունը ստացել է գերմանացի գիտնական Գ.Հերցի պատվին։

Զարկերի հաճախականությունը, որոնք առաջանում են մեկ ուղիղ գծի երկայնքով տարբեր, բայց նման հաճախականություններով ($(\nu )_1\ և\ (\nu)_2$) տատանումներ գումարելիս հավասար է.

\[(\nu =\nu )_1-\ (\nu )_2\ ձախ (3\ աջ):\]

Տատանողական գործընթացը բնութագրող մեկ այլ մեծություն է ցիկլային հաճախականությունը ($(\omega )_0$), որը կապված է հաճախականության հետ՝ որպես.

\[(\omega)_0=2\pi \nu \ձախ(4\աջ):\]

Ցիկլային հաճախականությունը չափվում է ռադիաններով՝ բաժանված վայրկյանում.

\[\ձախ[(\omega )_0\աջ]=\frac(rad)(s).\]

$\ m,$ զանգված ունեցող մարմնի տատանումների հաճախականությունը, որը կախված է $k$ առաձգականության գործակից ունեցող զսպանակի վրա, հավասար է.

\[\nu =\frac(1)(2\pi \sqrt((m)/(k)))\ձախ(5\աջ):\]

Բանաձևը (4) ճիշտ է առաձգական, փոքր թրթռումների համար: Բացի այդ, աղբյուրի զանգվածը պետք է փոքր լինի այս աղբյուրին ամրացված մարմնի զանգվածի համեմատ։

Մաթեմատիկական ճոճանակի համար տատանումների հաճախականությունը հաշվարկվում է հետևյալ կերպ՝ թելի երկարությունը.

\[\nu =\frac(1)(2\pi \sqrt((l)/(g)))\ձախ(6\աջ),\]

որտեղ $g$-ը ազատ անկման արագացումն է. $\l$-ը ճոճանակի թելի երկարությունն է (կախոցի երկարությունը):

Ֆիզիկական ճոճանակը տատանվում է հաճախականությամբ.

\[\nu =\frac(1)(2\pi \sqrt((J)/(mgd)))\ձախ(7\աջ),\]

որտեղ $J$-ը առանցքի շուրջ տատանվող մարմնի իներցիայի պահն է. $d$-ը ճոճանակի զանգվածի կենտրոնից մինչև տատանման առանցքը հեռավորությունն է։

(4) - (6) բանաձևերը մոտավոր են։ Որքան փոքր է տատանումների ամպլիտուդը, այնքան ավելի ճշգրիտ է դրանց օգնությամբ հաշվարկված տատանումների հաճախականության արժեքը։

Դիսկրետ իրադարձությունների հաճախականության, պտտման արագության հաշվարկման բանաձևեր

դիսկրետ տատանումներ ($n$) - կոչվում է ֆիզիկական մեծություն, որը հավասար է ժամանակի միավորի համար գործողությունների (իրադարձությունների) թվին: Եթե ​​մեկ իրադարձության տևող ժամանակը նշվում է որպես $\tau $, ապա դիսկրետ իրադարձությունների հաճախականությունը հավասար է.

Դիսկրետ իրադարձությունների հաճախականության չափման միավորը փոխադարձ երկրորդն է.

\[\left=\frac(1)(с).\]

Մի վայրկյանը մինուս առաջին հզորությանը հավասար է դիսկրետ իրադարձությունների հաճախականությանը, եթե մեկ իրադարձություն տեղի է ունենում մեկ վայրկյանին հավասար ժամանակում:

Պտտման հաճախականությունը ($n$) արժեք է, որը հավասար է մարմնի լրիվ պտույտների քանակին մեկ միավոր ժամանակում: Եթե ​​$\tau$-ը մեկ ամբողջական հեղափոխության վրա ծախսված ժամանակն է, ապա.

Լուծումների հետ կապված խնդիրների օրինակներ

Օրինակ 1

Զորավարժություններ.Տատանողական համակարգը մեկ րոպեին հավասար ժամանակում կատարել է 600 տատանումներ ($\Delta t=1\min$)։ Ո՞րն է այս թրթռումների հաճախականությունը:

Լուծում.Խնդիրը լուծելու համար մենք կօգտագործենք տատանումների հաճախականության սահմանումը. Հաճախականությունը, այս դեպքում, ժամանակի մեկ միավորում տեղի ունեցող ամբողջական տատանումների թիվն է:

\[\nu =\frac(N)(\Delta t)\ձախ (1.1\աջ):\]

Նախքան հաշվարկներին անցնելը, եկեք ժամանակը փոխարկենք SI միավորների՝ $\Delta t=1\ min=60\ s$։ Եկեք հաշվարկենք հաճախականությունը.