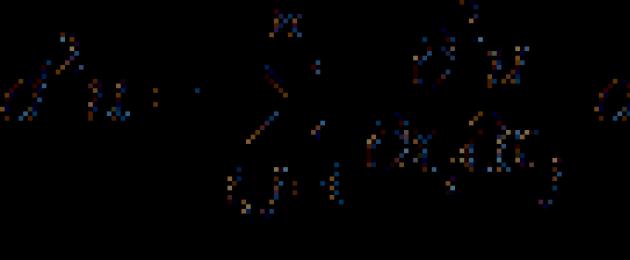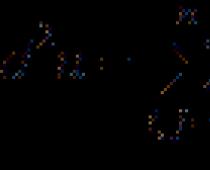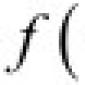Պայմանական էքստրեմում.

Մի քանի փոփոխականների ֆունկցիայի ծայրահեղություն

Նվազագույն քառակուսիների մեթոդ.

FNP-ի տեղական ծայրահեղություն

Թող ֆունկցիան տրվի Եվ= զ(P), РÎDÌR nև թողեք P 0 կետը ( Ա 1 , Ա 2 , ..., a p) –ներքինհավաքածուի կետ Դ.

Սահմանում 9.4.

1) P 0 կետը կոչվում է առավելագույն միավոր գործառույթները Եվ= զ(P), եթե այս կետի U(P 0) М D հարևանություն կա այնպես, որ ցանկացած P( կետի համար X 1 , X 2 , ..., x n)О U(P 0) , Р¹Р 0 , պայմանը բավարարված է զ(P)£ զ(P 0) . Իմաստը զ(P 0) ֆունկցիան առավելագույն կետում կոչվում է գործառույթի առավելագույնը և նշանակված է զ(P0) = առավելագույնը զ(P) .

2) P 0 կետը կոչվում է նվազագույն միավոր գործառույթները Եվ= զ(P), եթե այս կետի U(P 0)Ì D այնպիսի հարևանություն կա, որ ցանկացած P( կետի համար X 1 , X 2 , ..., x n)ОU(P 0), Р¹Р 0 , պայմանը բավարարված է զ(P)³ զ(P 0) . Իմաստը զ(P 0) ֆունկցիան նվազագույն կետում կոչվում է նվազագույն գործառույթ և նշանակված է զ(P 0) = min զ(P).

Ֆունկցիայի նվազագույն և առավելագույն կետերը կոչվում են ծայրահեղ միավորներ, ծայրահեղ կետերում ֆունկցիայի արժեքները կոչվում են ֆունկցիայի ծայրահեղություն:

Ինչպես հետևում է սահմանումից՝ անհավասարությունները զ(P)£ զ(P 0), զ(P)³ զ(P 0) պետք է բավարարվի միայն P 0 կետի որոշակի հարևանությամբ, և ոչ թե ֆունկցիայի սահմանման ողջ տիրույթում, ինչը նշանակում է, որ ֆունկցիան կարող է ունենալ միևնույն տիպի մի քանի ծայրահեղություններ (մի քանի նվազագույն, մի քանի առավելագույն) . Հետեւաբար, վերը սահմանված ծայրահեղությունները կոչվում են տեղական(տեղական) ծայրահեղություններ.

Թեորեմ 9.1 (անհրաժեշտ պայման FNP-ի ծայրահեղության համար)

Եթե ​​ֆունկցիան Եվ= զ(X 1 , X 2 , ..., x n) ունի ծայրահեղություն P 0 կետում, ապա նրա առաջին կարգի մասնակի ածանցյալներն այս կետում կամ հավասար են զրոյի, կամ գոյություն չունեն։

Ապացույց.Թողեք P 0 կետում ( Ա 1 , Ա 2 , ..., a p) գործառույթ Եվ= զ(P) ունի ծայրահեղություն, օրինակ, առավելագույնը: Եկեք շտկենք փաստարկները X 2 , ..., x n, դնելով X 2 =Ա 2 ,..., x n = a p. Հետո Եվ= զ(P) = զ 1 ((X 1 , Ա 2 , ..., a p) մեկ փոփոխականի ֆունկցիա է X 1. Քանի որ այս ֆունկցիան ունի X 1 = Ա 1 էքստրեմում (առավելագույնը), ապա զ 1 ¢=0 կամ գոյություն չունի, երբ X 1 =Ա 1 (անհրաժեշտ պայման մեկ փոփոխականի ֆունկցիայի ծայրահեղության գոյության համար): Բայց դա նշանակում է կամ գոյություն չունի P 0 կետում՝ ծայրահեղ կետում: Նմանապես, մենք կարող ենք դիտարկել մասնակի ածանցյալներ այլ փոփոխականների նկատմամբ: CTD.

Ֆունկցիայի տիրույթի այն կետերը, որոնցում առաջին կարգի մասնակի ածանցյալները հավասար են զրոյի կամ գոյություն չունեն, կոչվում են. կրիտիկական կետեր այս գործառույթը:

Ինչպես հետևում է 9.1 թեորեմից, FNP-ի ծայրահեղ կետերը պետք է փնտրել ֆունկցիայի կրիտիկական կետերի շարքում: Բայց, ինչ վերաբերում է մեկ փոփոխականի ֆունկցիային, ապա ամեն կրիտիկական կետ չէ, որ ծայրահեղ կետ է:

Թեորեմ 9.2 (բավարար պայման FNP-ի ծայրահեղության համար)

Թող P 0 լինի ֆունկցիայի կրիտիկական կետը Եվ= զ(P) և այս ֆունկցիայի երկրորդ կարգի դիֆերենցիալն է: Հետո

ա) եթե դ 2 u(P 0) > 0 ժամը , ապա P 0 կետ է նվազագույնըգործառույթները Եվ= զ(P);

բ) եթե դ 2 u(P0)< 0 при , то Р 0 – точка առավելագույնըգործառույթները Եվ= զ(P);

գ) եթե դ 2 u(P 0) նշանով սահմանված չէ, ապա P 0-ը ծայրահեղ կետ չէ.

Այս թեորեմը մենք կդիտարկենք առանց ապացույցի:

Նշենք, որ թեորեմը չի դիտարկում այն ​​դեպքը, երբ դ 2 u(P 0) = 0 կամ գոյություն չունի: Սա նշանակում է, որ նման պայմաններում P 0 կետում ծայրահեղության առկայության հարցը մնում է բաց. անհրաժեշտ է լրացուցիչ հետազոտություն, օրինակ՝ այս պահին ֆունկցիայի աճի ուսումնասիրություն։

Մաթեմատիկայի ավելի մանրամասն դասընթացներում ապացուցված է, որ, մասնավորապես, ֆունկցիայի համար z = f(x,y) երկու փոփոխականների, որոնց երկրորդ կարգի դիֆերենցիալը ձևի գումարն է

P 0 կրիտիկական կետում էքստրեմումի առկայության ուսումնասիրությունը կարելի է պարզեցնել:

Նշանակենք , , . Կազմենք որոշիչ

.

Պարզվում է՝

դ 2 զ> 0 P 0 կետում, այսինքն. P 0 – նվազագույն միավոր, եթե Ա(P 0) > 0 և D (P 0) > 0;

դ 2 զ < 0 в точке Р 0 , т.е. Р 0 – точка максимума, если Ա(P0)< 0 , а D(Р 0) > 0;

եթե D (P 0)< 0, то դ 2 զ P 0 կետի շրջակայքում այն ​​փոխում է նշանը և P 0 կետում ծայրահեղություն չկա.

եթե D(Р 0) = 0, ապա պահանջվում են նաև Р 0 կրիտիկական կետի շրջակայքում ֆունկցիայի լրացուցիչ ուսումնասիրություններ։

Այսպիսով, ֆունկցիայի համար z = f(x,y) երկու փոփոխականներից մենք ունենք հետևյալ ալգորիթմը (եկեք այն անվանենք «ալգորիթմ D») ծայրահեղություն գտնելու համար.

1) Գտեք սահմանման տիրույթը D( զ) գործառույթներ.

2) Գտեք կրիտիկական կետեր, այսինքն. միավորներ D-ից ( զ), որոնց համար և հավասար են զրոյի կամ գոյություն չունեն։

3) յուրաքանչյուր կրիտիկական կետում P 0 ստուգեք էքստրեմումի բավարար պայմանները: Դա անելու համար գտեք , որտեղ , , և հաշվարկել D(P 0) և Ա(P 0): Այնուհետև:

եթե D(P 0) >0, ապա P 0 կետում կա ծայրահեղություն, և եթե Ա(P 0) > 0 – ապա սա նվազագույնն է, և եթե Ա(P 0)< 0 – максимум;

եթե D (P 0)< 0, то в точке Р­ 0 нет экстремума;

Եթե ​​D(P 0) = 0, ապա լրացուցիչ հետազոտություն է անհրաժեշտ:

4) Գտնված ծայրամասային կետերում հաշվարկե՛ք ֆունկցիայի արժեքը.

Օրինակ 1.

Գտեք ֆունկցիայի ծայրահեղությունը զ = x 3 + 8y 3 – 3xy .

Լուծում.Այս ֆունկցիայի սահմանման տիրույթը ամբողջ կոորդինատային հարթությունն է։ Եկեք գտնենք կրիտիկական կետերը:

, , Þ P 0 (0,0) , .

Եկեք ստուգենք, թե արդյոք բավարարված են էքստրեմի համար բավարար պայմանները։ Մենք կգտնենք

6X, = -3, = 48ժամըԵվ = 288xy – 9.

Այնուհետեւ D(P 0) = 288×0×0 – 9 = -9< 0 , значит, в точке Р 0 экстремума нет.

D(Р 1) = 36-9>0 – Р 1 կետում կա էքստրեմում, և քանի որ. Ա(P 1) = 3 >0, ապա այս ծայրահեղությունը նվազագույն է: Այսպիսով, մին զ=զ(P 1) = .

Օրինակ 2.

Գտեք ֆունկցիայի ծայրահեղությունը .

Լուծում: D ( զ) =R 2. Կրիտիկական կետեր. ; գոյություն չունի, երբ ժամը= 0, ինչը նշանակում է, որ P 0 (0,0) այս ֆունկցիայի կրիտիկական կետն է:

2, = 0, = , = , բայց D(P 0) սահմանված չէ, ուստի նրա նշանն ուսումնասիրելը անհնար է։

Նույն պատճառով անհնար է ուղղակիորեն կիրառել 9.2 թեորեմը. դ 2 զայս պահին գոյություն չունի:

Դիտարկենք ֆունկցիայի աճը զ(x, y) P 0 կետում: Եթե ​​Դ զ =զ(P) - զ(P 0)>0 «P, ապա P 0-ը նվազագույն կետն է, բայց եթե D զ < 0, то Р 0 – точка максимума.

Մեր դեպքում ունենք

Դ զ = զ(x, y) – զ(0, 0) = զ(0+D x,0+D y) – զ(0, 0) = .

Դ x= 0,1 և Դ y= -0,008 ստանում ենք Դ զ = 0,01 – 0,2 < 0, а при Dx= 0,1 և Դ y= 0,001 Դ զ= 0.01 + 0.1 > 0, այսինքն. P 0 կետի շրջակայքում D ոչ մի պայման չի բավարարվում զ <0 (т.е. զ(x, y) < զ(0, 0) և, հետևաբար, P 0-ը առավելագույն միավոր չէ), ոչ էլ պայման D զ>0 (այսինքն. զ(x, y) > զ(0, 0), ապա P 0-ը նվազագույն միավոր չէ): Սա նշանակում է, որ ըստ էքստրեմի սահմանման՝ այս ֆունկցիան ծայրահեղություն չունի։

Պայմանական էքստրեմում.

Ֆունկցիայի դիտարկված ծայրահեղությունը կոչվում է անվերապահ, քանի որ ֆունկցիայի արգումենտների վրա սահմանափակումներ (պայմաններ) չեն դրվում։

Սահմանում 9.2.Ֆունկցիայի ծայրահեղություն Եվ = զ(X 1 , X 2 , ... , x n), գտնվել է պայմանով, որ դրա փաստարկները X 1 , X 2 , ... , x nբավարարել j 1 հավասարումները ( X 1 , X 2 , ... , x n) = 0, …, ժ Տ(X 1 , X 2 , ... , x n) = 0, որտեղ P ( X 1 , X 2 , ... , x n) О D( զ), կանչեց պայմանական ծայրահեղություն .

Հավասարումներ ժ կ(X 1 , X 2 , ... , x n) = 0 , կ = 1, 2,..., մ, կոչվում են կապի հավասարումներ.

Եկեք նայենք գործառույթներին z = f(x,y) երկու փոփոխական. Եթե ​​կապի հավասարումը մեկն է, այսինքն. , ապա պայմանական ծայրահեղություն գտնելը նշանակում է, որ ծայրահեղությունը որոնվում է ոչ թե ֆունկցիայի սահմանման ողջ տիրույթում, այլ D(-ում գտնվող որոշ կորի վրա։ զ) (այսինքն՝ մակերեսի ամենաբարձր կամ ամենացածր կետերը չեն, որոնք փնտրում են z = f(x,y), և ամենաբարձր կամ ամենացածր կետերը այս մակերեսի մխոցի հետ հատման կետերի միջև, Նկար 5):

Ֆունկցիայի պայմանական ծայրահեղություն z = f(x,y) երկու փոփոխականներից կարելի է գտնել հետևյալ կերպ( վերացման մեթոդ) Հավասարումից արտահայտի՛ր փոփոխականներից մեկը մյուսի ֆունկցիայով (օրինակ՝ գրել ) և փոփոխականի այս արժեքը փոխարինելով ֆունկցիայի մեջ՝ գրի՛ր վերջինս որպես մեկ փոփոխականի ֆունկցիա (դիտարկվող դեպքում. ) Գտե՛ք մեկ փոփոխականի ստացված ֆունկցիայի ծայրահեղությունը:

Մի քանի փոփոխականների ֆունկցիաների ծայրահեղություն: Էքստրեմի համար անհրաժեշտ պայման. Բավարար պայման էքստրեմումի համար. Պայմանական էքստրեմում. Լագրանժի բազմապատկիչ մեթոդ. Գտնել ամենամեծ և ամենափոքր արժեքները:

Դասախոսություն 5.

Սահմանում 5.1.Կետ M 0 (x 0, y 0)կանչեց առավելագույն միավորգործառույթները z = f (x, y),Եթե f (x o, y o) > f(x,y)բոլոր կետերի համար (x, y) Մ 0.

Սահմանում 5.2.Կետ M 0 (x 0, y 0)կանչեց նվազագույն միավորգործառույթները z = f (x, y),Եթե f (x o, y o) < f(x,y)բոլոր կետերի համար (x, y)կետի ինչ-որ հարևանությամբ Մ 0.

Ծանոթագրություն 1. Առավելագույն և նվազագույն միավորները կոչվում են ծայրահեղ կետերմի քանի փոփոխականների գործառույթներ.

Դիտողություն 2. Ցանկացած թվով փոփոխականների ֆունկցիայի ծայրահեղ կետը որոշվում է նույն կերպ:

Թեորեմ 5.1(էքստրեմումի համար անհրաժեշտ պայմաններ). Եթե M 0 (x 0, y 0)- ֆունկցիայի ծայրահեղ կետ z = f (x, y),ապա այս պահին այս ֆունկցիայի առաջին կարգի մասնակի ածանցյալները հավասար են զրոյի կամ գոյություն չունեն։

Ապացույց.

Եկեք ֆիքսենք փոփոխականի արժեքը ժամը, հաշվելով y = y 0. Այնուհետև գործառույթը f (x, y 0)կլինի մեկ փոփոխականի ֆունկցիա X, որի համար x = x 0ծայրահեղ կետն է: Հետևաբար, Ֆերմայի թեորեմով կամ գոյություն չունի: Նույն հայտարարությունը նույն կերպ ապացուցված է նաև .

Սահմանում 5.3.Մի քանի փոփոխականների ֆունկցիայի տիրույթին պատկանող կետերը, որոնցում ֆունկցիայի մասնակի ածանցյալները հավասար են զրոյի կամ գոյություն չունեն, կոչվում են. անշարժ կետերայս գործառույթը:

Մեկնաբանություն. Այսպիսով, ծայրահեղությանը կարելի է հասնել միայն անշարժ կետերում, բայց պարտադիր չէ, որ այն դիտարկվի դրանցից յուրաքանչյուրում:

Թեորեմ 5.2(բավարար պայմաններ էքստրեմումի համար): Թողեք կետի ինչ-որ հարևանությամբ M 0 (x 0, y 0), որը ֆունկցիայի անշարժ կետն է z = f (x, y),այս ֆունկցիան ունի շարունակական մասնակի ածանցյալներ մինչև 3-րդ կարգի ներառյալ: Նշենք Հետո.

1) f(x,y)ունի կետում Մ 0առավելագույնը, եթե AC–B² > 0, Ա < 0;

2) f(x,y)ունի կետում Մ 0նվազագույնը, եթե AC–B² > 0, Ա > 0;

3) կրիտիկական կետում ծայրահեղություն չկա, եթե AC–B² < 0;

4) եթե AC–B² = 0, անհրաժեշտ է լրացուցիչ հետազոտություն:

Ապացույց.

Եկեք գրենք ֆունկցիայի երկրորդ կարգի Թեյլորի բանաձևը f (x,y),հիշելով, որ անշարժ կետում առաջին կարգի մասնակի ածանցյալները հավասար են զրոյի.

Որտեղ Եթե ​​հատվածի միջև ընկած անկյունը M 0 M, Որտեղ M (x 0 +Δ x, y 0 +Δ ժամը), և O առանցքը XՆշել φ, ապա Δ x =Δ ρ cos φ, Δ y=Δρsinφ. Այս դեպքում Թեյլորի բանաձևը կունենա հետևյալ ձևը. Թող Հետո մենք կարող ենք բաժանել և բազմապատկել փակագծերում տրված արտահայտությունը Ա. Մենք ստանում ենք.

Այժմ դիտարկենք չորս հնարավոր դեպքեր.

1) AC-B² > 0, Ա < 0. Тогда , и բավականաչափ փոքր Դր. Հետեւաբար, ինչ-որ թաղամասում M 0 f (x 0 + Δ x, y 0 +Δ y)< f (x 0, y 0), այսինքն Մ 0- առավելագույն միավոր.

2) Թող AC–B² > 0, A > 0.Հետո , Եվ Մ 0- նվազագույն միավոր.

3) Թող AC-B² < 0, Ա> 0. Դիտարկենք արգումենտների աճը φ = 0 ճառագայթի երկայնքով: Այնուհետև (5.1)-ից հետևում է, որ , այսինքն՝ այս ճառագայթով շարժվելիս ֆունկցիան մեծանում է։ Եթե ​​մենք շարժվենք ճառագայթով այնպես, որ tg φ 0 = -A/B,Դա , հետևաբար, այս ճառագայթով շարժվելիս ֆունկցիան նվազում է։ Այսպիսով, ժամանակաշրջան Մ 0ծայրահեղ կետ չէ:

3`) Երբ AC–B² < 0, Ա < 0 доказательство отсутствия экстремума проводится

նման է նախորդին:

3``) Եթե AC–B² < 0, Ա= 0, ապա . Միևնույն ժամանակ. Այնուհետև բավական փոքր φ-ի համար 2 արտահայտությունը Բ cosφ + Գ sinφ մոտ է 2-ին IN, այսինքն՝ այն պահպանում է հաստատուն նշան, բայց sinφ նշանը փոխում է կետի մոտակայքում Մ 0.Սա նշանակում է, որ ֆունկցիայի աճը փոխում է նշանը անշարժ կետի մոտակայքում, որը հետևաբար ծայրահեղ կետ չէ:

4) Եթե AC–B² = 0 և , , այսինքն՝ աճի նշանը որոշվում է 2α 0 նշանով։ Միաժամանակ անհրաժեշտ է լրացուցիչ հետազոտություն՝ էքստրեմումի գոյության հարցը պարզաբանելու համար։

Օրինակ. Գտնենք ֆունկցիայի ծայրահեղ կետերը z = x² - 2 xy + 2y² + 2 x.Անշարժ կետեր գտնելու համար մենք լուծում ենք համակարգը . Այսպիսով, անշարժ կետը (-2,-1) է: Միևնույն ժամանակ A = 2, IN = -2, ՀԵՏ= 4. Հետո AC–B² = 4 > 0, հետևաբար, անշարժ կետում հասնում է ծայրահեղության, մասնավորապես նվազագույնի (քանի որ Ա > 0).

Սահմանում 5.4.Եթե ​​ֆունկցիայի արգումենտները f (x 1, x 2,…, x n)պարտադիր են ձևի լրացուցիչ պայմաններով մհավասարումներ ( մ< n) :

φ 1 ( x 1, x 2,…, x n) = 0, φ 2 ( x 1, x 2,…, x n) = 0, …, φ m ( x 1, x 2,…, x n) = 0, (5.2)

որտեղ φ i ֆունկցիաները ունեն շարունակական մասնակի ածանցյալներ, ապա կոչվում են (5.2) հավասարումները կապի հավասարումներ.

Սահմանում 5.5.Ֆունկցիայի ծայրահեղություն f (x 1, x 2,…, x n)երբ (5.2) պայմանները բավարարվում են, այն կոչվում է պայմանական ծայրահեղություն.

Մեկնաբանություն. Մենք կարող ենք առաջարկել երկու փոփոխականների ֆունկցիայի պայմանական ծայրահեղության հետևյալ երկրաչափական մեկնաբանությունը. թող ֆունկցիայի արգումենտները. f(x,y)կապված φ հավասարման հետ (x,y)= 0՝ O հարթությունում որոշ կորի սահմանում xy. Այս կորի յուրաքանչյուր կետից O հարթության ուղղահայացների վերակառուցում xyմինչև այն հատվի մակերեսի հետ z = f (x,y),մենք ստանում ենք տարածական կոր, որը ընկած է φ կորի վերևում գտնվող մակերեսի վրա (x,y)= 0. Խնդիրն է գտնել ստացված կորի ծայրահեղ կետերը, որոնք, իհարկե, ընդհանուր դեպքում չեն համընկնում ֆունկցիայի անվերապահ ծայրահեղ կետերի հետ։ f(x,y):

Եկեք որոշենք պայմանական ծայրահեղության համար անհրաժեշտ պայմանները երկու փոփոխականների ֆունկցիայի համար՝ նախ ներկայացնելով հետևյալ սահմանումը.

Սահմանում 5.6.Գործառույթ L (x 1 , x 2 ,…, x n) = f (x 1 , x 2 ,…, x n) + λ 1 φ 1 (x 1 , x 2 ,…, x n) +

+ λ 2 φ 2 (x 1 , x 2 ,…, x n) +…+λ m φ m (x 1 , x 2 ,…, x n), (5.3)

Որտեղ λi –ոմանք հաստատուն են, կոչվում են Լագրանժի ֆունկցիաև թվերը λi– անորոշ Lagrange բազմապատկիչներ.

Թեորեմ 5.3(պայմանական էքստրեմումի համար անհրաժեշտ պայմաններ). Ֆունկցիայի պայմանական ծայրահեղություն z = f (x, y)Ֆ զուգավորման հավասարման առկայության դեպքում x, y)= 0 կարելի է հասնել միայն Լագրանժի ֆունկցիայի անշարժ կետերում L (x, y) = f (x, y) + λφ (x, y):

Ապացույց. Միացման հավասարումը սահմանում է անուղղակի հարաբերություն ժամը-ից X, հետևաբար մենք կենթադրենք, որ ժամըկա մի ֆունկցիա ից X: y = y(x):Հետո զկա մի բարդ ֆունկցիա ից X, և դրա կրիտիկական կետերը որոշվում են պայմանով. . (5.4) Միացման հավասարումից հետևում է, որ . (5.5)

Եկեք բազմապատկենք (5.5) հավասարությունը որոշ λ թվով և ավելացնենք այն (5.4): Մենք ստանում ենք.

, կամ .

Վերջին հավասարությունը պետք է բավարարվի անշարժ կետերում, որից հետևում է.

(5.6)

Ստացվում է երեք անհայտների երեք հավասարումների համակարգ. x, yև λ, իսկ առաջին երկու հավասարումները Լագրանժի ֆունկցիայի անշարժ կետի պայմաններն են։ Օժանդակ անհայտ λ-ն հեռացնելով (5.6) համակարգից՝ մենք գտնում ենք այն կետերի կոորդինատները, որոնցում սկզբնական ֆունկցիան կարող է ունենալ պայմանական ծայրահեղություն։

Դիտողություն 1. Գտնված կետում պայմանական ծայրահեղության առկայությունը կարելի է ստուգել՝ ուսումնասիրելով Լագրանժի ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալները՝ 5.2 թեորեմի անալոգիայի միջոցով:

Դիտողություն 2. Կետեր, որտեղ կարելի է հասնել ֆունկցիայի պայմանական ծայրահեղությանը f (x 1, x 2,…, x n)երբ (5.2) պայմանները բավարարված են, կարող են սահմանվել որպես համակարգի լուծումներ (5.7)

Օրինակ. Գտնենք ֆունկցիայի պայմանական ծայրահեղությունը z = xyհաշվի առնելով, որ x + y= 1. Կազմենք Lagrange ֆունկցիան L(x, y) = xy + λ (x + y – 1). Համակարգը (5.6) ունի հետևյալ տեսքը.

Որտեղ -2λ=1, λ=-0.5, x = y = -λ = 0.5. Միևնույն ժամանակ L (x, y)կարող է ներկայացվել ձևով L(x, y) = - 0,5 (x–y)² + 0,5 ≤ 0,5, հետևաբար գտնված անշարժ կետում L (x, y)ունի առավելագույնը, և z = xy –պայմանական առավելագույնը.

Նախ դիտարկենք երկու փոփոխականների ֆունկցիայի դեպքը։ $z=f(x,y)$ ֆունկցիայի պայմանական ծայրահեղությունը $M_0(x_0;y_0)$ կետում այս ֆունկցիայի ծայրահեղությունն է, որը ձեռք է բերվել այն պայմանով, որ $x$ և $y$ փոփոխականները այս կետի մերձակայքում բավարարում է կապի հավասարումը $\ varphi (x,y)=0$:

«Պայմանական» էքստրեմում անվանումը պայմանավորված է նրանով, որ փոփոխականների վրա դրվում է լրացուցիչ պայման $\varphi(x,y)=0$։ Եթե ​​մի փոփոխականը կարող է արտահայտվել միացման հավասարումից մյուսի միջոցով, ապա պայմանական ծայրահեղության որոշման խնդիրը կրճատվում է մեկ փոփոխականի ֆունկցիայի սովորական ծայրահեղության որոշման խնդրին։ Օրինակ, եթե կապի հավասարումը ենթադրում է $y=\psi(x)$, ապա $y=\psi(x)$-ին փոխարինելով $z=f(x,y)$-ով, մենք ստանում ենք $z մեկ փոփոխականի ֆունկցիա: =f\ձախ (x,\psi(x)\աջ)$: Ընդհանուր դեպքում, սակայն, այս մեթոդը քիչ կիրառություն ունի, ուստի պահանջվում է նոր ալգորիթմի ներդրում։

Լագրանժի բազմապատկիչ մեթոդ երկու փոփոխականների ֆունկցիաների համար:

Լագրանժի բազմապատկիչ մեթոդը բաղկացած է Լագրանժի ֆունկցիայի կառուցումից՝ պայմանական ծայրահեղություն գտնելու համար՝ $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ ($\lambda$ պարամետրը կոչվում է. Լագրանժի բազմապատկիչ): Ծայրահեղության համար անհրաժեշտ պայմանները սահմանվում են հավասարումների համակարգով, որից որոշվում են անշարժ կետերը.

$$ \ձախ \( \սկիզբ(հավասարեցված) & \frac(\մասնակի F)(\մասնակի x)=0;\\ & \frac(\մասնակի F)(\մասնակի y)=0;\\ & \varphi (x,y)=0.

Բավարար պայման, որից կարելի է որոշել էքստրեմի բնույթը $d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy) նշանն է: ^("" )dy^2$. Եթե ​​անշարժ կետում $d^2F > 0$, ապա $z=f(x,y)$ ֆունկցիան այս պահին ունի պայմանական նվազագույն, բայց եթե $d^2F.< 0$, то условный максимум.

Ծայրահեղության բնույթը որոշելու մեկ այլ եղանակ կա. Միացման հավասարումից ստանում ենք՝ $\varphi_(x)^(")dx+\varphi_(y)^(")dy=0$, $dy=-\frac(\varphi_(x)^("))( \varphi_ (y)^("))dx$, հետևաբար ցանկացած անշարժ կետում ունենք.

$$d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=F_(xx)^( "")dx^2+2F_(xy)^("")dx\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\աջ)+ F_(yy)^("")\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)^2=\\ =-\frac (dx^2)(\left(\varphi_(y)^(") \աջ)^2)\cdot\left(-(\varphi_(y)^("))^2 F_(xx)^(" ")+2\varphi_(x)^(")\varphi_(y)^(")F_(xy)^("")-(\varphi_(x)^("))^2 F_(yy)^ ("") \աջ)$$

Երկրորդ գործոնը (գտնվում է փակագծերում) կարող է ներկայացվել այս ձևով.

$\left| որոշիչի տարրերն ընդգծված են կարմիրով: \սկիզբ(զանգված) (cc) F_(xx)^("") & F_(xy)^("") \\ F_(xy)^("") & F_(yy)^("") \վերջ (զանգված)\right|$, որը Լագրանժի ֆունկցիայի Հեսիան է։ Եթե ​​$H > 0$, ապա $d^2F< 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F >0 դոլար, այսինքն. ունենք $z=f(x,y)$ ֆունկցիայի պայմանական նվազագույնը։

Ծանոթագրություն $H$ որոշիչի նշման վերաբերյալ: ցույց տալ/թաքցնել

$$ H=-\ձախ|\սկիզբ(զանգված) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_ (xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \ վերջ(զանգված) \աջ| $$

Այս իրավիճակում վերևում ձևակերպված կանոնը կփոխվի հետևյալ կերպ. եթե $H > 0$, ապա ֆունկցիան ունի պայմանական նվազագույն, և եթե $H< 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

Պայմանական ծայրահեղության համար երկու փոփոխականի ֆունկցիան ուսումնասիրելու ալգորիթմ

1. Կազմել Lagrange ֆունկցիան $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. Լուծեք համակարգը $ \left \( \begin(adigned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \ varphi (x,y)=0 \end(հավասարեցված) \աջ
3. Որոշեք էքստրեմի բնույթը նախորդ պարբերությունում հայտնաբերված անշարժ կետերից յուրաքանչյուրում: Դա անելու համար օգտագործեք հետևյալ մեթոդներից որևէ մեկը.
   • Կազմի՛ր $H$-ի որոշիչը և պարզի՛ր դրա նշանը
   • Հաշվի առնելով միացման հավասարումը, հաշվարկեք $d^2F$ նշանը

Լագրանժի բազմապատկիչ մեթոդ n փոփոխականների ֆունկցիաների համար

Ենթադրենք, մենք ունենք $n$ փոփոխականների ֆունկցիա՝ $z=f(x_1,x_2,\ldots,x_n)$ և $m$ միացման հավասարումների ($n > m$):

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

Նշելով Լագրանժի բազմապատկիչները որպես $\lambda_1,\lambda_2,\ldots,\lambda_m$, մենք կազմում ենք Lagrange ֆունկցիան.

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

Պայմանական ծայրահեղության առկայության համար անհրաժեշտ պայմանները տրված են հավասարումների համակարգով, որից հայտնաբերվում են անշարժ կետերի կոորդինատները և Լագրանժի բազմապատկիչների արժեքները.

$$\ձախ\(\սկիզբ(հավասարեցված) & \frac(\մասնակի F)(\մասնակի x_i)=0; (i=\ overline(1,n))\\ & \varphi_j=0; (j=\ overline(1,m)) \end(aligned) \right.$$

Դուք կարող եք պարզել, թե արդյոք ֆունկցիան ունի պայմանական նվազագույն կամ պայմանական առավելագույն գտնված կետում, ինչպես նախկինում, օգտագործելով $d^2F$ նշանը: Եթե ​​գտնված կետում $d^2F > 0$, ապա ֆունկցիան ունի պայմանական նվազագույն, բայց եթե $d^2F< 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

$\left| մատրիցայի որոշիչ \սկիզբ(զանգված) (cccc) \frac(\մասնակի^2F)(\մասնակի x_(1)^(2)) & \frac(\մասնակի^2F)(\մասնակի x_(1)\մասնակի x_(2) ) & \frac(\մասնակի^2F)(\մասնակի x_(1)\մասնակի x_(3)) &\ldots & \frac(\մասնակի^2F)(\մասնակի x_(1)\մասնակի x_(n)) \\ \frac(\մասնակի^2F)(\մասնակի x_(2)\մասնակի x_1) & \frac(\մասնակի^2F)(\մասնակի x_(2)^(2)) & \frac(\մասնակի^2F) )(\մասնակի x_(2)\մասնակի x_(3)) &\ldots & \frac(\մասնակի^2F)(\մասնակի x_(2)\մասնակի x_(n))\\ \frac(\մասնակի^2F) )(\մասնակի x_(3) \մասնակի x_(1)) & \frac(\մասնակի^2F)(\մասնակի x_(3)\մասնակի x_(2)) & \frac(\մասնակի^2F)(\մասնակի x_(3)^(2)) &\ldots & \frac(\partial^2F)(\partial x_(3)\partial x_(n))\\ \ldots & \ldots & \ldots &\ldots & \ ldots\\ \frac(\մասնակի^2F)(\մասնակի x_(n)\մասնակի x_(1)) & \frac(\մասնակի^2F)(\մասնակի x_(n)\մասնակի x_(2)) & \ frac(\մասնակի^2F)(\մասնակի x_(n)\մասնակի x_(3)) &\ldots & \frac(\մասնակի^2F)(\մասնակի x_(n)^(2))\\ \վերջ( զանգված) \right|$, կարմիրով ընդգծված $L$ մատրիցում, Լագրանժի ֆունկցիայի Հեսիան է։ Մենք օգտագործում ենք հետևյալ կանոնը.

• Եթե ​​անկյունային անչափահասների նշանները $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ $L$ մատրիցները համընկնում են $(-1)^m$ նշանի հետ, ապա ուսումնասիրվող անշարժ կետը $ ֆունկցիայի պայմանական նվազագույն կետն է։ z=f(x_1,x_2,x_3,\ldots,x_n)$:
• Եթե ​​անկյունային անչափահասների նշանները $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ հերթափոխ, իսկ փոքր $H_(2m+1)$ նշանը համընկնում է $(-1)^(m+1 թվի նշանի հետ: )$, ապա անշարժ կետը $z=f(x_1,x_2,x_3,\ldots,x_n)$ ֆունկցիայի պայմանական առավելագույն կետն է։

Օրինակ թիվ 1

Գտե՛ք $z(x,y)=x+3y$ ֆունկցիայի պայմանական ծայրահեղությունը $x^2+y^2=10$ պայմանով։

Այս խնդրի երկրաչափական մեկնաբանությունը հետևյալն է. պահանջվում է գտնել $z=x+3y$ հարթության հավելվածի ամենամեծ և ամենափոքր արժեքները $x^2+y գլանով հատման կետերի համար։ ^2=10$.

Որոշ չափով դժվար է մի փոփոխականի միջոցով արտահայտել զուգավորման հավասարումից և այն փոխարինել $z(x,y)=x+3y$ ֆունկցիայի մեջ, ուստի մենք կօգտագործենք Լագրանժի մեթոդը:

Նշելով $\varphi(x,y)=x^2+y^2-10$՝ կազմում ենք Lagrange ֆունկցիան.

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac(\մասնակի Զ)(\մասնակի x)=1+2\լամբդա x; \frac(\մասնակի F)(\մասնակի y)=3+2\լամբդա y. $$

Լագրանժի ֆունկցիայի անշարժ կետերը որոշելու համար գրենք հավասարումների համակարգ.

$$ \ձախ \( \սկիզբ (հավասարեցված) & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0: \վերջ (հավասարեցված)\աջ.$$

Եթե ​​ենթադրենք $\lambda=0$, ապա առաջին հավասարումը դառնում է՝ $1=0$։ Ստացված հակասությունը ցույց է տալիս, որ $\lambda\neq 0$: $\lambda\neq 0$ պայմանով, առաջին և երկրորդ հավասարումներից ունենք՝ $x=-\frac(1)(2\lambda)$, $y=-\frac(3)(2\lambda) $. Ստացված արժեքները փոխարինելով երրորդ հավասարման մեջ՝ ստանում ենք.

$$ \left(-\frac(1)(2\lambda) \right)^2+\left(-\frac(3)(2\lambda) \աջ)^2-10=0;\\ \frac (1)(4\lambda^2)+\frac(9)(4\lambda^2)=10; \lambda^2=\frac(1)(4); \ձախ[ \begin(հավասարեցված) & \lambda_1=-\frac(1)(2);\\ & \lambda_2=\frac(1)(2): \end (հավասարեցված) \աջ.\\ \սկիզբ (հավասարեցված) & \lambda_1=-\frac(1)(2); \; x_1=-\frac(1)(2\lambda_1)=1; \; y_1=-\frac(3)(2\lambda_1)=3;\\ & \lambda_2=\frac(1)(2); \; x_2=-\frac(1)(2\lambda_2)=-1; \; y_2=-\frac(3)(2\lambda_2)=-3.\վերջ (հավասարեցված) $$

Այսպիսով, համակարգն ունի երկու լուծում՝ $x_1=1;\; y_1=3;\; \lambda_1=-\frac(1)(2)$ և $x_2=-1;\; y_2=-3;\; \lambda_2=\frac(1)(2)$: Եկեք պարզենք ծայրահեղության բնույթը յուրաքանչյուր անշարժ կետում՝ $M_1(1;3)$ և $M_2(-1;-3)$: Դա անելու համար մենք յուրաքանչյուր կետում հաշվարկում ենք $H$-ի որոշիչը:

$$ \varphi_(x)^(")=2x;\; \varphi_(y)^(")=2y;\; F_(xx)^("")=2\lambda;\; F_(xy)^("")=0;\; F_(yy)^("")=2\lambda.\\ H=\ձախ| \ սկիզբ (զանգված) (cc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \վերջ (զանգված) \աջ|= \ձախ| \սկիզբ (զանգված) (ccc) 0 & 2x & 2y\\ 2x & 2\lambda & 0 \\ 2y & 0 & 2\lambda \վերջ (զանգված) \աջ|= 8\cdot\ձախ| \սկիզբ (զանգված) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \վերջ (զանգված) \աջ| $$

$M_1(1;3)$ կետում ստանում ենք՝ $H=8\cdot\left| \սկիզբ (զանգված) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \վերջ (զանգված) \աջ|= 8\cdot\ ձախ| \սկիզբ(զանգված) (ccc) 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \վերջ (զանգված) \աջ|=40 > 0$, այնպես որ կետ $M_1(1;3)$ $z(x,y)=x+3y$ ֆունկցիան ունի պայմանական առավելագույն, $z_(\max)=z(1;3)=10$։

Նմանապես, $M_2(-1,-3)$ կետում մենք գտնում ենք՝ $H=8\cdot\left| \սկիզբ (զանգված) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \վերջ (զանգված) \աջ|= 8\cdot\ ձախ| \սկիզբ (զանգված) (ccc) 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \վերջ (զանգված) \աջ|=-40$: Քանի որ $H< 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

Ես նշում եմ, որ յուրաքանչյուր կետում $H$ որոշիչի արժեքը հաշվարկելու փոխարեն, շատ ավելի հարմար է այն ընդլայնել ընդհանուր տեսքով: Որպեսզի տեքստը չխառնվի մանրամասներով, այս մեթոդը կթաքցնեմ գրառման տակ։

$H$ որոշիչ գրելը ընդհանուր ձևով: ցույց տալ/թաքցնել

$$ H=8\cdot\ձախ|\սկիզբ(զանգված)(ccc)0&x&y\\x&\lambda&0\\y&0&\lambda\end(զանգված)\աջ| =8\cdot\left(-\lambda(y^2)-\lambda(x^2)\right) =-8\lambda\cdot\left(y^2+x^2\աջ): $$

Սկզբունքորեն արդեն ակնհայտ է, թե $H$ ինչ նշան ունի։ Քանի որ $M_1$ կամ $M_2$ կետերից ոչ մեկը չի համընկնում ծագման հետ, ապա $y^2+x^2>0$: Հետևաբար, $H$ նշանը հակառակ է $\lambda$ նշանին։ Դուք կարող եք լրացնել հաշվարկները.

$$ \սկիզբ (հավասարեցված) &H(M_1)=-8\cdot\left(-\frac(1)(2)\right)\cdot\left(3^2+1^2\աջ)=40;\ \ &H(M_2)=-8\cdot\frac(1)(2)\cdot\left((-3)^2+(-1)^2\աջ)=-40: \վերջ (հավասարեցված) $$

$M_1(1;3)$ և $M_2(-1;-3)$ անշարժ կետերում ծայրահեղության բնույթի մասին հարցը կարող է լուծվել առանց $H$ որոշիչ օգտագործելու: Եկեք յուրաքանչյուր անշարժ կետում գտնենք $d^2F$ նշանը.

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=2\lambda \ձախ( dx^2+dy^2\աջ) $$

Նշեմ, որ $dx^2$ նշումը նշանակում է ճիշտ $dx$ բարձրացված երկրորդ աստիճանի, այսինքն. $\ձախ(dx \աջ)^2$։ Այսպիսով, մենք ունենք՝ $dx^2+dy^2>0$, հետևաբար, $\lambda_1=-\frac(1)(2)$-ով մենք ստանում ենք $d^2F< 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Պատասխանել$(-1;-3)$ կետում ֆունկցիան ունի պայմանական նվազագույն, $z_(\min)=-10$: $(1;3)$ կետում ֆունկցիան ունի պայմանական առավելագույն, $z_(\max)=10$

Օրինակ թիվ 2

Գտե՛ք $z(x,y)=3y^3+4x^2-xy$ ֆունկցիայի պայմանական ծայրահեղությունը $x+y=0$ պայմանով։

Առաջին մեթոդ (Լագրանժի բազմապատկիչ մեթոդ)

Նշելով $\varphi(x,y)=x+y$՝ կազմում ենք Lagrange ֆունկցիան՝ $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+ 4x^2 -xy+\lambda(x+y)$։

$$ \frac(\մասնակի F)(\մասնակի x)=8x-y+\lambda; \; \frac(\մասնակի F)(\մասնակի y)=9y^2-x+\lambda.\\ \ձախ \( \սկիզբ (հավասարեցված) & 8x-y+\lambda=0;\\ & 9y^2-x+\ lambda=0 \\ & x+y=0.

Համակարգը լուծելուց հետո մենք ստանում ենք՝ $x_1=0$, $y_1=0$, $\lambda_1=0$ և $x_2=\frac(10)(9)$, $y_2=-\frac(10)( 9)$, $\lambda_2=-10$: Մենք ունենք երկու անշարժ կետ՝ $M_1(0;0)$ և $M_2 \left(\frac(10)(9);-\frac(10)(9) \right)$: Եկեք պարզենք ծայրահեղության բնույթը յուրաքանչյուր անշարժ կետում՝ օգտագործելով $H$ որոշիչը:

$$H=\ձախ| \ սկիզբ (զանգված) (cc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \վերջ (զանգված) \աջ|= \ձախ| \սկիզբ(զանգված) (ccc) 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18y \վերջ (զանգված) \աջ|=-10-18y $$

$M_1(0;0)$ $H=-10-18\cdot 0=-10 կետում< 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 >0$, հետևաբար այս պահին ֆունկցիան ունի պայմանական առավելագույն՝ $z_(\max)=\frac(500)(243)$։

Մենք ուսումնասիրում ենք էքստրեմի բնույթը յուրաքանչյուր կետում՝ օգտագործելով տարբեր մեթոդ՝ հիմնվելով $d^2F$ նշանի վրա.

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=8dx^2-2dxdy+ 18ydy ^2 $$

$x+y=0$ կապի հավասարումից ունենք՝ $d(x+y)=0$, $dx+dy=0$, $dy=-dx$։

$$ d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

Քանի որ $ d^2F \Bigr|_(M_1)=10 dx^2 > 0$, ապա $M_1(0;0)$-ը $z(x,y)=3y^3+ ֆունկցիայի պայմանական նվազագույն կետն է։ 4x^ 2-xy$. Նմանապես, $d^2F \Bigr|_(M_2)=-10 dx^2< 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

Երկրորդ ճանապարհ

$x+y=0$ կապի հավասարումից ստանում ենք՝ $y=-x$։ Փոխարինելով $y=-x$-ը $z(x,y)=3y^3+4x^2-xy$ ֆունկցիայի մեջ՝ մենք ստանում ենք $x$ փոփոխականի որոշ ֆունկցիա: Նշենք այս ֆունկցիան որպես $u(x)$:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

Այսպիսով, մենք կրճատեցինք երկու փոփոխականի ֆունկցիայի պայմանական ծայրահեղությունը գտնելու խնդիրը մեկ փոփոխականի ֆունկցիայի ծայրահեղությունը որոշելու խնդրին:

$$ u_(x)^(")=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \ y_1=-x_1=0;\\ x_2=\frac(10)(9);

Մենք ստացանք $M_1(0;0)$ և $M_2\left(\frac(10)(9); -\frac(10)(9)\right)$ միավորներ: Հետագա հետազոտությունները հայտնի են մեկ փոփոխականի ֆունկցիաների դիֆերենցիալ հաշվարկի ընթացքից: Քննելով $u_(xx)^("")$ նշանը յուրաքանչյուր անշարժ կետում կամ ստուգելով $u_(x)^(")$ նշանի փոփոխությունը գտնված կետերում, մենք ստանում ենք նույն եզրակացությունները, ինչ երբ. լուծելով առաջին մեթոդը, օրինակ, մենք կստուգենք $u_(xx)^(")$:

$$u_(xx)^("")=-18x+10;\\ u_(xx)^("")(M_1)=10;\;u_(xx)^("")(M_2)=- 10.$$

Քանի որ $u_(xx)^("")(M_1)>0$, ապա $M_1$-ը $u(x)$ ֆունկցիայի նվազագույն կետն է, իսկ $u_(\min)=u(0)=0: $ . Քանի որ $u_(xx)^("")(M_2)<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

Տրված կապի պայմանի համար $u(x)$ ֆունկցիայի արժեքները համընկնում են $z(x,y)$ ֆունկցիայի արժեքների հետ, այսինքն. $u(x)$ ֆունկցիայի հայտնաբերված ծայրահեղությունները $z(x,y)$ ֆունկցիայի որոնված պայմանական ծայրահեղություններն են:

Պատասխանել$(0;0)$ կետում ֆունկցիան ունի պայմանական նվազագույն, $z_(\min)=0$։ $\left(\frac(10)(9); -\frac(10)(9) \right)$ կետում ֆունկցիան ունի պայմանական առավելագույն, $z_(\max)=\frac(500)(243): ) $.

Դիտարկենք մեկ այլ օրինակ, որտեղ մենք կպարզենք էքստրեմի բնույթը՝ որոշելով $d^2F$ նշանը։

Օրինակ թիվ 3

Գտեք $z=5xy-4$ ֆունկցիայի ամենամեծ և ամենափոքր արժեքները, եթե $x$ և $y$ փոփոխականները դրական են և բավարարում են կապի հավասարումը $\frac(x^2)(8)+\frac( y^2)(2) -1=0$.

Եկեք կազմենք Lagrange ֆունկցիան՝ $F=5xy-4+\lambda \left(\frac(x^2)(8)+\frac(y^2)(2)-1 \աջ)$։ Գտնենք Լագրանժի ֆունկցիայի անշարժ կետերը.

$$ F_(x)^(")=5y+\frac(\lambda x)(4); \; F_(y)^(")=5x+\lambda y.\\ \ձախ \( \սկիզբ (հավասարեցված) & 5y+\frac(\lambda x)(4)=0;\\ & 5x+\lambda y=0;\\ & \frac(x^2)(8)+\frac(y^2)(2)- 1=0;\\ & x > y > 0. \end(հավասարեցված) \աջ;

Բոլոր հետագա փոխակերպումները կատարվում են հաշվի առնելով $x > 0; \; y > 0$ (սա նշված է խնդրի հայտարարության մեջ): Երկրորդ հավասարումից մենք արտահայտում ենք $\lambda=-\frac(5x)(y)$ և գտնված արժեքը փոխարինում ենք առաջին հավասարման մեջ՝ $5y-\frac(5x)(y)\cdot \frac(x)(4 )=0$ , $4y^2-x^2=0$, $x=2y$։ Փոխարինելով $x=2y$-ը երրորդ հավասարման մեջ՝ ստանում ենք՝ $\frac(4y^2)(8)+\frac(y^2)(2)-1=0$, $y^2=1$, $y =1$:

Քանի որ $y=1$, ապա $x=2$, $\lambda=-10$։ Մենք որոշում ենք էքստրեմի բնույթը $(2;1)$ կետում $d^2F$ նշանի հիման վրա։

$$ F_(xx)^("")=\frac(\lambda)(4); \; F_(xy)^("")=5; \; F_(yy)^("")=\lambda. $$

Քանի որ $\frac(x^2)(8)+\frac(y^2)(2)-1=0$, ապա.

$$ d\left(\frac(x^2)(8)+\frac(y^2)(2)-1\right)=0; \; d\left(\frac(x^2)(8) \right)+d\left(\frac(y^2)(2) \աջ)=0; \; \frac(x)(4)dx+ydy=0; \; dy=-\frac(xdx)(4y): $$

Սկզբունքորեն այստեղ կարող եք անմիջապես փոխարինել $x=2$, $y=1$ անշարժ կետի կոորդինատները և $\lambda=-10$ պարամետրը՝ ստանալով.

$$ F_(xx)^("")=\frac(-5)(2); \; F_(xy)^("")=-10; \; dy=-\frac(dx)(2).\\ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^(" ")dy^2=-\frac(5)(2)dx^2+10dx\cdot \left(-\frac(dx)(2) \right)-10\cdot \left(-\frac(dx) (2) \աջ)^2=\\ =-\frac(5)(2)dx^2-5dx^2-\frac(5)(2)dx^2=-10dx^2. $$

Այնուամենայնիվ, պայմանական էքստրեմումի այլ խնդիրների դեպքում կարող են լինել մի քանի անշարժ կետեր: Նման դեպքերում ավելի լավ է $d^2F$-ը ներկայացնել ընդհանուր տեսքով, այնուհետև գտած անշարժ կետերից յուրաքանչյուրի կոորդինատները փոխարինել ստացված արտահայտությամբ.

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=\frac(\lambda) (4)dx^2+10\cdot dx\cdot \frac(-xdx)(4y) +\lambda\cdot \left(-\frac(xdx)(4y) \աջ)^2=\\ =\frac (\lambda)(4)dx^2-\frac(5x)(2y)dx^2+\lambda \cdot \frac(x^2dx^2)(16y^2)=\left(\frac(\lambda )(4)-\frac(5x)(2y)+\frac(\lambda \cdot x^2)(16y^2) \աջ)\cdot dx^2 $$

Փոխարինելով $x=2$, $y=1$, $\lambda=-10$՝ ստանում ենք.

$$ d^2 F=\left(\frac(-10)(4)-\frac(10)(2)-\frac(10 \cdot 4)(16) \աջ)\cdot dx^2=- 10dx^2. $$

Քանի որ $d^2F=-10\cdot dx^2< 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

Պատասխանել$(2;1)$ կետում ֆունկցիան ունի պայմանական առավելագույն, $z_(\max)=6$։

Հաջորդ մասում կքննարկենք Լագրանժի մեթոդի կիրառումը ավելի մեծ թվով փոփոխականների ֆունկցիաների համար։

Թող z - /(x, y) ֆունկցիան սահմանվի D որոշ տիրույթում և թող Mo(xo, Vo) լինի այս տիրույթի ներքին կետը: Սահմանում. Եթե ​​կա այնպիսի թիվ, որ բոլոր պայմաններին բավարարող անհավասարությունը ճիշտ է, ապա Mo(xo, y) կետը կոչվում է f(x, y) ֆունկցիայի տեղական առավելագույն կետ; եթե բոլորի համար Dx, Du, պայմանները բավարարող | ապա Mo(xo,yo) կետը կոչվում է բարակ տեղային նվազագույն: Այլ կերպ ասած, M0(x0, y0) կետը /(x, y) ֆունկցիայի առավելագույնի կամ նվազագույնի կետն է, եթե կա A/o(x0, y0) կետի 6 հարևանություն, որ ընդհանրապես. սրա M(x, y) կետերը հարևանությամբ, ֆունկցիայի աճը պահպանում է իր նշանը: Օրինակներ. 1. Ֆունկցիոնալ կետի համար՝ նվազագույն կետ (նկ. 17): 2. Ֆունկցիայի համար 0(0,0) կետը առավելագույն կետն է (նկ. 18): 3. Ֆունկցիայի համար 0(0,0) կետը տեղական առավելագույն կետ է: 4 Իրոք, կա 0(0, 0) կետի հարևանություն, օրինակ՝ j շառավղով շրջան (տե՛ս Նկար 19), որի ցանկացած կետում, 0(0,0) կետից տարբերվող, /(x,y) ֆունկցիայի արժեքը 1-ից փոքր = Մենք կդիտարկենք միայն խիստ առավելագույն և նվազագույն ֆունկցիաների կետերը, երբ խիստ անհավասարությունը կամ խիստ անհավասարությունը բավարարված է M(x) y) որոշ ծակված 6 հարևանությամբ գտնվող կետերի համար: կետը Mq. Ֆունկցիայի արժեքը առավելագույն կետում կոչվում է առավելագույնը, իսկ ֆունկցիայի արժեքը նվազագույն կետում կոչվում է այս ֆունկցիայի նվազագույնը: Ֆունկցիայի առավելագույն և նվազագույն կետերը կոչվում են ֆունկցիայի ծայրահեղ կետեր, իսկ բուն ֆունկցիայի առավելագույն և նվազագույն կետերը կոչվում են դրա ծայրահեղություններ: 18 Նկ. 20 immt ածանցյալներ, որոնք վերածվում են զրոյի: Բայց այս ֆունկցիան բարակ է ստրումի իմվաթի վրա:< 0. Если же то в точке Мо(жо> F(x, y) ֆունկցիայի ծայրահեղությունը կարող է գոյություն ունենալ կամ չլինել: Այս դեպքում անհրաժեշտ է լրացուցիչ հետազոտություն: m Եկեք սահմանափակվենք թեորեմի 1) և 2) պնդումների ապացուցմամբ։ Գրենք երկրորդ կարգի Թեյլորի բանաձևը /(i, y) ֆունկցիայի համար, որտեղ. Ըստ պայմանի՝ երևում է, որ D/ աճի նշանը որոշվում է (1-ի աջ կողմի եռանդամի նշանով), այսինքն՝ երկրորդ դիֆերենցիալ d2f նշանով։ Համառոտության համար նշենք։ Այնուհետև (l) հավասարությունը կարելի է գրել հետևյալ կերպ. Թող MQ(so, V0) կետում ունենք... Քանի որ պայմանով f(s, y) ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալները շարունակական են, ապա. անհավասարությունը (3) կպահպանվի նաև M0(s0,yo) կետի որոշ հարևանությամբ: Եթե ​​պայմանը բավարարված է (Ա/0 կետում և շարունակականության պատճառով, /,z(s,y) ածանցյալը կպահպանի իր նշանը Af0 կետի որոշակի հարևանությամբ: Այն տարածաշրջանում, որտեղ А Ф 0, Սրանից պարզ է դառնում, որ եթե M0(x0) y0 կետի ինչ-որ հարևանությամբ ЛС - В2 > 0), ապա AAx2 -I- 2BAxAy + CDy2 եռանկյունի նշանը համընկնում է կետում: (այսպես, V0) (ինչպես նաև C-ի նշանով, քանի որ AC-ի համար - B2 > 0 A-ն և C-ն չեն կարող ունենալ տարբեր նշաններ): Քանի որ AAs2 + 2BAxAy + CAy2 գումարի նշանը (s0 + $ Ax, y0 + 0 Dyn) կետում որոշում է տարբերության նշանը, մենք գալիս ենք հետևյալ եզրակացության. եթե /(s,y) ֆունկցիայի համար անշարժ կետի (s0, V0) պայմանը, ապա բավական փոքր || անհավասարությունը կբավարարվի. Այսպիսով, կետում (sq, V0) /(s, y) ֆունկցիան ունի առավելագույնը: Եթե ​​պայմանը բավարարված է անշարժ կետում (s0, y0), ապա բոլորի համար բավականաչափ փոքր |Dr| եւ |Դու| անհավասարությունը ճշմարիտ է, ինչը նշանակում է, որ (so,yo) կետում /(s, y) ֆունկցիան ունի նվազագույնը: Օրինակներ. 1. Հետազոտել էքստրեմումի ֆունկցիան 4 Օգտվելով էքստրեմումի համար անհրաժեշտ պայմաններից՝ մենք փնտրում ենք ֆունկցիայի անշարժ կետերը: Դա անելու համար մենք գտնում ենք u մասնակի ածանցյալները և հավասարեցնում դրանք զրոյի: Մենք ստանում ենք հավասարումների համակարգ, որտեղից՝ անշարժ կետ: Այժմ օգտագործենք թեորեմ 12-ը: Մենք ունենք Սա նշանակում է, որ Ml կետում կա ծայրահեղություն: Որովհետև սա նվազագույնն է։ Եթե ​​r ֆունկցիան վերածենք ձևի, ապա հեշտ է տեսնել, որ աջ կողմը (“) կլինի նվազագույն, երբ այս ֆունկցիայի բացարձակ նվազագույնն է: 2. Հետազոտել էքստրեմի ֆունկցիան Մենք գտնում ենք ֆունկցիայի անշարժ կետերը, որոնց համար կազմում ենք հավասարումների համակարգ, որպեսզի կետը լինի անշարժ: Քանի որ 12-րդ թեորեմի ուժով Մ կետում ծայրահեղություն չկա։ * 3. Հետազոտել ֆունկցիայի ծայրահեղությունը: Հավասարումների համակարգից մենք ստանում ենք դա, ուստի կետը անշարժ է: Ավելին, մենք ունենք, որ թեորեմ 12-ը չի պատասխանում ծայրահեղության առկայության կամ բացակայության մասին հարցին: Եկեք դա անենք այսպես. Բոլոր կետերի վերաբերյալ ֆունկցիայի համար, որը տարբերվում է կետից, ըստ սահմանման, և A/o(0,0) կետից, r ֆունկցիան ունի բացարձակ նվազագույն: Նմանատիպ հաշվարկներով մենք հաստատում ենք, որ ֆունկցիան կետում ունի առավելագույնը, բայց կետում ֆունկցիան ծայրահեղություն չունի: Թող n անկախ փոփոխականներից կազմված ֆունկցիան լինի տարբերվող մի կետում Mo կետը կոչվում է ֆունկցիայի անշարժ կետ, եթե 13-րդ թեորեմը (մինչև ծայրահեղության համար բավարար պայմաններ): Թող ֆունկցիան սահմանվի և ունենա երկրորդ կարգի շարունակական մասնակի ածանցյալներ Mt(xi...) նուրբ Mt(xi...) որոշ հարևանությամբ, որը անշարժ նուրբ ֆունկցիա է, եթե քառակուսի ձևը (տուգանքի մեջ f ֆունկցիայի երկրորդ դիֆերենցիալը դրական է. Որոշակի (բացասական որոշիչ), f ֆունկցիայի նվազագույն կետը (համապատասխանաբար, նուրբ առավելագույնը) լավ է Քառակուսի ձևը (4) դրական կամ բացասական որոշիչ է, օրինակ՝ Sylvester չափանիշը դրական (բացասական) համար 15.2 Պայմանական ծայրահեղություն Մինչև հիմա մենք փնտրում էինք a-ի տեղական ծայրահեղությունները ֆունկցիան իր սահմանման ողջ տիրույթում, երբ ֆունկցիայի արգումենտները կապված չեն որևէ լրացուցիչ պայմանի հետ: x, y) սահմանվի D տիրույթում: Ենթադրենք, որ այս տիրույթում տրված է L կոր, և մենք պետք է գտնենք f(x> y) ֆունկցիայի ծայրահեղությունը միայն դրա արժեքների մեջ, որոնք համապատասխանում են: L կորի կետերին. Նույն ծայրահեղությունները կոչվում են L կորի վրա z = f(x) y) ֆունկցիայի պայմանական ծայրահեղություններ. Սահմանում Ասում են, որ L կորի վրա ընկած կետում ֆունկցիան /(x, y) ունի պայմանական առավելագույն (նվազագույն), եթե անհավասարությունը բավարարված է M (s, y) y) կորի L կետերում, որոնք պատկանում են M0(x0, V0) կետի ինչ-որ հարևանությանը և տարբերվում են M0 կետից (Եթե L կորը տրված է հավասարմամբ, այնուհետև խնդիրը կորի վրա r - f(x,y) ֆունկցիայի պայմանական ծայրահեղությունը գտնելն է։ կարելի է ձևակերպել հետևյալ կերպ. գտե՛ք x = /(z, y) ֆունկցիայի ծայրահեղությունը D տարածաշրջանում, պայմանով, որ այսպես, z = y ֆունկցիայի պայմանական ծայրահեղությունները գտնելիս, gnu-ի արգումենտներն այլևս չեն կարող. դիտարկել որպես անկախ փոփոխականներ. դրանք միմյանց հետ կապված են y ) = 0 հարաբերակցությամբ, որը կոչվում է միացման հավասարում: Անվերապահ և պայմանական ծայրահեղությունների միջև տարբերությունը պարզելու համար դիտարկենք մի օրինակ՝ ֆունկցիայի անվերապահ առավելագույնը (նկ. 23) հավասար է մեկի և ձեռք է բերվում (0,0) կետում: Այն համապատասխանում է M կետին - pvvboloid-ի գագաթին Ավելացնենք y = j միացման հավասարումը: Այնուհետև պայմանական առավելագույնը ակնհայտորեն հավասար կլինի դրան: Այն հասնում է (o,|) կետում, և այն համապատասխանում է գնդակի Afj գագաթին, որը գնդակի հատման գիծն է y = j հարթության հետ: Անվերապահ mvximum-ի դեպքում մենք ունենք mvximum հավելված մակերևույթի բոլոր vpplicvt-երի միջև * = 1 - l;2 ~ y1; պայմանականի summvv - միայն pvraboloidv-ի vllikvt կետերից, որոնք համապատասխանում են y = j ոչ xOy հարթության ուղիղ գծի կետին*: Առկայության և միացման դեպքում ֆունկցիայի պայմանական ծայրահեղությունը գտնելու մեթոդներից մեկը հետևյալն է. Պայմանական էքստրեմի գոյության և բնույթի հարցը լուծվում է Լագրանժի ֆունկցիայի երկրորդ դիֆերենցիալ նշանի ուսումնասիրության հիման վրա (8)-ից ստացված x0, V0, A արժեքների դիտարկված համակարգի համար, պայմանով, որ եթե. , ապա (x0, V0) կետում /(x, y ) ֆունկցիան ունի պայմանական առավելագույն; եթե d2F > 0 - ապա պայմանական նվազագույնը: Մասնավորապես, եթե անշարժ կետում (xo, J/o) F(x, y) ֆունկցիայի D որոշիչը դրական է, ապա (®o, Yo) կետում կա f( ֆունկցիայի պայմանական առավելագույնը. x, y), եթե և ֆունկցիայի պայմանական նվազագույնը /(x, y), եթե Օրինակ. Կրկին անդրադառնանք նախորդ օրինակի պայմաններին. գտե՛ք ֆունկցիայի ծայրահեղությունը x + y = 1 պայմանով: Խնդիրը կլուծենք Լագրանժի բազմապատկիչ մեթոդով: Լագրանժի ֆունկցիան այս դեպքում ունի անշարժ կետերի ձևը, մենք կազմում ենք համակարգ համակարգի առաջին երկու հավասարումներից, որ մենք ստանում ենք x = y: Այնուհետև համակարգի երրորդ հավասարումից (միացման հավասարում) գտնում ենք, որ x - y = j հնարավոր ծայրահեղ կետի կոորդինատներն են։ Այս դեպքում (նշվում է, որ A = -1: Այսպիսով, Լագրանժի ֆունկցիան. * = x2 + y2 ֆունկցիայի պայմանական նվազագույն կետն է՝ Լագրանժի ֆունկցիայի համար անվերապահ ծայրահեղություն չկա: P(x, y): ) դեռ չի նշանակում /(x, y) ֆունկցիայի պայմանական ծայրահեղության բացակայություն կապի առկայության դեպքում Օրինակ Գտեք ֆունկցիայի ծայրահեղությունը y պայմանով 4 Մենք կազմում ենք Լագրանժի ֆունկցիան և դուրս գրում ենք համակարգ: Որոշելով A-ն և հնարավոր ծայրահեղ կետերի կոորդինատները. Առաջին երկու հավասարումներից մենք ստանում ենք x + y = 0 և գալիս ենք համակարգին, որտեղից x = y = A = 0: Այսպիսով, համապատասխան Լագրանժի ֆունկցիան ունի կետում ձևը. (0,0), F(x, y; 0) ֆունկցիան չունի անվերապահ ծայրահեղություն, բայց կա r = xy ֆունկցիայի պայմանական ծայրահեղություն, երբ y = x2 Իրոք, այս դեպքում այստեղ պարզ է, որ (0,0) կետում կա պայմանական նվազագույն. «Լագրանժի բազմապատկիչների մեթոդը տարածվում է ցանկացած թվով արգումենտների ֆունկցիաների դեպքում։ Եկեք փնտրենք ֆունկցիայի ծայրահեղությունը՝ առկայության դեպքում։ Կազմենք Լագրանժի ֆունկցիան, որտեղ A|, Az,..., անորոշ գործակիցներ են: Հավասարեցնելով F ֆունկցիայի բոլոր առաջին կարգի մասնակի ածանցյալներին և ստացված հավասարումներին ավելացնելով կապի (9) հավասարումները՝ ստանում ենք n + m հավասարումների համակարգ, որից որոշում ենք Ab A3|..., At և x կոորդինատները։ \) x2). » պայմանական ծայրահեղության հնարավոր կետերի xn. Հարցը, թե արդյոք Լագրանժի մեթոդով հայտնաբերված կետերը իսկապես պայմանական ծայրահեղության կետեր են, հաճախ կարող է լուծվել ֆիզիկական կամ երկրաչափական բնույթի նկատառումների հիման վրա: 15.3. Շարունակական ֆունկցիաների ամենամեծ և ամենափոքր արժեքները Թող անհրաժեշտ լինի գտնել z = /(x, y) ֆունկցիայի ամենամեծ (ամենափոքր) արժեքը, շարունակական որոշ փակ սահմանափակ D տիրույթում: Համաձայն թեորեմ 3-ի՝ այս տարածաշրջանում կա մի կետ (xo, V0), որտեղ ֆունկցիան ընդունում է ամենամեծ (ամենափոքր) արժեքը։ Եթե ​​կետը (xo, y0) գտնվում է D տիրույթի ներսում, ապա / ֆունկցիան իր մեջ ունի առավելագույնը (նվազագույնը), ուստի այս դեպքում մեզ հետաքրքրող կետը պարունակվում է /(x,) ֆունկցիայի կրիտիկական կետերի մեջ։ y). Այնուամենայնիվ, /(x, y) ֆունկցիան կարող է հասնել իր ամենամեծ (ամենափոքր) արժեքին տարածաշրջանի սահմանին: Հետևաբար, z = /(x, y) ֆունկցիայի ամենամեծ (ամենափոքր) արժեքը գտնելու համար սահմանափակ փակ տարածքում 2), դուք պետք է գտնեք այս տարածքի ներսում ձեռք բերված ֆունկցիայի բոլոր առավելագույնը (նվազագույնը), ինչպես նաև այս տարածքի սահմանին գտնվող ֆունկցիայի ամենամեծ (ամենափոքր) արժեքը: Այս բոլոր թվերից ամենամեծը (ամենափոքրը) կլինի z = /(x,y) ֆունկցիայի ցանկալի ամենամեծ (փոքր) արժեքը 27-րդ շրջանում: Եկեք ցույց տանք, թե ինչպես է դա արվում դիֆերենցիալ ֆունկցիայի դեպքում: Պրմմր. Գտեք 4-րդ շրջանի ֆունկցիայի ամենամեծ և ամենափոքր արժեքները: Մենք գտնում ենք ֆունկցիայի կրիտիկական կետերը D շրջանի ներսում: Դա անելու համար մենք կազմում ենք հավասարումների համակարգ այստեղից ստանում ենք x = y «0, այնպես որ 0 (0,0) կետը x ֆունկցիայի կրիտիկական կետն է: Քանի որ հիմա եկեք գտնենք ֆունկցիայի ամենամեծ և ամենափոքր արժեքները D տիրույթի Г սահմանի վրա: Սահմանի մի մասում մենք ունենք, որ y = 0-ը կրիտիկական կետ է, և քանի որ = ապա այս կետում z= ֆունկցիան: 1 + y2 ունի նվազագույնը հավասար է մեկի: Г հատվածի ծայրերում», կետերում (, ունենք: Համաչափության նկատառումներով ստանում ենք նույն արդյունքները սահմանի մյուս մասերի համար: Վերջապես ստանում ենք. z = x2+y2 ֆունկցիայի ամենափոքր արժեքը տարածաշրջանում. «B-ն հավասար է զրոյի և այն ձեռք է բերվում 0( 0, 0) ներքին կետում, իսկ այս ֆունկցիայի առավելագույն արժեքը՝ հավասար երկուսի, ձեռք է բերվում սահմանի չորս կետերում (նկ. 25) Նկար 25. Վարժություններ Գտե՛ք ֆունկցիաների սահմանման տիրույթը. Կառուցե՛ք ֆունկցիաների մակարդակի գծերը. 9 Գտե՛ք երեք անկախ փոփոխականների ֆունկցիաների մակարդակի մակերևույթները. Հաշվե՛ք սահմանային ֆունկցիաները. Գտե՛ք ֆունկցիաների մասնակի ածանցյալները և դրանց ընդհանուր դիֆերենցիալները. Գտե՛ք բարդի ածանցյալները. ֆունկցիաներ՝ 3 Գտե՛ք J. Մի քանի փոփոխականի ֆունկցիայի ծայրահեղության հայեցակարգ Մի քանի փոփոխականի ֆունկցիայի ծայրահեղության հասկացություն Էքստրեմի համար անհրաժեշտ և բավարար պայմաններ Պայմանական էքստրեմում Շարունակական ֆունկցիաների ամենամեծ և ամենափոքր արժեքները 34. Օգտագործելով ածանցյալի բանաձևը. կոմպլեքս երկու փոփոխական, գտնել և ֆունկցիաներ. 35. Օգտագործելով երկու փոփոխականների բարդ ֆունկցիայի ածանցյալի բանաձևը, գտի՛ր |J և ֆունկցիաները. Գտի՛ր անուղղակիորեն տրված jj ֆունկցիաները. դրա հատման կետը x = 3 ուղիղի հետ: 41. Գտե՛ք այն կետերը, որոնցում x կորի շոշափողը զուգահեռ է Ox առանցքին: . Հետևյալ խնդիրներում գտե՛ք և Տ. Գրե՛ք շոշափողի հարթության և մակերևույթի նորմալի հավասարումները. + 6z = 0. Գտե՛ք ընդլայնման առաջին երեք կամ չորս անդամները՝ օգտագործելով Թեյլորի բանաձևը՝ 50. y կետի մոտակայքում (0, 0):

Երկու փոփոխականի ֆունկցիայի ծայրահեղության համար բավարար պայման

1. Թող ֆունկցիան լինի անընդհատ տարբերվող կետի ինչ-որ հարևանությամբ և ունենա երկրորդ կարգի շարունակական մասնակի ածանցյալներ (մաքուր և խառը):

2. Նշենք երկրորդ կարգի որոշիչով

ծայրահեղ փոփոխական դասախոսության գործառույթ

Թեորեմ

Եթե ​​կոորդինատներով կետը ֆունկցիայի անշարժ կետ է, ապա.

Ա) Դա տեղական ծայրահեղության կետ է, իսկ տեղական առավելագույնի դեպքում դա տեղական նվազագույն է.

Գ) կետում տեղական ծայրահեղ կետ չէ.

Գ) եթե, գուցե երկուսն էլ:

Ապացույց

Եկեք գրենք Թեյլորի բանաձևը ֆունկցիայի համար՝ սահմանափակվելով երկու տերմինով.

Քանի որ, ըստ թեորեմի պայմանների, կետը անշարժ է, երկրորդ կարգի մասնակի ածանցյալները հավասար են զրոյի, այսինքն. Եվ. Հետո

Նշենք

Այնուհետև ֆունկցիայի աճը կունենա հետևյալ ձևը.

Երկրորդ կարգի մասնակի ածանցյալների (մաքուր և խառը) շարունակականության պատճառով մի կետում թեորեմի պայմանների համաձայն կարող ենք գրել.

Որտեղ կամ; ,

1. Թող եւ, այսինքն. կամ.

2. Բազմապատկենք ֆունկցիայի աճը և բաժանենք վրա, ստանում ենք.

3. Գումարի լրիվ քառակուսին ավելացնենք գանգուր փակագծերում տրված արտահայտությունը.

4. Գանգուր բրեկետներում արտահայտությունը ոչ բացասական է, քանի որ

5. Հետևաբար, եթե միջոցը, ապա և, հետևաբար, ըստ սահմանման կետը տեղական նվազագույնի կետ է:

6. Եթե միջոցը, ապա, ըստ սահմանման, կոորդինատներով կետը տեղական առավելագույնի կետ է։

2. Դիտարկենք քառակուսի եռանկյունը, նրա դիսկրիմինանտը, .

3. Եթե, ապա կան այնպիսի կետեր, որ բազմանդամը

4. Ֆունկցիայի ընդհանուր աճը I-ում ստացված արտահայտությանը համապատասխան կետում գրում ենք հետևյալ կերպ.

5. Երկրորդ կարգի մասնակի ածանցյալների շարունակականության պատճառով մի կետում թեորեմի պայմանների համաձայն կարող ենք գրել, որ.

Հետևաբար, կա կետի այնպիսի հարևանություն, որ ցանկացած կետի համար քառակուսի եռանկյունը մեծ է զրոյից.

6. Դիտարկենք կետի հարեւանությունը:

Եկեք ընտրենք ցանկացած արժեք, ուստի կետ: Ենթադրելով, որ ֆունկցիայի աճի բանաձեւում

Ինչ ենք մենք ստանում.

7. Այդ ժամանակվանից:

8. Նմանապես վիճելով արմատի համար՝ մենք գտնում ենք, որ կետի ցանկացած հարևանությունում կա կետ, որի համար, հետևաբար, կետի հարևանությամբ նշանը չի պահպանվում, հետևաբար կետում ծայրահեղություն չկա:

Երկու փոփոխականի ֆունկցիայի պայմանական ծայրահեղություն

Երկու փոփոխականի ֆունկցիայի էքստրեմաներ գտնելիս հաճախ խնդիրներ են առաջանում՝ կապված այսպես կոչված պայմանական ծայրահեղության հետ։ Այս հայեցակարգը կարելի է բացատրել երկու փոփոխականների ֆունկցիայի օրինակով։

Թող 0xy հարթության վրա տրվեն ֆունկցիա և L ուղիղ։ Խնդիրն է գտնել P (x, y) կետ L գծի վրա, որտեղ ֆունկցիայի արժեքը ամենամեծն է կամ ամենափոքրը՝ համեմատած այս ֆունկցիայի արժեքների հետ L գծի կետերում, որոնք գտնվում են P կետի մոտ: Նման P կետերը: կոչվում են պայմանական ծայրահեղ կետերի գործառույթներ L գծի վրա: Ի տարբերություն սովորական ծայրահեղ կետի, ֆունկցիայի արժեքը պայմանական ծայրահեղ կետում համեմատվում է ֆունկցիայի արժեքների հետ ոչ թե նրա հարևանության բոլոր կետերում, այլ միայն նրանց, որոնք գտնվում են: գծի վրա Լ.

Միանգամայն պարզ է, որ սովորական ծայրահեղության կետը (ասում են նաև անվերապահ էքստրեմում) նաև պայմանական էքստրեմումի կետ է այս կետով անցնող ցանկացած գծի համար։ Հակառակը, իհարկե, ճիշտ չէ. պայմանական ծայրահեղ կետը կարող է լինել սովորական ծայրահեղ կետը: Եկեք սա բացատրենք օրինակով։

Օրինակ թիվ 1.Ֆունկցիայի գրաֆիկը վերին կիսագնդն է (նկ. 2):

Բրինձ. 2.

Այս ֆունկցիան սկզբում ունի առավելագույնը. այն համապատասխանում է կիսագնդի M գագաթին։ Եթե ​​L ուղիղը A և B կետերով անցնող ուղիղ գիծ է (դրա հավասարումը), ապա երկրաչափորեն պարզ է, որ այս ուղղի կետերի համար ֆունկցիայի ամենամեծ արժեքը ձեռք է բերվում A և B կետերի միջև ընկած կետում: Սա պայմանական ծայրահեղ (առավելագույն) ֆունկցիաների կետն է այս գծում. այն համապատասխանում է կիսագնդի M 1 կետին, և նկարից պարզ է դառնում, որ այստեղ որևէ սովորական ծայրահեղության մասին խոսք լինել չի կարող։

Նկատի ունեցեք, որ փակ տարածաշրջանում ֆունկցիայի ամենամեծ և ամենափոքր արժեքները գտնելու խնդրի վերջին մասում մենք պետք է գտնենք այս շրջանի սահմանին գտնվող ֆունկցիայի ծայրահեղ արժեքները, այսինքն. ինչ-որ գծի վրա և դրանով իսկ լուծել պայմանական էքստրեմումի խնդիրը։

Սահմանում 1.Նրանք ասում են, որ որտեղ կա հավասարումը բավարարող կետում պայմանական կամ հարաբերական առավելագույնը (նվազագույնը), եթե հավասարումը բավարարող որևէ կետի համար անհավասարություն կա.

Սահմանում 2.Ձևի հավասարումը կոչվում է սահմանափակման հավասարում:

Թեորեմ

Եթե ​​ֆունկցիաները և ֆունկցիաները շարունակաբար տարբերելի են կետի և մասնակի ածանցյալի հարևանությամբ, իսկ կետը ֆունկցիայի պայմանական ծայրահեղ կետն է սահմանափակման հավասարման նկատմամբ, ապա երկրորդ կարգի որոշիչը հավասար է զրոյի.

Ապացույց

1. Քանի որ, ըստ թեորեմի պայմանների, մասնակի ածանցյալի և ֆունկցիայի արժեքի, ապա որոշակի ուղղանկյունում.

Սահմանված է անուղղակի գործառույթ

Երկու փոփոխականների կոմպլեքս ֆունկցիան մի կետում կունենա տեղական ծայրահեղություն, հետևաբար կամ:

2. Իրոք, ըստ առաջին կարգի դիֆերենցիալ բանաձևի ինվարիանտության հատկության

3. Կապի հավասարումը կարելի է ներկայացնել այս տեսքով, ինչը նշանակում է

4. Բազմապատկել (2) և (3) հավասարումը և գումարել դրանք

Հետեւաբար, երբ

կամայական. և այլն:

Հետևանք

Երկու փոփոխականի ֆունկցիայի պայմանական ծայրահեղ կետերի որոնումը գործնականում իրականացվում է հավասարումների համակարգի լուծման միջոցով.

Այսպիսով, վերը նշված թիվ 1 օրինակում միացման հավասարումից մենք ունենք. Այստեղից հեշտ է ստուգել, ​​թե ինչն է հասնում առավելագույնին: Բայց հետո կապի հավասարումից. Մենք ստանում ենք P կետը, որը գտնվել է երկրաչափորեն:

Օրինակ թիվ 2.Գտեք ֆունկցիայի պայմանական ծայրահեղ կետերը միացման հավասարման նկատմամբ:

Գտնենք տրված ֆունկցիայի մասնակի ածանցյալները և միացման հավասարումը.

Եկեք ստեղծենք երկրորդ կարգի որոշիչ.

Պայմանական ծայրահեղ կետերը գտնելու համար գրենք հավասարումների համակարգ.

Սա նշանակում է, որ ֆունկցիայի պայմանական ծայրահեղության չորս կետ կա կոորդինատներով.

Օրինակ թիվ 3.Գտեք ֆունկցիայի ծայրահեղ կետերը:

Մասնակի ածանցյալները հավասարեցնելով զրոյի՝ մենք գտնում ենք մեկ անշարժ կետ՝ սկզբնաղբյուրը: Ահա,. Հետևաբար, կետը (0, 0) ծայրահեղ կետ չէ։ Հավասարումը հիպերբոլիկ պարաբոլոիդի հավասարումն է (նկ. 3) Նկարից երևում է, որ (0, 0) կետը ծայրահեղ կետ չէ:

Բրինձ. 3.

Փակ տարածաշրջանում ֆունկցիայի ամենամեծ և ամենափոքր արժեքը

1. Թող ֆունկցիան լինի սահմանված և շարունակական սահմանափակված փակ D տիրույթում։

2. Թող ֆունկցիան ունենա վերջավոր մասնակի ածանցյալներ այս տարածքում, բացառությամբ շրջանի առանձին կետերի:

3. Վայերշտրասի թեորեմի համաձայն՝ այս տարածաշրջանում կա մի կետ, որտեղ ֆունկցիան ընդունում է ամենամեծ և ամենափոքր արժեքները։

4. Եթե այդ կետերը Դ շրջանի ներքին կետեր են, ապա ակնհայտորեն դրանք կունենան առավելագույն կամ նվազագույն։

5. Այս դեպքում մեզ հետաքրքրող կետերը ծայրահեղության կասկածելի կետերից են։

6. Այնուամենայնիվ, ֆունկցիան կարող է վերցնել նաև ամենամեծ կամ ամենափոքր արժեքը D տարածաշրջանի սահմանին:

7. D տարածաշրջանում ֆունկցիայի ամենամեծ (ամենափոքր) արժեքը գտնելու համար անհրաժեշտ է գտնել բոլոր ներքին կետերը, որոնք կասկածելի են ծայրահեղության համար, հաշվարկել դրանցում առկա ֆունկցիայի արժեքը, այնուհետև համեմատել ֆունկցիայի արժեքի հետ: տարածաշրջանի սահմանային կետերը, իսկ հայտնաբերված բոլոր արժեքներից ամենամեծը կլինի ամենամեծը փակ տարածաշրջանում Դ.

8. Տեղական առավելագույնը կամ նվազագույնը գտնելու մեթոդը ավելի վաղ քննարկվել է 1.2 բաժնում: և 1.3.

9. Մնում է դիտարկել տարածաշրջանի սահմանի վրա ֆունկցիայի ամենամեծ և ամենափոքր արժեքները գտնելու մեթոդը:

10. Երկու փոփոխականների ֆունկցիայի դեպքում տարածքը սովորաբար սահմանափակվում է կորով կամ մի քանի կորով։

11. Նման կորի (կամ մի քանի կորերի) երկայնքով փոփոխականները կամ կախված են մեկը մյուսից, կամ երկուսն էլ կախված են մեկ պարամետրից:

12. Այսպիսով, սահմանում ֆունկցիան կախված է մեկ փոփոխականից։

13. Մեկ փոփոխականի ֆունկցիայի ամենամեծ արժեքը գտնելու մեթոդը քննարկվել է ավելի վաղ։

14. Դ շրջանի սահմանը տրվի պարամետրական հավասարումներով.

Այնուհետև այս կորի վրա երկու փոփոխականների ֆունկցիան կլինի պարամետրի բարդ ֆունկցիա՝ . Նման ֆունկցիայի համար ամենամեծ և ամենափոքր արժեքները որոշվում են՝ օգտագործելով մեկ փոփոխականի ֆունկցիայի ամենամեծ և ամենափոքր արժեքները որոշելու մեթոդը: