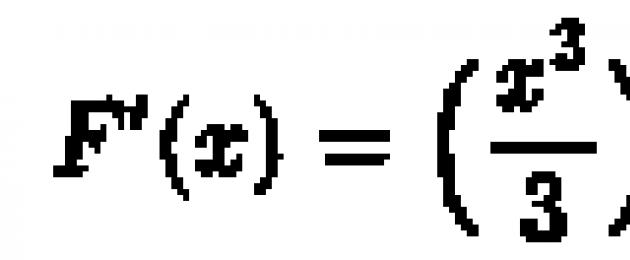Ինտեգրալների ամենապարզ հատկությունները. Ինտեգրալների ամենապարզ հատկությունները 2 անորոշ ինտեգրալի և նրա հատկությունների սահմանումը

Այս հատկությունները օգտագործվում են ինտեգրալի փոխակերպումներ իրականացնելու համար՝ այն տարրական ինտեգրալներից մեկին իջեցնելու և հետագա հաշվարկի համար։

1. Անորոշ ինտեգրալի ածանցյալը հավասար է ինտեգրանդին.

2. Անորոշ ինտեգրալի դիֆերենցիալը հավասար է ինտեգրանտին.

3. Որոշակի ֆունկցիայի դիֆերենցիալի անորոշ ինտեգրալը հավասար է այս ֆունկցիայի և կամայական հաստատունի գումարին.

4. Ինտեգրալ նշանից կարելի է հանել հաստատուն գործոնը.

Ավելին, a ≠ 0

5. Գումարի (տարբերության) ինտեգրալը հավասար է ինտեգրալների գումարին (տարբերությանը).

6. Սեփականությունը 4 և 5 հատկությունների համակցություն է.

Ավելին, a ≠ 0 ˄ b ≠ 0

7. Անորոշ ինտեգրալի անփոփոխ հատկություն.

Եթե, ապա

8. Գույք:

Եթե, ապա

Փաստորեն, այս գույքն է հատուկ դեպքինտեգրում` օգտագործելով փոփոխական փոփոխության մեթոդը, որն ավելի մանրամասն կքննարկվի հաջորդ բաժնում:

Դիտարկենք օրինակ.

Սկզբում կիրառեցինք հատկությունը 5, հետո հատկություն 4, հետո օգտագործեցինք հակաածանցյալների աղյուսակը և ստացանք արդյունքը։

Մեր առցանց ինտեգրալ հաշվիչի ալգորիթմը աջակցում է վերը թվարկված բոլոր հատկություններին և կարող է հեշտությամբ գտնել մանրամասն լուծումձեր ինտեգրալի համար:

Դիֆերենցիալ հաշվարկում խնդիրը լուծվում է. Այս ֆունկցիայի տակ ƒ(x) գտեք նրա ածանցյալը(կամ դիֆերենցիալ): Ինտեգրալ հաշվարկը լուծում է հակադարձ խնդիրը՝ գտե՛ք F(x) ֆունկցիան՝ իմանալով դրա ածանցյալը F "(x)=ƒ(x) (կամ դիֆերենցիալ): Փնտրվող F(x) ֆունկցիան կոչվում է ƒ(x) ֆունկցիայի հակաածանցյալ: )

F(x) ֆունկցիան կոչվում է հակաածանցյալƒ(x) ֆունկցիան (a; b) միջակայքի վրա, եթե որևէ x-ի համար є (a; բ) հավասարությունը

F "(x)=ƒ(x) (կամ dF(x)=ƒ(x)dx):

Օրինակ, y = x 2, x є R ֆունկցիայի հակաածանցյալը ֆունկցիան է, քանի որ

Ակնհայտ է, որ ցանկացած ֆունկցիա նույնպես հակաածանցյալ է լինելու

որտեղ C-ն հաստատուն է, քանի որ

Թեորեմ 29. 1. Եթե F(x) ֆունկցիան (a;b) ƒ(x) ֆունկցիայի հակաածանցյալն է, ապա ƒ(x)-ի բոլոր հակաածանցյալների բազմությունը տրվում է F(x)+ բանաձևով։ C, որտեղ C-ն հաստատուն թիվ է:

▲ F(x)+C ֆունկցիան ƒ(x) հակաածանցյալն է:

Իրոք, (F(x)+C) " =F" (x)=ƒ(x):

Թող Ф(х) լինի ƒ(x) ֆունկցիայի այլ հակաածանցյալ, որը տարբերվում է F(x-ից), այսինքն. Ф"(x)=ƒ(х): Այնուհետև ցանկացած x є (а;b)-ի համար մենք ունենք.

Իսկ սա նշանակում է (տես Հետևություն 25.1), որ

որտեղ C-ն հաստատուն թիվ է: Հետևաբար, Ф(x)=F(x)+С.▼

Բոլոր հակաածանցյալ ֆունկցիաների բազմությունը F(x)+С ƒ(x)-ի համար կոչվում է ƒ(x) ֆունկցիայի անորոշ ինտեգրալև նշանակվում է ∫ ƒ(x) dx նշանով։

Այսպիսով, ըստ սահմանման

∫ ƒ(x)dx= F(x)+C.

Այստեղ կոչվում է ƒ(x): ինտեգրացիոն ֆունկցիա, ƒ(x)dx — ինտեգրալ արտահայտություն, X - ինտեգրման փոփոխական, ∫ -անորոշ ինտեգրալի նշան.

Ֆունկցիայի անորոշ ինտեգրալը գտնելու գործողությունը կոչվում է այս ֆունկցիայի ինտեգրում։

Երկրաչափական առումով անորոշ ինտեգրալը «զուգահեռ» կորերի ընտանիք է y=F(x)+C (C-ի յուրաքանչյուր թվային արժեքը համապատասխանում է ընտանիքի որոշակի կորին) (տե՛ս նկ. 166): Յուրաքանչյուր հակաածանցյալի (կորի) գրաֆիկը կոչվում է ինտեգրալ կոր.

Արդյո՞ք յուրաքանչյուր ֆունկցիա ունի անորոշ ինտեգրալ:

Կա մի թեորեմ, որը նշում է, որ «ամեն մի շարունակական ֆունկցիա այս միջակայքում ունի հակաածանցյալ» և, հետևաբար, անորոշ ինտեգրալ։

Եկեք նշենք անորոշ ինտեգրալի մի շարք հատկություններ, որոնք բխում են դրա սահմանումից:

1. Անորոշ ինտեգրալի դիֆերենցիալը հավասար է ինտեգրալին, իսկ անորոշ ինտեգրալի ածանցյալը հավասար է ինտեգրալին.

դ(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) " =ƒ(x).

Իրոք, d(∫ ƒ(x) dx)=d(F(x)+C)=dF(x)+d(C)=F "(x) dx =ƒ(x) dx

(∫ ƒ (x) dx) " =(F(x)+C)"=F"(x)+0 =ƒ (x):

Այս հատկության շնորհիվ ինտեգրման ճիշտությունը ստուգվում է տարբերակմամբ։ Օրինակ՝ հավասարությունը

∫(3x 2 + 4) dx=х з +4х+С

ճշմարիտ, քանի որ (x 3 +4x+C)"=3x 2 +4:

2. Որոշ ֆունկցիայի դիֆերենցիալի անորոշ ինտեգրալ գումարին հավասարայս ֆունկցիան և կամայական հաստատունը՝

∫dF(x)= F(x)+C.

Իսկապես,

3. Ինտեգրալ նշանից կարելի է հանել հաստատուն գործոնը.

α ≠ 0 հաստատուն է:

Իսկապես,

(դնել C 1 / a = C.)

4. Վերջավոր թվով շարունակական ֆունկցիաների հանրահաշվական գումարի անորոշ ինտեգրալը հավասար է ֆունկցիաների գումարելիների ինտեգրալների հանրահաշվական գումարին.

Թող F"(x)=ƒ(x) և G"(x)=g(x): Հետո

որտեղ C 1 ± C 2 = C.

5. (Ինտեգրման բանաձեւի անփոփոխություն):

Եթե , որտեղ u=φ(x)-ը կամայական ֆունկցիա է՝ շարունակական ածանցյալով։

▲ Թող x լինի անկախ փոփոխական, ƒ(x) - շարունակական գործառույթիսկ F(x) նրա հակագենն է: Հետո

Այժմ սահմանենք u=φ(x), որտեղ φ(x)-ը շարունակաբար տարբերվող ֆունկցիա է: Դիտարկենք բարդ ֆունկցիան F(u)=F(φ(x)): Ֆունկցիայի առաջին դիֆերենցիալի ձևի անփոփոխության պատճառով (տե՛ս էջ 160) ունենք.

Այստեղից ▼

Այսպիսով, անորոշ ինտեգրալի բանաձևը մնում է ուժի մեջ՝ անկախ նրանից, թե ինտեգրման փոփոխականը անկախ փոփոխականն է, թե նրա որևէ ֆունկցիա, որն ունի շարունակական ածանցյալ։

Այսպիսով, բանաձեւից x-ը u-ով (u=φ(x)) փոխարինելով՝ ստանում ենք

Մասնավորապես,

Օրինակ 29.1.Գտե՛ք ինտեգրալը

որտեղ C=C1+C 2 +C 3 +C 4.

Օրինակ 29.2.Գտեք ամբողջական լուծումը.

• 29.3. Հիմնական անորոշ ինտեգրալների աղյուսակ

Օգտվելով այն հանգամանքից, որ ինտեգրումը տարբերակման հակադարձ գործողություն է, կարելի է ստանալ հիմնական ինտեգրալների աղյուսակ՝ շրջելով դիֆերենցիալ հաշվարկի համապատասխան բանաձևերը (դիֆերենցիալների աղյուսակ) և օգտագործելով անորոշ ինտեգրալի հատկությունները։

Օրինակ, որովհետեւ

d(sin u)=cos u . դու

Աղյուսակում մի շարք բանաձևերի ածանցումը կտրվի ինտեգրման հիմնական մեթոդները դիտարկելիս:

Ստորև բերված աղյուսակի ինտեգրալները կոչվում են աղյուսակային: Նրանք պետք է անգիր հայտնի լինեն։ Ինտեգրալ հաշվարկում տարրական ֆունկցիաների հակաածանցյալներ գտնելու պարզ և համընդհանուր կանոններ չկան, ինչպես դիֆերենցիալ հաշվում։ Հակաածանցյալներ գտնելու մեթոդները (այսինքն՝ ֆունկցիայի ինտեգրում) կրճատվում են՝ ցույց տալու այն տեխնիկան, որը տվյալ (փնտրվող) ինտեգրալը բերում է աղյուսակայինին: Ուստի անհրաժեշտ է իմանալ աղյուսակի ինտեգրալները և կարողանալ ճանաչել դրանք։

Նկատի ունեցեք, որ հիմնական ինտեգրալների աղյուսակում ինտեգրման փոփոխականը կարող է նշանակել ինչպես անկախ փոփոխական, այնպես էլ անկախ փոփոխականի ֆունկցիա (ըստ ինտեգրման բանաձևի ինվարիանտության հատկության):

Ստորև բերված բանաձևերի վավերականությունը կարելի է ստուգել՝ վերցնելով աջ կողմի դիֆերենցիալը, որը հավասար կլինի բանաձևի ձախ կողմի ինտեգրմանը:

Եկեք ապացուցենք, օրինակ, 2-րդ բանաձևի վավերականությունը: 1/u ֆունկցիան սահմանված և շարունակական է զրոյից բացի բոլոր արժեքների համար:

Եթե ​​u > 0, ապա ln|u|=lnu, ապա Ահա թե ինչու

Եթե ​​դու<0, то ln|u|=ln(-u). НоՄիջոցներ

Այսպիսով, բանաձև 2-ը ճիշտ է: Նմանապես, եկեք ստուգենք 15-րդ բանաձևը.

Հիմնական ինտեգրալների աղյուսակ

Ընկերներ! Հրավիրում ենք քննարկելու։ Եթե ​​ունեք ձեր կարծիքը, գրեք մեզ մեկնաբանություններում։

Այս հոդվածում մենք կթվարկենք որոշակի ինտեգրալի հիմնական հատկությունները։ Այս հատկությունների մեծ մասն ապացուցված է Ռիմանի և Դարբուի որոշակի ինտեգրալի հասկացությունների հիման վրա:

Որոշակի ինտեգրալի հաշվարկը շատ հաճախ կատարվում է օգտագործելով առաջին հինգ հատկությունները, ուստի անհրաժեշտության դեպքում մենք կանդրադառնանք դրանց: Որոշակի ինտեգրալի մնացած հատկությունները հիմնականում օգտագործվում են տարբեր արտահայտություններ գնահատելու համար։

Նախքան առաջ անցնելը Որոշակի ինտեգրալի հիմնական հատկությունները, համաձայնենք, որ a-ն չի գերազանցում b-ն։

x = a-ով սահմանված y = f(x) ֆունկցիայի համար հավասարությունը ճշմարիտ է:

Այսինքն՝ ինտեգրման նույն սահմաններով որոշակի ինտեգրալի արժեքը հավասար է զրոյի։ Այս հատկությունը Ռիմանի ինտեգրալի սահմանման հետևանք է, քանի որ այս դեպքում յուրաքանչյուր ինտեգրալ գումար ինտերվալի ցանկացած բաժանման և կետերի ցանկացած ընտրության համար հավասար է զրոյի, քանի որ, հետևաբար, ինտեգրալ գումարների սահմանը զրո է։

Ինտերվալի վրա ինտեգրվող ֆունկցիայի համար, .

Այլ կերպ ասած, երբ ինտեգրման վերին և ստորին սահմանները փոխվում են տեղերը, որոշակի ինտեգրալի արժեքը փոխվում է հակառակը: Որոշակի ինտեգրալի այս հատկությունը բխում է նաև Ռիմանի ինտեգրալի հասկացությունից, միայն հատվածի բաժանման համարակալումը պետք է սկսվի x = b կետից։

y = f(x) և y = g(x) միջակայքում ինտեգրվող ֆունկցիաների համար:

Ապացույց.

Գրենք ֆունկցիայի ինտեգրալ գումարը հատվածի տրված բաժանման և կետերի տվյալ ընտրության համար.

որտեղ և են y = f(x) և y = g(x) ֆունկցիաների ինտեգրալ գումարները համապատասխանաբար հատվածի տվյալ բաժանման համար:

Գնա դեպի սահմանը ժամը մենք ստանում ենք, որ Ռիմանի ինտեգրալի սահմանմամբ համարժեք է ապացուցված սեփականության հայտարարությանը:

Որոշակի ինտեգրալի նշանից կարելի է հանել հաստատուն գործոնը։ Այսինքն՝ y = f(x) ֆունկցիայի համար, որը ինտեգրելի է միջակայքի և կամայական k թվի վրա, գործում է հետևյալ հավասարությունը. .

Որոշակի ինտեգրալի այս հատկության ապացույցը բացարձակապես նման է նախորդին.


Թող y = f(x) ֆունկցիան ինտեգրելի լինի X միջակայքում, և եւ հետո .

Այս հատկությունը ճշմարիտ է և՛ և՛, և՛ համար:

Ապացուցումը կարող է իրականացվել որոշիչ ինտեգրալի նախորդ հատկությունների հիման վրա։

Եթե ​​ֆունկցիան ինտեգրելի է ինտերվալի վրա, ապա այն ինտեգրելի է ցանկացած ներքին ինտերվալի վրա:

Ապացույցը հիմնված է Դարբուի գումարների հատկության վրա. եթե հատվածի գոյություն ունեցող բաժանմանը ավելացվեն նոր կետեր, ապա ստորին Դարբուի գումարը չի նվազի, իսկ վերինը՝ չի ավելանա։

Եթե ​​y = f(x) ֆունկցիան ինտեգրելի է արգումենտի միջակայքում և ցանկացած արժեքի համար, ապա .

Այս հատկությունն ապացուցվում է Ռիմանի ինտեգրալի սահմանման միջոցով. հատվածի բաժանման կետերի ցանկացած ընտրության և մոտ կետերի ցանկացած ինտեգրալ գումար կլինի ոչ բացասական (ոչ դրական):

Հետևանք.

y = f(x) և y = g(x) ֆունկցիաների համար, որոնք ինտեգրվում են ինտերվալի վրա, գործում են հետևյալ անհավասարությունները.


Այս հայտարարությունը նշանակում է, որ անհավասարությունների ինտեգրումը թույլատրելի է։ Մենք կօգտագործենք այս եզրակացությունը՝ ապացուցելու հետևյալ հատկությունները.

Թող y = f(x) ֆունկցիան ինտեգրելի լինի ինտերվալի վրա, ապա անհավասարությունը պահպանվում է .

Ապացույց.

Ակնհայտ է, որ . Նախորդ հատկության մեջ պարզեցինք, որ անհավասարությունը կարող է ինտեգրվել տերմին առ տերմին, հետևաբար, դա ճիշտ է. . Այս կրկնակի անհավասարությունը կարելի է գրել այսպես .

Թող y = f(x) և y = g(x) ֆունկցիաները ինտեգրելի լինեն արգումենտի միջակայքում և ցանկացած արժեքի համար, ապա , Որտեղ Եվ .

Ապացուցումն իրականացվում է նույն կերպ. Քանի որ m-ը և M-ը y = f(x) ֆունկցիայի ամենափոքր և ամենամեծ արժեքներն են հատվածի վրա, ապա . Կրկնակի անհավասարությունը բազմապատկելով ոչ բացասական y = g(x) ֆունկցիայով մեզ տանում է հետևյալ կրկնակի անհավասարությունը. Ինտեգրելով այն ինտերվալի վրա՝ հասնում ենք ապացուցվող պնդումին։

Հակածանցյալ ֆունկցիա և անորոշ ինտեգրալ

Փաստ 1. Ինտեգրումը տարբերակման հակադարձ գործողություն է, այն է՝ ֆունկցիայի վերականգնում այս ֆունկցիայի հայտնի ածանցյալից: Գործառույթն այսպիսով վերականգնվեց Ֆ(x) կոչվում է հակաածանցյալֆունկցիայի համար զ(x).

Սահմանում 1. Ֆունկցիա Ֆ(x զ(x) որոշ ընդմիջումով X, եթե բոլոր արժեքների համար xայս միջակայքից պահպանվում է հավասարությունը Ֆ "(x)=զ(x), այսինքն՝ այս ֆունկցիան զ(x) հակաածանցյալ ֆունկցիայի ածանցյալն է Ֆ(x). .

Օրինակ՝ ֆունկցիան Ֆ(x) = մեղք x ֆունկցիայի հակաածանցյալն է զ(x) = cos x ամբողջ թվային տողի վրա, քանի որ x-ի ցանկացած արժեքի համար (մեղ x)» = (cos x) .

Սահմանում 2. Ֆունկցիայի անորոշ ինտեգրալ զ(x) նրա բոլոր հակաածանցյալների բազմությունն է. Այս դեպքում օգտագործվում է նշումը

∫

զ(x)dx

,

որտեղ է նշանը ∫ կոչվում է ինտեգրալ նշան, ֆունկցիա զ(x) – ինտեգրացիոն ֆունկցիա, և զ(x)dx - ինտեգրալ արտահայտություն:

Այսպիսով, եթե Ֆ(x) – որոշ հակաածանցյալ զ(x), Դա

∫

զ(x)dx = Ֆ(x) +Գ

Որտեղ Գ - կամայական հաստատուն (հաստատուն):

Որպես անորոշ ինտեգրալ ֆունկցիայի հակաածանցյալների բազմության իմաստը հասկանալու համար տեղին է հետևյալ անալոգիան. Թող լինի դուռ (ավանդական փայտե դուռ): Նրա գործառույթն է «դուռ լինել»։ Ինչի՞ց է պատրաստված դուռը։ Պատրաստված է փայտից։ Սա նշանակում է, որ «լինել դուռ» ֆունկցիայի ինտեգրացիայի հակաածանցյալների բազմությունը, այսինքն՝ նրա անորոշ ինտեգրալը, «լինել ծառ + C» ֆունկցիան է, որտեղ C-ն հաստատուն է, որն այս համատեքստում կարող է. Նշեք, օրինակ, ծառի տեսակը. Ինչպես որ դուռը պատրաստվում է փայտից՝ օգտագործելով որոշ գործիքներ, ֆունկցիայի ածանցյալը «պատրաստվում» է հակաածանցյալ ֆունկցիայից՝ օգտագործելով. բանաձևեր, որոնք սովորել ենք ածանցյալն ուսումնասիրելիս .

Այնուհետև սովորական առարկաների և դրանց համապատասխան հակաածանցյալների ֆունկցիաների աղյուսակը («լինել դուռ» - «ծառ լինել», «գդալ լինել» - «մետաղ լինել» և այլն) նման է հիմնական աղյուսակին. անորոշ ինտեգրալներ, որոնք կներկայացվեն ստորև։ Անորոշ ինտեգրալների աղյուսակը թվարկում է ընդհանուր ֆունկցիաները՝ նշելով այն հակաածանցյալները, որոնցից «ստեղծվել» են այդ ֆունկցիաները: Անորոշ ինտեգրալը գտնելու խնդիրների մի մասում տրված են ինտեգրանդներ, որոնք կարող են ուղղակիորեն ինտեգրվել առանց մեծ ջանքերի, այսինքն՝ օգտագործելով անորոշ ինտեգրալների աղյուսակը։ Ավելի բարդ խնդիրների դեպքում ինտեգրանդը նախ պետք է փոխակերպվի, որպեսզի աղյուսակի ինտեգրալները օգտագործվեն:

Փաստ 2. Ֆունկցիան որպես հակաածանցյալ վերականգնելիս պետք է հաշվի առնել կամայական հաստատունը (հաստատուն) Գ, և որպեսզի չգրեք հակաածանցյալների ցուցակ 1-ից մինչև անվերջ տարբեր հաստատուններով, պետք է գրել հակաածանցյալների մի շարք կամայական հաստատունով։ ԳՕրինակ՝ այսպես՝ 5 x³ + C. Այսպիսով, կամայական հաստատուն (հաստատուն) ներառված է հակաածանցյալի արտահայտման մեջ, քանի որ հակաածանցյալը կարող է լինել ֆունկցիա, օրինակ՝ 5. x³+4 կամ 5 x³+3 և երբ տարբերվում է, 4 կամ 3 կամ որևէ այլ հաստատուն գնում է զրոյի:

Եկեք առաջադրենք ինտեգրման խնդիրը՝ այս ֆունկցիայի համար զ(x) գտնել նման գործառույթ Ֆ(x), որի ածանցյալըհավասար է զ(x).

Օրինակ 1.Գտե՛ք ֆունկցիայի հակաածանցյալների բազմությունը

Լուծում. Այս ֆունկցիայի համար հակաածանցյալը ֆունկցիան է

Գործառույթ Ֆ(x) կոչվում է ֆունկցիայի հակաածանցյալ զ(x), եթե ածանցյալը Ֆ(x) հավասար է զ(x), կամ, որը նույն բանն է, դիֆերենցիալ Ֆ(x) հավասար է զ(x) dx, այսինքն.

(2)

Հետևաբար, ֆունկցիան ֆունկցիայի հակաածանցյալն է։ Այնուամենայնիվ, դա միակ հակաածանցյալը չէ . Նրանք նաև գործառույթներ են կատարում

Որտեղ ՀԵՏ- կամայական հաստատուն: Սա կարելի է ստուգել տարբերակման միջոցով:

Այսպիսով, եթե ֆունկցիայի համար կա մեկ հակաածանցյալ, ապա նրա համար կա անսահման թվով հակաածանցյալներ, որոնք տարբերվում են հաստատուն անդամով։ Ֆունկցիայի բոլոր հակաածանցյալները գրված են վերը նշված ձևով: Սա բխում է հետևյալ թեորեմից.

Թեորեմ (փաստի պաշտոնական շարադրանք 2):Եթե Ֆ(x) – ֆունկցիայի հակաածանցյալ զ(x) որոշ ընդմիջումով X, ապա ցանկացած այլ հակաածանցյալ համար զ(x) նույն միջակայքում կարող է ներկայացվել ձևով Ֆ(x) + Գ, Որտեղ ՀԵՏ- կամայական հաստատուն:

Հաջորդ օրինակում մենք դիմում ենք ինտեգրալների աղյուսակին, որը տրվելու է 3-րդ պարբերությունում՝ անորոշ ինտեգրալի հատկություններից հետո։ Մենք դա անում ենք ամբողջ աղյուսակը կարդալուց առաջ, որպեսզի պարզ լինի վերը նշվածի էությունը: Իսկ աղյուսակից և հատկություններից հետո մենք դրանք ամբողջությամբ կօգտագործենք ինտեգրման ժամանակ։

Օրինակ 2.Գտեք հակաածանցյալ ֆունկցիաների հավաքածուներ.

Լուծում. Մենք գտնում ենք հակաածանցյալ ֆունկցիաների մի շարք, որոնցից «ստեղծվում» են այդ ֆունկցիաները: Ինտեգրալների աղյուսակից բանաձևեր նշելիս, առայժմ միայն ընդունեք, որ այնտեղ կան այդպիսի բանաձևեր, և մենք անորոշ ինտեգրալների աղյուսակը կուսումնասիրենք մի փոքր ավելի հեռու։

1) ինտեգրալների աղյուսակից (7) բանաձևի կիրառում n= 3, մենք ստանում ենք

2) Օգտագործելով բանաձևը (10) ինտեգրալների աղյուսակից n= 1/3, մենք ունենք

3) Քանի որ

ապա համաձայն (7) բանաձևի հետ n= -1/4 մենք գտնում ենք

Ինտեգրալ նշանի տակ գրված է ոչ թե գործառույթն ինքնին։ զ, և դրա արտադրանքը դիֆերենցիալով dx. Սա արվում է հիմնականում, որպեսզի ցույց տա, թե որ փոփոխականով է որոնվում հակաածանցյալը: Օրինակ,

, ;

այստեղ երկու դեպքում էլ ինտեգրանդը հավասար է , բայց նրա անորոշ ինտեգրալները դիտարկված դեպքերում տարբեր են լինում։ Առաջին դեպքում այս ֆունկցիան դիտարկվում է որպես փոփոխականի ֆունկցիա x, իսկ երկրորդում՝ որպես ֆունկցիա զ .

Ֆունկցիայի անորոշ ինտեգրալը գտնելու գործընթացը կոչվում է այդ ֆունկցիայի ինտեգրում։

Անորոշ ինտեգրալի երկրաչափական նշանակությունը

Ենթադրենք, մենք պետք է գտնենք կոր y=F(x)և մենք արդեն գիտենք, որ շոշափողի անկյան շոշափումը նրա յուրաքանչյուր կետում տրված ֆունկցիա է f(x)այս կետի աբսցիսա:

Ըստ ածանցյալի երկրաչափական նշանակության՝ շոշափողի թեքության անկյան շոշափողը կորի տվյալ կետում. y=F(x)հավասար է ածանցյալի արժեքին F"(x). Այսպիսով, մենք պետք է գտնենք նման գործառույթ F(x), ինչի համար F"(x)=f(x). Առաջադրանքում պահանջվող գործառույթ F(x)-ի հակաածանցյալն է f(x). Խնդրի պայմանները բավարարվում են ոչ թե մեկ կորով, այլ կորերի ընտանիքով։ y=F(x)- այս կորերից մեկը և ցանկացած այլ կոր կարելի է ստանալ դրանից առանցքի երկայնքով զուգահեռ փոխադրման միջոցով Օյ.

Անվանենք հակաածանցյալ ֆունկցիայի գրաֆիկը f(x)ինտեգրալ կոր. Եթե F"(x)=f(x), ապա ֆունկցիայի գրաֆիկը y=F(x)կա ինտեգրալ կոր:

Փաստ 3. Անորոշ ինտեգրալը երկրաչափորեն ներկայացված է բոլոր ինտեգրալ կորերի ընտանիքով։ , ինչպես ստորև նկարում։ Յուրաքանչյուր կորի հեռավորությունը կոորդինատների սկզբնակետից որոշվում է կամայական ինտեգրման հաստատունով Գ.

Անորոշ ինտեգրալի հատկությունները

Փաստ 4. Թեորեմ 1. Անորոշ ինտեգրալի ածանցյալը հավասար է ինտեգրանդին, իսկ դիֆերենցիալը՝ ինտեգրանդին։

Փաստ 5. Թեորեմ 2. Ֆունկցիայի դիֆերենցիալի անորոշ ինտեգրալ զ(x) հավասար է ֆունկցիային զ(x) մինչև հաստատուն ժամկետ , այսինքն.

(3)

1-ին և 2-րդ թեորեմները ցույց են տալիս, որ տարբերակումը և ինտեգրումը փոխադարձ հակադարձ գործողություններ են:

Փաստ 6. Թեորեմ 3. Ինտեգրանդի հաստատուն գործոնը կարելի է դուրս բերել անորոշ ինտեգրալի նշանից. , այսինքն.

Թողեք գործառույթը y = զ(x) սահմանվում է միջակայքում [ ա, բ ], ա < բ. Եկեք կատարենք հետևյալ գործողությունները.

1) եկեք բաժանենք [ ա, բ] կետեր ա = x 0 < x 1 < ... < x ես- 1 < x ես < ... < x n = բ վրա nմասնակի հատվածներ [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x ես- 1 , x ես ], ..., [x n- 1 , x n ];

2) մասնակի հատվածներից յուրաքանչյուրում [ x ես- 1 , x ես ], ես = 1, 2, ... n, ընտրեք կամայական կետ և հաշվարկեք ֆունկցիայի արժեքը այս կետում. զ(z i ) ;

3) գտնել աշխատանքները զ(z i ) · Δ x ես , որտեղ է մասնակի հատվածի երկարությունը [ x ես- 1 , x ես ], ես = 1, 2, ... n;

4) եկեք դիմենք ինտեգրալ գումարգործառույթները y = զ(x) հատվածում [ ա, բ ]:

Երկրաչափական տեսանկյունից այս գումարը σ-ն ուղղանկյունների մակերեսների գումարն է, որոնց հիմքերը մասնակի հատվածներ են [ x 0 , x 1 ], [x 1 , x 2 ], ..., [x ես- 1 , x ես ], ..., [x n- 1 , x n ], իսկ բարձրությունները հավասար են զ(զ 1 ) , զ(զ 2 ), ..., զ(z n) համապատասխանաբար (նկ. 1): Նշենք ըստ λ ամենաերկար մասնակի հատվածի երկարությունը.

5) գտե՛ք ինտեգրալ գումարի սահմանը, երբ λ → 0.

Սահմանում.Եթե ​​կա ինտեգրալ գումարի (1) վերջավոր սահման, և դա կախված չէ հատվածի բաժանման եղանակից [ ա, բ] մասնակի հատվածներին, ոչ էլ կետերի ընտրությունից z iնրանց մեջ, ապա այս սահմանը կոչվում է որոշակի ինտեգրալֆունկցիայից y = զ(x) հատվածում [ ա, բ] և նշվում է

Այսպիսով,

Այս դեպքում գործառույթը զ(x) կոչվում է ինտեգրելիվրա [ ա, բ]։ Թվեր աԵվ բկոչվում են համապատասխանաբար ինտեգրման ստորին և վերին սահմաններ. զ(x) – ինտեգրացիոն ֆունկցիա, զ(x ) dx- ինտեգրալ արտահայտություն, x- ինտեգրման փոփոխական; գծի հատված [ ա, բ] կոչվում է ինտեգրման միջակայք։

Թեորեմ 1.Եթե ​​ֆունկցիան y = զ(x) շարունակական է [ ա, բ], ապա այն ինտեգրելի է այս միջակայքում:

Ինտեգրման միևնույն սահմաններով որոշակի ինտեգրալը հավասար է զրոյի.

Եթե ա > բ, ապա, ըստ սահմանման, մենք ենթադրում ենք

2. Որոշակի ինտեգրալի երկրաչափական նշանակությունը

Թող հատվածը [ ա, բ] նշված է շարունակական ոչ բացասական ֆունկցիա y = զ(x ) . Curvilinear trapezoidվերևում սահմանափակված ֆունկցիայի գրաֆիկով պատկեր է y = զ(x), ներքևից՝ Օքսի առանցքի երկայնքով, դեպի ձախ և աջ՝ ուղիղ գծեր x = aԵվ x = բ(նկ. 2):

Ոչ բացասական ֆունկցիայի որոշակի ինտեգրալ y = զ(x) երկրաչափական տեսանկյունից հավասար է կորագիծ տրապեզիի մակերեսին, որը սահմանափակված է վերևում ֆունկցիայի գրաֆիկով. y = զ(x) , ձախ և աջ – գծային հատվածներ x = aԵվ x = բ, ներքևից՝ Ox առանցքի մի հատված։

3. Որոշակի ինտեգրալի հիմնական հատկությունները

1. Որոշակի ինտեգրալի արժեքը կախված չէ ինտեգրման փոփոխականի նշանակումից.

2. Որոշակի ինտեգրալի նշանից կարելի է հանել հաստատուն գործոնը.

3. Երկու ֆունկցիաների հանրահաշվական գումարի որոշակի ինտեգրալը հավասար է այս ֆունկցիաների որոշակի ինտեգրալների հանրահաշվական գումարին.

4. Եթե գործառույթը y = զ(x) ինտեգրելի է [ ա, բ] Եվ ա < բ < գ, Դա

5. (միջին արժեքի թեորեմ). Եթե ​​ֆունկցիան y = զ(x) շարունակական է [ ա, բ], ապա այս հատվածի վրա կա այնպիսի կետ, որ

4. Նյուտոն-Լայբնից բանաձեւ

Թեորեմ 2.Եթե ​​ֆունկցիան y = զ(x) շարունակական է [ ա, բ] Եվ Ֆ(x) նրա հակաածանցյալներից որևէ մեկն է այս հատվածում, ապա վավեր է հետևյալ բանաձևը.

որը կոչվում է Նյուտոն-Լայբնից բանաձև.Տարբերություն Ֆ(բ) - Ֆ(ա) սովորաբար գրվում է հետևյալ կերպ.

որտեղ խորհրդանիշը կոչվում է կրկնակի նիշ:

Այսպիսով, բանաձևը (2) կարելի է գրել հետևյալ կերպ.

Օրինակ 1.Հաշվարկել ինտեգրալը

Լուծում. Ինտեգրադի համար զ(x ) = x 2 կամայական հակաածանցյալն ունի ձև

Քանի որ ցանկացած հակաածանցյալ կարող է օգտագործվել Նյուտոն-Լայբնից բանաձևում, ինտեգրալը հաշվարկելու համար մենք վերցնում ենք հակաածանցյալը, որն ունի ամենապարզ ձևը.

5. Փոփոխականի փոփոխություն որոշակի ինտեգրալում

Թեորեմ 3.Թողեք գործառույթը y = զ(x) շարունակական է [ ա, բ]։ Եթե:

1) գործառույթ x = φ ( տ) և դրա ածանցյալ φ "( տ) շարունակական են ժամը ;

2) ֆունկցիայի արժեքների մի շարք x = φ ( տ) համար է հատվածը [ ա, բ ];

3) φ ( ա) = ա, φ ( բ) = բ, ապա բանաձեւը վավեր է

որը կոչվում է Որոշակի ինտեգրալում փոփոխականը փոխելու բանաձև .

Ի տարբերություն անորոշ ինտեգրալի, այս դեպքում ոչ անհրաժեշտվերադառնալ սկզբնական ինտեգրման փոփոխականին - բավական է միայն գտնել α և β ինտեգրման նոր սահմաններ (դրա համար անհրաժեշտ է լուծել փոփոխականի համար տհավասարումներ φ ( տ) = աև φ ( տ) = բ).

Փոխարինման փոխարեն x = φ ( տ) կարող եք օգտագործել փոխարինումը տ = է(x) . Այս դեպքում փոփոխականի վրա ինտեգրման նոր սահմաններ գտնելը տպարզեցնում է՝ α = է(ա) , β = է(բ) .

Օրինակ 2. Հաշվարկել ինտեգրալը

Լուծում. Ներկայացնենք նոր փոփոխական՝ օգտագործելով բանաձևը. Հավասարության երկու կողմերը քառակուսելով՝ ստանում ենք 1 + x = տ 2 , որտեղ x = տ 2 - 1, dx = (տ 2 - 1)"dt= 2tdt. Մենք գտնում ենք ինտեգրման նոր սահմաններ: Դա անելու համար եկեք փոխարինենք հին սահմանները բանաձևով x = 3 և x = 8. Ստանում ենք՝ , որտեղից տ= 2 և α = 2; , որտեղ տ= 3 և β = 3: Այսպիսով,

Օրինակ 3.Հաշվիր

Լուծում. Թող u= մատյան x, Հետո, v = x. Ըստ բանաձևի (4)