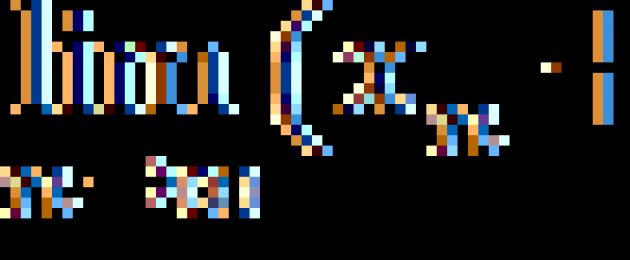Տվեք մի կետում անվերջ փոքր ֆունկցիայի սահմանումը: Անվերջ փոքր ֆունկցիաները և դրանց հիմնական հատկությունները

Գործառույթ y=f(x)կանչեց անսահման փոքրժամը x→aկամ երբ x→∞, եթե կամ, այսինքն. անվերջ փոքր ֆունկցիան այն ֆունկցիան է, որի սահմանը տվյալ կետում զրո է:

Օրինակներ.

1. Գործառույթ f(x)=(x-1) 2-ը անվերջ փոքր է x→1, քանի որ (տե՛ս նկարը):

2. Գործառույթ f(x)= tg x– անսահման փոքր ժամը x→0.

3. f(x)= տեղեկամատյան (1+ x) – անսահման փոքր ժամը x→0.

4. f(x) = 1/x– անսահման փոքր ժամը x→∞.

Եկեք հաստատենք հետևյալ կարևոր հարաբերությունները.

Թեորեմ.Եթե ​​ֆունկցիան y=f(x)հետ ներկայացվող x→aորպես հաստատուն թվի գումար բև անսահման փոքր մեծություն α(x): f (x)=b+ α(x)որ .

Եվ հակառակը, եթե, ապա f (x)=b+α(x), Որտեղ կացին)– անսահման փոքր ժամը x→a.

Ապացույց.

1. Փաստենք հայտարարության առաջին մասը. Հավասարությունից f(x)=b+α(x)պետք է |f(x) – b|=| α|. Բայց քանի որ կացին)անվերջ փոքր է, ապա կամայական ε-ի համար կա δ – կետի հարևանություն ա,բոլորի աչքի առաջ xորից՝ արժեքներ կացին)բավարարել հարաբերությունները |α(x)|< է. Հետո |f(x) – բ|< է. Եվ սա նշանակում է, որ.

2. Եթե , ապա ցանկացած ε >0 բոլորի համար Xորոշ δ – կետի հարևանությամբ ակամք |f(x) – բ|< է. Բայց եթե նշենք f(x) – b= α, Դա |α(x)|< ε, ինչը նշանակում է, որ ա- անսահման փոքր:

Դիտարկենք անվերջ փոքր ֆունկցիաների հիմնական հատկությունները։

Թեորեմ 1.Երկու, երեք և ընդհանրապես անվերջ փոքրերի ցանկացած վերջավոր թվի հանրահաշվական գումարը անվերջ փոքր ֆունկցիա է։

Ապացույց. Եկեք ապացույցներ տանք երկու ժամկետով. Թող f(x)=α(x)+β(x), որտեղ և. Մենք պետք է ապացուցենք, որ ցանկացած կամայական փոքր ε > Գտնվել է 0 δ> 0, այնպիսին, որ համար x, բավարարելով անհավասարությունը |x – ա|<δ , կատարվեց |զ(x)|< ε.

Այսպիսով, եկեք ամրագրենք կամայական ε > 0. Քանի որ թեորեմի պայմանների համաձայն α(x)անվերջ փոքր ֆունկցիա է, ուրեմն կա այդպիսի δ 1 > 0, որը |x – ա|< δ 1 ունենք |α(x)|< ε / 2. Նմանապես, քանի որ β(x)անվերջ փոքր է, ուրեմն կա այդպիսի δ 2 > 0, որը |x – ա|< δ 2 ունենք | β(x)|< ε / 2.

Վերցնենք δ=min(δ 1 , δ2 } .Այնուհետև կետի մոտակայքում աշառավիղը δ անհավասարություններից յուրաքանչյուրը կբավարարվի |α(x)|< ε / 2 և | β(x)|< ε / 2. Հետեւաբար, այս հարեւանությամբ կլինի

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

դրանք. |զ(x)|< ε, ինչը պետք է ապացուցվեր:

Թեորեմ 2.Անվերջ փոքր ֆունկցիայի արտադրյալ կացին)սահմանափակ գործառույթի համար f(x)ժամը x→a(կամ երբ x→∞) անվերջ փոքր ֆունկցիա է։

Ապացույց. Քանի որ գործառույթը f(x)սահմանափակ է, ապա կա քանակ Մայնպես, որ բոլոր արժեքների համար xկետի ինչ-որ հարևանությամբ a|f(x)|≤M.Ավելին, քանի որ կացին)ժամը անվերջ փոքր ֆունկցիա է x→a, ապա կամայական ε > 0 կա կետի հարևանություն ա, որում կպահպանվի անհավասարությունը |α(x)|< ε /Մ. Հետո այս թաղամասերից ավելի փոքրում մենք ունենք | αf|< ε /Մ= է. Իսկ սա նշանակում է, որ աֆ- անսահման փոքր: Առիթով x→∞ապացույցն իրականացվում է նույն կերպ.

Ապացուցված թեորեմից հետևում է.

Եզրակացություն 1.Եթե ​​և, ապա.

Եզրակացություն 2.Եթե գ= const, ապա .

Թեորեմ 3.Անվերջ փոքր ֆունկցիայի հարաբերակցությունը α(x)ըստ գործառույթի f(x), որի սահմանը տարբերվում է զրոյից, անվերջ փոքր ֆունկցիա է։

Ապացույց. Թող . Հետո 1 /f(x)սահմանափակ գործառույթ կա. Հետևաբար, կոտորակը անվերջ փոքր ֆունկցիայի և սահմանափակ ֆունկցիայի արտադրյալն է, այսինքն. ֆունկցիան անսահման փոքր է:

Սահմանում թվային ֆունկցիա. Գործառույթների ճշգրտման մեթոդներ:

Թող D լինի R թվային տողի բազմություն: Եթե D-ին պատկանող յուրաքանչյուր x կապված է y=f(x) մեկ թվի հետ, ապա ասում ենք, որ տրված է f ֆունկցիա:

Գործառույթների ճշգրտման մեթոդներ.

1) աղյուսակային՝ վերջավոր բազմության վրա սահմանված ֆունկցիաների համար։

2) վերլուծական

3) գրաֆիկական

2 և 3 - անսահման բազմության վրա սահմանված ֆունկցիաների համար:

Հակադարձ ֆունկցիայի հայեցակարգը:

Եթե ​​y=f(x) ֆունկցիան այնպիսին է, որ x արգումենտի տարբեր արժեքներ համապատասխանում են ֆունկցիայի տարբեր արժեքներին, ապա x փոփոխականը կարող է արտահայտվել որպես y փոփոխականի ֆունկցիա՝ x=g(y: ) g ֆունկցիան կոչվում է f-ի հակադարձ և նշանակվում է f^(-1):

Բարդ ֆունկցիայի հայեցակարգը:

Համալիր ֆունկցիա-գործառույթ, որի արգումենտը ցանկացած այլ ֆունկցիա է։

Տրված լինեն f(x) և g(x) ֆունկցիաները։ Դրանցից կազմենք երկու բարդ ֆունկցիա։ Համարելով f ֆունկցիան արտաքին (հիմնական), իսկ g ֆունկցիան՝ ներքին, մենք ստանում ենք u(x)=f(g(x)) բարդ ֆունկցիա:

Հերթականության սահմանի որոշում.

A թիվը կոչվում է հաջորդականության սահման (xn), եթե որևէ դրականի համար կա n0 թիվ, որից սկսած հաջորդականության բոլոր անդամները a-ից տարբերվում են ε-ից պակաս մոդուլով (այսինքն՝ դրանք ընկնում են ε-հարևանության մեջ։ ա կետից):

Կոնվերգենտ հաջորդականությունների սահմանների հաշվարկման կանոններ.

1. Յուրաքանչյուր կոնվերգենտ հաջորդականություն ունի միայն մեկ սահման: 2. Եթե (x n) հաջորդականության բոլոր տարրերը հավասար են C-ի (հաստատուն), ապա հաջորդականության սահմանը (x n) նույնպես հավասար է C-ի 3. ; 4. ; 5. .

Սահմանում սահմանափակ հաջորդականություն.

(x n) հաջորդականությունը կոչվում է սահմանափակ, եթե X=(x n) թվերի բազմությունը սահմանափակված է՝ .

Անվերջ փոքր հաջորդականության սահմանում.

Հաջորդականությունը (x n) կոչվում է անվերջ փոքր, եթե ցանկացած (անկախ նրանից, թե որքան փոքր է) >0-ի համար կա n 0 այնպիսի թիվ, որ ցանկացած n>n 0-ի համար անհավասարությունը |x n |< .

Անսահման մեծ հաջորդականության սահմանում.

Հերթականությունը կոչվում է անսահման մեծ, եթե ցանկացած (անկախ նրանից, թե որքան մեծ է) A>0 թվի համար կա n 0 այնպիսի թիվ, որ յուրաքանչյուր n>n 0 թվի համար գործում է |x n |>A անհավասարությունը:

Միապաղաղ հաջորդականությունների սահմանում.

Միապաղաղ հաջորդականություն. 1) աճող ifx n x n +1 բոլոր n-ի համար, 4) չաճող, եթե x n x n +1 բոլոր n-ի համար:

Մի կետում ֆունկցիայի սահմանի որոշումը:

y=f(x) ֆունկցիայի սահմանը x 0 կետում (կամ x x 0-ում) a թիվն է, եթե փաստարկի ցանկացած հաջորդականության (x n) արժեքների համար, որը համընկնում է x 0-ին (բոլորը x n x 0-ին), ֆունկցիայի (f(xn)) արժեքների հաջորդականությունը համընկնում է սահմանին a.

Անվերջ փոքր ֆունկցիայի սահմանում.

Ֆ-իյա f(x)-ն անվերջ փոքր է որպես x→A, եթե .

Անսահման մեծ ֆունկցիայի սահմանում:

Ֆ-իյա f(x)-ը x→A-ի համար անսահման մեծ է, եթե .

Մի կետում անսահման փոքր և անսահման մեծ ֆունկցիաների սահմանումներ և հատկություններ: Հատկությունների և թեորեմների ապացույցներ. Անսահման փոքր և անսահման մեծ ֆունկցիաների փոխհարաբերությունները:

Բովանդակություն

Տես նաեւ: Անսահման փոքր հաջորդականություններ - սահմանում և հատկություններ
Անսահման մեծ հաջորդականությունների հատկությունները

Անվերջ փոքր և անվերջ փոքր ֆունկցիաների սահմանում

Թող x 0 վերջավոր կամ անվերջ կետ է՝ ∞, -∞ կամ +∞:

Անվերջ փոքր ֆունկցիայի սահմանում
α ֆունկցիան (x)կանչեց անսահման փոքրքանի որ x-ը ձգտում է x-ին 0 0 , և այն հավասար է զրոյի.
.

Անսահման մեծ ֆունկցիայի սահմանում
Ֆունկցիան f (x)կանչեց անսահման մեծքանի որ x-ը ձգտում է x-ին 0 , եթե ֆունկցիան ունի սահման՝ x → x 0 , և այն հավասար է անսահմանության.
.

Անսահման փոքր ֆունկցիաների հատկությունները

Անվերջ փոքր ֆունկցիաների գումարի, տարբերության և արտադրյալի հատկությունը

Գումար, տարբերություն և արտադրանքվերջավոր թվով անվերջ փոքր ֆունկցիաներ, ինչպիսիք են x → x 0 անվերջ փոքր ֆունկցիա է որպես x → x 0 .

Այս հատկությունը ֆունկցիայի սահմանների թվաբանական հատկությունների անմիջական հետևանքն է։

Արտադրանքի թեորեմ սահմանափակ գործառույթդեպի անսահման փոքր

Սահմանափակված ֆունկցիայի արտադրյալ x կետի ինչ-որ ծակված հարևանությամբ 0 , մինչև անսահման փոքր, ինչպես x → x 0 , անվերջ փոքր ֆունկցիա է որպես x → x 0 .

Ֆունկցիան որպես հաստատունի և անվերջ փոքր ֆունկցիայի գումար ներկայացնելու հատկությունը

Որպեսզի f ֆունկցիան (x)ուներ վերջավոր սահման, անհրաժեշտ և բավարար է, որ
,
որտեղ է x → x անվերջ փոքր ֆունկցիան 0 .

Անսահման մեծ ֆունկցիաների հատկությունները

Թեորեմ սահմանափակված ֆունկցիայի և անսահման մեծի գումարի մասին

Սահմանափակված ֆունկցիայի գումարը կամ տարբերությունը x կետի ինչ-որ ծակված հարևանության վրա 0 , և անսահման մեծ ֆունկցիա, ինչպես x → x 0 , անսահման մեծ ֆունկցիա է որպես x → x 0 .

Սահմանափակված ֆունկցիայի անսահման մեծի վրա բաժանելու թեորեմ

Եթե ​​ֆունկցիան f (x)անսահման մեծ է որպես x → x 0 , և g ֆունկցիան (x)- սահմանափակված է x կետի ինչ-որ ծակված հարևանությամբ 0 , Դա
.

Թեորեմ ներքևում անվերջ փոքրով սահմանափակված ֆունկցիայի բաժանման մասին

Եթե ​​ֆունկցիան, կետի ինչ-որ ծակված հարևանությամբ, ներքևից սահմանափակված է բացարձակ արժեքով դրական թիվ:
,
իսկ ֆունկցիան անվերջ փոքր է որպես x → x 0 :
,
և կա կետի ծակված հարևանություն, որի վրա, ապա
.

Անսահման մեծ ֆունկցիաների անհավասարությունների հատկությունը

Եթե ​​ֆունկցիան անսահման մեծ է հետևյալում.
,
և ֆունկցիաները և , կետի որոշ ծակված հարևանության վրա բավարարում են անհավասարությունը.
,
ապա ֆունկցիան նույնպես անսահման մեծ է հետևյալում.
.

Այս գույքն ունի երկու հատուկ դեպք.

Թողեք կետի որոշ ծակված հարևանությամբ ֆունկցիաները և բավարարենք անհավասարությունը.
.
Ապա եթե , ապա եւ .
Եթե ​​, ապա եւ .

Անսահման մեծ և անվերջ փոքր ֆունկցիաների փոխհարաբերությունները

Նախորդ երկու հատկություններից հետևում է անսահման մեծ և անվերջ փոքր ֆունկցիաների կապը։

Եթե ​​ֆունկցիան անսահման մեծ է ժամը , ապա ֆունկցիան անվերջ փոքր է ժամը .

Եթե ​​ֆունկցիան անվերջ փոքր է , and-ի համար, ապա ֆունկցիան անսահման մեծ է համարի համար:

Անվերջ փոքրի և անսահման մեծ ֆունկցիայի միջև կապը կարող է արտահայտվել խորհրդանշականորեն.
, .

Եթե ​​անվերջ փոքր ֆունկցիան ունի որոշակի նշան , այսինքն՝ այն դրական է (կամ բացասական) կետի ինչ-որ ծակված հարևանության վրա, ապա այն կարող ենք գրել այսպես.
.
Նույն կերպ, եթե անսահման մեծ ֆունկցիան ունի որոշակի նշան , ապա գրում են.
, կամ ։

Այնուհետև անսահման փոքր և անսահման մեծ ֆունկցիաների խորհրդանշական կապը կարելի է լրացնել հետևյալ հարաբերություններով.
, ,
, .

Անսահմանության նշաններին վերաբերող լրացուցիչ բանաձևեր կարելի է գտնել էջում
«Կետերը անսահմանության վրա և դրանց հատկությունները»:

Հատկությունների և թեորեմների ապացույց

Սահմանափակ և անվերջ փոքր ֆունկցիայի արտադրյալի թեորեմի ապացուցում

Այս թեորեմն ապացուցելու համար մենք կօգտագործենք. Օգտագործում ենք նաև անվերջ փոքր հաջորդականությունների հատկությունը, ըստ որի

Թող ֆունկցիան անվերջ փոքր լինի , և թող ֆունկցիան սահմանափակված լինի կետի ծակված հարևանությամբ.
ժամը .

Քանի որ կա սահմանափակում, կա կետի ծակված հարևանություն, որի վրա սահմանված է գործառույթը: Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա:

.
,
հաջորդականությունը անվերջ փոքր է.
.

Եկեք օգտվենք այն հանգամանքից, որ սահմանափակ հաջորդականության և անվերջ փոքր հաջորդականության արտադրյալը անվերջ փոքր հաջորդականություն է.
.
.

Թեորեմն ապացուցված է.

Գործառույթը որպես հաստատուն և անվերջ փոքր ֆունկցիայի գումար ներկայացնելու հատկության ապացույց

Անհրաժեշտություն. Թող ֆունկցիան ունենա վերջավոր սահման մի կետում
.
Դիտարկենք գործառույթը.
.
Օգտագործելով ֆունկցիաների տարբերության սահմանի հատկությունը՝ ունենք.
.
Այսինքն, կա անվերջ փոքր ֆունկցիա .

Համարժեքություն. Թող այդպես լինի; թող դա լինի։
.

Կիրառենք ֆունկցիաների գումարի սահմանի հատկությունը.

Սեփականությունն ապացուցված է։

Սահմանափակված ֆունկցիայի և անսահման մեծի գումարի թեորեմի ապացույցը

ժամը .

Թեորեմն ապացուցելու համար մենք կօգտագործենք ֆունկցիայի սահմանի Հայնեի սահմանումը

Քանի որ կա սահմանափակում, կա կետի ծակված հարևանություն, որի վրա սահմանված է գործառույթը: Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա:
.
Թող լինի կամայական հաջորդականություն, որը համընկնում է , որի տարրերը պատկանում են հարևանությանը.
,
Այնուհետև սահմանվում են հաջորդականությունը: Ավելին, հաջորդականությունը սահմանափակ է.
.

հաջորդականությունը անսահման մեծ է.
.
Քանի որ սահմանափակ հաջորդականության և անսահման մեծի գումարը կամ տարբերությունը
.

Թեորեմն ապացուցված է.

Այնուհետև, ըստ Հայնեի հաջորդականության սահմանի սահմանման.

Սահմանափակված ֆունկցիայի անվերջ մեծի վրա բաժանման գործակցի վերաբերյալ թեորեմի ապացույց

Դա ապացուցելու համար մենք կօգտագործենք ֆունկցիայի սահմանի Հայնեի սահմանումը։ Մենք օգտագործում ենք նաև անվերջ մեծ հաջորդականությունների հատկությունը, ըստ որի՝ անվերջ փոքր հաջորդականություն է։
ժամը .

Թող ֆունկցիան անսահման մեծ լինի , և թող ֆունկցիան սահմանափակված լինի կետի ծակված հարևանությամբ.
ժամը .
Քանի որ ֆունկցիան անսահման մեծ է, կա մի ծակված հարևանություն այն կետի, որտեղ այն սահմանված է և չի անհետանում.

Քանի որ կա սահմանափակում, կա կետի ծակված հարևանություն, որի վրա սահմանված է գործառույթը: Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա:
.
Թող լինի կամայական հաջորդականություն, որը համընկնում է , որի տարրերը պատկանում են հարևանությանը.
,
Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա: մի հաջորդականություն անսահման մեծ է տարբեր:
, .

զրոյական անդամներ
.
Քանի որ սահմանափակ հաջորդականության և անսահման մեծի գումարը կամ տարբերությունը
.

Թեորեմն ապացուցված է.

Քանի որ սահմանափակ հաջորդականությունը անվերջ մեծի վրա բաժանելու գործակիցը անվերջ փոքր հաջորդականություն է, ուրեմն.

Ներքևում սահմանափակված ֆունկցիան անվերջ փոքրով բաժանելու գործակիցի թեորեմի ապացույց

Թող ֆունկցիան լինի անվերջ փոքր, և թող ֆունկցիան բացարձակ արժեքով սահմանափակված լինի ներքևից դրական թվով, կետի ծակված հարևանությամբ.
ժամը .

Ըստ պայմանի, կա կետի ծակված հարևանություն, որի վրա սահմանված է գործառույթը և չի անհետանում.
ժամը .
Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա: Ավելին, և.

Քանի որ կա սահմանափակում, կա կետի ծակված հարևանություն, որի վրա սահմանված է գործառույթը: Թող լինի թաղամասերի խաչմերուկ և . Այնուհետև գործառույթները և սահմանվում են դրա վրա:
.
Այնուհետև սահմանվում են հաջորդականությունը: Ավելին, հաջորդականությունը սահմանափակված է ստորև.
,
իսկ հաջորդականությունը անվերջ փոքր է՝ ոչ զրոյական անդամներով.
, .

Քանի որ ներքևում սահմանափակված հաջորդականությունը անվերջ փոքրով բաժանելու գործակիցը անսահման մեծ հաջորդականություն է, ապա
.
Եվ թող լինի այն կետի ծակված հարևանությունը, որի վրա
ժամը .

Վերցնենք կամայական հաջորդականություն, որը համընկնում է . Այնուհետև, սկսած ինչ-որ N թվից, հաջորդականության տարրերը կպատկանեն այս հարևանությանը.
ժամը .
Հետո
ժամը .

Ըստ Հայնեի ֆունկցիայի սահմանի սահմանման.
.
Այնուհետև, անսահման մեծ հաջորդականությունների անհավասարությունների հատկությամբ,
.
Քանի որ հաջորդականությունը կամայական է, համընկնում է , ապա, ըստ Հայնեի ֆունկցիայի սահմանի սահմանման,
.

Կիրառենք ֆունկցիաների գումարի սահմանի հատկությունը.

Հղումներ:
Լ.Դ. Կուդրյավցև. Դե ինչ մաթեմատիկական վերլուծություն. Հատոր 1. Մոսկվա, 2003 թ.

Տես նաեւ:

Անսահման փոքր ֆունկցիաներ

Կանչվում է %%f(x)%% ֆունկցիան անսահման փոքր(b.m.) %%x \-ով \in \overline(\mathbb(R))%%, եթե արգումենտի այս միտումով ֆունկցիայի սահմանը հավասար է զրոյի։

Հայեցակարգը բ.մ. ֆունկցիան անքակտելիորեն կապված է իր արգումենտը փոխելու հրահանգների հետ: Կարելի է խոսել բ.մ. գործում է %%a \-ից ​​+ 0%% և %%a \-ից ​​մինչև 0%%: Սովորաբար բ.մ. ֆունկցիաները նշվում են հունարեն այբուբենի առաջին տառերով %%\alpha, \beta, \gamma, \ldots%%

Օրինակներ

1. %%f(x) = x%% ֆունկցիան b.m է: %%x \մինչև 0%%, քանի որ դրա սահմանը %%a = 0%% կետում զրո է: Երկկողմանի սահմանի և միակողմանի սահմանի կապի թեորեմի համաձայն այս ֆունկցիան բ.մ. ինչպես %%x \մինչև +0%%, այնպես էլ %%x \մինչև -0%%:
2. Գործառույթ %%f(x) = 1/(x^2)%% - բ.մ. %%x \մինչև \infty%% (ինչպես նաև %%x \մինչև +\infty%% և %%x \մինչև -\infty%%):

Զրոյից տարբեր հաստատուն թիվը, որքան էլ փոքր լինի բացարձակ արժեքով, բ.մ. ֆունկցիան։ Հաստատուն թվերի դեպքում միակ բացառությունը զրոյական է, քանի որ %%f(x) \equiv 0%% ֆունկցիան ունի զրոյական սահման։

Թեորեմ

%%f(x)%% ֆունկցիան ընդլայնված թվային տողի %%a \in \overline(\mathbb(R))%% կետում ունի վերջնական սահման, որը հավասար է %%b%% թվին, եթե և միայն եթե այս ֆունկցիան հավասար է այս թվի գումարին %%b%% և b.m. %%\alpha(x)%% ֆունկցիաները %%x \մինչև a%%, կամ $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R) ) \Ձախ աջ սլաք \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\աջ): $$

Անսահման փոքր ֆունկցիաների հատկությունները

Ըստ %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%-ով սահմանին անցնելու կանոնների համաձայն, հետևում են հետևյալ պնդումները.

1. բ.մ-ի վերջնական թվի գումարը. %%x \-ից ​​մինչև a%% ֆունկցիաները b.m. %%x \մինչև a%%:
2. Ցանկացած թվի արտադրյալը b.m. %%x \-ից ​​մինչև a%% ֆունկցիաները b.m. %%x \մինչև a%%:

Ապրանք բ.մ. ֆունկցիաներ %%x \մինչև a%% և ֆունկցիա, որը սահմանափակված է որոշ ծակված հարևանությամբ %%\stackrel(\circ)(\text(U))(a)%% a կետում, կա b.m. %%x \մինչև a%% ֆունկցիան:

Հասկանալի է, որ հաստատուն ֆունկցիայի արտադրյալը և բ.մ. %%x \մինչև a%% կա բ.մ. ֆունկցիա %%x \-ից ​​մինչև a%%:

Համարժեք անվերջ փոքր ֆունկցիաներ

Անվերջ փոքր ֆունկցիաները %%\alpha(x), \beta(x)%% %%x \մինչև a%% կոչվում են համարժեքև գրել %%\alpha(x) \sim \beta(x)%%, եթե

$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x)) = \lim\limits_(x \to a)(\frac(\beta(x) )(\ալֆա(x))) = 1. $$

b.m-ի փոխարինման թեորեմ. համարժեք գործառույթներ

Թող %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% լինի b.m. գործառույթներ %%x \մինչև a%%, %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, ապա $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x)) = \lim\ սահմանափակումներ_(x \ a)(\frac(\alpha_1(x))(\beta_1(x))). $$

Համարժեք բ.մ. գործառույթները։

Թող %%\alpha(x)%% լինի b.m. գործառույթը %%x \-ից ​​մինչև a%%, ապա

1. %%\sin(\alpha(x)) \sim \alpha(x)%%
2. %%\ցուցադրման ոճ 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
3. %%\tan \alpha(x) \sim \alpha(x)%%
4. %%\arcsin\alpha(x) \sim \alpha(x)%%
5. %%\arctan\alpha(x) \sim \alpha(x)%%
6. %%\ln(1 + \ալֆա(x)) \sim \ալֆա(x)%%
7. %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
8. %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%

Օրինակ

$$ \սկիզբ(զանգված)(ll) \lim\limits_(x \մինչև 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \մինչև 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\սահմաններ_(x \մինչև 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\սահմանները_(x \մինչև 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \վերջ (զանգված) $$

Անսահման մեծ գործառույթներ

Կանչվում է %%f(x)%% ֆունկցիան անսահման մեծ(b.b.) %%x \-ով \in \overline(\mathbb(R))%%, եթե արգումենտի այս միտումով ֆունկցիան ունի անսահման սահման։

Նման է բ.մ. գործառույթների հայեցակարգ բ.բ. ֆունկցիան անքակտելիորեն կապված է իր արգումենտը փոխելու հրահանգների հետ: Կարելի է խոսել բ.բ. գործառույթներ %%x \-ից ​​մինչև + 0%% և %%x \-ից ​​մինչև a - 0%%: «Անսահման մեծ» տերմինը խոսում է ոչ թե ֆունկցիայի բացարձակ արժեքի, այլ տվյալ կետի մերձակայքում դրա փոփոխության բնույթի մասին։ Ոչ մի հաստատուն թիվ, որքան էլ մեծ լինի բացարձակ արժեքով, անսահման մեծ չէ:

Օրինակներ

1. Գործառույթ %%f(x) = 1/x%% - բ.բ. %%x \մինչև 0%%:
2. Գործառույթ %%f(x) = x%% - b.b. %%x \մինչև \infty%%:

Եթե ​​սահմանման պայմանները $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end (զանգված) $$

հետո խոսում են դրականկամ բացասականբ.բ. %%a%% ֆունկցիայի դեպքում:

Օրինակ

Գործառույթ %%1/(x^2)%% - դրական բ.բ. %%x \մինչև 0%%:

Կապը բ.բ. եւ բ.մ. գործառույթները

Եթե ​​%%f(x)%% բ.բ. %%x \ to a%% ֆունկցիայով, ապա %%1/f(x)%% - b.m.

%%x \մինչև a%%: Եթե ​​%%\ալֆա(x)%% - բ.մ. քանի որ %%x \ to a%%-ը ոչ զրոյական ֆունկցիա է %%a% կետի որոշ ծակված հարևանությամբ, ապա %%1/\alpha(x)%% է b.b. %%x \-ից ​​մինչև a%%:

Անսահման մեծ ֆունկցիաների հատկությունները

Ներկայացնենք b.b-ի մի քանի հատկություններ. գործառույթները։ Այս հատկությունները ուղղակիորեն բխում են b.b-ի սահմանումից: վերջավոր սահմաններ ունեցող ֆունկցիաների ֆունկցիաները և հատկությունները, ինչպես նաև բ.բ.-ի միջև կապի թեորեմից։ եւ բ.մ. գործառույթները։

1. B.b-ի վերջավոր թվի արտադրյալը. %%x \-ից ​​մինչև a%% ֆունկցիաները b.b. ֆունկցիա %%x \-ից ​​մինչև a%%: Իսկապես, եթե %%f_k(x), k = \overline(1, n)%% - b.b. գործում է %%x \մինչև a%%, ապա կետի որոշ ծակված հարևանությամբ %%a%% %%f_k(x) \ne 0%%, և կապի թեորեմով բ.բ. եւ բ.մ.ֆունկցիաներ %%1/f_k(x)%% - b.m. ֆունկցիա %%x \-ից ​​մինչև a%%: Ստացվում է %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m ֆունկցիա %%x \մինչև a%%, և %%\displaystyle\prod^(n) )_(k = 1)f_k(x)%% - բ.բ. ֆունկցիա %%x \-ից ​​մինչև a%%:
2. Ապրանք բ.բ. ֆունկցիաներ %%x \-ից ​​մինչև a%% և մի ֆունկցիա, որը %%a%% կետի որոշ ծակված հարևանությամբ բացարձակ արժեքով ավելի մեծ է, քան դրական հաստատունը, b.b. ֆունկցիա %%x \-ից ​​մինչև a%%: Մասնավորապես, ապրանքը b.b. %%x \մինչև a%% ֆունկցիան և այն ֆունկցիան, որն ունի վերջավոր ոչ զրոյական սահման %%a%% կետում կլինի b.b. ֆունկցիա %%x \-ից ​​մինչև a%%:

%%a%% կետի որոշ ծակված հարևանությամբ սահմանափակված ֆունկցիայի գումարը և b.b. %%x \-ից ​​մինչև a%% ֆունկցիաները b.b. ֆունկցիա %%x \-ից ​​մինչև a%%:

Օրինակ՝ %%x - \sin x%% և %%x + \cos x%% ֆունկցիաները b.b են: %%x \մինչև \infty%%:

3. Երկու բ.բ.-ի գումարը. %%x \-ից ​​մինչև a%% ֆունկցիաների դեպքում անորոշություն կա: Կախված տերմինների նշանից՝ նման գումարի փոփոխության բնույթը կարող է շատ տարբեր լինել։

   Օրինակ

   Տրված լինեն %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% ֆունկցիաները։ գործում է %%x \ից \infty%%: Ապա.

   • %%f(x) + g(x) = 3x%% - բ.բ. ֆունկցիա %%x \ից \infty%%;
   • %%f(x) + h(x) = 0%% - բ.մ. ֆունկցիա %%x \ից \infty%%;
   • %%h(x) + v(x) = \sin x%% չունի սահմանաչափ %%x \մինչև \infty%%:

Անվերջ փոքրերի և մեծերի հաշվարկ

Անսահման փոքր հաշվարկ- անվերջ փոքր մեծություններով կատարված հաշվարկներ, որոնցում ստացված արդյունքը համարվում է անվերջ փոքրերի գումար. Անսահման փոքր հաշվարկն է ընդհանուր հայեցակարգդիֆերենցիալ և ինտեգրալ հաշվարկների համար, որոնք կազմում են ժամանակակից բարձրագույն մաթեմատիկայի հիմքը։ Անվերջ փոքր մեծության հասկացությունը սերտորեն կապված է սահման հասկացության հետ։

Անսահման փոքր

Հաջորդականություն ա nկանչեց անսահման փոքր, Եթե . Օրինակ՝ թվերի հաջորդականությունը անվերջ փոքր է։

Ֆունկցիան կոչվում է անսահման փոքր՝ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման փոքր անսահմանության մեջ, Եթե կամ .

Նաև անվերջ փոքր է ֆունկցիան, որը ֆունկցիայի և նրա սահմանի տարբերությունն է, այսինքն՝ եթե , Դա զ(x) − ա = α( x) , .

Անսահման մեծ քանակությամբ

Հաջորդականություն ա nկանչեց անսահման մեծ, Եթե .

Ֆունկցիան կոչվում է անսահման մեծ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման մեծ անսահմանության մեջ, Եթե կամ .

Բոլոր դեպքերում, հավասարության իրավունքի անսահմանությունը ենթադրվում է ունենալ որոշակի նշան (կամ «գումարած» կամ «մինուս»): Դա, օրինակ, ֆունկցիան է xմեղք xանսահման մեծ չէ ժամը .

Անսահման փոքրի և անսահման մեծի հատկությունները

Անվերջ փոքրերի համեմատություն

Ինչպե՞ս համեմատել անսահման փոքր մեծությունները:
Անվերջ փոքր մեծությունների հարաբերակցությունը ձևավորում է այսպես կոչված անորոշություն։

Սահմանումներ

Ենթադրենք, որ մենք ունենք անվերջ փոքր արժեքներ α( x) և β( x) (կամ, որը սահմանման համար կարևոր չէ, անվերջ փոքր հաջորդականություններ)։

Նման սահմանները հաշվարկելու համար հարմար է օգտագործել L'Hopital-ի կանոնը։

Համեմատության օրինակներ

Օգտագործելով ՄԱՍԻՆ-սիմվոլիզմ, ստացված արդյունքները կարելի է գրել հետեւյալ ձեւով x 5 = o(x 3). Այս դեպքում ճշմարիտ են հետևյալ գրառումները. 2x 2 + 6x = Օ(x) Եվ x = Օ(2x 2 + 6x).

Համարժեք արժեքներ

Սահմանում

Եթե ​​, ապա կոչվում են α և β անվերջ փոքր մեծությունները համարժեք ().
Ակնհայտ է, որ համարժեք մեծությունները նույն փոքրության կարգի անվերջ փոքր մեծությունների հատուկ դեպք են։

Երբ վավեր են հետևյալ համարժեքության հարաբերությունները. .

Թեորեմ

Երկու անվերջ փոքր մեծությունների գործակցի (հարաբերակցության) սահմանը չի փոխվի, եթե դրանցից մեկը (կամ երկուսը) փոխարինվի համարժեք մեծությամբ..

Այս թեորեմը գործնական նշանակություն ունի սահմաններ գտնելիս (տես օրինակ)։

Օգտագործման օրինակ

Փոխարինելով սեսn 2x համարժեք արժեք 2 x, ստանում ենք

Պատմական ուրվագիծ

«Անվերջ փոքր» հասկացությունը քննարկվել է դեռևս հին ժամանակներում՝ կապված անբաժանելի ատոմների հայեցակարգի հետ, բայց դասական մաթեմատիկայի մեջ չի ներառվել։ Այն կրկին վերածնվեց 16-րդ դարում «անբաժանելիների մեթոդի» հայտնվելով՝ ուսումնասիրվող պատկերը բաժանելով անվերջ փոքր հատվածների։

17-րդ դարում տեղի է ունեցել անվերջ փոքր հաշվարկների հանրահաշիվը։ Դրանք սկսեցին սահմանվել որպես թվային մեծություններ, որոնք փոքր են ցանկացած վերջավոր (ոչ զրոյական) մեծությունից և դեռևս հավասար չեն զրոյի։ Վերլուծության արվեստը բաղկացած էր անվերջ փոքրեր (դիֆերենցիալներ) պարունակող հարաբերություն կազմելուց և այնուհետև ինտեգրելուց:

Հին դպրոցի մաթեմատիկոսները հայեցակարգը փորձության ենթարկեցին անսահման փոքրկոշտ քննադատություն. Միշել Ռոլեն գրել է, որ նոր հաշվարկը « հնարամիտ սխալների հավաքածու«; Վոլտերը կաուստիկ կերպով նկատեց, որ հաշվարկը այն իրերը հաշվարկելու և ճշգրիտ չափելու արվեստ է, որոնց գոյությունն ապացուցված չէ: Նույնիսկ Հյուգենսը խոստովանեց, որ չի հասկանում ավելի բարձր կարգի դիֆերենցիալների իմաստը:

Որպես ճակատագրի հեգնանք կարելի է համարել դարի կեսերին ոչ ստանդարտ վերլուծության ի հայտ գալը, որն ապացուցեց, որ սկզբնական տեսակետը` փաստացի անվերջ փոքրերը, նույնպես համահունչ էր և կարող էր օգտագործվել որպես վերլուծության հիմք:

տես նաեւ

Վիքիմեդիա հիմնադրամ. 2010 թ.

Տեսեք, թե ինչ է «Անսահման մեծ» բառը այլ բառարաններում.

Y փոփոխական մեծությունը X անվերջ փոքր մեծության հակադարձն է, այսինքն՝ Y = 1/X... Մեծ Հանրագիտարանային բառարան

y փոփոխականը անվերջ փոքր x-ի հակադարձն է, այսինքն՝ y = 1/x: * * * Անսահման մեծ, անսահման մեծ, փոփոխական քանակություն Y, անվերջ փոքր X արժեքի հակադարձ, այսինքն, Y = 1/X ... Հանրագիտարանային բառարան

Մաթեմատիկայի մեջ փոփոխական մեծություն, որը փոփոխության տվյալ գործընթացում դառնում և մնում է բացարձակ արժեքով ավելի մեծ, քան ցանկացած կանխորոշված ​​թիվ։ Բ.-ի ուսումնասիրություն. քանակները կարող են կրճատվել մինչև անվերջ փոքրերի ուսումնասիրությունը (Տես... ... Սովետական ​​մեծ հանրագիտարան