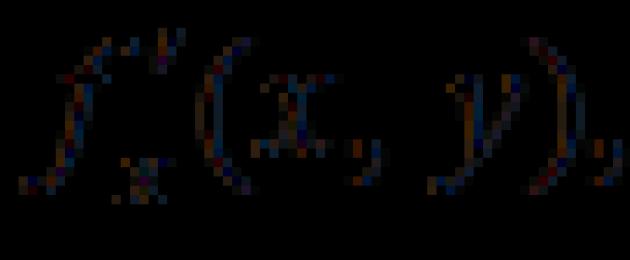Թող տրվի երկու փոփոխականի ֆունկցիա։ Եկեք արգումենտին ավելացնենք և փաստարկը թողնենք անփոփոխ: Այնուհետև ֆունկցիան կստանա աճ, որը փոփոխականով կոչվում է մասնակի աճ և նշվում է.
Նմանապես, արգումենտը ամրագրելով և արգումենտին ավելացում տալով, մենք ստանում ենք ֆունկցիայի մասնակի աճ ըստ փոփոխականի.
Մեծությունը կոչվում է ֆունկցիայի ընդհանուր աճը մի կետում:
Սահմանում 4. Երկու փոփոխականի ֆունկցիայի մասնակի ածանցյալը այս փոփոխականներից մեկի նկատմամբ ֆունկցիայի համապատասխան մասնակի աճի հարաբերակցության սահմանն է տվյալ փոփոխականի աճին, երբ վերջինս ձգտում է զրոյի (եթե այս սահմանը գոյություն ունի): Մասնակի ածանցյալը նշվում է հետևյալ կերպ՝ կամ, կամ.
Այսպիսով, ըստ սահմանման մենք ունենք.
Ֆունկցիաների մասնակի ածանցյալները հաշվարկվում են նույն կանոններով և բանաձևերով՝ որպես մեկ փոփոխականի ֆունկցիա՝ հաշվի առնելով, որ փոփոխականի նկատմամբ տարբերելիս այն համարվում է հաստատուն, իսկ փոփոխականի նկատմամբ տարբերելիս՝ հաստատուն։ .
Օրինակ 3. Գտեք ֆունկցիաների մասնակի ածանցյալներ.
Լուծում. ա) Գտնելու համար մենք այն համարում ենք հաստատուն արժեք և տարբերակում այն որպես մեկ փոփոխականի ֆունկցիա.
Նմանապես, ենթադրելով հաստատուն արժեք, մենք գտնում ենք.
Սահմանում 5. Ֆունկցիայի ընդհանուր դիֆերենցիալը այս ֆունկցիայի մասնակի ածանցյալների արտադրյալների և համապատասխան անկախ փոփոխականների ավելացումների գումարն է, այսինքն.
Հաշվի առնելով, որ անկախ փոփոխականների դիֆերենցիալները համընկնում են դրանց աճի հետ, այսինքն. , ընդհանուր դիֆերենցիալ բանաձեւը կարելի է գրել այսպես
Օրինակ 4. Գտե՛ք ֆունկցիայի լրիվ դիֆերենցիալը:
Լուծում. Քանի որ, օգտագործելով ընդհանուր դիֆերենցիալ բանաձևը, մենք գտնում ենք
Բարձր կարգի մասնակի ածանցյալներ
Մասնակի ածանցյալները կոչվում են առաջին կարգի մասնակի ածանցյալներ կամ առաջին մասնակի ածանցյալներ:
Սահմանում 6. Ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալները առաջին կարգի մասնակի ածանցյալների մասնակի ածանցյալներն են:
Կան չորս երկրորդ կարգի մասնակի ածանցյալներ: Դրանք նշանակված են հետևյալ կերպ.
Նմանապես սահմանվում են 3-րդ, 4-րդ և ավելի բարձր կարգերի մասնակի ածանցյալները: Օրինակ, ֆունկցիայի համար մենք ունենք.
Երկրորդ կամ ավելի բարձր կարգի մասնակի ածանցյալները, վերցված տարբեր փոփոխականների նկատմամբ, կոչվում են խառը մասնակի ածանցյալներ։ Ֆունկցիայի համար սրանք ածանցյալներ են: Նկատի ունեցեք, որ այն դեպքում, երբ խառը ածանցյալները շարունակական են, ապա հավասարությունը պահպանվում է։
Օրինակ 5. Գտեք ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալներ
Լուծում. Այս ֆունկցիայի առաջին կարգի մասնակի ածանցյալները գտնվում են Օրինակ 3-ում.
Տարբերակելով x և y փոփոխականների նկատմամբ՝ մենք ստանում ենք
Օրինակ։ Գտե՛ք y x yxz ֆունկցիայի մասնակի ածանցյալները
Լուծում. Ենթադրելով y =const, մենք գտնում ենք xy x z
Ենթադրելով x =const, մենք գտնում ենք 2 2) 1 (1 y x x y xx y z
Օրինակ։ Գտեք ֆունկցիայի մասնակի ածանցյալների արժեքները M կետում (1, – 1, 0): xyzyxu)ln(
Լուծում. Ենթադրելով y = const , z = const , մենք գտնում ենք 10 11 22 1)02(1 22 22 , М czy yz yx x yzx yxx u
Նմանապես մենք գտնում ենք 10 11 22 1)20 (1 22 22, M czx xz yx y xzy yxy u 110, M cyx xyxy z u
Մասնակի ածանցյալի երկրաչափական նշանակությունը (օրինակ) M 0 (x 0 , y 0 , z 0) կետում գծված շոշափողի թեքության անկյան շոշափումն է y = y հարթությամբ մակերեսի հատվածին։ 0. xz
Ենթադրենք, որ z = f (x, y) ֆունկցիան ունի շարունակական մասնակի ածանցյալներ), (yxf x z x), (yxf y z y):
Այս ածանցյալներն իրենց հերթին x և y անկախ փոփոխականների գործառույթներն են: Մենք դրանք կանվանենք նաև 1-ին կարգի մասնակի ածանցյալներ, (yxf x), (yxf y):
2-րդ կարգի մասնակի ածանցյալները կոչվում են 1-ին կարգի մասնակի ածանցյալներ: Երկու փոփոխականների z = f (x, y) ֆունկցիայի համար կարող եք գտնել 2-րդ կարգի չորս մասնակի ածանցյալներ, որոնք նշվում են հետևյալ կերպ.
Ընդհանուր դեպքում խառը մասնակի ածանցյալները կարող են չհամընկնել, բայց նրանց համար վավեր է թեորեմը՝ թեորեմ։ Եթե խառը մասնակի ածանցյալները M (x, y) մի կետում շարունակական են, ապա դրանք հավասար են, այսինքն՝ xyfyxf), (yxfyxf yxxy):
n-րդ կարգի մասնակի ածանցյալները կոչվում են (n – 1)-րդ կարգի մասնակի ածանցյալներ։ Դրանք նշանակված են և այլն 221, yx z x z n n n
Օրինակ։ Գտե՛ք ֆունկցիայի 2-րդ կարգի մասնակի ածանցյալները)1 sin(23 xyyxz
Լուծում. Մենք այն հաջորդաբար գտնում ենք); 1 cos(3 22 xyyyx x z cy); 1 cos(2 3 xyxyx y z cx
); 1 sin(6)1 cos(3 22 22 2 2 xyyxy xyyyx xx z cy cy); 1 sin()1 cos(6)1 cos(3 2 22 2 xyyx xyyyx z cx cx
)1 sin()1 cos(6 1 cos(2 2 3 2 xyyx xyxyx xxy z cy cy)1 sin(2)1 cos(2 23 3 2 2 xyxx xyxyx yy z cx cx
Դիտարկենք z = f (x, y) ֆունկցիան: Եկեք x արգումենտին տանք աճ Δ x, իսկ y արգումենտը՝ Δ y աճ: Այնուհետև z-ն կստանա աճ, որը կոչվում է z. ֆունկցիայի ընդհանուր աճ), (yxfyyxxfz):
Ենթադրենք, որ f(x, y) M(x, y) կետում ունի շարունակական մասնակի ածանցյալներ։
Սահմանում. z = f (x, y) ֆունկցիայի 1-ին կարգի դիֆերենցիալը այս ֆունկցիայի Δ z ընդհանուր աճի հիմնական մասն է, գծային Δ x և Δ y-ի նկատմամբ, որը նշվում է dz կամ df նշանով և հաշվարկվում է բանաձեւը y y z x x z zd
Քանի որ անկախ փոփոխականների դիֆերենցիալները համընկնում են դրանց աճի հետ, այսինքն՝ dx = Δ x, dy = Δ y, այս բանաձևը կարելի է գրել հետևյալ կերպ. dy y z dx x z zd.
F (x, y) երկու փոփոխականների ֆունկցիայի ընդհանուր դիֆերենցիալի երկրաչափական նշանակությունը (x 0, y 0) կետում շոշափող հարթության կիրառման (z կոորդինատների) ավելացումն է մակերևույթից շարժվելիս: կետը (x 0, y 0) մինչև կետը (x 0 + x, y 0 + y):
Երկու փոփոխականների ֆունկցիայի ընդհանուր դիֆերենցիալի երկրաչափական նշանակությունը մեկ փոփոխականի ֆունկցիայի դիֆերենցիալի երկրաչափական նշանակության տարածական անալոգն է։
Z = f (x, y) ֆունկցիայի 2-րդ կարգի դիֆերենցիալը նրա 1-ին կարգի դիֆերենցիալի դիֆերենցիալն է և նշանակվում է (zzddd)
Եթե z = f (x, y) ֆունկցիայի բոլոր 2-րդ կարգի մասնակի ածանցյալները շարունակական են, ապա գործում է բանաձևը՝ 2 2 2 y y z yx yx z x x z zddddd.
Օրինակ։ Գտե՛ք y x yz 2 x ֆունկցիայի 1-ին և 2-րդ կարգերի դիֆերենցիալները
Լուծում. Գտնենք 1-ին և 2-րդ կարգերի մասնակի ածանցյալները՝ y yx x z 1 2 2 2 y x x y z.
; 202 1 2 2 2 yy y xy xx z cy; 1 2 2 2 y xy yyx z cx 33 22 22 2)2(0 y x yx y x x y y z cy
Հետևաբար, 1-ին և 2-րդ կարգերի դիֆերենցիալները կգրվեն հետևյալ ձևով.
Թող f (x, y) ֆունկցիան տարբերելի լինի (x, y) կետում։ Գտնենք այս ֆունկցիայի ընդհանուր աճը:), (yxfyyxxfz zyxfyyxxf), (
Եթե արտահայտությունը փոխարինենք այս բանաձևով, ապա կստանանք մոտավոր բանաձև՝ y yf x xf dzz y y yxf x x yxf yyxxf), (
Օրինակ։ Մոտավորապես հաշվարկեք արժեքը՝ հիմնվելով x = 1, y = 2, z = 102, 1 ln 04, 1 99, 1 zxu y ln ֆունկցիայի արժեքի վրա:
Լուծում. Տրված արտահայտությունից որոշում ենք x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01, z = 1,02 – 1 = 0,02 Գտեք u (x, y, z) = 11 ln ֆունկցիայի արժեքը
Գտե՛ք մասնակի ածանցյալները՝ 1 12 12 ln 2 1 zx xy x u y y 0 ln 2 ln zx xx y u y y
u ֆունկցիայի ընդհանուր դիֆերենցիալը հավասար է՝ 2 1 ln 2 1 zx z z u y
05, 001, 004, 0 02, 0 21 01, 0004, 01 02, 001, 004, 0 zu yu xudu
Այս արտահայտության ճշգրիտ իմաստը հետևյալն է.
Մ 0 կետում գտնվող մակերևույթին շոշափող հարթությունը այն հարթությունն է, որը պարունակում է այս կետով մակերևույթի վրա գծված կորերի բոլոր շոշափումները:
Մ 0 կետում մակերևույթի նորմալը ուղիղ գիծ է, որն անցնում է այս կետով և ուղղահայաց է այս կետում գծված շոշափող հարթությանը:
Եթե մակերեսը տրված է F (x, y, z) = 0 հավասարմամբ, ապա շոշափողի հարթության հավասարումը M 0 կետում (x 0, y 0, z 0) ունի ձև՝ 0))((00) 0000 zz MF yy
M 0 (x 0, y 0, z 0) կետում մակերեսին գծված նորմալի հավասարումները կգրվեն հետևյալ կերպ.)()()(0 0 0 MF zz MF yy MF xx zyx.
Եթե մակերեսը տրված է z = f (x, y) հավասարմամբ, ապա շոշափողի հարթության հավասարումը M 0 (x 0, y 0, z 0) կետում ունի ձև:))(, (000 0000): yyyxf xxyxfzz y x
իսկ նորմալ հավասարումները կգրվեն հետևյալ կերպ. 1), (0 00 0 zz yxf yy yxf xx yx
Օրինակ։ M 0 (x 0 , y 0 , z 0) կետում շոշափող հարթության և մակերևույթի վրա նորմալ հարթության համար ստեղծե՛ք հավասարումներ, եթե 01332 22 yzxzxyyx: 1, 2 00 yx
Լուծում. Փոխարինելով x 0-ը և y 0-ը մակերեսային հավասարման մեջ՝ մենք գտնում ենք z 0 արժեքը. որտեղից մենք գտնում ենք z 0 = 1: Հետևաբար, M 0 (2, – 1, 1) շոշափման կետն է: 01)1(32)1(23)1(2400 2 zz
Ըստ խնդրի պայմանների՝ մակերեսը հստակեցվում է անուղղակիորեն։ Նշենք և գտնենք մասնակի ածանցյալները M կետում 0 (2, – 1, 1)՝ 1332), (22 yzxzxyyxzyx):
, 32 zyx. F x 21)1(322)(0 MF x, 334 zxy. F y 51323)1(4)(0 MF y, 3 yx. F z 1)1(32)(0 MF z
Մենք փոխարինում ենք մասնակի ածանցյալների հայտնաբերված արժեքները շոշափող հարթության 0))) ((00 0000 zz. MF yy. MFxx. MF z yx) հավասարման մեջ
Նորմալ հավասարումները ունեն 1 1 5 1 2 2 zyx ձև
Սահմանում. Z = f (x, y) ֆունկցիան ունի առավելագույնը M կետում 0 (x 0, y 0), եթե կա այս կետի այնպիսի հարևանություն, որ այս հարևանությունից ցանկացած M (x, y) կետերի համար հետևյալ անհավասարությունը. պահում է, (00 yxfyxf
Սահմանում.Ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալները նրա առաջին կարգի մասնակի ածանցյալների մասնակի ածանցյալներն են։
Երկրորդ կարգի մասնակի ածանցյալների նշում.
Գործնական օրինակների համար ճշմարիտ է հետևյալ հավասարությունը.
Այսպիսով, երկրորդ կարգի խառը ածանցյալների միջոցով շատ հարմար է ստուգել առաջին կարգի մասնակի ածանցյալներ գտնելու ճիշտությունը։
Օրինակներ.
Ա)Գտեք ֆունկցիայի երկրորդ կարգի մասնակի ածանցյալները
Լուծում.
1. Մենք հաշվում ենք փոփոխականը y
2. Ստացված ֆունկցիան նորից տարբերակենք «x»-ի նկատմամբ, այսինքն. Գտնենք երկրորդ ածանցյալը «x»-ի նկատմամբ.
3. Մենք հաշվում ենք փոփոխականը X հաստատուն, մենք կիրառում ենք գումարը տարբերելու կանոնը, հաստատուն գործակիցը ածանցյալի նշանից և հզորության ֆունկցիայի աղյուսակային ածանցյալից դուրս դնելու կանոնը.
4. Եվս մեկ անգամ տարբերակենք ստացված ֆունկցիան «y»-ի նկատմամբ, այսինքն. Գտնենք երկրորդ ածանցյալը «y»-ի նկատմամբ.
5. Գտնենք «x-ով» խառը ածանցյալը: Դա անելու համար մենք առաջին ածանցյալը «x»-ի նկատմամբ տարբերում ենք «y»-ի նկատմամբ:
5. Գտնենք «y» խառը ածանցյալը x-ի նկատմամբ: Դա անելու համար մենք առաջին ածանցյալը «y»-ի նկատմամբ տարբերում ենք «x»-ի նկատմամբ:
բ)Գտեք ֆունկցիայի առաջին կարգի մասնակի ածանցյալները Ստուգեք, որ Գրեք առաջին կարգի ընդհանուր դիֆերենցիալը ձ.
Լուծում.
1. Գտնենք առաջին կարգի մասնակի ածանցյալներ՝ օգտագործելով արտադրյալի ածանցյալը, գումարը, հաստատուն գործակիցը ածանցյալի նշանից դուրս և եռանկյունաչափական ֆունկցիաների աղյուսակային ինտեգրալները հաշվարկելու կանոնները.
2. Գտնենք երկրորդ կարգի խառը ածանցյալներ.
3. Կատարենք առաջին կարգի ամբողջական դիֆերենցիալ.
V)Ցույց տվեք, որ այս ֆունկցիան բավարարում է հավասարումը 
Լուծում.
1. Գտնենք տրված ֆունկցիայի մասնակի ածանցյալը «x»-ի նկատմամբ.
2. Ստացված արտահայտությունը բազմապատկեք x 2 :
3. Ստացված ֆունկցիայից մենք գտնում ենք մասնակի ածանցյալը «x»-ի նկատմամբ.
4. Գտնենք տրված ֆունկցիայի մասնակի ածանցյալը «y»-ի նկատմամբ.
5. Հաշվենք երկրորդ ածանցյալը «y»-ի նկատմամբ.
6. Ստացված ֆունկցիան բազմապատկե՛ք ժամը 2-ին :
7. 5-րդ քայլում ստացված արդյունքից հանել 6-րդ քայլի արդյունքը.
Դա այն էր, ինչ պետք էր ցույց տալ:
Առնչվող տեղեկություններ.
- V3: ((101)) 07/04/14. Գծային անհամասեռ երկրորդ կարգի դիֆերենցիալ հավասարումներ հաստատուն գործակիցներով (ընդհանուր լուծում)
Երկու փոփոխականների, մասնակի ածանցյալների, դիֆերենցիալների և գրադիենտի ֆունկցիաները
Թեմա 5.Երկու փոփոխականների ֆունկցիաներ.
մասնակի ածանցյալներ
Երկու փոփոխականի ֆունկցիայի սահմանում, տեղադրման մեթոդներ։
Մասնակի ածանցյալներ.
Մեկ փոփոխականի ֆունկցիայի գրադիենտ
Փակ սահմանափակ տիրույթում երկու փոփոխականների ֆունկցիայի ամենամեծ և ամենափոքր արժեքները գտնելը
1. Մի քանի փոփոխականների ֆունկցիայի սահմանում, տեղադրման մեթոդներ
Համար երկու փոփոխականների ֆունկցիաներ
սահմանման տիրույթ
որոշ է հարթության վրա կետերի հավաքածու
, իսկ արժեքների միջակայքը առանցքի միջակայքն է 
.
Տեսողական ներկայացման համար երկու փոփոխության գործառույթներ nyh կիրառվում են մակարդակի գծեր.
Օրինակ
.
Գործառույթի համար 
կառուցել գրաֆիկ և մակարդակի գծեր: Գրի՛ր կետով անցնող մակարդակի գծի հավասարումը 
.
Գծային ֆունկցիայի գրաֆիկէ Ինքնաթիռտարածության մեջ։
Ֆունկցիայի համար գրաֆիկը կետերով անցնող հարթություն է 
, 
, 
.
Ֆունկցիոնալ մակարդակի գծերզուգահեռ ուղիղներ են, որոնց հավասարումն է 
.
Համար երկու փոփոխականների գծային ֆունկցիա
մակարդակի գծերը տրված են հավասարմամբ 
և ներկայացնել հարթության մեջ զուգահեռ ուղիղների ընտանիք:
4
Ֆունկցիայի գրաֆիկ 0 1 2 X
Ֆունկցիոնալ մակարդակի գծեր
Մասնավոր նախագծերերկու փոփոխականների ածանցյալ ֆունկցիաներ
Դիտարկենք գործառույթը 
. Տանք փոփոխականը 
կետում 
կամայական աճ 
, հեռանալով փոփոխական արժեք 
անփոփոխ. Համապատասխան ֆունկցիայի ավելացում
կանչեց ֆունկցիայի մասնավոր ավելացում ըստ փոփոխականիկետում 
.
Սահմանված է նմանապես ֆունկցիայի մասնակի ավելացումըստ փոփոխականի: .
Նշանակումնկատմամբ մասնակի ածանցյալ: 
, 
,
, 
.
Ֆունկցիայի մասնակի ածանցյալը փոփոխականի նկատմամբ 
կոչվում է վերջնական սահման :
Նշումներ: 
, 
,
, 
.
Մասնակի ածանցյալը գտնելու համար 
ըստ փոփոխականի, օգտագործվում են մեկ փոփոխականի ֆունկցիան տարբերելու կանոնները, ենթադրելով, որ փոփոխականը հաստատուն է..
Նմանապես, փոփոխականի նկատմամբ մասնակի ածանցյալը գտնելու համար փոփոխականը համարվում է հաստատուն 
.
Օրինակ
. Գործառույթի համար 
գտնել մասնակի ածանցյալներ 
, 
և հաշվարկեք դրանց արժեքները տվյալ կետում 
.
Ֆունկցիայի մասնակի ածանցյալ 
ըստ փոփոխականի ենթադրվում է, որ այն հաստատուն է.
Գտնենք ֆունկցիայի մասնակի ածանցյալը ի նկատմամբ՝ հաստատուն ընդունելով.
Եկեք հաշվարկենք մասնակի ածանցյալների արժեքները 
, 
:
; 
.
Երկրորդ կարգի մասնակի ածանցյալներ Մի քանի փոփոխականների ֆունկցիաները կոչվում են առաջին կարգի մասնակի ածանցյալների մասնակի ածանցյալներ:
Եկեք գրենք 2-րդ կարգի մասնակի ածանցյալներ ֆունկցիայի համար.
; 
;
; 
.
; 
և այլն:
Եթե մի քանի փոփոխականների ֆունկցիաների խառը մասնակի ածանցյալները ինչ-որ պահի շարունակական են 
, ապա նրանք իրար հավասարայս պահին. Սա նշանակում է, որ երկու փոփոխականների ֆունկցիայի համար խառը մասնակի ածանցյալների արժեքները կախված չեն տարբերակման կարգից.
.
Օրինակ։
Ֆունկցիայի համար գտե՛ք երկրորդ կարգի մասնակի ածանցյալները 
Եվ 
.
Լուծում
Խառը մասնակի ածանցյալը հայտնաբերվում է ֆունկցիան հաջորդաբար տարբերելով 
ըստ (ենթադրելով հաստատուն), ապա տարբերակելով ածանցյալը 
կողմից (համարելով հաստատուն):
Ածանցյալը գտնում ենք՝ սկզբում ֆունկցիան տարբերելով , այնուհետև ածանցյալը .
Խառը մասնակի ածանցյալները հավասար են միմյանց. 
.
3. Երկու փոփոխականի ֆունկցիայի գրադիենտ
Գրադիենտ հատկություններ
Օրինակ
. Տրվում է ֆունկցիա 
. Գտեք գրադիենտը 
կետում 
և կառուցիր այն:
Լուծում
Գտնենք գրադիենտի կոորդինատները՝ մասնակի ածանցյալներ։
Կետում 
գրադիենտ
հավասար է ։ Վեկտորի սկիզբը 
կետում, իսկ վերջը` կետում:
5 
4. Փակ սահմանափակ տարածքում երկու փոփոխականի ֆունկցիայի ամենամեծ և ամենափոքր արժեքների հայտնաբերում
Խնդրի ձևակերպում.
Թող ինքնաթիռում լինի փակ սահմանափակ շրջան 
տրված է ձևի անհավասարությունների համակարգով 
. Պահանջվում է գտնել այն կետերը տարածաշրջանում, որտեղ ֆունկցիան ընդունում է ամենամեծ և ամենափոքր արժեքները:
Կարևոր է էքստրեմում գտնելու խնդիր, որի մաթեմատիկական մոդելը պարունակում է գծայինսահմանափակումներ (հավասարումներ, անհավասարություններ) և գծայինֆունկցիան 
.
Խնդրի ձևակերպում.
Գտեք ֆունկցիայի ամենամեծ և ամենափոքր արժեքները 
(2.1)
սահմանափակումների տակ
(2.2)
. (2.3)
Քանի որ շատ փոփոխականների գծային ֆունկցիայի համար կրիտիկական կետեր չկան ներսումշրջան 
, ապա ձեռք է բերվում միայն օպտիմալ լուծումը, որը ծայրահեղություն է հաղորդում օբյեկտիվ ֆունկցիային շրջանի սահմանին. Գծային սահմանափակումներով սահմանված շրջանի համար հնարավոր ծայրահեղության կետերն են անկյունային կետեր. Սա թույլ է տալիս դիտարկել խնդրի լուծումը գրաֆիկական մեթոդ.
Գծային անհավասարությունների համակարգի գրաֆիկական լուծում
Այս խնդիրը գրաֆիկորեն լուծելու համար դուք պետք է կարողանաք գրաֆիկորեն լուծել գծային անհավասարությունների համակարգեր երկու փոփոխականներով։
Ընթացակարգը:
Նշենք, որ անհավասարությունը 
սահմանում է աջ կոորդինատային կիսահարթություն(առանցքից 
), և անհավասարությունը 
- վերին կոորդինատային կիսահարթություն(առանցքից 
).
Օրինակ։
Գրաֆիկորեն լուծեք անհավասարությունը 
.
Եկեք գրենք սահմանային գծի հավասարումը 
և կառուցիր այն երկու կետի հիման վրա, օրինակ. 
Եվ 
. Ուղիղ գիծը հարթությունը բաժանում է երկու կիսահարթությունների։
Կետերի կոորդինատները 
բավարարել անհավասարությունը ( 
– ճշմարիտ), ինչը նշանակում է, որ կետը պարունակող կիսահարթության բոլոր կետերի կոորդինատները բավարարում են անհավասարությունը: Անհավասարության լուծումը կլինի սահմանագծից աջ կողմում գտնվող կիսահարթության կետերի կոորդինատները՝ ներառյալ սահմանի վրա գտնվող կետերը: Նկարում ընդգծված է ցանկալի կես հարթությունը:
Լուծում 
կոչվում է անհավասարությունների համակարգ ընդունելի, եթե դրա կոորդինատները ոչ բացասական են, . Անհավասարությունների համակարգի իրագործելի լուծումների բազմությունը կազմում է շրջան, որը գտնվում է կոորդինատային հարթության առաջին քառորդում։
Օրինակ։ Կառուցեք անհավասարությունների համակարգի լուծման տիրույթը
Անհավասարությունների լուծումներն են.
1) 
- ուղիղ գծի նկատմամբ ձախ և ներքև տեղակայված կիսահավասարություն ( 
) 
;
2) 
– ուղիղ գծի նկատմամբ ներքևի աջ կիսահավասարության մեջ գտնվող կիսահավասարություն ( 
) 
;
3) 
- ուղիղ գծի աջ կողմում գտնվող կիսահավասարություն ( 
) 
;
4) - կես հարթություն x առանցքի վերևում, այսինքն ուղիղ գիծ ( 
) 
.
0 
Իրագործելի լուծումների շրջանակըԳծային անհավասարությունների տրված համակարգի մի շարք կետեր, որոնք գտնվում են քառանկյունի ներսում և սահմանի վրա. 
, որն է խաչմերուկչորս կիսաինքնաթիռներ.
Գծային ֆունկցիայի երկրաչափական պատկերը
(մակարդակի գծեր և գրադիենտ)
Եկեք ֆիքսենք արժեքը 
, ստանում ենք հավասարումը 
, որը երկրաչափորեն սահմանում է ուղիղ գիծ։ Գծի յուրաքանչյուր կետում ֆունկցիան ընդունում է արժեքը 
և է մակարդակի գիծ.Տալ 
տարբեր իմաստներ, օրինակ 
, ..., մենք ստանում ենք շատ մակարդակի գծեր - զուգահեռների հավաքածու
ուղիղ.
Եկեք կառուցենք գրադիենտ- վեկտոր 
, որոնց կոորդինատները հավասար են ֆունկցիայի փոփոխականների գործակիցների արժեքներին 
. Այս վեկտորը՝ 1) ուղղահայաց է յուրաքանչյուր ուղիղ գծին (մակարդակի գիծ) 
; 2) ցույց է տալիս օբյեկտիվ ֆունկցիայի մեծացման ուղղությունը.
Օրինակ
. Հողամասի մակարդակի գծեր և գրադիենտ ֆունկցիաներ 
.
Մակարդակի գծերը , ,-ում ուղիղ են 
, 
, 
, միմյանց զուգահեռ. Գրադիենտը յուրաքանչյուր մակարդակի գծին ուղղահայաց վեկտոր է:
Գրաֆիկորեն գտնել գծային ֆունկցիայի ամենամեծ և ամենափոքր արժեքները տարածքում
Խնդրի երկրաչափական ձևակերպում. Գծային անհավասարությունների համակարգի լուծման տիրույթում գտե՛ք այն կետը, որով անցնում է մակարդակի ուղիղը, որը համապատասխանում է երկու փոփոխական ունեցող գծային ֆունկցիայի ամենամեծ (ամենափոքր) արժեքին։
Հաջորդականություն:
4. Գտե՛ք A կետի կոորդինատները՝ լուծելով A կետում հատվող ուղիղների հավասարումների համակարգը և հաշվարկե՛ք ֆունկցիայի ամենափոքր արժեքը. 
. Նմանապես - B կետի և ֆունկցիայի ամենամեծ արժեքի համար 
. կառուցված կետերի վրա.փոփոխականներ Մասնավորածանցյալներգործառույթներըմի քանիսը փոփոխականներև տարբերակման տեխնիկան։ Ծայրահեղ գործառույթներըերկուփոփոխականներև դրա անհրաժեշտությունը...
Շատ փոփոխականների ֆունկցիայի հայեցակարգ
Թող լինեն n-փոփոխականներ և յուրաքանչյուր x 1, x 2 ... x n x-ի որոշակի բազմությունից տրվում է սահմանում: Z թիվը, ապա x բազմության վրա տրված է բազմաթիվ փոփոխականների Z = f (x 1, x 2 ... x n) ֆունկցիան։
X - ֆունկցիայի սահմանման տարածք
x 1, x 2 ... x n – անկախ փոփոխական (փաստարկներ)
Z – ֆունկցիա Օրինակ՝ Z=P x 2 1 *x 2 (Գլանների ծավալը)
Դիտարկենք Z=f(x;y) – 2 փոփոխականի ֆունկցիան (x 1, x 2 փոխարինված x,y-ով): Արդյունքները անալոգիայի միջոցով փոխանցվում են բազմաթիվ փոփոխականների այլ գործառույթներին: 2 փոփոխականի ֆունկցիան որոշելու տարածքը ամբողջ լարն է (oh) կամ դրա մի մասը։ 2 փոփոխականի ֆունկցիայի արժեքների թիվը մակերես է եռաչափ տարածության մեջ:
Գրաֆիկների կառուցման տեխնիկա. - Դիտարկենք մակերեսի խաչմերուկը քառակուսիներով || կոորդինատային քառակուսիներ.
Օրինակ՝ x = x 0, zn. քառակուսի X || 0уz y = y 0 0хz Ֆունկցիայի տեսակը՝ Z=f(x 0 ,y); Z=f(x,y 0)
Օրինակ՝ Z=x 2 +y 2 -2y
Z= x 2 +(y-1) 2 -1 x=0 Z=(y-1) 2 -1 y=1 Z= x 2 -1 Z=0 x 2 +(y-1) 2 -1
Պարաբոլա շրջապատում (կենտրոն (0,1)
Երկու փոփոխականների ֆունկցիաների սահմանները և շարունակականությունը
Թող տրված լինի Z=f(x;y), ապա A-ն ֆունկցիայի սահմանն է t.(x 0 ,y 0), եթե ցանկացած կամայականորեն փոքր բազմության համար: թիվը E>0 դրական թիվ է b>0, որը բոլոր x, y բավարարող |x-x 0 |<б; |y-y 0 |<б выполняется нерав-во |f(x,y)-A| Z=f(x;y) t-ում (x 0 ,y 0) շարունակական է, եթե՝ - սահմանվում է այս տ. - եզրափակիչ ունի սահմանը x-ում, հակված է x 0-ին և y-ին դեպի y 0; - այս սահմանը = արժեք ֆունկցիաները t (x 0 ,y 0), այսինքն. limf(x;y)=f(x0,y 0) Եթե ֆունկցիան յուրաքանչյուրում շարունակական է t mn-va X, ապա այն շարունակական է այս տարածքում Դիֆերենցիալ ֆունկցիա, նրա երկրաչափական նշանակությունը: Դիֆերենցիալի կիրառումը մոտավոր արժեքներով. dy=f’(x)∆x – դիֆերենցիալ ֆունկցիա dy=dx, այսինքն. dy=f ’(x)dx եթե y=x Երկրաբանական տեսանկյունից ֆունկցիայի դիֆերենցիալը ֆունկցիայի գրաֆիկին գծված շոշափողի օրդինատի աճն է x 0 աբսցիսայով կետում: Dif-l-ն օգտագործվում է մոտ. ֆունկցիայի արժեքներն ըստ բանաձևի՝ f(x0 +∆x)~f(x0)+f’(x0)∆x Որքան ավելի մոտ է ∆x-ը x-ին, այնքան ավելի ճշգրիտ կլինի արդյունքը Առաջին և երկրորդ կարգի մասնակի ածանցյալներ Առաջին կարգի ածանցյալ (որը կոչվում է մասնակի) A. Թող x, y լինեն x և y անկախ փոփոխականների աճերը X շրջանից ինչ-որ կետում: Այնուհետև z = f(x+ x, y+ y) = f(x,y) արժեքը կոչվում է ընդհանուր: հավելում x 0 կետում, y 0: Եթե ֆիքսենք x փոփոխականը և y-ին տանք աճը y, ապա կստանանք zу = f(x,y,+ y) – f(x,y) Նմանապես որոշվում է y փոփոխականի մասնակի ածանցյալը, այսինքն. 2 փոփոխականի ֆունկցիայի մասնակի ածանցյալը գտնում ենք նույն կանոններով, ինչ մեկ փոփոխականի ֆունկցիաների համար: Տարբերությունն այն է, որ x փոփոխականի նկատմամբ ֆունկցիան տարբերակելիս y-ն համարվում է const, իսկ y, x-ի նկատմամբ տարբերելիս՝ const: Մեկուսացված const-ը միացված է ֆունկցիային՝ օգտագործելով գումարման/հանման գործողությունները: Կապված const-ը միացված է ֆունկցիային բազմապատկման/բաժանման գործողություններով: Մեկուսացված կոնստի ածանցյալ = 0 1.4.2 փոփոխականների ամբողջական դիֆերենցիալ ֆունկցիա և դրա կիրառությունները
Թող z = f(x,y), ապա tz = 2-րդ կարգի մասնակի ածանցյալ 2 փոփոխականների շարունակական ֆունկցիաների համար 2-րդ կարգի խառը մասնակի ածանցյալները համընկնում են։ Մասնակի ածանցյալների կիրառումը max և min ֆունկցիաների մասնակի ածանցյալների որոշման համար կոչվում են ծայրահեղություններ: A. Կետերը կոչվում են max կամ min z = f(x,y), եթե կան այնպիսի հատվածներ, որ բոլոր x և y այս հարևանությամբ f(x,y) T. Եթե տրված է 2 փոփոխականի ֆունկցիայի ծայրահեղ կետ, ապա մասնակի ածանցյալների արժեքը այս կետում հավասար է 0-ի, այսինքն. , Այն կետերը, որոնցում առաջին կարգի մասնակի ածանցյալները կոչվում են անշարժ կամ կրիտիկական: Հետևաբար, 2 փոփոխականների ֆունկցիայի ծայրահեղ կետերը գտնելու համար օգտագործվում են բավարար ծայրահեղական պայմաններ: Թող z = f(x,y) ֆունկցիան լինի երկու անգամ տարբերվող, և անշարժ կետ, 1) և maxA<0, minA>0. 1.4.(*)Ամբողջական դիֆերենցիալ. Դիֆերենցիալի երկրաչափական նշանակությունը. Դիֆերենցիալի կիրառումը մոտավոր հաշվարկներում
A. Թող y = f(x) ֆունկցիան որոշված լինի կետերում որոշակի հարևանությամբ: f(x) ֆունկցիան համարվում է տարբերվող մի կետում, եթե դրա աճն այս կետում է Այնտեղ, որտեղ A-ն հաստատուն արժեք է, որը անկախ x-ից է, և անսահման փոքր է . Համեմատաբար գծային A ֆունկցիան կոչվում է f(x) ֆունկցիայի դիֆերենցիալ կետում և նշանակվում է df() կամ dy։ Այսպիսով, արտահայտությունը (1) կարելի է գրել այսպես Ֆունկցիայի դիֆերենցիալը (1) արտահայտության մեջ ունի dy = A ձև: Ինչպես ցանկացած գծային ֆունկցիա, այն սահմանվում է ցանկացած արժեքի համար Դիֆերենցիալը գրելու հարմարության համար աճը նշանակվում է dx-ով և կոչվում է x անկախ փոփոխականի դիֆերենցիալ։ Հետևաբար, դիֆերենցիալը գրվում է dy = Adx: Եթե f(x) ֆունկցիան տարբերվում է որոշակի ինտերվալի յուրաքանչյուր կետում, ապա դրա դիֆերենցիալը երկու փոփոխականների՝ x կետի և dx փոփոխականի ֆունկցիա է. T. Որպեսզի y = g(x) ֆունկցիան ինչ-որ կետում տարբերվող լինի, անհրաժեշտ է և բավարար, որ այն այս կետում ունենա ածանցյալ, և (*) Ապացույց. Անհրաժեշտություն. Թող f(x) ֆունկցիան տարբերվող լինի կետում, այսինքն. Հետևաբար, f’() ածանցյալը գոյություն ունի և հավասար է A-ին: Հետևաբար, dy = f’()dx Համարժեքություն. Թող լինի f’( ածանցյալ), այսինքն. = f'(). Այնուհետև y = f(x) կորը շոշափող հատված է: Ֆունկցիայի արժեքը x կետում հաշվարկելու համար վերցրեք մի կետ նրա որոշ հարևանությամբ, որպեսզի դժվար չլինի գտնել f() և f’()/:
- կոչվում է լրիվ աճ
, որտեղ այն ներկայացված է (1) ձևով.
().
մինչդեռ ֆունկցիայի աճը պետք է դիտարկել միայն նրանց համար, որոնց համար + պատկանում է f(x) ֆունկցիայի սահմանման տիրույթին։. Հետո
