Սա քառանկյուն է, որի հակառակ կողմերը զույգերով զուգահեռ են:
Գույք 1. Զուգահեռագծի ցանկացած անկյունագիծ այն բաժանում է երկու հավասար եռանկյունների:
Ապացույց . Ըստ II բնութագրիչի (խաչաձև անկյուններ և ընդհանուր կողմ)։
Թեորեմն ապացուցված է.
Գույք 2. Զուգահեռագրում հակառակ կողմերը հավասար են, իսկ հակառակ անկյունները՝ հավասար։
Ապացույց .
Նմանապես,
Թեորեմն ապացուցված է.

Հատկություն 3. Զուգահեռագծի մեջ անկյունագծերը կիսվում են հատման կետով:
Ապացույց .
Թեորեմն ապացուցված է.

Գույք 4. Զուգահեռագծի անկյան կիսադիրը, հատելով հակառակ կողմը, այն բաժանում է հավասարաչափ եռանկյունեւ trapezoid. (Չ. բառեր - գագաթ - երկու հավասարաչափ. -կա):
Ապացույց .

Թեորեմն ապացուցված է.
Գույք 5. Զուգահեռագրում այս կետով կիսվում է ուղիղ հատվածը, որի ծայրերը հակառակ կողմերին են, որոնք անցնում են անկյունագծերի հատման կետով:
Ապացույց .
Թեորեմն ապացուցված է.

Գույք 6. Զուգահեռագծի բութ անկյան գագաթից իջած բարձրությունների միջև անկյունը հավասար է զուգահեռագծի սուր անկյան:
Ապացույց .

Թեորեմն ապացուցված է.
Գույք 7. Մի կողմին կից զուգահեռագծի անկյունների գումարը 180° է։
Ապացույց .
Թեորեմն ապացուցված է.

Անկյան կիսաչափի կառուցում. Եռանկյան անկյան կիսադիրի հատկությունները.
1) Կառուցեք կամայական DE ճառագայթ:
2) Տրված ճառագայթի վրա կառուցիր կամայական շրջան, որի կենտրոնը գագաթին է և նույնը
կենտրոնով կառուցված ճառագայթի սկզբում։
3) F և G - շրջանագծի հատման կետերը տրված անկյան կողմերի հետ, H - շրջանագծի հատման կետը կառուցված ճառագայթի հետ.

Կառուցեք շրջան, որի կենտրոնը գտնվում է H կետում և շառավիղը հավասար է FG-ին:
5) I-ը կառուցված փնջի շրջանագծերի հատման կետն է.
6) Գծեք ուղիղ գիծ գագաթի և I-ի միջով:
IDH-ն պահանջվող անկյունն է:
)
Գույք 1. Եռանկյան անկյան կիսադիրը հակառակ կողմը բաժանում է հարակից կողմերին համամասնորեն:

Ապացույց . Թող x, y-ը լինեն c կողմի հատվածներ: Շարունակենք ճառագայթը մ.թ.ա. BC ճառագայթի վրա մենք C-ից գծում ենք CK հատված, որը հավասար է AC-ին:
Զուգահեռագիծը այն քառանկյունն է, որի հակառակ կողմերը զուգահեռ են, այսինքն. պառկել զուգահեռ գծերի վրա
Զուգահեռագծի հատկությունները. 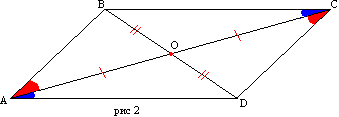 Թեորեմ 22.
Զուգահեռագծի հակառակ կողմերը հավասար են:
Թեորեմ 22.
Զուգահեռագծի հակառակ կողմերը հավասար են:
Ապացույց. ABCD զուգահեռագրում մենք գծում ենք AC անկյունագիծ: ACD և ACB եռանկյունները հավասար են, քանի որ ունեն ընդհանուր կողմ AC և երկու զույգ հավասար անկյուններ. դրան կից՝ ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (որպես խաչաձև անկյուններ՝ AD և BC զուգահեռ ուղիղներով): Սա նշանակում է, որ AB = CD և BC = AD, որպես հավասար եռանկյունների համապատասխան կողմեր և այլն: Այս եռանկյունների հավասարությունից հետևում է նաև, որ եռանկյունների համապատասխան անկյունները հավասար են.
Թեորեմ 23.
Զուգահեռագծի հակառակ անկյունները հավասար են՝ ∠ A=∠ C և ∠ B=∠ D:
Առաջին զույգի հավասարությունը գալիս է ABD և CBD եռանկյունների հավասարությունից, իսկ երկրորդը ՝ ABC և ACD:
Թեորեմ 24.
Զուգահեռագծի հարակից անկյունները, այսինքն. մի կողմին հարող անկյունները ավելացնում են մինչև 180 աստիճան:
Դա այդպես է, քանի որ դրանք ներքին միակողմանի անկյուններ են:
Թեորեմ 25.
Զուգահեռագծի անկյունագծերը հատվում են միմյանց հատման կետում:
Ապացույց. Դիտարկենք BOC և AOD եռանկյունները: Ըստ առաջին հատկության AD=BC ∠ OAD=∠ OCB և ∠ ODA=∠ OBC, որոնք գտնվում են AD և BC զուգահեռ ուղիղների համար խաչաձև: Այսպիսով, BOC և AOD եռանկյունները հավասար են կողային և հարակից անկյուններով: Սա նշանակում է BO=OD և AO=OS, ինչպես հավասար եռանկյունների համապատասխան կողմերը և այլն։
Զուգահեռագծի նշաններ
Թեորեմ 26.
Եթե քառանկյան հակառակ կողմերը զույգերով հավասար են, ապա այն զուգահեռագիծ է։
Ապացույց. Թող ABCD քառանկյունն ունենա AD և BC, AB և CD կողմերը համապատասխանաբար հավասար (նկ. 2): Եկեք գծենք AC անկյունագիծը: ABC և ACD եռանկյունները երեք կողմերից հավասար են: Այնուհետև BAC և DCA անկյունները հավասար են և, հետևաբար, AB-ն զուգահեռ է CD-ին: BC և AD կողմերի զուգահեռությունը բխում է CAD և ACB անկյունների հավասարությունից:
Թեորեմ 27.
Եթե քառանկյան հակառակ անկյունները զույգերով հավասար են, ապա այն զուգահեռագիծ է։
Թող ∠ A=∠ C և ∠ B=∠ D. Որովհետև ∠ A+∠ B+∠ C+∠ D=360 o, ապա ∠ A+∠ B=180 o և AD և BC կողմերը զուգահեռ են (ուղիղների զուգահեռության հիման վրա): Մենք նաև կապացուցենք AB և CD կողմերի զուգահեռականությունը և եզրակացնենք, որ ABCD-ն ըստ սահմանման զուգահեռագիծ է:
Թեորեմ 28.
Եթե քառանկյունի հարակից անկյունները, այսինքն. Մի կողմին կից անկյունները գումարվում են մինչև 180 աստիճան, այնուհետև այն զուգահեռագիծ է։
Եթե ներքին միակողմանի անկյունները ավելանում են մինչև 180 աստիճան, ապա ուղիղ գծերը զուգահեռ են: Այսպիսով, AB-ը զուգահեռ է CD-ին, իսկ BC-ն՝ AD-ին: Քառանկյունը պարզվում է, որ զուգահեռագիծ է:
Թեորեմ 29.
Եթե քառանկյան անկյունագծերը հատման կետում կիսում են միմյանց, ապա քառանկյունը զուգահեռագիծ է։
Ապացույց. Եթե AO = OC, BO = OD, ապա AOD և BOC եռանկյունները հավասար են, քանի որ ունեն հավասար անկյուններ (ուղղահայաց) O գագաթում, որը պարփակված է զույգերի միջև: հավասար կողմեր. Եռանկյունների հավասարությունից եզրակացնում ենք, որ AD և BC հավասար են։ AB և CD կողմերը նույնպես հավասար են, իսկ քառանկյունը 1-ին չափանիշով ստացվում է զուգահեռագիծ։
Թեորեմ 30.
Եթե քառանկյունն ունի զույգ հավասար, զուգահեռ կողմեր, ապա այն զուգահեռագիծ է։
Թող ABCD քառանկյան AB և CD կողմերը լինեն զուգահեռ և հավասար: Եկեք գծենք AC և BD անկյունագծերը: Այս ուղիղների զուգահեռությունից հետևում է, որ ABO = CDO և BAO = OCD խաչաձև անկյունները հավասար են: ABO և CDO եռանկյունները հավասար են կողային և հարակից անկյուններով: Հետեւաբար AO=OS, VO=ОD, այսինքն. Անկյունագծերը հատման կետով բաժանվում են կիսով չափ, և ըստ 4-րդ չափանիշի քառանկյունը ստացվում է զուգահեռագիծ։
Երկրաչափության մեջ դիտարկվում են զուգահեռագծի հատուկ դեպքեր։
Այս թեմայով խնդիրներ լուծելիս, բացառությամբ հիմնական հատկությունները զուգահեռագիծև համապատասխան բանաձևերը, կարող եք հիշել և կիրառել հետևյալը.
- Զուգահեռագծի ներքին անկյան կիսադիրը նրանից կտրում է հավասարաչափ եռանկյունին
- Զուգահեռագծի կողմերից մեկին կից ներքին անկյունների կիսադիրները փոխադարձաբար ուղղահայաց են
- Զուգահեռագծի հակառակ ներքին անկյուններից բիսեկտորները զուգահեռ են միմյանց կամ ընկած են նույն ուղիղ գծի վրա
- Զուգահեռագծի անկյունագծերի քառակուսիների գումարը հավասար է նրա կողմերի քառակուսիների գումարին
- Զուգահեռագծի մակերեսը հավասար է անկյունագծերի և նրանց միջև անկյան սինուսի արտադրյալի կեսին
Եկեք քննարկենք խնդիրները, որոնցում օգտագործվում են այս հատկությունները:
Առաջադրանք 1.
ABCD զուգահեռագծի C անկյան կիսորդը հատում է AD կողմը M կետում և AB կողմի շարունակությունը A կետից այն կողմ E կետում: Գտե՛ք զուգահեռագծի պարագիծը, եթե AE = 4, DM = 3:
Լուծում.
1. CMD եռանկյունը հավասարաչափ է: (Գույք 1): Հետեւաբար, CD = MD = 3 սմ:
2. EAM եռանկյունը հավասարաչափ է:
Հետեւաբար, AE = AM = 4 սմ:
3. AD = AM + MD = 7 սմ:
4. Պարագիծ ABCD = 20 սմ:
Պատասխանել. 20 սմ.
Առաջադրանք 2.
Անկյունագծերը գծված են ուռուցիկ քառանկյուն ABCD-ում: Հայտնի է, որ ABD, ACD, BCD եռանկյունների մակերեսները հավասար են։ Ապացուցեք, որ այս քառանկյունը զուգահեռագիծ է:

Լուծում.
1. Թող BE լինի ABD եռանկյան բարձրությունը, CF՝ ACD եռանկյան բարձրությունը: Քանի որ, ըստ խնդրի պայմանների, եռանկյունների մակերեսները հավասար են և ունեն ընդհանուր AD հիմք, ապա այդ եռանկյունների բարձրությունները հավասար են։ BE = CF:
2. BE, CF-ն ուղղահայաց են AD-ին: B և C կետերը գտնվում են AD ուղիղ գծի նկատմամբ նույն կողմում: BE = CF: Ուստի ուղիղ գիծ մ.թ.ա. || ՀԱՅՏԱՐԱՐՈՒԹՅՈՒՆ։ (*)
3. Թող AL լինի ACD եռանկյան բարձրությունը, BK՝ BCD եռանկյան բարձրությունը: Քանի որ, ըստ խնդրի պայմանների, եռանկյունների մակերեսները հավասար են և ունեն ընդհանուր հիմք CD, ապա այդ եռանկյունների բարձրությունները հավասար են։ AL = BK.
4. AL-ը և BK-ն ուղղահայաց են CD-ին: B և A կետերը գտնվում են ուղիղ գծի CD-ի նկատմամբ նույն կողմում: AL = BK. Ուստի ուղիղ AB || CD (**)
5. (*), (**) պայմաններից հետևում է, որ ABCD-ը զուգահեռագիծ է։
Պատասխանել. Ապացուցված է. ABCD-ն զուգահեռագիծ է:
Առաջադրանք 3.
ABCD զուգահեռագծի BC և CD կողմերի վրա համապատասխանաբար M և H կետերը նշված են այնպես, որ BM և HD հատվածները հատվում են O կետում;<ВМD = 95 о,
 Լուծում.
Լուծում.
1. DOM եռանկյունու մեջ<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. Ուղղանկյուն եռանկյունում DHC Հետո<НСD = 30 о. СD: НD = 2: 1 Բայց CD = AB: Այնուհետև AB: HD = 2: 1: 3. <С = 30 о, 4. <А = <С = 30 о, <В = Պատասխան՝ AB: HD = 2: 1,<А = <С = 30 о, <В = Առաջադրանք 4. 4√6 երկարությամբ զուգահեռագծի անկյունագծերից մեկը հիմքի հետ կազմում է 60° անկյուն, իսկ երկրորդը նույն հիմքով կազմում է 45° անկյուն։ Գտեք երկրորդ անկյունագիծը: Լուծում.
1. AO = 2√6: 2. Սինուսների թեորեմը կիրառում ենք AOD եռանկյան վրա: AO/sin D = OD/sin A. 2√6/sin 45 o = OD/sin 60 o: ОД = (2√6sin 60 о) / մեղք 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6: Պատասխան՝ 12.
Առաջադրանք 5. 5√2 և 7√2 կողմեր ունեցող զուգահեռագծի համար անկյունագծերի միջև փոքր անկյունը հավասար է զուգահեռագծի փոքր անկյան: Գտե՛ք շեղանկյունների երկարությունների գումարը: Լուծում.
Թող d 1, d 2 լինեն զուգահեռագծի անկյունագծերը, իսկ անկյունագծերի և զուգահեռագծի փոքր անկյան միջև ընկած անկյունը հավասար է φ-ի: 1. Հաշվենք երկու տարբեր S ABCD = AB AD sin A = 5√2 7√2 sin f, S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin f. Մենք ստանում ենք հավասարություն 5√2 · 7√2 · sin f = 1/2d 1 d 2 sin f կամ 2 · 5√2 · 7√2 = d 1 d 2; 2. Օգտագործելով զուգահեռագծի կողմերի և անկյունագծերի հարաբերությունները՝ գրում ենք հավասարությունը (AB 2 + AD 2) 2 = AC 2 + BD 2: ((5√2) 2 + (7√2) 2) 2 = դ 1 2 + դ 2 2: d 1 2 + d 2 2 = 296: 3. Եկեք ստեղծենք համակարգ. (d 1 2 + d 2 2 = 296, Համակարգի երկրորդ հավասարումը բազմապատկենք 2-ով և ավելացնենք առաջինին։ Մենք ստանում ենք (d 1 + d 2) 2 = 576: Այսպիսով, Id 1 + d 2 I = 24: Քանի որ d 1, d 2-ը զուգահեռագծի անկյունագծերի երկարություններն են, ապա d 1 + d 2 = 24: Պատասխան՝ 24։
Առաջադրանք 6. Զուգահեռագծի կողմերը 4 և 6 են։ Անկյունագծերի միջև սուր անկյունը 45 աստիճան է։ Գտե՛ք զուգահեռագծի մակերեսը: Լուծում.
1. AOB եռանկյունից, օգտագործելով կոսինուսի թեորեմը, գրում ենք զուգահեռագծի կողմի և անկյունագծերի հարաբերությունները։ AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOB. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1/2) · (d 2 /2)cos 45 o; d 1 2 /4 + d 2 2 /4 – 2 · (d 1/2) · (d 2 /2)√2/2 = 16: d 1 2 + d 2 2 – d 1 · d 2 √2 = 64: 2. Նմանապես մենք գրում ենք AOD եռանկյան հարաբերությունը: Հաշվի առնենք դա<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Մենք ստանում ենք d 1 2 + d 2 2 + d 1 · d 2 √2 = 144 հավասարումը: 3. Մենք ունենք համակարգ Առաջինը հանելով երկրորդ հավասարումից՝ ստանում ենք 2d 1 · d 2 √2 = 80 կամ. դ 1 դ 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin α = 1/2 20√2 √2/2 = 10: Նշում:Այս և նախորդ հարցում համակարգն ամբողջությամբ լուծելու կարիք չկա՝ ակնկալելով, որ այս հարցում տարածքը հաշվարկելու համար մեզ անհրաժեշտ է անկյունագծերի արտադրյալը։ Պատասխան՝ 10. Առաջադրանք 7. Զուգահեռագծի մակերեսը 96 է, իսկ կողմերը՝ 8 և 15։ Գտե՛ք ավելի փոքր անկյունագծի քառակուսին։ Լուծում.
1. S ABCD = AB · AD · sin VAD. Բանաձևում կատարենք փոխարինում. Մենք ստանում ենք 96 = 8 · 15 · sin VAD: Հետևաբար մեղքը VAD = 4/5: 2. Եկեք գտնենք cos VAD-ը: մեղք 2 VAD + cos 2 VAD = 1: (4 / 5) 2 + cos 2 VAD = 1. cos 2 VAD = 9 / 25: Ըստ խնդրի պայմանների՝ մենք գտնում ենք ավելի փոքր շեղանկյունի երկարությունը։ ՎԴ անկյունագիծը ավելի փոքր կլինի, եթե ВАD անկյունը սուր է: Այնուհետև cos VAD = 3/5: 3. ABD եռանկյունից, օգտագործելով կոսինուսի թեորեմը, գտնում ենք BD անկյունագծի քառակուսին: ВД 2 = АВ 2 + АД 2 – 2 · АВ · ВД · cos VAD. ВД 2 = 8 2 + 15 2 – 2 8 15 3 / 5 = 145: Պատասխան՝ 145։
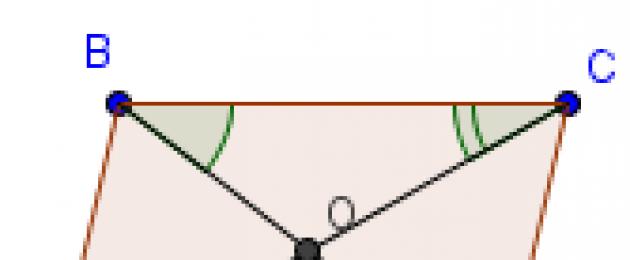
Դեռ ունե՞ք հարցեր: Չգիտե՞ք ինչպես լուծել երկրաչափության խնդիրը: կայքը, նյութը ամբողջությամբ կամ մասնակի պատճենելիս անհրաժեշտ է հղում աղբյուրին: Ինչպես էվկլիդեսյան երկրաչափության մեջ կետը և ուղիղ գիծը հարթությունների տեսության հիմնական տարրերն են, այնպես էլ զուգահեռագիծը ուռուցիկ քառանկյունների առանցքային պատկերներից է։ Դրանից, ինչպես գնդակից թելերը, հոսում են «ուղղանկյուն», «քառակուսի», «ռոմբ» և այլ երկրաչափական մեծություններ հասկացությունները։ հետ շփման մեջ ուռուցիկ քառանկյուն,կազմված ուղիղ հատվածներից, որոնց յուրաքանչյուր զույգ զուգահեռ է, երկրաչափության մեջ հայտնի է որպես զուգահեռագիծ։ Ինչ տեսք ունի դասական զուգահեռագիծը, պատկերված է ABCD քառանկյունով: Կողմերը կոչվում են հիմքեր (AB, BC, CD և AD), ցանկացած գագաթից այս գագաթին հակառակ կողմին գծված ուղղահայացը կոչվում է բարձրություն (BE և BF), AC և BD ուղիղները կոչվում են անկյունագծեր: Ուշադրություն.Քառակուսին, ռոմբը և ուղղանկյունը զուգահեռագծի հատուկ դեպքեր են: Հիմնական հատկությունները, մեծ հաշվով, կանխորոշված է հենց նշանակմամբ, դրանք ապացուցված են թեորեմով։ Այս բնութագրերը հետևյալն են. Ապացույց. Դիտարկենք ∆ABC և ∆ADC, որոնք ստացվում են ABCD քառանկյունը AC ուղիղ գծի հետ բաժանելով: ∠BCA=∠CAD և ∠BAC=∠ACD, քանի որ AC-ը նրանց համար սովորական է (համապատասխանաբար BC||AD և AB||CD-ի ուղղահայաց անկյունները): Այստեղից բխում է՝ ∆ABC = ∆ADC (եռանկյունների հավասարության երկրորդ նշանը)։ ∆ABC-ում AB և BC հատվածները զույգերով համապատասխանում են ∆ADC-ի CD և AD տողերին, ինչը նշանակում է, որ դրանք նույնական են՝ AB = CD, BC = AD: Այսպիսով, ∠B-ն համապատասխանում է ∠D-ին և դրանք հավասար են: Քանի որ ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, որոնք նույնպես զույգերով նույնական են, ապա ∠A = ∠C: Սեփականությունն ապացուցված է։ Հիմնական առանձնահատկությունըզուգահեռագծի այս ուղիղներից. հատման կետը դրանք կիսում է կիսով չափ: Ապացույց. Այսինքն՝ լինի ABCD նկարի AC և BD անկյունագծերի հատման կետը: Նրանք կազմում են երկու համաչափ եռանկյունիներ՝ ∆ABE և ∆CDE: AB=CD, քանի որ դրանք հակադիր են: Ըստ տողերի և սեկանտի՝ ∠ABE = ∠CDE և ∠BAE = ∠DCE: Համաձայն հավասարության երկրորդ չափանիշի՝ ∆ABE = ∆CDE։ Սա նշանակում է, որ ∆ABE և ∆CDE տարրերը՝ AE = CE, BE = DE և միևնույն ժամանակ AC և BD-ի համամասնական մասեր են։ Սեփականությունն ապացուցված է։ Հարակից կողմերն ունեն 180°-ի հավասար անկյունների գումար, քանի որ դրանք ընկած են զուգահեռ գծերի և լայնակի միևնույն կողմում: ABCD քառանկյունի համար. ∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º Բիսեկտորի հատկությունները. Այս գործչի առանձնահատկությունները բխում են նրա հիմնական թեորեմից, որտեղ ասվում է հետևյալը. քառանկյունը համարվում է զուգահեռագիծայն դեպքում, երբ նրա անկյունագծերը հատվում են, և այս կետը դրանք բաժանում է հավասար հատվածների: Ապացույց. թող ABCD քառանկյան AC և BD ուղիղները հատվեն, այսինքն. Քանի որ ∠AED = ∠BEC, և AE+CE=AC BE+DE=BD, ապա ∆AED = ∆BEC (եռանկյունների հավասարության առաջին չափանիշով): Այսինքն՝ ∠EAD = ∠ԵԿԲ: Դրանք նաև AC հատվածի ներքին խաչաձև անկյուններն են AD և BC գծերի համար: Այսպիսով, զուգահեռության սահմանմամբ - AD || Ք.ա. Ստացված է նաև BC և CD տողերի նմանատիպ հատկությունը։ Թեորեմն ապացուցված է. Այս գործչի տարածքը հայտնաբերվել է մի քանի մեթոդներովամենապարզներից մեկը՝ բազմապատկելով այն բարձրությունը և հիմքը, որին այն գծված է: Ապացույց. B և C գագաթներից նկարեք BE և CF ուղղահայացները: ∆ABE և ∆DCF հավասար են, քանի որ AB = CD և BE = CF: ABCD-ն իր չափերով հավասար է EBCF ուղղանկյունին, քանի որ դրանք բաղկացած են համաչափ թվերից՝ S ABE և S EBCD, ինչպես նաև S DCF և S EBCD: Այստեղից հետևում է, որ այս երկրաչափական գործչի մակերեսը նույնն է, ինչ ուղղանկյունը. S ABCD = S EBCF = BE×BC=BE×AD: Զուգահեռագծի մակերեսի ընդհանուր բանաձևը որոշելու համար եկեք բարձրությունը նշանակենք որպես hb, և կողք - բ. Համապատասխանաբար. Տարածքի հաշվարկներ զուգահեռագծի և անկյան կողմերի միջով, որը նրանք ձևավորում են, երկրորդ հայտնի մեթոդն է։ Spr-ma - տարածք; a և b-ն նրա կողմերն են α-ն անկյունն է a և b հատվածների միջև: Այս մեթոդը գործնականում հիմնված է առաջինի վրա, բայց այն դեպքում, երբ այն անհայտ է։ միշտ կտրում է ուղղանկյուն եռանկյունը, որի պարամետրերը հայտնաբերվում են եռանկյունաչափական նույնականությամբ, այսինքն. Փոխակերպելով հարաբերությունը, մենք ստանում ենք. Առաջին մեթոդի հավասարման մեջ մենք բարձրությունը փոխարինում ենք այս արտադրյալով և ստանում այս բանաձևի վավերականության ապացույց։ Զուգահեռագծի և անկյան անկյունագծերի միջով,որը նրանք ստեղծում են, երբ հատվում են, կարող ես գտնել նաև տարածքը: Ապացույց. AC-ը և BD-ն հատվում են՝ ձևավորելով չորս եռանկյուններ՝ ABE, BEC, CDE և AED: Դրանց գումարը հավասար է այս քառանկյան մակերեսին։ Այս ∆ներից յուրաքանչյուրի մակերեսը կարելի է գտնել արտահայտությամբ, որտեղ a=BE, b=AE, ∠γ =∠AEB: Քանի որ , հաշվարկները օգտագործում են մեկ սինուսային արժեք: Այն է ։ Քանի որ AE+CE=AC= d 1 և BE+DE=BD= d 2, տարածքի բանաձևը կրճատվում է հետևյալի. Այս քառանկյան բաղկացուցիչ մասերի հատկանիշները կիրառություն են գտել վեկտորային հանրահաշիվում, այն է՝ երկու վեկտորների գումարում։ Զուգահեռագծի կանոնը նշում է, որ եթե տրված են վեկտորներԵվՈչհամագիծ են, ապա դրանց գումարը հավասար կլինի այս թվի անկյունագծին, որի հիմքերը համապատասխանում են այս վեկտորներին։ Ապացույց՝ կամայականորեն ընտրված սկզբից, այսինքն. - կառուցել վեկտորներ և. Այնուհետև մենք կառուցում ենք OASV զուգահեռագիծ, որտեղ OA և OB հատվածները կողմեր են: Այսպիսով, ՕՀ-ն ընկած է վեկտորի կամ գումարի վրա: Ինքնությունը տրվում է հետևյալ պայմաններով. Զուգահեռագիծը այն քառանկյունն է, որի հակառակ կողմերը զույգերով զուգահեռ են: Հետևյալ նկարը ցույց է տալիս ABCD զուգահեռագիծը: Այն ունի AB կողմը զուգահեռ CD կողքին և BC կողմը AD կողմին զուգահեռ: Ինչպես կռահեցիք, զուգահեռագիծը ուռուցիկ քառանկյուն է: Դիտարկենք զուգահեռագծի հիմնական հատկությունները։ 1. Զուգահեռագրում հակառակ անկյուններն ու հակառակ կողմերը հավասար են: Եկեք ապացուցենք այս հատկությունը՝ դիտարկենք հետևյալ նկարում ներկայացված զուգահեռագիծը։ Diagonal BD-ն այն բաժանում է երկու հավասար եռանկյունների՝ ABD և CBD: Նրանք հավասար են BD կողքի և դրան հարող երկու անկյունների երկայնքով, քանի որ անկյունները խաչաձև ընկած են BC և AD և AB և CD, համապատասխանաբար, զուգահեռ ուղիղների BD հատվածում: Հետեւաբար AB = CD եւ 2. Զուգահեռագծի անկյունագծերը կիսով չափ բաժանվում են հատման կետով: Թող O կետը լինի ABCD զուգահեռագծի AC և BD անկյունագծերի հատման կետը: Այնուհետև AOB եռանկյունը և COD եռանկյունը հավասար են միմյանց կողքի երկայնքով և հարակից երկու անկյուններով: (AB = CD, քանի որ դրանք զուգահեռագծի հակառակ կողմերն են: Իսկ անկյունը 1 = անկյուն2 և անկյուն 3 = անկյուն4 նման են խաչաձև անկյունների, երբ AB և CD ուղիղները հատվում են համապատասխանաբար AC և BD հատվածների հետ:) Սրանից հետևում է, որ AO = OC: և OB = OD, որոնք և պետք է ապացուցվեին: Բոլոր հիմնական հատկությունները պատկերված են հետևյալ երեք նկարներում:
(
(Քանի որ ուղղանկյուն եռանկյունում 30° անկյան հակառակ ոտքը հավասար է հիպոթենուսի կեսին):
 ուղիները իր տարածքը.
ուղիները իր տարածքը.
(d 1 + d 2 = 140.
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Կրկնուսույցից օգնություն ստանալու համար գրանցվեք։
Առաջին դասն անվճար է։
Զուգահեռագծի սահմանում
Կողմերն ու անկյունները՝ հարաբերությունների առանձնահատկությունները
Ֆիգուրի անկյունագծերի բնութագրերը
Հարակից անկյունների առանձնահատկությունները
Զուգահեռագծի բնորոշ հատկանիշների որոշումը թեորեմի միջոցով
Նկարի մակերեսի հաշվարկ

Տարածք գտնելու այլ եղանակներ
![]() ,
,![]() .
.Կիրառում վեկտորային հանրահաշիվում

Զուգահեռագծի պարամետրերի հաշվարկման բանաձևեր
Պարամետր
Բանաձև
Գտնելով կողմերը
անկյունագծերի և նրանց միջև անկյան կոսինուսի երկայնքով
![]()
![]()
անկյունագծերի և կողմերի երկայնքով
![]()
![]()
բարձրության և հակառակ գագաթի միջոցով
Գտեք շեղանկյունների երկարությունը
կողմերի վրա և դրանց միջև եղած գագաթի չափը
Զուգահեռագծի հատկությունները

BC = մ.թ.ա. Իսկ 1, 2, 3 և 4 անկյունների հավասարությունից հետևում է, որ A անկյուն = անկյուն1 + անկյուն3 = անկյուն2 + անկյուն4 = անկյուն C: