Ինչպես լուծել հանրահաշվական և երկրաչափական առաջընթացները: GP-ի առաջին n անդամների գումարի բանաձևը

Օրինակ, հաջորդականություն \(3\); \(6\); \(12\); \(24\); \(48\)... երկրաչափական պրոգրեսիա է, քանի որ յուրաքանչյուր հաջորդ տարրը նախորդից տարբերվում է երկու գործակցով (այլ կերպ ասած՝ այն կարելի է ստանալ նախորդից՝ բազմապատկելով այն երկուսով).

Ինչպես ցանկացած հաջորդականություն, երկրաչափական առաջընթացը նշվում է փոքր լատինատառով: Այն թվերը, որոնք կազմում են պրոգրեսիա, կոչվում են անդամներ(կամ տարրեր): Նրանք նշվում են նույն տառով, ինչ երկրաչափական պրոգրեսիան, բայց թվային ինդեքսով, որը հավասար է տարրի թվին ըստ հերթականության։

Օրինակ, երկրաչափական պրոգրեսիան \(b_n = \(3; 6; 12; 24; 48…\)\) բաղկացած է տարրերից \(b_1=3\); \(b_2=6\); \(b_3=12\) և այլն: Այլ կերպ ասած:

Եթե ​​հասկանում եք վերը նշված տեղեկատվությունը, արդեն կկարողանաք լուծել այս թեմայի հետ կապված խնդիրների մեծ մասը:

Օրինակ (OGE):
Լուծում:

Պատասխանել : \(-686\).

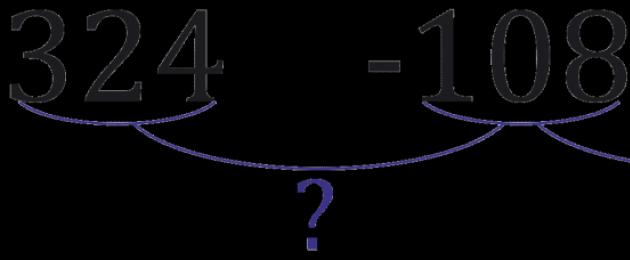
Օրինակ (OGE): Տրված են \(324\) առաջընթացի առաջին երեք անդամները. \(-108\); \(36\)…. Գտեք \(b_5\):
Լուծում:

	Հաջորդականությունը շարունակելու համար մենք պետք է իմանանք հայտարարը: Գտնենք այն երկու հարևան տարրերից. ինչո՞վ է պետք \(324\) բազմապատկել \(-108\) ստանալու համար:
\(324·q=-108\)	Այստեղից մենք հեշտությամբ կարող ենք հաշվարկել հայտարարը։
\(q=-\) \(\frac(108)(324)\) \(=-\) \(\frac(1)(3)\)	Այժմ մենք հեշտությամբ կարող ենք գտնել մեզ անհրաժեշտ տարրը:
	Պատասխանը պատրաստ է.

Պատասխանել : \(4\).

Օրինակ: Առաջընթացը նշվում է \(b_n=0.8·5^n\ պայմանով): Ո՞ր թիվն է այս առաջընթացի անդամ.

ա) \(-5\) բ) \(100\) գ) \(25\) դ) \(0.8\) ?

Լուծում: Առաջադրանքի ձեւակերպումից ակնհայտ է, որ այս թվերից մեկը միանշանակ մեր առաջընթացի մեջ է։ Հետևաբար, մենք կարող ենք պարզապես մեկ առ մեկ հաշվարկել դրա պայմանները, մինչև գտնենք մեզ անհրաժեշտ արժեքը։ Քանի որ մեր առաջընթացը տրվում է բանաձևով, մենք հաշվարկում ենք տարրերի արժեքները՝ փոխարինելով տարբեր \(n\):
\(n=1\); \(b_1=0.8·5^1=0.8·5=4\) – ցանկում նման թիվ չկա։ Շարունակենք.
\(n=2\); \(b_2=0.8·5^2=0.8·25=20\) - և սա նույնպես չկա:
\(n=3\); \(b_3=0.8·5^3=0.8·125=100\) - և ահա մեր չեմպիոնը:

Պատասխան. \(100\).

Օրինակ (OGE): Տրված են երկրաչափական պրոգրեսիայի մի քանի հաջորդական անդամներ...\(8\); \(x\); \(50\); \(-125\)…. Գտեք \(x\) պիտակավորված տարրի արժեքը:

Լուծում:

Պատասխան. \(-20\).

Օրինակ (OGE): Առաջընթացը սահմանվում է \(b_1=7\), \(b_(n+1)=2b_n\ պայմաններով: Գտեք այս առաջընթացի առաջին \(4\) անդամների գումարը:

Լուծում:

Պատասխան. \(105\).

Օրինակ (OGE): Հայտնի է, որ երկրաչափական պրոգրեսիայում \(b_6=-11\), \(b_9=704\): Գտե՛ք \(q\) հայտարարը:

Լուծում:

	Ձախ կողմի գծապատկերից երևում է, որ \(b_6\)-ից \(b_9\) «ստանալու» համար մենք կատարում ենք երեք «քայլ», այսինքն՝ \(b_6\)-ը երեք անգամ բազմապատկում ենք հայտարարով։ առաջընթացի։ Այլ կերպ ասած՝ \(b_9=b_6·q·q·q=b_6·q^3\):
\(b_9=b_6·q^3\)	Եկեք փոխարինենք մեր իմացած արժեքները։
\(704=(-11)·ք^3\)	Շրջենք հավասարումը և այն բաժանենք \((-11)\-ով):
\(q^3=\) \(\frac(704)(-11)\) \(\:\:\: ⇔ \:\:\: \)\(q^3=-\) \(64 \)	Ո՞ր թիվն է տալիս «-64» խորանարդը: Իհարկե, \(-4\)!
	Պատասխանը գտնվել է. Այն կարելի է ստուգել՝ վերականգնելով \(-11\)-ից \(704\) թվերի շղթան:
	Ամեն ինչ հավաքվեց - պատասխանը ճիշտ է:

Պատասխան. \(-4\).

Ամենակարևոր բանաձևերը

Ինչպես տեսնում եք, երկրաչափական պրոգրեսիայի խնդիրների մեծ մասը կարելի է լուծել մաքուր տրամաբանության միջոցով՝ պարզապես հասկանալով էությունը (սա ընդհանուր առմամբ բնորոշ է մաթեմատիկայի համար): Բայց երբեմն որոշակի բանաձեւերի ու օրինաչափությունների իմացությունը արագանում է և զգալիորեն հեշտացնում լուծումը: Մենք կուսումնասիրենք նման երկու բանաձև.

\(n\)-րդ անդամի բանաձևը՝ \(b_n=b_1·q^(n-1)\), որտեղ \(b_1\) առաջընթացի առաջին անդամն է; \(n\) – պահանջվող տարրի համարը; \(q\) – առաջընթացի հայտարար; \(b_n\) - առաջընթացի ժամկետ \(n\) թվով:

Օգտագործելով այս բանաձևը, դուք կարող եք, օրինակ, խնդիրը լուծել առաջին օրինակից բառացիորեն մեկ գործողությամբ։

Օրինակ (OGE): Երկրաչափական պրոգրեսիան որոշվում է \(b_1=-2\); \(q=7\): Գտեք \(b_4\):
Լուծում:

Պատասխան. \(-686\).

Այս օրինակը պարզ էր, ուստի բանաձևը մեզ համար շատ չհեշտացրեց հաշվարկները: Եկեք նայենք խնդրին մի փոքր ավելի բարդ:

Օրինակ: Երկրաչափական պրոգրեսիան որոշվում է \(b_1=20480\); \(q=\frac(1)(2)\): Գտեք \(b_(12)\):
Լուծում:

Պատասխան. \(10\).

Իհարկե, \(\frac(1)(2)\)-ը \(11\)-րդ հզորության բարձրացնելը այնքան էլ ուրախալի չէ, բայց դեռ ավելի հեշտ է, քան \(11\) \(20480\)-ը երկուսի բաժանելը:

Առաջին անդամների \(n\) գումարը՝ \(S_n=\)\(\frac(b_1·(q^n-1))(q-1)\) , որտեղ \(b_1\) առաջին անդամն է առաջընթացի; \(n\) – գումարված տարրերի քանակը; \(q\) – առաջընթացի հայտարար; \(S_n\) – առաջընթացի \(n\) առաջին անդամների գումարը:

Օրինակ (OGE): Տրվում է \(b_n\) երկրաչափական պրոգրեսիա, որի հայտարարը \(5\) է, իսկ առաջին անդամը՝ \(b_1=\frac(2)(5)\): Գտե՛ք այս առաջընթացի առաջին վեց անդամների գումարը:
Լուծում:

Պատասխան. \(1562,4\).

Եվ կրկին, մենք կարող էինք լուծել խնդիրը՝ հերթով գտնել բոլոր վեց տարրերը, այնուհետև ավելացնել արդյունքները: Այնուամենայնիվ, հաշվարկների քանակը և, հետևաբար, պատահական սխալի հավանականությունը կտրուկ կավելանա:

Երկրաչափական պրոգրեսիայի համար կան ևս մի քանի բանաձևեր, որոնք մենք այստեղ չենք դիտարկել դրանց ցածր գործնական օգտագործման պատճառով: Դուք կարող եք գտնել այս բանաձեւերը.

Երկրաչափական առաջընթացների ավելացում և նվազում

Հոդվածի հենց սկզբում դիտարկված \(b_n = \(3; 6; 12; 24; 48...\)\) առաջընթացի համար \(q\) հայտարարը մեկից մեծ է և հետևաբար յուրաքանչյուր հաջորդ անդամ: ավելի մեծ է, քան նախորդը. Նման առաջընթացները կոչվում են աճող.

Եթե ​​\(q\)-ը մեկից փոքր է, բայց դրական է (այսինքն, գտնվում է զրոյից մինչև մեկ միջակայքում), ապա յուրաքանչյուր հաջորդ տարր պակաս կլինի նախորդից: Օրինակ, առաջընթացի մեջ \(4\); \(2\); \(1\); \(0.5\); \(0.25\)... \(q\)-ի հայտարարը հավասար է \(\frac(1)(2)\):

Այս առաջընթացները կոչվում են նվազում է. Նկատի ունեցեք, որ նման պրոգրեսիայի տարրերից ոչ մեկը բացասական չի լինի, պարզապես ամեն քայլափոխի դրանք ավելի ու ավելի փոքրանում են: Այսինքն՝ մենք աստիճանաբար կմոտենանք զրոյին, բայց երբեք չենք հասնի դրան ու դրանից այն կողմ չենք անցնի։ Նման դեպքերում մաթեմատիկոսներն ասում են՝ «հակված են զրոյի»։

Նկատի ունեցեք, որ բացասական հայտարարի դեպքում երկրաչափական պրոգրեսիայի տարրերը անպայմանորեն կփոխեն նշանը: Օրինակ, y առաջընթաց \(5\); \(-15\); \(45\); \(-135\); \(675\)... \(q\)-ի հայտարարը \(-3\) է, և դրա պատճառով էլ տարրերի նշանները թարթում են։

Երկրաչափական պրոգրեսիան թվային հաջորդականության նոր տեսակ է, որին մենք պատրաստվում ենք ծանոթանալ։ Հաջող ծանոթության համար վնաս չէ գոնե իմանալն ու հասկանալը: Այդ դեպքում երկրաչափական առաջընթացի հետ կապված խնդիրներ չեն լինի:)

Ի՞նչ է երկրաչափական առաջընթացը: Երկրաչափական պրոգրեսիայի հայեցակարգը.

Շրջայցը, ինչպես միշտ, սկսում ենք հիմունքներով։ Ես գրում եմ թվերի անավարտ հաջորդականություն.

1, 10, 100, 1000, 10000, …

Կարո՞ղ եք նկատել օրինաչափությունը և ասել, թե որ թվերն են լինելու հաջորդը: Պղպեղը պարզ է, հետո կհետևեն 100.000, 1.000.000 թվերը և այլն։ Նույնիսկ առանց մեծ մտավոր ջանքերի, ամեն ինչ պարզ է, չէ՞):

ԼԱՎ։ Մեկ այլ օրինակ. Ես գրում եմ այս հաջորդականությունը.

1, 2, 4, 8, 16, …

Կարո՞ղ եք ասել, թե որ թվերն են հաջորդում՝ հետևելով 16 թվին և անունին ութերորդհաջորդականության անդամ. Եթե ​​դուք հասկացաք, որ դա կլինի 128 թիվը, ապա շատ լավ: Այսպիսով, գործի կեսը ըմբռնման մեջ է իմաստըԵվ հիմնական կետերըերկրաչափական պրոգրեսիա արդեն կատարվել է։ Դուք կարող եք ավելի մեծանալ:)

Իսկ հիմա սենսացիաներից նորից անցնում ենք խիստ մաթեմատիկայի։

Երկրաչափական առաջընթացի հիմնական կետերը.

Հիմնական կետ թիվ 1

Երկրաչափական առաջընթացն է թվերի հաջորդականություն.Այդպես է առաջընթացը: Ոչ մի շքեղ բան: Միայն այս հաջորդականությունն է դասավորված այլ կերպ.Ուստի, բնականաբար, այլ անուն ունի, այո...

Հիմնական կետ թիվ 2

Երկրորդ առանցքային կետով հարցն ավելի բարդ կլինի. Եկեք մի փոքր հետ գնանք և հիշենք թվաբանական առաջընթացի հիմնական հատկությունը։ Ահա այն: յուրաքանչյուր անդամ տարբերվում է նախորդից նույն չափով։

Հնարավո՞ր է երկրաչափական պրոգրեսիայի համար ձևակերպել նմանատիպ հիմնական հատկություն: Մի քիչ մտածեք... Ավելի ուշադիր նայեք բերված օրինակներին: Դուք գուշակեցի՞ք։ Այո՛ Երկրաչափական պրոգրեսիայով (ցանկացած!) նրա անդամներից յուրաքանչյուրը տարբերվում է նախորդից նույնքան անգամ:Միշտ!

Առաջին օրինակում այս թիվը տաս է։ Հերթականության որ անդամն էլ վերցնես, այն ավելի մեծ է, քան նախորդը տասն անգամ։

Երկրորդ օրինակում դա երկու է. յուրաքանչյուր անդամ ավելի մեծ է, քան նախորդը երկու անգամ։

Հենց այս առանցքային կետն է, որ երկրաչափական պրոգրեսիան տարբերվում է թվաբանական առաջընթացից: Թվաբանական առաջընթացում ստացվում է յուրաքանչյուր հաջորդ անդամ ավելացնելովնույն արժեքը նախորդ տերմինի հետ: Եվ այստեղ - բազմապատկումնախորդ ժամկետը նույն չափով։ Սա է ողջ տարբերությունը։)

Հիմնական կետ թիվ 3

Այս առանցքային կետը լիովին նույնական է թվաբանական առաջընթացի համար: Այսինքն: Երկրաչափական առաջընթացի յուրաքանչյուր անդամ կանգնած է իր տեղում:Ամեն ինչ ճիշտ նույնն է, ինչ թվաբանական առաջընթացում, և մեկնաբանությունները, կարծում եմ, ավելորդ են։ Կա առաջին տերմինը, կա հարյուր և առաջինը և այլն: Եկեք փոխանակենք առնվազն երկու տերմին. նախշը (և դրա հետ մեկտեղ երկրաչափական առաջընթացը) կվերանա: Այն, ինչ կմնա, պարզապես թվերի հաջորդականություն է՝ առանց որևէ տրամաբանության։

Այսքանը: Սա է երկրաչափական առաջընթացի ամբողջ իմաստը:

Պայմաններ և նշանակումներ.

Բայց հիմա, հասկանալով երկրաչափական պրոգրեսիայի իմաստն ու հիմնական կետերը, կարող ենք անցնել տեսությանը։ Թե չէ իմաստը չհասկանալով տեսությունն ի՞նչ է, չէ՞։

Ինչպե՞ս նշել երկրաչափական առաջընթացը:

Ինչպե՞ս է գրվում երկրաչափական պրոգրեսիան ընդհանուր ձևով: Ոչ մի խնդիր! Առաջընթացի յուրաքանչյուր տերմին գրված է նաև տառի տեսքով։ Միայն թվաբանական առաջընթացի համար սովորաբար օգտագործվում է տառը «Ա», երկրաչափական համար – տառ «բ». Անդամի համարը, ինչպես միշտ, նշված է ինդեքսը ներքևի աջ մասում. Մենք ուղղակի թվարկում ենք հենց իրենք պրոգրեսիայի անդամները՝ բաժանված ստորակետերով կամ կետ-ստորակետերով:

Սրա նման:

բ 1,բ 2 , բ 3 , բ 4 , բ 5 , բ 6 , …

Համառոտ այս առաջընթացը գրված է այսպես. (b n) .

Կամ այսպես՝ վերջավոր առաջընթացների համար.

բ 1, բ 2, բ 3, բ 4, բ 5, բ 6։

բ 1, բ 2, …, բ 29, բ 30:

Կամ, մի խոսքով.

(b n), n=30 .

Դա, ըստ էության, ամբողջ նշանակումն է։ Ամեն ինչ նույնն է, միայն տառն է տարբեր, այո։) Իսկ հիմա ուղղակիորեն անցնում ենք սահմանմանը։

Երկրաչափական առաջընթացի սահմանում.

Երկրաչափական պրոգրեսիան թվային հաջորդականություն է, որտեղ առաջին անդամը զրոյական չէ, և յուրաքանչյուր հաջորդ անդամը հավասար է նախորդ անդամին, որը բազմապատկվում է նույն ոչ զրոյական թվով։

Սա է ամբողջ սահմանումը: Բառերի և արտահայտությունների մեծ մասը ձեզ համար պարզ և ծանոթ է: Եթե, իհարկե, հասկանում եք երկրաչափական պրոգրեսիայի իմաստը «ձեր մատների վրա» և ընդհանրապես։ Բայց կան նաև մի քանի նոր արտահայտություններ, որոնց կուզենայի հատուկ ուշադրություն դարձնել։

Նախ, բառերը. «որի առաջին անդամը ոչ զրոյական".

Առաջին ժամկետի այս սահմանափակումը պատահական չի դրվել։ Ի՞նչ եք կարծում, ինչ կլինի, եթե առաջին անդամը բ 1 հավասար կլինի զրոյի? Ի՞նչ հավասար կլինի երկրորդ անդամը, եթե յուրաքանչյուր անդամ մեծ է նախորդից: նույնքան անգամ?Ասենք երեք անգամ. Տեսնենք... Առաջին անդամը (այսինքն 0) բազմապատկեք 3-ով և ստացեք... զրո: Ինչ վերաբերում է երրորդ անդամին: Նաև զրո: Եվ չորրորդ անդամը նույնպես զրո է: Եվ այսպես շարունակ…

Մենք պարզապես ստանում ենք մի պարկ թխուկներ, զրոների հաջորդականություն.

0, 0, 0, 0, …

Իհարկե, նման հաջորդականությունը կյանքի իրավունք ունի, բայց դա գործնական հետաքրքրություն չի ներկայացնում։ Ամեն ինչ պարզ է. Նրա ցանկացած անդամ զրո է: Ցանկացած թվով տերմինների գումարը նույնպես զրո է... Ի՞նչ հետաքրքիր բաներ կարող ես անել դրա հետ։ Ոչինչ…

Հետևյալ հիմնաբառերը. «բազմապատկված նույն ոչ զրոյական թվով»։

Այս նույն համարն ունի նաև իր հատուկ անվանումը. երկրաչափական պրոգրեսիայի հայտարար. Սկսենք ծանոթանալ։)

Երկրաչափական պրոգրեսիայի հայտարար.

Ամեն ինչ այնքան պարզ է, որքան տանձը ռմբակոծելը:

Երկրաչափական պրոգրեսիայի հայտարարը ոչ զրոյական թիվ է (կամ մեծություն), որը ցույց է տալիս.քանի անգամառաջընթացի յուրաքանչյուր տերմին ավելի շատ, քան նախորդը:

Կրկին, թվաբանական առաջընթացի նման, այս սահմանման մեջ փնտրելու հիմնական բառը բառն է «ավելի շատ». Դա նշանակում է, որ ստացված է երկրաչափական պրոգրեսիայի յուրաքանչյուր անդամ բազմապատկումհենց այս հայտարարին նախորդ անդամ.

Թույլ տուր բացատրեմ։

Հաշվարկելու համար ասենք երկրորդԴիկ, պետք է վերցնել առաջինանդամ և բազմապատկելայն հայտարարին: Հաշվարկի համար տասներորդԴիկ, պետք է վերցնել իններորդանդամ և բազմապատկելայն հայտարարին:

Ինքնին երկրաչափական պրոգրեսիայի հայտարարը կարող է լինել ցանկացած բան: Բացարձակապես որևէ մեկը: Ամբողջական, կոտորակային, դրական, բացասական, իռացիոնալ՝ ամեն ինչ: Բացի զրոյից։ Ահա թե ինչ է մեզ ասում սահմանման մեջ «ոչ զրոյական» բառը: Ինչու է այս բառը անհրաժեշտ այստեղ, դրա մասին ավելի ուշ:

Երկրաչափական պրոգրեսիայի հայտարարամենից հաճախ նշվում է տառով ք.

Ինչպես գտնել այն ք? Ոչ մի խնդիր! Մենք պետք է վերցնենք առաջընթացի ցանկացած տերմին և բաժանել նախորդ անդամի վրա. Բաժանում է մաս. Այստեղից էլ անվանումը՝ «առաջընթացի հայտարար»։ Հայտարարը սովորաբար կոտորակի մեջ է նստում, այո...) Չնայած, տրամաբանորեն, արժեքը. քպետք է կոչել մասնավորերկրաչափական պրոգրեսիա՝ նման տարբերությունըթվաբանական առաջընթացի համար. Բայց մենք պայմանավորվեցինք զանգահարել հայտարար. Եվ մենք նույնպես չենք հայտնագործի անիվը:)

Սահմանենք, օրինակ, քանակը քայս երկրաչափական առաջընթացի համար.

2, 6, 18, 54, …

Ամեն ինչ տարրական է։ Վերցնենք ցանկացածհաջորդականության համարը. Ինչ ուզում ենք՝ վերցնում ենք։ Բացառությամբ առաջինի. Օրինակ՝ 18. Եվ բաժանիր նախորդ համարը. Այսինքն՝ ժամը 6-ին։

Մենք ստանում ենք.

ք = 18/6 = 3

Այսքանը: Սա ճիշտ պատասխանն է։ Այս երկրաչափական առաջընթացի համար հայտարարը երեքն է:

Եկեք հիմա գտնենք հայտարարը քմեկ այլ երկրաչափական առաջընթացի համար: Օրինակ, այս մեկը.

1, -2, 4, -8, 16, …

Ամեն ինչ նույնն է։ Անկախ նրանից, թե անդամներն իրենք ինչ նշաններ ունեն, մենք դեռ վերցնում ենք ցանկացածհաջորդականության համարը (օրինակ՝ 16) և բաժանիր նախորդ համարը(այսինքն -8):

Մենք ստանում ենք.

դ = 16/(-8) = -2

Եվ վերջ։) Այս անգամ առաջընթացի հայտարարը բացասական է ստացվել։ Մինուս երկու. Պատահում է.)

Այժմ վերցնենք այս առաջընթացը.

1, 1/3, 1/9, 1/27, …

Եվ կրկին, անկախ հաջորդականության թվերի տեսակից (ամբողջ թվեր, զույգ կոտորակներ, նույնիսկ բացասական, նույնիսկ իռացիոնալ), վերցնում ենք ցանկացած թիվ (օրինակ՝ 1/9) և բաժանում նախորդ թվին (1/3)։ Կոտորակների հետ աշխատելու կանոններով, իհարկե։

Մենք ստանում ենք.

Այսքանը:) Այստեղ հայտարարը կոտորակային է ստացվել. ք = 1/3.

Ի՞նչ եք կարծում այս «առաջընթացի» մասին:

3, 3, 3, 3, 3, …

Ակնհայտորեն այստեղ ք = 1 . Ֆորմալ առումով սա նույնպես երկրաչափական պրոգրեսիա է, միայն հետ նույնական անդամներ.) Բայց նման առաջընթացները հետաքրքիր չեն ուսումնասիրության և գործնական կիրառման համար։ Նույնը, ինչ պինդ զրոներով առաջընթացները: Հետեւաբար, մենք դրանք չենք դիտարկի:

Ինչպես տեսնում եք, առաջընթացի հայտարարը կարող է լինել ցանկացած բան՝ ամբողջ թիվ, կոտորակային, դրական, բացասական՝ ամեն ինչ: Չի կարող պարզապես զրո լինել: Չե՞ք կարող կռահել, թե ինչու:

Դե, եկեք որոշ կոնկրետ օրինակ օգտագործենք՝ տեսնելու, թե ինչ կլինի, եթե որպես հայտարար վերցնենք քզրո։) Օրինակ՝ ունենանք բ 1 = 2 , Ա ք = 0 . Այդ դեպքում ինչի՞ն կհավասարվի երկրորդ անդամը:

Մենք հաշվում ենք.

բ 2 = բ 1 · ք= 2 0 = 0

Ինչ վերաբերում է երրորդ անդամին:

բ 3 = բ 2 · ք= 0 0 = 0

Երկրաչափական առաջընթացների տեսակներն ու վարքագիծը:

Ամեն ինչ քիչ թե շատ պարզ էր՝ եթե առաջընթացի տարբերությունը դդրական է, ապա առաջընթացը մեծանում է։ Եթե ​​տարբերությունը բացասական է, ապա առաջընթացը նվազում է։ Կա միայն երկու տարբերակ. Երրորդ չկա։)

Բայց երկրաչափական առաջընթացի վարքագծով ամեն ինչ շատ ավելի հետաքրքիր և բազմազան կլինի:)

Անկախ նրանից, թե ինչպես են տերմիններն իրենց պահում այստեղ. նրանք ավելանում և նվազում են, և անորոշ ժամանակով մոտենում են զրոյին, և նույնիսկ փոխում են նշանները, հերթափոխով նետվում են «գումարած», իսկ հետո «մինուս»: Եվ այս ամբողջ բազմազանության մեջ պետք է կարողանալ լավ հասկանալ, այո...

Եկեք պարզենք?) Սկսենք ամենապարզ դեպքից:

Հայտարարը դրական է ( ք >0)

Դրական հայտարարի դեպքում, առաջին հերթին, կարող են ներառվել երկրաչափական առաջընթացի պայմանները գումարած անսահմանություն(այսինքն՝ ավելացնել առանց սահմանի) և կարող է մտնել մինուս անսահմանություն(այսինքն, նվազում է առանց սահմանի): Մենք արդեն սովոր ենք պրոգրեսիաների այս պահվածքին։

Օրինակ:

(b n): 1, 2, 4, 8, 16, …

Այստեղ ամեն ինչ պարզ է. Ստացվում է առաջընթացի յուրաքանչյուր տերմին ավելի շատ, քան նախորդը. Ընդ որում, յուրաքանչյուր տերմին ստացվում է բազմապատկումնախորդ անդամը միացված է դրականհամարը +2 (այսինքն. ք = 2 ) Նման պրոգրեսիայի վարքագիծն ակնհայտ է՝ պրոգրեսիայի բոլոր անդամները աճում են անսահմանափակ՝ գնալով տիեզերք։ Գումարած անսահմանություն...

Եվ հիմա ահա առաջընթացը.

(b n): -1, -2, -4, -8, -16, …

Այստեղ նույնպես ստացվում է առաջընթացի յուրաքանչյուր տերմին բազմապատկումնախորդ անդամը միացված է դրականհամարը +2. Բայց նման պրոգրեսիայի վարքագիծը ճիշտ հակառակն է՝ ստացվում է պրոգրեսիայի յուրաքանչյուր տերմին ավելի քիչ, քան նախորդը, և նրա բոլոր անդամները նվազում են առանց սահմանի, գնալով մինուս անսահմանության։

Հիմա եկեք մտածենք՝ ի՞նչ ընդհանուր բան ունեն այս երկու առաջընթացները։ Ճիշտ է, հայտարար! Այստեղ, եւ այնտեղ ք = +2 . Դրական թիվ.Երկու. Եվ ահա վարքագիծԱյս երկու առաջընթացները սկզբունքորեն տարբեր են: Չե՞ք կարող կռահել, թե ինչու: Այո՛ Ամեն ինչի մասին է առաջին անդամ!Հենց նա է, ինչպես ասում են, մեղեդին կանչողը։) Ինքներդ տեսեք։

Առաջին դեպքում՝ առաջընթացի առաջին տերմինը դրական(+1) և, հետևաբար, բոլոր հաջորդ անդամները, որոնք ստացվում են բազմապատկելով դրականհայտարար ք = +2 , նույնպես կլինի դրական.

Բայց երկրորդ դեպքում՝ առաջին ժամկետը բացասական(-1): Հետևաբար, առաջընթացի բոլոր հաջորդ անդամները, որոնք ստացվում են բազմապատկելով դրական ք = +2 , նույնպես ձեռք կբերվի բացասական.Որովհետև «մինուս»-ը «պլյուս»-ին միշտ տալիս է «մինուս», այո):

Ինչպես տեսնում եք, ի տարբերություն թվաբանական առաջընթացի, երկրաչափական պրոգրեսիան կարող է բոլորովին այլ կերպ վարվել ոչ միայն կախված. հայտարարիցք, բայց նաև կախված առաջին անդամից, Այո։)

Հիշեք. երկրաչափական պրոգրեսիայի վարքագիծը եզակիորեն որոշվում է նրա առաջին անդամով բ 1 և հայտարարք .

Եվ հիմա մենք սկսում ենք վերլուծել ոչ այնքան ծանոթ, բայց շատ ավելի հետաքրքիր դեպքերը:

Վերցնենք, օրինակ, այս հաջորդականությունը.

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

Այս հաջորդականությունը նույնպես երկրաչափական պրոգրեսիա է: Այս առաջընթացի յուրաքանչյուր տերմին նույնպես ստացվում է բազմապատկումնախորդ անդամը՝ նույն թվով։ Դա պարզապես թիվ է - կոտորակային: ք = +1/2 . Կամ +0,5 . Ավելին (կարևոր է) թիվը մեկից պակաս:ք = 1/2<1.

Ինչու է այս երկրաչափական առաջընթացը հետաքրքիր: Ո՞ւր են գնում նրա անդամները: Եկեք նայենք.

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Ի՞նչ հետաքրքիր բաներ կարող եք նկատել այստեղ: Նախ, առաջընթացի անկումը անմիջապես նկատելի է. նրա յուրաքանչյուր անդամ պակասհենց նախորդը 2 անգամ։Կամ, ըստ երկրաչափական պրոգրեսիայի սահմանման, յուրաքանչյուր տերմին ավելիննախորդ 1/2 անգամ, որովհետեւ առաջընթացի հայտարար ք = 1/2 . Իսկ մեկից փոքր դրական թվով բազմապատկելիս արդյունքը սովորաբար նվազում է, այո...

Ինչ ավելինկարելի՞ է տեսնել այս առաջընթացի վարքագծում: Արդյո՞ք դրա անդամները նվազում են: անսահմանափակ, գնալով մինուս անսահմանությո՞ւն։ Ո՛չ։ Նրանք անհետանում են հատուկ ձևով: Սկզբում դրանք բավականին արագ են նվազում, իսկ հետո ավելի ու ավելի դանդաղ։ Եվ ամբողջ ժամանակ մնալով դրական. Թեև շատ, շատ փոքր: Իսկ ինչի՞ն են իրենք ձգտում։ Չե՞ք գուշակել։ Այո՛ Նրանք ձգտում են դեպի զրոյի: Ավելին, ուշադրություն դարձրեք, մեր պրոգրեսիայի անդամները զրոյից են երբեք չհասնես!Միայն մոտենալով նրան անսահման մոտ. Դա շատ կարեւոր է։)

Նմանատիպ իրավիճակ տեղի կունենա հետևյալ առաջընթացով.

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Այստեղ բ 1 = -1 , Ա ք = 1/2 . Ամեն ինչ նույնն է, միայն հիմա տերմինները մյուս կողմից՝ ներքեւից կմոտենան զրոյին։ Անընդհատ մնալը բացասական.)

Այդպիսի երկրաչափական պրոգրեսիա, որի տերմինները մոտենալ զրոյին առանց սահմանի(անկախ դրական կամ բացասական կողմից), մաթեմատիկայում հատուկ անուն ունի. անսահման նվազող երկրաչափական պրոգրեսիա:Այս առաջընթացն այնքան հետաքրքիր և անսովոր է, որ նույնիսկ կքննարկվի առանձին դաս .)

Այսպիսով, մենք ամեն ինչ համարել ենք հնարավոր դրականհայտարարները և՛ մեծերն են, և՛ փոքրերը: Մենք միավորն ինքնին որպես հայտարար չենք համարում վերը նշված պատճառներով (հիշեք օրինակը եռյակների հաջորդականությամբ...)

Ամփոփենք.

դրականԵվ մեկից ավել (ք>1), ապա առաջընթացի պայմանները.

ա) մեծացնել առանց սահմանի (եթեբ 1 >0);

բ) նվազում առանց սահմանի (եթեբ 1 <0).

Եթե ​​երկրաչափական պրոգրեսիայի հայտարարը դրական Եվ մեկից պակաս (0< ք<1), то члены прогрессии:

ա) անսահման մոտ զրոյին վերևում(Եթեբ 1 >0);

բ) մոտենում է զրոյին անսահման մոտ ներքեւից(Եթեբ 1 <0).

Այժմ մնում է քննել գործը բացասական հայտարար.

Հայտարարը բացասական է ( ք <0)

Օրինակի համար հեռու չենք գնա. Ինչու՞ հենց, բրդոտ տատիկ։) Թող, օրինակ, առաջընթացի առաջին տերմինը լինի բ 1 = 1 , և վերցնենք հայտարարը q = -2.

Մենք ստանում ենք հետևյալ հաջորդականությունը.

(b n): 1, -2, 4, -8, 16, …

Եվ այսպես շարունակ։) Ստացվում է առաջընթացի յուրաքանչյուր տերմին բազմապատկումնախորդ անդամը միացված է բացասական թիվ-2. Այս դեպքում կենտ տեղերում կանգնած բոլոր անդամները (առաջին, երրորդ, հինգերորդ և այլն) կլինեն. դրականև զույգ տեղերում (երկրորդ, չորրորդ և այլն) – բացասական.Նշանները խիստ հերթափոխ են։ Plus-minus-plus-minus... Այս երկրաչափական պրոգրեսիան կոչվում է - աճող նշանի փոփոխական.

Ո՞ւր են գնում նրա անդամները: Բայց ոչ մի տեղ:) Այո, բացարձակ արժեքով (այսինքն մոդուլ)մեր առաջընթացի անդամներն ավելանում են անսահմանափակ (այստեղից էլ՝ «աճող» անվանումը): Բայց միևնույն ժամանակ, պրոգրեսիայի յուրաքանչյուր անդամ հերթափոխով ձեզ գցում է շոգի մեջ, հետո՝ սառը: Կամ «գումարած» կամ «մինուս»: Մեր առաջընթացը տատանվում է... Ավելին, տատանումների շրջանակն ամեն քայլափոխի արագորեն մեծանում է, այո։) Հետևաբար, պրոգրեսիայի անդամների նկրտումները գնում են ինչ-որ տեղ։ կոնկրետԱյստեղ ՈչՈչ դեպի գումարած անսահմանություն, ոչ մինուս անվերջություն, ոչ էլ զրոյի՝ ոչ մի տեղ:

Այժմ դիտարկենք մի քանի կոտորակային հայտարար զրոյի և մինուս մեկի միջև:

Օրինակ, թող լինի բ 1 = 1 , Ա q = -1/2.

Այնուհետև մենք ստանում ենք առաջընթացը.

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

Եվ կրկին մենք ունենք նշանների փոփոխություն: Բայց, ի տարբերություն նախորդ օրինակի, այստեղ արդեն ակնհայտ է տերմինների զրոյին մոտենալու միտումը։) Միայն թե այս անգամ մեր տերմինները զրոյին մոտենում են ոչ թե խիստ վերեւից կամ ներքեւից, այլ նորից։ վարանելով. Դրական և բացասական արժեքների այլընտրանքային ընդունում: Բայց միևնույն ժամանակ նրանք մոդուլներավելի ու ավելի են մոտենում նվիրական զրոյին։)

Այս երկրաչափական պրոգրեսիան կոչվում է անսահման նվազող նշան, հերթափոխ.

Ինչու են այս երկու օրինակները հետաքրքիր: Եվ այն, որ երկու դեպքում էլ տեղի է ունենում նշանների փոփոխություն!Այս հնարքը բնորոշ է միայն բացասական հայտարար ունեցող պրոգրեսիաներին, այո։) Հետևաբար, եթե որևէ առաջադրանքի մեջ տեսնեք երկրաչափական պրոգրեսիա՝ փոփոխվող անդամներով, արդեն հաստատ կիմանաք, որ դրա հայտարարը 100% բացասական է և չեք սխալվի։ նշանի մեջ։)

Ի դեպ, բացասական հայտարարի դեպքում առաջին անդամի նշանը բացարձակապես չի ազդում բուն պրոգրեսիայի վարքագծի վրա։ Անկախ առաջընթացի առաջին կիսամյակի նշանից, ամեն դեպքում ժամկետների նշանը կնկատվի։ Միակ հարցն այն է, ինչ վայրերում(զույգ կամ կենտ) կլինեն կոնկրետ նշաններ ունեցող անդամներ:

Հիշեք.

Եթե ​​երկրաչափական պրոգրեսիայի հայտարարը բացասական , ապա առաջընթացի պայմանների նշանները միշտ են այլընտրանքային.

Միևնույն ժամանակ, իրենք՝ անդամները.

ա) ավելանալ առանց սահմանիմոդուլ, Եթեք<-1;

բ) անվերջ մոտենալ զրոյին, եթե -1< ք<0 (прогрессия бесконечно убывающая).

Այսքանը: Բոլոր բնորոշ դեպքերը վերլուծվել են։)

Երկրաչափական առաջընթացների մի շարք օրինակների վերլուծության ընթացքում ես պարբերաբար օգտագործում էի բառերը. «հակված է զրոյի», «հակված է գումարած անսահմանությանը», «հակված է մինուս անսահմանությանը»... Ոչինչ:) Այս խոսքի թվերը (և կոնկրետ օրինակները) ընդամենը նախնական ներածություն են. վարքագիծմի շարք թվային հաջորդականություններ. Օգտագործելով երկրաչափական պրոգրեսիայի օրինակ:

Ինչու՞ մեզ անհրաժեշտ է նույնիսկ իմանալ առաջընթացի վարքագիծը: Ի՞նչ տարբերություն, թե որտեղ է նա գնում: Դեպի զրոյ, դեպի գումարած անսահմանություն, մինուս անսահմանություն... Ի՞նչ է սա մեզ հետ անում:

Բանն այն է, որ արդեն համալսարանում, բարձրագույն մաթեմատիկայի կուրսում, ձեզ անհրաժեշտ կլինի թվային հաջորդականությունների լայն տեսականիով աշխատելու ունակություն (ցանկացած, ոչ միայն առաջընթացներով) և կարողություն պատկերացնել, թե ինչպես է այս կամ այն ​​հաջորդականությունը: վարվում է - մեծանում է, թե նվազում է անսահմանափակ, թե արդյոք այն հակված է որոշակի թվի (և պարտադիր չէ զրոյի), թե նույնիսկ ընդհանրապես չի հակված որևէ բանի... Մաթեմատիկականի ընթացքում այս թեմային է նվիրված մի ամբողջ բաժին. վերլուծություն - սահմանների տեսություն.Իսկ մի քիչ ավելի կոնկրետ՝ հայեցակարգը թվերի հաջորդականության սահմանը.Շատ հետաքրքիր թեմա! Իմաստ ունի գնալ քոլեջ և պարզել դա:)

Որոշ օրինակներ այս բաժնից (հաջորդականություններ, որոնք սահման ունեն) և մասնավորապես, անսահման նվազող երկրաչափական պրոգրեսիաԴպրոցում սկսում են ընտելանալ: Մենք սովորում ենք դրան:)

Ավելին, հաջորդականությունների վարքագիծը լավ ուսումնասիրելու կարողությունը ձեզ մեծ օգուտ կտա ապագայում և շատ օգտակար կլինի. ֆունկցիոնալ հետազոտություն:Ամենատարբեր. Բայց ֆունկցիաների հետ գրագետ աշխատելու ունակությունը (ածանցյալները հաշվարկել, դրանք ամբողջությամբ ուսումնասիրել, դրանց գրաֆիկները կառուցել) արդեն իսկ կտրուկ բարձրացնում է ձեր մաթեմատիկական մակարդակը: Դուք կասկածներ ունե՞ք։ Կարիք չկա։ Հիշիր նաև իմ խոսքերը։)

Եկեք նայենք կյանքի երկրաչափական առաջընթացին:

Մեզ շրջապատող կյանքում մենք շատ ու շատ հաճախ հանդիպում ենք երկրաչափական առաջընթացի: Նույնիսկ առանց իմանալու:)

Օրինակ՝ տարբեր միկրոօրգանիզմներ, որոնք մեզ շրջապատում են ամենուր՝ հսկայական քանակությամբ, և որոնք մենք նույնիսկ չենք կարող տեսնել առանց մանրադիտակի, ճշգրիտ բազմապատկվում են երկրաչափական առաջընթացով:

Ենթադրենք մեկ բակտերիան բազմանում է՝ կիսվելով կիսով չափ՝ սերունդ տալով 2 բակտերիաների։ Իր հերթին նրանցից յուրաքանչյուրը բազմանալիս նույնպես կիսով չափ կիսվում է՝ տալով 4 բակտերիաների ընդհանուր սերունդ։ Հաջորդ սերունդը կարտադրի 8 բակտերիա, հետո 16 բակտերիա, 32, 64 և այլն։ Յուրաքանչյուր հաջորդ սերնդի հետ բակտերիաների թիվը կրկնապատկվում է: Երկրաչափական առաջընթացի տիպիկ օրինակ):

Նաև որոշ միջատներ՝ աֆիդներ և ճանճեր, բազմապատկվում են էքսպոնենցիալ: Եվ երբեմն, ի դեպ, նաև նապաստակները:)

Երկրաչափական պրոգրեսիայի մեկ այլ օրինակ, որն ավելի մոտ է առօրյա կյանքին, այսպես կոչված բաղադրություն հետաքրքրությունը։Այս հետաքրքիր երեւույթը հաճախ հանդիպում է բանկային ավանդներում եւ կոչվում է տոկոսների կապիտալացում.Ինչ է դա?

Դուք ինքներդ դեռ, իհարկե, երիտասարդ եք: Դու գնում ես դպրոց, մի՛ գնա բանկ։ Բայց ձեր ծնողներն արդեն չափահաս ու անկախ մարդիկ են։ Գնում են աշխատանքի, օրվա հացի փող են աշխատում, գումարի մի մասը դնում բանկում՝ խնայողություններ անելով։)

Ենթադրենք, ձեր հայրը ցանկանում է որոշակի գումար կուտակել Թուրքիայում ընտանեկան հանգստի համար և 50,000 ռուբլի է դնում բանկում տարեկան 10 տոկոսով երեք տարի ժամկետով: տարեկան տոկոսադրույքով կապիտալիզացիայով:Ավելին, այս ամբողջ ընթացքում ավանդի հետ ոչինչ չի կարելի անել։ Դուք չեք կարող ոչ ավանդը համալրել, ոչ էլ հաշվից գումար հանել: Որքա՞ն շահույթ կունենա նա այս երեք տարի հետո։

Դե, նախ և առաջ մենք պետք է հասկանանք, թե որն է տարեկան 10%-ը: Դա նշանակում է որ մեկ տարումԲանկը ավանդի սկզբնական գումարին կավելացնի 10%: Ինչի՞ց։ Իհարկե, սկսած սկզբնական ավանդի գումարը.

Հաշվի չափը հաշվում ենք մեկ տարի հետո։ Եթե ​​ավանդի սկզբնական գումարը եղել է 50,000 ռուբլի (այսինքն՝ 100%), ապա մեկ տարի հետո ինչքա՞ն տոկոսներ կլինեն հաշվի վրա: Ճիշտ է, 110%: 50,000 ռուբլիից:

Այսպիսով, մենք հաշվարկում ենք 50,000 ռուբլու 110% -ը.

50000 · 1.1 = 55000 ռուբլի:

Հուսով եմ՝ հասկանում եք, որ արժեքի 110%-ը գտնելը նշանակում է այդ արժեքը բազմապատկել 1.1 թվով: Եթե ​​չեք հասկանում, թե ինչու է դա այդպես, հիշեք հինգերորդ և վեցերորդ դասարանները: Այսինքն – տոկոսների և կոտորակների և մասերի միջև կապը):

Այսպիսով, առաջին տարվա աճը կկազմի 5000 ռուբլի:

Որքա՞ն գումար կլինի հաշվում երկու տարվա ընթացքում: 60 000 ռուբլի՞ Ցավոք (ավելի ճիշտ, բարեբախտաբար), ամեն ինչ այնքան էլ պարզ չէ։ Տոկոսների կապիտալացման ամբողջ հնարքն այն է, որ յուրաքանչյուր նոր տոկոսագումարի հետ այս նույն տոկոսներն արդեն դիտարկվելու են նոր գումարից!Նրանից, ով արդենհաշվի վրա է Այս պահին։Իսկ նախորդ ժամանակաշրջանի համար հաշվարկված տոկոսները գումարվում են ավանդի սկզբնական գումարին և, այդպիսով, ինքն է մասնակցում նոր տոկոսների հաշվարկին: Այսինքն՝ նրանք դառնում են ընդհանուր հաշվի ամբողջական մասը։ Կամ ընդհանուր կապիտալ։Այստեղից էլ անունը - տոկոսների կապիտալացում.

Դա տնտեսագիտության մեջ է: Իսկ մաթեմատիկայում այդպիսի տոկոսներ են կոչվում բաղադրություն հետաքրքրությունը։Կամ տոկոսադրույքը:) Նրանց հնարքն այն է, որ հաջորդաբար հաշվարկելիս ամեն անգամ հաշվարկվում են տոկոսները նոր արժեքից։Եվ ոչ բնօրինակից...

Հետևաբար, գումարը հաշվարկելու համար երկու տարի, պետք է հաշվարկենք այն գումարի 110%-ը, որը կլինի հաշվում մեկ տարում։Այսինքն՝ արդեն 55000 ռուբլուց։

Մենք հաշվում ենք 55000 ռուբլու 110%-ը.

55000 · 1.1 = 60500 ռուբլի:

Սա նշանակում է, որ երկրորդ տարվա համար տոկոսային աճը կկազմի 5500 ռուբլի, իսկ երկու տարվա համար՝ 10500 ռուբլի։

Այժմ արդեն կարող եք կռահել, որ երեք տարի անց հաշվում գումարը կկազմի 60500 ռուբլու 110%-ը։ Դա կրկին 110% է նախորդից (նախորդ տարի)գումարներ։

Այստեղ մենք մտածում ենք.

60500 · 1.1 = 66550 ռուբլի:

Այժմ մենք դասավորում ենք մեր դրամական գումարները ըստ տարիների հաջորդականությամբ.

50000;

55000 = 50000 1.1;

60500 = 55000 1.1 = (50000 1.1) 1.1;

66550 = 60500 1.1 = ((50000 1.1) 1.1) 1.1

Այսպիսով, ինչպես է դա: Ինչու՞ ոչ երկրաչափական պրոգրեսիա: Առաջին անդամ բ 1 = 50000 , և հայտարարը ք = 1,1 . Յուրաքանչյուր տերմին խիստ 1,1 անգամ մեծ է նախորդից: Ամեն ինչ խստորեն համապատասխանում է սահմանմանը:)

Եվ քանի՞ հավելյալ տոկոսային բոնուսներ «կկուտակի» ձեր հայրը, երբ նրա 50,000 ռուբլին երեք տարի գտնվում է բանկային հաշվին:

Մենք հաշվում ենք.

66550 – 50000 = 16550 ռուբլի

Ոչ շատ, իհարկե: Բայց սա այն դեպքում, եթե նախնական ավանդի գումարը փոքր է: Իսկ եթե ավելին լինի: Ասենք՝ ոչ թե 50, այլ 200 հազար ռուբլի՞։ Այնուհետև երեք տարվա ընթացքում աճը կկազմի 66200 ռուբլի (եթե հաշվում եք): Ինչն արդեն շատ լավ է։) Իսկ եթե ներդրումն էլ ավելի մեծ լինի։ վերջ...

Եզրակացություն. որքան բարձր է նախնական ավանդը, այնքան ավելի շահավետ է դառնում տոկոսների կապիտալացումը: Այդ իսկ պատճառով տոկոսային կապիտալիզացիայով ավանդները բանկերի կողմից տրամադրվում են երկարաժամկետ ժամկետներով։ Ասենք հինգ տարի։

Նաև բոլոր տեսակի վատ հիվանդությունները, ինչպիսիք են գրիպը, կարմրուկը և նույնիսկ ավելի սարսափելի հիվանդությունները (նույն SARS-ը 2000-ականների սկզբին կամ ժանտախտը միջնադարում) սիրում են տարածվել երկրաչափական մակարդակով: Այստեղից էլ համաճարակների մասշտաբները, այո...) Եվ այս ամենը պայմանավորված է նրանով, որ երկրաչափական պրոգրեսիան ամբողջ դրական հայտարար (ք>1) - մի բան, որը շատ արագ է աճում: Հիշեք բակտերիաների վերարտադրությունը՝ մեկ բակտերիայից ստացվում է երկու, երկուսից՝ չորս, չորսից՝ ութ և այլն... Նույնը ցանկացած վարակի տարածման դեպքում է։)

Երկրաչափական առաջընթացի ամենապարզ խնդիրները.

Սկսենք, ինչպես միշտ, մի պարզ խնդրից. Զուտ իմաստը հասկանալու համար։

1. Հայտնի է, որ երկրաչափական պրոգրեսիայի երկրորդ անդամը հավասար է 6-ի, իսկ հայտարարը՝ -0,5: Գտե՛ք առաջին, երրորդ և չորրորդ անդամները:

Այսպիսով, մեզ տրված է անվերջերկրաչափական պրոգրեսիա, բայց հայտնի երկրորդ ժամկետըայս առաջընթացը.

բ 2 = 6

Բացի այդ, մենք նաև գիտենք առաջընթացի հայտարար:

q = -0,5

Եվ դուք պետք է գտնեք առաջին, երրորդԵվ չորրորդայս առաջընթացի անդամները:

Այսպիսով, մենք գործում ենք: Հաջորդականությունը գրում ենք ըստ խնդրի պայմանների։ Ուղղակի ընդհանուր ձևով, որտեղ երկրորդ տերմինը վեց է.

բ 1, 6,բ 3 , բ 4 , …

Հիմա եկեք սկսենք փնտրել: Մենք սկսում ենք, ինչպես միշտ, ամենապարզից: Դուք կարող եք հաշվարկել, օրինակ, երրորդ տերմինը բ 3? Կարող է Դուք և ես արդեն գիտենք (ուղղակիորեն երկրաչափական պրոգրեսիայի իմաստով), որ երրորդ տերմինը (բ 3)ավելին, քան երկրորդը (բ 2 ) Վ «ք»մեկ անգամ!

Այսպիսով, մենք գրում ենք.

բ 3 =բ 2 · ք

Այս արտահայտության փոխարեն մենք փոխարինում ենք վեցը բ 2իսկ փոխարենը -0,5 քև մենք հաշվում ենք. Եվ մինուսն էլ չենք անտեսում, իհարկե...

b 3 = 6·(-0.5) = -3

Սրա նման։ Երրորդ ժամկետը բացասական է ստացվել. Զարմանալի չէ՝ մեր հայտարարը ք- բացասական. Եվ գումարածը մինուսով բազմապատկելը, իհարկե, կլինի մինուս:)

Այժմ մենք հաշվում ենք առաջընթացի հաջորդ՝ չորրորդ ժամկետը.

բ 4 =բ 3 · ք

b 4 = -3·(-0.5) = 1.5

Չորրորդ ժամկետը կրկին պլյուսով է։ Հինգերորդ անդամը կրկին կլինի մինուս, վեցերորդը կլինի գումարած և այլն: Նշանները հերթափոխ են։

Այսպիսով, գտնվեցին երրորդ և չորրորդ տերմինները։ Արդյունքը հետևյալ հաջորդականությունն է.

բ 1; 6; -3; 1,5; ...

Այժմ մնում է գտնել առաջին տերմինը բ 1ըստ հայտնի երկրորդի. Դա անելու համար մենք քայլում ենք մյուս ուղղությամբ՝ դեպի ձախ: Սա նշանակում է, որ այս դեպքում մեզ հարկավոր չէ առաջընթացի երկրորդ անդամը բազմապատկել հայտարարով, այլ. բաժանել.

Բաժանում ենք և ստանում.

Այսքանը:) Խնդրի պատասխանը կլինի հետևյալը.

-12; 6; -3; 1,5; …

Ինչպես տեսնում եք, լուծման սկզբունքը նույնն է, ինչ . Մենք գիտենք ցանկացածանդամ և հայտարարերկրաչափական պրոգրեսիա - մենք կարող ենք գտնել դրա ցանկացած այլ անդամ: Մենք կգտնենք մեր ուզածին:) Միակ տարբերությունն այն է, որ գումարումը/հանումը փոխարինվում է բազմապատկմամբ/բաժանմամբ:

Հիշեք. եթե մենք գիտենք երկրաչափական պրոգրեսիայի առնվազն մեկ անդամ և հայտարար, ապա մենք միշտ կարող ենք գտնել այս պրոգրեսիայի որևէ այլ անդամ:

Հետևյալ խնդիրը, ըստ ավանդույթի, OGE-ի իրական տարբերակից է.

2.

...; 150; X; 6; 1.2; ...

Այսպիսով, ինչպես է դա: Այս անգամ չկա առաջին տերմին, չկա հայտարար ք, պարզապես տրված է թվերի հաջորդականություն... Արդեն ծանոթ բան, չէ՞։ Այո՛ Նմանատիպ խնդիր արդեն լուծվել է թվաբանական պրոգրեսիայով։

Այսպիսով, մենք չենք վախենում: Ամեն ինչ նույնն է։ Եկեք շրջվենք մեր գլխի վրա և հիշենք երկրաչափական առաջընթացի տարրական իմաստը: Մենք ուշադիր նայում ենք մեր հաջորդականությանը և պարզում, թե երեք հիմնականների երկրաչափական առաջընթացի որ պարամետրերն են թաքնված (առաջին անդամ, հայտարար, անդամի համար):

Անդամների համարներ? Անդամության համարներ չկան, այո... Բայց չորսն են հաջորդականթվեր։ Ես որևէ իմաստ չեմ տեսնում բացատրելու, թե ինչ է նշանակում այս բառը այս փուլում:) Երկուսն են հարևան հայտնի թվեր.Կերե՛ք Սրանք 6 և 1.2 են: Այսպիսով, մենք կարող ենք գտնել առաջընթացի հայտարար.Այսպիսով վերցնում ենք 1.2 թիվը և բաժանում նախորդ համարին։Դեպի վեց.

Մենք ստանում ենք.

Մենք ստանում ենք.

x= 150·0,2 = 30

Պատասխան. x = 30 .

Ինչպես տեսնում եք, ամեն ինչ բավականին պարզ է. Հիմնական դժվարությունը միայն հաշվարկների մեջ է։ Հատկապես դժվար է բացասական և կոտորակային հայտարարների դեպքում։ Այսպիսով, ովքեր խնդիրներ ունեն, կրկնեք թվաբանությունը: Ինչպես աշխատել կոտորակների հետ, ինչպես աշխատել բացասական թվերի հետ և այլն... Թե չէ այստեղ անխնա կդանդաղեցնեք։

Հիմա եկեք մի փոքր փոփոխենք խնդիրը։ Այժմ այն ​​հետաքրքիր է դառնալու: Նրանից հանենք վերջին 1.2 թիվը։ Հիմա եկեք լուծենք այս խնդիրը.

3. Երկրաչափական պրոգրեսիայի մի քանի հաջորդական անդամներ դուրս են գրվում.

...; 150; X; 6; ...

Գտե՛ք x տառով նշված առաջընթացի տերմինը:

Ամեն ինչ նույնն է, միայն երկու կից հայտնիՄենք այժմ պրոգրեսիայի անդամ չունենք: Սա է հիմնական խնդիրը։ Քանի որ մեծությունը քերկու հարևան տերմինների միջոցով մենք կարող ենք հեշտությամբ որոշել մենք չենք կարող։Մենք հնարավորություն ունե՞նք հաղթահարել առաջադրանքը: Անշուշտ։

Եկեք գրենք անհայտ տերմինը» x«ուղղակիորեն երկրաչափական պրոգրեսիայի իմաստով! Ընդհանրապես.

Այո այո! Ճիշտ անհայտ հայտարարով:

Մի կողմից, X-ի համար կարող ենք գրել հետևյալ հարաբերակցությունը.

x= 150 ·ք

Մյուս կողմից, մենք բոլոր իրավունքներն ունենք այս նույն X-ի միջոցով նկարագրելու հաջորդանդամ, միջոցով վեց! Վեցը բաժանեք հայտարարի վրա:

Սրա նման:

x = 6/ ք

Ակնհայտ է, որ այժմ մենք կարող ենք նույնացնել այս երկու գործակիցները: Քանի որ մենք արտահայտում ենք նույնըմեծություն (x), բայց երկու տարբեր ճանապարհներ։

Մենք ստանում ենք հավասարումը.

Ամեն ինչ բազմապատկելով ք, պարզեցնելով և կրճատելով՝ ստանում ենք հավասարումը.

q2 = 1/25

Մենք լուծում և ստանում ենք.

q = ±1/5 = ±0.2

Վա՜յ Հայտարարը կրկնակի է ստացվել։ +0.2 և -0.2: Իսկ ո՞ր մեկն ընտրել։ Փակուղի?

Հանգիստ. Այո, խնդիրն իսկապես կա երկու լուծում!Դրանում ոչ մի վատ բան չկա: Պատահում է։) Չե՞ք զարմանում, երբ, օրինակ, սովորական խնդիրը լուծելիս երկու արմատ եք ստանում։ Այստեղ նույն պատմությունն է։)

Համար q = +0.2մենք կստանանք.

X = 150 0,2 = 30

Եվ համար ք = -0,2 կամք:

X = 150 · (-0.2) = -30

Մենք ստանում ենք կրկնակի պատասխան. x = 30; x = -30.

Ի՞նչ է նշանակում այս հետաքրքիր փաստը։ Եվ այն, ինչ կա երկու առաջընթաց, բավարարելով խնդրի պայմանները։

Այսպիսիների նման.

…; 150; 30; 6; …

…; 150; -30; 6; …

Երկուսն էլ հարմար են:) Ինչու՞ եք կարծում, որ մենք պատասխանների մեջ բաժանվեցինք: Պարզապես պրոգրեսիայի կոնկրետ անդամի (1,2) վերացման պատճառով, որը գալիս է վեցից հետո։ Եվ իմանալով միայն երկրաչափական պրոգրեսիայի նախորդ (n-1)-րդ և հաջորդ (n+1) անդամները, մենք այլևս չենք կարող միանշանակ որևէ բան ասել նրանց միջև եղած n-րդ անդամի մասին։ Երկու տարբերակ կա՝ պլյուսով և մինուսով:

Բայց խնդիր չկա: Որպես կանոն, երկրաչափական պրոգրեսիայի առաջադրանքներում կա լրացուցիչ տեղեկատվություն, որը տալիս է միանշանակ պատասխան։ Ասենք բառերը. «փոխարինվող առաջընթաց»կամ «դրական հայտարարով առաջընթաց».և այլն... Հենց այս բառերը պետք է մատնանշեն, թե վերջնական պատասխանը պատրաստելիս որ նշանը, գումարած կամ մինուս, պետք է ընտրել։ Եթե ​​նման տեղեկություն չկա, ապա այո, առաջադրանքը կունենա երկու լուծում.)

Հիմա մենք ինքներս ենք որոշում.

4. Որոշեք, թե արդյոք 20 թիվը երկրաչափական պրոգրեսիայի անդամ է.

4 ; 6; 9; …

5. Տրված է փոփոխական երկրաչափական առաջընթացի նշանը.

…; 5; x ; 45; …

Գտե՛ք տառով նշված առաջընթացի տերմինը x .

6. Գտե՛ք երկրաչափական պրոգրեսիայի չորրորդ դրական անդամը.

625; -250; 100; …

7. Երկրաչափական պրոգրեսիայի երկրորդ անդամը հավասար է -360-ի, իսկ հինգերորդ անդամը հավասար է 23,04-ի: Գտեք այս առաջընթացի առաջին անդամը:

Պատասխաններ (անկարգության դեպքում) -15; 900; Ոչ; 2.56.

Շնորհավորում եմ, եթե ամեն ինչ ստացվեց:

Ինչ-որ բան չի՞ տեղավորվում: Ինչ-որ տեղ կրկնակի պատասխան կար. Ուշադիր կարդացեք առաջադրանքի պայմանները:

Վերջին խնդիրը չի՞ ստացվում։ Այնտեղ բարդ բան չկա։) Մենք աշխատում ենք ուղղակիորեն ըստ երկրաչափական պրոգրեսիայի իմաստի։ Դե, դուք կարող եք նկարել: Օգնում է։)

Ինչպես տեսնում եք, ամեն ինչ տարրական է։ Եթե ​​առաջընթացը կարճ է. Իսկ եթե երկար է: Թե՞ պահանջվող անդամի թիվը շատ մեծ է։ Ես կցանկանայի, թվաբանական առաջընթացի համեմատությամբ, ինչ-որ կերպ ստանալ հարմար բանաձև, որը հեշտացնում է գտնելը ցանկացածցանկացած երկրաչափական առաջընթացի տերմին իր համարով։Առանց շատ ու շատ անգամներ բազմապատկելու ք. Եվ կա այդպիսի բանաձև։) Մանրամասները՝ հաջորդ դասում։

Դաս և ներկայացում «Թվերի հաջորդականություններ. Երկրաչափական առաջընթաց» թեմայով.

Լրացուցիչ նյութեր
Հարգելի օգտատերեր, մի մոռացեք թողնել ձեր մեկնաբանությունները, ակնարկները, ցանկությունները: Բոլոր նյութերը ստուգվել են հակավիրուսային ծրագրով։

Ուսումնական միջոցներ և սիմուլյատորներ Ինտեգրալ առցանց խանութում 9-րդ դասարանի համար
Ուժեր և արմատներ Գործառույթներ և գրաֆիկներ

Տղերք, այսօր մենք կծանոթանանք պրոգրեսիայի մեկ այլ տեսակի հետ։
Այսօրվա դասի թեման երկրաչափական առաջընթացն է:

Երկրաչափական առաջընթաց

Սահմանում. Թվային հաջորդականությունը, որտեղ յուրաքանչյուր անդամ, սկսած երկրորդից, հավասար է նախորդի և որոշ ֆիքսված թվի արտադրյալին, կոչվում է երկրաչափական պրոգրեսիա։
Եկեք սահմանենք մեր հաջորդականությունը ռեկուրսիվ՝ $b_(1)=b$, $b_(n)=b_(n-1)*q$,
որտեղ b և q որոշակի թվեր են: q թիվը կոչվում է պրոգրեսիայի հայտարար։

Օրինակ։ 1,2,4,8,16... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է մեկի, իսկ $q=2$։

Օրինակ։ 8,8,8,8... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է ութի,
և $q=1$.

Օրինակ։ 3,-3,3,-3,3... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է երեքի,
և $q=-1$.

Երկրաչափական պրոգրեսիան ունի միապաղաղության հատկություններ։
Եթե ​​$b_(1)>0$, $q>1$,
ապա հաջորդականությունը մեծանում է:
Եթե ​​$b_(1)>0$, $0 Հերթականությունը սովորաբար նշվում է $b_(1), b_(2), b_(3), ..., b_(n), ...$:

Ինչպես թվաբանական պրոգրեսիայում, եթե երկրաչափական պրոգրեսիայում տարրերի թիվը վերջավոր է, ապա պրոգրեսիան կոչվում է վերջավոր երկրաչափական պրոգրեսիա։

$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$:
Նկատի ունեցեք, որ եթե հաջորդականությունը երկրաչափական պրոգրեսիա է, ապա տերմինների քառակուսիների հաջորդականությունը նույնպես երկրաչափական պրոգրեսիա է։ Երկրորդ հաջորդականում առաջին անդամը հավասար է $b_(1)^2$-ի, իսկ հայտարարը հավասար է $q^2$-ի։

Երկրաչափական պրոգրեսիայի n-րդ անդամի բանաձևը

Երկրաչափական պրոգրեսիան կարող է սահմանվել նաև վերլուծական ձևով: Տեսնենք, թե ինչպես դա անել.
$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$:
$b_(4)=b_(3)*q=b_(1)*q^3$:
$b_(5)=b_(4)*q=b_(1)*q^4$:
Մենք հեշտությամբ նկատում ենք օրինակը՝ $b_(n)=b_(1)*q^(n-1)$:
Մեր բանաձեւը կոչվում է «երկրաչափական պրոգրեսիայի n-րդ անդամի բանաձեւ»։

Վերադառնանք մեր օրինակներին։

Օրինակ։ 1,2,4,8,16... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է մեկի,
և $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$:

Օրինակ։ 16,8,4,2,1,1/2… Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է տասնվեցի, իսկ $q=\frac(1)(2)$:
$b_(n)=16*(\frac(1)(2))^(n-1)$:

Օրինակ։ 8,8,8,8... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է ութի, իսկ $q=1$։
$b_(n)=8*1^(n-1)=8$:

Օրինակ։ 3,-3,3,-3,3... Երկրաչափական պրոգրեսիա, որի առաջին անդամը հավասար է երեքի, իսկ $q=-1$:
$b_(n)=3*(-1)^(n-1)$:

Օրինակ։ Տրված է երկրաչափական պրոգրեսիա $b_(1), b_(2), …, b_(n), … $:
ա) Հայտնի է, որ $b_(1)=6, q=3$: Գտեք $b_(5)$:
բ) Հայտնի է, որ $b_(1)=6, q=2, b_(n)=768$: Գտեք n.
գ) Հայտնի է, որ $q=-2, b_(6)=96$: Գտեք $b_(1)$:
դ) Հայտնի է, որ $b_(1)=-2, b_(12)=4096$: Գտեք ք.

Լուծում.
ա) $b_(5)=b_(1)*q^4=6*3^4=486$:
բ) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$:
$2^(n-1)=\frac(768)(6)=128$, քանի որ $2^7=128 => n-1=7; n=8$.
գ) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$:
դ) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.

Օրինակ։ Երկրաչափական պրոգրեսիայի յոթերորդ և հինգերորդ անդամների տարբերությունը 192 է, առաջընթացի հինգերորդ և վեցերորդ անդամների գումարը 192 է։ Գտե՛ք այս պրոգրեսիայի տասներորդ անդամը։

Լուծում.
Մենք գիտենք, որ $b_(7)-b_(5)=192$ և $b_(5)+b_(6)=192$:
Մենք նաև գիտենք՝ $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Ապա.
$b_(1)*q^6-b_(1)*q^4=192$:
$b_(1)*q^4+b_(1)*q^5=192$:
Մենք ստացել ենք հավասարումների համակարգ.
$\սկիզբ(դեպքեր)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\վերջ(դեպքեր)$:
Հավասարեցնելով մեր հավասարումները՝ ստանում ենք.
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Ստացանք երկու լուծում q՝ $q_(1)=2, q_(2)=-1$:
Հաջորդաբար փոխարինեք երկրորդ հավասարման մեջ.
$b_(1)*2^4*3=192 => b_(1)=4$:
$b_(1)*(-1)^4*0=192 =>$ լուծումներ չկան:
Մենք ստացանք, որ $b_(1)=4, q=2$:
Գտնենք տասներորդ անդամը՝ $b_(10)=b_(1)*q^9=4*2^9=2048$։

Վերջավոր երկրաչափական պրոգրեսիայի գումարը

Եկեք ունենանք վերջավոր երկրաչափական պրոգրեսիա: Եկեք, ինչպես թվաբանական պրոգրեսիայի դեպքում, հաշվարկենք նրա անդամների գումարը։

Թող տրվի վերջավոր երկրաչափական պրոգրեսիա՝ $b_(1),b_(2),…,b_(n-1),b_(n)$:
Ներկայացնենք դրա տերմինների գումարի նշանակումը՝ $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$:
Այն դեպքում, երբ $q=1$. Երկրաչափական պրոգրեսիայի բոլոր անդամները հավասար են առաջին անդամին, ապա ակնհայտ է, որ $S_(n)=n*b_(1)$։
Այժմ դիտարկենք $q≠1$ դեպքը։
Վերը նշված գումարը բազմապատկենք q-ով։
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$:
Նշում:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$:
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$:

$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2 )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$:

$S_(n)(q-1)=b_(n)*q-b_(1)$:

$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.

$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$:

Մենք ստացել ենք վերջավոր երկրաչափական պրոգրեսիայի գումարի բանաձևը.

Օրինակ։
Գտե՛ք երկրաչափական պրոգրեսիայի առաջին յոթ անդամների գումարը, որի առաջին անդամը 4 է, իսկ հայտարարը՝ 3։

Լուծում.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$:

Օրինակ։
Գտե՛ք հայտնի երկրաչափական պրոգրեսիայի հինգերորդ անդամը՝ $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$:

Լուծում.
$b_(n)=(-3)*q^(n-1)=-3072$:
$q^(n-1)=1024$։
$q^(n)=1024q$.

$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$:
$-4095(q-1)=-3*(q^(n)-1)$:
$-4095(q-1)=-3*(1024q-1)$:
$1365q-1365=1024q-1$.
$341q=$1364.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$։

Երկրաչափական պրոգրեսիայի բնորոշ հատկություն

Տղերք, տրված է երկրաչափական պրոգրեսիա։ Դիտարկենք նրա երեք հաջորդական անդամները՝ $b_(n-1),b_(n),b_(n+1)$:
Մենք գիտենք, որ.
$\frac(b_(n))(q)=b_(n-1)$:
$b_(n)*q=b_(n+1)$.
Ապա.
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$:
Եթե ​​առաջընթացը վերջավոր է, ապա այս հավասարությունը գործում է բոլոր անդամների համար, բացի առաջինից և վերջինից:
Եթե ​​նախապես հայտնի չէ, թե ինչ ձև ունի հաջորդականությունը, բայց հայտնի է, որ $b_(n)^(2)=b_(n-1)*b_(n+1)$։
Ապա մենք կարող ենք վստահորեն ասել, որ սա երկրաչափական առաջընթաց է:

Թվերի հաջորդականությունը երկրաչափական պրոգրեսիա է միայն այն դեպքում, երբ յուրաքանչյուր անդամի քառակուսին հավասար է առաջընթացի երկու հարակից անդամների արտադրյալին: Մի մոռացեք, որ վերջավոր առաջընթացի համար այս պայմանը չի բավարարվում առաջին և վերջին տերմինների համար:

Դիտարկենք այս ինքնությունը՝ $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$:
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$-ը կոչվում է a և b թվերի երկրաչափական միջին։

Երկրաչափական պրոգրեսիայի ցանկացած անդամի մոդուլը հավասար է նրա երկու հարևան անդամների երկրաչափական միջինին:

Օրինակ։
Գտեք x այնպես, որ $x+2; 2x+2; 3x+3$-ը երկրաչափական պրոգրեսիայի երեք հաջորդական անդամներ էին:

Լուծում.
Եկեք օգտագործենք բնորոշ հատկությունը.
$(2x+2)^2=(x+2)(3x+3)$:
$4x^2+8x+4=3x^2+3x+6x+6$:
$x^2-x-2=0$.
$x_(1)=2$ և $x_(2)=-1$:
Եկեք հաջորդաբար փոխարինենք մեր լուծումները սկզբնական արտահայտության մեջ.
$x=2$-ով ստացանք հաջորդականությունը՝ 4;6;9 – $q=1,5$-ով երկրաչափական պրոգրեսիա:
$x=-1$-ի համար ստանում ենք հաջորդականությունը՝ 1;0;0:
Պատասխան՝ $x=2.$

Ինքնուրույն լուծելու խնդիրներ

1. Գտե՛ք երկրաչափական պրոգրեսիայի ութերորդ առաջին անդամը 16;-8;4;-2…:
2. Գտի՛ր 11,22,44 երկրաչափական պրոգրեսիայի տասներորդ անդամը:
3. Հայտնի է, որ $b_(1)=5, q=3$: Գտեք $b_(7)$:
4. Հայտնի է, որ $b_(1)=8, q=-2, b_(n)=512$: Գտեք n.
5. Գտե՛ք երկրաչափական պրոգրեսիայի առաջին 11 անդամների գումարը 3;12;48…:
6. Գտեք x այնպես, որ $3x+4; 2x+4; x+5$-ը երկրաչափական պրոգրեսիայի երեք հաջորդական անդամներ են:

Երկրաչափական առաջընթացի օրինակ: 2, 6, 18, 54, 162.

Այստեղ առաջինից հետո յուրաքանչյուր տերմին 3 անգամ մեծ է նախորդից։ Այսինքն՝ յուրաքանչյուր հաջորդ անդամը նախորդ անդամը 3-ով բազմապատկելու արդյունք է.

2 · 3 = 6

6 3 = 18

18 3 = 54

54 3 = 162 .

Մեր օրինակում երկրորդ անդամը առաջինի, երրորդը երկրորդի և այլնի վրա բաժանելիս։ ստանում ենք 3. 3 թիվը այս երկրաչափական պրոգրեսիայի հայտարարն է:

Օրինակ:

Վերադառնանք մեր երկրաչափական առաջընթացին՝ 2, 6, 18, 54, 162: Վերցնենք չորրորդ անդամը և քառակուսի դարձնենք այն.
54 2 = 2916.

Այժմ եկեք բազմապատկենք 54 թվի ձախ և աջ եզրերը.

18 162 = 2916։

Ինչպես տեսնում ենք, երրորդ անդամի քառակուսին հավասար է հարակից երկրորդ և չորրորդ անդամների արտադրյալին։

Օրինակ 1Վերցնենք որոշակի երկրաչափական պրոգրեսիա, որտեղ առաջին անդամը հավասար է 2-ի, իսկ երկրաչափական պրոգրեսիայի հայտարարը հավասար է 1,5-ի։ Պետք է գտնել այս առաջընթացի 4-րդ տերմինը։

Տրված է.
բ 1 = 2

ք = 1,5
n = 4

————
բ 4 - ?

Լուծում.

Կիրառեք բանաձևը b n= բ 1 · ք n- 1, դրա մեջ տեղադրելով համապատասխան արժեքները.
բ 4 = 2 1,5 4 - 1 = 2 1,5 3 = 2 3,375 = 6,75:

ՊատասխանելՏրված երկրաչափական առաջընթացի չորրորդ անդամը 6.75 թիվն է:

Օրինակ 2Գտե՛ք երկրաչափական պրոգրեսիայի հինգերորդ անդամը, եթե առաջին և երրորդ անդամները հավասար են համապատասխանաբար 12-ի և 192-ի:

Տրված է.
բ 1 = 12
բ 3 = 192
————
բ 5 - ?

Լուծում.

1) Նախ պետք է գտնել երկրաչափական պրոգրեսիայի հայտարարը, առանց որի հնարավոր չէ լուծել խնդիրը: Որպես առաջին քայլ, օգտագործելով մեր բանաձևը, մենք ստանում ենք b 3-ի բանաձևը.

բ 3 = b 1 q 3 - 1 = b 1 q 2

Այժմ մենք կարող ենք գտնել երկրաչափական պրոգրեսիայի հայտարարը.

բ 3 192
ք 2 = —— = —— = 16
բ 1 12

ք= √16 = 4 կամ -4:

2) Մնում է գտնել արժեքը բ 5 .
Եթե ք= 4, ապա

բ 5 = բ 1 q 5-1 = 12 4 4 = 12 256 = 3072:

ժամը ք= -4 արդյունքը կլինի նույնը: Այսպիսով, խնդիրն ունի մեկ լուծում.

ՊատասխանելՏվյալ երկրաչափական առաջընթացի հինգերորդ անդամը 3072 թիվն է։

ՕրինակԳտե՛ք երկրաչափական պրոգրեսիայի առաջին հինգ անդամների գումարը ( b n), որում առաջին անդամը 2 է, իսկ երկրաչափական պրոգրեսիայի հայտարարը՝ 3։

Տրված է.

բ 1 = 2

ք = 3

n = 5
————
Ս 5 - ?

Լուծում.

Մենք կիրառում ենք վերը նշված երկու բանաձևը.

բ 1 (ք 5 - 1) 2 (3 5 - 1) 2 (243 - 1) 484
Ս 5 = ————— = ————— = ———————— = ————— = 242
ք - 1 3 - 1 2 2

ՊատասխանելՏրված երկրաչափական պրոգրեսիայի առաջին հինգ անդամների գումարը 242 է:

Անսահման երկրաչափական պրոգրեսիայի գումարը:

Անհրաժեշտ է տարբերակել «անսահման երկրաչափական պրոգրեսիայի գումար» և «գումար nերկրաչափական պրոգրեսիայի անդամներ»։ Երկրորդ հայեցակարգը վերաբերում է ցանկացած երկրաչափական պրոգրեսիայի, իսկ առաջինը՝ միայն մեկին, որտեղ հայտարարը բացարձակ արժեքով 1-ից փոքր է:

Մաթեմատիկան ինչ էմարդիկ վերահսկում են բնությունը և իրենց:

Խորհրդային մաթեմատիկոս, ակադեմիկոս Ա.Ն. Կոլմոգորովը

Երկրաչափական առաջընթաց.

Թվաբանական պրոգրեսիաների խնդիրների հետ մեկտեղ մաթեմատիկայի ընդունելության քննությունների ժամանակ տարածված են նաև երկրաչափական պրոգրեսիա հասկացության հետ կապված խնդիրները։ Նման խնդիրները հաջողությամբ լուծելու համար դուք պետք է իմանաք երկրաչափական պրոգրեսիաների հատկությունները և ունենաք դրանք օգտագործելու լավ հմտություններ:

Այս հոդվածը նվիրված է երկրաչափական պրոգրեսիայի հիմնական հատկությունների ներկայացմանը: Այստեղ ներկայացված են նաև տիպիկ խնդիրների լուծման օրինակներ։, փոխառված մաթեմատիկայի ընդունելության քննությունների առաջադրանքներից։

Եկեք նախ նշենք երկրաչափական առաջընթացի հիմնական հատկությունները և հիշենք ամենակարևոր բանաձևերն ու պնդումները., կապված այս հայեցակարգի հետ։

Սահմանում.Թվերի հաջորդականությունը կոչվում է երկրաչափական պրոգրեսիա, եթե յուրաքանչյուր թիվ, սկսած երկրորդից, հավասար է նախորդին՝ բազմապատկված նույն թվով։ Թիվը կոչվում է երկրաչափական պրոգրեսիայի հայտարար։

Երկրաչափական առաջընթացի համարբանաձևերը վավեր են

, (1)

Որտեղ. Բանաձև (1) կոչվում է երկրաչափական պրոգրեսիայի ընդհանուր անդամի բանաձև, իսկ բանաձևը (2) ներկայացնում է երկրաչափական պրոգրեսիայի հիմնական հատկությունը. պրոգրեսիայի յուրաքանչյուր անդամ համընկնում է իր հարևան տերմինների երկրաչափական միջինին և .

Նշում, որ հենց այս հատկության պատճառով է, որ խնդրո առարկա առաջընթացը կոչվում է «երկրաչափական»:

Վերոնշյալ (1) և (2) բանաձևերը ընդհանրացված են հետևյալ կերպ.

, (3)

Գումարը հաշվարկելու համարառաջին երկրաչափական պրոգրեսիայի անդամներբանաձևը կիրառվում է

Եթե ​​մենք նշում ենք, ապա

Որտեղ. Քանի որ , բանաձևը (6) (5) բանաձևի ընդհանրացումն է։

Այն դեպքում, երբ և երկրաչափական առաջընթացանսահման նվազում է. Գումարը հաշվարկելու համարԱնսահման նվազող երկրաչափական պրոգրեսիայի բոլոր տերմինների համար օգտագործվում է բանաձևը

. (7)

Օրինակ , օգտագործելով (7) բանաձևը կարող ենք ցույց տալ, Ինչ

Որտեղ. Այս հավասարությունները ստացվում են (7) բանաձևից՝ , (առաջին հավասարություն) և , (երկրորդ հավասարություն) պայմանով։

Թեորեմ.Եթե, ապա

Ապացույց. Եթե, ապա

Թեորեմն ապացուցված է.

Եկեք անցնենք «Երկրաչափական առաջընթաց» թեմայով խնդիրների լուծման օրինակների դիտարկմանը:

Օրինակ 1.Տրված է՝ , և . Գտնել.

Լուծում.Եթե ​​կիրառենք (5) բանաձևը, ապա

Պատասխան.

Օրինակ 2.Թող այդպես լինի; թող դա լինի։ Գտնել.

Լուծում.Քանի որ և , մենք օգտագործում ենք (5), (6) բանաձևերը և ստանում հավասարումների համակարգ

Եթե ​​(9) համակարգի երկրորդ հավասարումը բաժանվի առաջինի վրա, ապա կամ . Այստեղից հետևում է, որ . Դիտարկենք երկու դեպք.

1. Եթե, ապա (9) համակարգի առաջին հավասարումից ունենք.

2. Եթե , ապա .

Օրինակ 3.Թող , և. Գտնել.

Լուծում.Բանաձևից (2) հետևում է, որ կամ. Այդ ժամանակվանից կամ .

Ըստ պայմանի. Այնուամենայնիվ, հետևաբար. Քանի որ և ապա այստեղ մենք ունենք հավասարումների համակարգ

Եթե ​​համակարգի երկրորդ հավասարումը բաժանվում է առաջինի վրա, ապա կամ .

Քանի որ հավասարումը ունի եզակի հարմար արմատ: Այս դեպքում դա բխում է համակարգի առաջին հավասարումից.

Հաշվի առնելով (7) բանաձևը, մենք ստանում ենք.

Պատասխան.

Օրինակ 4.Տրված է և . Գտնել.

Լուծում.Այդ ժամանակվանից։

Քանի որ, այն ժամանակ կամ

Համաձայն բանաձևի (2) մենք ունենք. Այս առումով հավասարությունից (10) մենք ստանում ենք կամ .

Այնուամենայնիվ, պայմանով, հետևաբար.

Օրինակ 5.Հայտնի է, որ. Գտնել.

Լուծում. Ըստ թեորեմի՝ ունենք երկու հավասարություն

Այդ ժամանակվանից կամ . Որովհետև, ուրեմն.

Պատասխան.

Օրինակ 6.Տրված է և . Գտնել.

Լուծում.Հաշվի առնելով (5) բանաձևը, մենք ստանում ենք

Այդ ժամանակվանից։ Քանի որ , և , այն ժամանակ .

Օրինակ 7.Թող այդպես լինի; թող դա լինի։ Գտնել.

Լուծում.Ըստ (1) բանաձևի կարող ենք գրել

Հետեւաբար, մենք ունենք կամ . Հայտնի է, որ և , հետևաբար և .

Պատասխան.

Օրինակ 8.Գտե՛ք անվերջ նվազող երկրաչափական պրոգրեսիայի հայտարարը, եթե

Եվ .

Լուծում. Բանաձևից (7) հետևում էԵվ . Այստեղից և խնդրի պայմաններից մենք ստանում ենք հավասարումների համակարգ

Եթե ​​համակարգի առաջին հավասարումը քառակուսի է, իսկ հետո ստացված հավասարումը բաժանեք երկրորդ հավասարման վրա, ապա մենք ստանում ենք

Կամ ։

Պատասխան.

Օրինակ 9.Գտեք բոլոր արժեքները, որոնց համար , , հաջորդականությունը երկրաչափական պրոգրեսիա է:

Լուծում.Թող , և. Համաձայն (2) բանաձևի, որը սահմանում է երկրաչափական պրոգրեսիայի հիմնական հատկությունը, մենք կարող ենք գրել կամ.

Այստեղից մենք ստանում ենք քառակուսի հավասարումը, որոնց արմատներն ենԵվ .

Եկեք ստուգենք՝ եթե, ապա , եւ ; եթե , ապա , եւ .

Առաջին դեպքում ունենքև , իսկ երկրորդում՝ և .

Պատասխան՝ , .

Օրինակ 10.Լուծե՛ք հավասարումը

, (11)

որտեղ և.

Լուծում. (11) հավասարման ձախ կողմը անսահման նվազող երկրաչափական պրոգրեսիայի գումարն է, որում և , ենթակա են՝ և .

Բանաձևից (7) հետևում է, Ինչ . Այս առումով, հավասարումը (11) ստանում է ձևկամ . Հարմար արմատ քառակուսային հավասարումն է

Պատասխան.

Օրինակ 11.Պ դրական թվերի հաջորդականությունկազմում է թվաբանական պրոգրեսիա, Ա - երկրաչափական առաջընթաց, ինչ կապ ունի . Գտնել.

Լուծում.Որովհետեւ թվաբանական հաջորդականություն, Դա (թվաբանական առաջընթացի հիմնական հատկությունը): Քանի որ, ապա կամ . Սա ենթադրում է, որ երկրաչափական պրոգրեսիան ունի ձև. Ըստ բանաձևի (2)Այնուհետև մենք գրում ենք դա:

ի վեր և, այնուհետև . Այս դեպքում արտահայտությունըընդունում է ձևը կամ . Պայմանով, այսպիսով հավասար.մենք ստանում ենք քննարկվող խնդրի յուրահատուկ լուծում, այսինքն. .

Պատասխան.

Օրինակ 12.Հաշվարկել գումարը

. (12)

Լուծում. Բազմապատկենք հավասարության երկու կողմերը (12) 5-ով և ստացենք

Եթե ​​ստացված արտահայտությունից հանենք (12)., Դա

կամ ։

Հաշվարկելու համար մենք արժեքները փոխարինում ենք (7) բանաձևով և ստանում: Այդ ժամանակվանից։

Պատասխան.

Այստեղ տրված խնդիրների լուծման օրինակները օգտակար կլինեն դիմորդներին ընդունելության քննություններին նախապատրաստվելիս։ Խնդիրների լուծման մեթոդների ավելի խորը ուսումնասիրության համար, կապված երկրաչափական առաջընթացի հետ, Դուք կարող եք օգտագործել ձեռնարկները առաջարկվող գրականության ցանկից:

1. Մաթեմատիկայի խնդիրների ժողովածու քոլեջների դիմորդների համար / Ed. Մ.Ի. Սկանավի. – M.: Mir and Education, 2013. – 608 p.

2. Սուպրուն Վ.Պ. Մաթեմատիկա ավագ դպրոցի աշակերտների համար. դպրոցական ծրագրի լրացուցիչ բաժիններ. – M.: Lenand / URSS, 2014. – 216 էջ.

3. Մեդինսկի Մ.Մ. Տարրական մաթեմատիկայի ամբողջական դասընթաց խնդիրներում և վարժություններում։ Գիրք 2. Թվերի հաջորդականություններ և առաջընթացներ. - Մ.: Էդիտուս, 2015. – 208 էջ.

Դեռ ունե՞ք հարցեր:

Կրկնուսույցից օգնություն ստանալու համար գրանցվեք։

կայքը, նյութը ամբողջությամբ կամ մասնակի պատճենելիս անհրաժեշտ է հղում աղբյուրին: