Սահմանի՛ր զուգահեռագիծը և ավարտի՛ր գծագիրը։ Զուգահեռագծի անկյունագծերի հատկությունը

1. Զուգահեռագծի սահմանում.

Եթե մի զույգ զուգահեռ ուղիղները հատենք մեկ այլ զույգ զուգահեռ ուղիղների հետ, ապա կստանանք քառանկյուն, որի հակառակ կողմերը զույգերով զուգահեռ են։

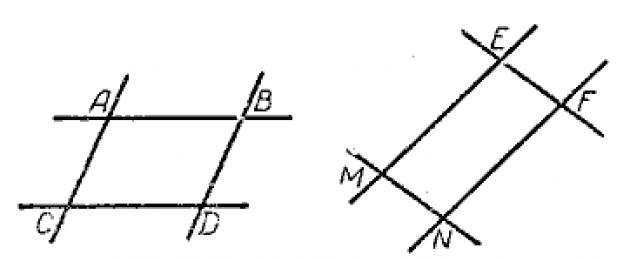
ABDC և EFNM քառանկյուններում (նկ. 224) ВD || AC և AB || CD;

EF || MN և EM || FN.

Այն քառանկյունը, որի հակառակ կողմերը զույգերով զուգահեռ են, կոչվում է զուգահեռագիծ:

2. Զուգահեռագծի հատկությունները.

Թեորեմ. Զուգահեռագծի անկյունագիծը այն բաժանում է երկու հավասար եռանկյունների։

Թող լինի ABDC զուգահեռագիծ (նկ. 225), որում AB || CD և AC || ՎԴ.

Դուք պետք է ապացուցեք, որ անկյունագիծը բաժանում է երկու հավասար եռանկյունների:

Եկեք գծենք CB անկյունագիծը ABDC զուգահեռագրում: Եկեք ապացուցենք, որ \(\Delta\)CAB = \(\Delta\)СДВ:

NE կողմը ընդհանուր է այս եռանկյունների համար. ∠ABC = ∠BCD, որպես ներքին խաչաձև անկյուններ զուգահեռ AB-ով և CD-ով և հատվածային CB-ով; ∠ACB = ∠СВD, ինչպես նաև ներքին խաչաձև անկյուններ զուգահեռ AC և BD և secant CB-ով:

Ուստի \(\Delta\)CAB = \(\Delta\)СДВ:

Նույն կերպ կարելի է ապացուցել, որ AD անկյունագիծը զուգահեռագիծը կբաժանի երկու հավասար եռանկյունների ACD և ABD:

Հետեւանքները:

1 . Զուգահեռագծի հակառակ անկյունները հավասար են միմյանց:

∠A = ∠D, սա բխում է CAB և CDB եռանկյունների հավասարությունից:

Նմանապես, ∠C = ∠B:

2. Զուգահեռագծի հակառակ կողմերը հավասար են միմյանց:

AB = CD և AC = BD, քանի որ դրանք հավասար եռանկյունների կողմեր են և գտնվում են հակառակ կողմերում հավասար անկյուններ.

Թեորեմ 2. Զուգահեռագծի անկյունագծերը իրենց հատման կետում բաժանվում են կիսով չափ։

Թող BC և AD լինեն ABC զուգահեռագծի անկյունագծերը (նկ. 226): Եկեք ապացուցենք, որ AO = OD և CO = OB:

Դա անելու համար համեմատեք միմյանց հակառակ տեղակայված եռանկյունների մի քանի զույգ, օրինակ՝ \(\Delta\)AOB և \(\Delta\)COD:

Այս եռանկյուններում AB = CD, ինչպես զուգահեռագծի հակառակ կողմերը;

∠1 = ∠2, որպես ներքին անկյուններ, որոնք գտնվում են խաչաձև AB-ի և CD-ի հետ զուգահեռ և AD հատվածով;

∠3 = ∠4 նույն պատճառով, քանի որ AB || CD-ն ու SV-ն իրենց սեկանտներն են։

Հետևում է, որ \(\Delta\)AOB = \(\Delta\)СOD: Իսկ հավասար եռանկյունների մեջ հակառակ հավասար անկյուններ են հավասար կողմեր. Հետևաբար, AO = OD և CO = OB:

Թեորեմ 3. Զուգահեռագծի մի կողմին կից անկյունների գումարը հավասար է 180°.

ABCD զուգահեռագրում գծում ենք AC անկյունագիծը և ստանում երկու եռանկյուն ABC և ADC:

Եռանկյունները հավասար են, քանի որ ∠1 = ∠4, ∠2 = ∠3 (զուգահեռ գծերի խաչաձև անկյունները), իսկ AC կողմը ընդհանուր է:
\(\Delta\)ABC = \(\Delta\)ADC հավասարությունից հետևում է, որ AB = CD, BC = AD, ∠B = ∠D:

Մի կողմին կից անկյունների գումարը, օրինակ՝ A և D անկյունները, հավասար է 180°-ի, որպես զուգահեռ ուղիղների միակողմանի:

«Ստացեք A» վիդեո դասընթացը ներառում է ձեզ անհրաժեշտ բոլոր թեմաները հաջող ավարտՄիասնական պետական քննություն մաթեմատիկայից 60-65 միավորով. Ամբողջովին բոլոր խնդիրները 1-13 Պրոֆիլ միասնական պետական քննությունՄաթեմատիկա։ Հարմար է նաև մաթեմատիկայի հիմնական միասնական պետական քննություն հանձնելու համար: Եթե ցանկանում եք միասնական պետական քննություն հանձնել 90-100 միավորով, ապա պետք է 1-ին մասը լուծեք 30 րոպեում և առանց սխալների։

Պետական միասնական քննության նախապատրաստական դասընթաց 10-11-րդ դասարանների, ինչպես նաև ուսուցիչների համար։ Այն ամենը, ինչ անհրաժեշտ է մաթեմատիկայի միասնական պետական քննության 1-ին մասի (առաջին 12 խնդիրների) և 13-րդ (եռանկյունաչափության) առաջադրանքները լուծելու համար: Իսկ սա միասնական պետական քննության 70 միավորից ավելին է, և ոչ 100 բալանոց ուսանողը, ոչ հումանիտար առարկան առանց դրանց չեն կարող։

Բոլոր անհրաժեշտ տեսությունը. Արագ ուղիներլուծումներ, ծուղակներ և միասնական պետական քննության գաղտնիքները. FIPI Task Bank-ի 1-ին մասի բոլոր ընթացիկ առաջադրանքները վերլուծվել են: Դասընթացը լիովին համապատասխանում է 2018 թվականի միասնական պետական քննության պահանջներին։

Դասընթացը պարունակում է 5 մեծ թեմա՝ յուրաքանչյուրը 2,5 ժամ: Յուրաքանչյուր թեմա տրված է զրոյից, պարզ ու հստակ։

Հարյուրավոր միասնական պետական քննության առաջադրանքներ. Բառային խնդիրներև հավանականությունների տեսությունը։ Պարզ և հեշտ հիշվող ալգորիթմներ խնդիրների լուծման համար: Երկրաչափություն. տեսություն, տեղեկատու նյութ, բոլոր տեսակի միասնական պետական քննական առաջադրանքների վերլուծություն. Ստերեոմետրիա. Բարդ լուծումներ, օգտակար խաբեբա թերթիկներ, տարածական երևակայության զարգացում: Եռանկյունաչափությունը զրոյից մինչև խնդիր 13. Խճճվելու փոխարեն հասկացողություն: Տեսողական բացատրություն բարդ հասկացություններ. Հանրահաշիվ. Արմատներ, հզորություններ և լոգարիթմներ, ֆունկցիա և ածանցյալ: Պետական միասնական քննության 2-րդ մասի բարդ խնդիրների լուծման հիմք.

Քաղաքապետարանի բյուջեն ուսումնական հաստատություն

Սավինսկայայի միջնակարգ դպրոց

Հետազոտություն

Զուգահեռագիծը և նրա նոր հատկությունները

Ավարտեց՝ 8Բ դասարանի աշակերտ

MBOU Սավինսկայայի միջնակարգ դպրոց

Կուզնեցովա Սվետլանա, 14 տարեկան

Ղեկավար՝ մաթեմատիկայի ուսուցիչ

Տուլչևսկայա Ն.Ա.

էջ Savino

Իվանովոյի մարզ, Ռուսաստան

2016թ

Ի. Ներածություն _________________________________________________ էջ 3

II. Զուգահեռագծի պատմությունից _________________________________ էջ 4

III Զուգահեռագծի լրացուցիչ հատկություններ ________________________________էջ 4

IV. Հատկությունների ապացույց _________________________________ էջ 5

Վ. Խնդիրների լուծում՝ օգտագործելով լրացուցիչ հատկություններ __________էջ 8

VI. Զուգահեռագծի հատկությունների կիրառումը կյանքում ___________________էջ 11

VII. Եզրակացություն _________________________________________________ էջ 12

VIII. Գրականություն _________________________________________________էջ 13

Ներածություն

"Հավասար մտքերի մեջ

ժամը այլ պայմանների հավասարություն

նա, ով գիտի երկրաչափություն, գերազանցում է»

(Բլեզ Պասկալ):

Երկրաչափության դասերին «Զուգահեռագիծ» թեման ուսումնասիրելիս դիտարկեցինք զուգահեռագծի երկու հատկություն և երեք հատկանիշ, բայց երբ սկսեցինք խնդիրներ լուծել, պարզվեց, որ դա բավարար չէ։

Ինձ մոտ հարց առաջացավ՝ զուգահեռագիծն այլ հատկություններ ունի՞, և ինչպե՞ս են դրանք օգնելու խնդիրների լուծմանը։

Եվ ես որոշեցի ուսումնասիրել զուգահեռագծի լրացուցիչ հատկությունները և ցույց տալ, թե ինչպես կարելի է դրանք կիրառել խնդիրները լուծելու համար:

Ուսումնասիրության առարկա : զուգահեռագիծ

Ուսումնասիրության օբյեկտ : զուգահեռագծի հատկությունները
Աշխատանքի նպատակը.

դպրոցում չուսումնասիրված զուգահեռագծի լրացուցիչ հատկությունների ձևակերպում և ապացուցում.

այս հատկությունների կիրառումը խնդիրների լուծման համար:

Առաջադրանքներ.

Ուսումնասիրել զուգահեռագծի արտաքին տեսքի պատմությունը և նրա հատկությունների զարգացման պատմությունը.

Գտեք հետագա ընթերցումուսումնասիրվող հարցի վերաբերյալ;

Ուսումնասիրել զուգահեռագծի լրացուցիչ հատկությունները և ապացուցել դրանք.

Ցույց տալ այս հատկությունների կիրառումը խնդիրների լուծման համար.

Դիտարկենք զուգահեռագծի հատկությունների կիրառումը կյանքում:
Հետազոտության մեթոդներ.

Ուսումնական և գիտահանրամատչելի գրականության, ինտերնետային ռեսուրսների հետ աշխատանք;

Տեսական նյութի ուսումնասիրություն;

Մի շարք խնդիրների բացահայտում, որոնք հնարավոր է լուծել զուգահեռագծի լրացուցիչ հատկությունների միջոցով.

Դիտարկում, համեմատություն, վերլուծություն, անալոգիա:

Ուսումնասիրության տեւողությունը 3 ամիս՝ հունվար-մարտ 2016թ

Երկրաչափության դասագրքում մենք կարդում ենք զուգահեռագծի հետևյալ սահմանումը. Զուգահեռագիծը այն քառանկյունն է, որի հակառակ կողմերը զույգերով զուգահեռ են:

«Զուգահեռագիծ» բառը թարգմանվում է որպես «զուգահեռ ուղիղներ» (հունարեն Parallelos - զուգահեռ և gramme - ուղիղ բառերից), այս տերմինը ներմուծել է Էվկլիդեսը։ Իր «Էլեմենտներ» գրքում Էվկլիդեսն ապացուցեց զուգահեռագծի հետևյալ հատկությունները՝ զուգահեռագծի հակառակ կողմերն ու անկյունները հավասար են, իսկ անկյունագիծը կիսում է այն։ Էվկլիդեսը չի նշում զուգահեռագծի հատման կետը։ Միայն միջնադարի վերջում զարգացավ զուգահեռագրությունների ամբողջական տեսությունը, և միայն 17-րդ դարում դասագրքերում հայտնվեցին զուգահեռագրերի թեորեմներ, որոնք ապացուցված են Էվկլիդեսի թեորեմի օգնությամբ:

III Զուգահեռագծի լրացուցիչ հատկությունները

Երկրաչափության դասագրքում տրված է զուգահեռագծի միայն 2 հատկություն.

Հակառակ անկյուններն ու կողմերը հավասար են

Զուգահեռագծի անկյունագծերը հատվում են և հատվում են հատման կետով:

Երկրաչափության տարբեր աղբյուրներում կարող եք գտնել հետևյալ լրացուցիչ հատկությունները.

Զուգահեռագծի հարակից անկյունների գումարը 180 0 է

Զուգահեռագծի անկյան կիսորդը կտրվում է դրանից հավասարաչափ եռանկյուն;

Զուգահեռագծի հակառակ անկյունների կիսադիրները գտնվում են զուգահեռ ուղիղների վրա.

Զուգահեռագծի հարակից անկյունների կիսադիրները հատվում են ուղիղ անկյան տակ.

Երբ զուգահեռագծի բոլոր անկյունների կիսադիրները հատվում են, նրանք կազմում են ուղղանկյուն;

Հեռավորությունները զուգահեռագծի հակառակ անկյուններից մինչև նույն անկյունագիծը հավասար են:

Եթե զուգահեռագծի հակառակ գագաթները միացնեք հակառակ կողմերի միջնակետերին, ապա կստանաք մեկ այլ զուգահեռագիծ:

Զուգահեռագծի անկյունագծերի քառակուսիների գումարը հավասար է նրա հարակից կողմերի քառակուսիների գումարի կրկնապատիկին:

Եթե զուգահեռագծի վրա երկու հակադիր անկյուններից գծեք բարձրություններ, ապա կստանաք ուղղանկյուն:

IV Զուգահեռագծի հատկությունների ապացույց

Զուգահեռագծի կից անկյունների գումարը 180 է 0

Տրված է:

ABCD - զուգահեռագիծ

Ապացուցել.

A+
B=

Ապացույց:

Ա և
B – BC զուգահեռ գծերով ներքին միակողմանի անկյուններ AD և հատված AB, ինչը նշանակում է
A+
B=

Տրված է.Ա Բ Գ Դ - զուգահեռագիծ,

AK բիսեկտոր
Ա.

Ապացուցել. AVK – հավասարաչափ

Ապացույց:

1)
1=
3 (խաչաձեւ ընկած մ.թ.ա AD և հատված AK),

2)
2=
3 քանի որ AK-ն կիսորդ է,

նշանակում է 1=
2.

3) ABC - հավասարաչափ, քանի որ եռանկյան 2 անկյունները հավասար են

. Զուգահեռագծի անկյան կիսորդը նրանից կտրում է հավասարաչափ եռանկյուն

Տրված է. ABCD-ն զուգահեռագիծ է,

AK – բիսեկտոր A,

CP - բիսեկտոր C.

Ապացուցել.ԱԿ ║ ՍՌ

Ապացույց:

1) 1=2 քանի որ AK-ն կիսորդ է

2) 4=5 քանի որ CP – բիսեկտոր

3) 3=1 (խաչաձեւ ընկած անկյունները ժամը

մ.թ.ա. ║ մ.թ. և AK-secant),

4) A =C (զուգահեռագծի հատկությամբ), որը նշանակում է 2=3=4=5։

4) 3-րդ և 4-րդ պարբերություններից հետևում է, որ 1 = 4, և այս անկյունները համապատասխանում են AK և CP ուղիղ գծերին և BC հատվածին,

սա նշանակում է AK ║ CP (հիմնված ուղիղների զուգահեռության վրա)

. Զուգահեռագծի հակառակ անկյունների կիսադիրները գտնվում են զուգահեռ ուղիղների վրա

Զուգահեռագծի հարակից անկյունների կիսադիրները հատվում են ուղիղ անկյան տակ

Տրված է. ABCD - զուգահեռագիծ,

AK-բիսեկտոր A,

DP բիսեկտոր Դ

Ապացուցել. DP Ա.Կ.

Ապացույց:

1) 1=2, քանի որ AK - բիսեկտոր

Թող 1=2=x, ապա A=2x,

2) 3=4, քանի որ D Р – բիսեկտոր

Թող 3=4=y, ապա D=2y

3) A + D =180 0, քանի որ զուգահեռագծի հարակից անկյունների գումարը 180 է

2) Հաշվի առեք A OD

1+3=90 0, ապա
<5=90 0 (сумма углов треугольников равна 180 0)

5. Զուգահեռագծի բոլոր անկյունների կիսադիրները հատվելիս կազմում են ուղղանկյուն.

Տրված է. ABCD - զուգահեռագիծ, AK-բիսեկտոր A,

DP-բիսեկտոր D,

CM բիսեկտոր C,

BF - բիսեկտոր B.

Ապացուցել KRNS - ուղղանկյուն

Ապացույց:

Նախորդ հատկության հիման վրա՝ 8=7=6=5=90 0,

նշանակում է, որ KRNS-ը ուղղանկյուն է:

Հեռավորությունները զուգահեռագծի հակառակ անկյուններից մինչև նույն անկյունագիծը հավասար են:

Տրված է. ABCD-զուգահեռագիծ, AC-անկյունագիծ:

VC AC, Դ.Պ. A.C.

Ապացուցել. BC=DP

Ապացույց: 1) DCP = KAB, որպես ներքին խաչեր, որոնք ընկած են AB ║ CD-ի և հատվածային AC-ի հետ:

2) AKB= CDP (կողքի և երկու հարակից անկյունների երկայնքով AB=CD CD P=AB K):

Իսկ հավասար եռանկյուններում համապատասխան կողմերը հավասար են, ինչը նշանակում է DP=BK։

Եթե զուգահեռագծի հակառակ գագաթները միացնեք հակառակ կողմերի միջնակետերին, ապա կստանաք մեկ այլ զուգահեռագիծ:

Տրված է. ABCD զուգահեռագիծ.

Ապացուցել. VKDR-ը զուգահեռագիծ է:

Ապացույց:

1) BP=KD (AD=BC, K և P կետեր

բաժանեք այս կողմերը կիսով չափ)

2) BP ║ KD (պառկած մ.թ մ.թ.ա.)

Եթե քառանկյան հակառակ կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է։

Եթե զուգահեռագծի վրա երկու հակադիր անկյուններից գծեք բարձրություններ, ապա կստանաք ուղղանկյուն:

Տրված է. ABCD-ն զուգահեռագիծ է: BD-ն և AC-ը անկյունագծեր են:

Ապացուցել. AC 2 + ВД 2 =2 (AB 2 + մ.թ 2 )

Ապացույց: 1)ՀԱՐՑՆԵԼ. A.C. ²=
+

2)Բ ՌԴ : ԲԴ 2 = Բ Ռ 2 + ՌԴ 2 (ըստ Պյութագորասի թեորեմի)

3) A.C. ²+ ԲԴ ²=SK²+Ա K²+Բ Р²+РԴ ²

4) SC = BP = N(բարձրություն )

5) AC 2 +ԲԴ 2 = Հ 2 + Ա TO 2 + Հ 2 +PԴ 2

6) Թող Դ K=Ա P=x, Հետո Գ TOԴ : Հ 2 = CD 2 - X 2 ըստ Պյութագորասի թեորեմի )

7) AC²+BԴ ² = CԴ 2 - x²+ AK 1 ²+ CD 2 -X 2 +PԴ 2 ,

AC²+BԴ ²=2СԴ 2 -2x 2 + Ա TO 2 +PԴ 2

8) Ա TO=AD+ X, ՌD=AD- X,

AC²+BԴ ² = 2CD 2 -2x 2 +(ՀԱՅՏԱՐԱՐՈՒԹՅՈՒՆ +x) 2 +(ՀԱՅՏԱՐԱՐՈՒԹՅՈՒՆ -X) 2 ,

AC²+ IND²=2 ՀԵՏD²-2 X² + մ.թ 2 +2AD X+ X 2 +AD 2 -2 մ.թ X+ X 2 ,
AC²+ IND²=2CD 2 +2AD 2 =2 (CD 2 +AD 2 ).

Վ . Խնդիրների լուծում՝ օգտագործելով այս հատկությունները

Մի կողմին կից զուգահեռագծի երկու անկյունների կիսորդների հատման կետը պատկանում է հակառակ կողմին: Զուգահեռագծի ամենակարճ կողմն է 5 . Գտեք նրա մեծ կողմը:

Տրված է. ABCD-ն զուգահեռագիծ է,

AK – բիսեկտոր
Ա,

D K – կիսաչափ
D, AB=5

Գտեք: Արև

որոշումը

Լուծում

Որովհետեւ AK - բիսեկտոր
Եվ հետո ABC-ն հավասարաչափ է:

Որովհետեւ D K – կիսաչափ
D, ապա DCK - հավասարաչափ

DC =C K= 5

Այնուհետև BC=VC+SC=5+5 = 10

Պատասխան՝ 10

2. Գտե՛ք զուգահեռագծի պարագիծը, եթե նրա անկյուններից մեկի կիսադիրը զուգահեռագծի կողմը բաժանում է 7 սմ և 14 սմ հատվածների։

1 դեպք

Տրված է.
Ա,

VK=14 սմ, KS=7 սմ

Գտնել. P զուգահեռագիծ

Լուծում

VS=VK+KS=14+7=21 (սմ)

Որովհետեւ AK – բիսեկտոր
Եվ հետո ABC-ն հավասարաչափ է:

AB=BK= 14 սմ

Այնուհետև P=2 (14+21) =70 (սմ)

տեղի է ունենում

Տրված է. ABCD-ն զուգահեռագիծ է,

D K – կիսաչափ
Դ

VK=14 սմ, KS=7 սմ

Գտեք P զուգահեռագիծ

Լուծում

VS=VK+KS=14+7=21 (սմ)

Որովհետեւ D K – կիսաչափ
D, ապա DCK - հավասարաչափ

DC =C K= 7

Այնուհետև P = 2 (21+7) = 56 (սմ)

Պատասխան. 70 սմ կամ 56 սմ

3. Զուգահեռագծի կողմերը 10 սմ և 3 սմ են. Մեծ կողմին կից երկու անկյունների կիսադիրները հակառակ կողմը բաժանում են երեք հատվածի: Գտեք այս հատվածները:

1 դեպք:կիսադիրները հատվում են զուգահեռագծից դուրս

Տրված է. ABCD – զուգահեռագիծ, AK – կիսադիր
Ա,

D K – կիսաչափ
D , AB=3 սմ, BC=10 սմ

Գտեք VM, MN, NC

Լուծում

Որովհետեւ AM - բիսեկտոր
Եվ հետո AVM-ն հավասարաչափ է:

Որովհետեւ DN - բիսեկտոր
D, ապա DCN - հավասարաչափ

DC=CN=3

Այնուհետև MN = 10 – (BM +NC) = 10 – (3+3)=4 սմ

Դեպք 2:կիսաչափերը հատվում են զուգահեռագծի ներսում

Որովհետեւ ԱՆ - բիսեկտոր
Եվ հետո ABN-ը հավասարաչափ է:

AB=BՆ = 3 Դ

Իսկ լոգարիթմական վանդակաճաղը պետք է տեղափոխվի դռան շեմում անհրաժեշտ հեռավորության վրա

Զուգահեռաչափ մեխանիզմ- չորս բարակ մեխանիզմ, որի կապերը կազմում են զուգահեռագիծ: Այն օգտագործվում է կախովի մեխանիզմներով թարգմանական շարժում իրականացնելու համար:

Զուգահեռագիծ ֆիքսված կապով- մի օղակը անշարժ է, հակառակը կատարում է ճոճվող շարժում՝ զուգահեռ մնալով անշարժին։ Մեկը մյուսի հետևից միացված երկու զուգահեռագիծը վերջի կապին տալիս է ազատության երկու աստիճան՝ այն թողնելով անշարժ կապին զուգահեռ։

Օրինակներ՝ ավտոբուսի դիմապակու մաքրիչներ, բեռնատարներ, եռոտանիներ, կախիչներ, մեքենաների կախոցներ:

Զուգահեռագիծ ֆիքսված հոդով- օգտագործվում է զուգահեռագծի հատկությունը երեք կետերի միջև հեռավորությունների մշտական հարաբերակցությունը պահպանելու համար: Օրինակ՝ գծագրող պանտոգրաֆ - գծագրերի մասշտաբավորման սարք:

Ռոմբուս- բոլոր օղակները նույն երկարությունն են, զույգ հակադիր ծխնիների մոտեցումը (կծկումը) հանգեցնում է մյուս երկու ծխնիների հեռացմանը: Բոլոր հղումները աշխատում են սեղմման մեջ:

Օրինակներ - ավտոմոբիլային ադամանդաձև բաճկոն, տրամվայի պանտոգրաֆ:

Մկրատկամ X-ձևավորված մեխանիզմ, հայտնի է նաեւ որպես Նյուրնբերգյան մկրատ- ռոմբի տարբերակ - երկու օղակ, որոնք մեջտեղում միացված են ծխնիով: Մեխանիզմի առավելություններն են կոմպակտությունն ու պարզությունը, թերությունը երկու սահող զույգերի առկայությունն է։ Երկու (կամ ավելի) նման մեխանիզմներ, որոնք միացված են հաջորդաբար, մեջտեղում ձևավորում են ադամանդ(ներ): Օգտագործվում է վերելակների և մանկական խաղալիքների մեջ:

VII Եզրակացություն

Ո՞վ է մանկուց սովորում մաթեմատիկա:

նա զարգացնում է ուշադրությունը, մարզում է իր ուղեղը,

սեփական կամքը, զարգացնում է հաստատակամությունը

և նպատակներին հասնելու համառություն

Ա.Մարկուշևիչ

Աշխատանքի ընթացքում ապացուցեցի զուգահեռագծի լրացուցիչ հատկությունները։

Ես համոզված էի, որ օգտագործելով այս հատկությունները, դուք կարող եք ավելի արագ լուծել խնդիրները:

Ես ցույց տվեցի, թե ինչպես են այս հատկությունները կիրառվում՝ օգտագործելով կոնկրետ խնդիրների լուծման օրինակներ:

Ես շատ բան իմացա զուգահեռագծի մասին, որը չկա մեր երկրաչափության դասագրքում

Ես համոզվեցի, որ երկրաչափության իմացությունը կյանքում շատ կարևոր է զուգահեռագծի հատկությունների կիրառման օրինակներով։

Իմ հետազոտական աշխատանքի նպատակն ավարտված է.

Մաթեմատիկական գիտելիքների կարևորության մասին է վկայում այն, որ մրցանակ է սահմանվել այն մարդու համար, ով գիրք է հրատարակում մի մարդու մասին, ով իր ողջ կյանքն ապրել է առանց մաթեմատիկայի օգնության։ Այս մրցանակը դեռ ոչ մի մարդ չի ստացել։

VIII գրականություն

Ապացույց

Նախ գծենք AC անկյունագիծը։ Ստանում ենք երկու եռանկյուն՝ ABC և ADC:

Քանի որ ABCD-ն զուգահեռագիծ է, ճիշտ է հետևյալը.

AD || BC \Աջ սլաք \անկյուն 1 = \անկյուն 2ինչպես խաչաձև պառկելը:

ԱԲ || CD\Rightarrow\angle3 =\անկյուն 4ինչպես խաչաձև պառկելը:

Հետևաբար, \եռանկյուն ABC = \եռանկյուն ADC (ըստ երկրորդ չափանիշի՝ և AC-ն ընդհանուր է):

Եվ, հետևաբար, \եռանկյուն ABC = \եռանկյուն ADC, ապա AB = CD և AD = BC:

Ապացուցված!

2. Հակառակ անկյունները նույնական են:

Ապացույց

Ըստ ապացույցի հատկություններ 1Մենք դա գիտենք \ անկյուն 1 = \անկյուն 2, \անկյուն 3 = \անկյուն 4. Այսպիսով, հակառակ անկյունների գումարը հետևյալն է. \անկյուն 1 + \անկյուն 3 = \անկյուն 2 + \անկյուն 4. Հաշվի առնելով, որ \եռանկյուն ABC = \եռանկյուն ADC մենք ստանում ենք \անկյուն A = \անկյուն C, \անկյուն B = \անկյուն D:

Ապացուցված!

3. Անկյունագծերը կիսով չափ բաժանվում են հատման կետով:

Ապացույց

Եկեք գծենք ևս մեկ անկյունագիծ:

Ըստ սեփականություն 1մենք գիտենք, որ հակառակ կողմերը նույնական են՝ AB = CD: Եվս մեկ անգամ նշեք խաչաձև պառկած հավասար անկյունները:

Այսպիսով, պարզ է, որ \եռանկյուն AOB = \եռանկյուն COD ըստ եռանկյունների հավասարության երկրորդ չափանիշի (երկու անկյուն և նրանց միջև գտնվող կողմ): Այսինքն՝ BO = OD (անկյան 2-ի և \անկյունի 1-ի դիմաց) և AO = OC (համապատասխանաբար \անկյունների 3 և 4 անկյունների դիմաց):

Ապացուցված!

Զուգահեռագծի նշաններ

Եթե ձեր խնդրի մեջ առկա է միայն մեկ հատկանիշ, ապա նկարը զուգահեռագիծ է և կարող եք օգտագործել այս նկարի բոլոր հատկությունները:

Ավելի լավ մտապահելու համար նշեք, որ զուգահեռագծի նշանը կպատասխանի հետևյալ հարցին. «Ինչպե՞ս պարզել»:. Այսինքն՝ ինչպես պարզել, որ տրված պատկերը զուգահեռագիծ է։

1. Զուգահեռագիծը այն քառանկյունն է, որի երկու կողմերը հավասար են և զուգահեռ:

AB = CD; ԱԲ || CD\Rightarrow ABCD-ն զուգահեռագիծ է:

Ապացույց

Եկեք ավելի սերտ նայենք: Ինչու AD || մ.թ.ա.

\եռանկյուն ABC = \եռանկյուն ADC ըստ սեփականություն 1 AB = CD, AC - ընդհանուր և \անկյուն 1 = \անկյուն 2 ընկած խաչաձև AB-ի և CD-ի հետ զուգահեռ AC-ի հետ:

Բայց եթե \եռանկյուն ABC = \եռանկյուն ADC , ապա \անկյուն 3 = \անկյուն 4 (համապատասխանաբար գտնվում է AB-ի և CD-ի դիմաց): Եվ ուրեմն մ.թ. || մ.թ.ա. (\անկյուն 3 և \անկյուն 4. խաչաձև պառկածները նույնպես հավասար են):

Առաջին նշանը ճիշտ է.

2. Զուգահեռագիծը այն քառանկյունն է, որի հակառակ կողմերը հավասար են:

AB = CD, AD = BC \Rightarrow ABCD-ը զուգահեռագիծ է:

Ապացույց

Դիտարկենք այս նշանը. Կրկին գծենք AC անկյունագիծը:

Ըստ սեփականություն 1\եռանկյուն ABC = \եռանկյուն ACD .

Հետևում է, որ. \անկյուն 1 = \անկյուն 2 \Աջ սլաք AD || Ք.ա.Եվ \անկյուն 3 = \անկյուն 4 \Աջ սլաք AB || CD, այսինքն՝ ABCD-ն զուգահեռագիծ է։

Երկրորդ նշանը ճիշտ է.

3. Զուգահեռագիծը այն քառանկյունն է, որի հակառակ անկյունները հավասար են:

\ անկյուն A = \անկյուն C, \ անկյուն B = \անկյուն D \Աջ սլաք ABCD- զուգահեռագիծ.

Ապացույց

2 \ալֆա + 2 \բետա = 360^(\circ)(քանի որ ABCD-ն քառանկյուն է, և \ անկյուն A = \անկյուն C , \անկյուն B = \անկյուն D ըստ պայմանի):

Ստացվում է, որ \ալֆա + \բետա = 180^(\circ) . Բայց \alpha-ն և \beta-ն ներքին միակողմանի են AB հատվածում:

Իսկ այն, որ \alpha + \beta = 180^(\circ) նշանակում է նաև, որ AD || Ք.ա.

Ավելին, \alpha-ն և \beta-ն ներքին միակողմանի են AD-ի հատվածում: Իսկ դա նշանակում է AB || CD.

Երրորդ նշանը ճիշտ է.

4. Զուգահեռագիծը այն քառանկյունն է, որի անկյունագծերը կիսով չափ բաժանված են հատման կետով:

AO = OC; BO = OD\Աջ սլաքի զուգահեռագիծ:

Ապացույց

BO = OD; AO = OC , \անկյուն 1 = \անկյուն 2 որպես ուղղահայաց \Աջ սլաք \եռանկյուն AOB = \եռանկյուն COD, \Աջ սլաք \անկյուն 3 = \անկյուն 4, և \Rightarrow AB || CD.

Նմանապես BO = OD; AO = OC, \անկյուն 5 = \անկյուն 6 \Աջ սլաք \եռանկյուն AOD = \եռանկյուն BOC \Աջ սլաք \անկյուն 7 = \անկյուն 8, և \Rightarrow AD || Ք.ա.

Չորրորդ նշանը ճիշտ է.

Ընդամենը:0
հետ շփման մեջ 0
Google+ 0
լավ 0
Ֆեյսբուք 0