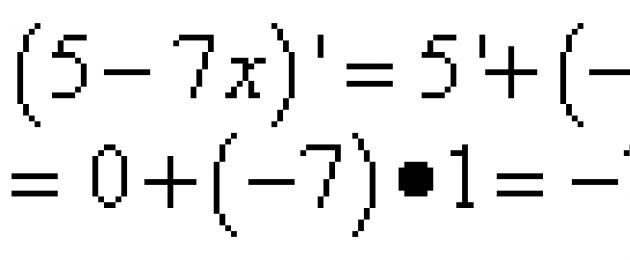La derivata della funzione y è la radice di x. Trova la derivata: algoritmo ed esempi di soluzioni

L'operazione per trovare una derivata è chiamata differenziazione.

Come risultato della risoluzione dei problemi di trovare derivate delle funzioni più semplici (e non molto semplici) definendo la derivata come il limite del rapporto tra l'incremento e l'incremento dell'argomento, è apparsa una tabella di derivate e regole di differenziazione definite con precisione . Isaac Newton (1643-1727) e Gottfried Wilhelm Leibniz (1646-1716) furono i primi a lavorare nel campo della ricerca di derivati.

Pertanto, ai nostri tempi, per trovare la derivata di una qualsiasi funzione, non è necessario calcolare il suddetto limite del rapporto tra l'incremento della funzione e l'incremento dell'argomento, ma basta usare la tabella delle derivate e le regole di differenziazione. Il seguente algoritmo è adatto per trovare la derivata.

Per trovare la derivata, hai bisogno di un'espressione sotto il segno del tratto scomporre semplici funzioni e determinare quali azioni (prodotto, somma, quoziente) queste funzioni sono correlate. Inoltre, troviamo le derivate delle funzioni elementari nella tabella delle derivate e le formule per le derivate del prodotto, somma e quoziente - nelle regole di differenziazione. La tabella delle derivate e le regole di differenziazione sono riportate dopo i primi due esempi.

Esempio 1 Trova la derivata di una funzione

Soluzione. Dalle regole di differenziazione scopriamo che la derivata della somma delle funzioni è la somma delle derivate delle funzioni, cioè

Dalla tabella delle derivate, scopriamo che la derivata di "X" è uguale a uno e la derivata del seno è coseno. Sostituiamo questi valori nella somma delle derivate e troviamo la derivata richiesta dalla condizione del problema:

Esempio 2 Trova la derivata di una funzione

Soluzione. Differenziare come derivata della somma, in cui il secondo termine con fattore costante, può essere dedotto dal segno della derivata:

Se ci sono ancora domande su da dove viene qualcosa, di norma diventano chiare dopo aver letto la tabella dei derivati e le regole di differenziazione più semplici. Stiamo andando da loro proprio ora.

Tabella delle derivate di funzioni semplici

1. Derivata di una costante (numero). Qualsiasi numero (1, 2, 5, 200...) che si trova nell'espressione della funzione. Sempre zero. Questo è molto importante da ricordare, poiché è richiesto molto spesso
2. Derivata della variabile indipendente. Molto spesso "x". Sempre uguale a uno. Anche questo è importante da ricordare
3. Derivato di laurea. Quando si risolvono i problemi, è necessario convertire le radici non quadrate in una potenza.
4. Derivata di una variabile alla potenza di -1
5. Derivata della radice quadrata
6. Derivata seno
7. Derivata del coseno
8. Derivata tangente
9. Derivato di cotangente
10. Derivata dell'arcoseno
11. Derivata dell'arcocoseno
12. Derivata dell'arcotangente
13. Derivata della tangente inversa
14. Derivata del logaritmo naturale
15. Derivata di una funzione logaritmica
16. Derivata dell'esponente
17. Derivata di funzione esponenziale

Regole di differenziazione

1. Derivata della somma o della differenza
2. Derivato di un prodotto
2a. Derivata di un'espressione moltiplicata per un fattore costante
3. Derivata del quoziente
4. Derivata di una funzione complessa

Regola 1Se funziona

ad un certo punto sono differenziabili, quindi nello stesso punto le funzioni

quelli. la derivata della somma algebrica delle funzioni è uguale alla somma algebrica delle derivate di queste funzioni.

Conseguenza. Se due funzioni differenziabili differiscono per una costante, allora lo sono le loro derivate, cioè.

Regola 2Se funziona

sono differenziabili ad un certo punto, quindi anche il loro prodotto è differenziabile nello stesso punto

quelli. la derivata del prodotto di due funzioni è uguale alla somma dei prodotti di ciascuna di queste funzioni e della derivata dell'altra.

Conseguenza 1. Il fattore costante può essere estratto dal segno della derivata:

Conseguenza 2. La derivata del prodotto di più funzioni differenziabili è uguale alla somma dei prodotti della derivata di ciascuno dei fattori e di tutti gli altri.

Ad esempio, per tre moltiplicatori:

Regola 3Se funziona

differenziabile a un certo punto e , allora a questo punto anche il loro quoziente è differenziabile.u/v , e

quelli. la derivata di un quoziente di due funzioni è uguale a una frazione il cui numeratore è la differenza tra i prodotti del denominatore e la derivata del numeratore e il numeratore e la derivata del denominatore, e il denominatore è il quadrato del numeratore precedente .

Dove cercare in altre pagine

Quando si trova la derivata del prodotto e il quoziente in problemi reali, è sempre necessario applicare più regole di differenziazione contemporaneamente, quindi nell'articolo ci sono più esempi su queste derivate."La derivata di un prodotto e un quoziente".

Commento. Non dovresti confondere una costante (cioè un numero) come un termine nella somma e come un fattore costante! Nel caso di un termine, la sua derivata è uguale a zero, e nel caso di un fattore costante, è tolta dal segno delle derivate. Questo è un errore tipico che si verifica nella fase iniziale dello studio delle derivate, ma poiché lo studente medio risolve diversi esempi a due componenti, questo errore non fa più.

E se, nel differenziare un prodotto o un quoziente, hai un termine tu"v, in quale tu- un numero, ad esempio 2 o 5, cioè una costante, quindi la derivata di questo numero sarà uguale a zero e, quindi, l'intero termine sarà uguale a zero (un caso del genere è analizzato nell'esempio 10) .

Un altro errore comune è la soluzione meccanica della derivata di una funzione complessa come derivata di una funzione semplice. Ecco perché derivata di una funzione complessa dedicato ad un articolo a parte. Ma prima impareremo a trovare le derivate di funzioni semplici.

Lungo la strada, non puoi fare a meno di trasformazioni di espressioni. Per fare ciò, potrebbe essere necessario aprire nuovi manuali di Windows Azioni con poteri e radici e Azioni con frazioni .

Se stai cercando soluzioni per derivate con poteri e radici, cioè quando appare la funzione , quindi segui la lezione "Derivata della somma delle frazioni con poteri e radici".

Se hai un compito come , allora sei nella lezione "Derivati di semplici funzioni trigonometriche".

Esempi passo passo: come trovare la derivata

Esempio 3 Trova la derivata di una funzione

Soluzione. Determiniamo le parti dell'espressione della funzione: l'intera espressione rappresenta il prodotto e i suoi fattori sono somme, nella seconda delle quali uno dei termini contiene un fattore costante. Applichiamo la regola di differenziazione del prodotto: la derivata del prodotto di due funzioni è uguale alla somma dei prodotti di ciascuna di queste funzioni e la derivata dell'altra:

Successivamente, applichiamo la regola di differenziazione della somma: la derivata della somma algebrica delle funzioni è uguale alla somma algebrica delle derivate di queste funzioni. Nel nostro caso, in ogni somma, il secondo termine con il segno meno. In ogni somma vediamo sia una variabile indipendente, la cui derivata è uguale a uno, sia una costante (numero), la cui derivata è uguale a zero. Quindi, "x" diventa uno e meno 5 - zero. Nella seconda espressione, "x" è moltiplicato per 2, quindi moltiplichiamo due per la stessa unità della derivata di "x". Otteniamo i seguenti valori di derivate:

Sostituiamo le derivate trovate nella somma dei prodotti e otteniamo la derivata dell'intera funzione richiesta dalla condizione del problema:

E puoi verificare la soluzione del problema sulla derivata su .

Esempio 4 Trova la derivata di una funzione

Soluzione. Dobbiamo trovare la derivata del quoziente. Applichiamo la formula per differenziare un quoziente: la derivata di un quoziente di due funzioni è uguale a una frazione il cui numeratore è la differenza tra i prodotti del denominatore e la derivata del numeratore e il numeratore e la derivata del denominatore, e il denominatore è il quadrato del precedente numeratore. Noi abbiamo:

Abbiamo già trovato la derivata dei fattori nel numeratore nell'esempio 2. Non dimentichiamo inoltre che il prodotto, che è il secondo fattore nel numeratore nell'esempio corrente, è preso con un segno meno:

Se stai cercando soluzioni a tali problemi in cui devi trovare la derivata di una funzione, dove c'è un mucchio continuo di radici e gradi, come, ad esempio, allora benvenuto in classe "La derivata della somma delle frazioni con potenze e radici" .

Se hai bisogno di saperne di più sulle derivate di seno, coseno, tangente e altre funzioni trigonometriche, cioè quando la funzione appare , allora hai una lezione "Derivati di semplici funzioni trigonometriche" .

Esempio 5 Trova la derivata di una funzione

Soluzione. In questa funzione vediamo un prodotto, uno dei cui fattori è la radice quadrata della variabile indipendente, con la derivata di cui abbiamo familiarizzato nella tabella delle derivate. In base alla regola di differenziazione del prodotto e al valore tabulare della derivata della radice quadrata, otteniamo:

Puoi controllare la soluzione del problema della derivata su calcolatrice derivati online .

Esempio 6 Trova la derivata di una funzione

Soluzione. In questa funzione vediamo il quoziente, il cui dividendo è la radice quadrata della variabile indipendente. Secondo la regola di differenziazione del quoziente, che abbiamo ripetuto e applicato nell'esempio 4, e il valore tabulare della derivata della radice quadrata, otteniamo:

Per eliminare la frazione nel numeratore, moltiplica il numeratore e il denominatore per .

Il caso generale della formula per la derivata di una radice di grado arbitrario- una frazione, il cui numeratore è uno, e denominatore un numero uguale al grado della radice per cui è stata calcolata la derivata, moltiplicato per la radice dello stesso grado, la cui espressione radice è una variabile nel grado della radice per cui è stata calcolata la derivata, ridotto di uno
Derivata della radice quadrata- è un caso speciale della formula precedente. Derivata della radice quadrata di xè una frazione il cui numeratore è uno e il denominatore è due volte la radice quadrata di x
Derivato della radice cubica, anche un caso speciale della formula generale. La derivata della radice cubica è l'unità divisa per le tre radici cubiche x al quadrato.

Di seguito sono riportate le trasformazioni che spiegano perché le formule per trovare la derivata delle radici quadrate e cubiche sono esattamente come mostrate nella figura.

Naturalmente queste formule non sono affatto memorizzabili, se si tiene conto che estrarre la radice di un grado derivato equivale a elevare a potenza una frazione il cui denominatore è uguale allo stesso grado. Quindi trovare la derivata della radice si riduce all'applicazione della formula per trovare la derivata del grado della frazione corrispondente.

Derivata di una variabile sotto la radice quadrata

(√x)" = 1 / (2√x) o 1/2 x -1/2

Spiegazione:
(√x)" = (x 1/2)"

La radice quadrata è esattamente la stessa operazione di elevare alla potenza di 1/2,questo significa che per trovare la derivata della radice, puoi applicare la formula della regola per trovare la derivata di una variabile in misura arbitraria:

(x 1/2)" \u003d 1/2 x -1/2 \u003d 1 / (2√x)

Derivato della radice cubica (derivato della radice del terzo grado)

La derivata della radice cubica è esattamente la stessa della radice quadrata.

Immagina la radice cubica come una potenza di 1/3 e trova la derivata secondo le regole generali di differenziazione. Una breve formula può essere vista nell'immagine sopra, e sotto c'è una spiegazione del perché è così.

La potenza -2/3 si ottiene sottraendo uno da 1/3

Le funzioni complesse non sempre si adattano alla definizione di una funzione complessa. Se esiste una funzione della forma y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, allora non può essere considerata complessa, a differenza di y \u003d sin 2 x.

Questo articolo mostrerà il concetto di una funzione complessa e la sua identificazione. Lavoriamo con formule per trovare la derivata con esempi di soluzioni nella conclusione. L'uso della tabella delle derivate e delle regole di differenziazione riduce notevolmente il tempo per trovare la derivata.

Definizioni di base

Definizione 1

Una funzione complessa è una funzione il cui argomento è anche una funzione.

È indicato in questo modo: f (g (x)) . Abbiamo che la funzione g (x) è considerata un argomento f (g (x)) .

Definizione 2

Se esiste una funzione f ed è una funzione cotangente, allora g(x) = ln x è la funzione del logaritmo naturale. Otteniamo che la funzione complessa f (g (x)) sarà scritta come arctg (lnx). Oppure una funzione f, che è una funzione elevata alla 4a potenza, dove g (x) \u003d x 2 + 2 x - 3 è considerata un'intera funzione razionale, otteniamo che f (g (x)) \u003d (x 2 + 2 x - 3) 4 .

Ovviamente g(x) può essere complicato. Dall'esempio y \u003d sin 2 x + 1 x 3 - 5, si può vedere che il valore di g ha una radice cubica con una frazione. Questa espressione può essere indicata come y = f (f 1 (f 2 (x))) . Da cui abbiamo che f è una funzione seno e f 1 è una funzione situata sotto la radice quadrata, f 2 (x) \u003d 2 x + 1 x 3 - 5 è una funzione razionale frazionaria.

Definizione 3

Il grado di annidamento è definito da qualsiasi numero naturale ed è scritto come y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Definizione 4

Il concetto di composizione della funzione si riferisce al numero di funzioni nidificate secondo l'affermazione del problema. Per la soluzione, la formula per trovare la derivata di una funzione complessa della forma

(f(g(x)))"=f"(g(x)) g"(x)

Esempi

Esempio 1

Trova la derivata di una funzione complessa della forma y = (2 x + 1) 2 .

Soluzione

Per convenzione, f è una funzione di quadratura e g(x) = 2 x + 1 è considerata una funzione lineare.

Applichiamo la formula derivata per una funzione complessa e scriviamo:

f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

È necessario trovare una derivata con una forma iniziale semplificata della funzione. Noi abbiamo:

y = (2x + 1) 2 = 4x2 + 4x + 1

Quindi abbiamo quello

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

I risultati corrispondevano.

Quando si risolvono problemi di questo tipo, è importante capire dove si troverà la funzione della forma feg (x).

Esempio 2

Dovresti trovare i derivati di funzioni complesse della forma y \u003d sin 2 x e y \u003d sin x 2.

Soluzione

La prima voce della funzione dice che f è la funzione di quadratura e g(x) è la funzione seno. Allora lo capiamo

y "= (peccato 2 x)" = 2 sin 2 - 1 x (peccato x)" = 2 sin x cos x

La seconda voce mostra che f è una funzione seno e g (x) = x 2 denota la funzione di potenza. Ne consegue che il prodotto di una funzione complessa può essere scritto come

y " \u003d (peccato x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

La formula per la derivata y \u003d f (f 1 (f 2 (f 3 (. . . (fn (x)))))) sarà scritta come y "= f" (f 1 (f 2 (f 3 (. . . ( fn (x)))))) f 1 "(f 2 (f 3 (. . . (fn (x))))) f 2 " (f 3 (. . . (fn (x) )) )) . . . f n "(x)

Esempio 3

Trova la derivata della funzione y = sin (ln 3 a r c t g (2 x)) .

Soluzione

Questo esempio mostra la complessità della scrittura e della determinazione della posizione delle funzioni. Quindi y \u003d f (f 1 (f 2 (f 3 (f 4 (x))))) indica, dove f , f 1 , f 2 , f 3 , f 4 (x) è la funzione seno, la funzione di elevare a 3 gradi una funzione con un logaritmo in base e, una funzione dell'arcotangente ed una lineare.

Dalla formula per la definizione di una funzione complessa, abbiamo quello

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Ottenere cosa trovare

f "(f 1 (f 2 (f 3 (f 4 (x))))) come derivata del seno nella tabella delle derivate, quindi f "(f 1 (f 2 (f 3 (f 4 (x ))))) ) = cos (ln 3 arctg (2 x)) .
f 1 "(f 2 (f 3 (f 4 (x)))) come derivata di una funzione di potenza, quindi f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctg (2 x) = 3 ln 2 arctg (2 x) .
f 2 "(f 3 (f 4 (x))) come derivata logaritmica, quindi f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
f 3 "(f 4 (x)) come derivata dell'arcotangente, quindi f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
Quando trovi la derivata f 4 (x) \u003d 2 x, prendi 2 dal segno della derivata usando la formula per la derivata della funzione di potenza con un esponente che è 1, quindi f 4 "(x) \u003d ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .

Uniamo i risultati intermedi e otteniamo quello

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)

L'analisi di tali funzioni ricorda le bambole che nidificano. Le regole di differenziazione non possono sempre essere applicate in modo esplicito utilizzando una tabella derivata. Spesso è necessario applicare la formula per trovare le derivate di funzioni complesse.

Ci sono alcune differenze tra una vista complessa e una funzione complessa. Con una chiara capacità di distinguere questo, trovare derivati sarà particolarmente facile.

Esempio 4

È necessario considerare di portare un tale esempio. Se esiste una funzione della forma y = tg 2 x + 3 tgx + 1 , allora può essere considerata come una funzione complessa della forma g (x) = tgx , f (g) = g 2 + 3 g + 1 . Ovviamente è necessario applicare la formula per la derivata complessa:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

Una funzione della forma y = t g x 2 + 3 t g x + 1 non è considerata complessa, poiché ha la somma t g x 2 , 3 t g x e 1 . Tuttavia, t g x 2 è considerata una funzione complessa, quindi otteniamo una funzione di potenza della forma g (x) \u003d x 2 ef, che è una funzione della tangente. Per fare ciò, è necessario differenziare per l'importo. Lo capiamo

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 cos 2 x

Passiamo a trovare la derivata di una funzione complessa (t g x 2) ":

f "(g (x)) \u003d (tg (g (x))) " \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g " (x) \u003d (x 2) " \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)

Otteniamo che y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Le funzioni complesse possono essere incluse in funzioni complesse e le funzioni complesse stesse possono essere funzioni complesse della forma complessa.

Esempio 5

Si consideri ad esempio una funzione complessa della forma y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Questa funzione può essere rappresentata come y = f (g (x)) , dove il valore di f è una funzione del logaritmo in base 3, e g (x) è considerata la somma di due funzioni della forma h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 e k (x) = ln 2 x (x 2 + 1) . Ovviamente, y = f (h (x) + k (x)) .

Considera la funzione h(x) . Questo è il rapporto tra l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e m (x) = e x 2 + 3 3

Abbiamo che l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) è la somma di due funzioni n (x) = x 2 + 7 e p ( x) \u003d 3 cos 3 (2 x + 1) , dove p (x) \u003d 3 p 1 (p 2 (p 3 (x))) è una funzione complessa con un coefficiente numerico di 3 e p 1 è una funzione cubo, p 2 funzione coseno, p 3 (x) = 2 x + 1 - funzione lineare.

Abbiamo trovato che m (x) = ex 2 + 3 3 = q (x) + r (x) è la somma di due funzioni q (x) = ex 2 e r (x) = 3 3 , dove q (x) = q 1 (q 2 (x)) è una funzione complessa, q 1 è una funzione con un esponente, q 2 (x) = x 2 è una funzione di potenza.

Ciò mostra che h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Quando si passa a un'espressione della forma k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), è chiaro che la funzione è rappresentata come un complesso s (x) \ u003d ln 2 x \u003d s 1 ( s 2 (x)) con un numero intero razionale t (x) = x 2 + 1, dove s 1 è una funzione di quadratura e s 2 (x) = ln x è logaritmico con base e.

Ne consegue che l'espressione assumerà la forma k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Allora lo capiamo

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Secondo le strutture della funzione, è diventato chiaro come e quali formule devono essere applicate per semplificare l'espressione quando è differenziata. Per familiarizzare con tali problemi e per comprenderne la soluzione, è necessario fare riferimento al punto di differenziare una funzione, cioè trovare la sua derivata.

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Derivazione della formula per la derivata di una funzione di potenza (x alla potenza di a). Si considerano le derivate delle radici da x. La formula per la derivata di una funzione di potenza di ordine superiore. Esempi di calcolo delle derivate.

Contenuto

Guarda anche: Funzione di potenza e radici, formule e grafico
Grafici delle funzioni di potenza

Formule di base

La derivata di x alla potenza di a è a volte x alla potenza di meno uno:
(1) .

La derivata della radice n-esima di x alla m-esima potenza è:
(2) .

Derivazione della formula per la derivata di una funzione di potenza

Caso x > 0

Consideriamo una funzione di potenza della variabile x con esponente a :
(3) .
Qui a è un numero reale arbitrario. Consideriamo prima il caso.

Per trovare la derivata della funzione (3), utilizziamo le proprietà della funzione di potenza e la trasformiamo nella forma seguente:
.

Ora troviamo la derivata applicando:
;
.
Qui .

La formula (1) è dimostrata.

Derivazione della formula per la derivata della radice del grado n di x al grado m

Consideriamo ora una funzione che è la radice della seguente forma:
(4) .

Per trovare la derivata, convertiamo la radice in una funzione di potenza:
.
Confrontando con la formula (3), lo vediamo
.
Quindi
.

Con la formula (1) troviamo la derivata:
(1) ;
;
(2) .

In pratica non è necessario memorizzare la formula (2). È molto più conveniente convertire prima le radici in funzioni di potenza e poi trovare le loro derivate usando la formula (1) (vedi esempi alla fine della pagina).

Caso x = 0

Se , allora la funzione esponenziale è definita anche per il valore della variabile x = 0 . Troviamo la derivata della funzione (3) per x = 0 . Per fare ciò, utilizziamo la definizione di derivata:
.

Sostituisci x = 0 :
.
In questo caso per derivata si intende il limite di destra per cui .

Quindi abbiamo trovato:
.
Da ciò si può vedere che a , .
In , .
In , .
Questo risultato si ottiene anche dalla formula (1):
(1) .
Pertanto, la formula (1) vale anche per x = 0 .

caso x< 0

Considera di nuovo la funzione (3):
(3) .
Per alcuni valori della costante a, viene definita anche per valori negativi della variabile x. Vale a dire, sia a un numero razionale. Quindi può essere rappresentato come una frazione irriducibile:
,
dove m e n sono interi senza divisore comune.

Se n è dispari, allora la funzione esponenziale è definita anche per valori negativi della variabile x. Ad esempio, per n = 3 e m = 1 abbiamo la radice cubica di x :
.
Viene anche definito per valori negativi di x .

Troviamo la derivata della funzione di potenza (3) per e per i valori razionali della costante a , per la quale è definita. Per fare ciò, rappresentiamo x nella forma seguente:
.
Quindi ,
.
Troviamo la derivata sottraendo la costante dal segno della derivata e applicando la regola di differenziazione di una funzione complessa:

.
Qui . Ma
.
Da allora
.
Quindi
.
Cioè, la formula (1) vale anche per:
(1) .

Derivati di ordini superiori

Ora troviamo le derivate di ordine superiore della funzione di potenza
(3) .
Abbiamo già trovato la derivata del primo ordine:
.

Prendendo la costante a fuori dal segno della derivata, troviamo la derivata del secondo ordine:
.
Allo stesso modo, troviamo derivate del terzo e quarto ordine:
;

.

Da qui è chiaro che derivata di un arbitrario ennesimo ordine ha la seguente forma:
.

notare che se a è un numero naturale, , allora la derivata n-esima è costante:
.
Allora tutte le derivate successive sono uguali a zero:
,
a .

Esempi derivati

Esempio

Trova la derivata della funzione:
.

Convertiamo le radici in poteri:
;
.
Quindi la funzione originale assume la forma:
.

Troviamo derivate di gradi:
;
.
La derivata di una costante è zero:
.

Istruzione

Prima di trovare la derivata della radice, prestare attenzione alle altre funzioni presenti nell'esempio da risolvere. Se il problema ha molte espressioni radicali, usa la seguente regola per trovare la derivata della radice quadrata:

(√x)" = 1 / 2√x.

E per trovare la derivata della radice cubica, applica la formula:

(³√x)" \u003d 1 / 3 (³√x)²,

dove ³√x denota la radice cubica di x.

Se, intesa per la differenziazione, esiste una variabile in fractional , converti la radice in una funzione di potenza con l'esponente appropriato. Per una radice quadrata, questa sarà una potenza di ½ e per una radice cubica, sarà ⅓:

√x \u003d x ^ ½,
³√x = x ^ ⅓,

dove ^ sta per esponenziazione.

Per trovare la derivata di una funzione di potenza in generale e x^1, x^⅓ in particolare, utilizzare la seguente regola:

(x ^ n)" = n * x^(n-1).

Per la derivata della radice, questa relazione implica:

(x^½)" = ½ x ^ (-½) e
(x^⅓)" = ⅓ x ^ (-⅔).

Dopo aver differenziato tutto, dai un'occhiata da vicino al resto dell'esempio. Se hai un'espressione molto ingombrante nella tua risposta, allora sicuramente può essere semplificata. La maggior parte degli esempi scolastici sono progettati in modo tale che il risultato sia un numero piccolo o un'espressione compatta.

In molti problemi derivati, le radici (quadrato e cubo) si verificano insieme ad altre funzioni. Per trovare la derivata della radice in questo caso, applica le seguenti regole:
la derivata di una costante (un numero costante, C) è uguale a zero: C" = 0;
il fattore costante è preso dal segno della derivata: (k*f)" = k * (f)" (f è una funzione arbitraria) ;
la derivata della somma di più funzioni è uguale alla somma delle derivate: (f + g)" = (f)" + (g)";
la derivata del prodotto di due funzioni è... no, non il prodotto delle derivate, ma la seguente espressione: (fg)" = (f)"g + f (g)";
anche la derivata del quoziente non è uguale al quoziente delle derivate, ma si trova secondo la seguente regola: (f / g)" = ((f)"g - f(g)") / g².

Nota

In questa pagina è possibile calcolare la derivata di una funzione online con una soluzione dettagliata del problema. La soluzione delle derivate di una funzione viene effettuata utilizzando le regole di differenziazione che gli studenti studiano nel corso di analisi matematica presso l'istituto. Per trovare la derivata di una funzione, è necessario inserire una funzione di differenziazione nel campo "Funzione" secondo le regole di immissione dati.

Consigli utili

La derivata di una funzione è il limite del rapporto tra l'incremento della funzione e l'incremento dell'argomento, quando l'incremento dell'argomento tende a zero: Il significato matematico di questa definizione non è molto facile da capire, poiché nella corso di algebra scolastica il concetto di limite di una funzione o non viene studiato affatto, oppure lo si studia in modo molto superficiale. Ma per imparare a trovare derivati di varie funzioni, questo non è necessario.

Fonti: