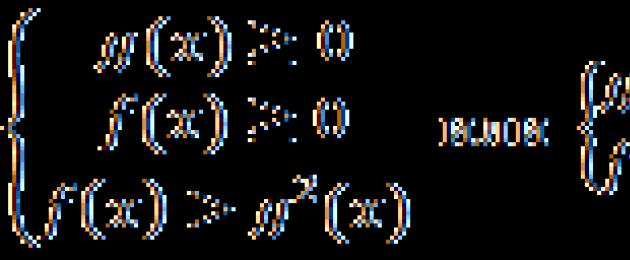Disuguaglianze con radici quadrate. Risolvere le disuguaglianze irrazionali

In questa lezione esamineremo la risoluzione delle disuguaglianze irrazionali e forniremo vari esempi.

Argomento: Equazioni e disequazioni. Sistemi di equazioni e disequazioni

Lezione:Disuguaglianze irrazionali

Quando si risolvono le disuguaglianze irrazionali, è molto spesso necessario sollevare in una certa misura entrambi i lati della disuguaglianza; questa è un’operazione piuttosto responsabile; Ricordiamo le caratteristiche.

Entrambi i lati della disuguaglianza possono essere quadrati se entrambi sono non negativi, solo allora otteniamo una vera disuguaglianza da una vera disuguaglianza.

Entrambi i lati della disuguaglianza possono essere in ogni caso ridotti al cubo; se la disuguaglianza originale fosse vera, una volta cubica otterremo la disuguaglianza vera.

Consideriamo una disuguaglianza della forma:

L'espressione radicale deve essere non negativa. La funzione può assumere qualsiasi valore; è necessario considerare due casi.

Nel primo caso, entrambi i lati della disuguaglianza sono non negativi, abbiamo il diritto di elevarlo al quadrato. Nel secondo caso lato destroè negativo e non abbiamo il diritto di elevarlo al quadrato. In questo caso è necessario guardare al significato della disuguaglianza: qui l'espressione positiva (radice quadrata) è maggiore dell'espressione negativa, il che significa che la disuguaglianza è sempre soddisfatta.

Abbiamo quindi il seguente schema risolutivo:

Nel primo sistema non proteggiamo separatamente l'espressione radicale, poiché quando è soddisfatta la seconda disuguaglianza del sistema, l'espressione radicale deve essere automaticamente positiva.

Esempio 1: risolvere la disuguaglianza:

Secondo il diagramma, passiamo a un insieme equivalente di due sistemi di disuguaglianze:

Illustriamo:

Riso. 1 - illustrazione della soluzione dell'esempio 1

Come vediamo, quando ci liberiamo dell'irrazionalità, ad esempio, durante la quadratura, otteniamo una serie di sistemi. A volte questo disegno complesso può essere semplificato. Nell'insieme risultante, abbiamo il diritto di semplificare il primo sistema e ottenere un insieme equivalente:

Come esercizio indipendente, è necessario dimostrare l'equivalenza di questi insiemi.

Consideriamo una disuguaglianza della forma:

Analogamente alla disuguaglianza precedente, consideriamo due casi:

Nel primo caso, entrambi i lati della disuguaglianza sono non negativi, abbiamo il diritto di elevarlo al quadrato. Nel secondo caso, il secondo membro è negativo e non abbiamo il diritto di elevarlo al quadrato. In questo caso è necessario guardare al significato della disuguaglianza: qui l'espressione positiva (radice quadrata) è inferiore all'espressione negativa, il che significa che la disuguaglianza è contraddittoria. Non è necessario considerare il secondo sistema.

Abbiamo un sistema equivalente:

A volte le disuguaglianze irrazionali possono essere risolte graficamente. Questo metodo è applicabile quando i grafici corrispondenti possono essere costruiti abbastanza facilmente e si possono trovare i loro punti di intersezione.

Esempio 2: risolvere graficamente le disuguaglianze:

UN)

B)

Abbiamo già risolto la prima disuguaglianza e conosciamo la risposta.

Per risolvere graficamente le disuguaglianze, è necessario costruire un grafico della funzione sul lato sinistro e un grafico della funzione sul lato destro.

Riso. 2. Grafici di funzioni e

Per rappresentare graficamente una funzione, è necessario trasformare la parabola in una parabola (specchiarla rispetto all'asse y) e spostare la curva risultante di 7 unità verso destra. Il grafico lo conferma questa funzione diminuisce monotonicamente nel suo dominio di definizione.

Il grafico di una funzione è una linea retta ed è facile da costruire. Il punto di intersezione con l'asse y è (0;-1).

La prima funzione diminuisce monotonicamente, la seconda aumenta monotonicamente. Se l'equazione ha una radice, allora è l'unica, è facile intuirla dal grafico: .

Quando il valore dell'argomento è inferiore alla radice, la parabola è sopra la retta. Quando il valore dell'argomento è compreso tra tre e sette, la retta passa sopra la parabola.

Abbiamo la risposta:

Metodo efficace Il metodo degli intervalli viene utilizzato per risolvere le disuguaglianze irrazionali.

Esempio 3: risolvi le disuguaglianze utilizzando il metodo degli intervalli:

UN)

B)

Secondo il metodo dell’intervallo, è necessario allontanarsi temporaneamente dalla disuguaglianza. Per fare ciò, sposta tutto nella disuguaglianza data sul lato sinistro (ottieni zero a destra) e introduci una funzione uguale al lato sinistro:

Ora dobbiamo studiare la funzione risultante.

ODZ:

Abbiamo già risolto graficamente questa equazione, quindi non ci soffermiamo a determinare la radice.

Ora è necessario selezionare gli intervalli di segno costante e determinare il segno della funzione su ciascun intervallo:

Riso. 3. Intervalli di costanza di segno ad esempio 3

Ricordiamo che per determinare i segni su un intervallo è necessario prendere un punto di prova e sostituirlo nella funzione, il segno risultante verrà mantenuto dalla funzione per tutto l'intervallo;

Controlliamo il valore al punto di confine:

La risposta è ovvia:

Consideriamo il seguente tipo di disuguaglianze:

Innanzitutto, scriviamo l'ODZ:

Le radici esistono, sono non negative, possiamo quadrare entrambi i lati. Otteniamo:

Abbiamo un sistema equivalente:

Il sistema risultante può essere semplificato. Quando la seconda e la terza disuguaglianza sono soddisfatte, la prima è automaticamente vera. Abbiamo::

Esempio 4: risolvere la disuguaglianza:

Agiamo secondo lo schema: otteniamo un sistema equivalente.

Viene chiamata qualsiasi disuguaglianza che includa una funzione sotto la radice irrazionale. Esistono due tipi di tali disuguaglianze:

Nel primo caso la radice è minore della funzione g(x), nel secondo è maggiore. Se g(x) - costante, la disuguaglianza è notevolmente semplificata. Nota: esteriormente queste disuguaglianze sono molto simili, ma i loro schemi di soluzione sono fondamentalmente diversi.

Oggi impareremo come risolvere le disuguaglianze irrazionali del primo tipo: sono le più semplici e comprensibili. Il segno di disuguaglianza può essere stretto o non stretto. Per loro vale la seguente affermazione:

Teorema. Qualsiasi disuguaglianza irrazionale della forma

Equivalente al sistema di disuguaglianze:

Non debole? Vediamo da dove viene questo sistema:

1. f (x) ≤ g 2 (x) - qui è tutto chiaro. Questa è la disuguaglianza originaria al quadrato;
2. f(x) ≥ 0 è ODZ della radice. Lascia che te lo ricordi: la radice quadrata aritmetica esiste solo da non negativo numeri;
3. g(x) ≥ 0 è l'intervallo della radice. Riequilibrando la disuguaglianza, bruciamo gli aspetti negativi. Di conseguenza, potrebbero apparire radici extra. La disuguaglianza g(x) ≥ 0 li esclude.

Molti studenti “rimangono bloccati” sulla prima disuguaglianza del sistema: f (x) ≤ g 2 (x) - e dimenticano completamente le altre due. Il risultato è prevedibile: decisione sbagliata, punti persi.

Poiché le disuguaglianze irrazionali sono sufficienti argomento complesso, diamo un'occhiata a 4 esempi contemporaneamente. Da base a veramente complesso. Tutti i problemi sono presi da esami di ammissione Università statale di Mosca dal nome MV Lomonosov.

Esempi di risoluzione dei problemi

Compito. Risolvi la disuguaglianza:

Davanti a noi c'è un classico disuguaglianza irrazionale: f(x) = 2x + 3; g(x) = 2 - costante. Abbiamo:

Delle tre disuguaglianze, solo due rimanevano alla fine della soluzione. Perché la disuguaglianza 2 ≥ 0 vale sempre. Incrociamo le restanti disuguaglianze:

Quindi, x ∈ [−1,5; 0,5]. Tutti i punti sono ombreggiati perché le disuguaglianze non sono rigorose.

Compito. Risolvi la disuguaglianza:

Applichiamo il teorema:

Risolviamo la prima disuguaglianza. Per fare ciò, riveleremo il quadrato della differenza. Abbiamo:

2x2 − 18x + 16< (x − 4) 2 ;
2x2 − 18x + 16< x 2 − 8x + 16:
x2-10x< 0;
x(x-10)< 0;
x∈ (0; 10).

Ora risolviamo la seconda disuguaglianza. Anche lì trinomio quadratico:

2x 2 − 18x + 16 ≥ 0;
x2 − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪)