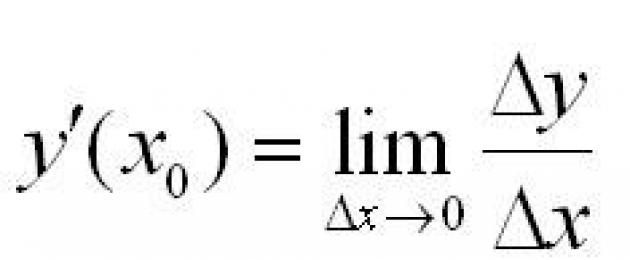Risolvere problemi fisici o esempi in matematica è completamente impossibile senza la conoscenza della derivata e dei metodi per calcolarla. La derivata è uno dei concetti più importanti nell'analisi matematica. Abbiamo deciso di dedicare l’articolo di oggi a questo argomento fondamentale. Cos'è una derivata, qual è il suo significato fisico e geometrico, come si calcola la derivata di una funzione? Tutte queste domande possono essere combinate in una sola: come comprendere la derivata?

Significato geometrico e fisico della derivata

Lascia che ci sia una funzione f(x) , specificato in un certo intervallo (a, b) . I punti x e x0 appartengono a questo intervallo. Quando x cambia, cambia la funzione stessa. Cambiare l'argomento: la differenza nei suoi valori x-x0 . Questa differenza è scritta come delta x ed è chiamato incremento dell'argomento. Una modifica o incremento di una funzione è la differenza tra i valori di una funzione in due punti. Definizione di derivato:

La derivata di una funzione in un punto è il limite del rapporto tra l'incremento della funzione in un dato punto e l'incremento dell'argomento quando quest'ultimo tende a zero.

Altrimenti si può scrivere così:

Che senso ha trovare un limite del genere? Ed ecco di cosa si tratta:

la derivata di una funzione in un punto è uguale alla tangente dell'angolo compreso tra l'asse OX e la tangente al grafico della funzione in un dato punto.

Significato fisico del derivato: la derivata del percorso rispetto al tempo è pari alla velocità del moto rettilineo.

Infatti, fin dai tempi della scuola tutti sanno che la velocità è un percorso particolare x=f(t) e tempo T . Velocità media in un certo periodo di tempo:

Per scoprire la velocità del movimento in un momento nel tempo t0 devi calcolare il limite:

Regola uno: imposta una costante

La costante può essere tolta dal segno della derivata. Inoltre, questo deve essere fatto. Quando risolvi esempi in matematica, prendilo come regola: Se puoi semplificare un'espressione, assicurati di semplificarla .

Esempio. Calcoliamo la derivata:

Seconda regola: derivata della somma di funzioni

La derivata della somma di due funzioni è uguale alla somma delle derivate di queste funzioni. Lo stesso vale per la derivata della differenza di funzioni.

Non daremo una dimostrazione di questo teorema, ma considereremo piuttosto un esempio pratico.

Trova la derivata della funzione:

Regola tre: derivata del prodotto di funzioni

La derivata del prodotto di due funzioni differenziabili si calcola con la formula:

Esempio: trova la derivata di una funzione:

Soluzione:

È importante parlare qui del calcolo delle derivate di funzioni complesse. La derivata di una funzione complessa è uguale al prodotto della derivata di questa funzione rispetto all'argomento intermedio e della derivata dell'argomento intermedio rispetto alla variabile indipendente.

Nell'esempio sopra ci imbattiamo nell'espressione:

In questo caso l'argomento intermedio è 8x elevato alla quinta potenza. Per calcolare la derivata di tale espressione, calcoliamo prima la derivata della funzione esterna rispetto all'argomento intermedio, quindi moltiplichiamo per la derivata dell'argomento intermedio stesso rispetto alla variabile indipendente.

Regola quattro: derivata del quoziente di due funzioni

Formula per determinare la derivata del quoziente di due funzioni:

Abbiamo provato a parlare di derivati for dummies partendo da zero. Questo argomento non è così semplice come sembra, quindi attenzione: negli esempi ci sono spesso delle insidie, quindi fai attenzione quando calcoli le derivate.

Per qualsiasi domanda su questo e altri argomenti è possibile contattare il servizio studenti. In breve tempo ti aiuteremo a risolvere i test più difficili e a comprendere i compiti, anche se non hai mai fatto calcoli derivativi prima.

Le derivate parziali di una funzione di più variabili sono funzioni delle stesse variabili. Queste funzioni, a loro volta, possono avere derivate parziali, che chiameremo derivate parziali seconde (o derivate parziali del secondo ordine) della funzione originaria.

Ad esempio, una funzione di due variabili ha quattro derivate parziali del secondo ordine, definite e denotate come segue:

Una funzione di tre variabili ha nove derivate parziali del secondo ordine:

Le derivate parziali del terzo e superiore ordine di una funzione a più variabili sono definite e denotate in modo simile: la derivata parziale dell'ordine di una funzione a più variabili è la derivata parziale del primo ordine della derivata parziale dell'ordine della stessa funzione.

Ad esempio, la derivata parziale del terzo ordine di una funzione è la derivata parziale del primo ordine rispetto a y della derivata parziale del secondo ordine

Una derivata parziale di secondo o ordine superiore presa rispetto a più variabili diverse è chiamata derivata parziale mista.

Ad esempio, le derivate parziali

sono derivate parziali miste di una funzione di due variabili.

Esempio. Trovare le derivate parziali miste del secondo ordine di una funzione

Soluzione. Determinazione delle derivate parziali del primo ordine

Troviamo poi le derivate parziali miste del secondo ordine

Vediamo che le derivate parziali miste, che differiscono tra loro solo nell'ordine di differenziazione, cioè nella sequenza in cui viene effettuata la differenziazione rispetto a varie variabili, si sono rivelate identicamente uguali. Questo risultato non è casuale. Per quanto riguarda le derivate parziali miste vale il seguente teorema, che accettiamo senza dimostrazione.

Derivate parziali di una funzione di due variabili.
Concetto ed esempi di soluzioni

In questa lezione continueremo la nostra conoscenza con la funzione di due variabili e considereremo forse il compito tematico più comune: la ricerca derivate parziali del primo e del secondo ordine, nonché differenziale totale della funzione. Gli studenti a tempo parziale, di regola, incontrano le derivate parziali nel 1° anno del 2° semestre. Inoltre, secondo le mie osservazioni, il compito di trovare le derivate parziali compare quasi sempre nell'esame.

Per studiare in modo efficace il materiale seguente, tu necessario essere in grado di trovare con maggiore o minore sicurezza le derivate “ordinarie” di funzioni di una variabile. Puoi imparare come gestire correttamente i derivati nelle lezioni Come trovare la derivata? E Derivata di una funzione complessa. Avremo anche bisogno di una tabella delle derivate delle funzioni elementari e delle regole di differenziazione, la cosa più conveniente è averla a portata di mano in forma stampata. È possibile ottenere materiale di riferimento nella pagina Formule e tabelle matematiche.

Ripetiamo velocemente il concetto di funzione di due variabili, cercherò di limitarmi al minimo indispensabile. Una funzione di due variabili viene solitamente scritta come , con le variabili chiamate variabili indipendenti O argomenti.

Esempio: – funzione di due variabili.

A volte viene utilizzata la notazione. Ci sono anche attività in cui viene utilizzata la lettera invece di una lettera.

Da un punto di vista geometrico, una funzione a due variabili rappresenta molto spesso una superficie nello spazio tridimensionale (piano, cilindro, sfera, paraboloide, iperboloide, ecc.). Ma in realtà questa è più geometria analitica, e nella nostra agenda c’è l’analisi matematica, che il mio professore universitario non mi ha mai lasciato cancellare ed è il mio “punto di forza”.

Passiamo alla questione della ricerca delle derivate parziali del primo e del secondo ordine. Ho alcune buone notizie per coloro che hanno bevuto qualche tazza di caffè e si stanno sintonizzando su materiale incredibilmente difficile: le derivate parziali sono quasi identiche alle derivate “ordinarie” di una funzione di una variabile.

Per le derivate parziali valgono tutte le regole di derivazione e la tabella delle derivate delle funzioni elementari. Ci sono solo un paio di piccole differenze, che vedremo subito:

...sì, comunque, per questo argomento che ho creato piccolo libro in pdf, che ti permetterà di “mettere i denti” in appena un paio d'ore. Ma utilizzando il sito, ovviamente, otterrai anche il risultato, forse solo un po' più lentamente:

Esempio 1

Trovare le derivate parziali del primo e del secondo ordine della funzione

Per prima cosa troviamo le derivate parziali del primo ordine. Ce ne sono due.

Designazioni:
oppure – derivata parziale rispetto a “x”
oppure – derivata parziale rispetto a “y”

Cominciamo con . Quando troviamo la derivata parziale rispetto a “x”, la variabile è considerata una costante (numero costante).

Commenti sulle azioni eseguite:

(1) La prima cosa che facciamo quando troviamo la derivata parziale è concludere Tutto funzione tra parentesi sotto il primo con pedice.

Attenzione, importante! NON PERDIAMO pedici durante il processo di soluzione. In questo caso, se disegni un "tratto" da qualche parte senza , l'insegnante, come minimo, può metterlo accanto al compito (mordere immediatamente parte del punto per disattenzione).

(2) Usiamo le regole di differenziazione , . Per un semplice esempio come questo, entrambe le regole possono essere facilmente applicate in un unico passaggio. Attenzione al primo termine: da allora è considerata una costante e qualsiasi costante può essere eliminata dal segno della derivata, quindi lo mettiamo tra parentesi. Cioè, in questa situazione non è migliore di un numero normale. Consideriamo ora il terzo termine: qui invece non c'è niente da togliere. Poiché è una costante, è anche una costante e in questo senso non è migliore dell'ultimo termine: "sette".

(3) Utilizziamo derivati tabulari e .

(4) Semplifichiamo o, come mi piace dire, “modifichiamo” la risposta.

Ora . Quando troviamo la derivata parziale rispetto a “y”, allora la variabileconsiderata una costante (numero costante).

(1) Usiamo le stesse regole di differenziazione , . Nel primo termine togliamo la costante dal segno della derivata, nel secondo termine non possiamo togliere nulla perché è già una costante.

(2) Utilizziamo la tabella delle derivate delle funzioni elementari. Cambiamo mentalmente tutte le “X” della tabella in “I”. Cioè, questa tabella è ugualmente valida per (e in effetti per quasi tutte le lettere). In particolare, le formule che utilizziamo assomigliano a questa: e .

Qual è il significato delle derivate parziali?

In sostanza, le derivate parziali del primo ordine somigliano derivata "ordinaria".:

- Questo funzioni, che caratterizzano tasso di cambiamento funziona rispettivamente nella direzione degli assi e . Quindi, ad esempio, la funzione caratterizza la pendenza di “rialzi” e “pendii” superfici nella direzione dell'asse delle ascisse, e la funzione ci informa del “rilievo” della stessa superficie nella direzione dell'asse delle ordinate.

! Nota : qui intendiamo indicazioni che parallelo assi coordinati.

Per una migliore comprensione, consideriamo un punto specifico sul piano e calcoliamo il valore della funzione (“altezza”) in esso:
– e ora immagina di essere qui (IN superficie).

Calcoliamo la derivata parziale rispetto a "x" in un dato punto:

Il segno negativo della derivata “X” ci parla di decrescente funziona in un punto nella direzione dell'asse delle ascisse. In altre parole, se facciamo un piccolo, piccolo (infinitesimale) passo verso la punta dell'asse (parallelo a questo asse), poi scenderemo lungo la pendenza della superficie.

Ora scopriamo la natura del “terreno” nella direzione dell'asse delle ordinate:

La derivata rispetto alla “y” è quindi positiva in un punto nella direzione dell'asse della funzione aumenta. Per dirla semplicemente, qui ci aspetta una salita.

Inoltre, la derivata parziale in un punto caratterizza tasso di cambiamento funzioni nella direzione corrispondente. Maggiore è il valore risultante modulo– più la superficie è ripida, e viceversa, più è vicina allo zero, più la superficie è piatta. Quindi, nel nostro esempio, la “pendenza” in direzione dell’asse delle ascisse è più ripida della “montagna” in direzione dell’asse delle ordinate.

Ma quelli erano due percorsi privati. È abbastanza chiaro che, dal punto in cui ci troviamo, (e in generale da qualsiasi punto di una data superficie) possiamo muoverci in qualche altra direzione. C'è quindi interesse a creare una "mappa di navigazione" generale che ci informi sul "paesaggio" della superficie se possibile in ogni punto dominio di definizione di questa funzione lungo tutti i sentieri disponibili. Di questo e di altre cose interessanti parlerò in una delle lezioni successive, ma per ora torniamo al lato tecnico della questione.

Sistematizziamo le regole elementari applicate:

1) Quando differenziamo rispetto a , la variabile è considerata una costante.

2) Quando la differenziazione viene effettuata secondo, allora è considerata una costante.

3) Le regole e la tabella delle derivate delle funzioni elementari sono valide e applicabili per qualsiasi variabile (o qualsiasi altra) mediante la quale si effettua la differenziazione.

Passo due. Troviamo le derivate parziali del secondo ordine. Ce ne sono quattro.

Designazioni:
oppure – derivata seconda rispetto a “x”
oppure – derivata seconda rispetto a “y”
O - misto derivato di “x per igr”
O - misto derivata di "Y"

Non ci sono problemi con la derivata seconda. In termini semplici, la derivata seconda è la derivata della derivata prima.

Per comodità riscrivo le derivate parziali del primo ordine già trovate:

Innanzitutto, troviamo le derivate miste:

Come puoi vedere, tutto è semplice: prendiamo la derivata parziale e la differenziamo di nuovo, ma in questo caso - questa volta secondo la "Y".

Allo stesso modo:

Negli esempi pratici, puoi concentrarti sulla seguente uguaglianza:

Pertanto, attraverso le derivate miste del secondo ordine è molto conveniente verificare se abbiamo trovato correttamente le derivate parziali del primo ordine.

Trovare la derivata seconda rispetto a “x”.
Niente invenzioni, prendiamolo e differenziarlo nuovamente con “x”:

Allo stesso modo:

Va notato che quando si trova è necessario mostrare maggiore attenzione, poiché non esistono uguaglianze miracolose che le possano verificare.

Anche le derivate seconde trovano ampie applicazioni pratiche, in particolare vengono utilizzate nel problema della ricerca estremi di una funzione di due variabili. Ma ogni cosa ha il suo tempo:

Esempio 2

Calcolare le derivate parziali del primo ordine della funzione nel punto. Trova le derivate del secondo ordine.

Questo è un esempio che puoi risolvere da solo (risposte alla fine della lezione). Se hai difficoltà a distinguere le radici, torna alla lezione Come trovare la derivata? In generale, molto presto imparerai a trovare tali derivati “al volo”.

Miglioriamo con esempi più complessi:

Esempio 3

Controlla quello. Annotare il differenziale totale del primo ordine.

Soluzione: Trovare le derivate parziali del primo ordine:

Attenzione al pedice: , accanto alla “X” non è vietato scrivere tra parentesi che è una costante. Questa nota può essere molto utile per i principianti per facilitare la navigazione nella soluzione.

Ulteriori commenti:

(1) Spostiamo tutte le costanti oltre il segno della derivata. In questo caso, e , e, quindi, il loro prodotto è considerato un numero costante.

(2) Non dimenticare come differenziare correttamente le radici.

(1) Togliamo tutte le costanti dal segno della derivata, in questo caso la costante è .

(2) Sotto il numero primo rimane il prodotto di due funzioni, quindi dobbiamo utilizzare la regola per differenziare il prodotto .

(3) Non dimenticare che questa è una funzione complessa (anche se la più semplice delle complesse). Usiamo la regola corrispondente: .

Troviamo ora le derivate miste del secondo ordine:

Ciò significa che tutti i calcoli sono stati eseguiti correttamente.

Scriviamo il differenziale totale. Nel contesto del compito in esame, non ha senso dire quale sia il differenziale totale di una funzione di due variabili. È importante che questo differenziale molto spesso debba essere scritto in problemi pratici.

Differenziale totale del primo ordine una funzione di due variabili ha la forma:

In questo caso:

Cioè, devi solo sostituire stupidamente le derivate parziali del primo ordine già trovate nella formula. In questa e in situazioni simili, è meglio scrivere i segni differenziali nei numeratori:

E secondo le ripetute richieste dei lettori, differenziale totale del secondo ordine.

Sembra questo:

Troviamo ATTENTAMENTE i derivati “di una lettera” del 2° ordine:

e annotare il “mostro”, “attaccando” con cura i quadrati, il prodotto e senza dimenticare di raddoppiare la derivata mista:

Non c'è problema se qualcosa sembra difficile; puoi sempre tornare alle derivate più tardi, dopo aver padroneggiato la tecnica di differenziazione:

Esempio 4

Trovare le derivate parziali del primo ordine di una funzione . Controlla quello. Annotare il differenziale totale del primo ordine.

Vediamo una serie di esempi con funzioni complesse:

Esempio 5

Trovare le derivate parziali del primo ordine della funzione.

Soluzione:

Esempio 6

Trovare le derivate parziali del primo ordine di una funzione .
Annotare il differenziale totale.

Questo è un esempio che puoi risolvere da solo (risposta alla fine della lezione). Non ti darò una soluzione completa perché è abbastanza semplice.

Molto spesso, tutte le regole di cui sopra vengono applicate in combinazione.

Esempio 7

Trovare le derivate parziali del primo ordine di una funzione .

(1) Usiamo la regola per differenziare la somma

(2) Il primo termine in questo caso è considerato una costante, poiché nell'espressione non c'è nulla che dipenda dalla “x” - solo “y”. Sai, è sempre bello quando una frazione può essere trasformata in zero). Per il secondo termine applichiamo la regola di differenziazione del prodotto. D'altronde in questo senso non sarebbe cambiato nulla se invece fosse stata data una funzione: qui l'importante è quella prodotto di due funzioni, OGNUNO dei quali dipende da "X", e pertanto è necessario utilizzare la regola di differenziazione del prodotto. Per il terzo termine applichiamo la regola di derivazione di una funzione complessa.

(1) Il primo termine sia del numeratore che del denominatore contiene una "Y", pertanto è necessario utilizzare la regola per differenziare i quozienti: . Il secondo termine dipende SOLO da “x”, il che significa che è considerato una costante e tende a zero. Per il terzo termine utilizziamo la regola per differenziare una funzione complessa.

Per quei lettori che coraggiosamente sono arrivati quasi alla fine della lezione, per sollievo racconterò una vecchia battuta di Mekhmatov:

Un giorno, nello spazio delle funzioni, è apparso un derivato malvagio che ha iniziato a differenziare tutti. Tutte le funzioni sono sparse in tutte le direzioni, nessuno vuole trasformarsi! E solo una funzione non scappa. Il derivato le si avvicina e le chiede:

- Perché non scappi da me?

- Ah. Ma non mi interessa, perché sono “e alla potenza di X”, e tu non mi farai niente!

Al che il derivato malvagio con un sorriso insidioso risponde:

- È qui che ti sbagli, ti differenzierò per “Y”, quindi dovresti essere uno zero.

Chiunque abbia capito lo scherzo padroneggia i derivati, almeno al livello “C”).

Esempio 8

Trovare le derivate parziali del primo ordine di una funzione .

Questo è un esempio che puoi risolvere da solo. La soluzione completa e l'esempio del problema si trovano alla fine della lezione.

Bene, questo è quasi tutto. Infine, non posso fare a meno di compiacere gli amanti della matematica con un altro esempio. Non si tratta nemmeno di dilettanti, ognuno ha un diverso livello di preparazione matematica: ci sono persone (e non così rare) a cui piace competere con compiti più difficili. Tuttavia, l'ultimo esempio di questa lezione non è tanto complesso quanto macchinoso da un punto di vista computazionale.

In questa lezione conosceremo il concetto di funzione di due variabili e considereremo anche in dettaglio il compito più comune: trovare derivate parziali primo e secondo ordine, differenziale completo di una funzione.

Per studiare in modo efficace il materiale seguente, tu necessario essere in grado di trovare con maggiore o minore sicurezza le derivate “ordinarie” di funzioni di una variabile. Puoi imparare come gestire correttamente i derivati nelle lezioni Come trovare la derivata? e Derivata di una funzione complessa. Avremo anche bisogno di una tabella delle derivate delle funzioni elementari e delle regole di differenziazione, la cosa più conveniente è averla a portata di mano in forma stampata.

Cominciamo con il concetto stesso di funzione di due variabili, cercheremo di limitarci al minimo teorico, poiché il sito ha un orientamento pratico. Una funzione di due variabili viene solitamente scritta come , con le variabili chiamate variabili indipendenti O argomenti.

Esempio: - funzione di due variabili.

A volte viene utilizzata la notazione. Ci sono anche attività in cui viene utilizzata la lettera invece di una lettera.

È utile conoscere il significato geometrico delle funzioni. Una funzione di una variabile corrisponde a una certa linea su un piano, ad esempio la parabola scolastica familiare. Qualsiasi funzione di due variabili dal punto di vista geometrico rappresenta una superficie nello spazio tridimensionale (piani, cilindri, sfere, paraboloidi, ecc.). Ma, in realtà, questa è già geometria analitica e l'analisi matematica è nella nostra agenda.

Per le derivate parziali valgono tutte le regole di derivazione e la tabella delle derivate delle funzioni elementari. Ci sono solo un paio di piccole differenze, di cui parleremo tra poco.

Esempio 1

Trovare le derivate parziali del primo e del secondo ordine della funzione

Per prima cosa troviamo le derivate parziali del primo ordine. Ce ne sono due.

Designazioni:

Oppure – derivata parziale rispetto a “x”

Oppure – derivata parziale rispetto a “y”

Cominciamo con .

Importante! Quando troviamo la derivata parziale rispetto a “x”, allora la variabile è considerata una costante (numero costante).

Decidiamo. In questa lezione forniremo immediatamente la soluzione completa e forniremo i commenti di seguito.

Commenti sulle azioni eseguite:

(1) La prima cosa che facciamo quando troviamo la derivata parziale è concludere Tutto funzione tra parentesi sotto il primo con pedice.

(2) Usiamo le regole di differenziazione ; . Per un semplice esempio come questo, entrambe le regole possono essere facilmente applicate in un unico passaggio. Attenzione al primo termine: da allora è considerata una costante e qualsiasi costante può essere eliminata dal segno della derivata, quindi lo mettiamo tra parentesi. Cioè, in questa situazione non è migliore di un numero normale. Consideriamo ora il terzo termine: qui invece non c'è niente da togliere. Poiché è una costante, è anche una costante e in questo senso non è migliore dell'ultimo termine: "sette".

(2) Utilizziamo la tabella delle derivate delle funzioni elementari. Cambiamo mentalmente tutte le “X” della tabella in “I”. Cioè, questa tabella è ugualmente valida per (e per qualsiasi lettera in generale). In questo caso le formule che utilizziamo sono: e .

Si ottengono quindi le derivate parziali del primo ordine

Le derivate parziali vengono utilizzate in problemi che coinvolgono funzioni di più variabili. Le regole per la ricerca sono esattamente le stesse delle funzioni di una variabile, con l'unica differenza che una delle variabili deve essere considerata una costante (numero costante) al momento della differenziazione.

Formula

Le derivate parziali di una funzione di due variabili $ z(x,y) $ sono scritte nella seguente forma $ z"_x, z"_y $ e si trovano utilizzando le formule:

Derivate parziali del primo ordine

$$ z"_x = \frac(\partial z)(\partial x) $$

$$ z"_y = \frac(\partial z)(\partial y) $$

Derivate parziali del secondo ordine

$$ z""_(xx) = \frac(\parziale^2 z)(\parziale x \parziale x) $$

$$ z""_(yy) = \frac(\partial^2 z)(\partial y \partial y) $$

Derivato misto

$$ z""_(xy) = \frac(\partial^2 z)(\partial x \partial y) $$

$$ z""_(yx) = \frac(\parziale^2 z)(\parziale y \parziale x) $$

Derivata parziale di una funzione complessa

a) Sia $ z (t) = f(x(t), y(t)) $, quindi la derivata di una funzione complessa è determinata dalla formula:

$$ \frac(dz)(dt) = \frac(\partial z)(\partial x) \cdot \frac(dx)(dt) + \frac(\partial z)(\partial y) \cdot \frac (dy)(dt)$$

b) Sia $ z (u,v) = z(x(u,v),y(u,v)) $, quindi le derivate parziali della funzione si trovano con la formula:

$$ \frac(\partial z)(\partial u) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial u) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial u) $$

$$ \frac(\partial z)(\partial v) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial v) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial v) $$

Derivate parziali di una funzione implicita

a) Sia $ F(x,y(x)) = 0 $, allora $$ \frac(dy)(dx) = -\frac(f"_x)(f"_y) $$

b) Sia $ F(x,y,z)=0 $, allora $$ z"_x = - \frac(F"_x)(F"_z); z"_y = - \frac(F"_y)( F"_z) $$

Esempi di soluzioni

Esempio 1
Trova le derivate parziali del primo ordine $ z (x,y) = x^2 - y^2 + 4xy + 10 $
Soluzione
Per trovare la derivata parziale rispetto a $ x $, considereremo $ y $ un valore (numero) costante: $$ z"_x = (x^2-y^2+4xy+10)"_x = 2x - 0 + 4y + 0 = 2x+4y $$ Per trovare la derivata parziale di una funzione rispetto a $y$, definiamo $y$ con una costante: $$ z"_y = (x^2-y^2+4xy+10)"_y = -2y+4x $$ Se non riesci a risolvere il tuo problema, inviacelo. Forniremo una soluzione dettagliata. Potrai visualizzare lo stato di avanzamento del calcolo e ottenere informazioni. Questo ti aiuterà a ottenere il voto dal tuo insegnante in modo tempestivo!
Risposta
$$ z"_x = 2x+4y; z"_y = -2y+4x $$

Esempio 2
Trova le derivate parziali della funzione del secondo ordine $ z = e^(xy) $
Soluzione
Per prima cosa devi trovare le derivate prime, poi conoscendole puoi trovare le derivate del secondo ordine. Sia $y$ una costante: $$ z"_x = (e^(xy))"_x = e^(xy) \cdot (xy)"_x = ye^(xy) $$ Impostiamo ora $ x $ come valore costante: $$ z"_y = (e^(xy))"_y = e^(xy) \cdot (xy)"_y = xe^(xy) $$ Conoscendo le derivate prime troviamo analogamente la seconda. Imposta $y$ su costante: $$ z""_(xx) = (z"_x)"_x = (ye^(xy))"_x = (y)"_x e^(xy) + y(e^(xy))"_x = 0 + ye^(xy)\cdot (xy)"_x = y^2e^(xy) $$ Impostiamo $ x $ su una costante: $$ z""_(yy) = (z"_y)"_y = (xe^(xy))"_y = (x)"_y e^(xy) + x(e^(xy))"_y = 0 + x^2e^(xy) = x^2e^(xy) $$ Ora non resta che trovare la derivata mista. Puoi differenziare $ z"_x $ per $ y $, e puoi differenziare $ z"_y $ per $ x $, poiché per il teorema $ z""_(xy) = z""_(yx) $ $$ z""_(xy) = (z"_x)"_y = (ye^(xy))"_y = (y)"_y e^(xy) + y (e^(xy))"_y = ye^(xy)\cdot (xy)"_y = yxe^(xy) $$
Risposta
$$ z"_x = ye^(xy); z"_y = xe^(xy); z""_(xy) = yxe^(xy) $$

Esempio 4
Sia $ 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ definisca la funzione implicita $ F(x,y,z) = 0 $. Trova le derivate parziali del primo ordine.
Soluzione
Scriviamo la funzione nel formato: $ F(x,y,z) = 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ e troviamo le derivate: $$ z"_x (y,z - cost) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_x = 3 x^2 z - 4 $$ $$ z"_y (x,y - cost) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_y = 3z^2 $$
Risposta
$$ z"_x = 3x^2 z - 4; z"_y = 3z^2; $$