REVISIONATO

Consiglio pedagogico dell'istituto scolastico di Mosca

"Scuola secondaria Zashizhemskaya"

Protocollo n. 1

CONCORDATO

Vicedirettore per le risorse umane

_______ /Sidorkina R.L./

HO APPROVATO

Dirigente scolastico:

A.P. Konakov

Ordine n. 63

Risoluzione di equazioni e disequazioni con il modulo

Lavoro di ricerca

Il programma è stato redatto da:

insegnante di matematica superiore

Sidorkina R.L.

Villaggio di Zashizhemye, 2014

Sommario

Introduzione………………………………3

Le più semplici equazioni e disuguaglianze con modulo…………5

Soluzione grafica di equazioni e disequazioni con modulo………….8

Altri modi per risolvere equazioni e disequazioni con modulo.........10

Conclusione..................................................................16

Riferimenti…………………………18

1. Introduzione

Il concetto di valore assoluto (modulo) è una delle caratteristiche più importanti di un numero, sia nel campo dei numeri reali che in quelli complessi.

Questo concetto è ampiamente utilizzato non solo in varie sezioni del corso di matematica scolastica, ma anche nei corsi di matematica superiore, fisica e scienze tecniche studiati nelle università. Ad esempio, nella teoria dei calcoli approssimativi vengono utilizzati i concetti di errori assoluti e relativi di un numero approssimativo. In meccanica e geometria si studiano i concetti di vettore e la sua lunghezza (modulo vettoriale). Nell'analisi matematica, il concetto di valore assoluto di un numero è contenuto nelle definizioni di concetti di base come limite, funzione limitata, ecc. Problemi relativi ai valori assoluti si trovano spesso nelle Olimpiadi matematiche, negli esami di ammissione all'università e nell'Unificazione Esame di Stato. E così è diventato importante per noi studiare alcuni aspetti di questo argomento.

Casa scopo Il nostro lavoro consiste nello studiare vari metodi per risolvere equazioni e disequazioni con moduli.

Questo obiettivo deve essere raggiunto risolvendo quanto segue compiti:

Studiare la definizione e alcune proprietà di un modulo.

Padroneggia la soluzione di semplici equazioni e disuguaglianze con modulo attraverso transizioni equivalenti

Considera vari metodi per risolvere equazioni e disuguaglianze con il modulo.

Oggetto gli studi sono alcuni tipi di equazioni e disequazioni con modulo.

Articolo ricerca - vari metodi per risolvere equazioni e disequazioni con un modulo, vale a dire: metodo grafico, metodo di interpretazione geometrica, uso dell'identità, applicazione del teorema dei segni, metodo di transizione a una conseguenza, metodo degli intervalli, metodo di moltiplicazione per un fattore positivo, metodo di rivelazione dei moduli.

Durante lo studio sono stati utilizzati metodi come lo studio della letteratura su questo tema e il metodo pratico.

Nel corso del nostro lavoro, abbiamo esaminato fonti come:

1. “Grande Enciclopedia Matematica” per scolari e studenti;

Matematica. Esame di Stato Unificato - 2011-2012. Opzioni tipiche dell'esame. / A cura di A.L. Semenova, I.V. Yashchenko.

Enciclopedia “Conosco il mondo” Matematica;

;

1. 1. Le più semplici equazioni e disuguaglianze con modulo

Tra le equazioni più semplici includeremo equazioni che possono essere risolte mediante una delle seguenti transizioni equivalenti:

Esempi di risoluzione di semplici equazioni.

Esempio 1 Risolviamo l'equazione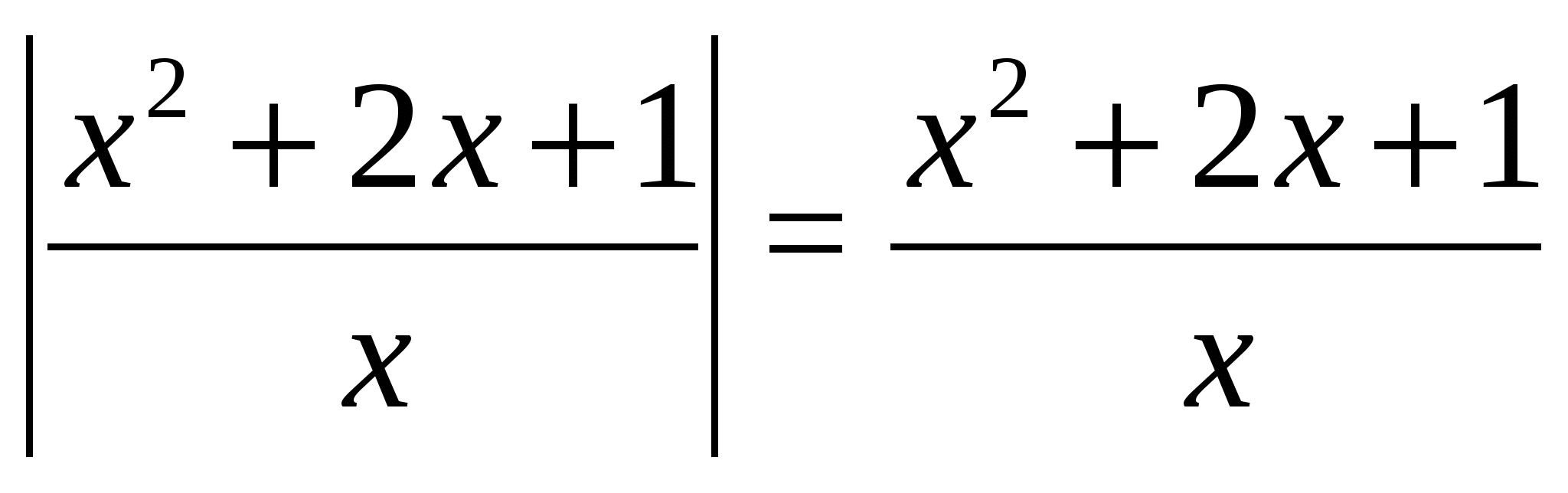
.

Soluzione.

Risposta.
.

Esempio 2 Risolviamo l'equazione.

Soluzione.

Risposta.
.

Esempio 3 Risolviamo l'equazione
.

Soluzione.

Risposta.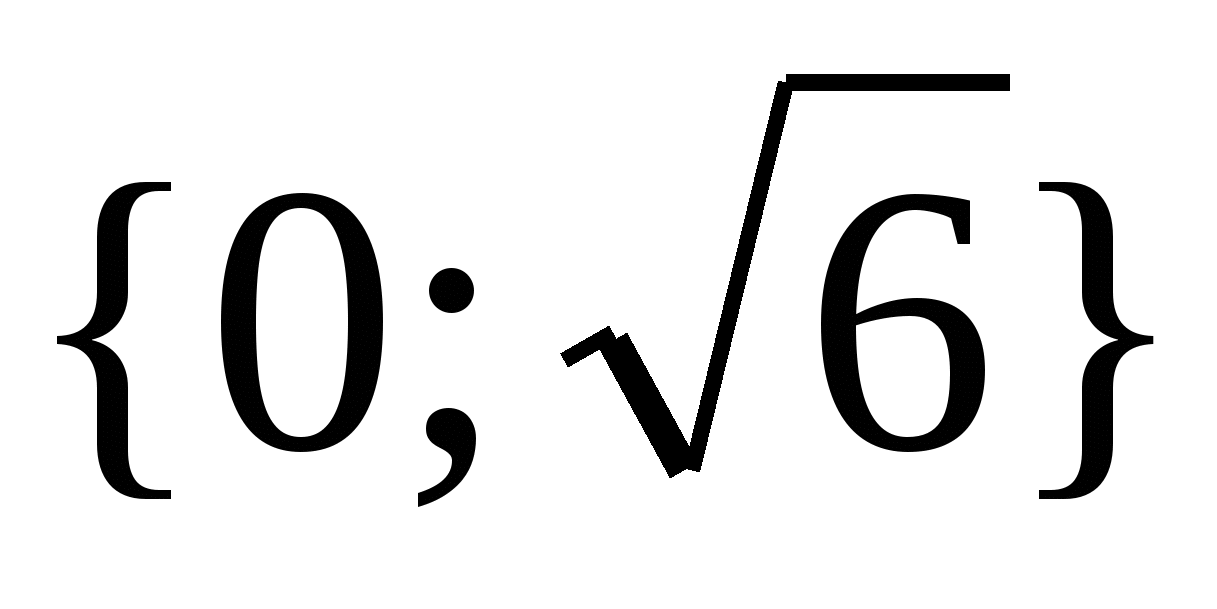
.

Una serie di equazioni vengono risolte utilizzando il seguente teorema.

Teorema.4 La somma dei moduli è uguale alla somma algebrica delle quantità submodulari se e solo se ciascuna quantità ha il segno con cui è compresa nella somma algebrica.

Esempio 5 Risolvi l'equazione

Soluzione. Poiché , allora abbiamo un'uguaglianza della forma , dove
,
. Pertanto, l’equazione originale è equivalente al sistema:

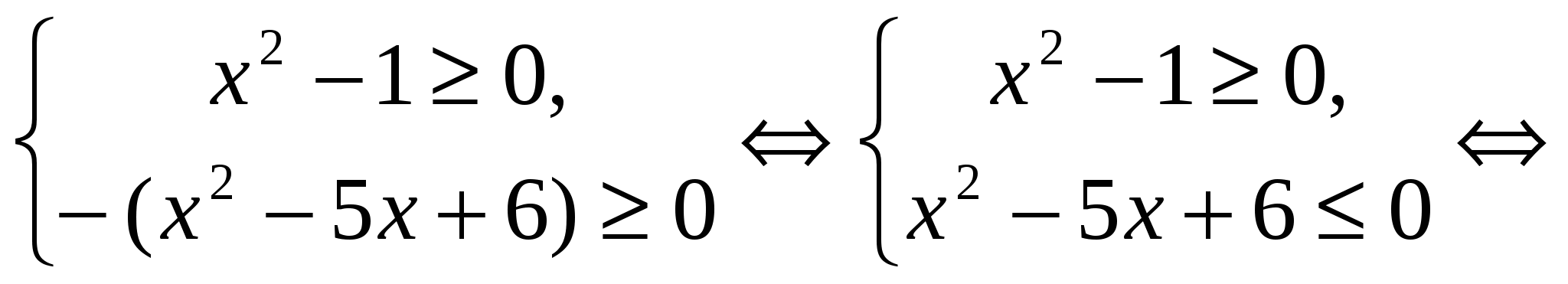
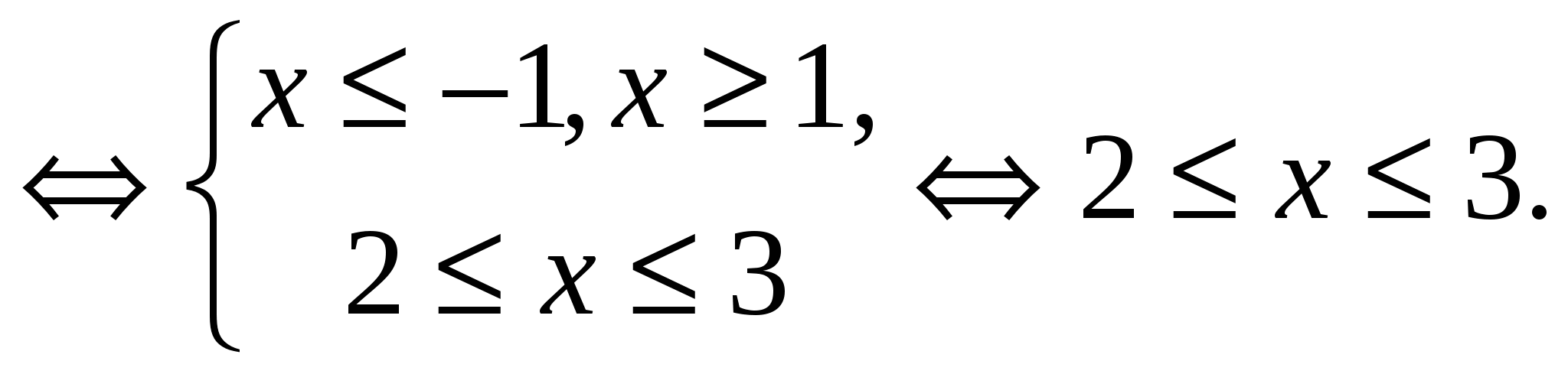
Risposta.
.

Esempi di risoluzione di disuguaglianze semplici.

Esempio 6 Risolviamo la disuguaglianza
.

Soluzione.

Risposta.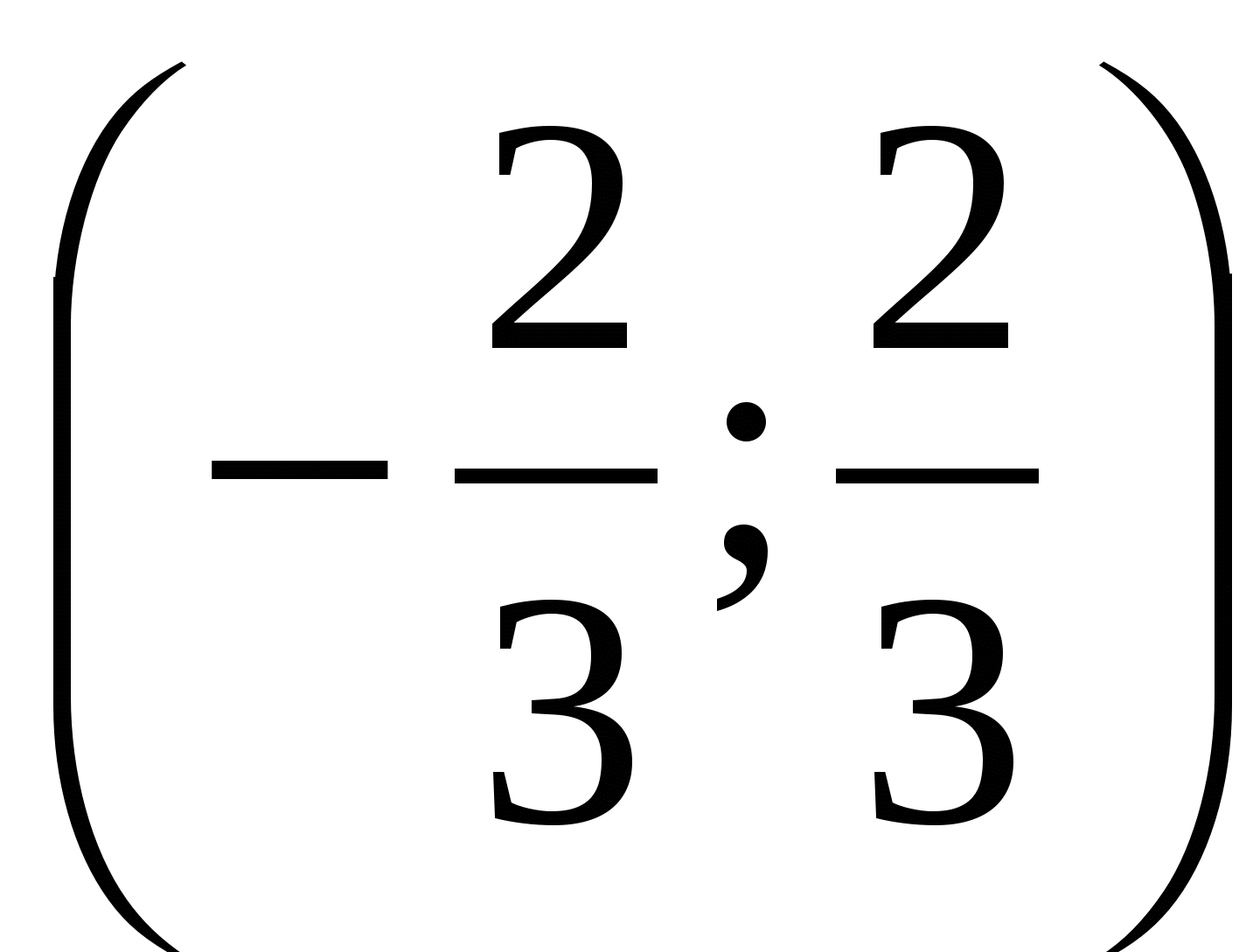
.

Esempio 7 Risolviamo la disuguaglianza
.

Soluzione.

Risposta.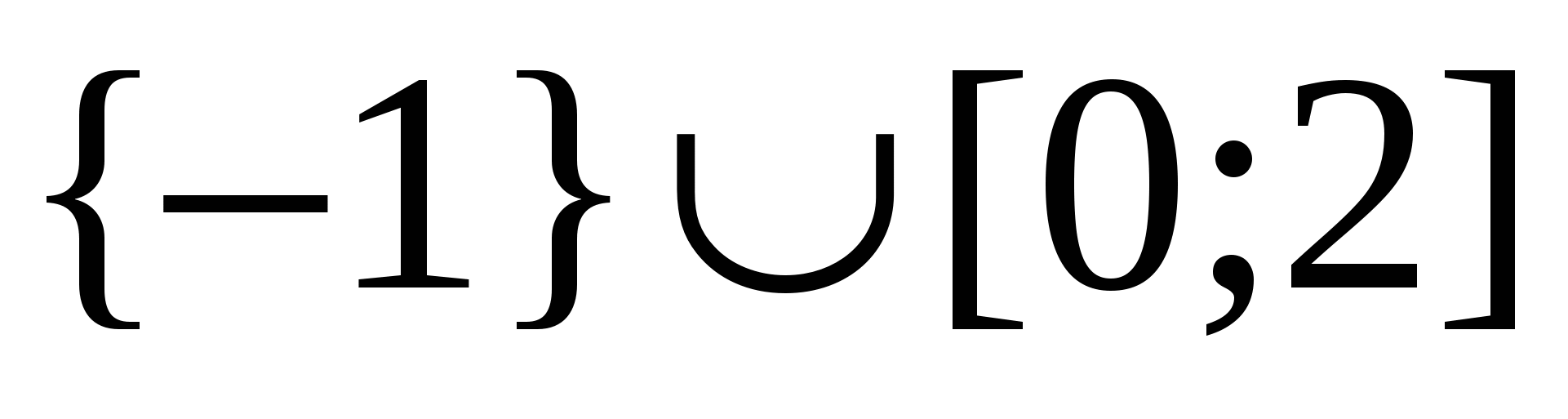
.

Stranamente, ma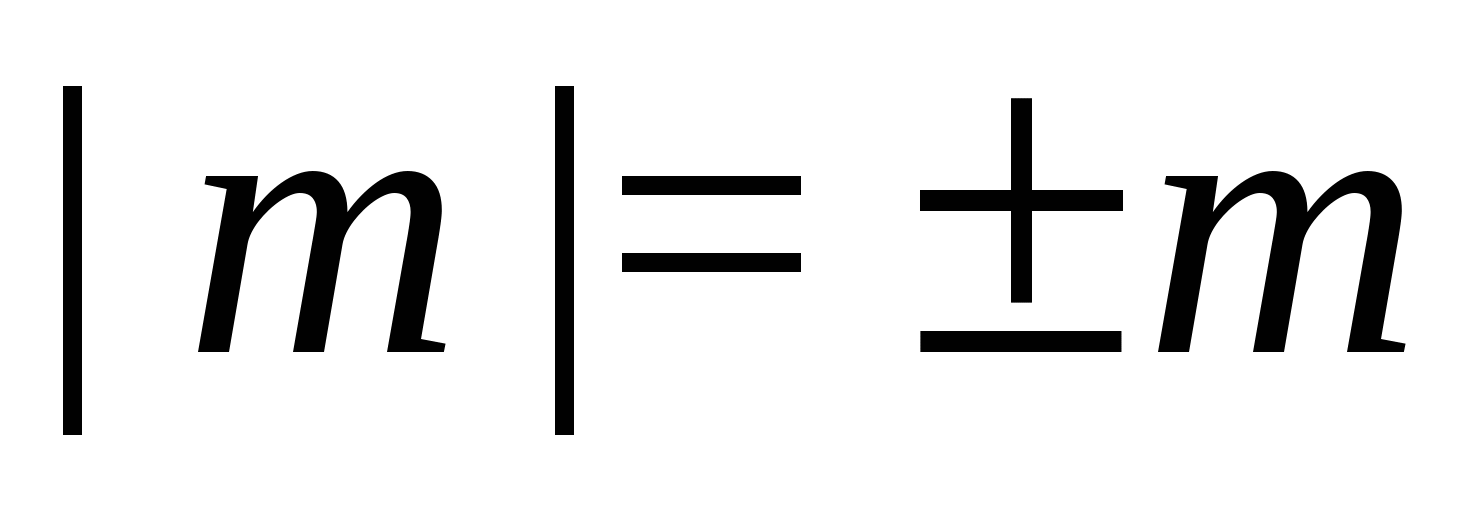
è sufficiente per eliminare il segno del modulo in eventuali disuguaglianze.

Esempio 8 Risolvere la disuguaglianza

Soluzione.

Risposta.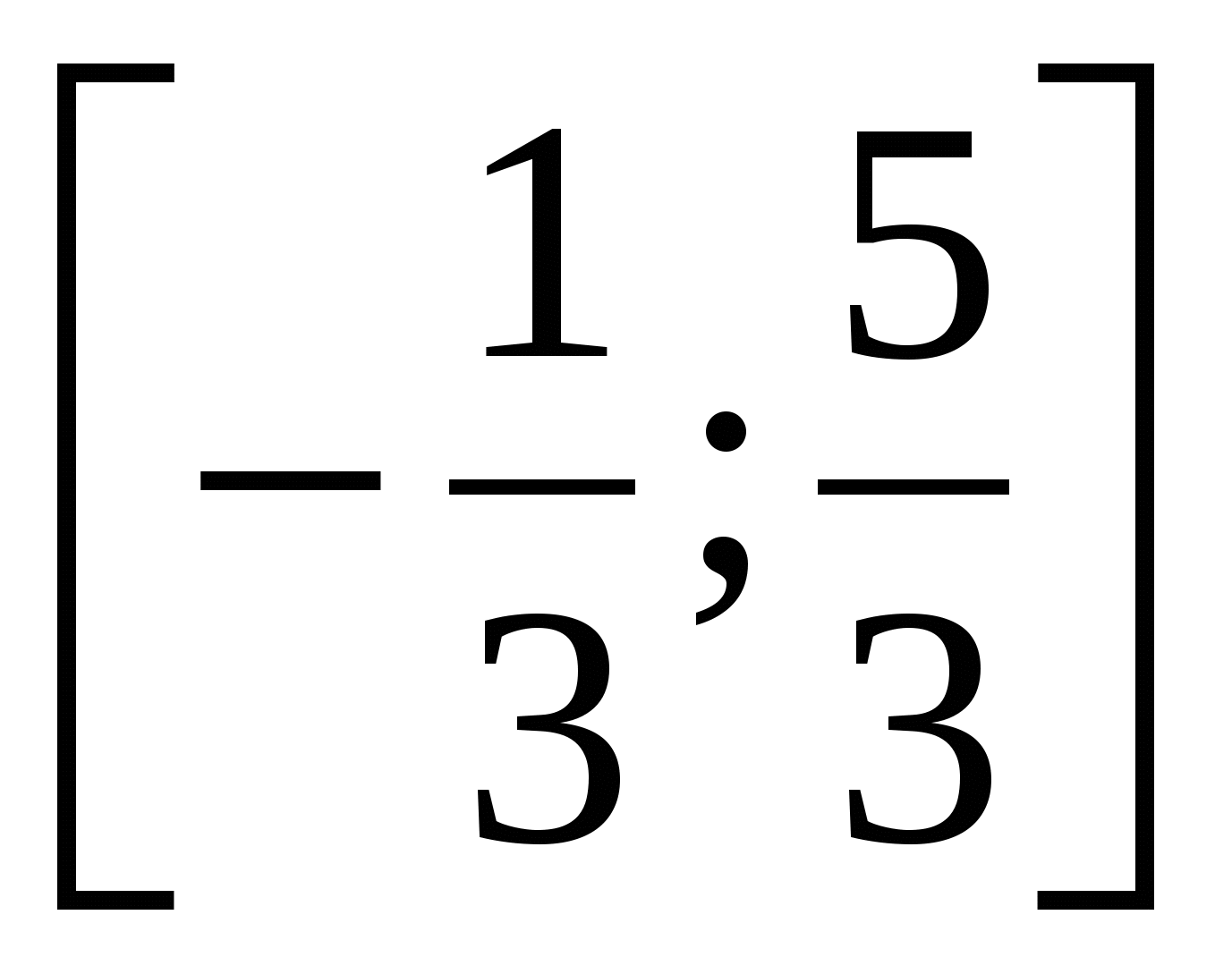
.

3. Soluzione grafica di equazioni e disequazioni con modulo

Risolvere equazioni contenenti il ​​segno di un valore assoluto è spesso molto più conveniente da risolvere non analiticamente, ma graficamente (specialmente equazioni contenenti parametri).

Esempio 9(C5, Esame di Stato Unificato - 2010)

C5. Per ciascun valoreUN indicare il numero di soluzioni dell'equazione

Soluzione.Tracciamo la funzione
. Per fare ciò, seleziona un quadrato completo:

Numero di punti di intersezione del grafico della funzione y =
con linee orizzontali y = a è uguale al numero di soluzioni dell'equazione.

DI risposta: Se < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а >4, allora ci sono due soluzioni.

Altri modi per risolvere equazioni e disequazioni con modulo

• Metodo di espansione del modulo

Diamo un'occhiata al metodo di espansione dei moduli utilizzando un esempio:

Esempio 10 Risolvi l'equazione

Soluzione. Questa equazione contiene più di un modulo.

Il metodo per risolvere equazioni contenenti variabili sotto il segno di due o più moduli è il seguente.

1. Trova i valori della variabile in cui ciascuno dei moduli diventa zero: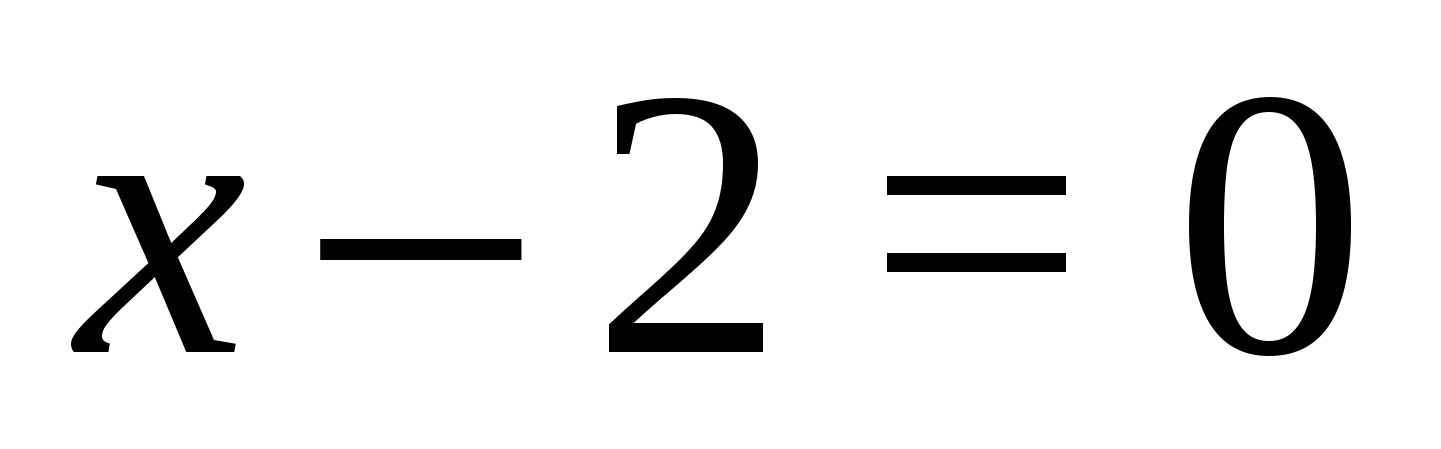
,
;
,
;
,
.

2. Segna questi punti sulla linea numerica.

3. Consideriamo l'equazione su ciascuno degli intervalli e impostiamo il segno delle espressioni che si trovano sotto i moduli.

1) Quando
O
. Per determinare il segno di ciascuna delle espressioni modulo su questo intervallo, è sufficiente assumere qualsiasi valore da questo intervallo e sostituirlo nell'espressione. Se il valore risultante è negativo, allora per tutti da questo intervallo l'espressione sarà negativa; se il valore numerico risultante è positivo, allora per tutti i valori da questo intervallo l'espressione sarà positiva.

Prendiamo il valore
di mezzo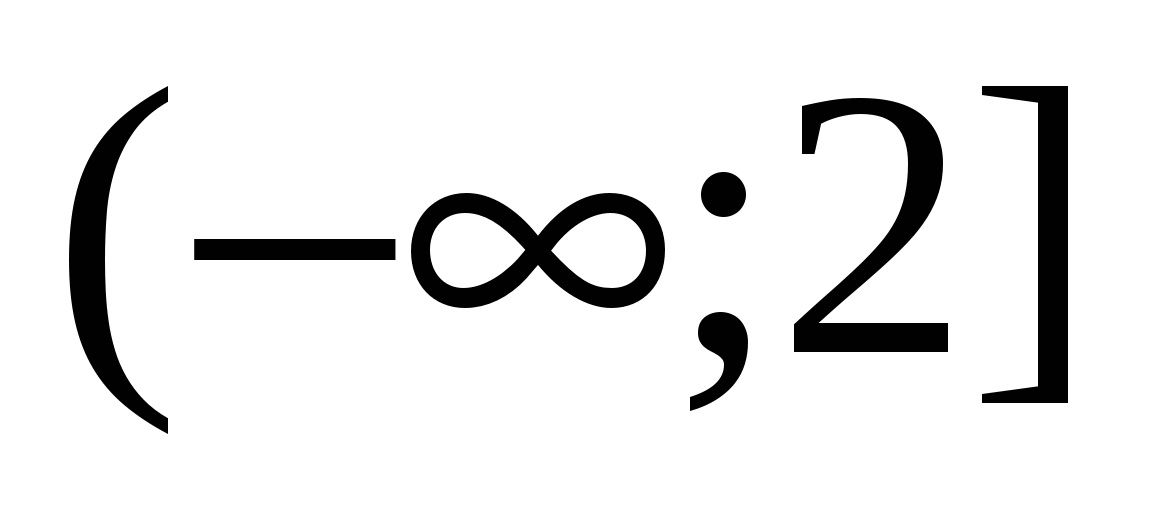
e sostituire il suo valore nell'espressione
, otteniamo
, il che significa in questo intervallo
negativo, e quindi ``uscirà"" da sotto il modulo con un segno ``meno"", otteniamo:
.

A questo valore , espressione
otterrà il valore
, il che significa che è nell'intervallo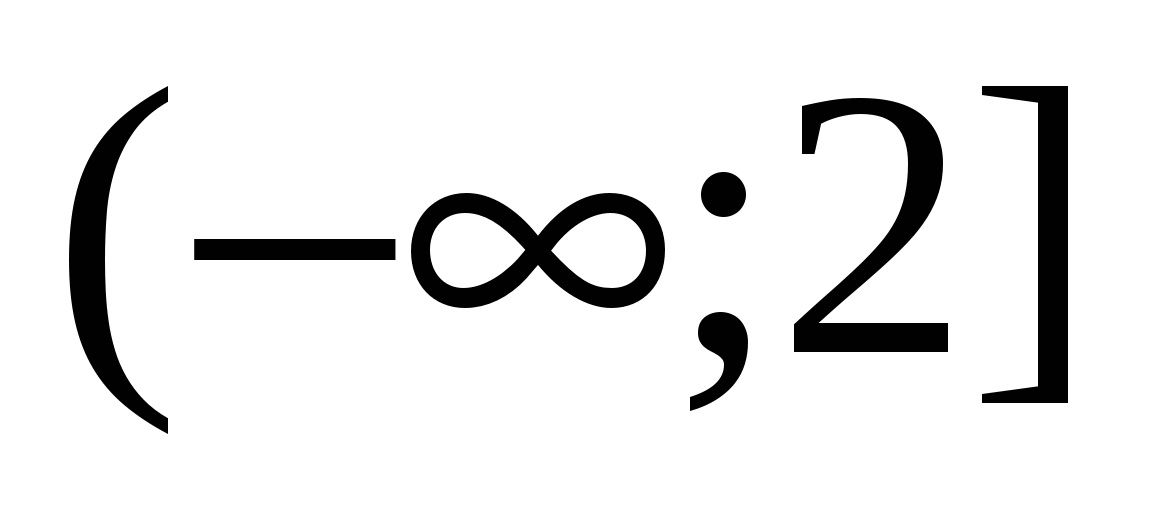
assume anche valori negativi e ``uscirà"" dal modulo con un segno ``meno"", otteniamo:
.

Espressione
otterrà il valore
e “uscirà” da sotto il modulo con un segno "meno":
.

L'equazione su questo intervallo risulterà così: risolvendola, troviamo:
.

Scopriamo se questo valore è incluso nell'intervallo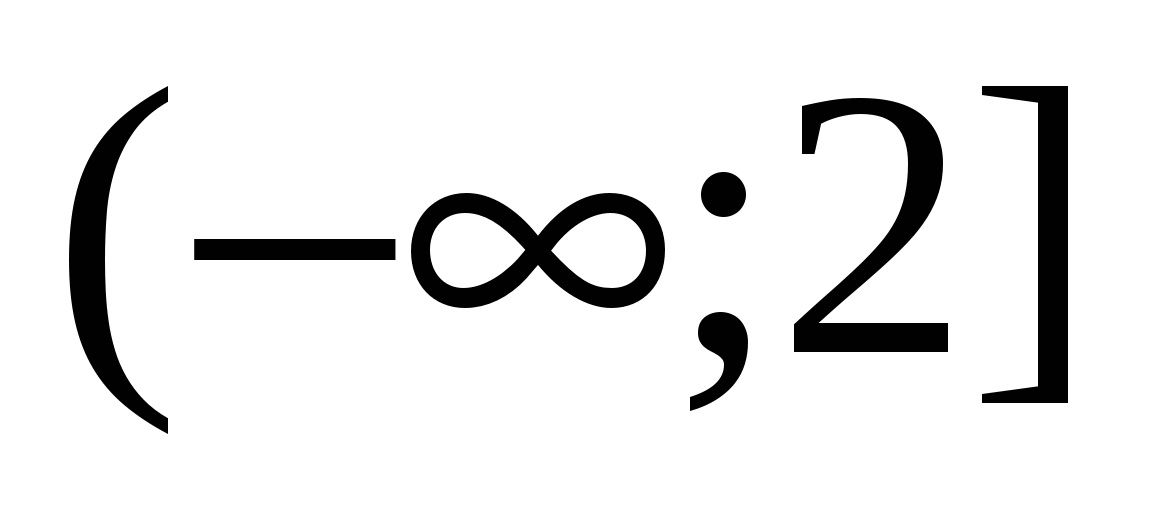
. Si scopre che è incluso, il che significa
è la radice dell'equazione.

2) Quando
. Scegli qualsiasi valore da questo divario. Permettere
. Determiniamo il segno di ciascuna delle espressioni sotto il modulo con questo valore . Si scopre che l'espressione
positivo e gli altri due negativi.

L'equazione su questo intervallo assumerà la forma: . Risolvendolo, troviamo
. Questo valore non è incluso nell'intervallo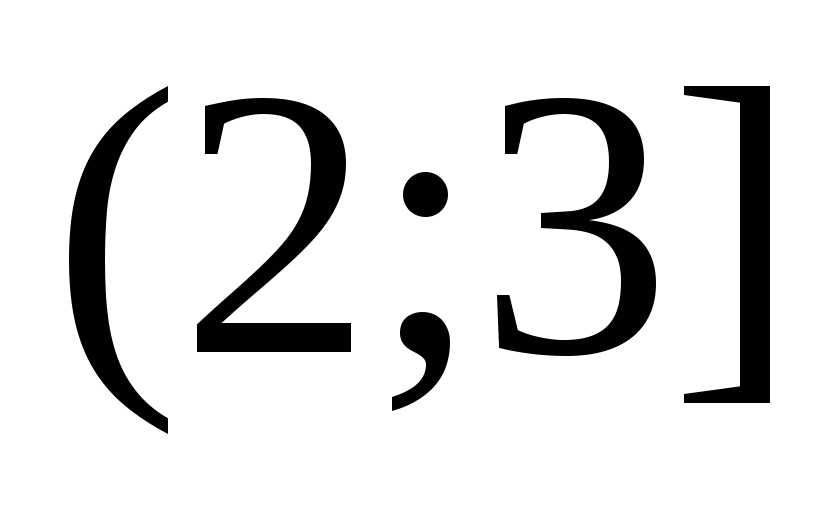
, il che significa che non è la radice dell'equazione.

3) Quando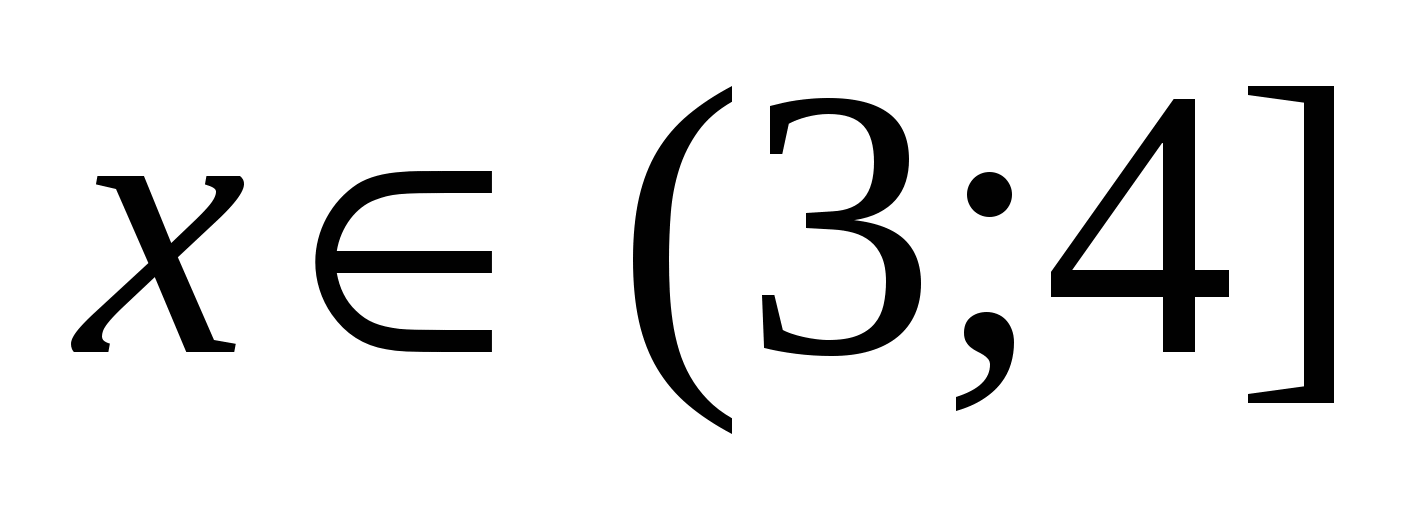
. Scegli un valore arbitrario da questo intervallo, diciamo
e sostituire in ciascuna delle espressioni. Troviamo che le espressioni
E
sono positivi e
- negativo. Otteniamo la seguente equazione: .

Dopo la trasformazione otteniamo: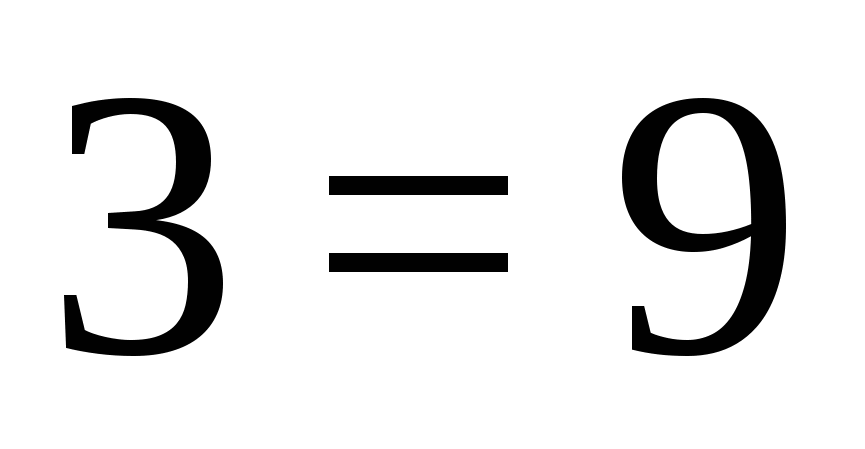
, il che significa che l'equazione non ha radici su questo intervallo.

4) Quando
. È facile stabilire che tutte le espressioni su questo intervallo sono positive, il che significa che otteniamo l'equazione: ,
,
che è incluso nell'intervallo ed è la radice dell'equazione.

Risposta.
,
.

• Risoluzione di equazioni contenenti moduli di espressioni non negative

Esempio 11 Qual è la somma delle radici dell'equazione (radice, se presente) dell'equazione

Soluzione. Considera l'espressione

e convertirlo nel modulo

È ovvio che il numeratore della frazione è un numero positivo per qualsiasi valore della variabile. Ciò significa che un'espressione frazionaria è positiva se
(Perché
). Trasformiamo l'espressione risultante, fornita
. Otteniamo un'equazione equivalente a quella originale:

Risposta.
.

Esempio 12 Risolvi l'equazione

Soluzione. Poiché il lato sinistro dell'equazione è non negativo, per tutti i valori ammissibili della variabile, sull'insieme delle radici dell'equazione anche il suo lato destro deve essere non negativo, da qui la condizione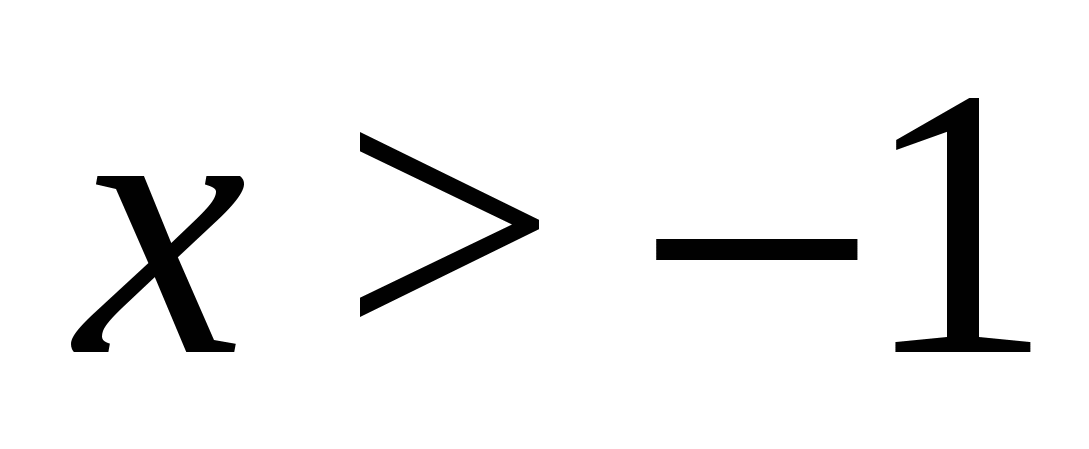
, su questo intervallo i denominatori di entrambe le frazioni sono uguali e resta da risolvere l'equazione
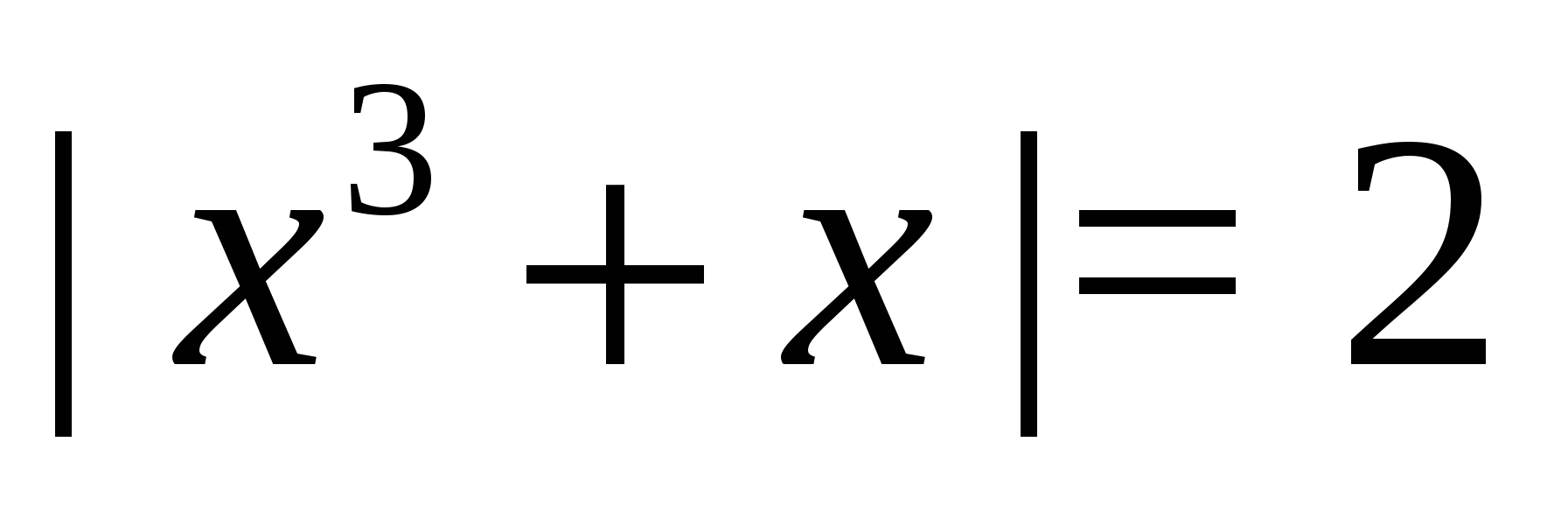. Risolverlo e tenere conto del vincolo
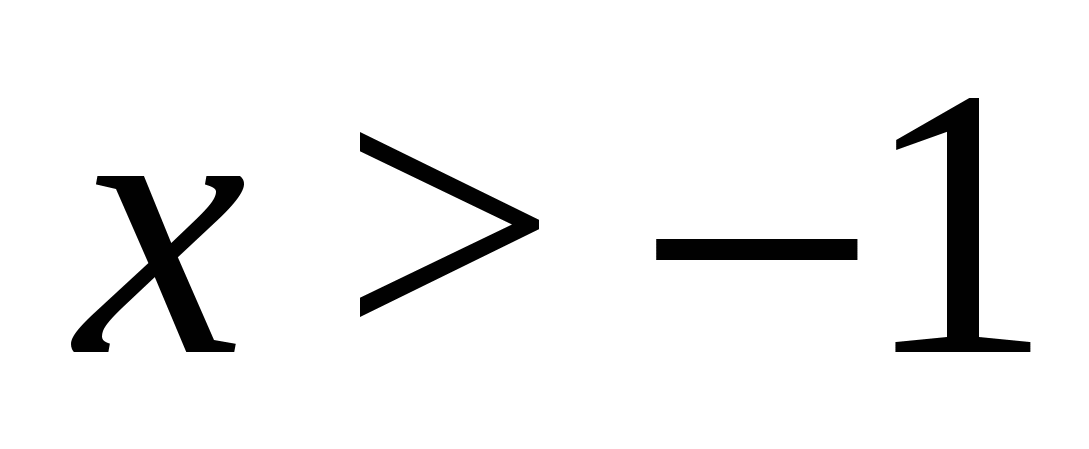, otteniamo

Risposta.
.

• Risoluzione di equazioni utilizzando l'interpretazione geometrica

Significato geometrico dell'espressione
- lunghezza del segmento dell'asse delle coordinate che collega i punti con le ascisse E . Tradurre un problema algebrico in linguaggio geometrico spesso permette di evitare calcoli scomodi.

Esempio 13 Risolviamo l'equazione
.

Soluzione. Ragioneremo così: in base all'interpretazione geometrica del modulo, il membro sinistro dell'equazione è la somma delle distanze da un certo punto con l'ascissa a due punti fissi con ascisse 1 e 2. Poi tutti i punti con ascisse del segmento
hanno la proprietà richiesta, ma i punti situati all'esterno di questo segmento no.

Risposta.
.

Esempio 14 Risolvere la disuguaglianza
.

Soluzione. Rappresentiamo i punti sulla linea delle coordinate, la somma delle distanze da cui ai punti
E esattamente uguale a . Questi sono tutti punti del segmento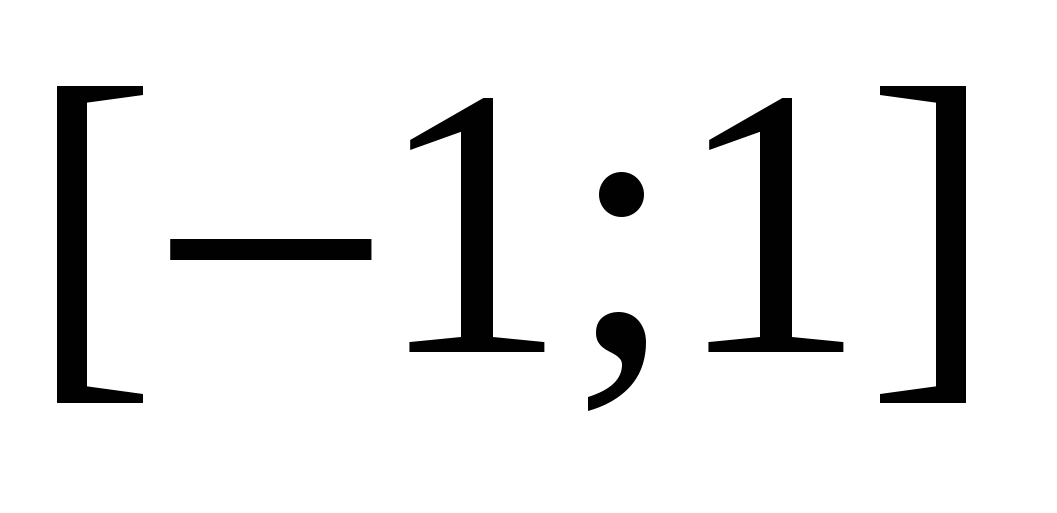
. Per tutti i numeri esterni a questo segmento, la somma delle distanze sarà maggiore di due.

Risposta.
.

Esempio(C3, Esame di Stato Unificato - 2010) 15 Risolvi l'equazione

Soluzione. Applicazione dell'identità due volte
, otteniamo l'equazione

la cui soluzione è l'intervallo
.

Risposta.
.

Esempio(C3, Esame di Stato Unificato - 2011) 16 17 Risolvi l'equazione

Soluzione. .

Risposta.
.

• Applicazione del teorema dei segni alla risoluzione di equazioni

Formuliamo un teorema utile per risolvere le disuguaglianze riguardanti prodotti o quozienti di differenze di moduli:

Teorema 18 Il segno della differenza tra i moduli di due espressioni coincide con il segno della differenza dei quadrati di tali espressioni. non si annulla per nessun valore della variabile. Ciò significa che la funzione ha segno costante in tutto il dominio di definizione. Calcolando ad es.
, troviamo che la funzione assume solo valori positivi.

Risposta.
.

Il metodo degli intervalli consente di risolvere equazioni e disuguaglianze più complesse con i moduli, ma in questo caso ha uno scopo leggermente diverso. Il punto è il seguente. Troviamo le radici di tutte le espressioni submodulari e dividiamo l'asse numerico in intervalli di segno costante di queste espressioni. Ciò ti consente di percorrere questi intervalli in sequenza, eliminare contemporaneamente tutti i moduli e risolvere un'equazione o disuguaglianza ordinaria (controllando che la risposta trovata sia inclusa in questo intervallo).

• Risolvere equazioni moltiplicando per un fattore positivo

Conclusione.

Per riassumere il nostro lavoro possiamo dire quanto segue.

L'obiettivo del lavoro era studiare vari metodi per risolvere equazioni e disuguaglianze con moduli.

Vengono considerate alcune varietà delle più semplici equazioni e disuguaglianze con un modulo, risolte utilizzando transizioni equivalenti, nonché il teorema sulla somma dei moduli; Metodo grafico per la risoluzione delle equazioni. Va detto che nel corso di matematica scolastica questi sono i metodi di soluzione che vengono utilizzati più spesso. Il metodo grafico è particolarmente rilevante quando si risolvono i problemi C 5 dai materiali di prova dell'Esame di Stato Unificato.

Successivamente, abbiamo studiato, utilizzando diversi esempi, altri modi per risolvere equazioni e disuguaglianze con moduli, vale a dire: il metodo per rivelare i moduli; risolvere equazioni contenenti moduli di espressioni non negative; risolvere equazioni utilizzando l'interpretazione geometrica; utilizzando l'identità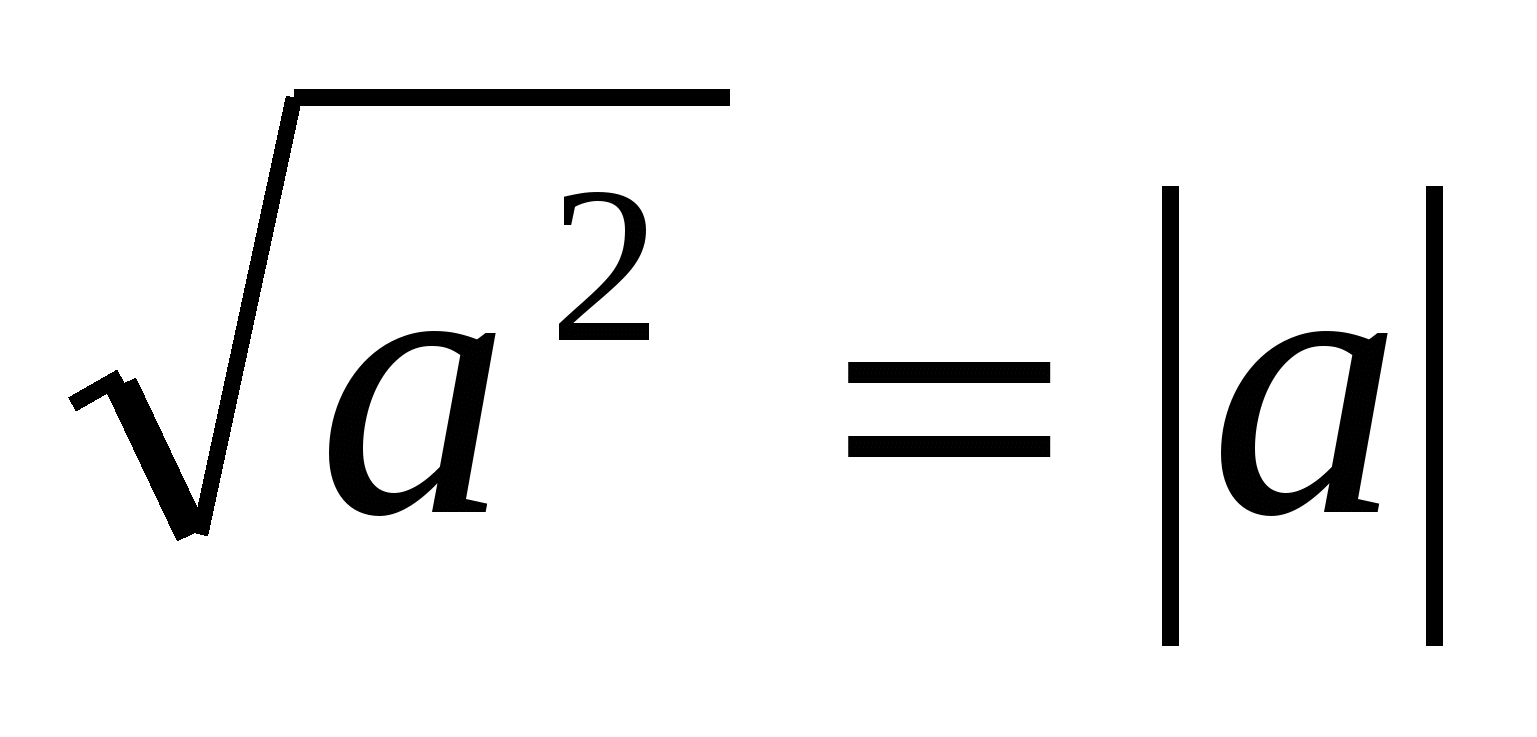
; applicazione del teorema dei segni; risolvere equazioni andando alla conseguenza, moltiplicando per un fattore positivo, nonché risolvere disuguaglianze con il metodo degli intervalli.

Pertanto, durante lo studio siamo giunti alle seguenti conclusioni.

Consideriamo il metodo di rivelazione dei moduli, il metodo grafico e il metodo degli intervalli i più universali e applicabili al maggior numero di problemi. Questa convinzione è nata come risultato della risoluzione di un gran numero di problemi dai materiali di prova dell'Esame di Stato Unificato, dei campionati tematici, dei problemi delle Olimpiadi, nonché dello studio della letteratura su questo tema. Consideriamo molto importante anche la conoscenza e l'applicazione dell'identità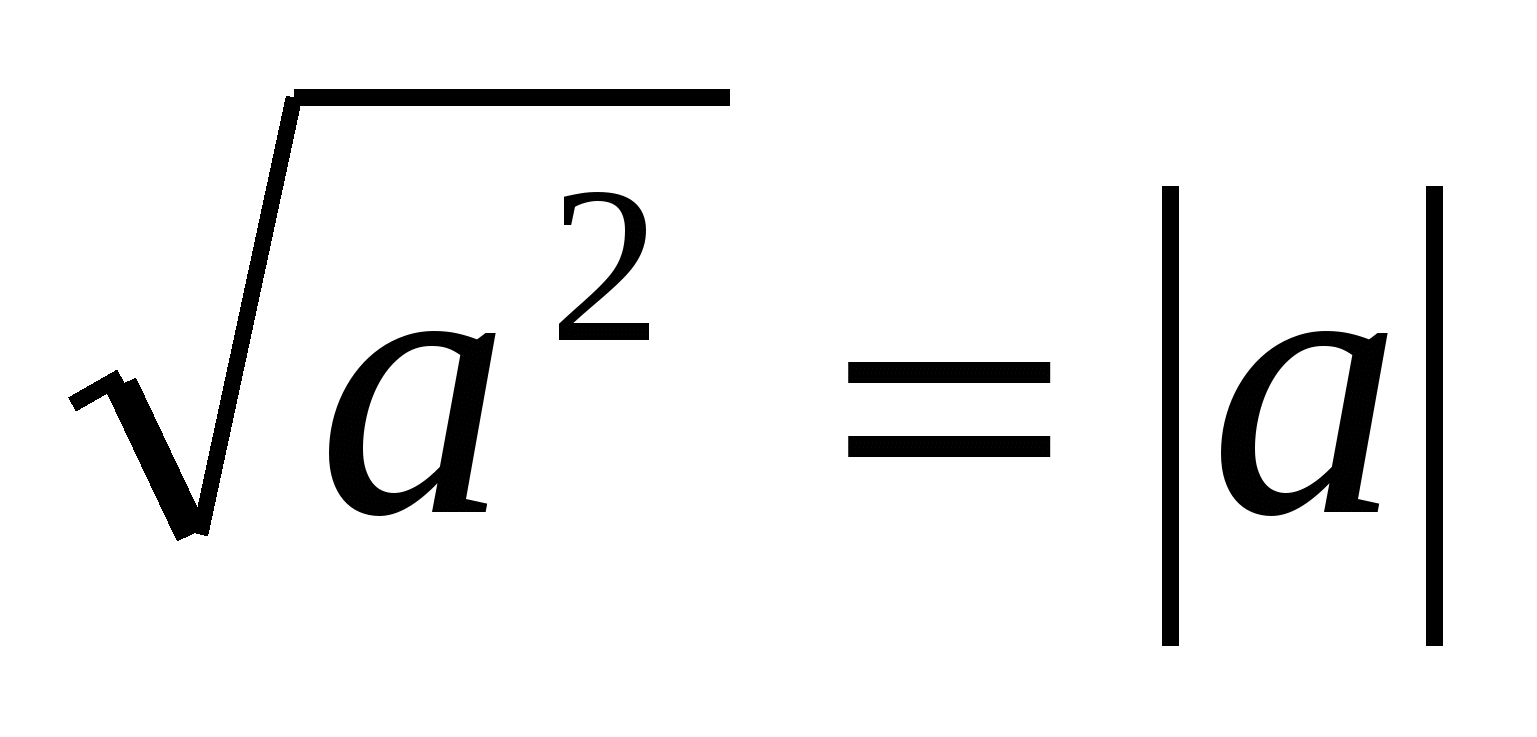
, poiché viene utilizzato non solo per risolvere equazioni e disequazioni, ma anche per trasformare molte espressioni con radicali. I rimanenti metodi risolutivi che abbiamo considerato sono certamente di grande interesse in termini di ampliamento degli orizzonti matematici e di sviluppo matematico generale. Pertanto, prevediamo di utilizzarli per prepararci alla certificazione finale statale sotto forma di Esame di Stato Unificato e alla preparazione per studiare presso un istituto di istruzione superiore.

Elenco della letteratura usata.

“Grande Enciclopedia Matematica” per scolari e studenti;

Matematica. Esame di Stato unificato - 2011, 2012. Opzioni di esame modello. / A cura di A.L. Semenova, I.V. Yashchenko.

M.Ya. Vygodskij. Manuale di matematica elementare

"Il nuovo libro di consultazione degli scolari";

Enciclopedia “Esploro il mondo. Matematica";

;

Matematica è un simbolo della saggezza della scienza,

un modello di rigore scientifico e semplicità,

lo standard di eccellenza e bellezza nella scienza.

Filosofo russo, professore A.V. Voloshinov

Disuguaglianze con modulo

I problemi più difficili da risolvere nella matematica scolastica sono le disuguaglianze, contenenti variabili sotto il segno del modulo. Per risolvere con successo tali disuguaglianze, è necessario avere una buona conoscenza delle proprietà del modulo e avere le competenze per utilizzarle.

Concetti e proprietà di base

Modulo (valore assoluto) di un numero reale indicato da ed è definito come segue:

Le proprietà semplici di un modulo includono le seguenti relazioni:

E .

Nota, che le ultime due proprietà sono valide per qualsiasi grado pari.

Inoltre, se, dove, allora e

Proprietà del modulo più complesse, che può essere efficacemente utilizzato per risolvere equazioni e disequazioni con moduli, sono formulati attraverso i seguenti teoremi:

Teorema 1.Per eventuali funzioni analitiche E la disuguaglianza è vera.

Teorema 2. Uguaglianza equivale a disuguaglianza.

Teorema 3. Uguaglianza equivale a disuguaglianza.

Le disuguaglianze più comuni nella matematica scolastica, contenenti variabili sconosciute sotto il segno del modulo, sono disuguaglianze della forma e, dove qualche costante positiva.

Teorema 4. Disuguaglianza equivale a una doppia disuguaglianza, e la soluzione alla disuguaglianzasi riduce a risolvere un insieme di disuguaglianze E .

Questo teorema è un caso speciale dei Teoremi 6 e 7.

Disuguaglianze più complesse, contenenti un modulo sono disuguaglianze della forma, E .

I metodi per risolvere tali disuguaglianze possono essere formulati utilizzando i seguenti tre teoremi.

Teorema 5. Disuguaglianza equivale alla combinazione di due sistemi di diseguaglianze

io (1)

Prova. Da allora

Ciò implica la validità della (1).

Teorema 6. Disuguaglianza equivale al sistema delle disuguaglianze

Prova. Perché , quindi dalla disuguaglianza ne consegue che . In questa condizione, la disuguaglianzae in questo caso il secondo sistema di diseguaglianze (1) risulterà inconsistente.

Il teorema è stato dimostrato.

Teorema 7. Disuguaglianza è equivalente alla combinazione di una disuguaglianza e di due sistemi di diseguaglianze

io (3)

Prova. Da allora la disuguaglianza sempre eseguito, Se .

Permettere quindi disuguaglianzasarà equivalente alla disuguaglianza, da cui segue un insieme di due disuguaglianze E .

Il teorema è stato dimostrato.

Diamo un'occhiata ad esempi tipici di risoluzione dei problemi sull'argomento “Diseguaglianze, contenente variabili sotto il segno del modulo."

Risolvere le disuguaglianze con il modulo

Il metodo più semplice per risolvere le disuguaglianze con il modulo è il metodo, in base all'espansione del modulo. Questo metodo è universale, tuttavia, nel caso generale, il suo utilizzo può portare a calcoli molto macchinosi. Pertanto, gli studenti dovrebbero conoscere altri metodi e tecniche (più efficaci) per risolvere tali disuguaglianze. In particolare, è necessario avere competenze nell'applicazione dei teoremi, dato in questo articolo.

Esempio 1.Risolvere la disuguaglianza

. (4)

Soluzione.Risolveremo la disuguaglianza (4) utilizzando il metodo “classico” – il metodo di rivelazione dei moduli. A questo scopo dividiamo l'asse dei numeri punti e in intervalli e consideriamo tre casi.

1. Se , allora , , , e la disuguaglianza (4) assume la forma O .

Poiché il caso qui considerato, è una soluzione alla disuguaglianza (4).

2. Se, allora dalla disuguaglianza (4) si ottiene O . Dall'intersezione degli intervalli E è vuoto, allora sull'intervallo di soluzione considerato non esiste disuguaglianza (4).

3. Se, allora assume la forma la disuguaglianza (4). O . E' ovvio è anche una soluzione alla disuguaglianza (4).

Risposta: , .

Esempio 2. Risolvere la disuguaglianza.

Soluzione. Supponiamolo. Perché , allora assume la forma la disuguaglianza data O . Da allora e da qui segue O .

Tuttavia, quindi o.

Esempio 3. Risolvere la disuguaglianza

. (5)

Soluzione. Perché , allora la disuguaglianza (5) è equivalente alle disuguaglianze O . Da qui, secondo il Teorema 4, abbiamo una serie di disuguaglianze E .

Risposta: , .

Esempio 4.Risolvere la disuguaglianza

. (6)

Soluzione. Indichiamo . Allora dalla disuguaglianza (6) si ottengono le disuguaglianze , , o .

Da qui, utilizzando il metodo dell'intervallo, otteniamo . Perché , allora qui abbiamo un sistema di disuguaglianze

La soluzione alla prima disuguaglianza del sistema (7) è l'unione di due intervalli E , e la soluzione alla seconda disuguaglianza è la doppia disuguaglianza. Ne consegue, che la soluzione del sistema di diseguaglianze (7) è l'unione di due intervalli E .

Risposta: ,

Esempio 5.Risolvere la disuguaglianza

. (8)

Soluzione. Trasformiamo la disuguaglianza (8) come segue:

O .

Utilizzando il metodo dell'intervallo, otteniamo una soluzione della disuguaglianza (8).

Risposta: .

Nota. Se poniamo e nelle condizioni del Teorema 5, otteniamo .

Esempio 6. Risolvere la disuguaglianza

. (9)

Soluzione. Dalla disuguaglianza (9) segue. Trasformiamo la disuguaglianza (9) come segue:

O

Dal , allora o .

Risposta: .

Esempio 7.Risolvere la disuguaglianza

. (10)

Soluzione. Da e , allora o .

A questo proposito e la disuguaglianza (10) assume la forma

O

. (11)

Ne consegue che o . Poiché , allora anche la disuguaglianza (11) implica o .

Risposta: .

Nota. Se applichiamo il Teorema 1 al membro sinistro della disuguaglianza (10), allora otteniamo . Da questo e dalla disuguaglianza (10) segue, cosa o . Perché , allora assume la forma la disuguaglianza (10). O .

Esempio 8. Risolvere la disuguaglianza

. (12)

Soluzione. Da allora e dalla disuguaglianza (12) segue O . Tuttavia, quindi o. Da qui otteniamo o .

Risposta: .

Esempio 9. Risolvere la disuguaglianza

. (13)

Soluzione. Secondo il Teorema 7, la soluzione della disuguaglianza (13) è o .

Lascia che sia adesso. In tal caso e la disuguaglianza (13) assume la forma O .

Se combini gli intervalli E , allora otteniamo una soluzione alla disuguaglianza (13) della forma.

Esempio 10. Risolvere la disuguaglianza

. (14)

Soluzione. Riscriviamo la disuguaglianza (14) in una forma equivalente: . Se applichiamo il Teorema 1 al lato sinistro di questa disuguaglianza, otteniamo la disuguaglianza .

Da qui e dal Teorema 1 segue, tale disuguaglianza (14) è soddisfatta per qualsiasi valore.

Risposta: qualsiasi numero.

Esempio 11. Risolvere la disuguaglianza

. (15)

Soluzione. Applicazione del Teorema 1 al membro sinistro della disuguaglianza (15), otteniamo . Questo e la disuguaglianza (15) danno l'equazione, che ha la forma.

Secondo il Teorema 3, equazione equivale a disuguaglianza. Da qui otteniamo.

Esempio 12.Risolvere la disuguaglianza

. (16)

Soluzione. Dalla disuguaglianza (16), secondo il Teorema 4, si ottiene un sistema di disuguaglianze

Quando si risolve la disuguaglianzaUtilizziamo il Teorema 6 e otteniamo un sistema di disuguaglianzeda cui segue.

Considera la disuguaglianza. Secondo il Teorema 7, otteniamo un insieme di disuguaglianze E . La seconda disuguaglianza della popolazione è valida per qualsiasi reale.

Quindi , la soluzione alla disuguaglianza (16) è.

Esempio 13.Risolvere la disuguaglianza

. (17)

Soluzione. Secondo il Teorema 1 possiamo scrivere

(18)

Tenendo conto della disuguaglianza (17), concludiamo che entrambe le disuguaglianze (18) si trasformano in uguaglianze, cioè c'è un sistema di equazioni

Per il Teorema 3, questo sistema di equazioni è equivalente al sistema di disequazioni

O

Esempio 14.Risolvere la disuguaglianza

. (19)

Soluzione. Da allora. Moltiplichiamo entrambi i lati della disuguaglianza (19) per l'espressione , che accetta solo valori positivi per qualsiasi valore. Quindi otteniamo una disuguaglianza equivalente alla disuguaglianza (19), della forma

Da qui arriviamo o , dove . Dal e allora la soluzione alla disuguaglianza è (19). E .

Risposta: , .

Per uno studio più approfondito dei metodi per risolvere le disuguaglianze con un modulo, si consiglia di rivolgersi ai libri di testo, riportati nell'elenco della letteratura consigliata.

1. Raccolta di problemi di matematica per i candidati alle università / Ed. MI. Scanavi. – M.: Pace ed educazione, 2013. – 608 pag.

2. Superare il V.P. Matematica per gli studenti delle scuole superiori: metodi per risolvere e dimostrare le disuguaglianze. – M.: Lenand/URSS, 2018. – 264 pag.

3. Superare il V.P. Matematica per studenti delle scuole superiori: metodi non standard per risolvere problemi. – M.: CD “Librocom” / URSS, 2017. – 296 pag.

Hai ancora domande?

Per ottenere aiuto da un tutor, registrati.

sito web, quando si copia materiale in tutto o in parte, è richiesto un collegamento alla fonte originale.

Più una persona capisce, più forte è il suo desiderio di capire

Tommaso d'Aquino

Il metodo dell'intervallo consente di risolvere qualsiasi equazione contenente un modulo. L'essenza di questo metodo è dividere l'asse dei numeri in più sezioni (intervalli) e l'asse deve essere diviso per gli zeri delle espressioni nei moduli. Quindi, su ciascuna delle sezioni risultanti, ogni espressione submodulare è positiva o negativa. Pertanto ciascuno dei moduli può essere aperto sia con il segno meno che con il segno più. Dopo questi passaggi non resta che risolvere ciascuna delle semplici equazioni risultanti sull'intervallo in esame e combinare le risposte ottenute.

Diamo un'occhiata a questo metodo utilizzando un esempio specifico.

|x+1| + |2x – 4| – |x + 3| = 2x-6.

1) Troviamo gli zeri delle espressioni nei moduli. Per fare ciò, dobbiamo equipararli a zero e risolvere le equazioni risultanti.

x + 1 = 0 2x – 4 = 0 x + 3 = 0

x = -1 2x = 4 x = -3

2) Posizionare i punti risultanti nell'ordine richiesto sulla linea delle coordinate. Divideranno l'intero asse in quattro sezioni.

3) Determiniamo su ciascuna delle sezioni risultanti i segni delle espressioni nei moduli. Per fare ciò, sostituiamo al loro interno qualsiasi numero degli intervalli che ci interessano. Se il risultato del calcolo è un numero positivo, inseriamo "+" nella tabella e se il numero è negativo, inseriamo "-". Questo può essere rappresentato in questo modo:

4) Ora risolveremo l'equazione su ciascuno dei quattro intervalli, rivelando i moduli con i segni che sono indicati nella tabella. Quindi, diamo un'occhiata al primo intervallo:

I intervallo (-∞; -3). Su di esso, tutti i moduli sono aperti con un segno “–”. Otteniamo la seguente equazione:

-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Presentiamo termini simili, aprendo prima le parentesi nell'equazione risultante:

X – 1 – 2x + 4 + x + 3 = 2x – 6

La risposta ricevuta non è compresa nell'intervallo considerato, quindi non è necessario scriverla nella risposta finale.

II intervallo [-3; -1). A questo intervallo nella tabella ci sono i segni “–”, “–”, “+”. Questo è esattamente il modo in cui apriamo i moduli dell'equazione originale:

-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Semplifichiamo aprendo le parentesi:

X – 1 – 2x + 4 – x – 3 = 2x – 6. Presentiamo quelli simili nell'equazione risultante:

x = 6/5. Il numero risultante non appartiene all'intervallo in esame, quindi non è la radice dell'equazione originale.

III intervallo [-1; 2). Espandiamo i moduli dell'equazione originale con i segni che compaiono nella terza colonna della figura. Otteniamo:

(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Eliminiamo le parentesi e spostiamo i termini contenenti la variabile x a sinistra dell'equazione, e quelli che non contengono x a il diritto. Avremo:

x + 1 – 2x + 4 – x – 3 = 2x – 6

Il numero 2 non è compreso nell'intervallo in esame.

intervallo IV)