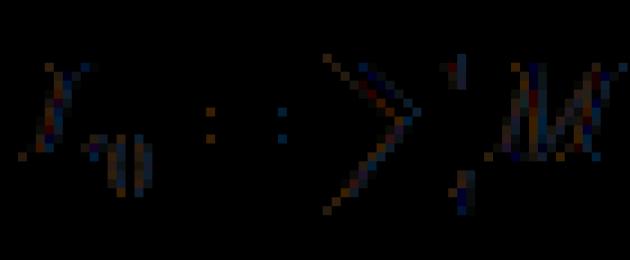Portare al centro un sistema di forze piatto e arbitrario. Portare al centro un sistema piano di forze

Lezione 5

Riepilogo: Portare forza in un dato centro. Portare un sistema di forze ad un dato centro. Condizioni di equilibrio per un sistema spaziale di forze parallele. Condizioni di equilibrio per un sistema piano di forze. Teorema dei tre momenti. Problemi staticamente definibili e staticamente indeterminati. Equilibrio del sistema dei corpi.

PORTARE IL SISTEMA DI FORZE AD UN CENTRO SPECIFICATO. CONDIZIONI DI EQUILIBRIO

Portare forza in un dato centro.

La risultante di un sistema di forze convergenti si trova direttamente sommando le forze secondo la regola del parallelogramma. Ovviamente, un problema simile può essere risolto per un sistema di forze arbitrario se troviamo un metodo che ci permetta di trasferire tutte le forze in un punto.

Teorema sul trasferimento parallelo di forze . Una forza applicata ad un corpo assolutamente rigido può, senza cambiare l'effetto che esercita, essere trasferita da un dato punto a qualsiasi altro punto del corpo, sommando una coppia con momento pari al momento della forza trasferita rispetto al punto in cui la forza viene trasferita.

Si applichi una forza al punto A. L'effetto di questa forza non cambia se al punto B vengono applicate due forze equilibrate. Il sistema di tre forze risultante è una forza uguale, ma applicata nel punto B, e una coppia con un momento. Il processo di sostituzione di una forza con una forza e una coppia di forze è chiamato portare la forza in un dato centro B.

Portare un sistema di forze ad un dato centro.

Teorema principale statica (Poinsot).

Qualsiasi sistema arbitrario di forze su cui agisce solido, può generalmente essere ridotto ad una forza e ad una coppia di forze. Questo processo di sostituzione di un sistema di forze con una forza e una coppia di forze viene chiamato portare il sistema di forze in un dato centro.

Il vettore principale del sistema forzaè chiamato un vettore uguale alla somma vettoriale di queste forze.

Il punto principale del sistema forza rispetto al punto O del corpo, viene chiamato un vettore uguale alla somma vettoriale dei momenti di tutte le forze del sistema rispetto a questo punto.

Formule per il calcolo del vettore principale e del momento principale

Formule per il calcolo del modulo e dei coseni direzionali

vettore principale e momento principale

Condizioni per l'equilibrio di un sistema di forze.

Forma vettoriale.

Per l'equilibrio di un sistema arbitrario di forze applicate ad un corpo rigido è necessario e sufficiente che vettore principale sistema di forze era uguale a zero e anche il momento principale del sistema di forze rispetto a qualsiasi centro di riduzione era uguale a zero.

Forma algebrica.

Per l'equilibrio di un sistema arbitrario di forze applicate ad un corpo solido, è necessario e sufficiente che le tre somme delle proiezioni di tutte le forze sugli assi delle coordinate cartesiane siano uguali a zero e le tre somme dei momenti di tutte le forze relative anche i tre assi coordinati sono uguali a zero.

Condizioni per l'equilibrio di un sistema spaziale

forze parallele.

Sul corpo agisce un sistema di forze parallele. Posizioniamo l'asse di Oz parallelo alle forze.

Equazioni

Per l'equilibrio di un sistema spaziale di forze parallele agenti su un corpo solido è necessario e sufficiente che la somma delle proiezioni di tali forze sia pari a zero e la somma dei momenti di tali forze rispetto a due assi coordinati, le forze perpendicolari, erano anch'esse pari a zero.

- proiezione della forza sull'asse di Oz.

SISTEMA DI FORZA PIANA.

Condizioni di equilibrio per un sistema piano di forze.

Sul corpo agisce un sistema piano di forze. Posizioniamo gli assi Ox e Oy nel piano d'azione delle forze.

Equazioni

Per l'equilibrio di un sistema piano di forze agenti su un corpo solido è necessario e sufficiente che le somme delle proiezioni di tali forze su ciascuno dei due assi coordinati rettangolari posti nel piano di azione delle forze siano pari a zero e anche la somma dei momenti di queste forze rispetto a qualsiasi punto situato nel piano d'azione era zero.

Teorema dei tre momenti.

Per l'equilibrio di un sistema piano di forze agenti su un corpo rigido, è necessario e sufficiente che le somme dei momenti di queste forze del sistema relative a tre punti qualsiasi situati nel piano di azione delle forze e non giacenti su la stessa retta sono uguali a zero.

Problemi staticamente definibili e staticamente indeterminati.

Per ogni sistema piano di forze agenti su un corpo rigido esistono tre condizioni di equilibrio indipendenti. Di conseguenza, per qualsiasi sistema piano di forze, non si possono trovare più di tre incognite dalle condizioni di equilibrio.

Nel caso di un sistema spaziale di forze agenti su un corpo rigido esistono sei condizioni di equilibrio indipendenti. Di conseguenza, per qualsiasi sistema spaziale di forze, non si possono trovare più di sei incognite dalle condizioni di equilibrio.

Problemi in cui il numero di incognite non lo è più numero vengono chiamate condizioni di equilibrio indipendenti per un dato sistema di forze applicate ad un corpo rigido staticamente definibili.

Altrimenti i problemi sono staticamente indeterminati.

Equilibrio del sistema dei corpi.

Consideriamo l'equilibrio delle forze applicate ad un sistema di corpi interagenti. I corpi possono essere collegati tra loro tramite cerniere o in altro modo.

Le forze che agiscono sul sistema di corpi in esame possono essere suddivise in esterne ed interne.

Esterno si chiamano le forze con le quali i corpi del sistema in esame vengono sollecitati da corpi che non sono compresi in tale sistema di forze.

Interno sono chiamate le forze di interazione tra i corpi del sistema in esame.

Quando si considera l'equilibrio delle forze applicate a un sistema di corpi, si può mentalmente dividere il sistema di corpi in singoli corpi solidi e applicare le condizioni di equilibrio ottenute per un corpo alle forze che agiscono su questi corpi. Queste condizioni di equilibrio includeranno sia le forze esterne che quelle interne del sistema di corpi. Le forze interne, basate sull'assioma dell'uguaglianza delle forze di azione e reazione in ciascun punto di articolazione di due corpi, formano un sistema di forze di equilibrio.

Dimostriamolo usando l'esempio di un sistema di due corpi e un sistema piano di forze.

Se stabiliamo condizioni di equilibrio per ciascun corpo rigido di un sistema di corpi, allora per il corpo I

.

per il corpo II

Inoltre, dall'assioma sull'uguaglianza delle forze di azione e reazione per due corpi interagenti abbiamo .

Le uguaglianze presentate sono le condizioni di equilibrio forze esterne, agendo sul sistema.

Reazione di sigillatura.

Consideriamo una trave di cui un'estremità AB è incastrata nel muro. Questo tipo di fissaggio dell'estremità della trave è chiamato AB sigillatura nel punto B. Sulla trave agisca un sistema piano di forze. Determiniamo le forze che devono essere applicate al punto B della trave se si scarta parte della trave AB. Alla sezione della trave (B) vengono applicate forze di reazione distribuite. Se queste forze vengono sostituite da forze elementari concentrate e poi portate al punto B, allora nel punto B otteniamo una forza (il vettore principale delle forze di reazione) e una coppia di forze con un momento M (il vettore principale delle forze di reazione rispetto a punto B). Momento M chiamato il momento di chiusura O momento direttivo. La forza di reazione può essere sostituita da due componenti e .

La guarnizione, a differenza di una cerniera, crea non solo una reazione sconosciuta in grandezza e direzione, ma anche una coppia di forze con momento M sconosciuto nella guarnizione.

Supponiamo che un sistema di forze piano arbitrario sia ridotto a una forza uguale al vettore principale e applicata al centro di riduzione, e a una coppia con un momento uguale al momento principale
(Figura 57, UN). Dimostriamo che il sistema di forze piano arbitrario in esame si riduce in questo caso generale alla forza risultante
, la cui retta d'azione passa per il punto UN, distanziato dal centro di riduzione selezionato DI sulla distanza
. Per fare questo, trasformiamo la coppia con momento
quindi quella forza E
, costituente questa coppia, si è rivelato uguale in grandezza al vettore principale R". In questo caso, è necessario selezionare il braccio della coppia in modo che il suo momento t
è rimasto pari a M 0. Per questo, la leva finanziaria della coppia
bisogna ovviamente ricavarlo dall'uguaglianza

. (1)

Approfittando del fatto che una coppia può sempre essere spostata nel suo piano d'azione come desiderato, muoviamo la coppia
in modo che la sua forza
si trovò attaccato al centro di adduzione DI e opposto al vettore principale
(Figura 57, B).

Il sistema di forze piano arbitrario in esame è quindi equivalente alla forza
e coppia
. Restituire le forze
E
in quanto equilibrato, otteniamo che l'intero sistema di forze in esame viene sostituito da un'unica forza
, che è quindi la risultante. In questo caso, la linea d'azione della risultante passerà attraverso il punto UN, la cui posizione rispetto al centro di riduzione selezionato è determinata dalla formula (1).

Se, come risultato dell'introduzione di un sistema di forze piano arbitrario, si scopre che
, UN
, allora in questo caso particolare questo sistema di forze viene immediatamente sostituito da una forza, cioè dalla risultante
, la cui linea d'azione passa per il centro di riduzione selezionato.

Problema 7. A punti IN E CON ai corpi vengono applicate rispettivamente forze uguali in grandezza e reciprocamente perpendicolari E
, distante dal punto DI corpi ad uguale distanza
. Porta questo sistema di forze a un punto DI(Figura 58).

Soluzione. Trasferiamo le forze E parallelo a noi stessi fino ad un punto DI. Come risultato di tale trasferimento otteniamo (Figura 58) forze
E
, applicato al punto DI e coppie aggiunte
E
, giacendo sullo stesso piano con i momenti
E
(le forze che formano queste coppie sono contrassegnate in figura con 58 trattini). Dalla somma geometrica delle forze E , applicato al punto DI, otteniamo il vettore principale di questo sistema di forze

il cui modulo è ovviamente uguale a

Dalla somma delle coppie aggiunte si ottiene una coppia risultante il cui momento è uguale al momento principale
di un dato sistema di forze rispetto ad un punto DI:

Pertanto, questo sistema di due forze E ha una risultante

,

applicato al punto UN, che è distante dal punto DI sulla distanza

.

;
,

cioè le forme risultanti con entrambe le forze date E angoli uguali di 45 0.

Compito 8. Sulla capriata del ponte agiscono forze verticali (Figura 59)
t e
t rispettivamente a una distanza di 10 M e 40 M dall'estremità sinistra della travatura reticolare e dalla forza orizzontale
t a livello della corda superiore della travatura, l'altezza della travatura è 6 M. Portare un sistema di forze ,E la forma più semplice.

Soluzione. Disegniamo gli assi delle coordinate come mostrato nella Figura 59, prendendo l'origine delle coordinate nel punto UN. Troviamo le proiezioni del vettore principale di un dato sistema di forze sull'asse del sistema di coordinate selezionato:

dove troviamo il modulo del vettore principale
:

T
.

Troviamo ora il momento principale del dato sistema di forze rispetto all'origine delle coordinate UN:

t m
.

Di conseguenza, questo sistema di forze ha una risultante
, il cui modulo
T.

Troviamo ora la retta d'azione della risultante. Momento risultante rispetto all'origine UN sarà determinato dalla formula

,

Dove X E sì - coordinate di un punto giacente sulla retta d'azione della risultante. Perché
t e
t, allora

.

CON d’altronde per il teorema di Varignon sul momento della risultante (5, § 11) abbiamo

Quindi,

.

Questa è l'equazione della retta d'azione della risultante.

Supponendo in questa equazione
, troviamo che il punto di intersezione della retta d'azione della risultante con la corda superiore della travatura reticolare posizionata a distanza
M dall'estremità sinistra della fattoria. Credere
M, troviamo che il punto di intersezione della retta d'azione della risultante con la corda inferiore della travatura reticolare è distanziata
M dall'estremità sinistra della fattoria. Le connessioni così definite sono i punti di intersezione delle linee d'azione della risultante con le corde superiore ed inferiore della travatura in linea retta si trova la linea d'azione della risultante .

Il metodo per portare una forza in un dato punto può essere applicato a qualsiasi numero di forze. Supponiamo che in alcuni punti del corpo (Fig. 1.24) vengano applicate delle forze Fa1 Fa2, Fa3 E F4.È necessario portare queste forze al punto DI aereo. Presentiamo innanzitutto la forza applicata nel punto UN. Applichiamo (vedi § 16) al punto DI due forze separatamente uguali in valore a una data forza, parallele ad essa e dirette in direzioni opposte. Come risultato del portare la forza, otteniamo la forza , applicato nel punto O e un paio di forze con la spalla . Facendo lo stesso con la forza , applicato al punto IN, otterremo il potere , applicato al punto DI, e un paio di forze con una spalla, ecc. Un sistema piatto di forze applicate nei punti A, B, C E D, abbiamo sostituito con forze convergenti , applicato in un punto DI, e coppie di forze con momenti uguali ai momenti delle forze date rispetto al punto DI:

Fig.1.24

Le forze convergenti in un punto possono essere sostituite da una forza uguale somma geometrica componenti,

Questa forza, pari alla somma geometrica delle forze date, si chiama il vettore principale del sistema di forze e denotare .

In base all'entità delle proiezioni del vettore principale sugli assi delle coordinate, troviamo il modulo del vettore principale:

In base alla regola per sommare le coppie di forze, queste possono essere sostituite dalla coppia risultante, il cui momento è uguale alla somma algebrica dei momenti delle forze date rispetto al punto DI e viene chiamato punto principale rispetto al punto di riferimento

Pertanto, un sistema di forze piano arbitrario è ridotto a una forza(il vettore principale del sistema di forze) e un momento(il momento principale del sistema di forze).

È necessario comprendere che il centovettore principale non è la risultante di un dato sistema di forze, poiché questo sistema non equivale ad una forza. Poiché il vettore principale è uguale alla somma geometrica delle forze in un dato sistema, né la sua grandezza né la sua direzione dipendono dalla scelta del centro di riduzione. Il valore e il segno del momento principale dipendono dalla posizione del centro di riduzione, poiché i bracci delle coppie componenti dipendono dalla posizione relativa delle forze e dal punto (centro) rispetto al quale vengono presi i momenti.

Casi particolari di riduzione di un sistema di forze:

1) ; il sistema è in equilibrio, cioè Per l'equilibrio di un sistema di forze piano è necessario e sufficiente che il suo vettore principale e il suo momento principale siano contemporaneamente pari a zero.

Anche un sistema piano di forze si riduce a una forza pari sia a quella applicata in un centro O scelto arbitrariamente sia a una coppia con un momento

in questo caso il vettore può essere determinato o geometricamente costruendo un poligono di forza (vedi punto 4), oppure analiticamente. Quindi, per un sistema di forze piano

R x = F kx , R y = F ky ,

dove tutti i momenti dell'ultima uguaglianza sono algebrici e anche la somma è algebrica.

Cerchiamo a quale forma più semplice può essere ridotto un dato sistema piatto di forze che non è in equilibrio. Il risultato dipende dai valori di R e M O.

• 1. Se per un dato sistema di forze R=0, a M O ?0, allora si riduce ad una coppia con momento M O , il cui valore non dipende dalla scelta del centro O.
• 2. Se per un dato sistema di forze R?0, allora si riduce a una forza, cioè alla risultante. In questo caso sono possibili due casi:
  • a) R?0, M O =0. In questo caso il sistema, come è immediatamente evidente, si riduce alla risultante R passante per il centro O;
  • b) R?0, M O?0. In questo caso, una coppia con momento M O può essere rappresentata da due forze R" e R", assumendo R"=R, e R"= - R. Inoltre, se d=OC è il braccio della coppia, allora esiste dovrebbe essere Rd=|M O |.

Rigettando ora le forze R e R" come equilibrate, troviamo che l'intero sistema di forze è sostituito dalla risultante R" = R passante per il punto C. La posizione del punto C è determinata da due condizioni: 1) la distanza OC = d() deve soddisfare l'uguaglianza Rd = |. M O |; 2) il segno del momento relativo al centro O della forza R" applicata nel punto C, cioè il segno di m O (R") deve coincidere con il segno di M O.

Lezione 3

Riepilogo: Portare al centro un sistema di forze arbitrario e piatto. Teorema sul trasferimento parallelo della forza, il teorema principale della statica Portare un sistema di forze ad un dato centro Il vettore principale e il momento principale del sistema di forze. Dipendenza del momento principale dalla scelta del centro. Determinazione analitica del vettore principale e del momento principale di un sistema di forze. Invarianti del sistema di forze. Riportare il sistema di forze alla sua forma più semplice. Casi particolari di introduzione di un sistema arbitrario di forze, vite dinamica. Teorema di Varignon sul momento della risultante.

Portare una forza in un dato centro (lemma di Poinsot)

La risultante di un sistema di forze convergenti si trova direttamente sommando le forze secondo la regola del parallelogramma. Ovviamente, un problema simile può essere risolto per un sistema di forze arbitrario se troviamo un metodo che ci permetta di trasferire tutte le forze in un punto.

Lemma di Poinsot sul trasferimento parallelo di forze. .Senza modificare l'azione della forza su un corpo rigido, essa può essere trasferita parallelamente a se stessa in qualsiasi punto del corpo, aggiungendo una coppia il cui momento è uguale al momento della forza data rispetto al nuovo punto di applicazione.

Si applichi una forza al punto A. L'effetto di questa forza non cambia se al punto B vengono applicate due forze equilibrate. Il sistema di tre forze risultante è una forza uguale, ma applicata al punto B, e una coppia con un momento. Il processo di sostituzione di una forza con una forza e una coppia di forze è chiamato portare la forza in un dato centro B. ■

Portare un sistema di forze ad un dato centro.

Il vettore principale del sistema di forzeè chiamato un vettore uguale alla somma vettoriale di queste forze.

Il punto principale del sistema di forze rispetto al punto O del corpo, viene chiamato un vettore uguale alla somma vettoriale dei momenti di tutte le forze del sistema rispetto a questo punto.

Teorema di Poinsot (Teorema fondamentale della statica)

Un sistema arbitrario di forze agenti su un corpo rigido può essere sostituito da un sistema equivalente costituito da una forza e da una coppia di forze. La forza è uguale al vettore principale del sistema di forze e viene applicata in un punto scelto arbitrariamente (centro di riduzione), il momento della coppia è uguale al vettore principale

il momento del sistema di forze relativo a questo punto.

PROVA.

Punto DI-centro di adduzione. Per il lemma di Poinsot trasferiamo la forza F1 esattamente DI. In questo caso, invece di F1, nel punto O abbiamo la stessa forza F1’ e un’ulteriore coppia di forze con momento m1.

Trasferiamo allo stesso modo tutte le altre forze. Di conseguenza, otteniamo un sistema di forze convergenti e un sistema di coppie di forze. Secondo il teorema sull'esistenza di un sistema risultante convergente

le forze possono essere sostituite da una forza R, uguale al vettore principale. Secondo il teorema dell’addizione di coppie, un sistema di coppie può essere sostituito da una coppia il cui momento è uguale al momento principale Mo. ■

Invarianti statici

Gli invarianti statici sono caratteristiche di un sistema di forze che non dipendono dalla scelta del centro di gravità.

Primo invariante la statica è il vettore principale del sistema di forze (per definizione).

Secondo invariante statica: il prodotto scalare del vettore principale e del momento principale.

Infatti, il punto principale dipende ovviamente dalla scelta del centro di riduzione. Consideriamo un sistema di forze arbitrario . Portiamolo prima al centro O, e poi al centro O 1.

Dalla figura è chiaro che . Pertanto, la formula per assumerà la forma

O .

Moltiplichiamo rispettivamente entrambi i lati di questa uguaglianza, tenendo conto che il vettore principale del sistema di forze è primo invariante statica: . Di

proprietà del prodotto misto di vettori , quindi:

.

Se usiamo la definizione prodotto scalare, allora per il secondo invariante possiamo ottenere un'altra forma:

Poiché , l'espressione precedente assumerà la forma:

Pertanto, la proiezione del momento principale sulla direzione del vettore principale è un valore costante per un dato sistema di forze e non dipende dalla scelta del centro di riduzione.

Casi particolari di riduzione di un sistema arbitrario di forze alla forma più semplice

1) Se, portando al centro il sistema di forze O allora in base alla (6.4) possiamo scrivere

.

risultante, applicato al centro di riduzione e coincidente in modulo e direzione con il vettore principale.

2) Se, portando al centro il sistema di forze O

presentandolo poi come una coppia di forze con una spalla,

noi abbiamo: .

In questo caso il sistema di forze si riduce a risultante, coincidente in grandezza e direzione con il vettore principale, e la linea d'azione della risultante si trova a una distanza dalla linea d'azione del vettore principale.

3) Se, portando al centro il sistema di forze O allora possiamo scrivere

, cioè il sistema di forze è ridotto a un paio di forze con un momento pari al momento principale del sistema di forze.

4) Se, portando al centro il sistema di forze O allora possiamo scrivere

Quelli. è presente il sistema di forze equilibrio.

Definizione: Un sistema costituito da una forza e da una coppia di forze, il cui momento è collineare alla forza (il piano della coppia è perpendicolare alla linea di azione della forza), è detto dinamo O vite dinamica.

Se, portando un sistema di forze al centro O, il secondo invariante non è uguale a zero, allora questo sistema di forze si riduce a dinamo.

Scomposto in due componenti - lungo il vettore principale e - perpendicolare al vettore principale, per e avremo il caso 2), e il vettore, come libero, può essere trasferito parallelo a se stesso al punto O 1:

I vettori rappresentano il dinamismo, dove , .

Nel caso considerato di portare un sistema di forze, il momento principale ha un valore minimo. Questo valore del momento viene preservato quando un dato sistema di forze viene portato in un punto qualsiasi che giace sulla linea d'azione del vettore principale e del momento principale. L'equazione di questa linea (l'asse centrale dell'elica del sistema di forze) è determinata dalla condizione di collinearità dei vettori e: .