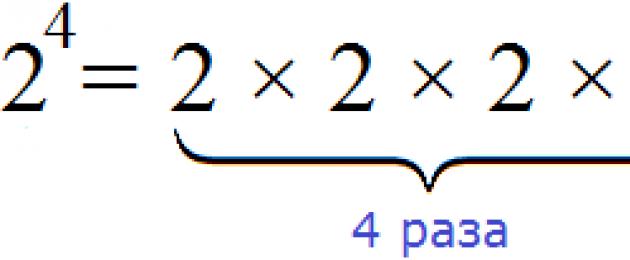È ovvio che i numeri dotati di potenze possono essere sommati come le altre quantità , sommandoli uno dopo l'altro con i relativi segni.
Quindi la somma di a 3 e b 2 è a 3 + b 2.
La somma di a 3 - b n e h 5 - d 4 è a 3 - b n + h 5 - d 4.
Probabilità potenze uguali di variabili identiche possono essere aggiunti o sottratti.
Quindi, la somma di 2a 2 e 3a 2 è uguale a 5a 2.
È anche ovvio che se prendi due quadrati a, o tre quadrati a, o cinque quadrati a.
Ma gradi varie variabili E vari gradi variabili identiche, devono essere composti sommandoli con i relativi segni.
Quindi la somma di a 2 e a 3 è la somma di a 2 + a 3.
È ovvio che il quadrato di a, e il cubo di a, non sono pari al doppio del quadrato di a, ma al doppio del cubo di a.
La somma di a 3 b n e 3a 5 b 6 è a 3 b n + 3a 5 b 6.
Sottrazione le potenze si eseguono allo stesso modo dell'addizione, tranne che i segni dei sottraendo devono essere cambiati di conseguenza.
O:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6
Moltiplicare i poteri
I numeri dotati di potenze possono essere moltiplicati, come le altre quantità, scrivendoli uno dopo l'altro, con o senza segno di moltiplicazione tra di loro.
Pertanto, il risultato della moltiplicazione di a 3 per b 2 è a 3 b 2 o aaabb.
O:
x -3 ⋅ un m = un m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Il risultato nell'ultimo esempio può essere ordinato aggiungendo variabili identiche.
L'espressione assumerà la forma: a 5 b 5 y 3.
Confrontando diversi numeri (variabili) con potenze, possiamo vedere che se ne moltiplicano due qualsiasi, il risultato è un numero (variabile) con una potenza pari a quantità gradi di termini.
Quindi, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Qui 5 è la potenza del risultato della moltiplicazione, pari a 2+3, la somma delle potenze dei termini.
Quindi, a n.a m = a m+n.
Per a n , a viene preso come fattore tante volte quanto la potenza di n;
E a m si prende come fattore tante volte quanto è uguale il grado m;
Ecco perché, le potenze con le stesse basi possono essere moltiplicate sommando gli esponenti delle potenze.
Quindi, a 2 .a 6 = a 2+6 = a 8 . E x 3 .x 2 .x = x 3+2+1 = x 6 .
O:
4a n ⋅ 2a n = 8a 2n
b2 y3 ⋅ b4 y = b6 y4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1
Moltiplica (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Risposta: x 4 - y 4.
Moltiplica (x 3 + x - 5) ⋅ (2x 3 + x + 1).
Questa regola vale anche per i numeri i cui esponenti sono negativo.
1. Quindi, a -2 .a -3 = a -5 . Questo può essere scritto come (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Se si moltiplicano a + b per a - b, il risultato sarà a 2 - b 2: cioè
Il risultato della moltiplicazione della somma o della differenza di due numeri è uguale alla somma o alla differenza dei loro quadrati.
Se moltiplichi la somma e la differenza di due numeri elevati a piazza, il risultato sarà uguale alla somma o alla differenza di questi numeri in quarto gradi.
Quindi, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.
Divisione dei gradi
I numeri con potenze possono essere divisi come gli altri numeri, sottraendo dal dividendo o trasformandoli in frazioni.
Quindi a 3 b 2 diviso b 2 è uguale a a 3.
O:
$\frac(9a^3y^4)(-3a^3) = -3y^4$
$\frac(a^2b + 3a^2)(a^2) = \frac(a^2(b+3))(a^2) = b + 3$
$\frac(d\cpunto (a - h + y)^3)((a - h + y)^3) = d$
Scrivere un 5 diviso per 3 assomiglia a $\frac(a^5)(a^3)$. Ma questo è uguale a 2 . In una serie di numeri
un +4, un +3, un +2, un +1, un 0, un -1, un -2, un -3, un -4.
qualsiasi numero può essere diviso per un altro e l'esponente sarà uguale a differenza indicatori dei numeri divisibili.
Quando si dividono i gradi con la stessa base, i loro esponenti vengono sottratti..
Quindi, y 3:y 2 = y 3-2 = y 1. Cioè $\frac(yyy)(yy) = y$.
E a n+1:a = a n+1-1 = a n . Cioè $\frac(aa^n)(a) = a^n$.
O:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3
La regola vale anche per i numeri con negativo valori dei gradi.
Il risultato della divisione -5 per -3 è -2.
Inoltre, $\frac(1)(aaaaa) : \frac(1)(aaa) = \frac(1)(aaaaa).\frac(aaa)(1) = \frac(aaa)(aaaaa) = \frac (1)(aa)$.
h 2:h -1 = h 2+1 = h 3 oppure $h^2:\frac(1)(h) = h^2.\frac(h)(1) = h^3$
È necessario padroneggiare molto bene la moltiplicazione e la divisione dei poteri, poiché tali operazioni sono molto utilizzate in algebra.
Esempi di risoluzione di esempi con frazioni contenenti numeri con potenze
1. Riduci gli esponenti di $\frac(5a^4)(3a^2)$ Risposta: $\frac(5a^2)(3)$.
2. Diminuire gli esponenti di $\frac(6x^6)(3x^5)$. Risposta: $\frac(2x)(1)$ o 2x.
3. Riduci gli esponenti a 2 /a 3 e a -3 /a -4 e portali a un denominatore comune.
a 2 .a -4 è a -2 il primo numeratore.
a 3 .a -3 è a 0 = 1, il secondo numeratore.
a 3 .a -4 è a -1 , il numeratore comune.
Dopo la semplificazione: a -2 /a -1 e 1/a -1 .
4. Riduci gli esponenti 2a 4 /5a 3 e 2 /a 4 e portali a un denominatore comune.
Risposta: 2a 3 /5a 7 e 5a 5 /5a 7 oppure 2a 3 /5a 2 e 5/5a 2.
5. Moltiplica (a 3 + b)/b 4 per (a - b)/3.
6. Moltiplica (a 5 + 1)/x 2 per (b 2 - 1)/(x + a).
7. Moltiplica b 4 /a -2 per h -3 /x e a n /y -3 .
8. Dividere a 4 /y 3 per a 3 /y 2 . Risposta: a/a.
9. Dividere (h 3 - 1)/d 4 per (d n + 1)/h.
Contenuto della lezioneCos'è una laurea?
Grado chiamato prodotto di più fattori identici. Per esempio:
2×2×2
Il valore di questa espressione è 8
2×2×2 = 8
Il lato sinistro di questa uguaglianza può essere accorciato: prima scrivi il fattore di ripetizione e indica sopra quante volte viene ripetuto. Il moltiplicatore ripetuto in questo caso è 2. Viene ripetuto tre volte. Pertanto, scriviamo un tre sopra i due:
2 3 = 8
Questa espressione recita così: “ due alla terza potenza fa otto" O " La terza potenza di 2 è 8."
La forma abbreviata di notazione per moltiplicare fattori identici viene utilizzata più spesso. Pertanto, dobbiamo ricordare che se un altro numero è scritto sopra un numero, si tratta di una moltiplicazione di più fattori identici.
Ad esempio, se viene data l'espressione 5 3, è necessario tenere presente che questa espressione equivale a scrivere 5 × 5 × 5.
Viene chiamato il numero che si ripete base di laurea. Nell'espressione 5 3 la base della potenza è il numero 5.
E viene chiamato il numero scritto sopra il numero 5 esponente. Nell'espressione 5 3, l'esponente è il numero 3. L'esponente mostra quante volte si ripete la base dell'esponente. Nel nostro caso la base 5 viene ripetuta tre volte
Si chiama l'operazione di moltiplicazione di fattori identici per esponenziazione.
Ad esempio, se devi trovare il prodotto di quattro fattori identici, ognuno dei quali è uguale a 2, allora diranno che il numero è 2 elevato alla quarta potenza:
Vediamo che il numero 2 alla quarta potenza è il numero 16.
Nota che in questa lezione stiamo guardando gradi con esponente naturale. Questo è un tipo di grado il cui esponente è un numero naturale. Ricordiamo che i numeri naturali sono numeri interi maggiori di zero. Ad esempio, 1, 2, 3 e così via.
In generale, la definizione di grado con esponente naturale si presenta così:
Potenza del numero UN con indicatore naturale Nè un'espressione della forma UN, che è uguale al prodotto N fattori, ciascuno dei quali è uguale UN
Esempi:
Dovresti fare attenzione quando elevi un numero a una potenza. Spesso, per disattenzione, una persona moltiplica la base dell'esponente per l'esponente.
Ad esempio, il numero 5 elevato alla seconda potenza è il prodotto di due fattori, ciascuno dei quali è pari a 5. Questo prodotto è pari a 25
Immaginiamo ora di aver inavvertitamente moltiplicato la base 5 per l'esponente 2
Si è verificato un errore perché il numero 5 elevato alla seconda non è uguale a 10.
Inoltre, va detto che la potenza di un numero con esponente 1 è il numero stesso:
Ad esempio, il numero 5 elevato alla prima potenza è il numero 5 stesso
Di conseguenza, se un numero non ha un indicatore, allora dobbiamo supporre che l'indicatore sia uguale a uno.
Ad esempio, i numeri 1, 2, 3 sono dati senza esponente, quindi i loro esponenti saranno uguali a uno. Ciascuno di questi numeri può essere scritto con esponente 1
E se elevi 0 a una certa potenza, ottieni 0. In effetti, non importa quante volte moltiplichi qualcosa per se stesso, non ottieni nulla. Esempi:
E l'espressione 0 0 non ha senso. Ma in alcuni rami della matematica, in particolare nell'analisi e nella teoria degli insiemi, l'espressione 0 0 può avere senso.
Per esercitazione, risolviamo alcuni esempi di elevazione dei numeri a potenze.
Esempio 1. Eleva il numero 3 alla seconda potenza.
Il numero 3 elevato alla seconda è il prodotto di due fattori, ciascuno dei quali è uguale a 3
3 2 = 3 × 3 = 9
Esempio 2. Eleva il numero 2 alla quarta potenza.
Il numero 2 alla quarta potenza è il prodotto di quattro fattori, ciascuno dei quali è uguale a 2
2 4 =2 × 2 × 2 × 2 = 16
Esempio 3. Eleva il numero 2 alla terza potenza.
Il numero 2 elevato alla terza è il prodotto di tre fattori, ciascuno dei quali è uguale a 2
2 3 =2 × 2 × 2 = 8
Elevare il numero 10 al potere
Per elevare il numero 10 a potenza è sufficiente aggiungere dopo l'uno un numero di zeri pari all'esponente.
Ad esempio, eleviamo il numero 10 alla seconda potenza. Innanzitutto, annotiamo il numero 10 stesso e indichiamo il numero 2 come indicatore
10 2
Ora mettiamo un segno uguale, scriviamo uno e dopo questo scriviamo due zeri, poiché il numero di zeri deve essere uguale all'esponente
10 2 = 100
Ciò significa che il numero 10 elevato alla seconda potenza è il numero 100. Ciò è dovuto al fatto che il numero 10 elevato alla seconda potenza è il prodotto di due fattori, ciascuno dei quali è uguale a 10
10 2 = 10 × 10 = 100
Esempio 2. Eleviamo il numero 10 alla terza potenza.
In questo caso, ci saranno tre zeri dopo l'uno:
10 3 = 1000
Esempio 3. Eleviamo il numero 10 alla quarta potenza.
In questo caso, ci saranno quattro zeri dopo l'uno:
10 4 = 10000
Esempio 4. Eleviamo il numero 10 alla prima potenza.
In questo caso, ci sarà uno zero dopo l'uno:
10 1 = 10
Rappresentazione dei numeri 10, 100, 1000 come potenze in base 10
Per rappresentare i numeri 10, 100, 1000 e 10000 come una potenza in base 10, è necessario scrivere la base 10 e come esponente specificare un numero uguale al numero di zeri del numero originale.
Immaginiamo il numero 10 come una potenza con base 10. Vediamo che ha uno zero. Ciò significa che il numero 10 come potenza con base 10 sarà rappresentato come 10 1
10 = 10 1
Esempio 2. Immaginiamo il numero 100 come una potenza con base 10. Vediamo che il numero 100 contiene due zeri. Ciò significa che il numero 100 come potenza con base 10 sarà rappresentato come 10 2
100 = 10 2
Esempio 3. Rappresentiamo il numero 1.000 come una potenza con base 10.
1 000 = 10 3
Esempio 4. Rappresentiamo il numero 10.000 come una potenza con base 10.
10 000 = 10 4
Elevando a potenza un numero negativo
Quando si eleva a potenza un numero negativo, è necessario racchiuderlo tra parentesi.
Ad esempio, eleviamo il numero negativo −2 alla seconda potenza. Il numero −2 elevato alla seconda potenza è il prodotto di due fattori, ciascuno dei quali è uguale a (−2)
(−2) 2 = (−2) × (−2) = 4
Se non racchiudessimo il numero −2 tra parentesi, risulterebbe che stiamo calcolando l'espressione −2 2, che non uguale 4. L'espressione −2² sarà uguale a −4. Per capirne il motivo, tocchiamo alcuni punti.
Quando mettiamo un segno meno davanti a un numero positivo, quindi eseguiamo operazione di assumere il valore opposto.
Diciamo che ti viene dato il numero 2 e devi trovare il numero opposto. Sappiamo che l'opposto di 2 è −2. In altre parole, per trovare il numero opposto a 2, basta mettere un meno davanti a questo numero. Inserire un meno prima di un numero è già considerato un'operazione a tutti gli effetti in matematica. Questa operazione, come detto sopra, è chiamata operazione di assunzione del valore opposto.
Nel caso dell'espressione −2 2 si verificano due operazioni: l'operazione di prendere il valore opposto ed elevarlo a potenza. Elevare a una potenza ha una priorità più alta rispetto a prendere il valore opposto.
Pertanto, l'espressione −2 2 viene calcolata in due fasi. Innanzitutto viene eseguita l’operazione di esponenziazione. In questo caso il numero positivo 2 è stato elevato alla seconda potenza
Quindi è stato preso il valore opposto. Questo valore opposto è stato trovato per il valore 4. E il valore opposto per 4 è −4
−2 2 = −4
Le parentesi hanno la massima priorità di esecuzione. Pertanto, nel caso del calcolo dell'espressione (−2) 2, viene prima preso il valore opposto, quindi il numero negativo −2 viene elevato alla seconda potenza. Il risultato è una risposta positiva pari a 4, poiché il prodotto dei numeri negativi è un numero positivo.
Esempio 2. Eleva il numero −2 alla terza potenza.
Il numero −2 elevato alla terza potenza è il prodotto di tre fattori, ciascuno dei quali è uguale a (−2)
(−2) 3 = (−2) × (−2) × (−2) = −8
Esempio 3. Eleva il numero −2 alla quarta potenza.
Il numero −2 alla quarta potenza è il prodotto di quattro fattori, ciascuno dei quali è uguale a (−2)
(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16
È facile vedere che elevando a potenza un numero negativo si può ottenere una risposta positiva o negativa. Il segno della risposta dipende dall'indice del grado originario.
Se l'esponente è pari, la risposta sarà positiva. Se l'esponente è dispari la risposta sarà negativa. Mostriamolo usando l'esempio del numero −3
Nel primo e nel terzo caso l'indicatore era strano numero, quindi la risposta è diventata negativo.
Nel secondo e nel quarto caso l'indicatore era Anche numero, quindi la risposta è diventata positivo.
Esempio 7. Eleva −5 alla terza potenza.
Il numero −5 elevato alla terza potenza è il prodotto di tre fattori, ciascuno dei quali è uguale a −5. L'esponente 3 è un numero dispari, quindi possiamo dire in anticipo che la risposta sarà negativa:
(-5) 3 = (-5) × (-5) × (-5) = -125
Esempio 8. Eleva −4 alla quarta potenza.
Il numero −4 alla quarta potenza è il prodotto di quattro fattori, ciascuno dei quali è uguale a −4. Inoltre l’esponente 4 è pari, quindi possiamo dire in anticipo che la risposta sarà positiva:
(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256
Trovare i valori di espressione
Quando si trovano i valori di espressioni che non contengono parentesi, verrà eseguita prima l'elevamento a potenza, seguito dalla moltiplicazione e divisione nell'ordine in cui appaiono, quindi dall'addizione e dalla sottrazione nell'ordine in cui appaiono.
Esempio 1. Trova il valore dell'espressione 2 + 5 2
Innanzitutto viene eseguito l'elevamento a potenza. In questo caso, il numero 5 viene elevato alla seconda potenza: otteniamo 25. Quindi questo risultato viene aggiunto al numero 2
2 + 5 2 = 2 + 25 = 27
Esempio 10. Trova il valore dell'espressione −6 2 × (−12)
Innanzitutto viene eseguito l'elevamento a potenza. Nota che il numero −6 non è tra parentesi, quindi il numero 6 verrà elevato alla seconda potenza, quindi verrà posto un segno meno davanti al risultato:
−6 2 × (−12) = −36 × (−12)
Completiamo l'esempio moltiplicando −36 per (−12)
−6 2 × (−12) = −36 × (−12) = 432
Esempio 11. Trova il valore dell'espressione −3 × 2 2
Innanzitutto viene eseguito l'elevamento a potenza. Quindi il risultato risultante viene moltiplicato per il numero −3
−3 × 2 2 = −3 × 4 = −12
Se l'espressione contiene parentesi, è necessario prima eseguire le operazioni tra parentesi, quindi l'elevamento a potenza, quindi la moltiplicazione e la divisione, quindi l'addizione e la sottrazione.
Esempio 12. Trova il valore dell'espressione (3 2 + 1 × 3) − 15 + 5
Per prima cosa eseguiamo le azioni tra parentesi. All'interno delle parentesi applichiamo le regole precedentemente apprese, ovvero prima eleviamo il numero 3 alla seconda potenza, quindi moltiplichiamo 1 × 3, quindi aggiungiamo il risultato dell'elevazione del numero 3 alla seconda potenza e della moltiplicazione 1 × 3. Successivamente, la sottrazione e l'addizione vengono eseguite nell'ordine in cui appaiono. Organizziamo il seguente ordine di esecuzione dell'azione sull'espressione originale:
(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Esempio 13. Trova il valore dell'espressione 2 × 5 3 + 5 × 2 3
Per prima cosa eleviamo i numeri a potenze, quindi moltiplichiamo e aggiungiamo i risultati:
2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Trasformazioni di potenza identiche
È possibile eseguire varie trasformazioni di identità sui poteri, semplificandoli così.
Diciamo che dobbiamo calcolare l'espressione (2 3) 2. In questo esempio, due alla terza potenza viene elevato alla seconda potenza. In altre parole, un grado viene elevato a un altro grado.
(2 3) 2 è il prodotto di due potenze, ciascuna delle quali è uguale a 2 3
Inoltre ciascuna di queste potenze è il prodotto di tre fattori, ciascuno dei quali è pari a 2
Abbiamo ottenuto il prodotto 2 × 2 × 2 × 2 × 2 × 2, che è uguale a 64. Ciò significa il valore dell'espressione (2 3) 2 o uguale a 64
Questo esempio può essere notevolmente semplificato. Per fare ciò, si possono moltiplicare gli esponenti dell'espressione (2 3) 2 e scrivere questo prodotto sulla base 2
Ne abbiamo ricevuti 2 6. Due alla sesta potenza è il prodotto di sei fattori, ciascuno dei quali è uguale a 2. Questo prodotto è uguale a 64
Questa proprietà funziona perché 2 3 è il prodotto di 2 × 2 × 2, che a sua volta si ripete due volte. Quindi risulta che la base 2 si ripete sei volte. Da qui possiamo scrivere che 2 × 2 × 2 × 2 × 2 × 2 è 2 6
In generale, per qualsiasi motivo UN con indicatori M E N, vale la seguente uguaglianza:
(UN)m = un n × m
Questa trasformazione identica si chiama elevare un potere a un potere. Può essere letto così: “Quando si eleva una potenza a potenza, la base resta invariata e gli esponenti si moltiplicano” .
Dopo aver moltiplicato gli indicatori, si ottiene un altro grado, il cui valore può essere trovato.
Esempio 2. Trova il valore dell'espressione (3 2) 2
In questo esempio, la base è 3 e i numeri 2 e 2 sono esponenti. Usiamo la regola di elevare una potenza a potenza. Lasceremo invariata la base e moltiplicheremo gli indicatori:
Ne abbiamo 3 4. E il numero 3 elevato alla quarta potenza è 81
Consideriamo le restanti trasformazioni.
Moltiplicare i poteri
Per moltiplicare le potenze, devi calcolare separatamente ciascuna potenza e moltiplicare i risultati.
Ad esempio, moltiplichiamo 2 2 per 3 3.
2 2 è il numero 4 e 3 3 è il numero 27. Moltiplicando i numeri 4 e 27, otteniamo 108
2 2 × 3 3 = 4 × 27 = 108
In questo esempio, le basi di laurea erano diverse. Se le basi sono le stesse, puoi scrivere una base e come indicatore annotare la somma degli indicatori dei gradi originali.
Ad esempio, moltiplica 2 2 per 2 3
In questo esempio, le basi per i gradi sono le stesse. In questo caso, puoi scrivere una base 2 e scrivere come esponente la somma degli esponenti delle potenze 2 2 e 2 3. In altre parole, lasciare invariata la base e sommare gli indicatori dei gradi originali. Apparirà così:
Ne abbiamo ricevuti 2 5. Il numero 2 elevato alla quinta potenza è 32
Questa proprietà funziona perché 2 2 è il prodotto di 2 × 2 e 2 3 è il prodotto di 2 × 2 × 2. Quindi otteniamo un prodotto di cinque fattori identici, ciascuno dei quali è uguale a 2. Questo prodotto può essere rappresentato come 2 5
In generale, per chiunque UN e indicatori M E N vale la seguente uguaglianza:
Questa trasformazione identica si chiama proprietà fondamentale del grado. Si può leggere così: “ PQuando si moltiplicano potenze con le stesse basi, la base viene lasciata invariata e si sommano gli esponenti. .
Si noti che questa trasformazione può essere applicata a qualsiasi numero di gradi. La cosa principale è che la base è la stessa.
Ad esempio, troviamo il valore dell'espressione 2 1 × 2 2 × 2 3. Base 2
In alcuni problemi può essere sufficiente eseguire la trasformazione opportuna senza calcolare il grado finale. Ciò è ovviamente molto conveniente, poiché calcolare grandi potenze non è così semplice.
Esempio 1. Esprimi come potenza l'espressione 5 8 × 25
In questo problema, devi assicurarti che invece dell'espressione 5 8 × 25, ottieni una potenza.
Il numero 25 può essere rappresentato come 5 2. Quindi otteniamo la seguente espressione:
In questa espressione puoi applicare la proprietà di base del grado: lascia invariata la base 5 e aggiungi gli esponenti 8 e 2:
Scriviamo brevemente la soluzione:
Esempio 2. Esprimi come potenza l'espressione 2 9 × 32
Il numero 32 può essere rappresentato come 2 5. Quindi otteniamo l'espressione 2 9 × 2 5. Successivamente, puoi applicare la proprietà base del grado: lascia invariata la base 2 e aggiungi gli esponenti 9 e 5. Il risultato sarà la seguente soluzione:
Esempio 3. Calcola il prodotto 3 × 3 utilizzando la proprietà di base delle potenze.
Tutti sanno bene che tre per tre fa nove, ma il problema richiede di utilizzare nella soluzione la proprietà fondamentale dei gradi. Come farlo?
Ricordiamo che se un numero è dato senza indicatore, allora l'indicatore deve essere considerato uguale a uno. Pertanto, i fattori 3 e 3 possono essere scritti come 3 1 e 3 1
31×31
Usiamo ora la proprietà base del grado. Lasciamo invariata la base 3 e sommiamo gli indicatori 1 e 1:
3 1 × 3 1 = 3 2 = 9
Esempio 4. Calcola il prodotto 2 × 2 × 3 2 × 3 3 utilizzando la proprietà di base delle potenze.
Sostituiamo il prodotto 2 × 2 con 2 1 × 2 1, poi con 2 1 + 1 e poi con 2 2. Sostituisci il prodotto 3 2 × 3 3 con 3 2 + 3 e poi con 3 5
Esempio 5. Esegui la moltiplicazione x×x
Questi sono due fattori di lettere identici con esponente 1. Per chiarezza, scriviamo questi esponenti. La prossima è la base X Lasciamo invariato e sommiamo gli indicatori:
Mentre sei alla lavagna, non dovresti scrivere la moltiplicazione delle potenze con le stesse basi in modo così dettagliato come viene fatto qui. Tali calcoli devono essere fatti nella tua testa. Una nota dettagliata molto probabilmente irriterà l'insegnante e gli ridurrà il voto. Qui viene fornita una registrazione dettagliata per rendere il materiale il più semplice possibile da comprendere.
Si consiglia di scrivere la soluzione di questo esempio come segue:
Esempio 6. Esegui la moltiplicazione X 2 ×x
L'esponente del secondo fattore è uguale a uno. Per chiarezza, scriviamolo. Successivamente, lasceremo invariata la base e sommeremo gli indicatori:
Esempio 7. Esegui la moltiplicazione sì 3 sì 2 sì
L'esponente del terzo fattore è uguale a uno. Per chiarezza, scriviamolo. Successivamente, lasceremo invariata la base e sommeremo gli indicatori:
Esempio 8. Esegui la moltiplicazione aa 3 a 2 a 5
L'esponente del primo fattore è uguale a uno. Per chiarezza, scriviamolo. Successivamente, lasceremo invariata la base e sommeremo gli indicatori:
Esempio 9. Rappresenta la potenza 3 8 come prodotto di potenze con le stesse basi.
In questo problema, devi creare un prodotto di potenze le cui basi saranno pari a 3 e la somma dei cui esponenti sarà pari a 8. È possibile utilizzare qualsiasi indicatore. Rappresentiamo la potenza 3 8 come il prodotto delle potenze 3 5 e 3 3
In questo esempio ci siamo affidati ancora una volta alla proprietà fondamentale del grado. Dopotutto, l'espressione 3 5 × 3 3 può essere scritta come 3 5 + 3, da cui 3 8.
Naturalmente era possibile rappresentare la potenza 3 8 come un prodotto di altre potenze. Ad esempio, nella forma 3 7 × 3 1, poiché anche questo prodotto è uguale a 3 8
Rappresentare una laurea come prodotto di poteri con le stesse basi è per lo più un lavoro creativo. Pertanto, non è necessario aver paura di sperimentare.
Esempio 10. Invia laurea X 12 sotto forma di vari prodotti di poteri con basi X .
Usiamo la proprietà base dei gradi. Immaginiamo X 12 sotto forma di prodotti con basi X, e la somma degli indicatori è 12
I costrutti con somme di indicatori sono stati registrati per chiarezza. Molto spesso puoi saltarli. Quindi ottieni una soluzione compatta:
Elevare alla potenza di un prodotto
Per elevare un prodotto a una potenza, è necessario elevare ciascun fattore di questo prodotto alla potenza specificata e moltiplicare i risultati.
Ad esempio, eleviamo alla seconda potenza il prodotto 2×3. Prendiamo questo prodotto tra parentesi e indichiamo 2 come indicatore
Ora eleviamo alla seconda potenza ciascun fattore del prodotto 2×3 e moltiplichiamo i risultati:
Il principio di funzionamento di questa regola si basa sulla definizione di laurea data all'inizio.
Elevare il prodotto 2×3 alla seconda potenza significa ripetere il prodotto due volte. E se lo ripeti due volte, ottieni quanto segue:
2×3×2×3
Riorganizzare i luoghi dei fattori non cambia il prodotto. Ciò ti consente di raggruppare fattori simili:
2×2×3×3
I fattori ripetitivi possono essere sostituiti con voci brevi - basi con indicatori. Il prodotto 2 × 2 può essere sostituito con 2 2 e il prodotto 3 × 3 può essere sostituito con 3 2. Quindi l'espressione 2 × 2 × 3 × 3 diventa l'espressione 2 2 × 3 2.
Permettere ab lavoro originale. Elevare a potenza un dato prodotto N, è necessario moltiplicare i fattori separatamente UN E B al grado specificato N
Questa proprietà è vera per qualsiasi numero di fattori. Sono valide anche le seguenti espressioni:
Esempio 2. Trova il valore dell'espressione (2 × 3 × 4) 2
In questo esempio è necessario elevare alla seconda potenza il prodotto 2×3×4. Per fare ciò, devi elevare ciascun fattore di questo prodotto alla seconda potenza e moltiplicare i risultati:
Esempio 3. Eleva il prodotto alla terza potenza a×b×c
Racchiudiamo questo prodotto tra parentesi e indichiamo il numero 3 come indicatore
Esempio 4. Eleva il prodotto 3 alla terza potenza xyz
Racchiudiamo questo prodotto tra parentesi e indichiamo 3 come indicatore
(3xyz) 3
Eleviamo alla terza potenza ciascun fattore di questo prodotto:
(3xyz) 3 = 3 3 X 3 sì 3 z 3
Il numero 3 elevato alla terza potenza è uguale al numero 27. Lasceremo invariato il resto:
(3xyz) 3 = 3 3 X 3 sì 3 z 3 = 27X 3 sì 3 z 3
In alcuni esempi la moltiplicazione di potenze con lo stesso esponente può essere sostituita dal prodotto di basi con lo stesso esponente.
Ad esempio, calcoliamo il valore dell'espressione 5 2 × 3 2. Eleviamo ogni numero alla seconda potenza e moltiplichiamo i risultati:
5 2 × 3 2 = 25 × 9 = 225
Ma non è necessario calcolare ciascun grado separatamente. Invece questo prodotto di potenze può essere sostituito da un prodotto con un esponente (5 × 3) 2 . Successivamente, calcola il valore tra parentesi ed eleva il risultato alla seconda potenza:
5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225
Anche in questo caso è stata utilizzata la regola dell’elevamento a potenza di un prodotto. Dopotutto, se (a×b)N = un n × b n , Quello un n × b n = (a×b)n. Cioè, i lati sinistro e destro dell’uguaglianza si sono scambiati di posto.
Elevare un grado a una potenza
Abbiamo considerato questa trasformazione come un esempio quando abbiamo cercato di comprendere l'essenza delle identiche trasformazioni di gradi.
Quando si eleva una potenza a potenza, la base viene lasciata invariata e gli esponenti vengono moltiplicati:
(UN)m = un n × m
Ad esempio, l'espressione (2 3) 2 è una potenza elevata a una potenza: due alla terza potenza viene elevata alla seconda potenza. Per trovare il valore di questa espressione, si può lasciare invariata la base e moltiplicare gli esponenti:
(2 3) 2 = 2 3 × 2 = 2 6
(2 3) 2 = 2 3 × 2 = 2 6 = 64
Questa regola si basa sulle regole precedenti: esponenziazione del prodotto e proprietà fondamentale del grado.
Torniamo all'espressione (2 3) 2. L'espressione tra parentesi 2 3 è un prodotto di tre fattori identici, ciascuno dei quali è uguale a 2. Quindi nell'espressione (2 3) la potenza 2 all'interno delle parentesi può essere sostituita dal prodotto 2 × 2 × 2.
(2×2×2) 2
E questa è l'esponenziazione del prodotto che abbiamo studiato prima. Ricordiamo che per elevare un prodotto a una potenza è necessario elevare ciascun fattore di un dato prodotto alla potenza indicata e moltiplicare i risultati ottenuti:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2
Ora abbiamo a che fare con la proprietà fondamentale del grado. Lasciamo invariata la base e sommiamo gli indicatori:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6
Come prima, ne abbiamo ricevuti 2 6. Il valore di questo grado è 64
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64
Anche un prodotto i cui fattori sono potenze può essere elevato a potenza.
Ad esempio, troviamo il valore dell'espressione (2 2 × 3 2) 3. Qui, gli indicatori di ciascun moltiplicatore devono essere moltiplicati per l’indicatore totale 3. Successivamente, trova il valore di ciascun grado e calcola il prodotto:
(2 2 × 3 2) 3 = 2 2 × 3 × 3 2 × 3 = 2 6 × 3 6 = 64 × 729 = 46656
Approssimativamente la stessa cosa accade quando si eleva un prodotto a una potenza. Abbiamo detto che elevando un prodotto a una potenza, ogni fattore di questo prodotto viene elevato alla potenza specificata.
Ad esempio, per elevare alla terza potenza il prodotto 2 × 4, scriveresti la seguente espressione:
Ma prima si diceva che se un numero viene dato senza un indicatore, allora l'indicatore deve essere considerato uguale a uno. Risulta che i fattori del prodotto 2 × 4 hanno inizialmente esponenti pari a 1. Ciò significa che l'espressione 2 1 × 4 1 è stata elevata alla terza potenza. E questo sta aumentando di grado in grado.
Riscriviamo la soluzione utilizzando la regola per elevare una potenza a potenza. Dovremmo ottenere lo stesso risultato:
Esempio 2. Trova il valore dell'espressione (3 3) 2
Lasciamo invariata la base e moltiplichiamo gli indicatori:
Ne abbiamo 3 6. Il numero 3 alla sesta potenza è il numero 729
Esempio 3xy)³
Esempio 4. Eseguire l'elevamento a potenza nell'espressione ( abc)⁵
Eleviamo alla quinta potenza ciascun fattore del prodotto:
Esempio 5ascia) 3
Eleviamo alla terza potenza ciascun fattore del prodotto:
Poiché il numero negativo −2 è stato elevato alla terza potenza, è stato messo tra parentesi.
Esempio 6. Eseguire l'elevamento a potenza nell'espressione (10 xy) 2
Esempio 7. Eseguire l'elevamento a potenza nell'espressione (−5 X) 3
Esempio 8. Eseguire l'elevamento a potenza nell'espressione (−3 sì) 4
Esempio 9. Eseguire l'elevamento a potenza nell'espressione (−2 abx)⁴
Esempio 10. Semplifica l'espressione X 5×( X 2) 3
Grado X Lasciamo per ora invariato 5 e nell'espressione ( X 2) 3 alziamo la potenza alla potenza:
X 5 × (X 2) 3 =x 5 ×x 2×3 =x 5 ×x 6
Adesso facciamo la moltiplicazione X 5 ×x 6. Per fare ciò utilizzeremo la proprietà fondamentale di un grado: la base X Lasciamo invariato e sommiamo gli indicatori:
X 5 × (X 2) 3 =x 5 ×x 2×3 =x 5 ×x 6 = X 5 + 6 = X 11
Esempio 9. Trova il valore dell'espressione 4 3 × 2 2 utilizzando la proprietà di base della potenza.
La proprietà base di un grado può essere utilizzata se le basi dei gradi originali sono le stesse. In questo esempio le basi sono diverse, quindi prima devi modificare un po' l'espressione originale, cioè assicurarti che le basi delle potenze diventino le stesse.
Osserviamo da vicino il grado 4 3. La base di questo grado è il numero 4, che può essere rappresentato come 2 2. Quindi l'espressione originale assumerà la forma (2 2) 3 × 2 2. Elevando la potenza a potenza nell'espressione (2 2) 3, otteniamo 2 6. Quindi l'espressione originale assumerà la forma 2 6 × 2 2, che può essere calcolata utilizzando la proprietà fondamentale della potenza.
Scriviamo la soluzione di questo esempio:
Divisione dei gradi
Per eseguire la divisione dei poteri, devi trovare il valore di ciascun potere, quindi dividere i numeri ordinari.
Ad esempio, dividiamo 4 3 per 2 2.
Calcoliamo 4 3, otteniamo 64. Calcola 2 2, ottieni 4. Ora dividi 64 per 4, ottieni 16
Se, quando si dividono le potenze, le basi risultano essere le stesse, allora la base può essere lasciata invariata e l'esponente del divisore può essere sottratto dall'esponente del dividendo.
Ad esempio, troviamo il valore dell'espressione 2 3: 2 2
Lasciamo invariata la base 2 e sottraiamo l'esponente del divisore dall'esponente del dividendo:
Ciò significa che il valore dell'espressione 2 3: 2 2 è uguale a 2.
Questa proprietà si fonda sulla moltiplicazione delle potenze per le stesse basi, o, come si diceva, sulla proprietà fondamentale di una potenza.
Torniamo all'esempio precedente 2 3: 2 2. Qui il dividendo è 2 3 e il divisore è 2 2.
Dividere un numero per un altro significa trovare un numero che, moltiplicato per il divisore, darà come risultato il dividendo.
Nel nostro caso, dividere 2 3 per 2 2 significa trovare una potenza che, moltiplicata per il divisore 2 2, dà come risultato 2 3. Quale potenza può essere moltiplicata per 2 2 per ottenere 2 3? Ovviamente solo il grado 2 è 1. Dalla proprietà fondamentale del grado abbiamo:
Puoi verificare che il valore dell'espressione 2 3: 2 2 è uguale a 2 1 calcolando direttamente l'espressione 2 3: 2 2 stessa. Per fare ciò, troviamo prima il valore della potenza 2 3, otteniamo 8. Quindi troviamo il valore della potenza 2 2, otteniamo 4. Dividi 8 per 4, otteniamo 2 o 2 1, poiché 2 = 2 1.
2 3: 2 2 = 8: 4 = 2
Pertanto, quando si dividono poteri con le stesse basi, vale la seguente uguaglianza:
Può anche succedere che non solo le ragioni, ma anche gli indicatori siano gli stessi. In questo caso la risposta sarà una.
Ad esempio, troviamo il valore dell'espressione 2 2: 2 2. Calcoliamo il valore di ciascun grado e dividiamo i numeri risultanti:
Quando risolvi l'esempio 2 2: 2 2, puoi anche applicare la regola di dividere le potenze con le stesse basi. Il risultato è un numero elevato a zero, poiché la differenza tra gli esponenti delle potenze 2 2 e 2 2 è uguale a zero:
Abbiamo scoperto sopra perché il numero 2 elevato alla potenza zero è uguale a uno. Se calcoli 2 2: 2 2 usando il metodo consueto, senza usare la regola della divisione delle potenze, ottieni uno.
Esempio 2. Trova il valore dell'espressione 4 12: 4 10
Lasciamo invariato 4 e sottraiamo l'esponente del divisore dall'esponente del dividendo:
4 12: 4 10 = 4 12 − 10 = 4 2 = 16
Esempio 3. Presenta il quoziente X 3: X sotto forma di potenza con base X
Usiamo la regola della divisione del potere. Base X Lasciamolo invariato e sottraiamo l'esponente del divisore dall'esponente del dividendo. L'esponente del divisore è uguale a uno. Per chiarezza scriviamolo:
Esempio 4. Presenta il quoziente X 3: X 2 come potenza con base X
Usiamo la regola della divisione del potere. Base X
La divisione dei poteri può essere scritta come una frazione. Quindi, l’esempio precedente può essere scritto come segue:
Il numeratore e il denominatore di una frazione possono essere scritti in forma estesa, cioè sotto forma di prodotti di fattori identici. Grado X 3 può essere scritto come x×x×x e il grado X 2 come x×x. Poi il disegno X 3 − 2 può essere saltato e la frazione può essere ridotta. Sarà possibile ridurre due fattori al numeratore e al denominatore X. Di conseguenza, rimarrà un moltiplicatore X
O anche più breve:
È utile anche poter ridurre velocemente le frazioni costituite da potenze. Ad esempio, una frazione può essere ridotta di X 2. Ridurre una frazione di X 2 devi dividere il numeratore e il denominatore della frazione per X 2
Non è necessario descrivere dettagliatamente la divisione dei gradi. L'abbreviazione sopra può essere abbreviata:
O anche più breve:
Esempio 5. Esegui la divisione X 12 :X 3
Usiamo la regola della divisione del potere. Base X lascialo invariato e sottrai l'esponente del divisore dall'esponente del dividendo:
Scriviamo la soluzione utilizzando la riduzione della frazione. Divisione dei gradi X 12 :X Scriviamo 3 nella forma . Successivamente, riduciamo questa frazione di X 3 .
Esempio 6. Trova il valore di un'espressione
Al numeratore eseguiamo la moltiplicazione delle potenze con le stesse basi:
Ora applichiamo la regola della divisione dei poteri con le stesse basi. Lasciamo invariata la base 7 e sottraiamo l'esponente del divisore dall'esponente del dividendo:
Completiamo l'esempio calcolando la potenza 7 2
Esempio 7. Trova il valore di un'espressione
Eleviamo la potenza alla potenza del numeratore. Devi farlo con l'espressione (2 3) 4
Ora moltiplichiamo le potenze con le stesse basi al numeratore.
Addizione e sottrazione di poteri
È ovvio che i numeri dotati di potenze possono essere sommati come le altre quantità , sommandoli uno dopo l'altro con i relativi segni.
Quindi la somma di a 3 e b 2 è a 3 + b 2.
La somma di a 3 - b n e h 5 - d 4 è a 3 - b n + h 5 - d 4.
Probabilità potenze uguali di variabili identiche possono essere aggiunti o sottratti.
Quindi, la somma di 2a 2 e 3a 2 è uguale a 5a 2.
È anche ovvio che se prendi due quadrati a, o tre quadrati a, o cinque quadrati a.
Ma gradi varie variabili E vari gradi variabili identiche, devono essere composti sommandoli con i relativi segni.
Quindi la somma di a 2 e a 3 è la somma di a 2 + a 3.
È ovvio che il quadrato di a, e il cubo di a, non sono pari al doppio del quadrato di a, ma al doppio del cubo di a.
La somma di a 3 b n e 3a 5 b 6 è a 3 b n + 3a 5 b 6.
Sottrazione le potenze si eseguono allo stesso modo dell'addizione, tranne che i segni dei sottraendo devono essere cambiati di conseguenza.
O:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6
Moltiplicare i poteri
I numeri dotati di potenze possono essere moltiplicati, come le altre quantità, scrivendoli uno dopo l'altro, con o senza segno di moltiplicazione tra di loro.
Pertanto, il risultato della moltiplicazione di a 3 per b 2 è a 3 b 2 o aaabb.
O:
x -3 ⋅ un m = un m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Il risultato nell'ultimo esempio può essere ordinato aggiungendo variabili identiche.
L'espressione assumerà la forma: a 5 b 5 y 3.
Confrontando diversi numeri (variabili) con potenze, possiamo vedere che se ne moltiplicano due qualsiasi, il risultato è un numero (variabile) con una potenza pari a quantità gradi di termini.
Quindi, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Qui 5 è la potenza del risultato della moltiplicazione, che è uguale a 2 + 3, la somma delle potenze dei termini.
Quindi, a n.a m = a m+n.
Per a n , a viene preso come fattore tante volte quanto la potenza di n;
E a m si prende come fattore tante volte quanto è uguale il grado m;
Ecco perché, le potenze con le stesse basi possono essere moltiplicate sommando gli esponenti delle potenze.
Quindi, a 2 .a 6 = a 2+6 = a 8 . E x 3 .x 2 .x = x 3+2+1 = x 6 .
O:
4a n ⋅ 2a n = 8a 2n
b2 y3 ⋅ b4 y = b6 y4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1
Moltiplica (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Risposta: x 4 - y 4.
Moltiplica (x 3 + x – 5) ⋅ (2x 3 + x + 1).
Questa regola vale anche per i numeri i cui esponenti sono negativo.
1. Quindi, a -2 .a -3 = a -5 . Questo può essere scritto come (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Se si moltiplicano a + b per a - b, il risultato sarà a 2 - b 2: cioè
Il risultato della moltiplicazione della somma o della differenza di due numeri è uguale alla somma o alla differenza dei loro quadrati.
Se moltiplichi la somma e la differenza di due numeri elevati a piazza, il risultato sarà uguale alla somma o alla differenza di questi numeri in quarto gradi.
Quindi, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.
Divisione dei gradi
I numeri con potenze possono essere divisi come gli altri numeri, sottraendo dal dividendo o trasformandoli in frazioni.
Quindi a 3 b 2 diviso b 2 è uguale a a 3.
Scrivere un 5 diviso per 3 assomiglia a $\frac $. Ma questo è uguale a 2 . In una serie di numeri
un +4, un +3, un +2, un +1, un 0, un -1, un -2, un -3, un -4.
qualsiasi numero può essere diviso per un altro e l'esponente sarà uguale a differenza indicatori dei numeri divisibili.
Quando si dividono i gradi con la stessa base, i loro esponenti vengono sottratti..
Quindi, y 3:y 2 = y 3-2 = y 1. Cioè $\frac = y$.
E a n+1:a = a n+1-1 = a n . Cioè $\frac = a^n$.
O:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3
La regola vale anche per i numeri con negativo valori dei gradi.
Il risultato della divisione -5 per -3 è -2.
Inoltre, $\frac: \frac = \frac .\frac = \frac = \frac $.
h 2:h -1 = h 2+1 = h 3 oppure $h^2:\frac = h^2.\frac = h^3$
È necessario padroneggiare molto bene la moltiplicazione e la divisione dei poteri, poiché tali operazioni sono molto utilizzate in algebra.
Esempi di risoluzione di esempi con frazioni contenenti numeri con potenze
1. Diminuire gli esponenti di $\frac $ Risposta: $\frac $.
2. Diminuire gli esponenti di $\frac$. Risposta: $\frac$ o 2x.
3. Riduci gli esponenti a 2 /a 3 e a -3 /a -4 e portali a un denominatore comune.
a 2 .a -4 è a -2 il primo numeratore.
a 3 .a -3 è a 0 = 1, il secondo numeratore.
a 3 .a -4 è a -1 , il numeratore comune.
Dopo la semplificazione: a -2 /a -1 e 1/a -1 .
4. Riduci gli esponenti 2a 4 /5a 3 e 2 /a 4 e portali a un denominatore comune.
Risposta: 2a 3 /5a 7 e 5a 5 /5a 7 oppure 2a 3 /5a 2 e 5/5a 2.
5. Moltiplica (a 3 + b)/b 4 per (a - b)/3.
6. Moltiplica (a 5 + 1)/x 2 per (b 2 - 1)/(x + a).
7. Moltiplica b 4 /a -2 per h -3 /x e a n /y -3 .
8. Dividere a 4 /y 3 per a 3 /y 2 . Risposta: a/a.
Proprietà del grado
Ti ricordiamo che in questa lezione capiremo proprietà dei gradi con indicatori naturali e zero. Le potenze con esponenti razionali e le loro proprietà verranno discusse nelle lezioni per la terza media.
Una potenza con esponente naturale ha diverse proprietà importanti che ci consentono di semplificare i calcoli negli esempi con potenze.
Proprietà n. 1
Prodotto di poteri
Quando si moltiplicano le potenze con le stesse basi, la base rimane invariata e si sommano gli esponenti delle potenze.
a m · a n = a m + n, dove “a” è un numero qualsiasi e “m”, “n” sono numeri naturali qualsiasi.
Questa proprietà delle potenze vale anche per il prodotto di tre o più potenze.
- Semplifica l'espressione.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Presentatelo come una laurea.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17 - Presentatelo come una laurea.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15 - Scrivi il quoziente come potenza
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2 - Calcolare.
Tieni presente che nella proprietà specificata si parlava solo della moltiplicazione di potenze con le stesse basi. Non si applica alla loro aggiunta.
Non è possibile sostituire la somma (3 3 + 3 2) con 3 5. Ciò è comprensibile se
calcolare (3 3 + 3 2) = (27 + 9) = 36 e 3 5 = 243
Proprietà n. 2
Gradi parziali
Quando si dividono potenze con la stessa base, la base rimane invariata e l'esponente del divisore viene sottratto dall'esponente del dividendo.
11 3 − 2 4 2 − 1 = 11 4 = 44
Esempio. Risolvi l'equazione. Utilizziamo la proprietà delle potenze quozienti.
3 8: t = 3 4
Risposta: t = 3 4 = 81
Utilizzando le proprietà n. 1 e n. 2, puoi facilmente semplificare le espressioni ed eseguire calcoli.
Esempio. Semplifica l'espressione.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Esempio. Trova il valore di un'espressione utilizzando le proprietà degli esponenti.
2 11 − 5 = 2 6 = 64
Si noti che nella Proprietà 2 si parlava solo di dividere poteri con le stesse basi.
Non è possibile sostituire la differenza (4 3 −4 2) con 4 1. Ciò è comprensibile se calcoli (4 3 −4 2) = (64 − 16) = 48 e 4 1 = 4
Proprietà n. 3
Elevare un grado a una potenza
Quando si eleva un grado a potenza, la base del grado rimane invariata e gli esponenti vengono moltiplicati.
(a n) m = a n · m, dove “a” è un numero qualsiasi e “m”, “n” sono numeri naturali qualsiasi.
Ti ricordiamo che un quoziente può essere rappresentato come una frazione. Pertanto, ci soffermeremo più in dettaglio sull'argomento dell'elevazione di una frazione a potenza nella pagina successiva.
Come moltiplicare i poteri
Come moltiplicare i poteri? Quali poteri possono essere moltiplicati e quali no? Come moltiplicare un numero per una potenza?
In algebra, puoi trovare un prodotto di potenze in due casi:
1) se i titoli hanno le stesse basi;
2) se i gradi hanno gli stessi indicatori.
Quando si moltiplicano potenze con le stesse basi, è necessario lasciare la base e aggiungere gli esponenti:
Quando si moltiplicano i gradi per gli stessi indicatori, l'indicatore complessivo può essere tolto tra parentesi:
Diamo un'occhiata a come moltiplicare i poteri utilizzando esempi specifici.
L'unità non si scrive nell'esponente, ma quando si moltiplicano le potenze si tiene conto di:
Quando si moltiplica, può esserci un numero qualsiasi di potenze. Va ricordato che non è necessario scrivere il segno di moltiplicazione prima della lettera:
Nelle espressioni, l'elevamento a potenza viene eseguito per primo.
Se devi moltiplicare un numero per una potenza, devi prima eseguire l'elevamento a potenza e solo dopo la moltiplicazione:
Moltiplicare le potenze con le stesse basi
Questo video tutorial è disponibile tramite abbonamento
Hai già un abbonamento? Login
In questa lezione studieremo la moltiplicazione di potenze con basi simili. Innanzitutto ricordiamo la definizione di grado e formuliamo un teorema sulla validità dell'uguaglianza . Quindi forniremo esempi della sua applicazione su numeri specifici e lo dimostreremo. Applicheremo il teorema anche per risolvere vari problemi.
Argomento: Potenza con esponente naturale e sue proprietà
Lezione: Moltiplicare le potenze con le stesse basi (formula)
1. Definizioni di base
Definizioni di base:
N- esponente,
— N l'esima potenza di un numero.
2. Enunciato del Teorema 1
Teorema 1. Per qualsiasi numero UN e qualsiasi naturale N E k l'uguaglianza è vera:
In altre parole: se UN– qualsiasi numero; N E k numeri naturali, quindi:
Quindi regola 1:
3. Compiti esplicativi
Conclusione: casi particolari hanno confermato la correttezza del Teorema n. 1. Proviamolo nel caso generale, cioè per qualsiasi UN e qualsiasi naturale N E k.
4. Dimostrazione del Teorema 1
Dato un numero UN- Qualunque; numeri N E k- naturale. Dimostrare:
La dimostrazione si basa sulla definizione di laurea.
5. Esempi di risoluzione utilizzando il Teorema 1
Esempio 1: Consideralo come una laurea.
Per risolvere i seguenti esempi utilizzeremo il Teorema 1.
E) 
6. Generalizzazione del Teorema 1
Una generalizzazione usata qui:
7. Risoluzione di esempi utilizzando una generalizzazione del Teorema 1
8. Risoluzione di vari problemi utilizzando il Teorema 1
Esempio 2: Calcola (puoi usare la tabella dei poteri di base).
UN) 
(secondo la tabella)
B) 
Esempio 3: Scrivilo come una potenza in base 2.
UN) 
Esempio 4: Determina il segno del numero:
, UN - negativo, poiché l'esponente a -13 è dispari.
Esempio 5: Sostituisci (·) con la potenza di un numero con base R:
Abbiamo, cioè.
9. Riassumendo
1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. e altri. M.: Illuminazione. 2010
1. Assistente scolastico (Fonte).
1. Presente come potere:
a) b) c) d) e) 
3. Scrivi come una potenza in base 2:
4. Determina il segno del numero:
UN) 
5. Sostituisci (·) con una potenza di un numero con base R:
a) r 4 · (·) = r 15; b) (·) · r 5 = r 6
Moltiplicazione e divisione di potenze con gli stessi esponenti
In questa lezione studieremo la moltiplicazione di potenze con esponenti uguali. Innanzitutto, ricordiamo le definizioni e i teoremi di base sulla moltiplicazione e divisione delle potenze con le stesse basi e sull'elevazione delle potenze a potenze. Quindi formuliamo e dimostriamo teoremi sulla moltiplicazione e divisione delle potenze con gli stessi esponenti. E poi con il loro aiuto risolveremo una serie di problemi tipici.
Richiami sulle definizioni e sui teoremi fondamentali
Qui UN- la base della laurea,
— N l'esima potenza di un numero.
Teorema 1. Per qualsiasi numero UN e qualsiasi naturale N E k l'uguaglianza è vera:
Quando si moltiplicano potenze con le stesse basi si sommano gli esponenti, la base rimane invariata.
Teorema 2. Per qualsiasi numero UN e qualsiasi naturale N E k, tale che N > k l'uguaglianza è vera:
Quando si dividono i gradi con le stesse basi, gli esponenti vengono sottratti, ma la base rimane invariata.
Teorema 3. Per qualsiasi numero UN e qualsiasi naturale N E k l'uguaglianza è vera:
Tutti i teoremi elencati riguardavano potenze con lo stesso principio ragioni, in questa lezione esamineremo i gradi con lo stesso indicatori.
Esempi di moltiplicazione di potenze con gli stessi esponenti
Considera i seguenti esempi:
Scriviamo le espressioni per determinare il grado.
Conclusione: Dagli esempi si può vedere che 
, ma questo deve ancora essere dimostrato. Formuliamo il teorema e dimostriamolo nel caso generale, cioè per qualsiasi UN E B e qualsiasi naturale N.
Formulazione e dimostrazione del Teorema 4
Per qualsiasi numero UN E B e qualsiasi naturale N l'uguaglianza è vera:
Prova Teorema 4 .
Per definizione di laurea:
Quindi lo abbiamo dimostrato .
Per moltiplicare le potenze con gli stessi esponenti è sufficiente moltiplicare le basi e lasciare invariato l'esponente.
Formulazione e dimostrazione del Teorema 5
Formuliamo un teorema per la divisione delle potenze con gli stessi esponenti.
Per qualsiasi numero UN E B() e qualsiasi naturale N l'uguaglianza è vera:
Prova Teorema 5 .
Scriviamo la definizione di laurea:
Enunciazione di teoremi in parole
Quindi, lo abbiamo dimostrato.
Per dividere tra loro potenze con lo stesso esponente è sufficiente dividere una base per un'altra e lasciare invariato l'esponente.
Risoluzione di problemi tipici utilizzando il Teorema 4
Esempio 1: Presente come prodotto dei poteri.
Per risolvere i seguenti esempi utilizzeremo il Teorema 4.
Per risolvere il seguente esempio, richiamare le formule:
Generalizzazione del Teorema 4
Generalizzazione del Teorema 4:
Risoluzione di esempi utilizzando il teorema generalizzato 4
Continuando a risolvere i problemi tipici
Esempio 2: Scrivilo come una potenza del prodotto.
Esempio 3: Scrivilo come una potenza con esponente 2.
Esempi di calcolo
Esempio 4: Calcola nel modo più razionale.
2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF
3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. e altri. Algebra 7.M.: Illuminismo. 2006
2. Assistente scolastico (Fonte).
1. Presente come prodotto dei poteri:
UN) ; B) ; V); G) ;
2. Scrivi come potenza del prodotto:
3. Scrivi come una potenza con esponente 2:
4. Calcola nel modo più razionale.
Lezione di matematica sul tema “Moltiplicazione e divisione delle potenze”
Sezioni: Matematica
Obiettivo pedagogico:
Compiti:
Unità di attività didattiche: determinazione del grado con indicatore naturale; componenti di laurea; definizione di privato; legge combinatoria della moltiplicazione.
I. Organizzare una dimostrazione della padronanza delle conoscenze esistenti da parte degli studenti. (passaggio 1)
a) Aggiornamento delle conoscenze:
2) Formulare una definizione di grado con esponente naturale.
a n =a a a a … a (n volte)
b k =b b b b a… b (k volte) Giustifica la risposta.
II. Organizzazione dell’autovalutazione del grado di competenza dello studente nell’esperienza attuale. (passaggio 2)
Autotest: (lavoro individuale in due versioni.)
A1) Presentare il prodotto 7 7 7 7 x x x come potenza:
A2) Rappresentare la potenza (-3) 3 x 2 come un prodotto
A3) Calcola: -2 3 2 + 4 5 3
Seleziono il numero di compiti nel test in base al livello di preparazione della classe.
Ti do la chiave del test per l'autotest. Criteri: superato - non superato.
III. Compito didattico e pratico (step 3) + step 4. (gli studenti stessi formuleranno le proprietà)
Mentre risolvono i problemi 1) e 2), gli studenti propongono una soluzione e io, come insegnante, organizzo la classe per trovare un modo per semplificare le potenze quando si moltiplicano con le stesse basi.
Insegnante: trova un modo per semplificare le potenze quando si moltiplicano con le stesse basi.
Sul cluster appare una voce:
L'argomento della lezione è formulato. Moltiplicazione dei poteri.
Insegnante: elaborare una regola per dividere i poteri con le stesse basi.
Ragionamento: quale azione viene utilizzata per verificare la divisione? un 5: un 3 = ? che a 2 a 3 = a 5
Torno al diagramma - un cluster e aggiungo alla voce - .. quando dividiamo, sottraiamo e aggiungiamo l'argomento della lezione. ...e divisione dei gradi.
IV. Comunicare agli studenti i limiti della conoscenza (come minimo e come massimo).
Insegnante: il compito minimo per la lezione di oggi è imparare ad applicare le proprietà di moltiplicazione e divisione delle potenze con le stesse basi, e il compito massimo è applicare moltiplicazione e divisione insieme.
Scriviamo alla lavagna : un m un n = un m+n ; un m: un n = un m-n
V. Organizzazione dello studio di nuovo materiale. (passaggio 5)
a) Secondo il libro di testo: n. 403 (a, c, e) compiti con formulazioni diverse
N. 404 (a,d,f) lavoro autonomo, poi organizzo un controllo reciproco, consegno le chiavi.
b) Per quale valore di m è vera l'uguaglianza? a 16 a m = a 32; xhx14 = x28; x8 (*) = x14
Compito: trovare esempi simili per la divisione.
c) N. 417 (a), N. 418 (a) Trappole per gli studenti: x3xn = x3n; 3 4 3 2 = 9 6 ; un 16: un 8 = un 2.
VI. Riassumere ciò che è stato appreso, condurre un lavoro diagnostico (che incoraggia gli studenti, non l'insegnante, a studiare questo argomento) (fase 6)
Lavoro diagnostico.
Test(posizionare le chiavi sul retro dell'impasto).
Opzioni del compito: rappresentare il quoziente x 15 come potenza: x 3; rappresentare come potenza il prodotto (-4) 2 (-4) 5 (-4) 7 ; per cui m è valida l'uguaglianza a 16 a m = a 32? trova il valore dell'espressione h 0: h 2 in h = 0,2; calcolare il valore dell'espressione (5 2 5 0) : 5 2 .
Riepilogo della lezione. Riflessione. Divido la classe in due gruppi.
Trova argomenti nel gruppo I: a favore della conoscenza delle proprietà della laurea e nel gruppo II - argomenti che diranno che puoi fare a meno delle proprietà. Ascoltiamo tutte le risposte e traiamo conclusioni. Nelle lezioni successive, puoi offrire dati statistici e intitolare la rubrica “È incredibile!”
VII. Compiti a casa.
Informazioni storiche. Quali numeri sono chiamati numeri di Fermat.
P.19. N. 403, N. 408, N. 417
Letteratura utilizzata:
Proprietà dei gradi, formulazioni, dimostrazioni, esempi.
Dopo che è stata determinata la potenza di un numero, è logico parlarne proprietà del grado. In questo articolo daremo le proprietà di base della potenza di un numero, toccando tutti i possibili esponenti. Qui forniremo prove di tutte le proprietà dei gradi e mostreremo anche come queste proprietà vengono utilizzate durante la risoluzione degli esempi.
Navigazione della pagina.
Proprietà dei gradi con esponente naturale
Per definizione di potenza con esponente naturale, la potenza a n è il prodotto di n fattori, ciascuno dei quali è uguale ad a. Sulla base di questa definizione e anche utilizzando proprietà della moltiplicazione dei numeri reali, possiamo ottenere e giustificare quanto segue proprietà del grado con esponente naturale:
- se a>0, allora a n>0 per qualsiasi numero naturale n;
- se a=0, allora a n =0;
- se a 2·m >0 , se a 2·m−1 n ;
- se m e n sono numeri naturali tali che m>n, allora per 0m n e per a>0 è vera la disuguaglianza a m >a n.
- a m · a n = a m+n ;
- un m:un n =un m−n ;
- (a·b) n =a n ·b n ;
- (a:b) n =a n:b n ;
- (a m) n = a m·n ;
- se n è un intero positivo, aeb sono numeri positivi e a n n e a −n >b −n ;
- se m e n sono interi, e m>n, allora per 0m n, e per a>1 vale la disuguaglianza a m >a n.
Notiamo subito che tutte le uguaglianze scritte lo sono identico alle condizioni specificate, sia la parte destra che quella sinistra possono essere scambiate. Ad esempio, la proprietà principale della frazione a m ·a n =a m+n con semplificazione delle espressioni spesso usato nella forma a m+n =a m ·a n .
Ora esaminiamo ciascuno di essi in dettaglio.
Cominciamo con la proprietà del prodotto di due potenze con le stesse basi, che si chiama la proprietà principale della laurea: per ogni numero reale a e ogni numero naturale m e n, l'uguaglianza a m ·a n = a m+n è vera.
Dimostriamo la proprietà principale del grado. Per la definizione di potenza con esponente naturale, il prodotto di potenze con basi identiche della forma a m ·a n può essere scritto come il prodotto 
. A causa delle proprietà della moltiplicazione, l'espressione risultante può essere scritta come 
, e questo prodotto è una potenza del numero a con esponente naturale m+n, cioè a m+n. Questo completa la dimostrazione.
Facciamo un esempio che confermi la proprietà principale della laurea. Prendiamo i gradi con le stesse basi 2 e potenze naturali 2 e 3, utilizzando la proprietà fondamentale dei gradi possiamo scrivere l'uguaglianza 2 2 ·2 3 =2 2+3 =2 5. Verifichiamo la sua validità calcolando i valori delle espressioni 2 2 · 2 3 e 2 5 . Eseguendo l'elevamento a potenza abbiamo 2 2 2 3 =(2 2) (2 2 2) = 4 8 = 32 e 2 5 =2 2 2 2 2 = 32 , poiché otteniamo valori uguali, allora l'uguaglianza 2 2 ·2 3 =2 5 è corretto e conferma la proprietà principale del grado.
La proprietà fondamentale di un grado, basata sulle proprietà della moltiplicazione, può essere generalizzata al prodotto di tre o più potenze con le stesse basi ed esponenti naturali. Quindi per ogni numero k di numeri naturali n 1 , n 2 , …, n k l'uguaglianza a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k è vera.
Ad esempio, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .
Possiamo passare alla proprietà successiva delle potenze con esponente naturale: proprietà dei quozienti di potenza con le stesse basi: per qualsiasi numero reale a diverso da zero e numeri naturali arbitrari m en che soddisfano la condizione m>n, l'uguaglianza a m:a n =a m−n è vera.
Prima di presentare la dimostrazione di questa proprietà, discutiamo il significato delle condizioni aggiuntive nella formulazione. La condizione a≠0 è necessaria per evitare la divisione per zero, poiché 0 n = 0, e quando abbiamo conosciuto la divisione, abbiamo convenuto che non possiamo dividere per zero. La condizione m>n viene introdotta in modo da non andare oltre gli esponenti naturali. Infatti per m>n l’esponente a m−n è un numero naturale, altrimenti sarà zero (cosa che accade per m−n) oppure un numero negativo (cosa accade per m m−n ·a n =a (m−n) +n =a m. Dall'uguaglianza risultante a m−n ·a n =a m e dalla connessione tra moltiplicazione e divisione segue che a m−n è un quoziente di potenze a m e a n. Ciò dimostra la proprietà dei quozienti di potenze con le stesse basi.
Facciamo un esempio. Prendiamo due gradi con le stesse basi π ed esponenti naturali 5 e 2, l'uguaglianza π 5:π 2 =π 5−3 =π 3 corrisponde alla proprietà considerata del grado.
Ora consideriamo proprietà di potenza del prodotto: la potenza naturale n del prodotto di due numeri reali qualsiasi a e b è uguale al prodotto delle potenze a n e b n , cioè (a·b) n =a n ·b n .
Infatti, per definizione di grado con esponente naturale abbiamo 
. In base alle proprietà della moltiplicazione, l'ultimo prodotto può essere riscritto come 
, che è uguale a a n · b n .
Ecco un esempio: 
.
Questa proprietà si estende alla potenza del prodotto di tre o più fattori. Cioè, la proprietà del grado naturale n di un prodotto di k fattori è scritta come (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Per chiarezza mostreremo questa proprietà con un esempio. Per il prodotto di tre fattori elevato a 7 abbiamo .
La seguente proprietà è proprietà di un quoziente in natura: il quoziente dei numeri reali a e b, b≠0 alla potenza naturale n è uguale al quoziente delle potenze a n e b n, cioè (a:b) n =a n:b n.
La dimostrazione può essere effettuata utilizzando la proprietà precedente. Allora (a:b) n ·b n =((a:b)·b) n =a n , e dall'uguaglianza (a:b) n ·b n =a n segue che (a:b) n è il quoziente di divisione a n su bn.
Scriviamo questa proprietà utilizzando numeri specifici come esempio: 
.
Adesso diamogli voce proprietà di elevare un potere a potere: per ogni numero reale a e ogni numero naturale m e n, la potenza di a m elevata a n è uguale alla potenza del numero a con esponente m·n, cioè (a m) n =a m·n.
Ad esempio, (5 2) 3 =5 2·3 =5 6.
La prova della proprietà potere-grado è la seguente catena di uguaglianze: 
.
La proprietà considerata può essere estesa di grado in grado, ecc. Ad esempio, per qualsiasi numero naturale p, q, r e s, l'uguaglianza 
. Per maggiore chiarezza, facciamo un esempio con numeri specifici: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10.
Resta da soffermarsi sulle proprietà di confrontare i gradi con un esponente naturale.
Cominciamo dimostrando la proprietà di confrontare zero e potenza con un esponente naturale.
Innanzitutto, dimostriamo che a n >0 per ogni a>0.
Il prodotto di due numeri positivi è un numero positivo, come segue dalla definizione di moltiplicazione. Questo fatto e le proprietà della moltiplicazione suggeriscono che anche il risultato della moltiplicazione di un numero qualsiasi di numeri positivi sarà un numero positivo. E la potenza di un numero a con esponente naturale n, per definizione, è il prodotto di n fattori, ciascuno dei quali è uguale ad a. Queste argomentazioni ci permettono di affermare che per ogni base positiva a, il grado a n è un numero positivo. Per la proprietà provata 3 5 >0, (0.00201) 2 >0 e 
.
È abbastanza ovvio che per ogni numero naturale n con a=0 il grado di a n è zero. Infatti, 0 n =0·0·…·0=0 . Ad esempio, 0 3 = 0 e 0 762 = 0.
Passiamo alle basi di grado negative.
Cominciamo con il caso in cui l'esponente è un numero pari, denotiamolo come 2·m, dove m è un numero naturale. Poi 
. Secondo la regola per moltiplicare i numeri negativi, ciascuno dei prodotti della forma a·a è uguale al prodotto dei valori assoluti dei numeri a e a, il che significa che è un numero positivo. Pertanto anche il prodotto sarà positivo 
e grado a 2·m. Facciamo degli esempi: (−6) 4 >0 , (−2,2) 12 >0 e .
Infine, quando la base a è un numero negativo e l'esponente è un numero dispari 2 m−1, allora 
. Tutti i prodotti a·a sono numeri positivi, anche il prodotto di questi numeri positivi è positivo e la sua moltiplicazione per il restante numero negativo a dà come risultato un numero negativo. Per questa proprietà (−5) 3 17 n n è il prodotto dei lati sinistro e destro di n disuguaglianze vere a proprietà delle disuguaglianze, è vera anche una disuguaglianza dimostrabile della forma a n n. Ad esempio, a causa di questa proprietà, le disuguaglianze 3 7 7 e 
.
Resta da dimostrare l'ultima delle proprietà elencate delle potenze con esponente naturale. Formuliamolo. Di due potenze con esponente naturale e basi positive identiche minori di uno, è maggiore quella il cui esponente è minore; e di due potenze con esponente naturale e base identica maggiore di uno, è maggiore quella il cui esponente è maggiore. Procediamo alla dimostrazione di questa proprietà.
Proviamolo per m>n e 0m n . Per fare ciò, scriviamo la differenza a m − a n e la confrontiamo con zero. La differenza registrata, dopo aver tolto a n tra parentesi, assumerà la forma a n ·(a m−n−1) . Il prodotto risultante è negativo come prodotto di un numero positivo a n e di un numero negativo a m−n −1 (a n è positivo come potenza naturale di un numero positivo e la differenza a m−n −1 è negativa, poiché m−n >0 per la condizione iniziale m>n, da cui segue che quando 0m−n è minore dell'unità). Quindi a m − a n m n , che è ciò che doveva essere dimostrato. Ad esempio, diamo la disuguaglianza corretta.
Resta da dimostrare la seconda parte della proprietà. Proviamo che per m>n e a>1 a m >a n è vero. La differenza a m − a n dopo aver tolto a n dalle parentesi assume la forma a n ·(a m − n −1) . Questo prodotto è positivo, poiché per a>1 il grado a n è un numero positivo, e la differenza a m−n −1 è un numero positivo, poiché m−n>0 per la condizione iniziale, e per a>1 il grado a m−n è maggiore di uno. Di conseguenza a m −a n >0 e a m >a n , che è ciò che occorreva dimostrare. Questa proprietà è illustrata dalla disuguaglianza 3 7 >3 2.
Proprietà dei gradi con esponente intero
Poiché gli interi positivi sono numeri naturali, allora tutte le proprietà delle potenze con esponente intero positivo coincidono esattamente con le proprietà delle potenze con esponente naturale elencate e dimostrate nel paragrafo precedente.
Abbiamo definito un grado con esponente intero negativo, nonché un grado con esponente zero, in modo tale che tutte le proprietà dei gradi con esponente naturale, espresse mediante uguaglianze, rimanessero valide. Tutte queste proprietà valgono quindi sia per esponenti nulli che per esponenti negativi, mentre, ovviamente, le basi delle potenze sono diverse da zero.
Quindi, per qualsiasi numero reale e diverso da zero a e b, così come per qualsiasi numero intero m e n, è vero quanto segue: proprietà delle potenze con esponente intero:
Quando a=0, le potenze a m e a n hanno senso solo quando sia m che n sono numeri interi positivi, cioè numeri naturali. Pertanto le proprietà appena scritte valgono anche per i casi in cui a=0 ed i numeri m e n sono interi positivi.
Dimostrare ciascuna di queste proprietà non è difficile; per farlo è sufficiente utilizzare le definizioni dei gradi con esponente naturale e intero, nonché le proprietà delle operazioni con numeri reali. Ad esempio, dimostriamo che la proprietà potere-potenza vale sia per gli interi positivi che per gli interi non positivi. Per fare ciò, devi dimostrare che se p è zero o un numero naturale e q è zero o un numero naturale, allora le uguaglianze (a p) q =a p·q, (a −p) q =a (−p) ·q, (a p ) −q =a p·(−q) e (a −p) −q =a (−p)·(−q) . Facciamolo.
Per p e q positivi, l'uguaglianza (ap) q =a p·q è stata dimostrata nel paragrafo precedente. Se p=0, allora abbiamo (a 0) q =1 q =1 e a 0·q =a 0 =1, da cui (a 0) q =a 0·q. Allo stesso modo, se q=0, allora (a p) 0 =1 e a p·0 =a 0 =1, da cui (a p) 0 =a p·0. Se sia p=0 che q=0, allora (a 0) 0 =1 0 =1 e a 0·0 =a 0 =1, da cui (a 0) 0 =a 0·0.
Ora dimostriamo che (a −p) q =a (−p)·q . Quindi per definizione di potenza con esponente intero negativo 
. Per la proprietà dei quozienti alle potenze che abbiamo 
. Poiché 1 p =1·1·…·1=1 e , allora . L'ultima espressione, per definizione, è una potenza della forma a −(p·q), che, a causa delle regole della moltiplicazione, può essere scritta come a (−p)·q.
Allo stesso modo 
.
E 
.
Utilizzando lo stesso principio, puoi dimostrare tutte le altre proprietà di un grado con esponente intero, scritto sotto forma di uguaglianze.
Nella penultima delle proprietà registrate, vale la pena soffermarsi sulla dimostrazione della disuguaglianza a −n >b −n, che vale per ogni intero negativo −n e ogni positivo a e b per i quali è soddisfatta la condizione a . Scriviamo e trasformiamo la differenza tra i lati sinistro e destro di questa disuguaglianza: 
. Poiché dalla condizione a n n , quindi, b n −a n >0 . Anche il prodotto a n · b n è positivo come prodotto dei numeri positivi a n e b n . Allora la frazione risultante è positiva come quoziente dei numeri positivi b n −an e a n ·b n . Donde dunque a −n >b −n , che è ciò che occorreva dimostrare.
L'ultima proprietà delle potenze con esponente intero si dimostra allo stesso modo di un'analoga proprietà delle potenze con esponente naturale.
Proprietà delle potenze con esponenti razionali
Abbiamo definito un grado con esponente frazionario estendendo le proprietà di un grado con esponente intero. In altre parole, le potenze con esponente frazionario hanno le stesse proprietà delle potenze con esponente intero. Vale a dire:
- proprietà del prodotto di potenze con le stesse basi
per a>0, e se e, allora per a≥0; - proprietà dei quozienti di potenza con le stesse basi
per a>0 ; - proprietà di un prodotto a una potenza frazionaria
per a>0 e b>0, e se e, allora per a≥0 e (o) b≥0; - proprietà di un quoziente a una potenza frazionaria
per a>0 e b>0, e se , allora per a≥0 e b>0; - proprietà di grado in grado
per a>0, e se e, allora per a≥0; - proprietà di confrontare potenze con esponenti razionali uguali: per ogni numero positivo a e b, a 0 è vera la disuguaglianza a p p, e per p p >b p ;
- la proprietà di confrontare potenze con esponenti razionali e basi uguali: per i numeri razionali p e q, p>q per 0p q, e per a>0 – disuguaglianza a p >a q.
- un p · un q = un p+q ;
- un p: un q = un p−q ;
- (a·b) p =a p ·b p ;
- (a:b) p =a p:b p ;
- (a p) q = a p·q ;
- per qualsiasi numero positivo a e b, a 0 è vera la disuguaglianza a p p, e per p p >b p ;
- per i numeri irrazionali p e q, p>q per 0p q, e per a>0 – la disuguaglianza a p >a q.
La dimostrazione delle proprietà delle potenze con esponente frazionario si basa sulla definizione di potenza con esponente frazionario, sulle proprietà della radice aritmetica di grado ennesimo e sulle proprietà di una potenza con esponente intero. Forniamo le prove.
Per definizione di potenza con esponente frazionario e , quindi 
. Le proprietà della radice aritmetica ci permettono di scrivere le seguenti uguaglianze. Inoltre, utilizzando la proprietà di un grado con esponente intero, otteniamo , da cui, per definizione di grado con esponente frazionario, abbiamo 
, e l'indicatore del titolo conseguito può essere trasformato come segue: . Questo completa la dimostrazione.
La seconda proprietà delle potenze con esponente frazionario si dimostra in modo assolutamente analogo: 
Le restanti uguaglianze vengono dimostrate utilizzando principi simili: 
Passiamo a dimostrare la prossima proprietà. Proviamo che per ogni positivo a e b , a 0 la disuguaglianza a p p è vera, e per p p >b p . Scriviamo il numero razionale p come m/n, dove m è un numero intero e n è un numero naturale. Le condizioni p 0 in questo caso saranno equivalenti rispettivamente alle condizioni m 0. Per m>0 e am m . Da questa disuguaglianza, per la proprietà delle radici, abbiamo, e poiché aeb sono numeri positivi, quindi, in base alla definizione di un grado con esponente frazionario, la disuguaglianza risultante può essere riscritta come, cioè a p p .
Similmente per m m >b m , donde cioè a p >b p .
Resta da dimostrare l'ultima delle proprietà elencate. Proviamo che per i numeri razionali p e q, p>q per 0p q, e per a>0 – la disuguaglianza a p >a q. Possiamo sempre ridurre i numeri razionali p e q a un denominatore comune, anche se otteniamo le frazioni ordinarie e , dove m 1 e m 2 sono numeri interi e n è un numero naturale. In questo caso, la condizione p>q corrisponderà alla condizione m 1 >m 2, che segue dalla regola per confrontare le frazioni ordinarie con gli stessi denominatori. Quindi, per la proprietà di confrontare i gradi con le stesse basi ed esponenti naturali, per 0m 1 m 2 e per a>1, la disuguaglianza a m 1 >a m 2. Queste disuguaglianze nelle proprietà delle radici possono essere riscritte di conseguenza come 
E 
. E la definizione di grado con esponente razionale ci consente di passare alle disuguaglianze e, di conseguenza. Da qui traiamo la conclusione finale: per p>q e 0p q , e per a>0 – la disuguaglianza a p >a q .
Proprietà delle potenze con esponenti irrazionali
Dal modo in cui viene definito un grado con esponente irrazionale, possiamo concludere che esso possiede tutte le proprietà dei gradi con esponente razionale. Quindi per ogni a>0, b>0 e numeri irrazionali p e q vale quanto segue Proprietà delle potenze con esponenti irrazionali:
Da ciò possiamo concludere che le potenze con qualsiasi esponente reale p e q per a>0 hanno le stesse proprietà.
- Algebra - 10a elementare. Equazioni trigonometriche Lezione e presentazione sull'argomento: "Risoluzione delle equazioni trigonometriche più semplici" Materiali aggiuntivi Cari utenti, non dimenticate di lasciare i vostri commenti, recensioni, suggerimenti! Tutti i materiali […]
- È stato aperto un concorso per la posizione "VENDITORE - CONSULENTE": Responsabilità: vendita di telefoni cellulari e accessori per comunicazioni mobili, servizio clienti per abbonati Beeline, Tele2, MTS, connessione di piani tariffari e servizi Beeline e Tele2, consulenza MTS [... ]
- Formula del parallelepipedo Un parallelepipedo è un poliedro con 6 facce, ciascuna delle quali è un parallelogramma. Un cuboide è un parallelepipedo le cui facce sono ciascuna un rettangolo. Qualsiasi parallelepipedo è caratterizzato da 3 […]
- Società per la protezione dei diritti dei consumatori Astana Per ricevere un codice PIN per accedere a questo documento sul nostro sito Web, inviare un messaggio SMS con il testo zan al numero Abbonati degli operatori GSM (Activ, Kcell, Beeline, NEO, Tele2) tramite inviando un SMS al numero, […]
- ORTOGRAFIA N E NN IN DIVERSE PARTI DEL DISCORSO S.G. ZELINSKAYA MATERIALE DIDATTICO Esercizio teorico 1. Quando si scrive nn negli aggettivi? 2. Nomina le eccezioni a queste regole. 3. Come distinguere un aggettivo verbale con il suffisso -n- da un participio con […]
- Adottare la legge sui patrimoni familiari Adottare la legge federale sull'assegnazione gratuita di un terreno a ciascun cittadino consenziente della Federazione Russa o a una famiglia di cittadini per la costruzione di un patrimonio familiare su di esso alle seguenti condizioni: 1. Il terreno è stanziato per […]
- ISPEZIONE DI GOSTEKHNADZOR DELLA REGIONE DI BRYANSK Ricevuta per il pagamento del dovere statale (Download-12.2 kb) Domande di registrazione per persone fisiche (Download-12 kb) Domande di registrazione per persone giuridiche (Download-11.4 kb) 1. Quando si registra una nuova auto: 1.domanda 2.passaporto […]
- È da un po' che non giochiamo tornei 1v1. Ed è probabilmente giunto il momento di riprendere questa tradizione. Anche se non possiamo organizzare una ladder separata e tornei per giocatori 1v1, ti suggeriamo di utilizzare i profili della tua squadra sul sito. I punti per le partite nelle partite possono essere rimossi o aggiunti [...]
Nell’articolo precedente abbiamo spiegato cosa sono i monomi. In questo materiale vedremo come risolvere esempi e problemi in cui vengono utilizzati. Qui considereremo azioni come sottrazione, addizione, moltiplicazione, divisione di monomi ed elevazione a una potenza con esponente naturale. Mostreremo come vengono definite tali operazioni, delineeremo le regole di base per la loro attuazione e quale dovrebbe essere il risultato. Tutti i concetti teorici, come di consueto, saranno illustrati con esempi di problemi con descrizione delle soluzioni.
È più conveniente lavorare con la notazione standard dei monomi, quindi presentiamo tutte le espressioni che verranno utilizzate nell'articolo in forma standard. Se originariamente erano specificati diversamente, si consiglia di ridurli prima a una forma generalmente accettata.
Regole per sommare e sottrarre monomi
Le operazioni più semplici che si possono eseguire con i monomi sono la sottrazione e l'addizione. In generale, il risultato di queste azioni sarà un polinomio (in alcuni casi particolari è possibile un monomio).
Quando aggiungiamo o sottraiamo monomi, prima scriviamo la somma e la differenza corrispondenti nella forma generalmente accettata, quindi semplifichiamo l'espressione risultante. Se ci sono termini simili, è necessario citarli e aprire le parentesi. Spieghiamo con un esempio.
Esempio 1
Condizione: eseguire l'addizione dei monomi − 3 x e 2, 72 x 3 y 5 z.
Soluzione
Scriviamo la somma delle espressioni originali. Aggiungiamo le parentesi e inseriamo un segno più tra di loro. Otterremo quanto segue:
(− 3 x) + (2, 72 x 3 y 5 z)
Quando espandiamo le parentesi, otteniamo - 3 x + 2, 72 x 3 y 5 z. Questo è un polinomio, scritto in forma standard, che sarà il risultato della somma di questi monomi.
Risposta:(− 3 x) + (2,72 x 3 y 5 z) = − 3 x + 2,72 x 3 y 5 z.
Se abbiamo tre, quattro o più termini, eseguiamo questa azione esattamente allo stesso modo.
Esempio 2
Condizione: eseguire le operazioni indicate con i polinomi nell'ordine corretto
3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c
Soluzione
Iniziamo aprendo le parentesi.
3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c
Vediamo che l'espressione risultante può essere semplificata aggiungendo termini simili:
3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = = (3 a 2 + a 2 - 7 a 2) + 4 a c - 2 2 3 a c + 4 9 = = - 3 a 2 + 1 1 3 a c + 4 9
Abbiamo un polinomio, che sarà il risultato di questa azione.
Risposta: 3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = - 3 a 2 + 1 1 3 a c + 4 9
In linea di principio, possiamo sommare e sottrarre due monomi, con alcune restrizioni, in modo da ottenere un monomio. Per fare ciò, è necessario soddisfare alcune condizioni relative agli addendi e ai monomi sottratti. Ti diremo come farlo in un articolo separato.
Regole per moltiplicare i monomi
L'azione di moltiplicazione non impone alcuna restrizione sui fattori. I monomi moltiplicati non devono soddisfare alcuna condizione aggiuntiva affinché il risultato sia un monomio.
Per eseguire la moltiplicazione dei monomi, è necessario seguire questi passaggi:
- Scrivi correttamente il pezzo.
- Espandi le parentesi nell'espressione risultante.
- Se possibile, raggruppare separatamente i fattori con le stesse variabili e i fattori numerici.
- Esegui le operazioni necessarie con i numeri e applica la proprietà della moltiplicazione delle potenze con le stesse basi ai fattori rimanenti.
Vediamo come questo viene fatto nella pratica.
Esempio 3
Condizione: moltiplicare i monomi 2 x 4 y z e - 7 16 t 2 x 2 z 11.
Soluzione
Iniziamo componendo l'opera.
Apriamo le parentesi al suo interno e otteniamo quanto segue:
2 x 4 y z - 7 16 t 2 x 2 z 11
2 - 7 16 t 2 x 4 x 2 y z 3 z 11
Tutto quello che dobbiamo fare è moltiplicare i numeri nelle prime parentesi e applicare la proprietà delle potenze per la seconda. Di conseguenza, otteniamo quanto segue:
2 - 7 16 t 2 x 4 x 2 y z 3 z 11 = - 7 8 t 2 x 4 + 2 y z 3 + 11 = = - 7 8 t 2 x 6 y z 14
Risposta: 2 x 4 y z - 7 16 t 2 x 2 z 11 = - 7 8 t 2 x 6 y z 14 .
Se la nostra condizione contiene tre o più polinomi, li moltiplichiamo utilizzando esattamente lo stesso algoritmo. Considereremo la questione della moltiplicazione dei monomi in modo più dettagliato in un materiale separato.
Regole per elevare un monomio a potenza
Sappiamo che una potenza con esponente naturale è il prodotto di un certo numero di fattori identici. Il loro numero è indicato dal numero nell'indicatore. Secondo questa definizione, elevare un monomio a potenza equivale a moltiplicare il numero specificato di monomi identici. Vediamo come è fatto.
Esempio 4
Condizione: eleva il monomio − 2 · a · b 4 alla potenza 3 .
Soluzione
Possiamo sostituire l'elevamento a potenza con la moltiplicazione di 3 monomi − 2 · a · b 4 . Scriviamolo e otteniamo la risposta desiderata:
(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12
Risposta:(− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .
Ma cosa succede se la laurea ha un indicatore di grandi dimensioni? È scomodo registrare un gran numero di fattori. Quindi, per risolvere un problema del genere, dobbiamo applicare le proprietà di un grado, vale a dire la proprietà di un grado di prodotto e la proprietà di un grado in un grado.
Risolviamo il problema che abbiamo presentato sopra utilizzando il metodo indicato.
Esempio 5
Condizione: eleva − 2 · a · b 4 alla terza potenza.
Soluzione
Conoscendo la proprietà potenza-grado, possiamo procedere ad un'espressione della forma seguente:
(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .
Successivamente eleviamo alla potenza - 2 e applichiamo la proprietà delle potenze alle potenze:
(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .
Risposta:− 2 · un · b 4 = − 8 · un 3 · b 12 .
Abbiamo anche dedicato un articolo a parte all'elevazione di un monomio a potenza.
Regole per dividere i monomi
L'ultima operazione con i monomi che esamineremo in questo materiale è la divisione di un monomio per un monomio. Di conseguenza, dovremmo ottenere una frazione razionale (algebrica) (in alcuni casi è possibile ottenere un monomio). Chiariamo subito che la divisione per zero monomiale non è definita, poiché la divisione per 0 non è definita.
Per eseguire la divisione dobbiamo scrivere i monomi indicati sotto forma di frazione e ridurli, se possibile.
Esempio 6
Condizione: dividere il monomio − 9 · x 4 · y 3 · z 7 per − 6 · p 3 · t 5 · x 2 · y 2 .
Soluzione
Iniziamo scrivendo i monomi in forma frazionaria.
9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2
Questa frazione può essere ridotta. Dopo aver eseguito questa azione otteniamo:
3 x 2 y z 7 2 p 3 t 5
Risposta:- 9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2 = 3 x 2 y z 7 2 p 3 t 5 .
Le condizioni alle quali, come risultato della divisione dei monomi, otteniamo un monomio, sono riportate in un articolo separato.
Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio
Come moltiplicare i poteri? Quali poteri possono essere moltiplicati e quali no? Come moltiplicare un numero per una potenza?
In algebra, puoi trovare un prodotto di potenze in due casi:
1) se i titoli hanno le stesse basi;
2) se i gradi hanno gli stessi indicatori.
Quando si moltiplicano potenze con le stesse basi, è necessario lasciare la base e aggiungere gli esponenti:
Quando si moltiplicano i gradi per gli stessi indicatori, l'indicatore complessivo può essere tolto tra parentesi:
Diamo un'occhiata a come moltiplicare i poteri utilizzando esempi specifici.
L'unità non si scrive nell'esponente, ma quando si moltiplicano le potenze si tiene conto di:
Quando si moltiplica, può esserci un numero qualsiasi di potenze. Va ricordato che non è necessario scrivere il segno di moltiplicazione prima della lettera:
Nelle espressioni, l'elevamento a potenza viene eseguito per primo.
Se devi moltiplicare un numero per una potenza, devi prima eseguire l'elevamento a potenza e solo dopo la moltiplicazione:
www.algebraclass.ru
Addizione, sottrazione, moltiplicazione e divisione di poteri
Addizione e sottrazione di poteri
È ovvio che i numeri dotati di potenze possono essere sommati come le altre quantità , sommandoli uno dopo l'altro con i relativi segni.
Quindi la somma di a 3 e b 2 è a 3 + b 2.
La somma di a 3 - b n e h 5 - d 4 è a 3 - b n + h 5 - d 4.
Probabilità potenze uguali di variabili identiche possono essere aggiunti o sottratti.
Quindi, la somma di 2a 2 e 3a 2 è uguale a 5a 2.
È anche ovvio che se prendi due quadrati a, o tre quadrati a, o cinque quadrati a.
Ma gradi varie variabili E vari gradi variabili identiche, devono essere composti sommandoli con i relativi segni.
Quindi la somma di a 2 e a 3 è la somma di a 2 + a 3.
È ovvio che il quadrato di a, e il cubo di a, non sono pari al doppio del quadrato di a, ma al doppio del cubo di a.
La somma di a 3 b n e 3a 5 b 6 è a 3 b n + 3a 5 b 6.
Sottrazione le potenze si eseguono allo stesso modo dell'addizione, tranne che i segni dei sottraendo devono essere cambiati di conseguenza.
O:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6
Moltiplicare i poteri
I numeri dotati di potenze possono essere moltiplicati, come le altre quantità, scrivendoli uno dopo l'altro, con o senza segno di moltiplicazione tra di loro.
Pertanto, il risultato della moltiplicazione di a 3 per b 2 è a 3 b 2 o aaabb.
O:
x -3 ⋅ un m = un m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Il risultato nell'ultimo esempio può essere ordinato aggiungendo variabili identiche.
L'espressione assumerà la forma: a 5 b 5 y 3.
Confrontando diversi numeri (variabili) con potenze, possiamo vedere che se ne moltiplicano due qualsiasi, il risultato è un numero (variabile) con una potenza pari a quantità gradi di termini.
Quindi, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Qui 5 è la potenza del risultato della moltiplicazione, che è uguale a 2 + 3, la somma delle potenze dei termini.
Quindi, a n.a m = a m+n.
Per a n , a viene preso come fattore tante volte quanto la potenza di n;
E a m si prende come fattore tante volte quanto è uguale il grado m;
Ecco perché, le potenze con le stesse basi possono essere moltiplicate sommando gli esponenti delle potenze.
Quindi, a 2 .a 6 = a 2+6 = a 8 . E x 3 .x 2 .x = x 3+2+1 = x 6 .
O:
4a n ⋅ 2a n = 8a 2n
b2 y3 ⋅ b4 y = b6 y4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1
Moltiplica (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Risposta: x 4 - y 4.
Moltiplica (x 3 + x – 5) ⋅ (2x 3 + x + 1).
Questa regola vale anche per i numeri i cui esponenti sono negativo.
1. Quindi, a -2 .a -3 = a -5 . Questo può essere scritto come (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Se si moltiplicano a + b per a - b, il risultato sarà a 2 - b 2: cioè
Il risultato della moltiplicazione della somma o della differenza di due numeri è uguale alla somma o alla differenza dei loro quadrati.
Se moltiplichi la somma e la differenza di due numeri elevati a piazza, il risultato sarà uguale alla somma o alla differenza di questi numeri in quarto gradi.
Quindi, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.
Divisione dei gradi
I numeri con potenze possono essere divisi come gli altri numeri, sottraendo dal dividendo o trasformandoli in frazioni.
Quindi a 3 b 2 diviso b 2 è uguale a a 3.
Scrivere un 5 diviso per 3 assomiglia a $\frac $. Ma questo è uguale a 2 . In una serie di numeri
un +4, un +3, un +2, un +1, un 0, un -1, un -2, un -3, un -4.
qualsiasi numero può essere diviso per un altro e l'esponente sarà uguale a differenza indicatori dei numeri divisibili.
Quando si dividono i gradi con la stessa base, i loro esponenti vengono sottratti..
Quindi, y 3:y 2 = y 3-2 = y 1. Cioè $\frac = y$.
E a n+1:a = a n+1-1 = a n . Cioè $\frac = a^n$.
O:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b + y) n-3
La regola vale anche per i numeri con negativo valori dei gradi.
Il risultato della divisione -5 per -3 è -2.
Inoltre, $\frac: \frac = \frac .\frac = \frac = \frac $.
h 2:h -1 = h 2+1 = h 3 oppure $h^2:\frac = h^2.\frac = h^3$
È necessario padroneggiare molto bene la moltiplicazione e la divisione dei poteri, poiché tali operazioni sono molto utilizzate in algebra.
Esempi di risoluzione di esempi con frazioni contenenti numeri con potenze
1. Diminuire gli esponenti di $\frac $ Risposta: $\frac $.
2. Diminuire gli esponenti di $\frac$. Risposta: $\frac$ o 2x.
3. Riduci gli esponenti a 2 /a 3 e a -3 /a -4 e portali a un denominatore comune.
a 2 .a -4 è a -2 il primo numeratore.
a 3 .a -3 è a 0 = 1, il secondo numeratore.
a 3 .a -4 è a -1 , il numeratore comune.
Dopo la semplificazione: a -2 /a -1 e 1/a -1 .
4. Riduci gli esponenti 2a 4 /5a 3 e 2 /a 4 e portali a un denominatore comune.
Risposta: 2a 3 /5a 7 e 5a 5 /5a 7 oppure 2a 3 /5a 2 e 5/5a 2.
5. Moltiplica (a 3 + b)/b 4 per (a - b)/3.
6. Moltiplica (a 5 + 1)/x 2 per (b 2 - 1)/(x + a).
7. Moltiplica b 4 /a -2 per h -3 /x e a n /y -3 .
8. Dividere a 4 /y 3 per a 3 /y 2 . Risposta: a/a.
Proprietà del grado
Ti ricordiamo che in questa lezione capiremo proprietà dei gradi con indicatori naturali e zero. Le potenze con esponenti razionali e le loro proprietà verranno discusse nelle lezioni per la terza media.
Una potenza con esponente naturale ha diverse proprietà importanti che ci consentono di semplificare i calcoli negli esempi con potenze.
Proprietà n. 1
Prodotto di poteri
Quando si moltiplicano le potenze con le stesse basi, la base rimane invariata e si sommano gli esponenti delle potenze.
a m · a n = a m + n, dove “a” è un numero qualsiasi e “m”, “n” sono numeri naturali qualsiasi.
Questa proprietà delle potenze vale anche per il prodotto di tre o più potenze.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Tieni presente che nella proprietà specificata si parlava solo della moltiplicazione di potenze con le stesse basi. Non si applica alla loro aggiunta.
Non è possibile sostituire la somma (3 3 + 3 2) con 3 5. Ciò è comprensibile se
calcolare (3 3 + 3 2) = (27 + 9) = 36 e 3 5 = 243
Proprietà n. 2
Gradi parziali
Quando si dividono potenze con la stessa base, la base rimane invariata e l'esponente del divisore viene sottratto dall'esponente del dividendo.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 4 2 − 1 = 11 4 = 44
Esempio. Risolvi l'equazione. Utilizziamo la proprietà delle potenze quozienti.
3 8: t = 3 4
Risposta: t = 3 4 = 81
Utilizzando le proprietà n. 1 e n. 2, puoi facilmente semplificare le espressioni ed eseguire calcoli.
- Esempio. Semplifica l'espressione.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Esempio. Trova il valore di un'espressione utilizzando le proprietà degli esponenti.
2 11 − 5 = 2 6 = 64
Si noti che nella Proprietà 2 si parlava solo di dividere poteri con le stesse basi.
Non è possibile sostituire la differenza (4 3 −4 2) con 4 1. Ciò è comprensibile se calcoli (4 3 −4 2) = (64 − 16) = 48 e 4 1 = 4
Proprietà n. 3
Elevare un grado a una potenza
Quando si eleva un grado a potenza, la base del grado rimane invariata e gli esponenti vengono moltiplicati.
(a n) m = a n · m, dove “a” è un numero qualsiasi e “m”, “n” sono numeri naturali qualsiasi.
Si prega di notare che la proprietà n. 4, come altre proprietà dei gradi, viene applicata anche in ordine inverso.
(a n · b n)= (a · b) n
Cioè, per moltiplicare potenze con gli stessi esponenti, puoi moltiplicare le basi, ma lasciare invariato l'esponente.
2 4 5 4 = (2 5) 4 = 10 4 = 10.000
0,5 16 2 16 = (0,5 2) 16 = 1
Negli esempi più complessi, potrebbero esserci casi in cui la moltiplicazione e la divisione devono essere eseguite su potenze con basi ed esponenti diversi. In questo caso, ti consigliamo di fare quanto segue.
Ad esempio, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
Un esempio di elevazione di un numero decimale a potenza.
4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = 4
Proprietà 5
Potenza di un quoziente (frazione)
Per elevare un quoziente a una potenza, puoi elevare separatamente il dividendo e il divisore a questa potenza e dividere il primo risultato per il secondo.
(a: b) n = a n: b n, dove “a”, “b” sono numeri razionali, b ≠ 0, n - qualsiasi numero naturale.
(5: 3) 12 = 5 12: 3 12
Ti ricordiamo che un quoziente può essere rappresentato come una frazione. Pertanto, ci soffermeremo più in dettaglio sull'argomento dell'elevazione di una frazione a potenza nella pagina successiva.
Poteri e radici
Operazioni con poteri e radici. Laurea con negativo ,
zero e frazionario indicatore. Di espressioni che non hanno significato.
Operazioni con i gradi.
1. Quando si moltiplicano le potenze con la stessa base, si sommano i loro esponenti:
Sono · un n = un m + n .
2. Quando si dividono i gradi con la stessa base, i loro esponenti vengono detratti .
3. Il grado del prodotto di due o più fattori è uguale al prodotto dei gradi di questi fattori.
4. Il grado di un rapporto (frazione) è uguale al rapporto tra i gradi del dividendo (numeratore) e del divisore (denominatore):
(a/b) n = un n / b n .
5. Quando si eleva una potenza a potenza, i suoi esponenti vengono moltiplicati:
Tutte le formule di cui sopra vengono lette ed eseguite in entrambe le direzioni da sinistra a destra e viceversa.
ESEMPIO (2 3 5 / 15)² = 2² · 3² · 5² / 15² = 900 / 225 = 4 .
Operazioni con le radici. In tutte le formule seguenti, il simbolo significa radice aritmetica(l'espressione radicale è positiva).
1. La radice del prodotto di più fattori è uguale al prodotto delle radici di questi fattori:
2. La radice di un rapporto è uguale al rapporto tra le radici del dividendo e il divisore:
3. Quando si eleva una radice a potenza, è sufficiente elevare a questa potenza numero radicale:
4. Se aumenti il grado della radice di m volte e allo stesso tempo elevi il numero radicale alla potenza m-esima, il valore della radice non cambierà:
5. Se riduci il grado della radice di m volte e contemporaneamente estrai la radice m-esima del numero radicale, il valore della radice non cambierà:
Ampliare il concetto di laurea. Finora abbiamo considerato solo i gradi con esponente naturale; ma possono portare anche operazioni con poteri e radici negativo, zero E frazionario indicatori. Tutti questi esponenti richiedono una definizione aggiuntiva.
Un grado con esponente negativo. La potenza di un certo numero con esponente negativo (intero) è definita come quella divisa per la potenza dello stesso numero con esponente uguale al valore assoluto dell'esponente negativo:
Ora la formula Sono : UN = un m - n può essere utilizzato non solo per M, più di N, ma anche con M, meno di N .
ESEMPIO UN 4: UN 7 = un 4 — 7 = un — 3 .
Se vogliamo la formula Sono : UN = Sono — N era giusto quando m = n, abbiamo bisogno di una definizione di grado zero.
Una laurea con indice pari a zero. La potenza di ogni numero diverso da zero con esponente zero è 1.
ESEMPI. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.
Grado con esponente frazionario. Per elevare un numero reale a alla potenza m / n, è necessario estrarre la radice n-esima della potenza m-esima di questo numero a:
Di espressioni che non hanno significato. Esistono molte di queste espressioni.
Dove UN ≠ 0 , non esiste.
In effetti, se lo assumiamo Xè un certo numero, quindi secondo la definizione dell'operazione di divisione abbiamo: UN = 0· X, cioè. UN= 0, che contraddice la condizione: UN ≠ 0
— qualsiasi numero.
In effetti, se assumiamo che questa espressione sia uguale a un numero X, allora secondo la definizione dell'operazione di divisione abbiamo: 0 = 0 · X. Ma questa uguaglianza si verifica quando qualsiasi numero x, che era ciò che doveva essere dimostrato.
0 0 — qualsiasi numero.
Soluzione Consideriamo tre casi principali:
1) X = 0 – questo valore non soddisfa questa equazione
2) quando X> 0 otteniamo: x/x= 1, cioè 1 = 1, il che significa
Che cosa X– qualsiasi numero; ma tenendo conto che in
nel nostro caso X> 0, la risposta è X > 0 ;
Regole per moltiplicare le potenze con basi diverse
LAUREA CON INDICATORE RAZIONALE,
FUNZIONE POTENZA IV
§ 69. Moltiplicazione e divisione dei poteri con le stesse basi
Teorema 1. Per moltiplicare le potenze con le stesse basi basta sommare gli esponenti e lasciare la base uguale, cioè
Prova. Per definizione di laurea
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Abbiamo esaminato il prodotto di due potenze. In effetti, la proprietà provata è vera per qualsiasi numero di potenze con le stesse basi.
Teorema 2. Per dividere i poteri con le stesse basi, quando l'indice del dividendo è maggiore dell'indice del divisore, basta sottrarre l'indice del divisore dall'indice del dividendo, e lasciare la base uguale, cioè A t > pag
(UN =/= 0)
Prova. Ricordiamo che il quoziente della divisione di un numero per un altro è il numero che, moltiplicato per il divisore, dà il dividendo. Pertanto, dimostra la formula dove UN =/= 0, equivale a dimostrare la formula
Se t > pag , quindi il numero t-p sarà naturale; quindi, per il Teorema 1
Il Teorema 2 è dimostrato.
Va notato che la formula
lo abbiamo dimostrato solo presupponendo che t > pag . Pertanto, da quanto dimostrato non è ancora possibile trarre, ad esempio, le seguenti conclusioni:
Inoltre non abbiamo ancora considerato i gradi con esponente negativo e non sappiamo ancora quale significato si possa dare all’espressione 3 - 2 .
Teorema 3. Per elevare un grado a potenza è sufficiente moltiplicare gli esponenti, lasciando la stessa base del grado, questo è
Prova. Utilizzando la definizione di grado e il Teorema 1 di questa sezione, otteniamo:
Q.E.D.
Ad esempio, (2 3) 2 = 2 6 = 64;
518 (Orale) Determinare X dalle equazioni:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 X ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 X ;
2) 3 3 3 3 5 3 7 3 9 = 3 X ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 X .
519. (Imposta n.) Semplificare:
520. (Imposta n.) Semplificare:
521. Presentare queste espressioni sotto forma di gradi con le stesse basi:
1) 32 e 64; 3) 8 5 e 16 3; 5) 4 100 e 32 50;
2) -1000 e 100; 4) -27 e -243; 6) 81 75 8 200 e 3 600 4 150.
- VKontakte 0
- Google+ 0
- OK 0
- Facebook 0
