Współrzędne środka wektora w przestrzeni. Wektory dla manekinów

Wreszcie wpadłem w obszerny i długo oczekiwany temat geometria analityczna. Najpierw trochę o tej sekcji matematyki wyższej…. Z pewnością pamiętasz szkolny kurs geometrii z licznymi twierdzeniami, ich dowodami, rysunkami itp. Co ukrywać, temat niekochany i często niejasny dla znacznej części uczniów. Co dziwne, geometria analityczna może wydawać się bardziej interesująca i przystępna. Co oznacza przymiotnik „analityczny”? Natychmiast przychodzą na myśl dwa stemplowane zwroty matematyczne: „graficzna metoda rozwiązywania” i „analityczna metoda rozwiązywania”. Metoda graficzna Oczywiście wiąże się to z budowaniem wykresów, rysunków. Analityczny to samo metoda wiąże się z rozwiązywaniem problemów przeważnie poprzez operacje algebraiczne. Pod tym względem algorytm rozwiązywania prawie wszystkich problemów geometrii analitycznej jest prosty i przejrzysty, często wystarczy dokładnie zastosować niezbędne formuły - i odpowiedź jest gotowa! Nie, oczywiście nie obejdzie się bez rysunków, poza tym dla lepszego zrozumienia materiału postaram się je w nadmiarze sprowadzić.

Otwarty kurs lekcji geometrii nie rości sobie pretensji do teoretycznej kompletności, jest nastawiony na rozwiązywanie praktycznych problemów. W swoich wykładach będę włączał tylko to, co z mojego punktu widzenia jest ważne z praktycznego punktu widzenia. Jeśli potrzebujesz bardziej kompletnego odniesienia do dowolnego podrozdziału, polecam następującą dość przystępną literaturę:

1) Rzecz, która, bez żartów, jest znana kilku pokoleniom: Podręcznik szkolny do geometrii, autorzy - L.S. Atanasyan i Spółka. Ten wieszak do szatni szkolnej wytrzymał już 20 (!) reedycji, co oczywiście nie jest limitem.

2) Geometria w 2 tomach. Autorzy L.S. Atanasjan, Bazylew W.T.. To jest literatura dla szkolnictwa wyższego, będziesz potrzebować pierwszy tom. Rzadko pojawiające się zadania mogą wypaść z mojego pola widzenia, a samouczek będzie nieocenioną pomocą.

Obie książki można pobrać bezpłatnie online. Dodatkowo możesz skorzystać z mojego archiwum z gotowymi rozwiązaniami, które znajdziesz na stronie Pobierz przykłady z wyższej matematyki.

Z narzędzi ponownie oferuję własny rozwój - pakiet oprogramowania na geometrii analitycznej, która znacznie uprości życie i zaoszczędzi dużo czasu.

Zakłada się, że czytelnik zna podstawowe pojęcia i figury geometryczne: punkt, prosta, płaszczyzna, trójkąt, równoległobok, równoległościan, sześcian itp. Wskazane jest, aby pamiętać niektóre twierdzenia, przynajmniej twierdzenie Pitagorasa, hello repeaters)

A teraz rozważymy kolejno: pojęcie wektora, działania z wektorami, współrzędne wektora. Dalej polecam lekturę najważniejszy artykuł Iloczyn skalarny wektorów, jak również Iloczyn wektorowy i mieszany wektorów. Zadanie lokalne nie będzie zbędne - Podział segmentu pod tym względem. Na podstawie powyższych informacji możesz równanie prostej w płaszczyźnie od najprostsze przykłady rozwiązań co pozwoli naucz się rozwiązywać problemy z geometrii. Pomocne są również następujące artykuły: Równanie płaszczyzny w przestrzeni, Równania prostej w przestrzeni, Podstawowe zagadnienia na linii i płaszczyźnie, inne przekroje geometrii analitycznej. Oczywiście po drodze będą brane pod uwagę standardowe zadania.

Pojęcie wektora. wolny wektor

Najpierw powtórzmy szkolną definicję wektora. Wektor nazywa się skierowany segment, dla którego wskazany jest jego początek i koniec:

W tym przypadku początkiem odcinka jest punkt , końcem odcinka jest punkt . Sam wektor jest oznaczony przez . Kierunek jest niezbędne, jeśli przestawisz strzałkę na drugi koniec segmentu, otrzymasz wektor, a to już jest zupełnie inny wektor. Wygodnie jest utożsamiać pojęcie wektora z ruchem ciała fizycznego: trzeba przyznać, że wejście w drzwi instytutu lub wyjście z instytutu to zupełnie inne rzeczy.

Wygodne jest rozpatrywanie poszczególnych punktów płaszczyzny, przestrzeni jako tzw wektor zerowy. Taki wektor ma ten sam koniec i początek.

!!! Notatka: Tutaj i poniżej możesz założyć, że wektory leżą na tej samej płaszczyźnie lub możesz założyć, że znajdują się w przestrzeni - istota przedstawionego materiału dotyczy zarówno płaszczyzny, jak i przestrzeni.

Oznaczenia: Wielu od razu zwróciło uwagę na patyk bez strzałki w oznaczeniu i powiedział, że umieścili również strzałę na górze! Tak, możesz napisać strzałką: , ale dopuszczalne i zapis, którego użyję później. Czemu? Najwyraźniej taki nawyk wyrósł z praktycznych względów, moi strzelcy w szkole i na uniwersytecie okazali się zbyt różnorodni i kudłaci. W literaturze edukacyjnej czasami w ogóle nie zawracają sobie głowy pismem klinowym, ale podkreślają litery pogrubione: , tym samym sugerując, że jest to wektor.

Taki był styl, a teraz o sposobach pisania wektorów:

1) Wektory można zapisać dwoma wielkimi literami łacińskimi:
itp. Podczas gdy pierwsza litera koniecznie oznacza punkt początkowy wektora, a druga litera oznacza punkt końcowy wektora.

2) Wektory są również pisane małymi literami łacińskimi:
W szczególności, nasz wektor może być oznaczony małą literą łacińską dla zwięzłości.

Długość lub moduł wektor niezerowy nazywany jest długością segmentu. Długość wektora zerowego wynosi zero. Logicznie.

Długość wektora oznaczamy znakiem modulo: ,

Jak znaleźć długość wektora, dowiemy się (lub powtórzymy, dla kogo jak) nieco później.

To były elementarne informacje o wektorze, znane wszystkim uczniom w wieku szkolnym. W geometrii analitycznej tzw wolny wektor.

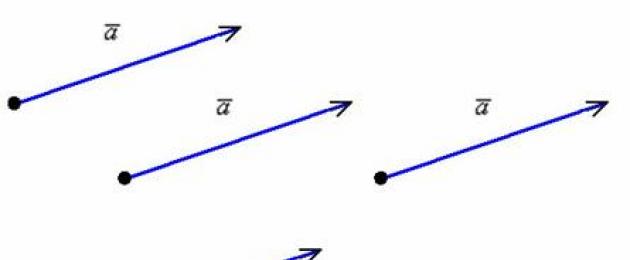
Jeśli to całkiem proste - wektor można narysować z dowolnego punktu:

Kiedyś nazywaliśmy takie wektory równymi (definicja równych wektorów zostanie podana poniżej), ale z czysto matematycznego punktu widzenia jest to TEN SAM WEKTOR lub wolny wektor. Dlaczego za darmo? Ponieważ w trakcie rozwiązywania problemów możesz „dołączyć” ten lub inny wektor „szkolny” do DOWOLNEGO punktu na płaszczyźnie lub przestrzeni, której potrzebujesz. To bardzo fajna nieruchomość! Wyobraź sobie skierowany odcinek o dowolnej długości i kierunku - można go "sklonować" nieskończoną ilość razy i w dowolnym punkcie przestrzeni, w rzeczywistości istnieje WSZĘDZIE. Jest takie przysłowie studenta: Każdy wykładowca w f ** u w wektorze. W końcu to nie tylko dowcipna rymowanka, wszystko jest prawie w porządku – tam też można doczepić wyreżyserowany segment. Ale nie spiesz się, by się radować, sami uczniowie cierpią częściej =)

Więc, wolny wektor- ten wiele identyczne segmenty kierunkowe. Szkolna definicja wektora, podana na początku akapitu: „Segment skierowany to wektor…”, implikuje konkretny skierowany segment wzięty z danego zbioru, który jest dołączony do pewnego punktu na płaszczyźnie lub przestrzeni.

Należy zauważyć, że z punktu widzenia fizyki pojęcie wektora swobodnego jest generalnie błędne, a znaczenie ma punkt zastosowania. Rzeczywiście, bezpośredni cios tej samej siły w nos lub w czoło wystarczy, by rozwinąć mój głupi przykład, pociąga za sobą różne konsekwencje. Jednakże, nie darmowy wektory znajdują się również w trakcie vyshmat (nie idź tam :)).

Akcje z wektorami. Kolinearność wektorów

Na szkolnym kursie geometrii bierze się pod uwagę szereg działań i reguł z wektorami: dodawanie zgodnie z zasadą trójkąta, dodawanie zgodnie z zasadą równoległoboku, zasada różnicy wektorów, mnożenie wektora przez liczbę, iloczyn skalarny wektorów itp. Jako ziarno powtarzamy dwie zasady, które są szczególnie istotne przy rozwiązywaniu problemów geometrii analitycznej.

Zasada dodawania wektorów zgodnie z zasadą trójkątów

Rozważ dwa dowolne niezerowe wektory i :

Wymagane jest znalezienie sumy tych wektorów. Ze względu na fakt, że wszystkie wektory są uważane za wolne, odkładamy wektor od koniec wektor :

Suma wektorów to wektor . Aby lepiej zrozumieć regułę, warto nadać jej znaczenie fizyczne: niech jakieś ciało poprowadzi ścieżkę wzdłuż wektora , a następnie wzdłuż wektora . Wtedy suma wektorów jest wektorem ścieżki wynikowej, rozpoczynającej się w punkcie wyjścia i kończącej się w punkcie przybycia. Podobną zasadę formułuje się dla sumy dowolnej liczby wektorów. Jak mówią, ciało może poruszać się mocno zygzakiem, a może na autopilocie - wzdłuż wynikowego wektora sumy.

Nawiasem mówiąc, jeśli wektor jest przełożony z początek wektor , to otrzymujemy ekwiwalent reguła równoległoboku dodawanie wektorów.

Najpierw o kolinearności wektorów. Te dwa wektory nazywają się współliniowy jeśli leżą na tej samej linii lub na równoległych liniach. Z grubsza mówimy o wektorach równoległych. Ale w odniesieniu do nich zawsze używany jest przymiotnik „współliniowy”.

Wyobraź sobie dwa współliniowe wektory. Jeśli strzałki tych wektorów są skierowane w tym samym kierunku, wówczas nazywane są takie wektory współkierunkowy. Jeśli strzałki będą skierowane w różnych kierunkach, wektory będą przeciwnie skierowane.

Oznaczenia: kolinearność wektorów jest zapisywana zwykłą ikoną równoległości: , natomiast detalowanie jest możliwe: (wektory są współkierunkowe) lub (wektory są skierowane przeciwnie).

Praca niezerowego wektora przez liczbę jest wektorem, którego długość jest równa , a wektory i są współkierunkowe i skierowane przeciwnie do .

Zasada mnożenia wektora przez liczbę jest łatwiejsza do zrozumienia za pomocą obrazu:

Rozumiemy bardziej szczegółowo:

1) Kierunek. Jeśli mnożnik jest ujemny, to wektor zmienia kierunek na odwrót.

2) Długość. Jeśli czynnik jest zawarty w lub , to długość wektora maleje. Zatem długość wektora jest dwukrotnie mniejsza niż długość wektora . Jeśli mnożnik modulo jest większy niż jeden, to długość wektora wzrasta w samą porę.

3) Należy pamiętać, że wszystkie wektory są współliniowe, podczas gdy jeden wektor jest wyrażany przez inny, na przykład . Odwrotność też jest prawdziwa: jeśli jeden wektor może być wyrażony w kategoriach innego, to takie wektory są koniecznie współliniowe. W ten sposób: jeśli pomnożymy wektor przez liczbę, otrzymamy współliniowość(w stosunku do oryginału) wektor.

4) Wektory są współkierunkowe. Wektory i są również współkierunkowe. Dowolny wektor z pierwszej grupy jest przeciwny do dowolnego wektora z drugiej grupy.

Jakie wektory są równe?

Dwa wektory są równe, jeśli są współkierunkowe i mają tę samą długość. Zauważ, że współkierunek implikuje, że wektory są współliniowe. Definicja będzie niedokładna (zbędna), jeśli powiesz: „Dwa wektory są równe, jeśli są współliniowe, współkierowane i mają tę samą długość”.

Z punktu widzenia koncepcji wektora swobodnego, równe wektory to ten sam wektor, co zostało już omówione w poprzednim akapicie.

Współrzędne wektorowe na płaszczyźnie i w przestrzeni

Pierwszym punktem jest rozważenie wektorów na płaszczyźnie. Narysuj kartezjański prostokątny układ współrzędnych i odłóż go na bok od początku pojedynczy wektory i :

Wektory i prostokątny. Ortogonalny = Prostopadły. Polecam powoli przyzwyczajać się do terminów: zamiast równoległości i prostopadłości używamy odpowiednio słów kolinearność I ortogonalność.

Przeznaczenie: ortogonalność wektorów zapisujemy zwykłym znakiem prostopadłym, na przykład: .

Rozważane wektory nazywają się wektory współrzędnych lub orts. Te wektory tworzą podstawa na powierzchni. Jaka jest podstawa, jak sądzę, jest intuicyjnie zrozumiała dla wielu, bardziej szczegółowe informacje można znaleźć w artykule Liniowa (nie) zależność wektorów. Podstawa wektorowa.W prostych słowach podstawa i pochodzenie współrzędnych określają cały układ - jest to swego rodzaju fundament, na którym gotuje się pełne i bogate geometryczne życie.

Czasami skonstruowana podstawa nazywa się ortonormalny podstawa płaszczyzny: „orto” - ponieważ wektory współrzędnych są ortogonalne, przymiotnik „znormalizowany” oznacza jednostkę, tj. długości wektorów bazowych są równe jeden.

Przeznaczenie: podstawa jest zwykle pisana w nawiasach, wewnątrz których w ścisłej kolejności wymienione są wektory bazowe, na przykład: . Wektory współrzędnych to jest zabronione zamiana miejsc.

Każdy samolot wektor jedyny sposób wyrażony jako:
, gdzie - liczby, które nazywają się współrzędne wektora na tej podstawie. Ale samo wyrażenie nazywa się rozkład wektorowypodstawa .

Kolacja serwowana:

Zacznijmy od pierwszej litery alfabetu: . Z rysunku wyraźnie widać, że przy rozkładaniu wektora pod kątem podstawy używa się tych właśnie rozważanych:
1) zasada mnożenia wektora przez liczbę: i ;
2) dodawanie wektorów zgodnie z regułą trójkąta: .

Teraz mentalnie odsuń wektor od dowolnego innego punktu na płaszczyźnie. Jest całkiem oczywiste, że jego zepsucie „będzie za nim nieustannie podążać”. Oto wolność wektora - wektor „niesie wszystko ze sobą”. Ta właściwość jest oczywiście prawdziwa dla każdego wektora. Zabawne, że same wektory bazowe (wolne) nie muszą być odkładane na bok od początku, jeden można narysować np. w lewym dolnym rogu, a drugi w prawym górnym i nic się od tego nie zmieni! To prawda, że nie musisz tego robić, ponieważ nauczyciel również wykaże się oryginalnością i narysuje „przepustkę” w nieoczekiwanym miejscu.

Wektory , dokładnie ilustrują zasadę mnożenia wektora przez liczbę , wektor jest współkierunkowy z wektorem bazy , wektor jest skierowany przeciwnie do wektora bazy . Dla tych wektorów jedna ze współrzędnych jest równa zeru, można ją skrupulatnie zapisać w następujący sposób:

Nawiasem mówiąc, wektory bazowe są takie: (w rzeczywistości są wyrażane przez siebie).

I w końcu: , . Przy okazji, co to jest odejmowanie wektorów i dlaczego nie powiedziałem ci o regule odejmowania? Gdzieś w algebrze liniowej, nie pamiętam gdzie, zauważyłem, że odejmowanie jest szczególnym przypadkiem dodawania. Tak więc rozwinięcia wektorów „de” i „e” są spokojnie zapisane jako suma: . Postępuj zgodnie z rysunkiem, aby zobaczyć, jak dobrze w takich sytuacjach działa stare, dobre dodawanie wektorów zgodnie z regułą trójkąta.

Rozważany rozkład formy czasami nazywany rozkładem wektorowym w systemie ort(tj. w systemie wektorów jednostkowych). Ale to nie jedyny sposób na napisanie wektora, powszechna jest następująca opcja:

Lub ze znakiem równości:

Same wektory bazowe są zapisane w następujący sposób: i

Oznacza to, że współrzędne wektora są podane w nawiasach. W zadaniach praktycznych wykorzystywane są wszystkie trzy opcje nagrywania.

Wątpiłem, czy mówić, ale i tak powiem: nie można zmienić układu współrzędnych wektora. Ściśle na pierwszym miejscu zapisz współrzędną odpowiadającą wektorowi jednostkowemu , ściśle na drugim miejscu zapisz współrzędną odpowiadającą wektorowi jednostkowemu . Rzeczywiście i są to dwa różne wektory.

Ustaliliśmy współrzędne w samolocie. Rozważmy teraz wektory w przestrzeni trójwymiarowej, tutaj wszystko jest prawie takie samo! Zostanie dodana tylko jedna współrzędna. Ciężko jest wykonać rysunki trójwymiarowe, więc ograniczę się do jednego wektora, który dla uproszczenia odłożę od początku:

Każdy 3d wektor kosmiczny jedyny sposób rozwiń w bazie ortonormalnej:
, gdzie są współrzędne wektora (liczby) w danej bazie.

Przykład ze zdjęcia: . Zobaczmy, jak działają tutaj reguły akcji wektorowej. Najpierw pomnożenie wektora przez liczbę: (czerwona strzałka), (zielona strzałka) i (magenta strzałka). Po drugie, oto przykład dodawania kilku, w tym przypadku trzech, wektorów: . Wektor sumy zaczyna się w początkowym punkcie wyjścia (początek wektora ) i kończy w końcowym punkcie przybycia (koniec wektora ).

Wszystkie wektory przestrzeni trójwymiarowej są oczywiście również wolne, spróbuj mentalnie odsunąć wektor z dowolnego innego punktu, a zrozumiesz, że jego rozszerzenie „pozostaje z nim”.

Podobnie jak w przypadku samolotu, oprócz pisania powszechnie stosowane są wersje z nawiasami: albo .

Jeśli w rozwinięciu brakuje jednego (lub dwóch) wektorów współrzędnych, zamiast tego wstawiane są zera. Przykłady:
wektor (drobiazgowo ) - zanotować ;
wektor (drobiazgowo ) - zanotować ;
wektor (drobiazgowo ) - zanotować .

Wektory bazowe są zapisywane w następujący sposób:

Tutaj być może znajduje się cała minimalna wiedza teoretyczna niezbędna do rozwiązywania problemów geometrii analitycznej. Być może terminów i definicji jest zbyt wiele, więc polecam głupkom ponowne przeczytanie i ponowne zrozumienie tych informacji. I przyda się każdemu czytelnikowi od czasu do czasu odwołanie się do podstawowej lekcji, aby lepiej przyswoić materiał. Kolinearność, ortogonalność, baza ortonormalna, rozkład wektorów - te i inne pojęcia będą często używane w dalszej części. Zaznaczam, że materiały strony nie wystarczą do zdania testu teoretycznego, kolokwium z geometrii, ponieważ wszystkie twierdzenia starannie szyfruję (oprócz bez dowodów) - ze szkodą dla naukowego stylu prezentacji, ale na plus za zrozumienie tematu. W celu uzyskania szczegółowych informacji teoretycznych proszę kłaniać się profesorowi Atanasyanowi.

Przejdźmy teraz do części praktycznej:

Najprostsze problemy geometrii analitycznej.
Działania z wektorami we współrzędnych

Zadania, które będą brane pod uwagę, bardzo pożądane jest nauczenie się ich rozwiązywania w pełni automatycznie oraz formuł zapamiętać, nawet nie pamiętaj tego celowo, sami to zapamiętają =) Jest to bardzo ważne, ponieważ inne problemy geometrii analitycznej opierają się na najprostszych elementarnych przykładach, a spędzanie dodatkowego czasu na jedzeniu pionków będzie denerwujące. Nie musisz zapinać górnych guzików na koszuli, wiele rzeczy znasz ze szkoły.

Prezentacja materiału będzie przebiegała równolegle – zarówno dla płaszczyzny, jak i przestrzeni. Z tego powodu, że wszystkie formuły… przekonasz się sam.

Jak znaleźć wektor mając dwa punkty?

Jeżeli dane są dwa punkty płaszczyzny i, to wektor ma następujące współrzędne:

Jeśli dane są dwa punkty w przestrzeni i, to wektor ma następujące współrzędne:

Tj, ze współrzędnych końca wektora musisz odjąć odpowiednie współrzędne początek wektora.

Zadanie: Dla tych samych punktów zapisz wzory na znalezienie współrzędnych wektora. Wzory na koniec lekcji.

Przykład 1

Biorąc pod uwagę dwa punkty na płaszczyźnie i . Znajdź współrzędne wektora

Rozwiązanie: zgodnie z odpowiednią formułą:

Alternatywnie można zastosować następującą notację:

Esteci zdecydują tak:

Osobiście jestem przyzwyczajony do pierwszej wersji płyty.

Odpowiedź:

Zgodnie z warunkiem nie było wymagane budowanie rysunku (co jest typowe dla problemów geometrii analitycznej), ale w celu wyjaśnienia niektórych punktów manekinom nie będę zbyt leniwy:

Musi być zrozumiany różnica między współrzędnymi punktu a współrzędnymi wektora:

Współrzędne punktu są zwykłymi współrzędnymi w prostokątnym układzie współrzędnych. Myślę, że każdy wie, jak wykreślić punkty na płaszczyźnie współrzędnych od klasy 5-6. Każdy punkt ma ściśle określone miejsce w samolocie i nie można ich nigdzie przesunąć.

Współrzędne tego samego wektora jest jego rozbudowa w stosunku do podstawy, w tym przypadku. Każdy wektor jest swobodny, dlatego w razie potrzeby lub konieczności możemy go łatwo przesunąć z innego punktu płaszczyzny (zmieniając jego nazwę, na przykład na , aby uniknąć nieporozumień). Co ciekawe, dla wektorów nie można w ogóle budować osi, prostokątny układ współrzędnych, wystarczy podstawa, w tym przypadku ortonormalna podstawa płaszczyzny.

Zapisy współrzędnych punktu i współrzędnych wektorowych wydają się być podobne: , oraz poczucie współrzędnych absolutnie inny; różny i powinieneś zdawać sobie sprawę z tej różnicy. Ta różnica oczywiście dotyczy również przestrzeni.

Szanowni Państwo, wypełniamy ręce:

Przykład 2

a) Podane punkty i . Znajdź wektory i .
b) Punkty są przyznawane I . Znajdź wektory i .
c) Podane punkty i . Znajdź wektory i .
d) Punkty są przyznawane. Znajdź wektory .

Być może wystarczy. To są przykłady na samodzielną decyzję, postaraj się ich nie zaniedbywać, to się opłaci ;-). Rysunki nie są wymagane. Rozwiązania i odpowiedzi na koniec lekcji.

Co jest ważne w rozwiązywaniu problemów geometrii analitycznej? Ważne jest, aby być NIEZWYKLE OSTROŻNYM, aby uniknąć mistrzowskiego błędu „dwa plus dwa równa się zero”. Z góry przepraszam jeśli popełniłem błąd =)

Jak znaleźć długość odcinka?

Długość, jak już wspomniano, jest oznaczona znakiem modułu.

Jeżeli podane są dwa punkty płaszczyzny i, to długość odcinka można obliczyć ze wzoru

Jeżeli dane są dwa punkty w przestrzeni i, to długość odcinka można obliczyć ze wzoru

Notatka: Wzory pozostaną poprawne, jeśli odpowiednie współrzędne zostaną zamienione: i , ale pierwsza opcja jest bardziej standardowa

Przykład 3

Rozwiązanie: zgodnie z odpowiednią formułą:

Odpowiedź:

Dla jasności zrobię rysunek

Sekcja - to nie jest wektor i oczywiście nie można go nigdzie przenieść. Dodatkowo jeśli uzupełnisz rysunek w skali: 1 jednostka. \u003d 1 cm (dwie komórki tetrad), odpowiedź można sprawdzić za pomocą zwykłej linijki, bezpośrednio mierząc długość segmentu.

Tak, rozwiązanie jest krótkie, ale jest w nim kilka ważnych punktów, które chciałbym wyjaśnić:

Najpierw w odpowiedzi ustalamy wymiar: „jednostki”. Warunek nie mówi CO to jest, milimetry, centymetry, metry czy kilometry. Dlatego ogólne sformułowanie będzie matematycznie kompetentnym rozwiązaniem: „jednostki” - w skrócie „jednostki”.

Po drugie powtórzmy materiał szkolny, który jest przydatny nie tylko w rozważanym problemie:

Zwróć uwagę na ważna sztuczka techniczna – wyjęcie mnożnika spod korzenia. W wyniku obliczeń otrzymaliśmy wynik, a dobry styl matematyczny polega na wyjęciu mnożnika spod pierwiastka (jeśli to możliwe). Bardziej szczegółowo proces wygląda tak: . Oczywiście pozostawienie odpowiedzi w formularzu nie będzie błędem - ale na pewno jest to wada i ważki argument za czepianiem się ze strony nauczyciela.

Oto inne typowe przypadki:

Często na przykład pod korzeniem uzyskuje się wystarczająco dużą liczbę. Jak być w takich przypadkach? Na kalkulatorze sprawdzamy, czy liczba jest podzielna przez 4:. Tak, podziel całkowicie, a więc: . A może tę liczbę można znów podzielić przez 4? . W ten sposób: . Ostatnia cyfra liczby jest nieparzysta, więc dzielenie przez 4 po raz trzeci jest oczywiście niemożliwe. Próba dzielenia przez dziewięć: . W rezultacie:
Gotowy.

Wyjście: jeśli pod pierwiastkiem otrzymamy liczbę zupełnie nieusuwalną, to staramy się wyciągnąć czynnik spod pierwiastka - na kalkulatorze sprawdzamy, czy liczba jest podzielna przez: 4, 9, 16, 25, 36, 49, itp.

W trakcie rozwiązywania różnych problemów często znajdują się korzenie, zawsze staraj się wydobyć czynniki spod korzenia, aby uniknąć niższego wyniku i niepotrzebnych kłopotów z finalizacją swoich rozwiązań zgodnie z uwagą nauczyciela.

Powtórzmy jednocześnie kwadraturę korzeni i innych potęg:

Zasady postępowania ze stopniami w formie ogólnej można znaleźć w podręczniku szkolnym do algebry, ale myślę, że wszystko lub prawie wszystko jest już jasne z podanych przykładów.

Zadanie samodzielnego rozwiązania z segmentem w przestrzeni:

Przykład 4

Podane punkty i . Znajdź długość segmentu.

Rozwiązanie i odpowiedź na końcu lekcji.

Jak znaleźć długość wektora?

Jeśli podano wektor płaski, to jego długość oblicza się ze wzoru.

Jeżeli podano wektor przestrzenny, to jego długość oblicza się ze wzoru .

Te wzory (podobnie jak wzory na długość odcinka) można łatwo wyprowadzić za pomocą słynnego twierdzenia Pitagorasa.

W tym artykule rozpoczniemy dyskusję na temat jednej „magicznej różdżki”, która pozwoli zredukować wiele problemów geometrii do prostej arytmetyki. Ta „różdżka” może znacznie ułatwić Ci życie, zwłaszcza gdy czujesz się niepewnie w budowaniu przestrzennych figur, przekrojów itp. Wszystko to wymaga pewnej wyobraźni i praktycznych umiejętności. Metoda, którą zaczniemy tutaj rozważać, pozwoli ci niemal całkowicie abstrahować od wszelkiego rodzaju konstrukcji geometrycznych i rozumowania. Metoda nazywa się „metoda współrzędnych”. W tym artykule rozważymy następujące pytania:

Płaszczyzna współrzędnych
Punkty i wektory na płaszczyźnie
Budowanie wektora z dwóch punktów
Długość wektora (odległość między dwoma punktami)
Współrzędne punktu środkowego
Iloczyn skalarny wektorów
Kąt między dwoma wektorami

Myślę, że już zgadłeś, dlaczego metoda współrzędnych jest tak nazywana? Prawdą jest, że otrzymał taką nazwę, ponieważ nie operuje obiektami geometrycznymi, ale ich cechami liczbowymi (współrzędnymi). A sama transformacja, która umożliwia przejście od geometrii do algebry, polega na wprowadzeniu układu współrzędnych. Jeśli oryginalna figura była płaska, współrzędne są dwuwymiarowe, a jeśli figura jest trójwymiarowa, współrzędne są trójwymiarowe. W tym artykule rozważymy tylko przypadek dwuwymiarowy. A głównym celem artykułu jest nauczenie Cię, jak korzystać z podstawowych technik metody współrzędnych (czasami okazują się przydatne przy rozwiązywaniu problemów planimetrycznych w części B Unified State Examination). Kolejne dwa rozdziały na ten temat poświęcone są omówieniu metod rozwiązywania problemów C2 (problem stereometrii).

Gdzie logiczne byłoby rozpoczęcie omawiania metody współrzędnych? Prawdopodobnie z pojęciem układu współrzędnych. Pamiętaj, kiedy ją poznałeś. Wydaje mi się, że w 7 klasie, kiedy dowiedziałeś się na przykład o istnieniu funkcji liniowej. Przypomnę, że zbudowałeś go punkt po punkcie. Pamiętasz? Wybrałeś dowolną liczbę, wstawiłeś ją do wzoru i obliczyłeś w ten sposób. Na przykład, jeśli, to, jeśli, to itd. Co uzyskałeś w rezultacie? I otrzymałeś punkty ze współrzędnymi: i. Następnie narysowałeś „krzyżyk” (układ współrzędnych), wybrałeś na nim skalę (ile komórek będziesz miał jako jeden odcinek) i zaznaczyłeś na nim otrzymane punkty, które następnie połączyłeś linią prostą, powstałą linią jest wykresem funkcji.

Jest kilka rzeczy, które należy wyjaśnić bardziej szczegółowo:

1. Ze względu na wygodę wybierasz jeden segment, aby wszystko ładnie i kompaktowo mieściło się na zdjęciu

2. Zakłada się, że oś biegnie od lewej do prawej, a oś od dołu do góry

3. Przecinają się pod kątem prostym, a punkt ich przecięcia nazywa się początkiem. Jest oznaczony literą.

4. W zapisie współrzędnej punktu np. po lewej stronie w nawiasie znajduje się współrzędna punktu wzdłuż osi, a po prawej wzdłuż osi. W szczególności oznacza po prostu, że punkt

5. Aby ustawić dowolny punkt na osi współrzędnych należy podać jego współrzędne (2 cyfry)

6. Dla dowolnego punktu leżącego na osi,

7. Dla dowolnego punktu leżącego na osi,

8. Oś nazywa się osią x

9. Oś nazywa się osią y

Teraz zróbmy z tobą kolejny krok: zaznacz dwa punkty. Połącz te dwa punkty linią. I postawmy strzałkę tak, jakbyśmy rysowali odcinek od punktu do punktu: to znaczy, że uczynimy nasz odcinek skierowanym!

Pamiętasz, jaka jest inna nazwa kierowanego segmentu? Zgadza się, nazywa się to wektorem!

Tak więc, jeśli połączymy kropkę z kropką, a początkiem będzie punkt A, a końcem punkt B, wtedy otrzymujemy wektor. Ty też robiłeś tę konstrukcję w 8 klasie, pamiętasz?

Okazuje się, że wektory, podobnie jak punkty, mogą być oznaczone dwiema liczbami: liczby te nazywane są współrzędnymi wektora. Pytanie: czy uważasz, że wystarczy znać współrzędne początku i końca wektora, aby znaleźć jego współrzędne? Okazuje się, że tak! A to bardzo proste:

Tak więc, ponieważ w wektorze punktem jest początek, a koniec wektor ma następujące współrzędne:

Na przykład, jeśli, to współrzędne wektora

Teraz zróbmy odwrotnie, znajdź współrzędne wektora. Co musimy w tym celu zmienić? Tak, musisz zamienić początek i koniec: teraz początek wektora będzie w punkcie, a koniec w punkcie. Następnie:

Przyjrzyj się uważnie, jaka jest różnica między wektorami i? Ich jedyną różnicą są znaki we współrzędnych. Są przeciwne. Ten fakt jest napisany tak:

Czasami, jeśli nie jest wyraźnie określone, który punkt jest początkiem wektora, a który końcem, wektory są oznaczone nie dwiema wielkimi literami, ale jedną małą literą, na przykład: itp.

Teraz trochę ćwiczyć i znajdź współrzędne następujących wektorów:

Badanie:

Teraz rozwiąż problem nieco trudniejszy:

Torus wektorowy ze złomem typu on-cha-scrap w punkcie ma co-lub-di-on-you. Znajdź di-te punkty abs-cis-su.

Wszystko to jest dość prozaiczne: niech będą współrzędne punktu. Następnie

Skompilowałem system, określając współrzędne wektora. Wtedy punkt ma współrzędne. Interesuje nas odcięta. Następnie

Odpowiedź:

Co jeszcze można zrobić z wektorami? Tak, prawie wszystko jest takie samo jak w przypadku zwykłych liczb (z wyjątkiem tego, że nie można dzielić, ale można mnożyć na dwa sposoby, z których jeden omówimy tutaj nieco później)

Wektory można łączyć ze sobą
Wektory można od siebie odejmować
Wektory można mnożyć (lub dzielić) przez dowolną liczbę niezerową
Wektory można mnożyć ze sobą

Wszystkie te operacje mają dość wizualną reprezentację geometryczną. Na przykład trójkąt (lub równoległobok) rządzi dodawaniem i odejmowaniem:

Wektor rozciąga się, kurczy lub zmienia kierunek po pomnożeniu lub podzieleniu przez liczbę:

Tutaj jednak interesuje nas pytanie, co dzieje się ze współrzędnymi.

1. Przy dodawaniu (odejmowaniu) dwóch wektorów dodajemy (odejmujemy) ich współrzędne element po elemencie. Tj:

2. Podczas mnożenia (dzielenia) wektora przez liczbę wszystkie jego współrzędne są mnożone (dzielone) przez tę liczbę:

Na przykład:

· Znajdź-di-suma ko-or-di-nat od stulecia do ra.

Najpierw znajdźmy współrzędne każdego z wektorów. Oba mają ten sam początek - punkt początkowy. Ich końce są inne. Następnie, . Teraz obliczamy współrzędne wektora Następnie suma współrzędnych wektora wynikowego jest równa.

Odpowiedź:

Teraz samodzielnie rozwiąż następujący problem:

· Znajdź sumę współrzędnych wektora

Sprawdzamy:

Rozważmy teraz następujący problem: mamy dwa punkty na płaszczyźnie współrzędnych. Jak znaleźć odległość między nimi? Niech będzie pierwszy punkt, a drugi. Oznaczmy odległość między nimi jako . Zróbmy następujący rysunek dla jasności:

Co ja zrobiłem? Najpierw połączyłem punkty, a także narysowałem linię równoległą do osi z punktu i narysowałem linię równoległą do osi z punktu. Czy przecinały się w pewnym momencie, tworząc cudowną figurę? Dlaczego jest cudowna? Tak, ty i ja wiemy prawie wszystko o trójkącie prostokątnym. Cóż, na pewno twierdzenie Pitagorasa. Pożądanym segmentem jest przeciwprostokątna tego trójkąta, a segmenty to nogi. Jakie są współrzędne punktu? Tak, łatwo je znaleźć na zdjęciu: ponieważ segmenty są równoległe do osi i odpowiednio ich długości są łatwe do znalezienia: jeśli oznaczymy odpowiednio długości segmentów przez, to

Użyjmy teraz twierdzenia Pitagorasa. Znamy długości nóg, znajdziemy przeciwprostokątną:

Zatem odległość między dwoma punktami jest sumą pierwiastków kwadratów różnic względem współrzędnych. Lub - odległość między dwoma punktami to długość łączącego je odcinka. Łatwo zauważyć, że odległość między punktami nie zależy od kierunku. Następnie:

Z tego wyciągamy trzy wnioski:

Poćwiczmy trochę obliczanie odległości między dwoma punktami:

Na przykład, jeśli, to odległość między i wynosi

Albo chodźmy inaczej: znajdź współrzędne wektora

I znajdź długość wektora:

Jak widać, jest tak samo!

Teraz poćwicz trochę na własną rękę:

Zadanie: znajdź odległość między podanymi punktami:

Sprawdzamy:

Oto kilka innych problemów związanych z tą samą formułą, choć brzmią one nieco inaczej:

1. Znajdź-di-te kwadrat długości powieki do-ra.

2. Nai-di-te kwadrat długości powieki do ra

Domyślam się, że łatwo sobie z nimi poradzisz? Sprawdzamy:

1. A to dla uwagi) Już wcześniej znaleźliśmy współrzędne wektorów: . Wtedy wektor ma współrzędne. Kwadrat jego długości będzie wynosił:

2. Znajdź współrzędne wektora

Wtedy kwadrat jego długości wynosi

Nic skomplikowanego, prawda? Prosta arytmetyka, nic więcej.

Poniższe zagadki nie dają się jednoznacznie sklasyfikować, służą raczej ogólnej erudycji i umiejętności rysowania prostych obrazków.

1. Znajdź-d-te sinusy kąta-od-przycięcie-od-cięcia, połącz-jeden-ty-ty punkt, z osią odciętych.

Jak zamierzamy to zrobić tutaj? Musisz znaleźć sinus kąta między osią a osią. A gdzie możemy szukać sinusa? Zgadza się, w trójkącie prostokątnym. Więc co musimy zrobić? Zbuduj ten trójkąt!

Ponieważ współrzędne punktu i, to odcinek jest równy, a odcinek. Musimy znaleźć sinus kąta. Przypomnę, że sinus to stosunek przeciwprostokątnej do przeciwprostokątnej

Co nam zostało do zrobienia? Znajdź przeciwprostokątną. Możesz to zrobić na dwa sposoby: używając twierdzenia Pitagorasa (nogi są znane!) lub używając wzoru na odległość między dwoma punktami (właściwie tak samo jak pierwsza metoda!). Pójdę w drugą stronę:

Odpowiedź:

Następne zadanie wyda ci się jeszcze łatwiejsze. Ona - na współrzędnych punktu.

Zadanie 2. Od tego momentu per-pen-di-kular jest opuszczany na oś odciętych. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.

Zróbmy rysunek:

Podstawą pionu jest punkt, w którym przecina oś x (oś) dla mnie jest to punkt. Rysunek pokazuje, że ma współrzędne: . Interesuje nas odcięta - czyli składnik "X". Jest równa.

Odpowiedź: .

Zadanie 3. W warunkach poprzedniego zadania znajdź sumę odległości od punktu do osi współrzędnych.

Zadanie jest generalnie elementarne, jeśli wiesz, jaka jest odległość od punktu do osi. Wiesz, że? Mam nadzieję, ale nadal przypominam:

Czyli na moim rysunku, położonym nieco wyżej, przedstawiłem już jedną taką prostopadłą? Jaka to oś? do osi. A jaka jest jego długość? Jest równa. Teraz sam narysuj prostopadłą do osi i znajdź jej długość. Będzie równy, prawda? Wtedy ich suma jest równa.

Odpowiedź: .

Zadanie 4. W warunkach zadania 2 znajdź rzędną punktu symetrycznego do punktu wokół osi x.

Myślę, że intuicyjnie rozumiesz, czym jest symetria? Ma ją bardzo wiele obiektów: wiele budynków, stołów, płaszczyzn, wiele kształtów geometrycznych: kula, walec, kwadrat, romb itp. Z grubsza mówiąc symetrię można rozumieć następująco: figura składa się z dwóch (lub więcej) identyczne połówki. Ta symetria nazywa się osiową. Czym więc jest oś? Jest to dokładnie ta linia, wzdłuż której figurę można, względnie mówiąc, „pociąć” na identyczne połówki (na tym rysunku oś symetrii jest prosta):

Wróćmy teraz do naszego zadania. Wiemy, że szukamy punktu symetrycznego względem osi. Wtedy ta oś jest osią symetrii. Musimy więc zaznaczyć punkt, aby oś przecięła segment na dwie równe części. Spróbuj sam oznaczyć taki punkt. Teraz porównaj z moim rozwiązaniem:

Czy zrobiłeś to samo? Dobry! W znalezionym punkcie interesuje nas rzędna. Ona jest równa

Odpowiedź:

Teraz powiedz mi, po chwili zastanowienia, jaka będzie odcięta punktu symetrycznego względem punktu A względem osi y? Jaka jest twoja odpowiedź? Poprawna odpowiedź: .

Ogólnie regułę można napisać tak:

Punkt symetryczny do punktu wokół osi X ma współrzędne:

Punkt symetryczny do punktu wokół osi y ma współrzędne:

Cóż, teraz to jest naprawdę przerażające. zadanie: Znajdź współrzędne punktu symetrycznego względem punktu względem początku. Najpierw myślisz sam, a potem patrzysz na mój rysunek!

Odpowiedź:

Ale już problem równoległoboku:

Zadanie 5: Punkty to ver-shi-na-mi-pa-ral-le-lo-gram-ma. Znajdź punkty dee-te lub-dee-on-tu.

Możesz rozwiązać ten problem na dwa sposoby: logicznie i metodą współrzędnych. Najpierw zastosuję metodę współrzędnych, a potem powiem, jak możesz inaczej zdecydować.

Jest całkiem jasne, że odcięta punktu jest równa. (leży na prostopadłej narysowanej od punktu do osi x). Musimy znaleźć rzędnego. Wykorzystajmy fakt, że nasza figura jest równoległobokiem, co oznacza, że. Znajdź długość odcinka, korzystając ze wzoru na odległość między dwoma punktami:

Obniżamy prostopadłość łączącą punkt z osią. Punkt przecięcia jest oznaczony literą.

Długość segmentu jest równa. (znajdź problem sam, gdzie omawialiśmy ten moment), wtedy znajdziemy długość odcinka za pomocą twierdzenia Pitagorasa:

Długość odcinka jest dokładnie taka sama jak jego rzędna.

Odpowiedź: .

Inne rozwiązanie (dostarczę tylko zdjęcie, które to ilustruje)

Postęp rozwiązania:

1. Wydaj

2. Znajdź współrzędne i długość punktu

3. Udowodnij to.

Jeszcze jeden problem z długością cięcia:

Punkty to-la-yut-xia top-shi-on-mi tri-angle-no-ka. Znajdź długość jego linii środkowej, par-ral-lel-noy.

Czy pamiętasz, jaka jest środkowa linia trójkąta? Wtedy dla ciebie to zadanie jest elementarne. Jeśli nie pamiętasz, to ci przypomnę: linia środkowa trójkąta to linia łącząca punkty środkowe przeciwległych boków. Jest równoległy do podstawy i równy jej połowie.

Baza jest segmentem. Musieliśmy wcześniej poszukać jego długości, jest równa. Wtedy długość linii środkowej jest o połowę krótsza i równa.

Odpowiedź: .

Komentarz: Ten problem można rozwiązać w inny sposób, do którego przejdziemy nieco później.

Tymczasem oto kilka zadań dla Ciebie, poćwicz na nich, są dość proste, ale pomagają „wypełnić rękę” metodą współrzędnych!

1. Punkty pojawiają się-la-yut-xia top-shi-on-mi tra-pe-tion. Znajdź długość jego linii środkowej.

2. Punkty i yav-la-yut-xia ver-shi-na-mi pa-ral-le-lo-gram-ma. Znajdź punkty dee-te lub-dee-on-tu.

3. Znajdź długość od cięcia, połącz drugi punkt i

4. Znajdź-di-te obszar dla-red-shen-noy fi-gu-ry na samolocie ko-or-di-nat-noy.

5. Okrąg o środku na-cha-le ko-or-di-nat przechodzi przez punkt. Znajdź-de-te jej ra-di-wąsy.

6. Nai-di-te ra-di-us circle-no-sti, opisz-san-noy w pobliżu kąta-no-ka, szczyty-shi-ny czegoś-ro-go mają ko-lub - di-na-you współ-od-odpowiedz-ale

Rozwiązania:

1. Wiadomo, że linia środkowa trapezu jest równa połowie sumy jego podstaw. Podstawa jest równa, ale podstawa. Następnie

Odpowiedź:

2. Najłatwiejszym sposobem rozwiązania tego problemu jest zauważenie tego (reguła równoległoboku). Oblicz współrzędne wektorów i nie jest trudne: . Podczas dodawania wektorów dodawane są współrzędne. Następnie ma współrzędne. Punkt ma te same współrzędne, ponieważ początek wektora to punkt o współrzędnych. Interesuje nas rz. Jest równa.

Odpowiedź:

3. Działamy natychmiast według wzoru na odległość między dwoma punktami:

Odpowiedź:

4. Spójrz na zdjęcie i powiedz, pomiędzy którymi dwiema figurami jest zacieniony obszar „ściśnięty”? Jest umieszczony pomiędzy dwoma kwadratami. Wtedy powierzchnia pożądanej figury jest równa powierzchni dużego kwadratu minus powierzchnia małego. Bok małego kwadratu to odcinek łączący punkty, a jego długość wynosi

Wtedy powierzchnia małego kwadratu to

To samo robimy z dużym kwadratem: jego bok to odcinek łączący punkty, a jego długość jest równa

Wtedy powierzchnia dużego placu to

Obszar pożądanej figury znajduje się według wzoru:

Odpowiedź:

5. Jeśli okrąg ma początek jako środek i przechodzi przez punkt, to jego promień będzie dokładnie równy długości odcinka (zrób rysunek, a zrozumiesz, dlaczego jest to oczywiste). Znajdź długość tego segmentu:

Odpowiedź:

6. Wiadomo, że promień okręgu opisanego na prostokącie jest równy połowie jego przekątnej. Znajdźmy długość dowolnej z dwóch przekątnych (w końcu w prostokącie są one równe!)

Odpowiedź:

Cóż, poradziłeś sobie ze wszystkim? Nie było to takie trudne, prawda? Jest tu tylko jedna zasada – móc zrobić obraz wizualny i po prostu „odczytać” z niego wszystkie dane.

Zostało nam bardzo niewiele. Są jeszcze dwa punkty, które chciałbym omówić.

Spróbujmy rozwiązać ten prosty problem. Niech dwa punkty i zostaną podane. Znajdź współrzędne środka segmentu. Rozwiązanie tego problemu jest następujące: niech punkt będzie pożądanym środkiem, wtedy ma współrzędne:

Tj: współrzędne środka odcinka = średnia arytmetyczna odpowiednich współrzędnych końców odcinka.

Ta zasada jest bardzo prosta i zazwyczaj nie sprawia uczniom trudności. Zobaczmy, w jakich problemach i jak jest używany:

1. Znajdź-di-te or-di-na-tu se-re-di-us from-cut, connect-nya-yu-th-th-th-th-th punkt i

2. Punkty to yav-la-yut-xia ver-shi-na-mi-che-you-reh-coal-no-ka. Znajdź-di-te or-di-na-tu punkty re-se-che-niya jego dia-go-on-lei.

3. Znajdź-di-te abs-cis-su środka koła, opisz-san-noy w pobliżu prostokąta-no-ka, wierzchołki-shi-mamy coś-ro-go co-or-di- na-ty współ-z-vet-stvenno-ale.

Rozwiązania:

1. Pierwsze zadanie to po prostu klasyka. Działamy natychmiast, określając środek odcinka. Ma współrzędne. Rzędna jest równa.

Odpowiedź:

2. Łatwo zauważyć, że dany czworokąt jest równoległobokiem (nawet rombem!). Możesz to udowodnić sam, obliczając długości boków i porównując je ze sobą. Co wiem o równoległoboku? Jego przekątne są przecinane przez punkt przecięcia! Aha! Więc jaki jest punkt przecięcia przekątnych? To jest środek dowolnej przekątnej! Wybiorę w szczególności przekątną. Wtedy punkt ma współrzędne.Rzędna punktu jest równa.

Odpowiedź:

3. Jaki jest środek okręgu opisanego wokół prostokąta? Zbiega się z punktem przecięcia jego przekątnych. Co wiesz o przekątnych prostokąta? Są równe, a punkt przecięcia jest podzielony na pół. Zadanie zostało zredukowane do poprzedniego. Weźmy na przykład przekątną. Wtedy jeśli jest środkiem opisanego koła, to jest środkiem. Szukam współrzędnych: odcięta jest równa.

Odpowiedź:

Teraz poćwicz trochę na własną rękę, podam tylko odpowiedzi na każdy problem, abyś mógł się sprawdzić.

1. Nai-di-te ra-di-us circle-no-sti, opisz-san-noy w pobliżu trójkąta-no-ka, wierzchołki kogoś-ro-go mają ko-or-di -bez panów

2. Znajdź-di-te or-di-na-tu środek okręgu, opisz san-noy w pobliżu trójkąta-no-ka, wierzchołki-shi-mamy coś-ro-go współrzędne

3. Jakie promienie powinny mieć okrąg ze środkiem w punkcie stykającym się z osią odciętych?

4. Znajdź-di-te lub-di-w tym punkcie ponownego ponownego sprawdzenia osi i od-cięcia, połącz-nya-yu-ty-ty punkt i

Odpowiedzi:

Czy wszystko się udało? Naprawdę mam na to nadzieję! Teraz - ostatnie pchnięcie. Teraz bądź szczególnie ostrożny. Materiał, który teraz wyjaśnię, dotyczy nie tylko problemów z prostymi metodami współrzędnych w części B, ale można go również znaleźć w zadaniu C2.

Której z moich obietnic jeszcze nie dotrzymałem? Pamiętasz, jakie operacje na wektorach obiecałem wprowadzić, a które ostatecznie wprowadziłem? Czy na pewno niczego nie zapomniałem? Zapomniałem! Zapomniałem wyjaśnić, co oznacza mnożenie wektorów.

Istnieją dwa sposoby pomnożenia wektora przez wektor. W zależności od wybranej metody otrzymamy przedmioty o różnym charakterze:

Produkt wektorowy jest dość skomplikowany. Jak to zrobić i dlaczego jest to potrzebne, omówimy z Tobą w następnym artykule. I w tym skupimy się na produkcie skalarnym.

Istnieją już dwa sposoby, które pozwalają nam to obliczyć:

Jak się domyślasz, wynik powinien być taki sam! Spójrzmy więc najpierw na pierwszy sposób:

Iloczyn skalarny przez współrzędne

Znajdź: - wspólny zapis iloczynu skalarnego

Wzór na obliczenia jest następujący:

To znaczy iloczyn skalarny = suma iloczynów współrzędnych wektorów!

Przykład:

Znajdź-dee-te

Rozwiązanie:

Znajdź współrzędne każdego z wektorów:

Iloczyn skalarny obliczamy według wzoru:

Odpowiedź:

Widzisz, absolutnie nic skomplikowanego!

Cóż, teraz spróbuj sam:

Find-di-te-scalar-noe pro-from-ve-de-nie-wiek-to-ditch i

Czy udało Ci się? Może zauważył małą sztuczkę? Sprawdźmy:

Współrzędne wektorowe, jak w poprzednim zadaniu! Odpowiedź: .

Oprócz współrzędnej istnieje inny sposób obliczania iloczynu skalarnego, a mianowicie poprzez długości wektorów i cosinus kąta między nimi:

Oznacza kąt między wektorami i.

Oznacza to, że iloczyn skalarny jest równy iloczynowi długości wektorów i cosinusowi kąta między nimi.

Po co nam ta druga formuła, skoro mamy pierwszą, która jest o wiele prostsza, przynajmniej nie ma w niej cosinusów. I potrzebujemy tego, abyśmy z pierwszego i drugiego wzoru mogli wywnioskować, jak znaleźć kąt między wektorami!

Zapamiętajmy więc wzór na długość wektora!

Następnie, jeśli połączę te dane z formułą iloczynu skalarnego, otrzymam:

Ale w inny sposób:

Więc co mamy? Mamy teraz wzór do obliczenia kąta między dwoma wektorami! Czasami, dla zwięzłości, jest to również napisane tak:

Oznacza to, że algorytm obliczania kąta między wektorami jest następujący:

Obliczamy iloczyn skalarny poprzez współrzędne
Znajdź długości wektorów i pomnóż je
Wynik z punktu 1 podzielić przez wynik z punktu 2

Poćwiczmy na przykładach:

1. Znajdź kąt między powiekami-do-ra-mi i. Podaj swoją odpowiedź w stopniach.

2. W warunkach poprzedniego zadania znajdź cosinus między wektorami

Zróbmy tak: pomogę ci rozwiązać pierwszy problem, a drugi spróbuję zrobić sam! Zgadzać się? W takim razie zacznijmy!

1. Te wektory to nasi starzy przyjaciele. Rozważaliśmy już ich iloczyn skalarny i był równy. Ich współrzędne to: , . Następnie znajdujemy ich długości:

Następnie szukamy cosinusa między wektorami:

Jaki jest cosinus kąta? To jest róg.

Odpowiedź:

Cóż, teraz sam rozwiąż drugi problem, a następnie porównaj! Podam tylko bardzo krótkie rozwiązanie:

2. ma współrzędne, ma współrzędne.

Niech będzie kątem między wektorami i wtedy

Odpowiedź:

Należy zauważyć, że zadania bezpośrednio na wektorach i metoda współrzędnych w części B pracy egzaminacyjnej są dość rzadkie. Jednak zdecydowaną większość problemów C2 można łatwo rozwiązać, wprowadzając układ współrzędnych. Możesz więc potraktować ten artykuł jako podkład, na podstawie którego wykonamy dość podchwytliwe konstrukcje, które będą nam potrzebne do rozwiązywania złożonych problemów.

WSPÓŁRZĘDNE I WEKTORY. POZIOM ŚREDNIOZAAWANSOWANY

Ty i ja nadal studiujemy metodę współrzędnych. W ostatniej części wyprowadziliśmy szereg ważnych formuł, które pozwalają:

Znajdź współrzędne wektora
Znajdź długość wektora (alternatywnie: odległość między dwoma punktami)
Dodaj, odejmij wektory. Pomnóż je przez liczbę rzeczywistą
Znajdź środek segmentu
Oblicz iloczyn skalarny wektorów
Znajdź kąt między wektorami

Oczywiście cała metoda współrzędnych nie mieści się w tych 6 punktach. Leży u podstaw takiej nauki, jak geometria analityczna, z którą zapoznasz się na uniwersytecie. Chcę tylko zbudować fundament, który pozwoli rozwiązywać problemy w jednym stanie. egzamin. Ustaliliśmy zadania części B w Teraz nadszedł czas, aby przejść na jakościowo nowy poziom! Ten artykuł będzie poświęcony metodzie rozwiązywania tych problemów C2, w których zasadne byłoby przejście na metodę współrzędnych. O tej racjonalności decyduje to, co należy znaleźć w problemie i jaka jest podana liczba. Więc użyłbym metody współrzędnych, jeśli pytania brzmią:

Znajdź kąt między dwiema płaszczyznami
Znajdź kąt między linią a płaszczyzną
Znajdź kąt między dwiema liniami
Znajdź odległość od punktu do samolotu
Znajdź odległość od punktu do linii
Znajdź odległość od linii prostej do płaszczyzny
Znajdź odległość między dwiema liniami

Jeśli liczba podana w warunku problemu jest ciałem obrotowym (kula, walec, stożek ...)

Odpowiednie liczby dla metody współrzędnych to:

prostopadłościan
Piramida (trójkątna, czworokątna, sześciokątna)

Również z mojego doświadczenia niewłaściwe jest stosowanie metody współrzędnych dla:

Znajdowanie obszarów przekrojów
Obliczenia objętości ciał

Należy jednak od razu zauważyć, że trzy „niekorzystne” sytuacje dla metody współrzędnych są w praktyce dość rzadkie. W większości zadań może stać się twoim wybawcą, zwłaszcza jeśli nie jesteś zbyt silny w konstrukcjach trójwymiarowych (które czasami są dość skomplikowane).

Jakie są wszystkie liczby, które wymieniłem powyżej? Nie są już płaskie, takie jak kwadrat, trójkąt, koło, ale obszerne! W związku z tym musimy wziąć pod uwagę nie dwuwymiarowy, ale trójwymiarowy układ współrzędnych. Jest zbudowana dość łatwo: oprócz odciętej i rzędnych wprowadzimy kolejną oś, oś aplikacji. Rysunek schematycznie pokazuje ich względne położenie:

Wszystkie są wzajemnie prostopadłe, przecinają się w jednym punkcie, który nazwiemy początkiem. Oś odciętych, jak poprzednio, będzie oznaczona, oś rzędnych - , a wprowadzoną oś aplikacyjną - .

Jeżeli wcześniej każdy punkt na płaszczyźnie charakteryzowały się dwiema liczbami - odciętą i rzędną, to każdy punkt w przestrzeni jest już opisany trzema liczbami - odcięta, rzędna, aplikacja. Na przykład:

W związku z tym odcięta punktu jest równa, rzędna to , a aplikacja to .

Czasami odcięta punktu nazywana jest również rzutem punktu na oś odciętych, rzędna to rzut punktu na oś rzędnych, a aplikacja to rzut punktu na oś aplikacji. W związku z tym, jeśli podano punkt, to punkt o współrzędnych:

nazwany rzutem punktu na płaszczyznę

Powstaje naturalne pytanie: czy wszystkie wzory wyprowadzone dla przypadku dwuwymiarowego są poprawne w przestrzeni? Odpowiedź brzmi tak, są po prostu i mają ten sam wygląd. Dla małego szczegółu. Myślę, że już zgadłeś, który. We wszystkich formułach będziemy musieli dodać jeszcze jeden termin odpowiadający za oś aplikacji. Mianowicie.

1. Jeżeli zostaną podane dwa punkty: , to:

Współrzędne wektora:
Odległość między dwoma punktami (lub długość wektora)
Środek segmentu ma współrzędne

2. Jeśli dane są dwa wektory: a, to:

Ich iloczyn skalarny to:
Cosinus kąta między wektorami wynosi:

Jednak przestrzeń nie jest taka prosta. Jak rozumiesz, dodanie jeszcze jednej współrzędnej wprowadza znaczne urozmaicenie spektrum postaci „żyjących” w tej przestrzeni. A dla dalszej narracji muszę wprowadzić pewną, z grubsza rzecz biorąc, „uogólnienie” linii prostej. Ta „uogólnienie” będzie samolotem. Co wiesz o samolocie? Spróbuj odpowiedzieć na pytanie, czym jest samolot? Bardzo trudno powiedzieć. Jednak wszyscy intuicyjnie wyobrażamy sobie, jak to wygląda:

Z grubsza mówiąc, jest to rodzaj niekończącego się „listka” wbitego w kosmos. Przez „nieskończoność” należy rozumieć, że płaszczyzna rozciąga się we wszystkich kierunkach, czyli jej powierzchnia jest równa nieskończoności. Jednak to wyjaśnienie „na palcach” nie daje najmniejszego pojęcia o budowie samolotu. I będziemy tym zainteresowani.

Zapamiętajmy jeden z podstawowych aksjomatów geometrii:

Linia prosta przechodzi przez dwa różne punkty na płaszczyźnie, a ponadto tylko jeden:

Lub jego analog w kosmosie:

Oczywiście pamiętasz, jak wyprowadzić równanie prostej z dwóch podanych punktów, to wcale nie jest trudne: jeśli pierwszy punkt ma współrzędne: a drugi, to równanie prostej będzie wyglądało następująco:

Przeszedłeś przez to w 7 klasie. W przestrzeni równanie prostej wygląda tak: załóżmy, że mamy dwa punkty o współrzędnych: , wtedy równanie przechodzącej przez nie prostej ma postać:

Na przykład linia przechodzi przez punkty:

Jak należy to rozumieć? Należy przez to rozumieć: punkt leży na prostej, jeśli jego współrzędne spełniają układ:

Nie będziemy zbytnio zainteresowani równaniem prostej, ale musimy zwrócić uwagę na bardzo ważną koncepcję wektora kierunkowego prostej. - dowolny niezerowy wektor leżący na danej linii lub równolegle do niej.

Na przykład oba wektory są wektorami kierunku linii prostej. Niech będzie punktem leżącym na linii prostej i będzie jego wektorem kierunkowym. Wtedy równanie prostej można zapisać w postaci:

Po raz kolejny nie będę się zbytnio interesował równaniem linii prostej, ale naprawdę muszę pamiętać, czym jest wektor kierunku! Jeszcze raz: jest to KAŻDY niezerowy wektor leżący na linii lub równolegle do niej.

Wycofać trzypunktowe równanie płaszczyzny nie jest już taka trywialna i zwykle nie jest objęta kursem w szkole średniej. Ale na próżno! Ta technika jest niezbędna, gdy do rozwiązywania złożonych problemów uciekamy się do metody współrzędnych. Zakładam jednak, że masz ochotę nauczyć się czegoś nowego? Co więcej, będziesz mógł zaimponować swojemu nauczycielowi na uniwersytecie, gdy okaże się, że już wiesz, jak posługiwać się techniką, którą zwykle uczy się na kursach geometrii analitycznej. Więc zacznijmy.

Równanie płaszczyzny nie różni się zbytnio od równania prostej na płaszczyźnie, a mianowicie ma postać:

niektóre liczby (nie wszystkie równe zeru), ale zmienne, na przykład: itp. Jak widać, równanie płaszczyzny nie różni się zbytnio od równania prostej (funkcja liniowa). Jednak pamiętasz, o czym się z tobą kłóciliśmy? Powiedzieliśmy, że jeśli mamy trzy punkty, które nie leżą na jednej prostej, to równanie płaszczyzny jest z nich jednoznacznie przywracane. Ale jak? Spróbuję ci to wyjaśnić.

Ponieważ równanie płaszczyzny to:

A punkty należą do tej płaszczyzny, to podstawiając współrzędne każdego punktu do równania płaszczyzny, powinniśmy uzyskać poprawną tożsamość:

Tak więc istnieje potrzeba rozwiązania trzech równań już z niewiadomymi! Dylemat! Jednak zawsze możemy tak założyć (w tym celu musimy podzielić przez). W ten sposób otrzymujemy trzy równania z trzema niewiadomymi:

Nie rozwiążemy jednak takiego systemu, tylko wypiszemy zagadkowe wyrażenie, które z niego wynika:

Równanie płaszczyzny przechodzącej przez trzy podane punkty

\[\lewo| (\begin(tablica)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(tablica)) \right| = 0\]

Zatrzymać! Co to jeszcze jest? Jakiś bardzo nietypowy moduł! Jednak obiekt, który widzisz przed sobą, nie ma nic wspólnego z modułem. Obiekt ten nazywany jest wyznacznikiem trzeciego rzędu. Odtąd, kiedy będziesz miał do czynienia z metodą współrzędnych na samolocie, często natkniesz się na te właśnie wyznaczniki. Co to jest wyznacznik trzeciego rzędu? Co dziwne, to tylko liczba. Pozostaje zrozumieć, jaką konkretną liczbę porównamy z wyznacznikiem.

Napiszmy najpierw wyznacznik trzeciego rzędu w bardziej ogólnej formie:

Gdzie są jakieś liczby. Ponadto przez pierwszy indeks rozumiemy numer wiersza, a przez indeks numer kolumny. Na przykład oznacza to, że podana liczba znajduje się na przecięciu drugiego rzędu i trzeciej kolumny. Zadajmy pytanie: jak dokładnie wyliczymy taki wyznacznik? To znaczy, z jaką konkretną liczbą będziemy ją porównywać? Dla wyznacznika dokładnie trzeciego rzędu istnieje heurystyczna (wizualna) reguła trójkąta, która wygląda tak:

Iloczyn elementów głównej przekątnej (od lewego górnego rogu do prawego dolnego) iloczynu elementów tworzących pierwszy trójkąt „prostopadły” do głównej przekątnej iloczynu elementów tworzących drugi trójkąt „prostopadle” do głównej przekątna
Iloczyn elementów przekątnej drugorzędnej (od prawego górnego do lewego dolnego) iloczynu elementów tworzących pierwszy trójkąt „prostopadły” do przekątnej drugorzędnej iloczynu elementów tworzących drugi trójkąt „prostopadle” do druga przekątna
Wtedy wyznacznik jest równy różnicy między wartościami uzyskanymi na etapie a

Jeśli zapiszemy to wszystko liczbami, otrzymamy następujące wyrażenie:

Nie musisz jednak zapamiętywać metody obliczania w tej formie, wystarczy po prostu trzymać trójkąty w głowie i samą ideę, co jest dodawane do czego, a co następnie od czego odejmowane).

Zilustrujmy metodę trójkątów na przykładzie:

1. Oblicz wyznacznik:

Zastanówmy się, co dodajemy, a co odejmujemy:

Warunki, które są oznaczone „plusem”:

To jest główna przekątna: iloczyn elementów wynosi

Pierwszy trójkąt „prostopadle do głównej przekątnej: iloczyn elementów wynosi

Drugi trójkąt „prostopadle do głównej przekątnej: iloczyn elementów wynosi

Dodajemy trzy liczby:

Terminy z „minusem”

To jest przekątna boczna: iloczyn elementów wynosi

Pierwszy trójkąt „prostopadle do przekątnej wtórnej: iloczyn elementów wynosi

Drugi trójkąt „prostopadle do przekątnej wtórnej: iloczyn elementów wynosi

Dodajemy trzy liczby:

Pozostaje tylko odjąć od sumy składników plus sumę składników minus:

W ten sposób,

Jak widać, w obliczaniu wyznaczników trzeciego rzędu nie ma nic skomplikowanego i nadprzyrodzonego. Po prostu ważne jest, aby pamiętać o trójkątach i nie popełniać błędów arytmetycznych. Teraz spróbuj sam policzyć:

Sprawdzamy:

Pierwszy trójkąt prostopadły do głównej przekątnej:
Drugi trójkąt prostopadły do głównej przekątnej:
Suma warunków plus:
Pierwszy trójkąt prostopadły do bocznej przekątnej:
Drugi trójkąt prostopadły do bocznej przekątnej:
Suma terminów z minusem:
Suma składników plus minus suma składników minus:

Oto jeszcze kilka wyznaczników dla Ciebie, sam oblicz ich wartości i porównaj z odpowiedziami:

Odpowiedzi:

Cóż, czy wszystko się zgadzało? Świetnie, możesz iść dalej! Jeśli są trudności, moja rada jest taka: w Internecie jest kilka programów do obliczania wyznacznika online. Wystarczy wymyślić własny wyznacznik, samemu go obliczyć, a następnie porównać z tym, co wylicza program. I tak dalej, aż wyniki zaczną się zgadzać. Jestem pewien, że ten moment nie potrwa długo!

Wróćmy teraz do wyznacznika, który napisałem, mówiąc o równaniu płaszczyzny przechodzącej przez trzy dane punkty:

Wystarczy bezpośrednio obliczyć jego wartość (metodą trójkątów) i ustawić wynik na zero. Oczywiście, ponieważ są to zmienne, otrzymasz wyrażenie zależne od nich. To właśnie to wyrażenie będzie równaniem płaszczyzny przechodzącej przez trzy dane punkty, które nie leżą na jednej linii prostej!

Zilustrujmy to prostym przykładem:

1. Skonstruuj równanie płaszczyzny przechodzącej przez punkty

Tworzymy wyznacznik dla tych trzech punktów:

Upraszczanie:

Teraz obliczamy to bezpośrednio zgodnie z zasadą trójkątów:

\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ right| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]

Zatem równanie płaszczyzny przechodzącej przez punkty to:

Teraz spróbuj samodzielnie rozwiązać jeden problem, a następnie omówimy go:

2. Znajdź równanie płaszczyzny przechodzącej przez punkty

Omówmy teraz rozwiązanie:

Wykonujemy wyznacznik:

I oblicz jego wartość:

Wtedy równanie płaszczyzny ma postać:

Albo redukując przez, otrzymujemy:

Teraz dwa zadania do samokontroli:

Skonstruuj równanie płaszczyzny przechodzącej przez trzy punkty:

Odpowiedzi:

Czy wszystko się zgadzało? Ponownie, jeśli są pewne trudności, to moja rada jest taka: bierzesz z głowy trzy punkty (z dużym prawdopodobieństwem nie będą leżeć na jednej prostej), budujesz na nich samolot. A potem sprawdź się online. Na przykład na stronie:

Jednak za pomocą wyznaczników zbudujemy nie tylko równanie płaszczyzny. Pamiętaj, powiedziałem ci, że dla wektorów definiowany jest nie tylko iloczyn skalarny. Istnieje również wektor, a także produkt mieszany. A jeśli iloczyn skalarny dwóch wektorów będzie liczbą, to iloczyn wektorowy dwóch wektorów będzie wektorem, a ten wektor będzie prostopadły do podanych:

Co więcej, jego moduł będzie równy powierzchni równoległoboku zbudowanego na wektorach i. Będziemy potrzebować tego wektora do obliczenia odległości od punktu do prostej. Jak obliczyć iloczyn poprzeczny wektorów i czy podano ich współrzędne? Znowu z pomocą przychodzi nam wyznacznik trzeciego porządku. Zanim jednak przejdę do algorytmu obliczania iloczynu krzyżowego, muszę zrobić małą dygresję liryczną.

Ta dygresja dotyczy wektorów bazowych.

Schematycznie pokazano je na rysunku:

Jak myślisz, dlaczego nazywa się je podstawowymi? Fakt jest taki :

Lub na zdjęciu:

Trafność tej formuły jest oczywista, ponieważ:

produkt wektorowy

Teraz mogę zacząć wprowadzać produkt krzyżowy:

Iloczyn wektorowy dwóch wektorów to wektor obliczany zgodnie z następującą zasadą:

Podajmy teraz kilka przykładów obliczania iloczynu krzyżowego:

Przykład 1: Znajdź iloczyn krzyżowy wektorów:

Rozwiązanie: Dokonuję wyznacznika:

I obliczam to:

Teraz, od pisania przez wektory bazowe, powrócę do zwykłej notacji wektorowej:

W ten sposób:

Spróbuj teraz.

Gotowy? Sprawdzamy:

I tradycyjnie dwa zadania do kontroli:

Znajdź iloczyn krzyżowy następujących wektorów:
Znajdź iloczyn krzyżowy następujących wektorów:

Odpowiedzi:

Produkt mieszany trzech wektorów

Ostatnią potrzebną mi konstrukcją jest iloczyn mieszany trzech wektorów. Podobnie jak skalar, jest liczbą. Można to obliczyć na dwa sposoby. - przez wyznacznik, - przez mieszany produkt.

Mianowicie załóżmy, że mamy trzy wektory:

Następnie mieszany iloczyn trzech wektorów, oznaczony jako, można obliczyć jako:

1. - czyli iloczyn mieszany jest iloczynem skalarnym wektora i iloczynem wektorowym dwóch innych wektorów

Na przykład mieszany produkt trzech wektorów to:

Spróbuj sam to obliczyć za pomocą iloczynu wektorowego i upewnij się, że wyniki się zgadzają!

I znowu - dwa przykłady na samodzielną decyzję:

Odpowiedzi:

Wybór układu współrzędnych

Cóż, teraz mamy wszystkie niezbędne podstawy wiedzy do rozwiązywania złożonych problemów stereometrycznych w geometrii. Jednak zanim przejdziemy bezpośrednio do przykładów i algorytmów ich rozwiązywania, uważam, że warto zastanowić się nad pytaniem: jak dokładnie wybierz układ współrzędnych dla konkretnej figury. W końcu to wybór względnego położenia układu współrzędnych i figury w przestrzeni ostatecznie określi, jak uciążliwe będą obliczenia.

Przypominam, że w tej sekcji rozważamy następujące liczby:

prostopadłościan
Pryzmat prosty (trójkątny, sześciokątny…)
Piramida (trójkątna, czworokątna)
Czworościan (taki sam jak trójkątna piramida)

Do prostopadłościanu lub sześcianu polecam następującą konstrukcję:

Oznacza to, że umieszczę figurę „w rogu”. Kostka i pudełko to bardzo dobre figury. Dla nich zawsze możesz łatwo znaleźć współrzędne jego wierzchołków. Na przykład, jeśli (jak pokazano na rysunku)

wtedy współrzędne wierzchołków to:

Oczywiście nie musisz o tym pamiętać, ale pamiętanie, jak najlepiej ustawić sześcian lub prostokątne pudełko, jest pożądane.

prosty pryzmat

Pryzmat jest postacią bardziej szkodliwą. Możesz go zaaranżować w przestrzeni na różne sposoby. Myślę jednak, że najlepszą opcją jest:

Trójkątny pryzmat:

Oznacza to, że umieszczamy jeden z boków trójkąta całkowicie na osi, a jeden z wierzchołków pokrywa się z początkiem.

Pryzmat sześciokątny:

Oznacza to, że jeden z wierzchołków pokrywa się z początkiem, a jeden z boków leży na osi.

Piramida czworokątna i sześciokątna:

Sytuacja podobna do sześcianu: łączymy dwa boki podstawy z osiami współrzędnych, jeden z wierzchołków łączymy z początkiem. Jedyną małą trudnością będzie obliczenie współrzędnych punktu.

Dla heksagonalnej piramidy - tak samo jak dla heksagonalnego graniastosłupa. Głównym zadaniem ponownie będzie znalezienie współrzędnych wierzchołka.

Czworościan (trójkątna piramida)

Sytuacja jest bardzo podobna do tej, którą podałem dla trójkątnego graniastosłupa: jeden wierzchołek pokrywa się z początkiem, jeden bok leży na osi współrzędnych.

Cóż, teraz ty i ja jesteśmy wreszcie blisko rozpoczęcia rozwiązywania problemów. Z tego, co powiedziałem na samym początku artykułu, można wyciągnąć następujący wniosek: większość problemów C2 można podzielić na 2 kategorie: problemy dotyczące kąta i problemy dotyczące odległości. Najpierw rozważymy problemy ze znalezieniem kąta. Z kolei dzielą się na następujące kategorie (w miarę wzrostu złożoności):

Problemy ze znalezieniem narożników

Znajdowanie kąta między dwiema liniami
Znajdowanie kąta między dwiema płaszczyznami

Rozważmy te problemy po kolei: zacznijmy od znalezienia kąta między dwiema liniami prostymi. Daj spokój, pamiętaj, czy ty i ja rozwiązywaliśmy już podobne przykłady? Pamiętasz, bo już mieliśmy coś podobnego... Szukaliśmy kąta między dwoma wektorami. Przypominam, jeśli dane są dwa wektory: a, to kąt między nimi znajduje się z relacji:

Teraz mamy cel - znalezienie kąta między dwiema liniami prostymi. Przejdźmy do „płaskiego obrazu”:

Ile kątów otrzymujemy, gdy przecinają się dwie linie? Już rzeczy. To prawda, że tylko dwa z nich nie są równe, podczas gdy inne są względem nich pionowe (a zatem pokrywają się z nimi). Więc jaki kąt powinniśmy wziąć pod uwagę jako kąt między dwiema liniami prostymi: lub? Tutaj zasada brzmi: kąt między dwiema liniami prostymi zawsze nie przekracza stopni. Oznacza to, że z dwóch kątów zawsze wybierzemy kąt o najmniejszym stopniu. Oznacza to, że na tym zdjęciu kąt między dwiema liniami jest równy. Aby nie zawracać sobie głowy znajdowaniem za każdym razem najmniejszego z dwóch kątów, sprytni matematycy zaproponowali skorzystanie z modułu. Zatem kąt między dwiema liniami prostymi jest określony wzorem:

Jako uważny czytelnik powinien był zadać sobie pytanie: skąd właściwie bierzemy te liczby, których potrzebujemy do obliczenia cosinusa kąta? Odpowiedź: weźmiemy je z wektorów kierunkowych linii! Tak więc algorytm znajdowania kąta między dwiema liniami jest następujący:

Stosujemy formułę 1.

Lub bardziej szczegółowo:

Szukamy współrzędnych wektora kierunkowego pierwszej prostej
Szukamy współrzędnych wektora kierunkowego drugiej linii
Oblicz moduł ich iloczynu skalarnego
Szukamy długości pierwszego wektora
Szukamy długości drugiego wektora
Pomnóż wyniki z punktu 4 przez wyniki z punktu 5
Wynik z punktu 3 dzielimy przez wynik z punktu 6. Otrzymujemy cosinus kąta między prostymi
Jeśli ten wynik pozwala nam dokładnie obliczyć kąt, szukamy go
W przeciwnym razie piszemy przez arcus cosinus

Cóż, teraz pora przejść do zadań: zademonstruję szczegółowo rozwiązanie dwóch pierwszych, krótko przedstawię rozwiązanie drugiego, a odpowiedzi podam tylko w dwóch ostatnich zadaniach, musisz zrób dla nich wszystkie obliczenia.

Zadania:

1. W prawym tet-ra-ed-re znajdź-di-te kąt między tobą-tak-te-ra-ed-ra a stroną me-di-a-noy bo-ko-jak.

2. W prawym do przodu six-coal-pi-ra-mi-de sto-ro-na-os-no-va-niya są w jakiś sposób równe, a boczne żebra są równe, znajdź kąt między prostą linie i.

3. Długości wszystkich krawędzi prawoskrzydłowych czterech-ty-rech-węgla-noy pi-ra-mi-dy są sobie równe. Znajdź-di-kąt między liniami prostymi i jeśli od-re-zok - ty-tak-tam, biorąc pod uwagę pi-ra-mi-dy, punkt to se-re-di-na jej bo-ko-th żebrze

4. Na krawędzi sześcianu od-me-che-do punktu, tak aby Znajdź-di-te kąt między liniami prostymi i

5. Punkt - se-re-di-na krawędziach sześcianu Nai-di-te kąt między liniami prostymi i.

To nie przypadek, że ułożyłem zadania w takiej kolejności. Chociaż nie miałeś jeszcze czasu, aby zacząć nawigować metodą współrzędnych, ja sam przeanalizuję najbardziej „problematyczne” liczby i zostawię ci najprostszą kostkę! Stopniowo musisz nauczyć się pracować ze wszystkimi figurami, będę zwiększał złożoność zadań z tematu na temat.

Zacznijmy rozwiązywać problemy:

1. Narysuj czworościan, umieść go w układzie współrzędnych, jak sugerowałem wcześniej. Ponieważ czworościan jest regularny, wszystkie jego powierzchnie (w tym podstawa) są regularnymi trójkątami. Ponieważ nie podano nam długości boku, mogę przyjąć ją równą. Myślę, że rozumiesz, że kąt tak naprawdę nie będzie zależał od tego, jak bardzo nasz czworościan będzie „rozciągnięty”?. Narysuję również wysokość i medianę w czworościanie. Po drodze narysuję jego podstawę (przyda się też nam).

Muszę znaleźć kąt między a. Co wiemy? Znamy tylko współrzędne punktu. Musimy więc znaleźć więcej współrzędnych punktów. Teraz myślimy: punkt jest punktem przecięcia wysokości (lub dwusiecznych lub środkowych) trójkąta. Kropka to podwyższony punkt. Punkt jest środkiem segmentu. W końcu musimy znaleźć: współrzędne punktów: .

Zacznijmy od najprostszego: współrzędnych punktu. Spójrz na rysunek: Widać wyraźnie, że przyłożenie punktu jest równe zeru (punkt leży na płaszczyźnie). Jego rzędna jest równa (ponieważ jest to mediana). Trudniej jest znaleźć jego odciętą. Można to jednak łatwo zrobić na podstawie twierdzenia Pitagorasa: Rozważ trójkąt. Jej przeciwprostokątna jest równa, a jedna z nóg jest równa Wtedy:

Wreszcie mamy:

Teraz znajdźmy współrzędne punktu. Jest jasne, że jego zastosowanie jest znowu równe zeru, a jego rzędna jest taka sama jak punktu. Znajdźmy jego odciętą. Robi się to dość trywialnie, jeśli się o tym pamięta wysokości trójkąta równobocznego są podzielone przez punkt przecięcia w proporcji licząc od góry. Ponieważ:, to pożądana odcięta punktu, równa długości odcinka, jest równa:. Zatem współrzędne punktu to:

Znajdźmy współrzędne punktu. Oczywiste jest, że jego odcięta i rzędna pokrywają się z odciętą i rzędną punktu. A aplikacja jest równa długości segmentu. - to jedna z nóg trójkąta. Przeciwprostokątna trójkąta to segment - noga. Jest wyszukiwana z powodów, które zaznaczyłem pogrubioną czcionką:

Punkt jest środkiem segmentu. Następnie musimy zapamiętać wzór na współrzędne środka odcinka:

To wszystko, teraz możemy poszukać współrzędnych wektorów kierunkowych:

Cóż, wszystko gotowe: podstawiamy wszystkie dane do formuły:

W ten sposób,

Odpowiedź:

Nie należy bać się takich „strasznych” odpowiedzi: w przypadku problemów C2 jest to powszechna praktyka. Raczej byłbym zaskoczony „piękną” odpowiedzią w tej części. Ponadto, jak zauważyłeś, praktycznie nie uciekałem się do niczego innego niż twierdzenie Pitagorasa i własność wysokości trójkąta równobocznego. To znaczy, aby rozwiązać problem stereometryczny, użyłem minimum stereometrii. Zysk w tym jest częściowo „wygaszony” przez dość kłopotliwe obliczenia. Ale są dość algorytmiczne!

2. Narysuj regularną sześciokątną piramidę wraz z układem współrzędnych oraz jej podstawą:

Musimy znaleźć kąt między liniami i. Zatem nasze zadanie sprowadza się do znalezienia współrzędnych punktów: . Znajdziemy współrzędne ostatnich trzech z małego rysunku, a współrzędną wierzchołka znajdziemy poprzez współrzędną punktu. Dużo pracy, ale muszę zacząć!

a) Współrzędna: jasne jest, że jej aplikacja i rzędna wynoszą zero. Znajdźmy odciętą. Aby to zrobić, rozważ trójkąt prostokątny. Niestety, znamy w nim tylko przeciwprostokątną, która jest równa. Spróbujemy znaleźć nogę (ponieważ jasne jest, że dwukrotna długość nogi da nam odciętą punktu). Jak możemy tego szukać? Pamiętajmy, jaką figurę mamy u podstawy piramidy? To jest foremny sześciokąt. Co to znaczy? Oznacza to, że wszystkie boki i wszystkie kąty są równe. Musimy znaleźć jeden taki zakątek. Jakieś pomysły? Pomysłów jest dużo, ale jest formuła:

Suma kątów regularnego n-kąta wynosi .

Zatem suma kątów sześciokąta foremnego to stopnie. Wtedy każdy z kątów jest równy:

Spójrzmy jeszcze raz na zdjęcie. Oczywiste jest, że segment jest dwusieczną kąta. Wtedy kąt to stopnie. Następnie:

Więc gdzie.

Więc ma współrzędne

b) Teraz możemy łatwo znaleźć współrzędne punktu: .

c) Znajdź współrzędne punktu. Ponieważ jego odcięta pokrywa się z długością segmentu, jest równa. Znalezienie rzędnej również nie jest bardzo trudne: jeśli połączymy punkty i oznaczymy punkt przecięcia prostej, powiedzmy. (zrób to sam, prosta konstrukcja). Zatem rzędna punktu B jest równa sumie długości odcinków. Spójrzmy ponownie na trójkąt. Następnie

Wtedy od Wtedy punkt ma współrzędne

d) Teraz znajdź współrzędne punktu. Rozważ prostokąt i udowodnij, że Tak więc współrzędne punktu to:

e) Pozostaje znaleźć współrzędne wierzchołka. Oczywiste jest, że jego odcięta i rzędna pokrywają się z odciętą i rzędną punktu. Znajdźmy aplikację. Od tego czasu. Rozważmy trójkąt prostokątny. Według stanu problemu, boczna krawędź. To jest przeciwprostokątna mojego trójkąta. Wtedy wysokość piramidy to noga.

Wtedy punkt ma współrzędne:

To wszystko, mam współrzędne wszystkich interesujących mnie punktów. Poszukuję współrzędnych wektorów kierunkowych linii prostych:

Szukamy kąta między tymi wektorami:

Odpowiedź:

Znowu przy rozwiązywaniu tego problemu nie zastosowałem żadnych wyrafinowanych sztuczek, z wyjątkiem wzoru na sumę kątów n-kąta foremnego oraz definicji cosinusa i sinusa trójkąta prostokątnego.

3. Ponieważ znowu nie podano nam długości krawędzi w piramidzie, uznam je za równe jeden. Tak więc, ponieważ WSZYSTKIE krawędzie, a nie tylko boczne, są sobie równe, to u podstawy piramidy i ja leży kwadrat, a ściany boczne są regularnymi trójkątami. Narysujmy taką piramidę, a także jej podstawę na płaszczyźnie, zaznaczając wszystkie dane podane w tekście zadania:

Szukamy kąta między a. Dokonuję bardzo krótkich obliczeń, gdy będę szukał współrzędnych punktów. Będziesz musiał je „odszyfrować”:

b) - środek segmentu. Jej współrzędne:

c) Znajdę długość odcinka korzystając z twierdzenia Pitagorasa w trójkącie. Znajdę według twierdzenia Pitagorasa w trójkącie.

Współrzędne:

d) - środek segmentu. Jego współrzędne to

e) Współrzędne wektorowe

f) Współrzędne wektorowe

g) Szukam kąta:

Kostka to najprostsza figura. Jestem pewien, że sam sobie z tym poradzisz. Odpowiedzi na problemy 4 i 5 są następujące:

Znajdowanie kąta między linią a płaszczyzną

Cóż, czas na proste łamigłówki się skończył! Teraz przykłady będą jeszcze trudniejsze. Aby znaleźć kąt między linią a płaszczyzną, postępujemy następująco:

Używając trzech punktów, budujemy równanie płaszczyzny
,
za pomocą wyznacznika trzeciego rzędu.
Przez dwa punkty szukamy współrzędnych wektora kierunkowego prostej:
Stosujemy wzór do obliczenia kąta między linią prostą a płaszczyzną:

Jak widać, ten wzór jest bardzo podobny do tego, którego użyliśmy do znalezienia kątów między dwiema liniami. Struktura prawej strony jest taka sama, a po lewej szukamy teraz sinusa, a nie cosinusa, jak poprzednio. Cóż, dodano jedną paskudną akcję - poszukiwanie równania samolotu.

Nie odkładajmy rozwiązywanie przykładów:

1. Os-no-va-ni-em prosto-moja nagroda-jesteśmy-la-et-xia równy-ale-biedny-ren-ny trójkąt-zdobądź-z-tą nagrodą-jesteśmy równi. Znajdź kąt między linią prostą a płaszczyzną

2. W prostokątnym pa-ral-le-le-pi-pe-de z zachodniego Nai-di-te kąt między linią prostą a płaszczyzną

3. W prawoskrętnym sześciowęglowym pryzmacie wszystkie krawędzie są równe. Znajdź kąt między linią prostą a płaszczyzną.

4. W prawym trójkątnym pi-ra-mi-de z os-but-va-ni-em od zachodu żebra kąt Nai-di-te, ob-ra-zo-van -ny płaszczyzna os -no-va-niya i prosto-my, przechodząc przez se-re-di-na żeber i

5. Długości wszystkich krawędzi prawego czworokątnego pi-ra-mi-dy z wierzchołkiem są sobie równe. Znajdź kąt między linią prostą a płaszczyzną, jeśli punkt jest se-re-di-na bo-ko-in-tej krawędzi pi-ra-mi-dy.

Znowu dwa pierwsze problemy rozwiążę szczegółowo, trzeci krótko, a dwa ostatnie pozostawiam do samodzielnego rozwiązania. Ponadto miałeś już do czynienia z piramidami trójkątnymi i czworokątnymi, ale jeszcze nie z pryzmatami.

Rozwiązania:

1. Narysuj pryzmat oraz jego podstawę. Połączmy to z układem współrzędnych i zaznaczmy wszystkie dane, które są podane w opisie problemu:

Przepraszam za pewne nieprzestrzeganie proporcji, ale dla rozwiązania problemu to w rzeczywistości nie jest tak ważne. Samolot to tylko „tylna ściana” mojego pryzmatu. Wystarczy zgadnąć, że równanie takiej płaszczyzny ma postać:

Można to jednak również pokazać bezpośrednio:

Wybieramy dowolne trzy punkty na tej płaszczyźnie: na przykład .

Zróbmy równanie samolotu:

Ćwiczenie dla Ciebie: sam oblicz ten wyznacznik. Udało Ci się? Wtedy równanie płaszczyzny ma postać:

Lub po prostu

W ten sposób,

Aby rozwiązać ten przykład, muszę znaleźć współrzędne wektora kierującego prostej. Ponieważ punkt pokrywał się z początkiem, współrzędne wektora po prostu pokrywają się ze współrzędnymi punktu.Aby to zrobić, najpierw znajdujemy współrzędne punktu.

Aby to zrobić, rozważ trójkąt. Narysujmy wysokość (jest to również mediana i dwusieczna) od góry. Ponieważ wtedy rzędna punktu jest równa. Aby znaleźć odciętą tego punktu, musimy obliczyć długość odcinka. Z twierdzenia Pitagorasa mamy:

Wtedy punkt ma współrzędne:

Kropka to „podwyższona” kropka:

Następnie współrzędne wektora:

Odpowiedź:

Jak widać, w rozwiązaniu takich problemów nie ma nic fundamentalnie trudnego. W rzeczywistości „prostość” figury, takiej jak pryzmat, upraszcza nieco ten proces. Przejdźmy teraz do następnego przykładu:

2. Rysujemy równoległościan, rysujemy w nim płaszczyznę i linię prostą, a także osobno rysujemy jego dolną podstawę:

Najpierw znajdujemy równanie płaszczyzny: współrzędne trzech leżących w niej punktów:

(pierwsze dwie współrzędne są uzyskiwane w sposób oczywisty, a ostatnią współrzędną z obrazka można łatwo znaleźć z punktu). Następnie układamy równanie płaszczyzny:

Obliczamy:

Szukamy współrzędnych wektora kierunku: jasne jest, że jego współrzędne pokrywają się ze współrzędnymi punktu, prawda? Jak znaleźć współrzędne? Są to współrzędne punktu podniesione o jeden wzdłuż osi aplikacji! . Następnie szukamy pożądanego kąta:

Odpowiedź:

3. Narysuj regularną sześciokątną piramidę, a następnie narysuj w niej płaszczyznę i linię prostą.

Tutaj nawet problematyczne jest narysowanie samolotu, nie wspominając o rozwiązaniu tego problemu, ale metoda współrzędnych nie obchodzi! To w jego wszechstronności leży jego główna zaleta!

Samolot przechodzi przez trzy punkty: . Szukamy ich współrzędnych:

jeden) . Samodzielnie wyświetl współrzędne dwóch ostatnich punktów. W tym celu będziesz musiał rozwiązać problem za pomocą sześciokątnej piramidy!

2) Budujemy równanie samolotu:

Szukamy współrzędnych wektora: . (Znowu zobacz problem piramidy trójkątnej!)

3) Szukamy kąta:

Odpowiedź:

Jak widać, w tych zadaniach nie ma nic nadnaturalnie trudnego. Musisz tylko bardzo uważać na korzenie. Na dwa ostatnie problemy podam tylko odpowiedzi:

Jak widać, technika rozwiązywania problemów jest wszędzie taka sama: głównym zadaniem jest znalezienie współrzędnych wierzchołków i zastąpienie ich niektórymi formułami. Pozostaje nam rozważyć jeszcze jedną klasę problemów do obliczania kątów, a mianowicie:

Obliczanie kątów między dwiema płaszczyznami

Algorytm rozwiązania będzie następujący:

Dla trzech punktów szukamy równania pierwszej płaszczyzny:
Dla pozostałych trzech punktów szukamy równania drugiej płaszczyzny:
Stosujemy formułę:

Jak widać, wzór jest bardzo podobny do dwóch poprzednich, za pomocą których szukaliśmy kątów między liniami prostymi oraz między linią prostą a płaszczyzną. Więc zapamiętanie tego nie będzie dla ciebie trudne. Przejdźmy od razu do problemu:

1. Sto ro-na podstawie prawego trójkątnego graniastosłupa jest równa, a przekątna ściany bocznej jest równa. Znajdź kąt między płaszczyzną a płaszczyzną podstawy nagrody.

2. W prawym do przodu four-you-re-coal-noy pi-ra-mi-de wszystkie krawędzie kogoś są równe, znajdź sinus kąta między samolotem a samolotem Ko-Stu, przechodzącym punkt per-pen-di-ku-lyar-ale prosto-my.

3. W zwykłym pryzmacie czterowęglowym boki os-no-va-nia są równe, a krawędzie boczne są równe. Na krawędzi od-mnie-che-do rzeczy tak. Znajdź kąt między płaszczyznami i

4. W prawym czworokątnym pryzmacie boki podstaw są równe, a krawędzie boczne są równe. Na krawędzi od-mnie-che-do punktu, tak aby Znajdź kąt między płaszczyznami i.

5. W sześcianie znajdź co-si-nus kąta między płaszczyznami i

Rozwiązania problemów:

1. Rysuję regularny (u podstawy - trójkąt równoboczny) trójkątny graniastosłup i zaznaczam na nim płaszczyzny, które pojawiają się w stanie zadania:

Musimy znaleźć równania dwóch płaszczyzn: Równanie bazowe otrzymuje się banalnie: możesz zrobić odpowiedni wyznacznik dla trzech punktów, ale od razu zrobię równanie:

Teraz znajdźmy równanie Punkt ma współrzędne Punkt - Ponieważ - mediana i wysokość trójkąta, łatwo jest znaleźć za pomocą twierdzenia Pitagorasa w trójkącie. Wtedy punkt ma współrzędne: Znajdź aplikację punktu Aby to zrobić, rozważ trójkąt prostokątny

Następnie otrzymujemy następujące współrzędne: Układamy równanie płaszczyzny.

Obliczamy kąt między płaszczyznami:

Odpowiedź:

2. Wykonanie rysunku:

Najtrudniej jest zrozumieć, co to za tajemnicza płaszczyzna, przechodząca przez punkt prostopadle. Cóż, najważniejsze jest to, co to jest? Najważniejsze jest uważność! Rzeczywiście, linia jest prostopadła. Linia jest również prostopadła. Wtedy płaszczyzna przechodząca przez te dwie linie będzie prostopadła do prostej, a przy okazji będzie przechodzić przez punkt. Ta płaszczyzna przechodzi również przez szczyt piramidy. Potem pożądany samolot - A samolot jest już nam dany. Poszukujemy współrzędnych punktów.

Znajdujemy współrzędną punktu przez punkt. Z małego rysunku łatwo wywnioskować, że współrzędne punktu będą wyglądały następująco: Co pozostało do znalezienia, aby znaleźć współrzędne wierzchołka piramidy? Nadal trzeba obliczyć jego wysokość. Odbywa się to za pomocą tego samego twierdzenia Pitagorasa: najpierw udowodnij to (trywialnie z małych trójkątów tworzących kwadrat u podstawy). Ponieważ pod warunkiem mamy:

Teraz wszystko gotowe: współrzędne wierzchołków:

Układamy równanie samolotu:

Jesteś już ekspertem w obliczaniu wyznaczników. Z łatwością otrzymasz:

Lub inaczej (jeśli obie części pomnożymy przez pierwiastek z dwójki)

Teraz znajdźmy równanie samolotu:

(Nie zapomniałeś, jak otrzymujemy równanie samolotu, prawda? Jeśli nie rozumiesz, skąd się wzięło to minus jeden, wróć do definicji równania samolotu! Po prostu zawsze okazywało się, że mój samolot należał do pochodzenia!)

Obliczamy wyznacznik:

(Możesz zauważyć, że równanie płaszczyzny pokrywało się z równaniem prostej przechodzącej przez punkty i! Pomyśl dlaczego!)

Teraz obliczamy kąt:

Musimy znaleźć sinus:

Odpowiedź:

3. Podchwytliwe pytanie: co to jest pryzmat prostokątny, co myślisz? Dla ciebie to tylko dobrze znany równoległościan! Rysowanie od razu! Nie możesz nawet osobno przedstawić podstawy, tutaj nie ma z niej większego pożytku:

Płaszczyzna, jak zauważyliśmy wcześniej, jest zapisana jako równanie:

Teraz robimy samolot

Natychmiast układamy równanie samolotu:

Szukasz kąta

Teraz odpowiedzi na dwa ostatnie problemy:

Cóż, teraz jest czas na przerwę, ponieważ ty i ja jesteśmy wspaniali i wykonaliśmy świetną robotę!

Współrzędne i wektory. Poziom zaawansowany

W tym artykule omówimy z Tobą inną klasę problemów, które można rozwiązać za pomocą metody współrzędnych: problemy odległościowe. Mianowicie rozważymy następujące przypadki:

Obliczanie odległości między liniami skośnymi.

Porządkowałem dane zadania wraz ze wzrostem ich złożoności. Najłatwiej jest znaleźć odległość od punktu do płaszczyzny a najtrudniejsze jest znalezienie odległość między przecinającymi się liniami. Chociaż oczywiście nie ma rzeczy niemożliwych! Nie zwlekajmy i od razu przystąpmy do rozważenia pierwszej klasy problemów:

Obliczanie odległości od punktu do płaszczyzny

Czego potrzebujemy, aby rozwiązać ten problem?

1. Współrzędne punktu

Tak więc, gdy tylko zdobędziemy wszystkie niezbędne dane, stosujemy wzór:

Powinieneś już wiedzieć, jak budujemy równanie samolotu z poprzednich problemów, które analizowałem w ostatniej części. Przejdźmy od razu do rzeczy. Schemat jest następujący: 1, 2 - pomogę ci zdecydować, a dokładniej 3, 4 - tylko odpowiedź, sam podejmujesz decyzję i porównujesz. Zaczęło się!

Zadania:

1. Dana kostka. Długość krawędzi sześcianu wynosi Znajdź-di-te odległość od se-re-di-ny od cięcia do płaskiego

2. Biorąc pod uwagę prawe-vil-naya cztery-ty-rekh-węgiel-naya pi-ra-mi-da Bo-ko-voe krawędź sto-ro-na os-no-va-nia jest równa. Znajdź-di-te odległości od punktu do płaszczyzny, gdzie - se-re-di-na krawędziach.

3. W prawym trójkątnym pi-ra-mi-de z os-but-va-ni-em, druga krawędź jest równa, a sto ro-on os-no-vaniya jest równe. Znajdź te odległości od góry do samolotu.

4. W prawoskrętnym sześciowęglowym pryzmacie wszystkie krawędzie są równe. Znajdź te odległości od punktu do płaszczyzny.

Rozwiązania:

1. Narysuj sześcian o pojedynczych krawędziach, zbuduj odcinek i płaszczyznę, oznacz literą środek odcinka

Najpierw zacznijmy od prostego: znajdź współrzędne punktu. Od tego czasu (pamiętaj o współrzędnych środka segmentu!)

Teraz składamy równanie płaszczyzny na trzy punkty

\[\lewo| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]

Teraz mogę zacząć szukać odległości:

2. Zaczynamy od rysunku, na którym zaznaczamy wszystkie dane!

W przypadku piramidy dobrze byłoby narysować jej podstawę osobno.

Nawet to, że rysuję jak łapa kurczaka, nie przeszkodzi nam w łatwym rozwiązaniu tego problemu!

Teraz łatwo jest znaleźć współrzędne punktu

Ponieważ współrzędne punktu

2. Skoro współrzędne punktu a są środkiem odcinka, to

Możemy łatwo znaleźć współrzędne dwóch kolejnych punktów na płaszczyźnie, układamy równanie płaszczyzny i upraszczamy je:

\[\lewo| (\left| (\begin(tablica)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(array)) \right|) \right| = 0\]

Ponieważ punkt ma współrzędne: , obliczamy odległość:

Odpowiedź (bardzo rzadko!):

Cóż, zrozumiałeś? Wydaje mi się, że wszystko tutaj jest tak samo techniczne, jak w przykładach, które rozważaliśmy z tobą w poprzedniej części. Jestem więc pewien, że jeśli opanowałeś ten materiał, to nie będzie Ci trudno rozwiązać pozostałe dwa problemy. Po prostu dam ci odpowiedzi:

Obliczanie odległości od linii do płaszczyzny

W rzeczywistości nie ma tu nic nowego. Jak można ustawić linię i płaszczyznę względem siebie? Mają wszystkie możliwości: przecinają się, czyli linia prosta jest równoległa do płaszczyzny. Jak myślisz, jaka jest odległość od linii do płaszczyzny, z którą przecina się dana linia? Wydaje mi się, że jasne jest, że taka odległość jest równa zeru. Nieciekawy przypadek.

Drugi przypadek jest trudniejszy: tutaj odległość jest już niezerowa. Ponieważ jednak linia jest równoległa do płaszczyzny, każdy punkt linii znajduje się w równej odległości od tej płaszczyzny:

W ten sposób:

A to oznacza, że moje zadanie zostało zredukowane do poprzedniego: szukamy współrzędnych dowolnego punktu na prostej, szukamy równania płaszczyzny, obliczamy odległość od punktu do płaszczyzny. W rzeczywistości takie zadania na egzaminie są niezwykle rzadkie. Udało mi się znaleźć tylko jeden problem, a dane w nim zawarte były takie, że metoda współrzędnych nie miała do niego zastosowania!

Przejdźmy teraz do innej, znacznie ważniejszej klasy problemów:

Obliczanie odległości punktu od linii

Czego będziemy potrzebować?

1. Współrzędne punktu, z którego szukamy odległości:

2. Współrzędne dowolnego punktu leżącego na linii prostej

3. Kierunkowe współrzędne wektora prostej

Jakiej formuły używamy?

Co oznacza dla Ciebie mianownik tego ułamka i dlatego powinno być jasne: jest to długość wektora kierunkowego prostej. Oto bardzo skomplikowany licznik! Wyrażenie oznacza moduł (długość) iloczynu wektorowego wektorów i Jak obliczyć iloczyn wektorowy, omówiliśmy w poprzedniej części pracy. Odśwież swoją wiedzę, teraz nam się przyda!

Zatem algorytm rozwiązywania problemów będzie następujący:

1. Szukamy współrzędnych punktu, z którego szukamy odległości:

2. Szukamy współrzędnych dowolnego punktu na linii, do której szukamy odległości:

3. Budowanie wektora

4. Budujemy wektor kierunkowy prostej

5. Oblicz iloczyn krzyżowy

6. Szukamy długości otrzymanego wektora:

7. Oblicz odległość:

Mamy dużo pracy, a przykłady będą dość złożone! Więc teraz skup całą swoją uwagę!

1. Dana jest praworęcznym trójkątnym pi-ra-mi-da z wierzchołkiem. Sto-ro-na os-no-va-niya pi-ra-mi-dy jest równe, ty-tak-ta jest równe. Znajdź-di-te odległości od se-re-di-ny krawędzi bo-ko-tej do linii prostej, gdzie punkty i są se-re-di-ny żeber i co-from-vet -stven-ale.

2. Długości żeber i kąt prosty-no-para-ral-le-le-pi-pe-da są odpowiednio równe, a odległość Find-di-te od top-shi-ny do straight-my

3. W prawym sześciowęglowym pryzmacie wszystkie krawędzie roju są równe odległości znajdź-d-tych od punktu do linii prostej

Rozwiązania:

1. Wykonujemy zgrabny rysunek, na którym zaznaczamy wszystkie dane:

Mamy dla Ciebie dużo pracy! Na początek chciałbym opisać słowami czego będziemy szukać i w jakiej kolejności:

1. Współrzędne punktów i

2. Współrzędne punktu

3. Współrzędne punktów i

4. Współrzędne wektorów i

5. Ich produkt krzyżowy

6. Długość wektora

7. Długość produktu wektorowego

8. Odległość od do

Cóż, mamy dużo pracy! Podwińmy rękawy!

1. Aby znaleźć współrzędne wysokości piramidy, musimy znać współrzędne punktu, jego zastosowanie wynosi zero, a rzędna jest równa odciętej. Wreszcie otrzymaliśmy współrzędne:

Współrzędne punktu

2. - środek segmentu

3. - środek segmentu

punkt środkowy

4. Współrzędne

Współrzędne wektorowe

5. Oblicz iloczyn wektorowy:

6. Długość wektora: najprościej zamienić, że odcinek jest linią środkową trójkąta, czyli jest równy połowie podstawy. Więc.

7. Rozważamy długość produktu wektorowego:

8. Na koniec znajdź odległość:

Uff, to wszystko! Powiem szczerze: rozwiązanie tego problemu tradycyjnymi metodami (poprzez konstrukcje) byłoby znacznie szybsze. Ale tutaj sprowadziłem wszystko do gotowego algorytmu! Myślę, że algorytm rozwiązania jest dla Ciebie jasny? Dlatego poproszę o samodzielne rozwiązanie pozostałych dwóch problemów. Porównaj odpowiedzi?

Powtarzam: łatwiej (szybciej) rozwiązać te problemy za pomocą konstrukcji, niż uciekać się do metody współrzędnych. Zademonstrowałem ten sposób rozwiązywania tylko po to, by pokazać ci uniwersalną metodę, która pozwala ci „niczego nie uzupełniać”.

Na koniec rozważ ostatnią klasę problemów:

Obliczanie odległości między liniami skośnymi

Tutaj algorytm rozwiązywania problemów będzie podobny do poprzedniego. Co mamy:

3. Dowolny wektor łączący punkty pierwszej i drugiej linii:

Jak znaleźć odległość między liniami?

Formuła to:

Licznikiem jest moduł iloczynu mieszanego (wprowadziliśmy go w poprzedniej części), a mianownikiem - tak jak w poprzednim wzorze (moduł iloczynu wektorowego wektorów kierujących prostych, odległości między którymi patrzymy dla).

Przypomnę ci, że

następnie wzór na odległość można przepisać jako:

Podziel ten wyznacznik przez wyznacznik! Chociaż, szczerze mówiąc, nie mam tu ochoty na żarty! Ta formuła jest w rzeczywistości bardzo kłopotliwa i prowadzi do dość skomplikowanych obliczeń. Na twoim miejscu używałbym tego tylko w ostateczności!

Spróbujmy rozwiązać kilka problemów powyższą metodą:

1. W prawym trójkątnym pryzmacie wszystkie krawędzie są w jakiś sposób równe, znajdź odległość między liniami prostymi i.

2. Biorąc pod uwagę trójkątny pryzmat w kształcie prawego dziobu, wszystkie krawędzie os-no-va-niya kogoś są równe Se-che-tion, przechodząc przez drugie żebro i se-re-di-nu żebra są yav-la-et-sya kwadrat-ra-tom. Find-di-te dis-sto-I-nie między prostymi-we-mi i

Ja decyduję o pierwszym, a na jego podstawie Ty decydujesz o drugim!

1. Rysuję pryzmat i zaznaczam linie i

Współrzędne punktu C: wtedy

Współrzędne punktu

Współrzędne wektorowe

Współrzędne punktu

Współrzędne wektorowe

\[\left((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \right) = \left| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(tablica))\\(\begin(tablica)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(tablica))\end(tablica)) \right| = \frac((\sqrt 3 ))(2)\]

Rozważamy iloczyn krzyżowy między wektorami i

\[\overrightarrow (A(A_1)) \cdot \overrightarrow (B(C_1)) = \left| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(tablica)\end(tablica) \right| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]

Teraz rozważymy jego długość:

Odpowiedź:

Teraz postaraj się dokładnie wykonać drugie zadanie. Odpowiedzią na to będzie:.

Współrzędne i wektory. Krótki opis i podstawowe formuły

Wektor jest segmentem skierowanym. - początek wektora, - koniec wektora.
Wektor jest oznaczony przez lub.

Całkowita wartość wektor - długość odcinka reprezentującego wektor. Oznaczony jako.

Współrzędne wektora:

,
gdzie są końce wektora \displaystyle a .

Suma wektorów: .

Iloczyn wektorów:

Iloczyn skalarny wektorów:

Iloczyn skalarny wektorów jest równy iloczynowi ich wartości bezwzględnych i cosinusa kąta między nimi:

POZOSTAŁE 2/3 ARTYKUŁÓW DOSTĘPNE TYLKO DLA MĄDRYCH UCZNIÓW!

Zostań uczniem YouClever,

Przygotuj się do OGE lub USE w matematyce w cenie „filiżanki kawy miesięcznie”,

A także nieograniczony dostęp do podręcznika „YouClever”, programu szkoleniowego „100gia” (książka rozwiązań), nielimitowanego próbnego USE i OGE, 6000 zadań z analizą rozwiązań i innych usług YouClever i 100gia.

Wektor to wielkość charakteryzująca się wartością liczbową i kierunkiem. Innymi słowy, wektor jest segmentem skierowanym. Pozycja wektor AB w przestrzeni jest określone przez współrzędne punktu początkowego wektor A i punkty końcowe wektor B. Zastanów się, jak określić współrzędne środka wektor.

Instrukcja

Najpierw zdefiniujmy zapis początku i końca wektor. Jeśli wektor jest zapisany jako AB, to punkt A jest początkiem wektor, a punkt B to koniec. Odwrotnie, dla wektor BA punkt B to początek wektor, a punkt A to koniec. Dajmy wektor AB ze współrzędnymi początku wektor A = (a1, a2, a3) i koniec wektor B = (b1, b2, b3). Następnie współrzędne wektor AB będzie wyglądać następująco: AB = (b1 - a1, b2 - a2, b3 - a3), tj. od końca współrzędnej wektor musisz odjąć odpowiednią współrzędną początkową wektor. Długość wektor AB (lub jego moduł) oblicza się jako pierwiastek kwadratowy z sumy kwadratów jego współrzędnych: |AB| = ?((b1 – a1)^2 + (b2 – a2)^2 + (b3 – a3)^2).

Znajdź współrzędne punktu, który jest punktem środkowym wektor. Oznacz to literą O = (o1, o2, o3). Znajdź współrzędne środka wektor analogicznie jak współrzędne środka odcinka regularnego, według wzorów: o1 = (a1 + b1)/2, o2 = (a2 + b2)/2 , o3 = (a3 + b3)/2 . Znajdźmy współrzędne wektor AO: AO = (o1 - a1, o2 - a2, o3 - a3) = ((b1 - a1)/2, (b2 - a2)/2, (b3 - a3)/2).

Rozważ przykład. Niech wektor AB będzie podany ze współrzędnymi początku wektor A = (1, 3, 5) i koniec wektor B = (3, 5, 7). Następnie współrzędne wektor AB można zapisać jako AB = (3 - 1, 5 - 3, 7 - 5) = (2, 2, 2). Znajdźmy moduł wektor AB: |AB| = ?(4 + 4 + 4) = 2 * ?3. Wartość długości określonego wektor pomoże nam dokładniej sprawdzić poprawność współrzędnych środka wektor. Następnie znajdujemy współrzędne punktu O: O = ((1 + 3)/2, (3 + 5)/2, (5 + 7)/2) = (2, 4, 6). Następnie współrzędne wektor AO jest obliczane jako AO = (2 - 1, 4 - 3, 6 - 5) = (1, 1, 1).

Sprawdźmy. Długość wektor AO = ?(1 + 1 + 1) = ?3. Przypomnij sobie, że długość oryginału wektor jest równy 2 * ?3, tj. połowa wektor jest naprawdę równa połowie długości oryginału wektor. Teraz obliczmy współrzędne wektor OB: OB = (3 - 2, 5 - 4, 7 - 6) = (1, 1, 1). Znajdźmy sumę wektorów AO i OB: AO + OB = (1 + 1, 1 + 1, 1 + 1) = (2, 2, 2) = AB. Dlatego współrzędne środka wektor zostały znalezione poprawnie.

Przydatna rada

Po obliczeniu współrzędnych środka wektora koniecznie wykonaj przynajmniej najprostszą kontrolę - oblicz długość wektora i porównaj ją z długością tego wektora.

całkowity:0
W kontakcie z 0
Google Plus 0
ok 0
Facebook 0

Współrzędne środka wektora w przestrzeni. Wektory dla manekinów

Pojęcie wektora. wolny wektor

Akcje z wektorami. Kolinearność wektorów

Zasada dodawania wektorów zgodnie z zasadą trójkątów

Jakie wektory są równe?

Współrzędne wektorowe na płaszczyźnie i w przestrzeni

Najprostsze problemy geometrii analitycznej.Działania z wektorami we współrzędnych

Jak znaleźć wektor mając dwa punkty?

Jak znaleźć długość odcinka?

Jak znaleźć długość wektora?

WSPÓŁRZĘDNE I WEKTORY. POZIOM ŚREDNIOZAAWANSOWANY

Równanie płaszczyzny przechodzącej przez trzy podane punkty

produkt wektorowy

Produkt mieszany trzech wektorów

Wybór układu współrzędnych

prosty pryzmat

Trójkątny pryzmat:

Pryzmat sześciokątny:

Piramida czworokątna i sześciokątna:

Czworościan (trójkątna piramida)

Znajdowanie kąta między linią a płaszczyzną

Obliczanie kątów między dwiema płaszczyznami

Współrzędne i wektory. Poziom zaawansowany

Obliczanie odległości od punktu do płaszczyzny

Obliczanie odległości od linii do płaszczyzny

Obliczanie odległości punktu od linii

Obliczanie odległości między liniami skośnymi

Współrzędne i wektory. Krótki opis i podstawowe formuły

POZOSTAŁE 2/3 ARTYKUŁÓW DOSTĘPNE TYLKO DLA MĄDRYCH UCZNIÓW!

Instrukcja

Najprostsze problemy geometrii analitycznej.
Działania z wektorami we współrzędnych