Siła wypadkowa. Wzór na siłę wypadkową Wypadkowa wszystkich sił działających na ciało

Pierwsze prawo Newtona mówi nam, że w inercjalnych układach odniesienia ciała mogą zmieniać prędkość tylko pod wpływem innych ciał. Za pomocą siły ($\overline(F)$) wyrażają wzajemne działanie ciał na siebie. Siła może zmienić wielkość i kierunek prędkości ciała. $\overline(F)$ jest wielkością wektorową, to znaczy ma moduł (wielkość) i kierunek.

Definicja i wzór wypadkowej wszystkich sił

W dynamice klasycznej główną zasadą wyznaczania kierunku i wielkości siły wypadkowej jest drugie prawo Newtona:

\[\overline(F)=m\overline(a)\ \left(1\right),\]

gdzie $m$ jest masą ciała, na którą działa siła $\overline(F)$; $\overline(a)$ jest przyspieszeniem, jakie siła $\overline(F)$ nadaje danemu ciału. Znaczenie drugiego prawa Newtona jest takie, że siły działające na ciało determinują zmianę prędkości ciała, a nie tylko jego prędkość. Powinieneś wiedzieć, że drugie prawo Newtona obowiązuje w przypadku inercjalnych układów odniesienia.

Na ciało może oddziaływać nie jedna, ale pewna kombinacja sił. Całkowite działanie tych sił scharakteryzowano za pomocą pojęcia siły wypadkowej. Niech kilka sił działa na ciało w tym samym momencie. Przyspieszenie ciała w tym przypadku jest równe sumie wektorów przyspieszeń, które powstałyby w obecności każdej siły z osobna. Siły działające na ciało należy sumować zgodnie z zasadą dodawania wektorów. Siła wypadkowa ($\overline(F)$) jest sumą wektorową wszystkich sił działających na ciało w rozpatrywanym momencie:

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\suma\limits^N_(i=1)((\ overline(F))_i)\\lewo(2\prawo).\]

Wzór (2) jest wzorem na wypadkową wszystkich sił przyłożonych do ciała. Siła wypadkowa jest wielkością sztuczną, którą wprowadza się dla wygody obliczeń. Wypadkowa siła jest skierowana jako wektor przyspieszenia ciała.

Podstawowe prawo dynamiki ruchu postępowego w obecności kilku sił

Jeżeli na ciało działa kilka sił, wówczas drugie prawo Newtona można zapisać jako:

\[\suma\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]

$\overline(F)=0$, jeśli siły przyłożone do ciała znoszą się. Wtedy w inercjalnym układzie odniesienia prędkość ciała jest stała.

Przedstawiając siły działające na ciało na rysunku, w przypadku ruchu jednostajnie przyspieszonego, siła wypadkowa jest przedstawiana jako większa niż suma sił skierowanych przeciwnie do niej. Jeżeli ciało porusza się ze stałą prędkością lub pozostaje w spoczynku, długości wektorów sił (wypadkowa i suma pozostałych sił) są takie same i są skierowane w przeciwne strony.

Po znalezieniu wypadkowej sił na rysunku pokazano wszystkie siły uwzględnione w zadaniu. Siły te sumuje się zgodnie z zasadami dodawania wektorów.

Przykłady zagadnień dotyczących sił wypadkowych

Przykład 1

Ćwiczenia. Na punkt materialny działają dwie siły skierowane względem siebie pod kątem $\alpha =60()^\circ $. Jaka jest wypadkowa tych sił, jeśli $F_1=20\ $N; $F_2=10\ $H?

Rozwiązanie. Zróbmy rysunek.

Siły na rys. Dodajemy 1 zgodnie z zasadą równoległoboku. Długość wypadkowej siły $\overline(F)$ można obliczyć korzystając z twierdzenia o cosinusie:

Obliczmy moduł siły wypadkowej:

Odpowiedź.$F = 26,5 $ N

Przykład 2

Ćwiczenia. Siły działają na punkt materialny (ryc. 2). Jaki jest wynik działania tych sił?

Rozwiązanie. Wypadkowa sił przyłożonych do punktu (rys. 2) jest równa:

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+(\overline(F))_3+(\overline(F))_4\left(2.1\right).\]

Znajdźmy wypadkową sił $(\overline(F))_1$ i $(\overline(F))_2$. Siły te są skierowane wzdłuż tej samej linii prostej, ale w przeciwnych kierunkach, zatem:

Ponieważ $F_1>F_2$, to siła $(\overline(F))_(12)$ jest skierowana w tym samym kierunku, co siła $(\overline(F))_1$.

Znajdźmy wypadkową sił $(\overline(F))_3$ i $(\overline(F))_4$. Siły te są skierowane wzdłuż jednej pionowej linii prostej (rys. 1), co oznacza:

Kierunek siły $(\overline(F))_(34)$ pokrywa się z kierunkiem wektora $(\overline(F))_3$, ponieważ $(\overline(F))_3>(\overline (F))_4 $.

Wynik, który działa na punkt materialny, znajdujemy jako:

\[\overline(F)=(\overline(F))_(12)+(\overline(F))_(34)\left(2.2\right).\]

Siły $(\overline(F))_(12)$ i $(\overline(F))_(34)$ są wzajemnie prostopadłe. Znajdźmy długość wektora $\overline(F)$ korzystając z twierdzenia Pitagorasa:

DEFINICJA

Siła jest wielkością wektorową będącą miarą działania innych ciał lub pól na dane ciało, w wyniku czego następuje zmiana stanu tego ciała. W tym przypadku zmiana stanu oznacza zmianę lub odkształcenie.

Pojęcie siły odnosi się do dwóch ciał. Zawsze możesz wskazać ciało, na które działa siła i ciało, z którego działa.

Siłę charakteryzuje:

• moduł;
• kierunek;
• punkt aplikacji.

Wielkość i kierunek siły są niezależne od wyboru.

Jednostką siły w układzie C jest 1 Newton.

W naturze nie ma ciał materialnych, na które nie mają wpływu inne ciała, dlatego wszystkie ciała znajdują się pod wpływem sił zewnętrznych lub wewnętrznych.

Na ciało może działać jednocześnie kilka sił. W tym przypadku obowiązuje zasada niezależności działania: działanie każdej siły nie zależy od obecności lub braku innych sił; połączone działanie kilku sił jest równe sumie niezależnych działań poszczególnych sił.

Siła wypadkowa

Do opisu ruchu ciała w tym przypadku używa się pojęcia siły wypadkowej.

DEFINICJA

Siła wypadkowa to siła, której działanie zastępuje działanie wszystkich sił działających na ciało. Inaczej mówiąc, wypadkowa wszystkich sił przyłożonych do ciała jest równa sumie wektorowej tych sił (ryc. 1).

Ryc.1. Wyznaczanie sił wypadkowych

Ponieważ ruch ciała jest zawsze uwzględniany w pewnym układzie współrzędnych, wygodnie jest brać pod uwagę nie samą siłę, ale jej rzuty na osie współrzędnych (ryc. 2, a). W zależności od kierunku siły jej rzuty mogą być dodatnie (ryc. 2, b) lub ujemne (ryc. 2, c).

Ryc.2. Rzuty siły na osie współrzędnych: a) na płaszczyznę; b) na linii prostej (rzut jest dodatni);
c) na linii prostej (rzut jest ujemny)

Ryc.3. Przykłady ilustrujące wektorową sumację sił

Często spotykamy przykłady ilustrujące wektorową sumację sił: lampa wisi na dwóch linkach (rys. 3, a) – w tym przypadku równowaga zostaje osiągnięta dzięki temu, że wypadkowa sił rozciągających jest kompensowana przez ciężar lampy lampa; blok ślizga się po nachylonej płaszczyźnie (rys. 3, b) - ruch następuje pod wpływem wypadkowych sił tarcia, grawitacji i reakcji podporowej. Słynne wersety z bajki I.A. Krylova „a wózek nadal tam jest!” - także ilustracja równości wypadkowej trzech sił do zera (ryc. 3, c).

Przykłady rozwiązywania problemów

PRZYKŁAD 1

Ćwiczenia	Na ciało działają dwie siły i . Wyznaczyć moduł i kierunek wypadkowej tych sił, jeśli: a) siły są skierowane w jednym kierunku; b) siły są skierowane w przeciwnych kierunkach; c) siły są skierowane prostopadle do siebie.
Rozwiązanie	a) siły są skierowane w jednym kierunku; Siła wypadkowa: b) siły są skierowane w przeciwnych kierunkach; Siła wypadkowa: Rzutujmy tę równość na oś współrzędnych: c) siły są skierowane prostopadle do siebie; Siła wypadkowa:

Kiedy mówią o wyniku, mają na myśli siła równa działaniu dwóch lub więcej sił działających jednocześnie na ciało.

Kiedy na ciało działa kilka sił, ich łączny efekt może być różny; zależy to zarówno od kierunku różnych sił, jak i od ich wartości liczbowych. W każdym razie zawsze można znaleźć jedną siłę, która je powoduje.

Na przykład cegła została umieszczona na trampolinie. Na cegłę działają dwie siły - grawitacja i siła sprężystości trampoliny. W momencie układania cegły siła ciężkości była większa od siły sprężystości i cegła przesuwała się w dół. Gdy siły się wyrównały, cegła zatrzymała się.

Gdyby cegła nie została położona na trampolinie, ale rzucona z całej siły z góry, wówczas poruszałaby się w dół nie tylko pod wpływem grawitacji, ale także przeniesionej na nią siły rzucania. Pod wpływem tych dwóch sił trampolina ugina się bardziej, gdyż siła sprężystości, która równoważy te siły, powinna być większa.

Kiedy równowaga sił zostanie osiągnięta i ruch ustanie, równowaga zostanie ponownie zakłócona, ponieważ siła rzucania nie będzie już działać na cegłę, a jedynie siły ciężkości i sprężystości. Ale siłę sprężystą osiągnięto nie tylko dzięki ciężarowi cegły, ale także dzięki sile rzutu. Dlatego siła sprężystości będzie większa niż siła grawitacji, a cegła podskoczy, to znaczy zacznie się poruszać w górę.

W najprostszych przypadkach uwzględnia się wypadkową sił skierowanych w jednym lub przeciwnym kierunku.

Jeżeli dwie siły działające na ciało są skierowane w tym samym kierunku, to ich wypadkowa będzie równa ich sumie: F 1 + F 2. Na przykład, jeśli ciało jest pchane w jednym kierunku przez dwie siły 10 N i 20 N, to wypadkowa siła tych dwóch będzie równa 30 N.

Jeżeli dwie siły działające na ciało są skierowane w przeciwne strony, to ich wypadkowa jest równa wielkości różnicy sił i jest skierowana w stronę większej: |F 1 – F 2 |. Przykładowo, jeśli jedna siła 10 N pcha ciało w lewo, a druga siła 15 N w prawo, to ciało przesunie się w prawo pod wpływem siły 5 N (|10 – 15 |. = 5).

Gdy siły są skierowane przeciwnie, ale mają taką samą wartość liczbową, wówczas ich wypadkowa będzie równa zeru. Oznacza to, że wypadkowa siła nie działa na ciało. Jeśli ciało było w spoczynku, pozostanie tam. Jeśli ciało poruszało się prosto i równomiernie, będzie się poruszać nadal. Zatem chociaż na ciało zadziałały dwie nowe siły, „wzajemnie się unicestwiły”.

Załóżmy, że na ciało działają trzy siły, z których dwie są skierowane w jednym kierunku, a trzecia w drugim. W takim przypadku należy najpierw znaleźć wypadkową dwóch sił skierowanych w jednym kierunku, dodając je. Następnie porównaj ją z trzecią siłą, aby określić, w którą stronę zostanie skierowana wypadkowa trzech sił. I znajdź moduł różnicy między sumą pierwszych dwóch i trzeciego: |F 1 + F 2 – F 3 |.

Często na ciało działa nie jedna, ale kilka sił jednocześnie. Rozważmy przypadek, gdy na ciało działają dwie siły ( i ). Przykładowo na ciało spoczywające na poziomej powierzchni działa siła ciężkości () i reakcja podpory powierzchniowej () (rys. 1).

Te dwie siły można zastąpić jedną, która nazywa się siłą wypadkową (). Znajdź to jako wektorową sumę sił i:

Wyznaczanie wypadkowej dwóch sił

DEFINICJA

Wynik dwóch sił nazywana siłą, która wywołuje na ciele skutek podobny do działania dwóch oddzielnych sił.

Należy zauważyć, że działanie każdej siły nie zależy od tego, czy istnieją inne siły, czy nie.

Drugie prawo Newtona dotyczące wypadkowej dwóch sił

Jeżeli na ciało działają dwie siły, wówczas drugie prawo Newtona zapisujemy jako:

Kierunek wypadkowej zawsze pokrywa się z kierunkiem przyspieszenia ciała.

Oznacza to, że jeśli na ciało działają jednocześnie dwie siły (), to przyspieszenie () tego ciała będzie wprost proporcjonalne do sumy wektorów tych sił (lub proporcjonalne do sił wypadkowych):

M jest masą danego ciała. Istotą drugiego prawa Newtona jest to, że siły działające na ciało determinują sposób, w jaki zmienia się prędkość ciała, a nie tylko wielkość prędkości ciała. Należy zauważyć, że drugie prawo Newtona jest spełnione wyłącznie w inercjalnych układach odniesienia.

Wypadkowa dwóch sił może być równa zeru, jeśli siły działające na ciało są skierowane w różne strony i mają taką samą wielkość.

Znalezienie wielkości wypadkowej dwóch sił

Aby znaleźć wynik, należy przedstawić na rysunku wszystkie siły, które należy uwzględnić w zadaniu działającym na ciało. Siły należy dodawać zgodnie z zasadami dodawania wektorów.

Załóżmy, że na ciało działają dwie siły skierowane wzdłuż tej samej linii prostej (rys. 1). Na rysunku widać, że są one skierowane w różnych kierunkach.

Siły wypadkowe () przyłożone do ciała będą równe:

Aby znaleźć moduł sił wypadkowych, wybieramy oś, oznaczamy ją X i kierujemy wzdłuż kierunku działania sił. Następnie rzutując wyrażenie (4) na oś X, otrzymujemy, że wielkość (moduł) wypadkowej (F) jest równa:

gdzie są moduły odpowiednich sił.

Wyobraźmy sobie, że na ciało działają dwie siły i, skierowane względem siebie pod pewnym kątem (ryc. 2). Wypadkową tych sił wyznaczamy korzystając z reguły równoległoboku. Wielkość wynikowej będzie równa długości przekątnej tego równoległoboku.

Przykłady rozwiązywania problemów

PRZYKŁAD 1

Ćwiczenia	Ciało o masie 2 kg porusza się pionowo w górę za pomocą nici, a jego przyspieszenie jest równe 1. Jaka jest wielkość i kierunek siły wypadkowej? Jakie siły działają na ciało?
Rozwiązanie	Na korpus działa siła ciężkości () i siła reakcji gwintu (ryc. 3). Wypadkową powyższych sił można wyznaczyć korzystając z drugiego prawa Newtona: W rzucie na oś X równanie (1.1) przyjmuje postać: Obliczmy wielkość siły wypadkowej:
Odpowiedź	N, wypadkowa siła jest skierowana w taki sam sposób, jak przyspieszenie ciała, czyli pionowo w górę. Na ciało działają dwie siły i .

Siła działa jako ilościowa miara interakcji ciał. Jest to ważna wielkość fizyczna, ponieważ w inercjalnym układzie odniesienia jakakolwiek zmiana prędkości ciała może nastąpić tylko podczas interakcji z innymi ciałami. Innymi słowy, gdy na ciało działa siła.

Oddziaływania ciał mogą mieć różny charakter, na przykład istnieją interakcje elektryczne, magnetyczne, grawitacyjne i inne. Jednak przy badaniu ruchu mechanicznego ciała charakter sił powodujących przyspieszenie w tym ciele nie ma znaczenia. Mechanika nie zajmuje się problemem pochodzenia interakcji. W przypadku każdej interakcji siła staje się miarą liczbową. Siły o różnym charakterze mierzy się w tych samych jednostkach (w międzynarodowym układzie jednostek w niutonach) i stosuje się te same standardy. Ze względu na tę uniwersalność mechanika zajmuje się badaniem i opisem ruchu ciał, na które wpływają siły dowolnego rodzaju.

Skutkiem działania siły na ciało jest przyspieszenie ciała (zmiana prędkości jego ruchu) i/lub jego odkształcenie.

Dodawanie sił

Siła jest wielkością wektorową. Oprócz modułu posiada kierunek i punkt zastosowania. Niezależnie od ich charakteru, wszystkie siły sumują się jako wektory.

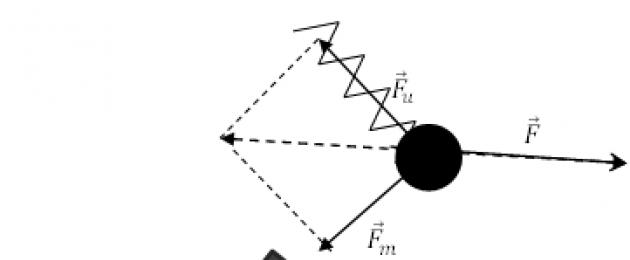
Niech metalowa kulka będzie trzymana przez elastyczną sprężynę i przyciągana przez magnes (ryc. 1). Następnie działają na niego dwie siły: siła sprężystości sprężyny ($(\overline(F))_u$) i siła magnetyczna ($(\overline(F))_m$) magnesu. Zakładamy, że ich wartości są znane. Pod wpływem połączonego działania tych sił piłka będzie w spoczynku, jeśli zadziała na nią trzecia siła ($\overline(F)$), która spełnia równość:

\[\overline(F)=-\left((\overline(F))_u+(\overline(F))_m\right)\left(1\right).\]

Doświadczenie to pozwala stwierdzić, że kilka sił działających na jedno ciało można zastąpić jedną wypadkową, przy czym charakter tych sił nie jest istotny. Wynik otrzymuje się w wyniku wektorowego sumowania sił działających na ciało.

Definicja i wzór siły wypadkowej

I tak wektorową sumę wszystkich sił działających na ciało w tym samym momencie nazywamy siłą wypadkową ($\overline(F)$):

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\suma\limits^N_(i=1)((\ overline(F))_i)\\lewo(2\prawo).\]

Czasami wypadkowa siła jest oznaczana dla podkreślenia $\overline(R)$, ale nie jest to konieczne.

Sumowanie sił można przeprowadzić graficznie. W tym przypadku stosowane są zasady wielokąta, równoległoboku i trójkąta. Jeśli po tym dodaniu sił wielokąt okaże się domknięty, to wynik będzie równy zeru. Gdy wynik jest równy zero, układ nazywa się zrównoważonym.

Zapisanie drugiego prawa Newtona z wykorzystaniem siły wypadkowej

Drugie prawo Newtona jest podstawowym prawem dynamiki klasycznej. Łączy siły działające na ciało i jego przyspieszenie i pozwala rozwiązać główny problem dynamiki. Jeśli na ciało działa kilka sił, wówczas drugie prawo Newtona piszę w następujący sposób:

\[\overline(R)=\suma\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]

Wzór (3) oznacza, że ​​wypadkowa wszystkich sił przyłożonych do ciała może być równa zeru, jeżeli nastąpi wzajemne kompensowanie sił. Wtedy ciało porusza się ze stałą prędkością lub pozostaje w spoczynku w inercjalnym układzie odniesienia. Można powiedzieć odwrotnie: jeśli ciało porusza się w inercjalnym układzie odniesienia ruchem jednostajnym i prostoliniowym, to nie działają na nie żadne siły lub ich wypadkowa wynosi zero.

Przy rozwiązywaniu zadań i wskazywaniu na wykresach sił działających na ciało, gdy ciało porusza się ze stałym przyspieszeniem, siła wypadkowa jest kierowana wzdłuż przyspieszenia i jest przedstawiana jako dłuższa niż siła skierowana przeciwnie (suma sił). Przy ruchu jednostajnym (lub gdy ciało jest w spoczynku) długość wektorów siły o przeciwnych kierunkach jest taka sama (wynik wynosi zero).

Badając przesłanki zadania, należy określić, jakie siły działają na ciało i zostaną uwzględnione w wyniku wypadkowym, które siły nie mają istotnego wpływu na ruch ciała i można je odrzucić. Znaczące siły pokazano na rysunku. Siły dodawane są zgodnie z zasadami dodawania wektorów.

Przykłady problemów z rozwiązaniami

Przykład 1

Ćwiczenia. Pod jakim kątem powinny być rozmieszczone siły z rys.? 2, tak że ich wypadkowa jest równa wielkości każdej z sił składowych?

Rozwiązanie. Aby rozwiązać problem, używamy twierdzenia o cosinusie:

Ponieważ zgodnie z warunkami problemu:

następnie przekształcamy wyrażenie (1.1) do postaci: $\ $

Rozwiązaniem otrzymanego równania trygonometrycznego są kąty:

\[\alpha =\frac(2\pi )(3)+\pi n\ ;;\ \alpha =\frac(4\pi )(3)+\pi n\ \left(gdzie\ n jest liczbą całkowitą \ liczba\po prawej).\ \]

Na podstawie rysunku (rys. 2) odpowiedź brzmi $\alpha =\frac(2\pi )(3)$.

Odpowiedź.$\alfa =\frac(2\pi )(3)$

Przykład 2

Ćwiczenia. Jaka będzie wypadkowa siła, jeśli na ciało zadziałają siły pokazane na rys. 3?

Rozwiązanie. Siłę wypadkową obliczamy przez sumowanie wektorów, korzystając z reguły wielokąta. Kolejno każdy kolejny wektor siły jest odkładany na bok od końca poprzedniego. W rezultacie wektor wypadkowej wszystkich sił będzie miał swój początek w punkcie, z którego wychodzi pierwszy wektor (mamy wektor $(\overline(F))_1$), jego koniec dotrze do punktu gdzie kończy się ostatni wektor ($(\overline(F) ))_4$). W rezultacie otrzymujemy rys. 4.

W wyniku konstrukcji otrzymuje się wielokąt zamknięty, co oznacza, że ​​wypadkowa sił przyłożonych do ciała jest równa zeru.

Odpowiedź.$\overline(R)=0$