Wyznaczanie kąta pomiędzy prostymi. Kąt pomiędzy liniami prostymi

Każdemu uczniowi przygotowującemu się do egzaminu państwowego z matematyki przydatne będzie powtórzenie tematu „Znajdowanie kąta między liniami prostymi”. Jak pokazują statystyki, przy zdaniu egzaminu certyfikacyjnego zadania z tej części stereometrii sprawiają dużej liczbie uczniów trudności. Jednocześnie zadania wymagające znalezienia kąta między prostymi znajdują się na egzaminie Unified State Exam zarówno na poziomie podstawowym, jak i specjalistycznym. Oznacza to, że każdy powinien być w stanie je rozwiązać.

Podstawowe momenty

Istnieją 4 rodzaje względnych pozycji linii w przestrzeni. Mogą się pokrywać, przecinać, być równoległe lub przecinać się. Kąt między nimi może być ostry lub prosty.

Aby znaleźć kąt między liniami w ujednoliconym egzaminie państwowym lub na przykład podczas rozwiązywania, uczniowie w Moskwie i innych miastach mogą skorzystać z kilku sposobów rozwiązywania problemów w tej części stereometrii. Zadanie możesz wykonać korzystając z klasycznych konstrukcji. Aby to zrobić, warto poznać podstawowe aksjomaty i twierdzenia stereometrii. Aby sprowadzić zadanie do zagadnienia planimetrycznego, uczeń musi umieć logicznie rozumować i tworzyć rysunki.

Metodę wektorów współrzędnych można również zastosować, korzystając z prostych formuł, reguł i algorytmów. Najważniejsze w tym przypadku jest prawidłowe wykonanie wszystkich obliczeń. Projekt edukacyjny Shkolkovo pomoże Ci udoskonalić umiejętności rozwiązywania problemów w zakresie stereometrii i innych części kursu szkolnego.

Kąt pomiędzy liniami prostymi w przestrzeni nazwiemy dowolny z sąsiednich kątów utworzonych przez dwie linie proste poprowadzone przez dowolny punkt równoległy do ​​danych.

Niech w przestrzeni zostaną dane dwie proste:

Oczywiście kąt φ między prostymi można przyjąć jako kąt między ich wektorami kierunkowymi i . Ponieważ , to korzystając ze wzoru na cosinus kąta między wektorami otrzymujemy

Warunki równoległości i prostopadłości dwóch prostych są równoważne warunkom równoległości i prostopadłości ich wektorów kierunkowych oraz:

Dwa proste równoległy wtedy i tylko wtedy, gdy odpowiadające im współczynniki są proporcjonalne, tj. l 1 równoległy l 2 wtedy i tylko wtedy, gdy jest równoległe do .

Dwa proste prostopadły wtedy i tylko wtedy, gdy suma iloczynów odpowiednich współczynników jest równa zeru: .

U cel między linią a płaszczyzną

Niech będzie prosto D- nie prostopadle do płaszczyzny θ;
D′− rzut linii D do płaszczyzny θ;
Najmniejszy kąt pomiędzy liniami prostymi D I D' zadzwonimy kąt między linią prostą a płaszczyzną.
Oznaczmy to jako φ=( D,θ)
Jeśli D⊥θ, następnie ( D,θ)=π/2

Oj→J→k→− prostokątny układ współrzędnych.
Równanie płaszczyzny:

θ: Topór+Przez+Cz+D=0

Zakładamy, że prostą wyznacza punkt i wektor kierunkowy: D[M 0,P→]
Wektor N→(A,B,C)⊥θ
Następnie pozostaje znaleźć kąt między wektorami N→ i P→ oznaczmy to jako γ=( N→,P→).

Jeżeli kąt γ<π/2 , то искомый угол φ=π/2−γ .

Jeżeli kąt wynosi γ>π/2, to pożądany kąt wynosi φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Następnie, kąt między prostą a płaszczyzną można obliczyć korzystając ze wzoru:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Kp 3∣ ∣ √A 2+B 2+C 2√P 21+P 22+P 23

Pytanie 29. Pojęcie formy kwadratowej. Określoność znaku form kwadratowych.

Postać kwadratowa j (x 1, x 2, …, x n) n zmienne rzeczywiste x 1, x 2, …, x n nazywa się sumą postaci , (1)

Gdzie ij – niektóre liczby zwane współczynnikami. Bez utraty ogólności możemy to założyć ij = ji.

Forma kwadratowa nazywa się ważny, Jeśli ij Î GR. Macierz postaci kwadratowej nazywa się macierzą złożoną z jej współczynników. Postać kwadratowa (1) odpowiada pojedynczej macierzy symetrycznej, tj. T = A. W konsekwencji postać kwadratową (1) można zapisać w postaci macierzowej j ( X) = x T Ah, Gdzie x T = (X 1 X 2 … x rz). (2)

I odwrotnie, każda macierz symetryczna (2) odpowiada unikalnej formie kwadratowej aż do zapisu zmiennych.

Ranga formy kwadratowej nazywa się rzędem jego macierzy. Forma kwadratowa nazywa się niezdegenerowany, jeśli jego macierz nie jest osobliwa A. (przypomnijmy, że matrix A nazywa się niezdegenerowanym, jeżeli jego wyznacznik nie jest równy zero). W przeciwnym razie forma kwadratowa jest zdegenerowana.

dodatnio określony(lub ściśle dodatnie) if

J ( X) > 0 , dla kazdego X = (X 1 , X 2 , …, x rz), z wyjątkiem X = (0, 0, …, 0).

Matryca A dodatnia określona forma kwadratowa j ( X) jest również nazywany dodatnio określonym. Dlatego dodatnio określona forma kwadratowa odpowiada unikalnej dodatnio określonej macierzy i odwrotnie.

Nazywa się postać kwadratową (1). zdefiniowane negatywnie(lub ściśle ujemne) if

J ( X) < 0, для любого X = (X 1 , X 2 , …, x rz), z wyjątkiem X = (0, 0, …, 0).

Podobnie jak powyżej, macierz o postaci kwadratowej ujemnie określonej nazywana jest również ujemnie określoną.

W konsekwencji dodatnia (ujemna) określona forma kwadratowa j ( X) osiąga minimalną (maksymalną) wartość j ( X*) = 0 w X* = (0, 0, …, 0).

Należy zauważyć, że większość form kwadratowych nie ma znaku określonego, to znaczy nie jest ani dodatnia, ani ujemna. Takie formy kwadratowe zwracają się do 0 nie tylko w początku układu współrzędnych, ale także w innych punktach.

Gdy N> 2, do sprawdzania znaku postaci kwadratowej wymagane są specjalne kryteria. Przyjrzyjmy się im.

Ważni nieletni forma kwadratowa nazywana jest mollami:

to znaczy są to nieletni rzędu 1, 2, ..., N matryce A, znajdujący się w lewym górnym rogu, ostatni z nich pokrywa się z wyznacznikiem macierzy A.

Kryterium pozytywnej określoności (kryterium Sylwestra)

X) = x T Ah był dodatnio określony, konieczne i wystarczające jest, aby wszystkie główne minory macierzy A były pozytywne, tj.: M 1 > 0, M 2 > 0, …, Mn > 0. Kryterium pewności ujemnej Aby postać kwadratowa j ( X) = x T Ah była ujemnie określona, ​​konieczne i wystarczające jest, aby jej molle główne parzystego rzędu były dodatnie, a nieparzystego – ujemne, tj.: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)N

Materiał ten poświęcony jest takiej koncepcji, jak kąt między dwiema przecinającymi się liniami. W pierwszym akapicie wyjaśnimy co to jest i pokażemy to na ilustracjach. Następnie przyjrzymy się sposobom znalezienia sinusa, cosinusa tego kąta i samego kąta (oddzielnie rozważymy przypadki z płaszczyzną i przestrzenią trójwymiarową), podamy niezbędne wzory i dokładnie pokażemy na przykładach jak się je wykorzystuje w praktyce.

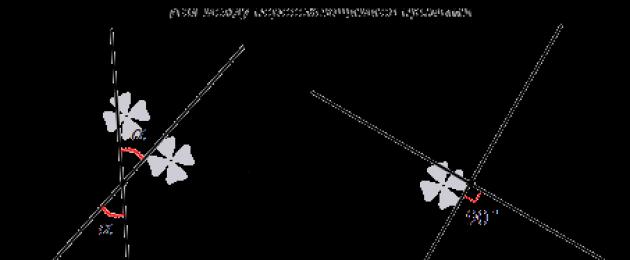
Aby zrozumieć, jaki jest kąt powstały na przecięciu dwóch prostych, należy pamiętać o samej definicji kąta, prostopadłości i punktu przecięcia.

Definicja 1

Dwie linie nazywamy przecinającymi się, jeśli mają jeden punkt wspólny. Punkt ten nazywany jest punktem przecięcia dwóch linii.

Każda linia prosta jest podzielona przez punkt przecięcia na promienie. Obie linie proste tworzą 4 kąty, z których dwa są pionowe, a dwa sąsiadują ze sobą. Jeśli znamy miarę jednego z nich, możemy wyznaczyć pozostałe.

Powiedzmy, że wiemy, że jeden z kątów jest równy α. W tym przypadku kąt pionowy względem niego będzie również równy α. Aby znaleźć pozostałe kąty, musimy obliczyć różnicę 180 ° - α. Jeśli α jest równe 90 stopni, wówczas wszystkie kąty będą kątami prostymi. Linie przecinające się pod kątem prostym nazywane są prostopadłymi (pojęciu prostopadłości poświęcony jest osobny artykuł).

Spójrz na zdjęcie:

Przejdźmy do sformułowania głównej definicji.

Definicja 2

Kąt utworzony przez dwie przecinające się linie jest miarą mniejszego z 4 kątów tworzących te dwie linie.

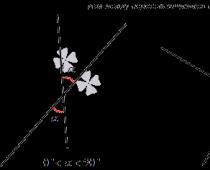
Z definicji należy wyciągnąć ważny wniosek: wielkość kąta w tym przypadku będzie wyrażona dowolną liczbą rzeczywistą z przedziału (0, 90). Jeżeli proste są prostopadłe, to kąt między nimi i tak będzie wynosił równy 90 stopni.

Umiejętność znalezienia miary kąta pomiędzy dwiema przecinającymi się liniami jest przydatna do rozwiązywania wielu praktycznych problemów. Metodę rozwiązania można wybrać spośród kilku opcji.

Na początek możemy zastosować metody geometryczne. Jeśli wiemy coś o kątach dopełniających, możemy je powiązać z potrzebnym nam kątem, korzystając z właściwości figur równych lub podobnych. Na przykład, jeśli znamy boki trójkąta i musimy obliczyć kąt między liniami, na których znajdują się te boki, wówczas do naszego rozwiązania nadaje się twierdzenie cosinus. Jeśli w naszym warunku mamy trójkąt prostokątny, to do obliczeń będziemy musieli także znać sinus, cosinus i tangens kąta.

Metoda współrzędnych jest również bardzo wygodna przy rozwiązywaniu problemów tego typu. Wyjaśnijmy, jak prawidłowo go używać.

Mamy prostokątny (kartezjański) układ współrzędnych O x y, w którym dane są dwie linie proste. Oznaczmy je literami a i b. Linie proste można opisać za pomocą równań. Oryginalne linie mają punkt przecięcia M. Jak wyznaczyć wymagany kąt (oznaczmy go α) pomiędzy tymi prostymi?

Zacznijmy od sformułowania podstawowej zasady znajdowania kąta w danych warunkach.

Wiemy, że pojęcie linii prostej jest ściśle powiązane z takimi pojęciami, jak wektor kierunkowy i wektor normalny. Jeśli mamy równanie pewnej prostej, możemy z niej pobrać współrzędne tych wektorów. Możemy to zrobić dla dwóch przecinających się linii jednocześnie.

Kąt wyznaczony przez dwie przecinające się linie można znaleźć za pomocą:

• kąt między wektorami kierunkowymi;
• kąt między wektorami normalnymi;
• kąt między wektorem normalnym jednej linii a wektorem kierunku drugiej.

Przyjrzyjmy się teraz każdej metodzie osobno.

1. Załóżmy, że mamy prostą a z wektorem kierunku a → = (a x, a y) i linię b z wektorem kierunku b → (b x, b y). Narysujmy teraz dwa wektory a → i b → z punktu przecięcia. Następnie zobaczymy, że każdy z nich będzie zlokalizowany na własnej linii prostej. Mamy wówczas cztery możliwości ich względnego ułożenia. Zobacz ilustrację:

Jeśli kąt między dwoma wektorami nie jest rozwarty, to będzie to kąt, którego potrzebujemy między przecinającymi się liniami a i b. Jeśli jest rozwarty, pożądany kąt będzie równy kątowi przylegającemu do kąta a →, b → ^. Zatem α = a → , b → ^ jeśli a → , b → ^ ≤ 90 ° , i α = 180 ° - a → , b → ^ jeśli a → , b → ^ > 90 ° .

Bazując na tym, że cosinusy równych kątów są równe, możemy przepisać powstałe równości w następujący sposób: cos α = cos a →, b → ^, jeśli a →, b → ^ ≤ 90 °; cos α = cos 180 ° - a →, b → ^ = - cos a →, b → ^, jeśli a →, b → ^ > 90 °.

W drugim przypadku wykorzystano wzory redukcyjne. Zatem,

sałata α sałata a → , b → ^ , sałata a → , b → ^ ≥ 0 - sałata a → , b → ^ , sałata a → , b → ^< 0 ⇔ cos α = cos a → , b → ^

Zapiszmy ostatnią formułę słownie:

Definicja 3

Cosinus kąta utworzonego przez dwie przecinające się linie proste będzie równy modułowi cosinusa kąta między jego wektorami kierunkowymi.

Ogólna postać wzoru na cosinus kąta między dwoma wektorami a → = (a x , a y) i b → = (b x , b y) wygląda następująco:

sałata za → , b → ^ = a → , b → ^ a → b → = a x b x + za y + b y a x 2 + za y 2 b x 2 + b y 2

Można z niego wyprowadzić wzór na cosinus kąta pomiędzy dwiema danymi prostymi:

cos α = za x b x + za y + b y a x 2 + za y 2 b x 2 + b y 2 = za x b x + a y + b y za x 2 + za y 2 b x 2 + b y 2

Następnie sam kąt można znaleźć za pomocą następującego wzoru:

α = za r do cos za x b x + za y + b y a x 2 + za y 2 b x 2 + b y 2

Tutaj a → = (a x , a y) i b → = (b x , b y) są wektorami kierunku danych prostych.

Podajmy przykład rozwiązania problemu.

Przykład 1

W prostokątnym układzie współrzędnych na płaszczyźnie dane są dwie przecinające się linie a i b. Można je opisać równaniami parametrycznymi x = 1 + 4 · λ y = 2 + λ λ ∈ R i x 5 = y - 6 - 3. Oblicz kąt między tymi liniami.

Rozwiązanie

W naszym warunku mamy równanie parametryczne, co oznacza, że ​​dla tej prostej możemy od razu zapisać współrzędne jej wektora kierunkowego. W tym celu musimy przyjąć wartości współczynników dla parametru, tj. linia prosta x = 1 + 4 · λ y = 2 + λ λ ∈ R będzie miała wektor kierunkowy a → = (4, 1).

Druga prosta jest opisana równaniem kanonicznym x 5 = y - 6 - 3. Tutaj możemy pobrać współrzędne z mianowników. Zatem ta linia ma wektor kierunkowy b → = (5 , - 3) .

Następnie przechodzimy bezpośrednio do znalezienia kąta. Aby to zrobić, wystarczy podstawić istniejące współrzędne dwóch wektorów do powyższego wzoru α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . Otrzymujemy co następuje:

α = za r do cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = za r do cos 17 17 34 = za r do cos 1 2 = 45 °

Odpowiedź: Te linie proste tworzą kąt 45 stopni.

Podobny problem możemy rozwiązać, znajdując kąt między wektorami normalnymi. Jeśli mamy prostą a z wektorem normalnym n a → = (n a x , n a y) i linię b z wektorem normalnym n b → = (n b x , n b y), to kąt między nimi będzie równy kątowi pomiędzy n a → i n b → lub kąt, który będzie przylegał do n a →, n b → ^. Metodę tę pokazano na obrazku:

Wzory do obliczania cosinusa kąta między przecinającymi się prostymi i samego tego kąta przy użyciu współrzędnych wektorów normalnych wyglądają następująco:

sałata α = sałata n za → , n b → ^ = n za x n b x + n za y + n b y n za x 2 + n za y 2 n b x 2 + n b y 2 α = za r do cos n za x n b x + n za y + n b y n za x 2 + n za y 2 n b x 2 + n b y 2

Tutaj n a → i n b → oznaczają wektory normalne dwóch danych prostych.

Przykład 2

W prostokątnym układzie współrzędnych dwie proste wyznacza się za pomocą równań 3 x + 5 y - 30 = 0 i x + 4 y - 17 = 0. Znajdź sinus i cosinus kąta między nimi oraz wielkość tego kąta.

Rozwiązanie

Oryginalne linie są określone za pomocą równań linii normalnych w postaci A x + B y + C = 0. Oznaczamy wektor normalny jako n → = (A, B). Znajdźmy współrzędne pierwszego wektora normalnego dla jednej linii i zapiszmy je: n a → = (3, 5) . Dla drugiej linii x + 4 y - 17 = 0 wektor normalny będzie miał współrzędne n b → = (1, 4). Dodajmy teraz uzyskane wartości do wzoru i obliczmy sumę:

sałata α = sałata n za → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34

Jeśli znamy cosinus kąta, możemy obliczyć jego sinus, korzystając z podstawowej tożsamości trygonometrycznej. Ponieważ kąt α utworzony przez linie proste nie jest rozwarty, wówczas sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.

W tym przypadku α = a r do cos 23 2 34 = a r do sin 7 2 34.

Odpowiedź: cos α = 23 2 34 , sin α = 7 2 34 , α = za r do cos 23 2 34 = za r do grzech 7 2 34

Przeanalizujmy ostatni przypadek - znalezienie kąta między prostymi, jeśli znamy współrzędne wektora kierunku jednej prostej i wektora normalnego drugiej.

Załóżmy, że prosta a ma wektor kierunkowy a → = (a x , a y) , a prosta b ma wektor normalny n b → = (n b x , n b y) . Musimy odsunąć te wektory od punktu przecięcia i rozważyć wszystkie opcje ich względnych pozycji. Zobacz na zdjęciu:

Jeżeli kąt pomiędzy podanymi wektorami nie będzie większy niż 90 stopni, to okaże się, że dopełni kąt pomiędzy a i b do kąta prostego.

a → , n b → ^ = 90 ° - α jeśli a → , n b → ^ ≤ 90 ° .

Jeśli jest mniejsza niż 90 stopni, wówczas otrzymujemy:

a → , n b → ^ > 90 ° , następnie a → , n b → ^ = 90 ° + α

Korzystając z zasady równości cosinusów równych kątów piszemy:

cos za → , n b → ^ = cos (90 ° - α) = sin α dla a → , n b → ^ ≤ 90 ° .

cos za → , n b → ^ = cos 90° + α = - sin α dla a → , n b → ^ > 90° .

Zatem,

sin α = sałata za → , n b → ^ , za → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , za → , n b → ^ > 90 ° ⇔ sin α = sałata a → , n b → ^ , za → , n b → ^ > 0 - sałata za → , n b → ^ , za → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^

Sformułujmy wniosek.

Definicja 4

Aby znaleźć sinus kąta między dwiema liniami przecinającymi się na płaszczyźnie, należy obliczyć moduł cosinusa kąta między wektorem kierunkowym pierwszej linii a wektorem normalnym drugiej linii.

Zapiszmy niezbędne formuły. Znajdowanie sinusa kąta:

grzech α = sałata za → , n b → ^ = za x n b x + za y n b y a x 2 + za y 2 n b x 2 + n b y 2

Znalezienie samego kąta:

α = za r do grzech = za x n b x + za y n b y za x 2 + za y 2 n b x 2 + n b y 2

Tutaj a → jest wektorem kierunku pierwszej linii, a n b → jest wektorem normalnym drugiej linii.

Przykład 3

Dwie przecinające się linie są dane równaniami x - 5 = y - 6 3 i x + 4 y - 17 = 0. Znajdź kąt przecięcia.

Rozwiązanie

Bierzemy współrzędne wektora prowadzącego i normalnego z podanych równań. Okazuje się, że a → = (- 5, 3) i n → b = (1, 4). Bierzemy wzór α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 i obliczamy:

α = za r do grzech = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = za r do grzech 7 2 34

Należy pamiętać, że wzięliśmy równania z poprzedniego zadania i otrzymaliśmy dokładnie ten sam wynik, ale w inny sposób.

Odpowiedź:α = za r do grzech 7 2 34

Przedstawmy inny sposób znalezienia żądanego kąta za pomocą współczynników kątowych danych prostych.

Mamy linię a zdefiniowaną w prostokątnym układzie współrzędnych za pomocą równania y = k 1 x + b 1 oraz linię b zdefiniowaną jako y = k 2 x + b 2. Są to równania prostych ze współczynnikami nachylenia. Aby znaleźć kąt przecięcia, używamy wzoru:

α = a r do cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, gdzie k 1 i k 2 są współczynnikami nachylenia danych prostych. Aby uzyskać ten zapis, wykorzystano wzory na wyznaczenie kąta poprzez współrzędne wektorów normalnych.

Przykład 4

Na płaszczyźnie przecinają się dwie proste, określone równaniami y = - 3 5 x + 6 i y = - 1 4 x + 17 4. Oblicz wartość kąta przecięcia.

Rozwiązanie

Współczynniki kątowe naszych linii są równe k 1 = - 3 5 i k 2 = - 1 4. Dodajmy je do wzoru α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 i obliczmy:

α = za r do cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = za r do cos 23 20 34 24 · 17 16 = za r do cos 23 2 34

Odpowiedź:α = za r do cos 23 2 34

We wnioskach z tego akapitu należy zauważyć, że podanych tutaj wzorów na znalezienie kąta nie trzeba uczyć się na pamięć. Aby to zrobić, wystarczy znać współrzędne prowadnic i/lub wektorów normalnych danych linii i umieć je wyznaczyć za pomocą różnego rodzaju równań. Ale lepiej zapamiętać lub zapisać wzory na obliczenie cosinusa kąta.

Jak obliczyć kąt między przecinającymi się liniami w przestrzeni

Obliczenie takiego kąta można sprowadzić do obliczenia współrzędnych wektorów kierunkowych i określenia wielkości kąta utworzonego przez te wektory. W przypadku takich przykładów stosuje się to samo rozumowanie, które podaliśmy wcześniej.

Załóżmy, że mamy prostokątny układ współrzędnych umiejscowiony w przestrzeni trójwymiarowej. Zawiera dwie proste a i b z punktem przecięcia M. Aby obliczyć współrzędne wektorów kierunkowych, musimy znać równania tych prostych. Oznaczmy wektory kierunkowe a → = (a x , a y , a z) i b → = (b x , b y , b z) . Aby obliczyć cosinus kąta między nimi, używamy wzoru:

sałata α = sałata za → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z za x 2 + za y 2 + a z 2 b x 2 + b y 2 + b z 2

Aby znaleźć sam kąt, potrzebujemy następującego wzoru:

α = za r do cos za x b x + a y b y + a z b z za x 2 + za y 2 + a z 2 b x 2 + b y 2 + b z 2

Przykład 5

Mamy linię zdefiniowaną w przestrzeni trójwymiarowej za pomocą równania x 1 = y - 3 = z + 3 - 2. Wiadomo, że przecina się z osią O z. Oblicz kąt przecięcia i cosinus tego kąta.

Rozwiązanie

Oznaczmy kąt, który należy obliczyć, literą α. Zapiszmy współrzędne wektora kierunku pierwszej prostej – a → = (1, - 3, - 2) . Dla osi zastosowania możemy przyjąć wektor współrzędnych k → = (0, 0, 1) jako wskazówkę. Otrzymaliśmy niezbędne dane i możemy je dodać do pożądanej formuły:

sałata α = sałata a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2

W rezultacie odkryliśmy, że potrzebny nam kąt będzie równy a r c cos 1 · 2 = 45 °.

Odpowiedź: cos α = 1 2 , α = 45 ° .

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Niech dwie proste l i m na płaszczyźnie w kartezjańskim układzie współrzędnych zostaną określone za pomocą ogólnych równań: l: A 1 x + B 1 y + C 1 = 0, m: A 2 x + B 2 y + C 2 = 0

Wektory normalne do tych prostych: = (A 1 , B 1) – do prostej l,

= (A 2 , B 2) – do linii m.

Niech j będzie kątem pomiędzy liniami l i m.

Ponieważ kąty o wzajemnie prostopadłych bokach są albo równe, albo sumują się do p, to , czyli cos j = .

Udowodniliśmy zatem następujące twierdzenie.

Twierdzenie. Niech j będzie kątem pomiędzy dwiema prostymi na płaszczyźnie i niech te proste zostaną określone w kartezjańskim układzie współrzędnych za pomocą ogólnych równań A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 = 0. Wtedy cos j = .

Ćwiczenia.

1) Wyprowadź wzór na obliczenie kąta między prostymi, jeżeli:

(1) obie linie są określone parametrycznie; (2) obie proste są dane równaniami kanonicznymi; (3) jedna linia jest określona parametrycznie, druga za pomocą równania ogólnego; (4) obie proste są dane równaniem ze współczynnikiem kątowym.

2) Niech j będzie kątem pomiędzy dwiema prostymi na płaszczyźnie i niech te proste zostaną określone w kartezjańskim układzie współrzędnych za pomocą równań y = k 1 x + b 1 i y = k 2 x + b 2 .

Następnie tan j = .

3) Zbadaj względne położenie dwóch prostych, określone przez ogólne równania w kartezjańskim układzie współrzędnych i wypełnij tabelę:

Odległość punktu od prostej na płaszczyźnie.

Niech prostą l na płaszczyźnie w kartezjańskim układzie współrzędnych wyznaczymy za pomocą równania ogólnego Ax + By + C = 0. Znajdźmy odległość punktu M(x 0 , y 0) od prostej l.

Odległość punktu M od prostej l jest długością prostopadłej HM (H О l, HM ^ l).

Wektor i wektor normalny do prostej l są współliniowe, zatem | | = | | | | i | | = .

Niech współrzędnymi punktu H będą (x,y).

Ponieważ punkt H należy do prostej l, to Ax + By + C = 0 (*).

Współrzędne wektorów i: = (x 0 - x, y 0 - y), = (A, B).

| | = = =

(C = -Ax - By, patrz (*))

Twierdzenie. Niech prostą l określimy w kartezjańskim układzie współrzędnych ogólnym równaniem Ax + By + C = 0. Następnie odległość punktu M(x 0 , y 0) od tej prostej obliczamy ze wzoru: r ( M; l) = .

Ćwiczenia.

1) Wyprowadź wzór na obliczenie odległości punktu od prostej, jeśli: (1) linia jest dana parametrycznie; (2) podana jest prosta równań kanonicznych; (3) linię prostą wyznacza równanie ze współczynnikiem kątowym.

2) Zapisz równanie okręgu stycznego do prostej 3x – y = 0, którego środek znajduje się w punkcie Q(-2,4).

3) Zapisz równania linii dzielących kąty utworzone przez przecięcie linii 2x + y - 1 = 0 i x + y + 1 = 0, na pół.

§ 27. Analityczna definicja płaszczyzny w przestrzeni

Definicja. Wektor normalny do płaszczyzny nazwiemy wektorem niezerowym, którego dowolny przedstawiciel jest prostopadły do ​​danej płaszczyzny.

Komentarz. Oczywiste jest, że jeśli co najmniej jeden przedstawiciel wektora jest prostopadły do ​​płaszczyzny, to wszyscy pozostali przedstawiciele wektora są prostopadłe do tej płaszczyzny.

Niech w przestrzeni będzie dany kartezjański układ współrzędnych.

Niech będzie dana płaszczyzna, = (A, B, C) – wektor normalny do tej płaszczyzny, punkt M (x 0 , y 0 , z 0) należy do płaszczyzny a.

Dla dowolnego punktu N(x, y, z) płaszczyzny a wektory i są ortogonalne, czyli ich iloczyn skalarny jest równy zero: = 0. Ostatnią równość napiszmy we współrzędnych: A(x - x 0 ) + B(y - y 0) + C(z - z 0) = 0.

Niech -Ax 0 - By 0 - Cz 0 = D, następnie Ax + By + Cz + D = 0.

Weźmy punkt K (x, y) taki, że Ax + By + Cz + D = 0. Ponieważ D = -Ax 0 - By 0 - Cz 0, to A(x - x 0) + B(y - y 0) + C(z - z 0) = 0. Ponieważ współrzędne skierowanego odcinka = (x - x 0, y - y 0, z - z 0), ostatnia równość oznacza, że ​​^, a zatem K О a.

Udowodniliśmy zatem następujące twierdzenie:

Twierdzenie. Dowolną płaszczyznę w przestrzeni w kartezjańskim układzie współrzędnych można określić równaniem w postaci Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0), gdzie (A, B, C) są współrzędne wektora normalnego do tej płaszczyzny.

Jest też odwrotnie.

Twierdzenie. Dowolne równanie postaci Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) w kartezjańskim układzie współrzędnych określa pewną płaszczyznę, a (A, B, C) są współrzędnymi normalnej wektor do tej płaszczyzny.

Dowód.

Weźmy punkt M (x 0 , y 0 , z 0) taki, że Ax 0 + By 0 + Cz 0 + D = 0 i wektor = (A, B, C) ( ≠ q).

Płaszczyzna (i tylko jedna) przechodzi przez punkt M prostopadle do wektora. Zgodnie z poprzednim twierdzeniem płaszczyznę tę wyznacza równanie Ax + By + Cz + D = 0.

Definicja. Nazywa się równanie postaci Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) ogólne równanie płaszczyzny.

Przykład.

Zapiszmy równanie płaszczyzny przechodzącej przez punkty M (0,2,4), N (1,-1,0) i K (-1,0,5).

1. Znajdź współrzędne wektora normalnego do płaszczyzny (MNK). Ponieważ iloczyn wektorowy ` jest ortogonalny do wektorów niewspółliniowych i , to wektor jest współliniowy ` .

= (1, -3, -4), = (-1, -2, 1);

´ = (-11, 3, -5).

Zatem jako wektor normalny bierzemy wektor = (-11, 3, -5).

2. Skorzystajmy teraz z wyników pierwszego twierdzenia:

równanie tej płaszczyzny A(x - x 0) + B(y - y 0) + C(z - z 0) = 0, gdzie (A, B, C) są współrzędnymi wektora normalnego, (x 0 , y 0 , z 0) – współrzędne punktu leżącego na płaszczyźnie (np. punkt M).

11(x - 0) + 3(y - 2) - 5(z - 4) = 0

11x + 3y – 5z + 14 = 0

Odpowiedź: -11x + 3y - 5z + 14 = 0.

Ćwiczenia.

1) Napisz równanie płaszczyzny jeśli

(1) płaszczyzna przechodzi przez punkt M (-2,3,0) równoległy do ​​płaszczyzny 3x + y + z = 0;

(2) płaszczyzna zawiera oś (Ox) i jest prostopadła do płaszczyzny x + 2y – 5z + 7 = 0.

2) Zapisz równanie płaszczyzny przechodzącej przez trzy dane punkty.

§ 28. Analityczna definicja półprzestrzeni*

Komentarz*. Niech jakiś samolot zostanie naprawiony. Pod połowa przestrzeni będziemy rozumieć zbiór punktów leżących po jednej stronie danej płaszczyzny, czyli dwa punkty leżą w tej samej półprzestrzeni, jeśli łączący je odcinek nie przecina danej płaszczyzny. Ten samolot nazywa się granicę tej półprzestrzeni. Nazwiemy połączenie tej płaszczyzny i półprzestrzeni zamknięta półprzestrzeń.

Niech kartezjański układ współrzędnych zostanie ustalony w przestrzeni.

Twierdzenie. Niech płaszczyzna a będzie dana równaniem ogólnym Ax + By + Cz + D = 0. Wtedy jedną z dwóch półprzestrzeni, na które płaszczyzna a dzieli przestrzeń, jest dana nierówność Ax + By + Cz + D > 0 , a drugą półprzestrzeń wyznacza nierówność Ax + By + Cz + D< 0.

Dowód.

Narysujmy wektor normalny = (A, B, C) do płaszczyzny a z punktu M (x 0 , y 0 , z 0) leżącego na tej płaszczyźnie: = , M О a, MN ^ a. Płaszczyzna dzieli przestrzeń na dwie półprzestrzenie: b 1 i b 2. Jest oczywiste, że punkt N należy do jednej z tych półprzestrzeni. Bez utraty ogólności założymy, że N О b 1 .

Udowodnimy, że półprzestrzeń b 1 jest określona przez nierówność Ax + By + Cz + D > 0.

1) Weźmy punkt K(x,y,z) znajdujący się w półprzestrzeni b 1 . Kąt Ð NMK jest kątem pomiędzy wektorami a - ostrym, dlatego iloczyn skalarny tych wektorów jest dodatni: > 0. Zapiszmy tę nierówność we współrzędnych: A(x - x 0) + B(y - y 0) + C(z - z 0) > 0, czyli Ax + By + Cy - Ax 0 - By 0 - C z 0 > 0.

Ponieważ M О b 1, to Ax 0 + By 0 + C z 0 + D = 0, zatem -Ax 0 - By 0 - C z 0 = D. Dlatego ostatnią nierówność można zapisać w następujący sposób: Ax + By + Cz + D > 0.

2) Wybierz punkt L(x,y) taki, że Ax + By + Cz + D > 0.

Przepiszmy nierówność, zastępując D przez (-Ax 0 - By 0 - C z 0) (ponieważ M О b 1, następnie Ax 0 + By 0 + C z 0 + D = 0): A(x - x 0) + B(y - y 0) + C(z - z 0) > 0.

Wektor o współrzędnych (x - x 0,y - y 0, z - z 0) jest wektorem, zatem wyrażenie A(x - x 0) + B(y - y 0) + C(z - z 0) można rozumieć jako iloczyn skalarny wektorów i . Ponieważ iloczyn skalarny wektorów i jest dodatni, kąt między nimi jest ostry i punkt L О b 1 .

Podobnie możemy udowodnić, że półprzestrzeń b 2 jest dana przez nierówność Ax + By + Cz + D< 0.

Notatki.

1) Jest oczywiste, że dowód podany powyżej nie zależy od wyboru punktu M na płaszczyźnie a.

2) Jest oczywiste, że tę samą półprzestrzeń można zdefiniować za pomocą różnych nierówności.

Jest też odwrotnie.

Twierdzenie. Dowolna nierówność liniowa postaci Ax + By + Cz + D > 0 (lub Ax + By + Cz + D< 0) (A 2 + B 2 + C 2 ≠ 0) задает в пространстве в декартовой системе координат полупространство с границей Ax + By + Cz + D = 0.

Dowód.

Równanie Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) w przestrzeni definiuje pewną płaszczyznę a (patrz § ...). Jak wykazano w poprzednim twierdzeniu, jedna z dwóch półprzestrzeni, na które płaszczyzna dzieli przestrzeń, jest dana przez nierówność Ax Ax + By + Cz + D > 0.

Notatki.

1) Jest oczywiste, że zamkniętą półprzestrzeń można zdefiniować za pomocą nieścisłej nierówności liniowej, a każda nieścisła nierówność liniowa w kartezjańskim układzie współrzędnych definiuje zamkniętą półprzestrzeń.

2) Każdy wielościan wypukły można zdefiniować jako przecięcie zamkniętych półprzestrzeni (których granicami są płaszczyzny zawierające ściany wielościanu), czyli analitycznie - przez układ liniowych nieścisłych nierówności.

Ćwiczenia.

1) Udowodnić dwa twierdzenia przedstawione dla dowolnego afinicznego układu współrzędnych.

2) Czy prawdą jest odwrotność, że dowolny system nieścisłych nierówności liniowych definiuje wielokąt wypukły?

Ćwiczenia.

1) Zbadaj względne położenie dwóch płaszczyzn określonych równaniami ogólnymi w kartezjańskim układzie współrzędnych i wypełnij tabelę.