Każdy z 24 uczestników zawodów strzeleckich. Rozwiązywanie zadań na temat „średnia arytmetyczna, moda, zakres i mediana

Zadania na statystykach

1. W ciągu kwartału Siergiej otrzymał następujące oceny z matematyki: jedną „dwójkę”, trzy „trójki”, pięć „czwórek” i jedną „pięć”. Znajdź sumę średniej arytmetycznej i tryb jej oszacowań.

Odpowiadać. 8,6.

2. Zarejestrowana średnia dzienna temperatura (w stopniach) w Moskwie przez pięć dni w miesiącu październiku: 6; 7; 7; 9; 11. Czym różni się średnia arytmetyczna tego zbioru liczb od jego mediany?

Odpowiadać. 1.

3. Rejestruje się wzrost (w centymetrach) pięciu uczniów: 156, 166, 134, 132, 132. Na ile średnia arytmetyczna tego zestawu liczb różni się od jego mediany?

Odpowiadać. 10.

4. W tabeli przedstawiono wyniki czterech strzelców, pokazane przez nich podczas treningu.

Imię strzelca	Liczba strzałów	Liczba trafień
Weronika

Odpowiadać. 2.

5. Pięciu znajomych znalazło odchylenia (w minutach) swoich zegarków na rękę od dokładnego czasu: -2, 0, 3, -5, -1. Znajdź sumę średniej arytmetycznej tego zbioru liczb i jego mediany.

Odpowiadać. - 2.

6. Koszt (w rublach) glazurowanego twarogu „Vkusnyashka” w sklepach dzielnicy jest rejestrowany: 3, 5, 6, 7, 9, 4, 8. Jak bardzo różni się średnia arytmetyczna tego zestawu od jego mediany ?

Odpowiadać. 0.

7. W serii cyfr 3, 7, 15, ___, 23 brakuje jednej cyfry. Znajdź tę liczbę, jeśli wiesz, że średnia arytmetyczna tej serii liczb wynosi 13.

Odpowiadać. 17.

8. Rejestruje się zużycie energii elektrycznej (w kW) przez określoną rodzinę w ciągu pierwszych pięciu miesięcy roku: 138, 140, 135, 132, 125. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany ?

Odpowiadać. 2.

9. Tabela przedstawia dane o sprzedaży ziemniaków na pewnym stoisku warzywnym w ciągu tygodnia.

Dzień tygodnia	Poniedziałek	Wtorek	Środa	Czwartek	Piątek	Sobota	Niedziela
Ilość sprzedanych ziemniaków, kg

Ile kilogramów ziemniaków sprzedawano średnio dziennie w tym tygodniu?

Odpowiadać. 125.

10. Średnia arytmetyczna ciągu dziesięciu liczb wynosi 16. Szeregowi temu przypisano liczbę 27. Jaka jest średnia arytmetyczna nowego ciągu liczb?

Odpowiadać. 17.

11. Średnia arytmetyczna szeregu dziesięciu liczb wynosi 16. Z tego szeregu została wykreślona liczba 7. Jaka jest średnia arytmetyczna nowego szeregu liczb?

Odpowiadać. 17.

12. Każdy z dziewięciu uczestników zawodów strzeleckich oddał dziesięć strzałów. Rejestrowana jest liczba trafień w tarczę każdego z tych uczestników: 12, 10, 5, 4, 6, 8, 9, 5, 4. Na ile średnia arytmetyczna tego zestawu liczb różni się od jego mediany?

Odpowiadać. 1.

13. Pięciu pracowników departamentu kupiło akcje o tej samej wartości jakiejś spółki akcyjnej. Zapisywana jest liczba tych akcji nabytych przez każdego z pracowników: 5, 10, 12, 7, 3. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 0,4.

14. Uczelnia prowadzi codzienną ewidencję otrzymanych pism. Na podstawie tego zestawienia uzyskano następujące serie danych (liczba listów otrzymywanych dziennie w tym tygodniu): 39, 43, 40, 56, 38, 21,1. Jak bardzo średnia tego zestawu liczb różni się od jego mediany?

Odpowiadać. 5.

15. W ciągu kwartału Aleksiej otrzymał następujące stopnie z fizyki: dwie „dwójki”, dwie „trójki”, cztery „czwórki” i dwie „piątki”. Znajdź sumę średniej arytmetycznej i mediany jej wyników.

Odpowiadać. 8.

16. Średnia dzienna temperatura (w stopniach) w Moskwie została zarejestrowana przez pięć dni we wrześniu: 15, 10, 18, 11, 11. Jak bardzo różni się średnia arytmetyczna tego zestawu liczb od jego trybu?

Odpowiadać. 2.

17. Rejestruje się wzrost (w centymetrach) pięciu uczniów: 164, 162, 156, 132, 136. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 6.

18. W tabeli przedstawiono wyniki czterech strzelców, pokazane przez nich na treningu.

Imię strzelca	Liczba strzałów	Liczba trafień
Weronika

Trener zdecydował się wysłać na zawody strzelca z wyższym względnym współczynnikiem trafień. Którego strzelca wybierze trener?

1) Weronika 2) Evgenia 3) Oleg 4) Irina

Odpowiadać. 2.

19. Pięciu znajomych znalazło odchylenia (w minutach) odczytów ich zegarków na rękę od dokładnego czasu: -1, 0, -4, -1, 1. Znajdź sumę średniej arytmetycznej tego zestawu liczb i jego trybu.

Odpowiadać. - 2.

20. Koszt (w rublach) glazurowanego skrzepu serowego „Baby” w sklepach osiedla jest rejestrowany: 4, 4, 6, 7, 11, 9, 8. Znajdź sumę średniej arytmetycznej tego zestawu i jego tryb.

Odpowiadać. 11.

21. W serii cyfr 3, 7, 15, ___, 21 brakuje jednej cyfry. Znajdź tę liczbę, jeśli wiesz, że średnia arytmetyczna tej serii liczb wynosi 12.

Odpowiadać. 14.

22. Rejestruje się zużycie energii elektrycznej (w kW) przez pewną rodzinę w ciągu pierwszych pięciu miesięcy roku: 146, 140, 138, 136, 130. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany ?

Odpowiadać. 0.

23. Rejestruje się zużycie energii elektrycznej (w kW) przez pewną rodzinę w ciągu pierwszych pięciu miesięcy roku: 152, 150, 148, 140, 130. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 4.

24. W tabeli przedstawiono dane dotyczące sprzedaży ziemniaków na pewnym stoisku warzywnym w ciągu tygodnia.

Dzień tygodnia	Poniedziałek	Wtorek		Czwartek	Piątek	Sobota	Niedziela
Ilość sprzedanych ziemniaków, kg

Ile wynosi średnia arytmetyczna liczby ziemniaków (w kg) sprzedanych dziennie na tym stoisku od mediany?

Odpowiadać. 5.

25. Średnia arytmetyczna ciągu dziesięciu liczb wynosi 18. Szeregowi temu przypisano liczbę 29. Jaka jest średnia arytmetyczna nowego ciągu liczb?

Odpowiadać. 19.

26. Średnia arytmetyczna szeregu dziesięciu liczb wynosi 18. Z tego szeregu została skreślona liczba 36. Jaka jest średnia arytmetyczna nowego szeregu liczb?

Odpowiadać. 16.

27. Każdy z dziewięciu uczestników zawodów strzeleckich oddał dziesięć strzałów. Rejestrowana jest liczba trafień w tarczę każdego z tych uczestników: 9, 8, 6, 5, 6, 9, 6, 5, 9. Na ile średnia arytmetyczna tego zestawu liczb różni się od jego mediany?

Odpowiadać. 1.

28. Pięciu pracowników departamentu nabyło akcje o tej samej wartości jakiejś spółki akcyjnej. Rejestrowana jest liczba tych akcji nabytych przez każdego z pracowników: 5, 7, 10, 11, 7. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 1.

29. Uczelnia prowadzi codzienną ewidencję otrzymanych listów. Na podstawie tego zestawienia uzyskano następujące serie danych (liczba listów otrzymywanych dziennie w tym tygodniu): 39, 42, 45, 50, 38, 0,17. Jak bardzo średnia tego zestawu liczb różni się od jego mediany?

Odpowiadać. 6.

30. Średnia dzienna temperatura (w stopniach) w Moskwie została zarejestrowana przez pięć dni w miesiącu czerwcu: 25, 27, 29, 24, 25. Na ile średnia arytmetyczna tego zestawu liczb różni się od jego mediany?

Odpowiadać. 1.

31. Rejestruje się wzrost (w centymetrach) pięciu uczniów: 164, 161, 152, 150, 148. Na ile średnia arytmetyczna tego zestawu liczb różni się od jego mediany?

Odpowiadać. 3.

32. W tabeli przedstawiono wyniki czterech strzelców, pokazane przez nich podczas treningu.

Imię strzelca	Liczba strzałów	Liczba trafień
Anastazja

Trener zdecydował się wysłać na zawody strzelca z wyższym względnym współczynnikiem trafień.

Którego strzelca wybierze trener?

1) Anastazja 2) Jewgienij 3) Siergiej 4) Irina

Odpowiadać. 3.

33. Odnotowuje się koszt (w rublach) śmietany w sklepach osiedla: 24, 25, 27, 27, 27, 24, 28. Na ile średnia arytmetyczna tego zestawu różni się od jego mediany?

Odpowiadać. 1.

34. W serii cyfr 3, 7, 17, ___, 23 brakuje jednej cyfry. Znajdź tę liczbę, jeśli wiesz, że średnia arytmetyczna tej serii liczb wynosi 14.

Odpowiadać. 20.

35. Rejestruje się zużycie energii elektrycznej (w kWh) przez pewną rodzinę w ciągu pierwszych pięciu miesięcy roku: 141, 130, 130, 124, 120. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 1.

36. W tabeli przedstawiono dane dotyczące sprzedaży marchwi na pewnym straganie z warzywami w ciągu tygodnia.

Dzień tygodnia	Poniedziałek	Wtorek		Czwartek	Piątek	Sobota	Niedziela
Ilość sprzedanych marchwi, kg

Ile kilogramów marchwi sprzedawano średnio dziennie w tym tygodniu?

Odpowiadać. 54.

37. Kością rzuca się 100 razy. Wyniki przedstawiono w tabeli.

Liczba odrzuconych punktów
Liczba wystąpień zdarzenia

Jaka jest względna częstotliwość zdobywania co najmniej pięciu punktów?

Odpowiadać. 0,35.

38. Średnia arytmetyczna ciągu dziesięciu liczb wynosi 12. Szeregowi temu przypisano liczbę 34. Jaka jest średnia arytmetyczna nowego ciągu liczb?

Odpowiadać. 14.

39. Koszykarz, po wykonaniu 50 rzutów na treningu, uderzył w ring 36 razy. Jaka jest względna częstotliwość uderzeń tego koszykarza?

Odpowiadać. Czernow w białym garniturze, Biełow w szarym, Sierow w czarnym.

40. Średnia arytmetyczna szeregu dziesięciu liczb wynosi 14. Z tego szeregu została wykreślona liczba 32. Jaka jest średnia arytmetyczna nowego szeregu liczb?

Odpowiadać. 12.

41. Każdy z siedmiu uczniów 9 klasy w danym dniu notował czas (w minutach) poświęcony na odrabianie lekcji z algebry. Wynikiem jest następujący ciąg liczb: 24, 45, 40, 50, 30, 35, 42. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 2.

42. Pięciu pracowników pewnej spółki akcyjnej nabyło akcje o tej samej wartości tej spółki. Zapisywana jest liczba tych akcji nabytych przez każdego z pracowników: 7, 12, 15, 8, 3. Na ile średnia arytmetyczna tego zbioru liczb różni się od jego mediany?

Odpowiadać. 1.

43. Każdy z siedmiu uczestników zawodów strzeleckich oddał dziesięć strzałów. Rejestrowana jest liczba trafień w tarczę każdego z tych uczestników: 9, 6, 5, 8, 9, 6, 6. Na ile średnia arytmetyczna drugiego zestawu liczb różni się od jego trybu?

Odpowiadać. 1.

44. Tabela przedstawia dane o sprzedaży aparatów cyfrowych w jednym z biur kampanii w ciągu tygodnia.

Dzień tygodnia	Poniedziałek	Wtorek		Czwartek	Piątek	Sobota	Niedziela
Ilość sprzedanych aparatów cyfrowych, szt.

Jaka jest średnia liczba aparatów cyfrowych sprzedawanych dziennie w tym biurze?

Odpowiadać. 19.

45. Tabela przedstawia dane o sprzedaży telefonów komórkowych w jednym z biur kampanii w ciągu tygodnia.

Dzień tygodnia	Poniedziałek	Wtorek	Środa	Czwartek	Piątek	Sobota	Niedziela
Ilość sprzedanych telefonów, szt.

Jaka jest średnia liczba telefonów komórkowych sprzedawanych dziennie w tym biurze?

Odpowiadać. 37.

46. ​​​​Tabela przedstawia wyniki czterech strzelców, pokazane przez nich na treningu.

Imię strzelca	Liczba strzałów	Liczba trafień
Weronika

Trener zdecydował się wysłać na zawody strzelca z wyższym względnym współczynnikiem trafień. Którego strzelca wybierze trener?

1) Weronika 2) Evgenia 3) Oleg 4) Irina

Odpowiadać. 2.

47. Pięciu znajomych znalazło odchylenia (w minutach) odczytów ich zegarków na rękę od dokładnego czasu: -1, 0 -3, -2, 1. Znajdź sumę średniej arytmetycznej tego zestawu liczb i jego mediany.

Odpowiadać. -2.

48. Na lekcji teorii prawdopodobieństwa sześciu facetów rzuciło monetami. W tabeli zapisali, ile razy dostali orły i reszki.

1. Ile razy Vova dostała głowy?

2. Co Dasha dostawała częściej: głowy czy ogony i ile razy?

3. Który z facetów ma najwięcej ogonów?

4. Ile razy wyszło to na głowę?

5. Ile razy Olya rzuciła monetą?

6. Który z uczniów rzucił monetą najczęściej i ile?

7. Ile razy w sumie uczniowie rzucili monetą?

Odpowiadać. 1) 11; 2) ogony, 8; 3) w Azji; 4) 48; 5) 13; 6) Asiu, 22 lata;

49. Na lekcji teorii prawdopodobieństwa Tanya, Wania, Mitya i Vika rzucali kośćmi. W tabeli zapisali, ile razy wypadła każda liczba.

Tanya
Wania
Mitya
Vika

1. Ile razy Vika wyrzuciła trójkę?

2. Jaką wartość Wania najczęściej odpadała i ile razy?

3. Który ma najwięcej czwórek?

4. Ile razy w sumie padło pięć?

5. Ile razy Tanya rzuciła kostką?

6. Ile razy w sumie uczniowie rzucili kostką?

Odpowiadać. czternaście; 2) Dwa, 11; 3) Vicki; 4) 28; 5) 56;

50. Szkoła ma dwie szóste klasy. Na pracy kontrolnej w 6 klasie "A" otrzymano 5 dwójek, aw 6 "B" - 4 dwójki. W tym samym czasie 20 studentów uczy się na 6 "A", a 25 na 6 "B".

a) Jaki procent uczniów w 6 „A” otrzymał dwójkę?

b) Jaki procent uczniów w 6 „B” otrzymał dwójkę?

c) Znajdź średnią arytmetyczną wyników zadań a) ib).

d) Sprawdź, jaki procent wszystkich szóstoklasistów otrzymało
licho.

e) Wyjaśnij, dlaczego wyniki w zadaniach c) id) są różne.

Odpowiadać. a) 25%; b) 16%; c) 20,5%; d) 20%; e) ponieważ w klasach jest różna liczba uczniów.

III. Zadania do samodzielnej pracy nad badanym tematem

III. Zadania do samodzielnej pracy nad badanym tematem

III. Zadania do samodzielnej pracy nad badanym tematem

IV. Zadania do samodzielnej pracy nad badanym tematem

Otrzymasz zadania z wyborem odpowiedzi (w każdym zadaniu tylko jedna odpowiedź jest poprawna). Wybierz poprawną odpowiedź (10 punktów).

„PODSTAWOWE POJĘCIA STATYSTYKI MATEMATYCZNEJ”

1. Poniżej przedstawiamy rozmiary ubrań dla 50 uczniów w klasie 9:

50 40 44 44 46 46 44 48 46 44

38 44 48 50 40 42 50 46 54 44

42 42 52 44 46 38 46 42 44 48

46 48 44 40 52 44 48 50 46 46

48 40 46 42 44 50 46 44 46 48.

Na podstawie tych danych skompiluj tabele rozkładów według częstości i względnej częstości wartości zmiennej losowej X - rozmiary ubrań dla uczniów w klasie 9.

2. Próbka składa się ze wszystkich liter zawartych w dwuwierszu: „... To drzewo to sosna,

A los sosny jest jasny…”.

a) Zapisz serie danych (wartości wariantów) próbki;

b) znaleźć wielkość próby;

c) określić opcje krotności i częstotliwości „O”;

d) Jaka jest najwyższa procentowa częstotliwość opcji próbkowania?

3. Badając obciążenie pracą, poproszono 32 uczniów klas ósmych o zapisanie czasu (z dokładnością do 0,1 godziny), jaki spędzili danego dnia na odrabianiu prac domowych. Otrzymaliśmy następujące dane:

2,7; 2,5; 3,1; 3,2; 3,4; 1,6; 1,8; 4,2;

2,6; 3,4; 3,2; 2,9; 1,9; 1,5; 3,7; 3,6;

3,1; 2,9; 2,8; 1,5; 3,1; 3,4; 2,2; 2,8;

4,1; 2,4; 4,3; 1,9; 3,6; 1,8; 2,8; 3.9.

Przedstaw uzyskane dane jako szeregi przedziałowe z przedziałami o długości 0,5.

4. W tabeli przedstawiono rozkład rekrutów okręgowych według wzrostu.

Wzrost (cm	Częstotliwość
155-160
160-165
165-170
170-175
175-180
180-185
185-190
190-195

Zgodnie z tą tabelą sporządź nową tabelę w odstępie 10 cm Znajdź średnią wysokość rekrutów.

5. Średnie dobowe przeróbki cukru (w tys. centów) przez zakłady przemysłu cukrowniczego danego regionu przedstawiono poniżej:

12,0; 13,6; 14,7; 18,9; 17,3; 16,1;

20,1; 16,9; 19,1; 18,4; 17,8; 15,6;

20,8; 19,7; 18,9; 19,0; 16,1; 15,8.

Przedstaw te dane jako szereg przedziałów z przedziałami trzech jednostek. Sprawdź, ile cukru roślina w regionie przetwarza średnio dziennie: a) zastępując każdy przedział jego środkiem; b) za pomocą danego wiersza. W którym przypadku średni wynik będzie dokładniejszy?

6. W gospodarstwie przeznaczono trzy działki pod pszenicę o powierzchni 12 ha, 8 ha i 6 ha. Przeciętny plon na pierwszym poletku wynosi 18 centów z hektara, na drugim 19 centów z hektara, na trzecim 23 centów z hektara. Jaki jest średni plon pszenicy w tym gospodarstwie?

7. Na zawodach w łyżwiarstwie figurowym sędziowie przyznali zawodnikowi następujące oceny: 5.2; 5.4; 5,5; 5.4; 5.1; 5.1; 5.4; 5.5 5.3.

8. Każdy z 24 uczestników zawodów strzeleckich oddał 10 strzałów. Odnotowując za każdym razem liczbę trafień w cel, otrzymaliśmy następującą serię danych:

6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9,

7, 7, 9, 8, 6, 6, 5, 6, 4, 3, 6, 5.

Dla wynikowych serii danych znajdź średnią arytmetyczną, medianę, zakres i tryb. Co charakteryzuje każdy z tych wskaźników?

9. Poniżej przedstawiono średnie dzienne przeróbki cukru (w tys. centów) przez zakłady przemysłu cukrowniczego danego regionu.

12,2; 13,2; 13,7; 18,0; 18,6; 12,2; 18,5; 12,4; 14,2; 17,8.

Dla wynikowych serii danych znajdź średnią arytmetyczną, medianę, zakres i tryb. Co charakteryzuje każdy z tych wskaźników?

10. Znajdź zakres, tryb i medianę próbki:

a) 1, 3, -2, 4, -2, 0, 2, 3, 1, -2, 4;

b) 0,2; 0,4; 0,1; 0,5; 0,1; 0,2; 0,3; 0,5; 0,4; 0,6.

11. W tabeli przedstawiono dane dotyczące stażu pracy (w latach) pracowników laboratorium. Znajdź średnią, tryb, medianę rozważanej populacji.

12. Znajdź wariancję zbioru wartości zmiennej losowej X określonej przez rozkład częstości.

15. Określ, która próbka -1, 0, 2, 3, 5, 3 lub -5, -3, 0, -3, -1 ma mniej danych rozproszonych wokół średniej.

16. Podczas sprawdzania 70 prac w języku rosyjskim odnotowano liczbę błędów ortograficznych popełnionych przez uczniów. Otrzymane serie danych przedstawiono w postaci tabeli częstości.

Jaka jest największa różnica w liczbie popełnionych błędów? Jaka jest typowa liczba błędów dla tej grupy uczniów? Wskaż, jakie cechy statystyczne zostały użyte w odpowiedzi na pytania.

Data __________

Temat lekcji: Średnia arytmetyczna, zakres i tryb.

Cele Lekcji: powtarzanie pojęć takich cech statystycznych jak średnia arytmetyczna, zakres i moda, kształtowanie umiejętności znajdowania średnich cech statystycznych różnych szeregów; rozwijać logiczne myślenie, pamięć i uwagę; wychowywać u dzieci pracowitość, dyscyplinę, wytrwałość, dokładność; rozwijać u dzieci zainteresowanie matematyką.

Podczas zajęć

Organizacja klas

Powtórzenie ( Równanie i jego pierwiastki)

Zdefiniuj równanie z jedną zmienną.

Jaki jest pierwiastek równania?

Co to znaczy rozwiązać równanie?

Rozwiązać równanie:

6x + 5 \u003d 23 -3x 2 (x - 5) + 3x \u003d 11 -2x 3x - (x - 5) \u003d 14 -2x

Aktualizacja wiedzy powtórz koncepcje takich cech statystycznych, jak średnia arytmetyczna, zakres, tryb i mediana.

Statystyka jest nauką, która gromadzi, przetwarza, analizuje dane ilościowe dotyczące różnorodnych zjawisk masowych występujących w przyrodzie i społeczeństwie.

Przeciętny to suma wszystkich liczb podzielona przez ich liczbę. (Średnia arytmetyczna nazywana jest średnią wartością szeregu liczbowego).

Zakres liczb to różnica między największą a najmniejszą z tych liczb.

Moda z serii numer - To liczba, która w tej serii występuje częściej niż w innych.

Mediana uporządkowany ciąg liczb o nieparzystej liczbie członków nazywamy liczbą zapisaną w środku, a o parzystej liczbie członków nazywamy średnią arytmetyczną dwóch liczb zapisanych w środku.

Statystyka słowa jest tłumaczona z języka łacińskiego status - stan, stan rzeczy.

Charakterystyki statystyczne: średnia arytmetyczna, zakres, moda, mediana.

Asymilacja nowego materiału

Zadanie numer 1: 12 siódmoklasistów zostało poproszonych o zaznaczenie czasu (w minutach) spędzonego na odrabianiu zadań domowych z algebry. Otrzymaliśmy następujące dane: 23,18,25,20,25,25,32,37,34,26,34,25. Ile minut średnio spędzali uczniowie na odrabianiu lekcji?

Rozwiązanie: 1) znajdź średnią arytmetyczną:

2) znajdź zakres serii: 37-18=19 (min)

3) moda 25.

Zadanie nr 2: W mieście Schastlivy mierzono ją codziennie o 18 00 temperatura powietrza (w stopniach Celsjusza przez 10 dni), w wyniku czego tabela została wypełniona:

T Poślubić = 0 Z,

Zakres = 25-13=12 0 Z,

Zadanie numer 3: Znajdź zakres liczb 2, 5, 8, 12, 33.

Rozwiązanie: Największa liczba to 33, najmniejsza to 2. Zatem zakres to: 33 - 2 = 31.

Zadanie nr 4: Znajdź tryb serii dystrybucyjnej:

a) 23 25 27 23 26 29 23 28 33 23 (tryb 23);

b) 14 18 22 26 30 28 26 24 22 20 (tryby: 22 i 26);

c) 14 18 22 26 30 32 34 36 38 40 (bez mody).

Zadanie numer 5 : Znajdź średnią arytmetyczną, zakres i mody szeregu liczb 1, 7, 3, 8, 7, 12, 22, 7, 11,22,8.

Rozwiązanie: 1) Najczęściej w tej serii liczb pojawia się liczba 7 (3 razy). Jest to tryb danej serii liczb.

Rozwiązanie do ćwiczeń

ALE) Znajdź średnią arytmetyczną, medianę, zakres i modę szeregu liczb:

1) 32, 26, 18, 26, 15, 21, 26;

2) 21, 18, 5, 25, 3, 18, 5, 17, 9;

3) 67,1 68,2 67,1 70,4 68,2;

4) 0,6 0,8 0,5 0,9 1,1.

B) Średnia arytmetyczna ciągu dziesięciu liczb wynosi 15. Szeregowi temu przypisano liczbę 37. Jaka jest średnia arytmetyczna nowego ciągu liczb.

W) W serii liczb 2, 7, 10, __, 18, 19, 27 jeden numer został wymazany. Przywróć to, wiedząc, że średnia arytmetyczna tej serii liczb wynosi 14.

G) Każdy z 24 uczestników zawodów strzeleckich oddał dziesięć strzałów. Odnotowując każdorazowo liczbę trafień w cel, otrzymywaliśmy następujące serie danych: 6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9, 7, 7, 9, 8 , 6, 6, 5 , 6, 4, 3, 6, 5. Znajdź zakres i modę dla tej serii. Co charakteryzuje każdy z tych wskaźników.

Zreasumowanie

Co to jest średnia arytmetyczna? Moda? Mediana? Trzepnąć?

Praca domowa:

№164 (powtórzenie), s.36-39 przeczytaj

№167(a,b), #177, 179

Sekcje: Matematyka

Statystyka(od łac. stan rzeczy, stan rzeczy) to nauka zajmująca się pozyskiwaniem, przetwarzaniem i analizowaniem danych ilościowych o różnych zjawiskach masowych występujących w przyrodzie i społeczeństwie. Statystyka bada liczebność poszczególnych grup ludności, produkcję i konsumpcję różnego rodzaju produktów, zasoby naturalne. Wyniki badań statystycznych są szeroko wykorzystywane do praktycznych i naukowych wniosków. Załącznik 2.

Średnia arytmetyczna, zakres i tryb.

• Średnia arytmetyczna szeregu liczb nazywamy ilorazem dzielenia sumy tych liczb przez liczbę członów.

Badając obciążenie dydaktyczne uczniów, wyodrębniono grupę 12 siódmoklasistów. Poproszono ich o zaznaczenie czasu (w minutach) spędzonego w danym dniu na odrabianiu zadań domowych z algebry. Otrzymaliśmy następujące dane:

23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Dzięki tej serii danych możemy określić, ile minut uczniowie spędzili średnio na odrabianiu zadań domowych z algebry.

Aby to zrobić, te liczby muszą zostać dodane, a suma podzielona przez 12.

= = 27

Powstała liczba 27 nazywa się Średnia arytmetyczna rozważane serie liczb.

Nr 1. Znajdź średnią arytmetyczną liczb:

A) 24, 22, 27, 20.16, 31
B) 11, 9, 7, 6, 2, 0,1
C) 30, 5, 23, 5, 28, 30
D) 144, 146, 114, 138.

Nr 2. Tabela przedstawia dane dotyczące sprzedaży w ciągu tygodnia ziemniaków przywożonych do namiotu warzywnego:

Ile średnio dziennie sprzedawano w tym tygodniu ziemniaki?

Nr 3. Na świadectwie dojrzałości czterech przyjaciół - absolwentów szkół - miało następujące oceny:

Ilyin: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4
Romanow: 3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4
Semenov: 3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4
Popow: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4.

Z jakim średnim wynikiem każdy z tych absolwentów ukończył szkołę średnią?

• Przeciągnij rząd liczb

to różnica między największą a najmniejszą z tych liczb.

Zakres serii jest znajdowany, gdy chcą określić, jak duży jest rozrzut danych w serii.

Nr 1. Każdy z 24 uczestników zawodów strzeleckich oddał dziesięć strzałów. Odnotowując każdorazowo liczbę trafień w cel, otrzymano następującą serię danych:

6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9, 7, 7, 9, 8, 6, 6, 5, 6, 4, 3, 6, 5.

Znajdź asortyment dla tej serii.

Nr 2. Na zawodach w łyżwiarstwie figurowym sędziowie przyznali zawodnikowi następujące oceny:

5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3.

Dla wynikowych serii liczb znajdź zakres i średnią arytmetyczną. Jakie jest znaczenie każdego z tych wskaźników?

Nr 3. Znajdź zakres szeregu liczb.

A) 32, 26, 18, 26, 15, 21, 26;
B) 21, 18,5, 25,3, 18,5, 17,9;
C) 67,1, 68,2, 67,1, 70,4, 68,2;
D) 0,6, 0,8, 0,5, 0,9, 1,1.

• Modne serie liczb

numer najczęściej występujący w danej serii to tzw.

Seria liczb może mieć więcej niż jeden tryb lub wcale.

47, 46, 50, 52, 47, 52, 49, 45, 43, 53 - (ma)

69, 68, 66, 70, 67, 71, 74, 63, 73, 72 - (nie posiada)

Przykład. Niech po uwzględnieniu części wyprodukowanych podczas zmiany przez pracowników jednego zespołu otrzymaliśmy następującą serię danych:

36, 35, 35,36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38 ,38, 39 ,39, 36.

Znajdź dla niego tryb szeregu liczb. W tym celu wygodnie jest wstępnie skompilować uporządkowaną serię liczb z uzyskanych danych, tj. taki szereg, w którym każda kolejna liczba jest mniejsza (lub większa) od poprzedniej.

Dostał:

35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39 ,39.

Odpowiadać. Numer 36 jest trybem tej serii liczb.

Nr 1. Znajdź modę szeregu liczb.

45, 48, 85, 31, 23, 45, 67, 45, 19, 48, 45, 85, 19, 27,45, 62, 45, 23, 67, 45, 89, 19, 87, 45, 56, 45, 43, 23, 12, 45, 78, 28, 19, 45, 65, 45, 81, 83, 45.

Nr 2. Tabela zawiera wyniki pomiarów dobowych na stacji meteorologicznej w południe temperatury powietrza (w stopniach Celsjusza) w pierwszej dekadzie marca:

Znajdź tryb szeregu liczb i wyciągnij wniosek, w jakich dniach w marcu temperatura powietrza była taka sama. Znajdź średnią temperaturę powietrza. Sporządź tabelę odchyleń od średniej temperatury powietrza w południe każdego dnia dekady.

Nr 3. W tabeli przedstawiono ilość części wyprodukowanych na zmianę przez pracowników jednego zespołu:

Dla serii liczb przedstawionych w tabeli znajdź tryb. Jakie jest znaczenie tego wskaźnika?

Mediana jako cecha statystyczna.

• Mediana uporządkowanego szeregu liczb o nieparzystej liczbie członków to liczba zapisana w środku, a mediana uporządkowanego szeregu liczb o parzystej liczbie członków to średnia arytmetyczna dwóch liczb zapisanych w środku.
  Mediana dowolnego szeregu liczb nazywana jest medianą odpowiedniego szeregu uporządkowanego.

Tabela przedstawia zużycie energii elektrycznej w styczniu przez mieszkańców dziewięciu mieszkań:

Z danych podanych w tabeli stwórzmy uporządkowaną serię:

64, 72, 72, 75, 78, 82, 85, 91, 93.

W wynikowej uporządkowanej serii jest dziewięć liczb. Łatwo zauważyć, że w środku rzędu znajduje się liczba 78 : cztery cyfry są zapisane po lewej stronie i cztery cyfry po prawej. Mówią, że liczba 78 jest liczbą środkową, czyli innymi słowy mediana, uporządkowany ciąg branych pod uwagę liczb (od łacińskiego słowa mediana co oznacza "średni"). Ta liczba jest uważana za medianę oryginalnej serii danych.

Załóżmy, że podczas zbierania danych o zużyciu energii elektrycznej do wskazanych dziewięciu mieszkań dodano jedną dziesiątą. Mamy ten stół:

Podobnie jak w pierwszym przypadku, otrzymane dane przedstawiamy w postaci uporządkowanej serii liczb:

64, 72, 72, 75, 78, 82, 85, 88, 91, 93.

Ta seria liczb ma parzystą liczbę członków, a w środku serii znajdują się dwie liczby: 78 oraz 82. Znajdźmy średnią arytmetyczną tych liczb: =80. Liczba 80, nie należąca do serii, dzieli tę serię na dwie grupy o równej wielkości: po lewej stronie znajduje się pięć członków serii, a po prawej również pięciu członków serii:

64, 72, 72, 75, , 85, 88, 91, 93.

Mówi się, że w tym przypadku medianą rozpatrywanych szeregów uporządkowanych, a także pierwotnych szeregów danych zapisanych w tabeli, jest liczba 80 .

Nr 1. Znajdź medianę szeregu liczb:

A) 30, 32, 37, 40, 41, 42, 45, 49, 52;
B) 102,104,205,207,327.408,417;
C) 16, 18, 20, 22, 24, 26;
D) 1,2 1,4 2,2, 2,6, 3,2 3,8 4,4 5, 6.

Nr 2. Tabela pokazuje liczbę zwiedzających wystawę w różne dni tygodnia:

Znajdź medianę szeregu liczb. Zbuduj histogram i zobacz, w którym dniu było więcej odwiedzających.

Nr 3. Poniżej przedstawiono średnie dobowe przeróbki cukru (w tys. centów) przez zakłady przemysłu cukrowniczego w niektórych regionach:

12,2, 13,2, 13,7, 18,0 18,6 12,2 18,5 12,4 14,2 17,8.

Znajdź medianę dla danej serii danych. Co charakteryzuje ten wskaźnik?

Zadania do samodzielnej pracy.

1. Na burmistrza miasta wystartuje trzech kandydatów: Aleksiejewa, Iwanow, Karpow (oznaczmy ich literami A, I, K). Przeprowadzając ankietę wśród 50 wyborców, dowiedzieliśmy się, na którego z kandydatów będą głosować. Otrzymaliśmy następujące dane: I, A, I, I, K, K, I, I, I, A, K, A, A, A, K, K, I, K, A, A, I, K, I, I, K, I, K, A, I, I, I, A, I, I, K, I, A, I, K, K, I, K, A, I, I, I, A, A, K, I. Przedstaw te dane w formie tabeli liczności.

2. Tabela przedstawia wydatki studenta na 4 dni:

Ktoś przetworzył te dane i zapisał:

a) 18 + 25 + 24 + 25 = 92; 92:4 = 23. (……………………….………..) = 23(p.)
b) 18, 24, 25, 25; (24 + 25): 2 = 24,5. (……………………………….) = 24,5 (p.)
c) 18, 25, 24, 25 (…………………….) = 25 (p.)
d) 25 - 18 \u003d 7. (……………………………) \u003d 7 (s.)

Nazwy charakterystyk statystycznych podano w nawiasach. Określ, która ze statystyk znajduje się w każdym zadaniu.

3. W ciągu roku za sprawdziany kontrolne z algebry Lena otrzymała następujące oceny: jedna „dwójka”, trzy „trójki”, cztery „czwórki” i trzy „piątki”. Znajdź średnią, tryb i medianę tych danych.

4. Prezes firmy otrzymuje 100 000 rubli. rocznie czterech jego zastępców otrzymuje po 20 000 rubli. rocznie, a 20 pracowników firmy otrzymuje 10 000 rubli. W roku. Znajdź wszystkie średnie (średnia arytmetyczna, tryb, mediana) wynagrodzeń w firmie.

Wizualna prezentacja informacji statystycznych.

1. Jednym z dobrze znanych sposobów przedstawiania serii danych jest konstruowanie wykresy słupkowe.

Wykresy kolumnowe są wykorzystywane, gdy chcą zilustrować dynamikę zmian danych w czasie lub rozkład danych uzyskanych w wyniku badań statystycznych.

Wykres słupkowy składa się z prostokątów o równej szerokości, o dowolnie wybranych podstawach, rozmieszczonych w takiej samej odległości od siebie. Wysokość każdego prostokąta jest równa (w wybranej skali) wartości badanej (częstotliwość).

2. Dla wizualnego przedstawienia relacji między częściami badanej populacji wygodnie jest użyć wykresy kołowe.

Jeżeli wynik badania statystycznego przedstawia się w postaci tabeli liczności względnych, to w celu skonstruowania wykresu kołowego okrąg dzieli się na sektory, których kąty środkowe są proporcjonalne do liczności względnych wyznaczonych dla każdej grupy.

Wykres kołowy zachowuje swoją widoczność i wyrazistość tylko w przypadku niewielkiej liczby części populacji.

3. Dynamikę zmian danych statystycznych w czasie ilustruje się często za pomocą wysypisko śmieci. Aby skonstruować wielokąt, na płaszczyźnie współrzędnych zaznacza się punkty, których odcięte są punkty w czasie, a rzędne są odpowiednimi danymi statystycznymi. Łącząc te punkty szeregowo z segmentami, uzyskuje się polilinię, która nazywa się wielokątem.

Jeżeli dane przedstawione są w postaci tabeli liczności lub liczności względnej, to aby zbudować wielokąt, na płaszczyźnie współrzędnych zaznacza się punkty, których odcięte są danymi statystycznymi, a rzędnymi są ich licznościami lub licznościami względnymi. Łącząc te punkty szeregowo z segmentami, uzyskuje się wielokąt dystrybucji danych.

4. Serie danych interwałowych są przedstawione za pomocą histogramy. Histogram to schodkowa figura składająca się z zamkniętych prostokątów. Podstawa każdego prostokąta jest równa długości interwału, a wysokość jest równa częstotliwości lub częstotliwości względnej. Na histogramie, w przeciwieństwie do wykresu słupkowego, podstawy prostokątów nie są wybierane arbitralnie, ale ściśle określone przez długość interwału.

Zadania do samodzielnej decyzji.

Nr 1. Zbuduj wykres słupkowy przedstawiający rozkład pracowników sklepów według kategorii płacowych, który przedstawia poniższa tabela:

Nr 2. W gospodarstwie tereny przeznaczone pod uprawy zbóż rozkładają się następująco: pszenica - 63%; owies - 16%; proso - 12%; kasza gryczana - 9%. Skonstruuj wykres kołowy ilustrujący rozkład powierzchni przeznaczonej na zboża.

Nr 3. W tabeli przedstawiono plony zbóż w 43 gospodarstwach regionu.

Skonstruuj wielokąt do podziału gospodarstw według plonu ziarna.

Nr 4. Badając rozkład rodzin mieszkających w domu, według liczby członków rodziny, sporządzono tabelę, w której dla każdej rodziny o tej samej liczbie członków wskazana jest względna częstotliwość:

Korzystając z tabeli, skonstruuj wielokąt częstości względnych.

Nr 5. Na podstawie ankiety sporządzono poniższą tabelę rozkładu uczniów według czasu spędzonego na oglądaniu telewizji w określonym dniu szkolnym:

Czas, h	Częstotliwość
0–1	12
1–2	24
2–3	8
3–4	5

Korzystając z tabeli, zbuduj odpowiedni histogram.

Nr 6. W obozie zdrowia uzyskano następujące dane dotyczące wagi 28 chłopców (z dokładnością do 0,1 kg):

21,8; 29,3, 30,2, 20,0, 23,8, 24,5, 24,0, 20,8, 22,0, 20,8, 22,0, 25,0, 25,5, 28,2, 22,5, 21,0, 24,5, 24,8, 24,6, 24,3, 26,0, 26,8, 23,2, 27,0, 29,5, 23,0 22,8, 31,2.

Wypełnij tabele, korzystając z tych danych:

Waga (kg	Częstotliwość		Waga (kg	Częstotliwość
20–22			20–23
22–24			23–26
24–26			26–29
26–28			29–32
28–30
30–32

Zgodnie z tymi tabelami zbuduj dwa histogramy na różnych figurach w tej samej skali. Co te histogramy mają wspólnego i czym się różnią?

Nr 7. Według kwartalnych ocen z geometrii, uczniowie jednej klasy zostali podzieleni w następujący sposób: „5” - 4 uczniów; „4” - 10 uczniów; „3” - 18 uczniów; „2” - 2 uczniów. Skonstruuj wykres słupkowy, który charakteryzuje rozkład uczniów według ćwiartek ocen geometrycznych.

Bibliografia:

1. Tkaczewa M.V.„Elementy statystyki i prawdopodobieństwa”: podręcznik. dodatek na 7-9 komórek. ogólne wykształcenie instytucje / Śr. Tkaczewa, N.E. Fiodorow. - M .: Edukacja, 2005.
2. Makarychev Yu.N. Algebra: elementy statystyki i rachunku prawdopodobieństwa: podręcznik. dodatek na 7-9 komórek. ogólne wykształcenie Instytucje / Yu.N. Makarychev, N.G. Mindiuk; wyd. SA Teliakowski - M. : Edukacja, 2004.
3. Sheveleva N.V. Matematyka (algebra, elementy statystyki i rachunku prawdopodobieństwa). Klasa 9 / N.V. Sheveleva, T.A. Koreshkova, V.V. Miroszyn. - M. : Edukacja narodowa, 2011.

Podczas zawodów tenisowych można używać następujących systemów:

System olimpijski oprócz wersji klasycznej posiada kilka modyfikacji:

W systemie olimpijskim zawodnik lub drużyna (dalej w tekście słowa „zawodnik” lub „uczestnik” będą oznaczać również „drużynę”) odpada z rozgrywek po pierwszej porażce, a przy ulepszonych systemach olimpijskich – po kilku porażkach.

System round robin obejmuje udział graczy w zawodach, dopóki każdy uczestnik nie spotka się ze wszystkimi innymi. Zwycięzcą zostaje uczestnik z największą liczbą punktów.

System mieszany opiera się na zasadzie połączenia systemu kołowego z systemem olimpijskim. Z reguły na wstępnym (wstępnym) etapie zawodów stosowany jest system kołowy, a na ostatnim etapie – olimpijski. Na wstępnym etapie losowania uczestnicy są dzieleni na podgrupy według kwalifikacji lub terytorialnej (z reguły w zawodach drużynowych). Najsilniejsi w podgrupach przechodzą do ostatniego etapu, w którym stosowany jest system olimpijski.

Przyjrzyjmy się bliżej każdemu z systemów.

(czasami nazywany „systemem eliminacji”) służy wyłącznie do wyłonienia zwycięzcy. Po pierwszej porażce uczestnik zostaje wyeliminowany z zawodów. W rezultacie zwycięzcą zostaje uczestnik, który nie przegrał ani jednego meczu.

Używany we wszystkich turniejach ITF, ATP, WTA(poza turniejem finałowym najsilniejszych) oraz na Igrzyskach Olimpijskich.

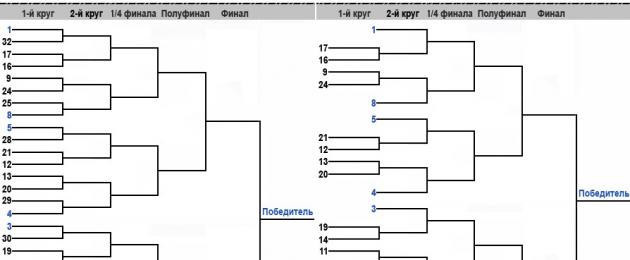
Zasada wyznaczania meczów pomiędzy uczestnikami zawodów i odnotowywania ich wyników odbywa się według specjalnej tabeli, zwanej potocznie „siatką turniejową”. Ma niezmieniony schemat i jest tworzony dla liczby uczestników 8; 16; 32; 64; 128. Losowania turniejowe mogą być również wykorzystywane dla 24 lub 48 uczestników, które są niepełnymi losowaniami odpowiednio dla 32 i 64 uczestników. Jako przykład podano przedziały turniejowe dla odpowiednio 32 i 24 uczestników. Maksymalna liczba graczy, ograniczona powyższymi seriami liczb, nazywa się rozmiar siatka turniejowa.

W skrajnym lewym rzędzie nazwiska uczestników znajdują się w odpowiednich wierszach zgodnie z jedną z trzech opcji:

• rozstawienie (miejsce) na podstawie oceny (w tym przypadku pierwsze mecze między uczestnikami są tworzone zgodnie z zasadą „silny przeciwko słabemu”);
• partie (losowo);
• kombinacje dwóch pierwszych opcji: najpierw wysiewa się określoną liczbę uczestników z najwyższą oceną, a następnie losuje się w ciemno dla pozostałych uczestników.

Tabela 1 pokazuje dozwoloną liczbę rozstawionych graczy w zależności od wielkości drabinki turniejowej.

Tabela 1

Zasadę sporządzania siatek turniejowych opisano w rozdziale „Kompilacja siatek turniejowych”.

Konkurs odbywa się w kilku kręgach lub rundach (w terminologii międzynarodowej „rundy” - Okrągły). Każde koło na siatce turniejowej odpowiada jednemu pionowemu rzędowi. Każdy taki wiersz składa się z poziomych linii, w których wskazane są nazwiska uczestników lub nazwy drużyn. W każdym kręgu uczestnicy spotykają się między sobą, których nazwiska znajdują się w tym samym rzędzie na sąsiednich (sąsiadujących) liniach połączonych z prawej strony pionową linią, czyli uczestnicy są podzieleni na pary, w których się spotykają.

Zwycięzcy meczu 1st kręgi wpadają w 2. kółko (w drabince turniejowej - do następnego pionowego rzędu), zwycięzcy w meczach 2. koło - w 3rd itp.

Runda, w której spotyka się 8 uczestników, nazywana jest ćwierćfinałem ( Ćwierćfinał), 4 uczestników – półfinały ( półfinał, Półksiężyc), 2 uczestników – finał ( Finał). Zwycięzcą meczu finałowego zostaje zwycięzca ( Zwycięzca) konkurencja.

Zależność liczby kółek od liczby uczestników przedstawia tabela 2.

Tabela 2

Liczba dni gry wymagana do zawodów (przy założeniu, że każdy uczestnik rozgrywa jeden mecz dziennie) jest równa liczbie okrążeń.

Całkowita liczba dopasowań ( MO ) jest określone wzorem M O \u003d N - 1 , gdzie N - liczba uczestników.

Niekiedy w zawodach rozgrywanych systemem olimpijskim trzecie miejsce rozgrywane jest pomiędzy uczestnikami, którzy przegrali mecze półfinałowe (np. Igrzyska Olimpijskie).

Wadą systemu olimpijskiego jest to, że awans w siatce turniejowej jest dość przypadkowy. Oczywiście silny zawodnik może przegrać ze słabym („no cóż, to nie był jego dzień”) i na tym zakończyć swoje występy. Jednocześnie jego zwycięzca z reguły przegrywa w kolejnej rundzie. Ponadto większość uczestników odpada po stosunkowo niewielkiej liczbie rozegranych meczów.

Przeznaczony do rozgrywania wszystkich miejsc, w których po każdej porażce zawodnik nie jest eliminowany z rywalizacji, a jedynie z walki o określone miejsce. W efekcie zwycięzcą zostaje uczestnik, który nie przegrał ani jednego meczu, a ostatnie miejsce zajmuje gracz, który nie odniósł ani jednego zwycięstwa. Wszystkie inne miejsca są rozdzielone pomiędzy pozostałych uczestników, w zależności od kolejności ich zwycięstw i porażek.

Turniej podzielony jest na kilka drabinek turniejowych – główną (ramkę zwycięzców) i dodatkową (ramkę przegranych), które nazywane są „ramionami repasażowymi”. Wszyscy uczestnicy rozpoczynają turniej w losowaniu głównym. Zasada kompilacji siatki głównej jest taka sama jak w systemie olimpijskim. Nazwiska uczestników mieszczą się w dodatkowych nawiasach z głównej po pierwszej porażce gracza, w zależności od przegranej rundy. W każdej rundzie, zaczynając od drugiej, pojawiają się uczestnicy, którzy mają taką samą kolejność zwycięstw i porażek w poprzednich rundach zawodów.

Jako przykład podano główne i dodatkowe plansze dla 16 uczestników.

Wyjaśnienie. W siatce każdej parze w I rundzie iw kolejnych rundach przypisywany jest własny numer (numeracja jest warunkowa i nie jest stosowana w siatkach wykorzystywanych w zawodach). Gracz, który przegra mecz w parze, otrzymuje numer odpowiadający tej parze ze znakiem „-” i jest oznaczony na czerwono. Spośród przegranych uczestników tworzy się siatka repasażowa odpowiadająca określonemu miejscu rozgrywania.

Przez analogię z siatką dla 16 uczestników, łatwo jest stworzyć siatki turniejowe dla 24, 32, 64 uczestników.

Liczbę meczów i rund w zależności od liczby uczestników podano w tabeli 3.

Tabela 3

Liczba uczestników	Wszystkie dopasowania	Liczba meczów w każdej rundzie
		1m	2.	3m	4.	5th	6.

Pozwala uczestnikom, którzy przegrali w pierwszych rundach, kontynuować udział do następnej porażki. Dodatkowe nawiasy są tworzone jak dla zwykłego, ulepszonego systemu olimpijskiego, jednak nie wszystkie miejsca są w nich rozgrywane. Np. dla siatki 16 uczestników wyznaczane są 1, 2, 3, 4, 5, 6, 9 i 10 miejsc, a dla 64 uczestników 1, 2, 3, 4, 5, 6, 9, 10, 17, 18, 33, 34. Jako przykład podano siatkę turniejową dla 16 uczestników.

Zasada awansowania uczestników w siatce głównej i dodatkowej jest taka sama, jak wyjaśniono w poprzedniej wersji (zaawansowany system olimpijski).

Według tego systemu często rozgrywane są zawody z wpisowym (startowym).

Uczestnik, który przegra jeden mecz w ciągu całych rozgrywek, zagra tylko o jeden mecz mniej od zwycięzcy rozgrywek.

Tabela 4 pokazuje całkowitą liczbę meczów na podstawie liczby uczestników.

Tabela 4

(Czasem nazywany " podkład") wiąże się z udziałem zawodnika do 2 porażek. Jest bardziej obiektywny niż system olimpijski i wszystkie jego odmiany, ale dłuższy. Głównym wyróżnikiem jest to, że raz przegrany zawodnik nie traci prawa do wygrania turnieju.

Zawody rozgrywane są w dwóch siatkach - górnym (głównym) i dolnym (dodatkowym). Jako przykład drabinki turniejowej dla 16 uczestników. W losowaniu głównym mecze odbywają się systemem olimpijskim.

W każdej parze przeciwników zwycięski uczestnik przechodzi do następnej rundy. Zawodnicy, którzy przegrali w 1. rundzie drabinki górnej, przechodzą do drabinki dolnej w drugiej rundzie. W przyszłości odliczanie okręgów odbywa się na górnej siatce. Uczestnik, który przegra w 2. rundzie górnej drabinki, w III rundzie przechodzi do dolnej drabinki i tak dalej.

Uczestnik, który przegra w dolnej drabince, zostaje wyeliminowany z zawodów.

W ostatniej rundzie (superfinale) spotykają się uczestnik, który bez porażki przeszedł przez losowanie główne i uczestnik, który dotarł do superfinału w dolnej drabince. Trzecie miejsce zajmuje przegrany finału w dolnej drabince.

• jeśli wygra zwycięzca górnej drabinki, rywalizacja się kończy, a jeśli wygra zwycięzca dolnej drabinki, to uczestnicy rozgrywają jeszcze jeden mecz (z pełnym superfinałem);
• odbywa się tylko jedno spotkanie (z prostym superfinałem).

Zaletą tego systemu jest to, że działa tak samo dla dowolnej liczby uczestników i jest najbardziej obiektywny w wyłonieniu zwycięzcy i zdobywców nagród. Wadą jest determinacja tylko trzech pierwszych miejsc i w dużej liczbie meczów, a także różnica w liczbie meczów, które zawodnicy rozgrywają, aby dojść do finału w górnej i dolnej drabince. Na przykład w przypadku turnieju z 8 uczestnikami finalista dolnej drabinki musi rozegrać 6 meczów więcej, z 16 uczestnikami - do 12, z 32 uczestnikami - do 24. Jednak ci, którzy nie przegrali z nikim, grają w górnej drabince i możemy założyć, że im wyższy poziom rywali rekompensuje różnicę w liczbie meczów.

Tabela 5 pokazuje liczbę dopasowań w nawiasach (górne/dolne) w przypadku korzystania z pierwszej wersji systemu.

Tabela 5

Liczba uczestników	Liczba meczów	1 koło	2 koła	3 koła	4 koła	5 kółek	6 kółek	7 kółek	8 kółek	9 koło

System ten był używany podczas finałowych turniejów WTA w latach 1978-1982.

Aby zmniejszyć liczbę meczów, można zastosować siatkę, w której raz przegrani walczą nie o pierwsze miejsce, ale o trzecie. Siatkę pokazano poniżej.

ULEPSZONY SYSTEM OLIMPIJSKI Z NAGRODĄ ZA KONFUZJĘ polega na przeprowadzeniu konkursu repasaży z tymi uczestnikami, którzy przegrali w pierwszej rundzie. Zwycięzca turnieju pocieszenia otrzymuje pamiątkową nagrodę lub wyróżnienie. Obie siatki turniejowe: główny i repasaże są zestawiane jak dla zwykłego systemu olimpijskiego (z eliminacją), czyli np. dla 22 uczestników, którzy brali udział w zawodach, rozgrywane są miejsca 1., 2. i 13..

Zaletą takiego systemu jest to, że silny uczestnik, który nie ma ochoty na mecz lub z jakiegoś innego powodu przegrywa z wyraźnie słabszym przeciwnikiem (co często się zdarza) ma możliwość kontynuowania gry w turnieju i rywalizacji o nagroda pocieszenia, która może być całkiem godna. W takim systemie odbywają się np. Mistrzostwa Świata wśród weteranów.

SYSTEM OKRĄGŁY przewiduje losowanie wszystkich miejsc podczas meczów pomiędzy wszystkimi uczestnikami zawodów.

O miejscach zajętych przez uczestników decyduje liczba zdobytych punktów. Za wygrany mecz (osobisty lub drużynowy) przyznawany jest jeden punkt, za przegrany - zero. W przypadku nie pojawienia się uczestnika na meczu lub odmowy z niego, porażka jest mu liczona (bez określania wyniku). Jeżeli uczestnik rozegrał mniej niż połowę meczów przewidzianych w tabeli rozgrywek, wszystkie jego wyniki zostaną anulowane (tylko w celu określenia miejsca w tabeli, ale nie należy brać pod uwagę w klasyfikacji).

W tenisie, co do zasady, wynik meczu jest wpisywany do tabeli tylko w polu zwycięzcy. Jeśli wyniki dowolnego uczestnika są wyświetlane w wierszu tabeli, a odpowiednie pole zawiera tylko „ 0 ”, to nie jest trudno znaleźć pole swojego przeciwnika na ten mecz (po przekątnej, biorąc pod uwagę numer układu) i wyjaśnić wynik. W przykładzie rachunek jest wskazany we wszystkich polach.

Zwycięzcą zostaje uczestnik z największą liczbą punktów.

Jeśli dwóch uczestników ma taką samą liczbę punktów (w konkursie osobistym lub drużynowym), zwycięzca meczu między nimi uzyskuje przewagę. W przypadku równej liczby punktów dla trzech lub więcej uczestników w poszczególnych zawodach, korzyść otrzymuje uczestnik zgodnie z następującymi konsekwentnie stosowanymi zasadami :

1. W meczach między nimi:

b) według najlepszej różnicy między wygranymi a przegranymi setami;

c) według najlepszej różnicy między wygranymi a przegranymi meczami.

2. We wszystkich meczach:

b) według najlepszej różnicy między wygranymi a przegranymi meczami;

c) w drodze losowania.

W przykładzie pierwsi trzej uczestnicy zdobyli taką samą liczbę punktów - każdy 5. Liczba punktów zdobytych między nimi również okazała się taka sama - każdy 1. Przy obliczaniu wygranych i przegranych zestawów wskaźniki są następujące: 1st uczestnik - 4 (zwycięski) /3 (Stracony); 2. uczestnik - 4/3 ; 3rd uczestnik - 5/2 . Najlepsza różnica w zestawie 3rd uczestnik, jest zwycięzcą. Na 1st oraz 2. uczestnik, różnica jest taka sama. Podział miejsc wśród zwycięzców w tym przypadku ustalany jest na podstawie ich osobistego spotkania.

W przypadku równej liczby punktów trzech lub więcej uczestników w rywalizacji drużynowej, drużyna uzyskuje przewagę w następujących kolejno stosowanych wskaźnikach:

1. W meczach drużynowych między nimi:

a) według liczby zdobytych punktów;

b) według najlepszej różnicy między wygranymi a przegranymi meczami singlowymi i deblowymi;

c) według najlepszej różnicy między wygranymi a przegranymi setami;

d) według najlepszej różnicy między wygranymi a przegranymi meczami

2. We wszystkich meczach drużynowych:

a) według najlepszej różnicy między wygranymi a przegranymi setami;

b) według najlepszej różnicy między wygranymi a przegranymi meczami.

Jeśli uczestnik odmówi po pierwszej rundzie, istnieją trzy możliwości wzięcia pod uwagę (lub nieuwzględnienia) wyników rozegranych przez niego meczów:

• anulowanie wyników;
• przyznawanie zwycięstw technicznych w pozostałych meczach;
• jeśli wyeliminowany uczestnik rozegrał połowę lub więcej swoich meczów, w pozostałych meczach jego przeciwnicy otrzymują zwycięstwo techniczne, w przeciwnym razie wyniki jego gier są anulowane.

W pierwszym przypadku uczestnicy znajdują się w nierównych warunkach: ci, którzy wygrali wyeliminowanego gracza, tracą punkty, a ci, którzy z nim przegrywają, nie tracą nic. W drugiej przewagę uzyskają ci, którzy nie zdążyli się z nim spotkać. Dlatego zaleca się skorzystanie z trzeciej opcji.

Sposób podjęcia decyzji w przypadku eliminacji uczestnika powinien być określony w Regulaminie turnieju.

Kolejność meczów przeciwników ze sobą w systemie round-robin nie ma większego znaczenia, ale zaleca się planowanie zgodnie z poniższą zasadą (Tal.6).

Tabela 6

Dla 8 uczestników
						5↔6

Opiera się na zasadzie obracania wszystkich liczb przeciwnie do ruchu wskazówek zegara wokół pierwszej liczby. W każdej kolejnej rundzie liczby są przesuwane o jedno zamówienie. Przy parzystej liczbie graczy będzie nieparzysta liczba kółek, tj. o jeden mniej niż całkowita liczba uczestników. Jeśli liczba uczestników jest nieparzysta, to okrążenia liczone są od liczby parzystej, tj. jeszcze jeden. W tym przypadku ostatnia liczba w tabeli pozostaje niezajęta, a gracz, który w kolejnej rundzie zdobędzie mecz z tym numerem jest wolny.

Liczba dni gry wymagana do przeprowadzenia turnieju „każdy z każdym” (pod warunkiem, że każdy uczestnik gra nie więcej niż jeden mecz dziennie) jest o jeden mniej niż liczba uczestników, jeśli jest parzysta, i jest równa liczbie uczestników, jeśli to jest dziwne.

Całkowita liczba dopasowań ( M K ) określa wzór: M K \u003d N (N - 1) / 2 , gdzie N - liczba uczestników konkursu.

Liczba okrążeń (jeśli istnieje techniczna możliwość przeprowadzenia odpowiedniej liczby meczów w tym samym czasie) jest równa N–1 dla parzystej liczby uczestników i N dla nieparzystej (w tym drugim przypadku każdy uczestnik traci jedną rundę, w której nie ma przeciwnika).

Zaletami tego systemu jest osiągnięcie maksymalnej obiektywności turnieju: wszyscy zagrają z każdym, o ostatecznym wyniku decyduje równowaga sił wszystkich par przeciwników.

Wadą jest duża liczba meczów (maksymalna wśród wszystkich systemów) i odpowiednio duża liczba dni na turniej. Liczba spotkań rośnie czterokrotnie wraz z liczbą uczestników. Praktyczny limit dla rundy z każdym w tenisie wynosi 8 graczy. W rezultacie duże turnieje round-robin są rzadkie. Ponadto pod koniec turnieju odbywają się mecze, które częściowo lub całkowicie nie wpływają na pozycje niektórych uczestników. A to może prowadzić do ustawiania meczów.

Możliwy jest dwustopniowy system kołowy. W fazie wstępnej uczestnicy dzielą się na kilka podgrup: 3, 4, 5 itd. z reguły 3–4 uczestników w podgrupie, a następnie na etapie głównym (końcowym) tworzą się zwycięzcy podgrup grupa, w której grają również w systemie „każdy z każdym” w celu wyłonienia zwycięzcy i zdobywców nagród. Jeśli są dwie podgrupy, do etapu głównego przechodzi dwóch uczestników z najlepszymi wynikami z każdej podgrupy. W przykładzie są 4 podgrupy z 4 uczestnikami każda, ale w jednej lub trzech podgrupach może być 3 uczestników.

Według tego systemu możliwe jest losowanie kolejnych miejsc na scenie głównej. W tym celu zestawiane są tabele, które łączą osobno 2., 3., 4. i kolejne miejsca.

SYSTEMY MIESZANE to różne kombinacje systemów okrężnych, olimpijskich i zaawansowanych olimpijskich, z których każdy może być używany na różnych etapach zawodów. Najbardziej rozpowszechniony jest system mieszany, który przewiduje, że w pierwszym (wstępnym) etapie rozgrywek mecze rozgrywane są w systemie „każdy z każdym” w podgrupach, a w finale (finał) – według systemu olimpijskiego (play-off) lub ulepszonego systemu olimpijskiego . Liczbę grup oraz liczbę uczestników z każdej grupy biorących udział w finałowej części zawodów należy wskazać w Regulaminie turnieju. Przykład pokazuje system mieszany, składający się na etapie wstępnym z 4 grup po 3-4 uczestników w każdej, spotykających się w systemie „każdy z każdym”, z późniejszym utworzeniem drabinki olimpijskiej z dwóch najlepszych uczestników z każdej grupy.

Grupy, w oparciu o rozstawienie i liczbę uczestników, tworzone są zgodnie z tzw.

Tabela 7

Grupa I	Grupa II	Grupa III	Grupa IV
itp.

Liczba rzędów odpowiada liczbie tworzonych grup, liczba rzędów odpowiada liczbie uczestników w każdej grupie.

Jeśli są tylko dwie grupy, na ostatnim etapie można wykonać następujące czynności:

1. Mecze dokowania między uczestnikami, którzy zajęli te same miejsca w grupach. Zwycięzcy w podgrupach pierwszego etapu konkursu spotykają się między sobą o 1-2 miejsca, ci, którzy zajęli 2 miejsca w grupach – o 3-4 miejsca itd.
2. Półfinały, w których zwycięzca z jednej grupy spotyka gracza, który zajął 2 miejsce z innej grupy. Zwycięzcy półfinałów spotykają się w finale, a mecz o 3 miejsce rozgrywany jest pomiędzy przegranymi półfinałami.

Faza grupowa ma swoje oczywiste plusy i minusy. Z jednej strony gwarantuje udział zawodników w kilku meczach (np. przy 4 uczestnikach - trzy mecze). Dodatkowo wszyscy uczestnicy mają szansę na awans z grupy do ostatniego etapu, nawet jeśli przegrają. Z drugiej strony złożoność percepcji i konieczność liczenia zestawów, a czasem gier, aby wyłonić zwycięzcę grupy. Często sami gracze nie zawsze rozumieją istotę wyznaczania miejsc w grupie. Na przykład na finałach ATP 2012, Andy Murray, po wygraniu pierwszego seta z Jo-Wilfriedem Tsonga w ostatnim meczu (miał jedno zwycięstwo i jedną porażkę), zapytał sędziego, czy idzie do półfinału. A w drugiej grupie „B” David Ferrer został pominięty w play-off, pomimo dwóch zwycięstw, podobnie jak Roger Federer i Juan Martin del Potro, którzy zajęli odpowiednio 1. i 2. miejsce.