Definition 1
Antiderivatan $F(x)$ för funktionen $y=f(x)$ på segmentet $$ är en funktion som är differentierbar vid varje punkt i detta segment och följande likhet gäller för dess derivata:
Definition 2
Mängden av alla antiderivator av en given funktion $y=f(x)$, definierade på ett visst segment, kallas den obestämda integralen av en given funktion $y=f(x)$. Den obestämda integralen betecknas med symbolen $\int f(x)dx $.
Från tabellen över derivator och Definition 2 får vi tabellen över grundläggande integraler.
Exempel 1
Kontrollera giltigheten av formel 7 från tabellen över integraler:
\[\int tgxdx =-\ln |\cos x|+C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $-\ln |\cos x|+C$.
\[\left(-\ln |\cos x|+C\right)"=-\frac(1)(\cos x) \cdot (-\sin x)=\frac(\sin x)(\cos x) =tgx\]
Exempel 2
Kontrollera giltigheten av formel 8 från tabellen över integraler:
\[\int ctgxdx =\ln |\sin x|+C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\ln |\sin x|+C$.
\[\left(\ln |\sin x|\right)"=\frac(1)(\sin x) \cdot \cos x=ctgx\]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 3
Kontrollera giltigheten av formel 11" från tabellen över integraler:
\[\int \frac(dx)(a^(2) +x^(2) ) =\frac(1)(a) arctg\frac(x)(a) +C,\, \, C=const .\]
Låt oss skilja på den högra sidan: $\frac(1)(a) arctg\frac(x)(a) +C$.
\[\left(\frac(1)(a) arctg\frac(x)(a) +C\right)"=\frac(1)(a) \cdot \frac(1)(1+\left( \frac(x)(a) \right)^(2) ) \cdot \frac(1)(a) =\frac(1)(a^(2) ) \cdot \frac(a^(2) ) (a^(2) +x^(2) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 4
Kontrollera giltigheten av formel 12 från tabellen över integraler:
\[\int \frac(dx)(a^(2) -x^(2) ) =\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+ C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C$.
$\left(\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C\right)"=\frac(1)(2a) \cdot \frac( 1)(\frac(a+x)(a-x) ) \cdot \left(\frac(a+x)(a-x) \right)"=\frac(1)(2a) \cdot \frac(a-x)( a+x) \cdot \frac(a-x+a+x)((a-x)^(2) ) =\frac(1)(2a) \cdot \frac(a-x)(a+x) \cdot \ frac(2a)((a-x)^(2) ) =\frac(1)(a^(2) -x^(2) ) $Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 5
Kontrollera giltigheten av formel 13" från tabellen över integraler:
\[\int \frac(dx)(\sqrt(a^(2) -x^(2) ) ) =\arcsin \frac(x)(a) +C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\arcsin \frac(x)(a) +C$.
\[\left(\arcsin \frac(x)(a) +C\right)"=\frac(1)(\sqrt(1-\left(\frac(x)(a) \right)^(2 ) ) ) \cdot \frac(1)(a) =\frac(a)(\sqrt(a^(2) -x^(2) ) ) \cdot \frac(1)(a) =\frac( 1)(\sqrt(a^(2) -x^(2) ) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 6
Kontrollera giltigheten av formel 14 från tabellen över integraler:
\[\int \frac(dx)(\sqrt(x^(2) \pm a^(2) ) =\ln |x+\sqrt(x^(2) \pm a^(2) ) |+ C ,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C$.
\[\left(\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C\right)"=\frac(1)(x+\sqrt(x^(2) \pm a^(2) ) \cdot \left(x+\sqrt(x^(2) \pm a^(2) ) \right)"=\frac(1)(x+\sqrt(x^(2) \ pm a^(2) ) \cdot \left(1+\frac(1)(2\sqrt(x^(2) \pm a^(2) ) ) \cdot 2x\right)=\] \[ =\ frac(1)(x+\sqrt(x^(2) \pm a^(2) ) \cdot \frac(\sqrt(x^(2) \pm a^(2) ) +x)( \sqrt( x^(2) \pm a^(2) ) =\frac(1)(\sqrt(x^(2) \pm a^(2) ) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 7
Hitta integralen:
\[\int \left(\cos (3x+2)+5x\right) dx.\]
Låt oss använda summaintegralsatsen:
\[\int \left(\cos (3x+2)+5x\right) dx=\int \cos (3x+2)dx +\int 5xdx .\]
Låt oss använda satsen om att placera en konstant faktor utanför integraltecknet:
\[\int \cos (3x+2)dx +\int 5xdx =\int \cos (3x+2)dx +5\int xdx .\]
Enligt tabellen över integraler:
\[\int \cos x dx=\sin x+C;\] \[\int xdx =\frac(x^(2) )(2) +C.\]
När vi beräknar den första integralen använder vi regel 3:
\[\int \cos (3x+2) dx=\frac(1)(3) \sin (3x+2)+C_(1) .\]
Därav,
\[\int \left(\cos (3x+2)+5x\right) dx=\frac(1)(3) \sin (3x+2)+C_(1) +\frac(5x^(2) )(2) +C_(2) =\frac(1)(3) \sin (3x+2)+\frac(5x^(2) )(2) +C,\, \, C=C_(1) ) +C_(2) \]
Tabell över antiderivat ("integraler"). Tabell över integraler. Tabellformade obestämda integraler. (De enklaste integralerna och integralerna med en parameter). Formler för integrering av delar. Newton-Leibniz formel.
|
Tabell över antiderivat ("integraler"). Tabellformade obestämda integraler. (De enklaste integralerna och integralerna med en parameter). |
|
|
Integral av en effektfunktion. |
Integral av en effektfunktion. |
|
En integral som reduceras till integralen av en effektfunktion om x drivs under differentialtecknet. |
|
|
|
Integral av en exponential, där a är ett konstant tal. |
|
Integral av en komplex exponentialfunktion. |
Integral av en exponentialfunktion. |
|
En integral lika med den naturliga logaritmen. |
Integral: "Lång logaritm". |
|
Integral: "Lång logaritm". |
|
|
Integral: "Hög logaritm". |
En integral, där x i täljaren placeras under differentialtecknet (konstanten under tecknet kan antingen adderas eller subtraheras), liknar i slutändan en integral lika med den naturliga logaritmen. |
|
Integral: "Hög logaritm". |
|
|
Cosinusintegral. |
Sinus integral. |
|
Integral lika med tangent. |
Integral lika med cotangens. |
|
Integral lika med både arcsine och arccosine |
|
|
En integral lika med både arcsine och arccosine. |
En integral lika med både arctangens och arccotangent. |
|
Integral lika med cosecant. |
Integral lika med sekant. |
|
Integral lika med ljusbåge. |
Integral lika med arccosecant. |
|
Integral lika med ljusbåge. |
Integral lika med ljusbåge. |
|
Integral lika med hyperbolisk sinus. |
Integral lika med hyperbolisk cosinus. |
|
|
|
|
Integral lika med hyperbolisk sinus, där sinhx är hyperbolisk sinus i den engelska versionen. |
Integral lika med hyperbolisk cosinus, där sinhx är hyperbolisk sinus i den engelska versionen. |
|
Integral lika med hyperbolisk tangent. |
Integral lika med hyperbolisk cotangens. |
|
Integral lika med den hyperboliska sekanten. |
Integral lika med den hyperboliska cosekanten. |
Formler för integrering av delar. Integrationsregler.
|
Formler för integrering av delar. Newton-Leibniz formel. |
|
|
Integrera en produkt (funktion) med en konstant: |
|
|
Integrera summan av funktioner: |
|
|
obestämda integraler: |
|
|
Formel för integrering av delar bestämda integraler: |
|
|
Newton-Leibniz formel bestämda integraler: |
Där F(a),F(b) är värdena för antiderivaten vid punkterna b respektive a. |
Tabell över derivat. Tabellformiga derivator. Derivat av produkten. Derivat av kvoten. Derivat av en komplex funktion.
Om x är en oberoende variabel, då:
|
Tabell över derivat. Tabellderivat."tabellderivat" - ja, tyvärr, det är precis så de söks efter på Internet |
|
|
Derivat av en potensfunktion |
|
|
|
Exponentens derivata |
|
|
Derivat av exponentiell funktion |
|
Derivat av en logaritmisk funktion |
|
|
Derivat av den naturliga logaritmen för en funktion |
|
|
|
|
|
Derivat av cosecant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Derivat av arc cotangens |
|
|
|
|
|
Derivat av arccosecant |
|
|
|
|
|
|
|
|
|
|
Regler för differentiering. Derivat av produkten. Derivat av kvoten. Derivat av en komplex funktion. |
|
|
Derivat av en produkt (funktion) med en konstant: |
|
|
Derivata av summa (funktioner): |
|
|
Derivat av produkten (funktioner): |
|
|
Derivat av kvoten (av funktioner): |
|
|
Derivat av en komplex funktion: |
|
Egenskaper för logaritmer. Grundformler för logaritmer. Decimala (lg) och naturliga logaritmer (ln).
|
|
|
|
|
|
|
|
|
|
|
Grundläggande logaritmisk identitet |
|
|
Låt oss visa hur vilken funktion som helst av formen a b kan göras exponentiell. Eftersom en funktion av formen e x kallas exponentiell, alltså |
|
|
Vilken funktion som helst av formen a b kan representeras som en potens av tio |
|
Naturlig logaritm ln (logaritm till bas e = 2,718281828459045...) ln(e)=1; ln(1)=0
Taylor-serien. Taylor-seriens expansion av en funktion.
Det visar sig att majoriteten praktiskt taget stött på matematiska funktioner kan representeras med vilken noggrannhet som helst i närheten av en viss punkt i form av potensserier som innehåller potenser av en variabel i ökande ordning. Till exempel, i närheten av punkten x=1:

När du använder serier kallas Taylors rader blandade funktioner som innehåller till exempel algebraiska, trigonometriska och exponentiella funktioner kan uttryckas som rent algebraiska funktioner. Med hjälp av serier kan du ofta snabbt utföra differentiering och integration.
Taylor-serien i närheten av punkt a har formen:
1)
, där f(x) är en funktion som har derivator av alla ordningar vid x = a. R n - den återstående termen i Taylor-serien bestäms av uttrycket 
2)
Seriens k:te koefficient (vid x k) bestäms av formeln

3) Ett specialfall av Taylor-serien är Maclaurin (=McLaren)-serien (expansionen sker runt punkten a=0)
vid a=0 
medlemmar i serien bestäms av formeln

Villkor för användning av Taylor-serien.
1. För att funktionen f(x) ska kunna expanderas till en Taylor-serie på intervallet (-R;R) är det nödvändigt och tillräckligt att den återstående termen i Taylor (Maclaurin (=McLaren)) formel för detta funktion tenderar till noll som k →∞ på det specificerade intervallet (-R;R).
2. Det är nödvändigt att det finns derivator för en given funktion vid den punkt i närheten av vilken vi ska konstruera Taylor-serien.
Egenskaper för Taylor-serien.
Om f är en analytisk funktion, så konvergerar dess Taylor-serie vid vilken punkt som helst i definitionsdomänen för f till f i någon grannskap av a.
Det finns oändligt differentierbara funktioner vars Taylor-serie konvergerar, men som samtidigt skiljer sig från funktionen i vilket område som helst av a. Till exempel:

Taylorserier används i approximation (approximation är en vetenskaplig metod som består i att ersätta vissa objekt med andra, i en eller annan mening nära de ursprungliga, men enklare) av en funktion med polynom. I synnerhet linjärisering ((från linjär - linjär), en av metoderna för ungefärlig representation av slutna olinjära system, där studien av ett olinjärt system ersätts med analys av ett linjärt system, i någon mening ekvivalent med det ursprungliga. .) ekvationer uppstår genom att expandera till en Taylor-serie och skära bort alla termer över första ordningen.
Således kan nästan vilken funktion som helst representeras som ett polynom med en given noggrannhet.
Exempel på några vanliga expansioner av potensfunktioner i Maclaurin-serien (=McLaren, Taylor i närheten av punkt 0) och Taylor i närheten av punkt 1. De första termerna för expansioner av huvudfunktionerna i Taylor- och McLaren-serierna.
Exempel på några vanliga expansioner av potensfunktioner i Maclaurin-serien (=McLaren, Taylor i närheten av punkt 0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exempel på några vanliga Taylor-serieexpansioner i närheten av punkt 1
|
|
|
|
|
|
Rektorintegraler som varje elev bör känna till
De listade integralerna är grunden, grunden för grunderna. Dessa formler bör definitivt komma ihåg. När du beräknar mer komplexa integraler måste du använda dem hela tiden.
Var särskilt uppmärksam på formlerna (5), (7), (9), (12), (13), (17) och (19). Glöm inte att lägga till en godtycklig konstant C till ditt svar när du integrerar!
Integral av en konstant
∫ A d x = A x + C (1)Integrera en Power-funktion
I själva verket var det möjligt att begränsa oss till endast formlerna (5) och (7), men resten av integralerna från denna grupp förekommer så ofta att det är värt att uppmärksamma dem lite.
∫ x d x = x 2 2 + C (2)
∫ x 2 d x = x 3 3 + C (3)
∫ 1 x d x = 2 x + C (4)
∫ 1 x d x = ln | x | +C (5)
∫ 1 x 2 d x = − 1 x + C (6)
∫ x n d x = x n + 1 n + 1 + C (n ≠ − 1) (7)
Integraler av exponentialfunktioner och hyperboliska funktioner
Naturligtvis kan formel (8) (kanske den mest bekväma för memorering) betraktas som ett specialfall av formel (9). Formlerna (10) och (11) för integralerna av hyperbolisk sinus och hyperbolisk cosinus härleds lätt från formel (8), men det är bättre att helt enkelt komma ihåg dessa relationer.
∫ e x d x = e x + C (8)
∫ a x d x = a x ln a + C (a > 0, a ≠ 1) (9)
∫ s h x d x = c h x + C (10)
∫ c h x d x = s h x + C (11)
Grundläggande integraler av trigonometriska funktioner
Ett misstag som elever ofta gör är att de blandar ihop tecknen i formlerna (12) och (13). Kom ihåg att derivatan av sinus är lika med cosinus, av någon anledning tror många att integralen av funktionen sinx är lika med cosx. Det är inte sant! Integralen av sinus är lika med "minus cosinus", men integralen av cosx är lika med "bara sinus":
∫ sin x d x = − cos x + C (12)
∫ cos x d x = sin x + C (13)
∫ 1 cos 2 x d x = t g x + C (14)
∫ 1 sin 2 x d x = − c t g x + C (15)
Integraler som reducerar till inversa trigonometriska funktioner
Formel (16), som leder till arctangensen, är naturligtvis ett specialfall av formel (17) för a=1. På samma sätt är (18) ett specialfall av (19).
∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C (16)
∫ 1 x 2 + a 2 = 1 a a r c t g x a + C (a ≠ 0) (17)
∫ 1 1 − x 2 d x = båge x + C = − bågar x + C (18)
∫ 1 a 2 − x 2 d x = båge x a + C = − bågar x a + C (a > 0) (19)
Mer komplexa integraler
Det är också lämpligt att komma ihåg dessa formler. De används också ganska ofta, och deras produktion är ganska tråkig.
∫ 1 x 2 + a 2 d x = ln | x + x 2 + a 2 | +C (20)
∫ 1 x 2 − a 2 d x = ln | x + x 2 − a 2 | +C (21)
∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 båge x a + C (a > 0) (22)
∫ x 2 + a 2 d x = x 2 x 2 + a 2 + a 2 2 ln | x + x 2 + a 2 | + C (a > 0) (23)
∫ x 2 − a 2 d x = x 2 x 2 − a 2 − a 2 2 ln | x + x 2 − a 2 | + C (a > 0) (24)
Allmänna regler för integration
1) Integralen av summan av två funktioner är lika med summan av motsvarande integraler: ∫ (f (x) + g (x)) d x = ∫ f (x) d x + ∫ g (x) d x (25)
2) Integralen av skillnaden mellan två funktioner är lika med skillnaden mellan motsvarande integraler: ∫ (f (x) − g (x)) d x = ∫ f (x) d x − ∫ g (x) d x (26)
3) Konstanten kan tas ut ur heltecknet: ∫ C f (x) d x = C ∫ f (x) d x (27)
Det är lätt att se att fastighet (26) helt enkelt är en kombination av fastigheter (25) och (27).
4) Integral av en komplex funktion om den inre funktionen är linjär: ∫ f (A x + B) d x = 1 A F (A x + B) + C (A ≠ 0) (28)
Här är F(x) en antiderivata för funktionen f(x). Observera: denna formel fungerar bara när den inre funktionen är Ax + B.
Viktigt: det finns ingen universell formel för integralen av produkten av två funktioner, såväl som för integralen av en bråkdel:
∫ f (x) g (x) d x = ? ∫ f (x) g (x) d x = ? (trettio)
Detta betyder naturligtvis inte att en fraktion eller produkt inte kan integreras. Det är bara det att varje gång du ser en integral som (30), måste du uppfinna ett sätt att "bekämpa" det. I vissa fall kommer integrering av delar att hjälpa dig, i andra kommer du att behöva göra en förändring av variabel, och ibland kan till och med "skola" algebra eller trigonometriformler hjälpa dig.
Ett enkelt exempel på beräkning av den obestämda integralen
Exempel 1. Hitta integralen: ∫ (3 x 2 + 2 sin x − 7 e x + 12) d xLåt oss använda formlerna (25) och (26) (integralen av summan eller skillnaden av funktioner är lika med summan eller skillnaden av motsvarande integraler. Vi får: ∫ 3 x 2 d x + ∫ 2 sin x d x − ∫ 7 e x d x + ∫ 12 d x
Låt oss komma ihåg att konstanten kan tas ut ur integraltecknet (formel (27)). Uttrycket konverteras till formen
3 ∫ x 2 d x + 2 ∫ sin x d x − 7 ∫ e x d x + 12 ∫ 1 d x
Låt oss nu bara använda tabellen över grundläggande integraler. Vi kommer att behöva tillämpa formlerna (3), (12), (8) och (1). Låt oss integrera potensfunktionen, sinus, exponential och konstant 1. Glöm inte att lägga till en godtycklig konstant C i slutet:
3 x 3 3 − 2 cos x − 7 e x + 12 x + C
Efter elementära transformationer får vi det slutliga svaret:
X 3 − 2 cos x − 7 e x + 12 x + C
Testa dig själv genom differentiering: ta derivatan av den resulterande funktionen och se till att den är lika med den ursprungliga integranden.
Sammanfattande tabell över integraler
| ∫ A d x = A x + C |
| ∫ x d x = x 2 2 + C |
| ∫ x 2 d x = x 3 3 + C |
| ∫ 1 x d x = 2 x + C |
| ∫ 1 x d x = ln | x | +C |
| ∫ 1 x 2 d x = − 1 x + C |
| ∫ x n d x = x n + 1 n + 1 + C (n ≠ − 1) |
| ∫ e x d x = e x + C |
| ∫ a x d x = a x ln a + C (a > 0, a ≠ 1) |
| ∫ s h x d x = c h x + C |
| ∫ c h x d x = s h x + C |
| ∫ sin x d x = − cos x + C |
| ∫ cos x d x = sin x + C |
| ∫ 1 cos 2 x d x = t g x + C |
| ∫ 1 sin 2 x d x = − c t g x + C |
| ∫ 1 1 + x 2 d x = a r c t g x + C = − a r c c t g x + C |
| ∫ 1 x 2 + a 2 = 1 a a r c t g x a + C (a ≠ 0) |
| ∫ 1 1 − x 2 d x = båge x + C = − bågar x + C |
| ∫ 1 a 2 − x 2 d x = båge x a + C = − bågar x a + C (a > 0) |
| ∫ 1 x 2 + a 2 d x = ln | x + x 2 + a 2 | +C |
| ∫ 1 x 2 − a 2 d x = ln | x + x 2 − a 2 | +C |
| ∫ a 2 − x 2 d x = x 2 a 2 − x 2 + a 2 2 båge x a + C (a > 0) |
| ∫ x 2 + a 2 d x = x 2 x 2 + a 2 + a 2 2 ln | x + x 2 + a 2 | + C (a > 0) |
| ∫ x 2 − a 2 d x = x 2 x 2 − a 2 − a 2 2 ln | x + x 2 − a 2 | + C (a > 0) |

Ladda ner tabellen över integraler (del II) från denna länk
Om du studerar vid ett universitet, om du har svårigheter med högre matematik (matematisk analys, linjär algebra, sannolikhetsteori, statistik), om du behöver tjänster från en kvalificerad lärare, gå till sidan för en högre matematiklärare. Vi löser dina problem tillsammans!
Du kanske också är intresserad av
Antiderivativ funktion och obestämd integral
Fakta 1. Integration är den omvända verkan av differentiering, nämligen att återställa en funktion från den kända derivatan av denna funktion. Funktionen återställdes därmed F(x) kallas antiderivat för funktion f(x).
Definition 1. Funktion F(x f(x) på något intervall X, om för alla värden x från detta intervall håller jämlikheten F "(x)=f(x), det vill säga denna funktion f(x) är derivatan av antiderivatfunktionen F(x). .
Till exempel funktionen F(x) = synd x är ett antiderivat av funktionen f(x) = cos x på hela tallinjen, eftersom för valfritt värde på x (synd x)" = (cos x) .
Definition 2. Obestämd integral av en funktion f(x) är uppsättningen av alla dess antiderivat. I det här fallet används notationen
∫
f(x)dx
,var är skylten ∫ kallas integraltecknet, funktionen f(x) – integrand funktion, och f(x)dx – integrant uttryck.
Alltså om F(x) – något antiderivat för f(x) , Den där
∫
f(x)dx = F(x) +C
Var C - godtycklig konstant (konstant).
För att förstå innebörden av uppsättningen av antiderivator av en funktion som en obestämd integral, är följande analogi lämplig. Låt det finnas en dörr (traditionell trädörr). Dess funktion är att "vara en dörr". Vad är dörren gjord av? Gjort av trä. Detta betyder att uppsättningen av antiderivator av integranden för funktionen "att vara en dörr", det vill säga dess obestämda integral, är funktionen "att vara ett träd + C", där C är en konstant, vilket i detta sammanhang kan beteckna till exempel typen av träd. Precis som en dörr är gjord av trä med hjälp av vissa verktyg, är en derivata av en funktion "gjord" från en antiderivatfunktion med formler vi lärde oss när vi studerade derivatan .
Sedan liknar funktionstabellen för vanliga föremål och deras motsvarande antiderivat ("att vara en dörr" - "att vara ett träd", "att vara en sked" - "att vara metall", etc.) som tabellen för grundläggande obestämda integraler, som kommer att ges nedan. Tabellen över obestämda integraler listar vanliga funktioner med en indikation på de antiderivator från vilka dessa funktioner är "gjorda". I en del av problemen med att hitta den obestämda integralen ges integrander som kan integreras direkt utan större ansträngning, det vill säga att använda tabellen över obestämda integraler. I mer komplexa problem måste integranden först transformeras så att tabellintegraler kan användas.
Fakta 2. När vi återställer en funktion som en antiderivata måste vi ta hänsyn till en godtycklig konstant (konstant) C, och för att inte skriva en lista med antiderivator med olika konstanter från 1 till oändlighet, måste du skriva en uppsättning antiderivator med en godtycklig konstant C till exempel så här: 5 x³+C. Så en godtycklig konstant (konstant) ingår i uttrycket av antiderivatan, eftersom antiderivatan kan vara en funktion, till exempel, 5 x³+4 eller 5 x³+3 och vid differentiering går 4 eller 3, eller någon annan konstant till noll.
Låt oss ställa integrationsproblemet: för denna funktion f(x) hitta en sådan funktion F(x), vars derivat lika med f(x).
Exempel 1. Hitta mängden antiderivator av en funktion
Lösning. För denna funktion är antiderivatan funktionen
Fungera F(x) kallas ett antiderivat för funktionen f(x), om derivatan F(x) är lika med f(x), eller, vilket är samma sak, differential F(x) är jämställd f(x) dx, dvs.
![]() (2)
(2)
Därför är funktionen ett antiderivat av funktionen. Det är dock inte det enda antiderivatet för . De fungerar också som funktioner
Var MED– godtycklig konstant. Detta kan verifieras genom differentiering.
Således, om det finns en antiderivata för en funktion, så finns det för den ett oändligt antal antiderivator som skiljer sig åt med en konstant term. Alla antiderivator för en funktion skrivs i ovanstående form. Detta följer av följande teorem.
Sats (formell faktapåstående 2). Om F(x) – antiderivata för funktionen f(x) på något intervall X, sedan något annat antiderivat för f(x) på samma intervall kan representeras i formuläret F(x) + C, Var MED– godtycklig konstant.
I nästa exempel vänder vi oss till tabellen över integraler, som kommer att ges i punkt 3, efter egenskaperna för den obestämda integralen. Vi gör detta innan vi läser hela tabellen så att kärnan i ovanstående är tydlig. Och efter tabellen och fastigheterna kommer vi att använda dem i sin helhet under integrationen.
Exempel 2. Hitta uppsättningar av antiderivata funktioner:
Lösning. Vi hittar uppsättningar av antiderivata funktioner från vilka dessa funktioner är "gjorda". När du nämner formler från tabellen över integraler, acceptera nu bara att det finns sådana formler där, så kommer vi att studera själva tabellen med obestämda integraler lite längre.
1) Tillämpa formel (7) från tabellen över integraler för n= 3, vi får
![]()
2) Använd formel (10) från tabellen över integraler för n= 1/3, vi har
3) Sedan
sedan enligt formel (7) med n= -1/4 finner vi
![]()
Det är inte själva funktionen som skrivs under integraltecknet. f, och dess produkt av skillnaden dx. Detta görs i första hand för att indikera med vilken variabel antiderivatet söks. Till exempel,
![]() ,
,
![]() ;
;
här i båda fallen är integranden lika med , men dess obestämda integraler i de övervägda fallen visar sig vara olika. I det första fallet betraktas denna funktion som en funktion av variabeln x, och i den andra - som en funktion av z .
Processen att hitta den obestämda integralen av en funktion kallas att integrera den funktionen.
Geometrisk betydelse av den obestämda integralen
Antag att vi måste hitta en kurva y=F(x) och vi vet redan att tangenten till tangentvinkeln vid var och en av dess punkter är en given funktion f(x) abskissan av denna punkt.
Enligt den geometriska betydelsen av derivatan, tangenten för tangentens lutningsvinkel vid en given punkt på kurvan y=F(x) lika med värdet på derivatet F"(x). Så vi måste hitta en sådan funktion F(x), för vilka F"(x)=f(x). Funktion som krävs i uppgiften F(x)är ett antiderivat av f(x). Villkoren för problemet uppfylls inte av en kurva, utan av en familj av kurvor. y=F(x)- en av dessa kurvor och vilken annan kurva som helst kan erhållas från den genom parallell translation längs axeln Oj.
Låt oss kalla grafen för antiderivatans funktion för f(x) integralkurva. Om F"(x)=f(x), sedan grafen för funktionen y=F(x) det finns en integralkurva.
Fakta 3. Den obestämda integralen representeras geometriskt av familjen av alla integralkurvor , som på bilden nedan. Avståndet för varje kurva från utgångspunkten för koordinaterna bestäms av en godtycklig integrationskonstant C.

Egenskaper för den obestämda integralen
Fakta 4. Sats 1. Derivatan av en obestämd integral är lika med integranden och dess differential är lika med integranden.
Fakta 5. Sats 2. Obestämd integral av differentialen för en funktion f(x) är lika med funktionen f(x) upp till en konstant term , dvs.
![]() (3)
(3)
Satserna 1 och 2 visar att differentiering och integration är ömsesidigt inversa operationer.
Fakta 6. Sats 3. Konstantfaktorn i integranden kan tas ur den obestämda integralens tecken , dvs.
Definition 1
Antiderivatan $F(x)$ för funktionen $y=f(x)$ på segmentet $$ är en funktion som är differentierbar vid varje punkt i detta segment och följande likhet gäller för dess derivata:
Definition 2
Mängden av alla antiderivator av en given funktion $y=f(x)$, definierade på ett visst segment, kallas den obestämda integralen av en given funktion $y=f(x)$. Den obestämda integralen betecknas med symbolen $\int f(x)dx $.
Från tabellen över derivator och Definition 2 får vi tabellen över grundläggande integraler.
Exempel 1
Kontrollera giltigheten av formel 7 från tabellen över integraler:
\[\int tgxdx =-\ln |\cos x|+C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $-\ln |\cos x|+C$.
\[\left(-\ln |\cos x|+C\right)"=-\frac(1)(\cos x) \cdot (-\sin x)=\frac(\sin x)(\cos x) =tgx\]
Exempel 2
Kontrollera giltigheten av formel 8 från tabellen över integraler:
\[\int ctgxdx =\ln |\sin x|+C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\ln |\sin x|+C$.
\[\left(\ln |\sin x|\right)"=\frac(1)(\sin x) \cdot \cos x=ctgx\]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 3
Kontrollera giltigheten av formel 11" från tabellen över integraler:
\[\int \frac(dx)(a^(2) +x^(2) ) =\frac(1)(a) arctg\frac(x)(a) +C,\, \, C=const .\]
Låt oss skilja på den högra sidan: $\frac(1)(a) arctg\frac(x)(a) +C$.
\[\left(\frac(1)(a) arctg\frac(x)(a) +C\right)"=\frac(1)(a) \cdot \frac(1)(1+\left( \frac(x)(a) \right)^(2) ) \cdot \frac(1)(a) =\frac(1)(a^(2) ) \cdot \frac(a^(2) ) (a^(2) +x^(2) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 4
Kontrollera giltigheten av formel 12 från tabellen över integraler:
\[\int \frac(dx)(a^(2) -x^(2) ) =\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+ C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C$.
$\left(\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C\right)"=\frac(1)(2a) \cdot \frac( 1)(\frac(a+x)(a-x) ) \cdot \left(\frac(a+x)(a-x) \right)"=\frac(1)(2a) \cdot \frac(a-x)( a+x) \cdot \frac(a-x+a+x)((a-x)^(2) ) =\frac(1)(2a) \cdot \frac(a-x)(a+x) \cdot \ frac(2a)((a-x)^(2) ) =\frac(1)(a^(2) -x^(2) ) $Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 5
Kontrollera giltigheten av formel 13" från tabellen över integraler:
\[\int \frac(dx)(\sqrt(a^(2) -x^(2) ) ) =\arcsin \frac(x)(a) +C,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\arcsin \frac(x)(a) +C$.
\[\left(\arcsin \frac(x)(a) +C\right)"=\frac(1)(\sqrt(1-\left(\frac(x)(a) \right)^(2 ) ) ) \cdot \frac(1)(a) =\frac(a)(\sqrt(a^(2) -x^(2) ) ) \cdot \frac(1)(a) =\frac( 1)(\sqrt(a^(2) -x^(2) ) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 6
Kontrollera giltigheten av formel 14 från tabellen över integraler:
\[\int \frac(dx)(\sqrt(x^(2) \pm a^(2) ) =\ln |x+\sqrt(x^(2) \pm a^(2) ) |+ C ,\, \, C=konst.\]
Låt oss skilja på den högra sidan: $\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C$.
\[\left(\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C\right)"=\frac(1)(x+\sqrt(x^(2) \pm a^(2) ) \cdot \left(x+\sqrt(x^(2) \pm a^(2) ) \right)"=\frac(1)(x+\sqrt(x^(2) \ pm a^(2) ) \cdot \left(1+\frac(1)(2\sqrt(x^(2) \pm a^(2) ) ) \cdot 2x\right)=\] \[ =\ frac(1)(x+\sqrt(x^(2) \pm a^(2) ) \cdot \frac(\sqrt(x^(2) \pm a^(2) ) +x)( \sqrt( x^(2) \pm a^(2) ) =\frac(1)(\sqrt(x^(2) \pm a^(2) ) ) \]
Derivatan visade sig vara lika med integranden. Därför är formeln korrekt.
Exempel 7
Hitta integralen:
\[\int \left(\cos (3x+2)+5x\right) dx.\]
Låt oss använda summaintegralsatsen:
\[\int \left(\cos (3x+2)+5x\right) dx=\int \cos (3x+2)dx +\int 5xdx .\]
Låt oss använda satsen om att placera en konstant faktor utanför integraltecknet:
\[\int \cos (3x+2)dx +\int 5xdx =\int \cos (3x+2)dx +5\int xdx .\]
Enligt tabellen över integraler:
\[\int \cos x dx=\sin x+C;\] \[\int xdx =\frac(x^(2) )(2) +C.\]
När vi beräknar den första integralen använder vi regel 3:
\[\int \cos (3x+2) dx=\frac(1)(3) \sin (3x+2)+C_(1) .\]
Därav,
\[\int \left(\cos (3x+2)+5x\right) dx=\frac(1)(3) \sin (3x+2)+C_(1) +\frac(5x^(2) )(2) +C_(2) =\frac(1)(3) \sin (3x+2)+\frac(5x^(2) )(2) +C,\, \, C=C_(1) ) +C_(2) \]
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0

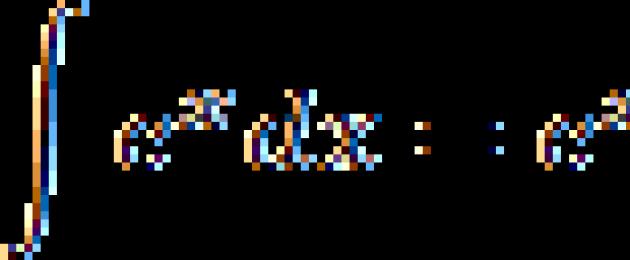








 Derivat av den naturliga logaritmen
Derivat av den naturliga logaritmen
 Derivat av en sekant
Derivat av en sekant Derivat av arcsine
Derivat av arcsine Derivat av bågekosinus
Derivat av bågekosinus Derivat av arcsine
Derivat av arcsine Derivat av bågekosinus
Derivat av bågekosinus Tangentderivat
Tangentderivat Derivat av cotangens
Derivat av cotangens Derivat av arctangens
Derivat av arctangens Derivat av arc cotangens
Derivat av arc cotangens Derivat av arctangens
Derivat av arctangens Derivat av ljusbåge
Derivat av ljusbåge Derivat av arccosecant
Derivat av arccosecant Derivat av ljusbåge
Derivat av ljusbåge Derivat av hyperbolisk sinus
Derivat av hyperbolisk sinus Derivat av hyperbolisk sinus i den engelska versionen
Derivat av hyperbolisk sinus i den engelska versionen Derivat av hyperbolisk cosinus
Derivat av hyperbolisk cosinus Derivat av hyperbolisk cosinus i engelsk version
Derivat av hyperbolisk cosinus i engelsk version Derivat av hyperbolisk tangent
Derivat av hyperbolisk tangent Derivat av hyperbolisk cotangens
Derivat av hyperbolisk cotangens Derivat av den hyperboliska sekanten
Derivat av den hyperboliska sekanten Derivat av den hyperboliska cosekanten
Derivat av den hyperboliska cosekanten