Rita ett diagram över systemet och markera tyngdpunkten på det. Om den hittade tyngdpunkten ligger utanför objektsystemet fick du ett felaktigt svar. Du kan ha mätt avstånd från olika referenspunkter. Upprepa mätningarna.
- Till exempel, om barn sitter på en gunga, kommer tyngdpunkten att vara någonstans mellan barnen och inte till höger eller vänster om gungan. Tyngdpunkten kommer heller aldrig att sammanfalla med punkten där barnet sitter.
- Dessa argument är giltiga i tvådimensionellt utrymme. Rita en kvadrat som kommer att innehålla alla objekt i systemet. Tyngdpunkten ska vara inuti denna ruta.
Kontrollera din matte om du får ett litet resultat. Om referenspunkten är i ena änden av systemet, placerar ett litet resultat tyngdpunkten nära slutet av systemet. Detta kan vara det korrekta svaret, men i de allra flesta fall indikerar detta resultat ett fel. När du beräknade momenten, multiplicerade du motsvarande vikter och avstånd? Om du istället för att multiplicera adderade vikterna och avstånden skulle du få ett mycket mindre resultat.
Rätta till felet om du hittat flera tyngdpunkter. Varje system har bara en tyngdpunkt. Om du hittade flera tyngdpunkter har du sannolikt inte lagt ihop alla momenten. Tyngdpunkten är lika med förhållandet mellan det "totala" momentet och den "totala" vikten. Det finns ingen anledning att dela "varje" ögonblick med "varje" vikt: på så sätt hittar du positionen för varje objekt.
Kontrollera referenspunkten om svaret skiljer sig med något heltalsvärde. I vårt exempel är svaret 3,4 m. Låt oss säga att du fick svaret 0,4 m eller 1,4 m, eller ett annat tal som slutar på ".4". Detta beror på att du inte valde den vänstra änden av brädan som utgångspunkt, utan en punkt som ligger en hel del till höger. Faktum är att ditt svar är korrekt oavsett vilken referenspunkt du väljer! Kom bara ihåg: referenspunkten är alltid vid position x = 0. Här är ett exempel:
- I vårt exempel var referenspunkten vid den vänstra änden av tavlan och vi fann att tyngdpunkten var 3,4 m från denna referenspunkt.
- Väljer du som referenspunkt en punkt som ligger 1 m till höger från tavlans vänstra ände får du svaret 2,4 m. Dvs tyngdpunkten är 2,4 m från den nya referenspunkten, vilket , är i sin tur placerad 1 m från den vänstra änden av brädan. Tyngdpunkten är alltså på ett avstånd av 2,4 + 1 = 3,4 m från brädans vänstra ände. Det visade sig vara ett gammalt svar!
- Observera: när du mäter avstånd, kom ihåg att avstånden till "vänster" referenspunkt är negativa och till "höger" referenspunkt är positiva.
Mät avstånd i raka linjer. Anta att det finns två barn på en gunga, men det ena barnet är mycket längre än det andra, eller så hänger ett barn under brädan istället för att sitta på den. Ignorera denna skillnad och mät avstånden längs den raka linjen på brädan. Att mäta avstånd i vinklar ger nära men inte helt exakta resultat.
- För problemet med gungbräda, kom ihåg att tyngdpunkten är mellan brädans högra och vänstra ände. Senare får du lära dig att beräkna tyngdpunkten för mer komplexa tvådimensionella system.
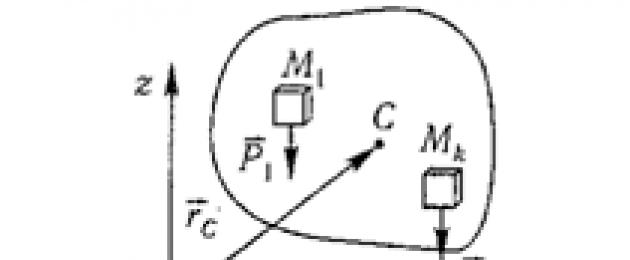
Tyngdpunkt av en solid kropp är en geometrisk punkt som är stelt ansluten till denna kropp och är centrum för parallella gravitationskrafter som appliceras på enskilda elementarpartiklar i kroppen (Figur 1.6).
Radievektor för denna punkt

Figur 1.6
För en homogen kropp är läget för kroppens tyngdpunkt inte beroende av materialet, utan bestäms av kroppens geometriska form.
Om den specifika vikten hos en homogen kropp γ , vikten av en elementarpartikel i kroppen
P k = γΔV k (P = γV ) ersätt i formeln för att bestämma r C , vi har
Varifrån vi skjuter ut på axlarna och passerar till gränsen, får vi koordinaterna för tyngdpunkten för en homogen volym

På samma sätt för koordinaterna för tyngdpunkten för en homogen yta med area S (Figur 1.7, a)


Figur 1.7
För koordinaterna för tyngdpunkten för en homogen längdlinje L (Figur 1.7, b)

Metoder för att bestämma koordinaterna för tyngdpunkten
Baserat på de allmänna formlerna som erhållits tidigare kan vi indikera metoder för att bestämma koordinaterna för tyngdpunkterna för fasta kroppar:
1 Analytisk(genom integration).
2 Symmetrimetod. Om en kropp har ett plan, en axel eller ett symmetricentrum, så ligger dess tyngdpunkt i respektive symmetriplan, symmetriaxeln eller symmetricentrum.
3 Experimentell(kroppsupphängningsmetod).
4 Splittring. Kroppen är uppdelad i ett ändligt antal delar, för var och en av vilka tyngdpunktens position är C och område S känd. Till exempel projektionen av en kropp på ett plan xOy (Figur 1.8) kan representeras som två platta figurer med ytor S 1 Och S 2 (S=S 1 +S 2 ). Tyngdpunkterna för dessa figurer är belägna på punkter C 1 (x 1 , y 1 ) Och C 2 (x 2 , y 2 ) . Då är koordinaterna för kroppens tyngdpunkt lika


Figur 1.8
5Tillägg(metod för negativa ytor eller volymer). Ett specialfall av partitioneringsmetoden. Det gäller kroppar som har utskärningar om kroppens tyngdpunkter utan utskärningen och utskärningsdelen är kända. Till exempel måste du hitta koordinaterna för tyngdpunkten för en platt figur (Figur 1.9):


Figur 1.9
Tyngdpunkter för de enklaste figurerna

Figur 1.10
1 triangel
Tyngdpunkten för triangelns område sammanfaller med skärningspunkten för dess medianer (Figur 1.10, a).
DM = MB , CM= (1/3)A.M. .
2 Cirkelbåge
Bågen har en symmetriaxel (Figur 1.10, b). Tyngdpunkten ligger på denna axel, dvs. y C = 0 .

dl – bågelement, dl = Rdφ , R – cirkelns radie, x = Rcosφ , L= 2αR ,
Därav:
x C = R(sinα/α) .
3 Cirkulär sektor
Radiesektor R med mittvinkel 2 α har en symmetriaxel Oxe , på vilken tyngdpunkten är belägen (Figur 1.10, c).
Vi delar upp sektorn i elementära sektorer, som kan betraktas som trianglar. Tyngdpunkterna för elementära sektorer är belägna på en cirkelbåge med radie (2/3) R .
Sektorns tyngdpunkt sammanfaller med bågens tyngdpunkt AB :

14. Metoder för att specificera en punkts rörelse.
Med vektormetoden för att specificera rörelse bestäms positionen för en punkt av en radievektor som ritas från en fast punkt i det valda referenssystemet.
Med koordinatmetoden för att specificera rörelse specificeras koordinaterna för en punkt som en funktion av tiden:

Dessa är parametriska ekvationer för en rörlig punkts bana, där tiden spelar rollen som en parameter t . För att skriva sin ekvation i explicit form är det nödvändigt att utesluta från dem t .
Med den naturliga metoden för att specificera rörelse specificeras punktens bana, ursprunget för referensen på banan som anger referensens positiva riktning och lagen för förändring i bågkoordinaten: s=s(t) . Denna metod är bekväm att använda om punktens bana är känd i förväg.
15. 1,2 punkthastighet
Tänk på rörelsen av en punkt under en kort tidsperiod AT :
![]()
medelhastighet för en punkt under en tidsperiod Dt . Hastigheten för en punkt vid en given tidpunkt


Punkthastighetär ett kinematiskt mått på dess rörelse, lika med tidsderivatan av radievektorn för denna punkt i referenssystemet i fråga. Hastighetsvektorn riktas tangentiellt till punktens bana i rörelseriktningen.
Instruktioner
Försök att hitta centrum allvar platt siffror empiriskt. Ta en ny, oslipad penna och placera den vertikalt. Placera en platt figur ovanpå den. Markera punkten på figuren där den är stabil på pennan. Detta kommer att vara centrum allvar din siffror. Istället för en penna använder du helt enkelt pekfingret uppåt. Men det beror på att du måste se till att fingret står rakt, inte svajar eller darrar.
För att visa att den resulterande punkten är massans centrum, gör ett hål i den med en nål. Trä en tråd genom hålet och knyt en knut i ena änden så att tråden inte hoppar ut. Håll i den andra änden av tråden och häng kroppen från den. Om centrum allvar Det stämmer, figuren kommer att placeras exakt, parallellt med golvet. Hennes sidor kommer inte att svaja.
Hitta centrum allvar siffror geometriskt. Om du får en triangel, konstruera . Dessa segment förbinder triangelns hörn till mitten av den motsatta sidan. Poängen kommer att bli Centrum triangelmassor. För att hitta mittpunkten på en sida kan du till och med vika figuren på mitten, men tänk på att detta kommer att störa enhetligheten siffror.
Jämför de erhållna resultaten geometriskt och experimentellt. Rapportera experimentets framsteg. Små fel anses vara normala. De förklaras av ofullkomlighet siffror, felaktigheter i instrument, mänsklig faktor (mindre brister i arbetet, ofullkomlighet i det mänskliga ögat, etc.).
Källor:
- Beräkna koordinaterna för en platt figurs tyngdpunkt
I ett enhetligt gravitationsfält sammanfaller tyngdpunkten med masscentrum. I geometri är begreppen "tyngdpunkt" och "massacentrum" också likvärdiga, eftersom förekomsten av ett gravitationsfält inte beaktas. Masscentrum kallas också tröghetscentrum och barycentrum (av grekiskan barus - tung, kentron - centrum). Det kännetecknar rörelsen hos en kropp eller ett system av partiklar. Sålunda, under fritt fall, roterar en kropp runt sitt tröghetscentrum.
Instruktioner
Låt systemet bestå av två identiska punkter. Då, uppenbarligen, ligger i mitten mellan dem. Om punkter med koordinater x1 och x2 har olika massor m1 och m2, så är koordinaten för masscentrum x(c)=(m1 x1+m2 x2)/(m1+m2). Beroende på referenssystemets valda "nolla" kan koordinaterna också vara negativa.
Punkter på ett plan har två koordinater: x och y. När det anges i rymden läggs en tredje z-koordinat till. För att inte beskriva varje koordinat separat, är det bekvämt att överväga radievektorn för punkten: r=x i+y j+z· k, Var i,j,k− enhetsvektorer för koordinataxlar.
Låt nu systemet bestå av tre punkter med massorna m1, m2 och m3. Deras radievektorer, respektive, r1, r2 Och r3. Sedan radievektorn för deras tyngdpunkt r(c)=(m1· r1+m2· r2+m3· r3)/(m1+m2+m3).
Om systemet består av godtyckliga punkter, så hittas radievektorn, per definition, av formeln:
r(c)=∑m(i) r(i)/∑m(i). Summeringen utförs med hjälp av index i (skrivet under summatecknet ∑). Här är m(i) något i:te system, r(i)− dess radievektor.
Om kroppen är homogen i massa går summan in i en integral. Bryt kroppen mentalt i oändligt små bitar av massa dm. Eftersom kroppen är homogen kan massan av varje del skrivas som dm=ρ·dV, där dV är den elementära volymen av denna bit, ρ är densiteten (samma genom hela volymen av en homogen kropp).
Den integrerade summan av massan av alla bitar ger massan av hela kroppen: ∑m(i)=∫dm=M. Så visar det sig r(c)=1/M·∫ρ·dV· dr. Densitet, ett konstant värde, kan tas ut under integraltecknet: r(c)=ρ/M·∫dV· dr. För direkt integration måste du ställa in en specifik funktion mellan dV och dr, vilket beror på figurens parametrar.
Till exempel är tyngdpunkten för ett segment (en lång homogen stav) i mitten. Sfärens och kulans masscentrum ligger i mitten. Konens barycentrum är beläget i höjd med det axiella segmentet, räknat från basen.
Centrum kan också bestämmas experimentellt. Klipp ut valfri form från ett ark tjockt papper eller kartong (till exempel samma triangel). Försök att placera den på toppen av ett vertikalt utsträckt finger. Platsen för vilken detta kan göras kommer att vara kroppens tröghetscentrum.
Källor:
- "Mekanik", D.V. Sivukhin, 2006.
- Bestämma koordinaterna för fartygets tyngdpunkt
I vanlig mening uppfattas tyngdpunkten som den punkt till vilken resultatet av alla krafter som verkar på kroppen kan appliceras. Det enklaste exemplet är en barngunga i form av en vanlig bräda. Utan några beräkningar kommer vilket barn som helst att välja brädans stöd på ett sådant sätt att det balanserar (och kanske till och med uppväger) en tung man på en gunga. När det gäller komplexa kroppar och sektioner är exakta beräkningar och motsvarande formler oumbärliga. Även om du får krångliga uttryck är det viktigaste att inte vara rädd för dem, utan att komma ihåg att vi initialt talar om en nästan elementär uppgift.

Instruktioner
Betrakta den enklaste spaken (se figur 1) i jämviktsläget. Placera x₁₂ på den horisontella axeln med abskissan och placera materialpunkter med massorna m₁ och m₂ på kanterna. Betrakta deras koordinater längs 0x-axeln som kända och lika med x₁ och x₂. Spaken är i jämviktsläge om momenten för viktkrafterna Р₁=m₁g och P₂=m₂g är lika. Momentet är lika med produkten av kraften från dess arm, vilket kan hittas som längden på vinkelrät sänkt från kraftens appliceringspunkt till vertikalen x=x₁₂. Därför, i enlighet med figur 1, är mlg11= m2gl2, 11=512-х1, 12=х2-х12. Därefter m₁(х₁₂-х₁)=m₂(х₂-х₁₂). Lös denna ekvation och få x₁₂=(m₁x₁+m₂x₂)/(m₁+m₂).

För att ta reda på ordinatan y₁₂, använd samma resonemang och beräkningar som i steg 1. Följ fortfarande illustrationen som visas i figur 1, där m₁gh₁= m₂gh₂, h1=y₁₂-y₁, h₂=y₂-y₁₂. Därefter m1(y12-y1)=m2(y2-y12). Resultatet är y12=(m1u1+m2u2)/(m1+m2). Tänk sedan på att istället för ett system med två punkter finns det en punkt M12(x12,у12) av den totala massan (m₁+m₂).
Till systemet med två punkter, lägg till ytterligare en massa (m₃) med koordinater (x₃, y₃). När du räknar ska du ändå utgå från att du har att göra med två punkter, där den andra har massa (m₁+m₂) och koordinater (x12,y12). Genom att upprepa alla åtgärderna i steg 1 och 2 för dessa två punkter kommer du till mitten av de tre punkterna x₁x₁+m₂x₂+m₃x₃)/(m₁+m₂+m₃), y₁₂₃₃=(m₁₂₃₃=(m₁₂у₁+m₁₂у₁+m) m1+ m2 +m3). Lägg sedan till den fjärde, femte och så vidare punkterna. Efter att ha upprepat samma procedur många gånger, se till att för ett system med n punkter beräknas koordinaterna för tyngdpunkten med hjälp av formeln (se fig. 2). Notera själv det faktum att under arbetet minskade tyngdaccelerationen g. Därför sammanfaller koordinaterna för massacentrum och tyngdpunkten.

Föreställ dig att det i det aktuella avsnittet finns ett visst område D, vars ytdensitet är ρ=1. Uppifrån och under begränsas figuren av graferna för kurvorna y=φ(x) och y=ψ(x), x є [a,b]. Dela area D med vertikaler x=x₍i-1₎, x=x₍i₎ (i=1,2,...,n) i tunna remsor, så att de ungefär kan betraktas som rektanglar med baser ∆хi (se fig. ..3). Betrakta i det här fallet att mitten av segmentet ∆хi sammanfaller med abskissan för massacentrum ξi=(1/2). Anse att rektangelns höjd är ungefär lika med [φ(ξi)-ψ(ξi)]. Då är ordinatan för det elementära områdets masscentrum ηi=(1/2)[φ(ξi)+ψ(ξi)].

På grund av den enhetliga densitetsfördelningen, tänk på att remsans masscentrum kommer att sammanfalla med dess geometriska centrum. Den motsvarande elementära massan ∆mi=ρ[φ(ξi)-ψ(ξi)]∆хi=[φ(ξi)-ψ(ξi)]∆хi är koncentrerad vid punkten (ξi,ηi). Ögonblicket har kommit för den omvända övergången från massa presenterad i diskret form till kontinuerlig. I enlighet med formlerna för beräkning av koordinaterna (se fig. 2) för tyngdpunkten, bildas integralsummor, illustrerade i fig. 4a. När du går över till gränsen vid ∆xi→0 (ξi→xi) från summor till bestämda integraler, få det slutliga svaret (Fig. 4b). Det finns ingen massa i svaret. Jämlikheten S=M ska endast förstås som kvantitativ. Måtten här skiljer sig från varandra.

Baserat på de allmänna formlerna som erhållits ovan är det möjligt att ange specifika metoder för att bestämma koordinaterna för kropparnas tyngdpunkter.
1. Symmetri. Om en homogen kropp har ett plan, axel eller symmetricentrum (fig. 7), så ligger dess tyngdpunkt i respektive symmetriplan, symmetriaxel eller i symmetricentrum.
Fig. 7
2. Splittring. Kroppen är uppdelad i ett ändligt antal delar (fig. 8), för var och en av vilka tyngdpunktens läge och area är kända.

Fig. 8
3.Negativ area metod. Ett specialfall av partitioneringsmetoden (fig. 9). Det gäller kroppar som har utskärningar om kroppens tyngdpunkter utan utskärningen och utskärningsdelen är kända. En kropp i form av en platta med en utskärning representeras av en kombination av en solid platta (utan en utskärning) med ett område S 1 och ett område av den utskurna delen S 2 .

Fig. 9
4.Grupperingsmetod. Det är ett bra komplement till de två sista metoderna. Efter att ha delat upp en figur i dess beståndsdelar är det bekvämt att kombinera några av dem igen för att sedan förenkla lösningen genom att ta hänsyn till denna grupps symmetri.
Tyngdpunkter för vissa homogena kroppar.
1) Tyngdpunkten för en cirkelbåge. Tänk på bågen AB radie R med en central vinkel. På grund av symmetri ligger tyngdpunkten för denna båge på axeln Oxe(Fig. 10).

Fig. 10
Låt oss hitta koordinaten med hjälp av formeln. För att göra detta, välj på bågen AB element MM' längd, vars position bestäms av vinkeln. Samordna X element MM' kommer . Ersätter dessa värden X och d l och med tanke på att integralen måste sträckas ut över bågens hela längd får vi:

Var L- båglängd AB, lika med .
Härifrån finner vi slutligen att tyngdpunkten för en cirkelbåge ligger på dess symmetriaxel på avstånd från centrum HANDLA OM, likvärdig
där vinkeln mäts i radianer.
2) Tyngdpunkten för triangelns område. Betrakta en triangel som ligger i planet Oxy, vars koordinater är kända: A i(x i,y i), (i= 1,2,3). Bryt triangeln i smala remsor parallellt med sidan A 1 A 2 kommer vi fram till att triangelns tyngdpunkt måste tillhöra medianen A 3 M 3 (Fig. 11).

Fig. 11
Bryt en triangel i remsor parallella med sidan A 2 A 3 kan vi verifiera att den måste ligga på medianen A 1 M 1 . Således, tyngdpunkten för en triangel ligger i skärningspunkten för dess medianer, som som bekant skiljer en tredje del från varje median, räknat från motsvarande sida.
I synnerhet för medianen A 1 M 1 erhåller vi, med hänsyn till att punktens koordinater M 1 är det aritmetiska medelvärdet av koordinaterna för hörnen A 2 och A 3:
x c = x 1 + (2/3)∙(x M 1 - x 1) = x 1 + (2/3)∙[(x 2 + x 3)/2-x 1 ] = (x 1 +x 2 +x 3)/3.
Således är koordinaterna för triangelns tyngdpunkt det aritmetiska medelvärdet av koordinaterna för dess hörn:
x c =(1/3)Σ x i ; y c =(1/3)Σ y i.
3) Tyngdpunkten för området för en cirkulär sektor. Betrakta en sektor av en cirkel med radie R med en central vinkel på 2α, placerad symmetriskt i förhållande till axeln Oxe(Fig. 12).
Det är uppenbart y c = 0, och avståndet från mitten av cirkeln från vilken denna sektor skärs till dess tyngdpunkt kan bestämmas med formeln:


Fig. 12
Det enklaste sättet att beräkna denna integral är genom att dela upp integrationsdomänen i elementära sektorer med en vinkel dφ. Exakt till infinitesimals av första ordningen kan en sådan sektor ersättas med en triangel med en bas lika med R× dφ och höjd R. Arean av en sådan triangel dF=(1/2)R 2 ∙dφ, och dess tyngdpunkt är på ett avstånd av 2/3 R från spetsen, därför sätter vi i (5). x = (2/3)R∙cosφ. Ersätter i (5) F= α R 2, vi får:

Med den sista formeln beräknar vi i synnerhet avståndet till tyngdpunkten halvcirkel.
Genom att ersätta α = π/2 i (2) får vi: x c = (4R)/(3π) ≅ 0,4 R .
Exempel 1. Låt oss bestämma tyngdpunkten för den homogena kroppen som visas i fig. 13.

Fig. 13
Kroppen är homogen, bestående av två delar med en symmetrisk form. Koordinater för deras tyngdpunkter:
Deras volymer:
Därför koordinaterna för kroppens tyngdpunkt
Exempel 2. Låt oss hitta tyngdpunkten för en platta böjd i rät vinkel. Mått finns på ritningen (Fig. 14).

Fig. 14
Koordinater för tyngdpunkterna:
Områden:
![]()
|

Fig. 15
I det här problemet är det bekvämare att dela kroppen i två delar: en stor fyrkant och ett fyrkantigt hål. Endast hålets yta bör betraktas som negativ. Sedan koordinaterna för arkets tyngdpunkt med hålet:
samordna ![]() eftersom kroppen har en symmetriaxel (diagonal).
eftersom kroppen har en symmetriaxel (diagonal).
Exempel 4. Trådfästet (fig. 16) består av tre lika långa sektioner l.

Fig. 16
Koordinater för sektionernas tyngdpunkter:
Därför är koordinaterna för tyngdpunkten för hela fästet:
Exempel 5. Bestäm läget för fackverkets tyngdpunkt, vars alla stavar har samma linjära densitet (Fig. 17).
Låt oss komma ihåg att i fysiken är tätheten hos en kropp ρ och dess specifika vikt g relaterade till förhållandet: γ= ρ g, Var g- tyngdacceleration. För att hitta massan av en sådan homogen kropp måste du multiplicera densiteten med dess volym.

Fig. 17
Termen "linjär" eller "linjär" densitet betyder att för att bestämma massan av en fackverksstav måste den linjära densiteten multipliceras med längden på denna stav.
För att lösa problemet kan du använda partitioneringsmetoden. Genom att representera en given fackverk som summan av 6 individuella stavar får vi:
Var L i längd i fackverksstång, och x i, y i- koordinater för dess tyngdpunkt.
Lösningen på detta problem kan förenklas genom att gruppera de sista 5 stängerna av fackverket. Det är lätt att se att de bildar en figur med ett symmetricentrum placerat i mitten av den fjärde staven, där tyngdpunkten för denna grupp av stavar finns.
Således kan en given fackverk representeras av en kombination av endast två grupper av stavar.
Den första gruppen består av den första spöet, för den L 1 = 4 m, x 1 = 0 m, y 1 = 2 m. Den andra gruppen av stavar består av fem stavar, för den L 2 = 20 m, x 2 = 3 m, y 2 = 2 m.
Koordinaterna för fackverkets tyngdpunkt hittas med formeln:
x c = (L 1 ∙x 1 +L 2 ∙x 2)/(L 1 + L 2) = (4∙0 + 20∙3)/24 = 5/2 m;
y c = (L 1 ∙y 1 +L 2 ∙y 2)/(L 1 + L 2) = (4∙2 + 20∙2)/24 = 2 m.
Observera att mitten MED ligger på den raka linjen som ansluter MED 1 och MED 2 och delar segmentet MED 1 MED 2 angående: MED 1 MED/SS 2 = (x c - x 1)/(x 2 - x c ) = L 2 /L 1 = 2,5/0,5.
Självtestfrågor
Vad kallas mitten av parallella krafter?
Hur bestäms koordinaterna för mitten av parallella krafter?
Hur bestämmer man mitten av parallella krafter vars resultant är noll?
Vilka egenskaper har centrum av parallella krafter?
Vilka formler används för att beräkna koordinaterna för mitten av parallella krafter?
Vad är en kropps tyngdpunkt?
Varför kan jordens gravitationskrafter som verkar på en punkt på en kropp ses som ett system av parallella krafter?
Skriv ner formeln för att bestämma tyngdpunktsläget för inhomogena och homogena kroppar, formeln för att bestämma tyngdpunktsläget för plana sektioner?
Skriv ner formeln för att bestämma tyngdpunktens position för enkla geometriska former: rektangel, triangel, trapets och halvcirkel?
Vad är det statiska momentet för arean?
Ge ett exempel på en kropp vars tyngdpunkt ligger utanför kroppen.
Hur används symmetrins egenskaper för att bestämma kropparnas tyngdpunkter?
Vad är kärnan i metoden med negativa vikter?
Var är tyngdpunkten för en cirkelbåge?
Vilken grafisk konstruktion kan användas för att hitta en triangels tyngdpunkt?
Skriv ner formeln som bestämmer tyngdpunkten för en cirkulär sektor.
Använd formler som bestämmer tyngdpunkterna för en triangel och en cirkulär sektor, härled en liknande formel för ett cirkulärt segment.
Vilka formler används för att beräkna koordinaterna för tyngdpunkterna för homogena kroppar, platta figurer och linjer?
Vad kallas det statiska momentet för arean av en plan figur i förhållande till axeln, hur beräknas det och vilken dimension har det?
Hur bestämmer man läget för ett områdes tyngdpunkt om läget för tyngdpunkterna för dess enskilda delar är känt?
Vilka hjälpsatser används för att bestämma tyngdpunktens position?
I ingenjörspraktik händer det att det finns ett behov av att beräkna koordinaterna för tyngdpunkten för en komplex platt figur som består av enkla element för vilka tyngdpunktens placering är känd. Denna uppgift är en del av uppgiften att bestämma...
Geometriska egenskaper hos sammansatta tvärsnitt av balkar och stänger. Ofta måste konstruktörer av skärformar möta liknande frågor när de bestämmer koordinaterna för tryckcentrum, utvecklare av lastscheman för olika fordon vid placering av last, designers av byggnadsmetallkonstruktioner när de väljer tvärsnitt av element och, naturligtvis, studenter när de studerar disciplinerna "Teoretisk mekanik" och "Materialstyrka."
Bibliotek med elementära figurer.

För symmetriska plana figurer sammanfaller tyngdpunkten med symmetricentrum. Den symmetriska gruppen av elementära objekt inkluderar: cirkel, rektangel (inklusive kvadrat), parallellogram (inklusive romb), vanlig polygon.
Av de tio siffrorna som presenteras i figuren ovan är endast två grundläggande. Det vill säga, med hjälp av trianglar och sektorer av cirklar kan du kombinera nästan vilken figur som helst av praktiskt intresse. Eventuella godtyckliga kurvor kan delas upp i sektioner och ersättas med cirkelbågar.
De återstående åtta figurerna är de vanligaste, varför de ingick i detta unika bibliotek. I vår klassificering är dessa element inte grundläggande. En rektangel, parallellogram och trapets kan bildas av två trianglar. En hexagon är summan av fyra trianglar. Ett cirkelsegment är skillnaden mellan en sektor av en cirkel och en triangel. Den ringformade sektorn i en cirkel är skillnaden mellan två sektorer. En cirkel är en sektor av en cirkel med vinkeln α=2*π=360˚. En halvcirkel är följaktligen en sektor av en cirkel med vinkeln α=π=180˚.
Beräkning i Excel av koordinaterna för tyngdpunkten för en sammansatt figur.
Det är alltid lättare att förmedla och uppfatta information genom att ta ett exempel än att studera frågan med rent teoretiska beräkningar. Låt oss överväga lösningen på problemet "Hur hittar man tyngdpunkten?" med hjälp av exemplet på den sammansatta figuren som visas i figuren nedanför denna text.

Den sammansatta sektionen är en rektangel (med dimensioner a1 =80 mm, b1 =40 mm), till vilken en likbent triangel lades till överst till vänster (med basens storlek a2 =24 mm och höjd h2 =42 mm) och från vilken en halvcirkel skars ut uppifrån till höger (med mitten i punkten med koordinaterna x03 =50 mm och y03 =40 mm, radie r3 =26 mm).
Vi kommer att använda ett program för att hjälpa dig utföra beräkningarna MS Excel eller program OOo Beräknat . Någon av dem kommer lätt att klara av vår uppgift!
I celler med gul vi kommer att fylla den extra preliminär beräkningar .
Vi beräknar resultaten i celler med en ljusgul fyllning.
Blå teckensnitt är initiala data .
Svart teckensnitt är mellanliggande beräkningsresultat .
Röd teckensnitt är slutlig beräkningsresultat .
Vi börjar lösa problemet - vi börjar leta efter koordinaterna för sektionens tyngdpunkt.
Initial data:
1. Vi kommer att skriva namnen på de elementära figurerna som bildar en sammansatt sektion därefter
till cell D3: Rektangel
till cell E3: Triangel
till cell F3: Halvcirkel
2. Med hjälp av "Library of Elementary Figures" som presenteras i den här artikeln kommer vi att bestämma koordinaterna för tyngdpunkterna för elementen i den sammansatta sektionen xci Och yci i mm i förhållande till godtyckligt valda axlar 0x och 0y och skriv
till cell D4: =80/2 = 40,000
xc 1 = a 1 /2
till cell D5: =40/2 =20,000
yc 1 = b 1 /2
till cell E4: =24/2 =12,000
xc 2 = a 2 /2
till cell E5: =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
till cell F4: =50 =50,000
xc 3 = x03
till cell F5: =40-4*26/3/PI() =28,965
yc 3 = y 03 -4* r3 /3/ π
3. Låt oss beräkna elementens area F 1 , F 2 , F3 i mm2, återigen med formlerna från avsnittet "Bibliotek med elementära figurer"
i cell D6: =40*80 =3200
F1 = a 1 * b1
i cell E6: =24*42/2 =504
F2 = a2 *h2 /2
i cell F6: =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
Arean av det tredje elementet - halvcirkeln - är negativ eftersom det är en utskärning - ett tomt utrymme!

Beräkning av tyngdpunktskoordinater:
4. Bestäm den totala ytan av den slutliga figuren F0 i mm2
i sammanslagen cell D8E8F8: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Låt oss beräkna de statiska momenten för en sammansatt figur Sx Och Sy i mm3 relativt de valda axlarna 0x och 0y
i sammanslagen cell D9E9F9: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
i den sammanslagna cellen D10E10F10: =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. Och slutligen, låt oss beräkna koordinaterna för tyngdpunkten för den sammansatta sektionen Xc Och Yc i mm i det valda koordinatsystemet 0x - 0y
i sammanslagen cell D11E11F11: =D10/D8 =30,640
Xc = Sy / F0
i sammanslagen cell D12E12F12: =D9/D8 =22,883
Yc =Sx/FO
Problemet är löst, beräkningen i Excel är klar - koordinaterna för sektionens tyngdpunkt, sammanställda med hjälp av tre enkla element, har hittats!
Slutsats.
Exemplet i artikeln valdes för att vara mycket enkelt för att göra det lättare att förstå metodiken för att beräkna tyngdpunkten för ett komplext avsnitt. Metoden är att varje komplex figur ska delas upp i enkla element med kända placeringar av tyngdpunkterna och slutliga beräkningar ska göras för hela sektionen.
Om sektionen består av rullade profiler - vinklar och kanaler, finns det inget behov av att dela upp dem i rektanglar och kvadrater med utskurna cirkulära "π/2" sektorer. Koordinaterna för tyngdpunkterna för dessa profiler anges i GOST-tabellerna, det vill säga både vinkeln och kanalen kommer att vara de grundläggande elementära elementen i dina beräkningar av sammansatta sektioner (det är ingen mening att prata om I-balkar, rör, stavar och hexagoner - dessa är centralt symmetriska sektioner).
Placeringen av koordinataxlarna påverkar naturligtvis inte läget för figurens tyngdpunkt! Välj därför ett koordinatsystem som förenklar dina beräkningar. Om jag till exempel skulle rotera koordinatsystemet 45˚ medurs i vårt exempel, då skulle beräkning av koordinaterna för tyngdpunkterna för en rektangel, triangel och halvcirkel förvandlas till ett annat separat och besvärligt steg av beräkningar som inte kan utföras " i huvudet".
Excel-beräkningsfilen som presenteras nedan är inte ett program i detta fall. Det är snarare en skiss av en miniräknare, en algoritm, en mall som följer i varje specifikt fall skapa din egen sekvens av formler för celler med en ljusgul fyllning.
Så nu vet du hur du hittar tyngdpunkten för vilken sektion som helst! Den fullständiga beräkningen av alla geometriska egenskaper hos godtyckliga komplexa sammansatta sektioner kommer att övervägas i en av de kommande artiklarna i avsnittet "". Följ nyheterna på bloggen.
För tar emot information om lanseringen av nya artiklar och för ladda ner fungerande programfiler Jag ber dig att prenumerera på meddelanden i fönstret som finns i slutet av artikeln eller i fönstret högst upp på sidan.
Efter att ha angett din e-postadress och klickat på knappen "Ta emot artikelmeddelanden". GLÖM INTE BEKRÄFTA DIN PRENUMERATION genom att klicka på länken i ett brev som omedelbart kommer till dig på angiven e-postadress (ibland i mappen « Spam » )!
Några ord om glaset, myntet och två gafflar, som avbildas i "illustrationsikonen" i början av artikeln. Många av er är säkert bekanta med detta "trick", som framkallar beundrande blickar från barn och oinvigda vuxna. Ämnet för den här artikeln är tyngdpunkten. Det är han och stödpunkten, som leker med vårt medvetande och vår erfarenhet, som helt enkelt lurar våra sinnen!
Tyngdpunkten för "gaffel+mynt"-systemet är alltid placerad på fast distans vertikalt ner från myntkanten, som i sin tur är stödpunkten. Detta är en position med stabil jämvikt! Skakar man gafflarna blir det direkt uppenbart att systemet strävar efter att ta sin tidigare stabila position! Föreställ dig en pendel - en fästpunkt (= stödpunkten för ett mynt på kanten av ett glas), en stavaxel på pendeln (= i vårt fall är axeln virtuell, eftersom massan av de två gafflarna är utspridda i olika riktningar av rymden) och en last längst ner på axeln (= tyngdpunkten för hela "gaffelsystemet + mynt"). Om du börjar avleda pendeln från vertikalen i någon riktning (framåt, bakåt, vänster, höger), kommer den oundvikligen att återgå till sin ursprungliga position under påverkan av gravitationen. stabilt jämviktstillstånd(samma sak händer med våra gafflar och mynt)!
Om du inte förstår, men vill förstå, ta reda på det själv. Det är väldigt intressant att "komma dit" själv! Jag kommer att tillägga att samma princip att använda stabil jämvikt också är implementerad i leksaken Vanka-ståupp. Endast tyngdpunkten för denna leksak är placerad ovanför stödjepunkten, men under mitten av halvklotet av den stödjande ytan.
Jag blir alltid glad att se dina kommentarer, kära läsare!!!
Fråga, RESPEKTERANDE författarens verk, ladda ner fil EFTER PRENUMERERA för artikelmeddelanden.
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0