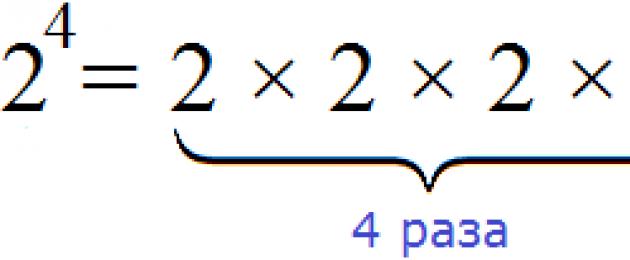Maktuttryck (uttryck med krafter) och deras omvandling. Lektion "Multiplikation och division av potenser" Subtraktion av tal med samma potenser

Det är uppenbart att tal med potenser kan adderas som andra storheter , genom att lägga till dem en efter en med sina tecken.

Så summan av a 3 och b 2 är a 3 + b 2.
Summan av a 3 - b n och h 5 -d 4 är a 3 - b n + h 5 - d 4.

Odds lika styrka av identiska variabler kan läggas till eller subtraheras.

Så summan av 2a 2 och 3a 2 är lika med 5a 2.

Det är också uppenbart att om du tar två rutor a, eller tre rutor a, eller fem rutor a.

Men grader olika variabler Och olika grader identiska variabler, måste komponeras genom att lägga till dem med sina tecken.

Så summan av en 2 och en 3 är summan av en 2 + en 3.

Det är uppenbart att kvadraten av a, och kuben av a, inte är lika med två gånger kvadraten av a, utan två gånger kuben av a.

Summan av a 3 b n och 3a 5 b 6 är a 3 b n + 3a 5 b 6.

Subtraktion befogenheter utförs på samma sätt som addition, förutom att subtrahendernas tecken måste ändras i enlighet med detta.

Eller:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Multiplicera makter

Tal med potenser kan multipliceras, precis som andra storheter, genom att skriva dem efter varandra, med eller utan ett multiplikationstecken mellan dem.

Således blir resultatet av att multiplicera a 3 med b 2 a 3 b 2 eller aaabb.

Eller:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Resultatet i det sista exemplet kan beställas genom att lägga till identiska variabler.
Uttrycket kommer att ha formen: a 5 b 5 y 3.

Genom att jämföra flera tal (variabler) med potenser kan vi se att om två av dem multipliceras så blir resultatet ett tal (variabel) med en potens lika med belopp grader av termer.

Så, a 2 .a 3 = aa.aaa = aaaaa = en 5 .

Här är 5 potensen av resultatet av multiplikationen, lika med 2 + 3, summan av termernas potenser.

Så, a n.am = a m+n.

För a n tas a som en faktor lika många gånger som potensen av n;

Och ett m tas som en faktor lika många gånger som graden m är lika med;

Det är därför, potenser med samma baser kan multipliceras genom att addera potensernas exponenter.

Så, a 2 .a 6 = a 2+6 = a 8 . Och x 3 .x 2 .x = x 3+2+1 = x 6 .

Eller:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Multiplicera (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Svar: x 4 - y 4.
Multiplicera (x 3 + x - 5) ⋅ (2x 3 + x + 1).

Denna regel gäller även för tal vars exponenter är negativ.

1. Så, a -2 .a -3 = a -5 . Detta kan skrivas som (1/aa).(1/aaa) = 1/aaaaa.

2. y-n.y-m = y-n-m.

3. a -n .a m = a m-n .

Om a + b multipliceras med a - b, blir resultatet a 2 - b 2: det vill säga

Resultatet av att multiplicera summan eller skillnaden mellan två tal är lika med summan eller skillnaden av deras kvadrater.

Om du multiplicerar summan och skillnaden av två tal upphöjda till fyrkant, blir resultatet lika med summan eller skillnaden av dessa siffror i fjärde grader.

Så, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.

Indelning av examina

Tal med potenser kan delas som andra tal, genom att subtrahera från utdelningen, eller genom att placera dem i bråkform.

Således är a 3 b 2 dividerat med b 2 lika med a 3.

Eller:
$\frac(9a^3y^4)(-3a^3) = -3y^4$
$\frac(a^2b + 3a^2)(a^2) = \frac(a^2(b+3))(a^2) = b + 3$
$\frac(d\cdot (a - h + y)^3)((a - h + y)^3) = d$

Att skriva 5 dividerat med 3 ser ut som $\frac(a^5)(a^3)$. Men detta är lika med en 2 . I en serie siffror
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
vilket tal som helst kan delas med ett annat, och exponenten blir lika med skillnad indikatorer för delbara tal.

När man dividerar grader med samma bas, subtraheras deras exponenter..

Så, y 3:y 2 = y 3-2 = y 1. Det vill säga $\frac(yyy)(yy) = y$.

Och a n+1:a = a n+1-1 = a n . Det vill säga $\frac(aa^n)(a) = a^n$.

Eller:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b +y) n-3

Regeln gäller även för siffror med negativ värden på grader.
Resultatet av att dividera en -5 med en -3 är en -2.
Dessutom, $\frac(1)(aaaaa) : \frac(1)(aaa) = \frac(1)(aaaaa).\frac(aaa)(1) = \frac(aaa)(aaaaa) = \frac (1)(aa)$.

h 2:h -1 = h 2+1 = h 3 eller $h^2:\frac(1)(h) = h^2.\frac(h)(1) = h^3$

Det är nödvändigt att behärska multiplikation och division av potenser mycket väl, eftersom sådana operationer används mycket i algebra.

Exempel på att lösa exempel med bråk som innehåller tal med potenser

1. Minska exponenterna med $\frac(5a^4)(3a^2)$ Svar: $\frac(5a^2)(3)$.

2. Minska exponenterna med $\frac(6x^6)(3x^5)$. Svar: $\frac(2x)(1)$ eller 2x.

3. Minska exponenterna a 2 /a 3 och a -3 /a -4 och ta till en gemensam nämnare.
a 2 .a -4 är a -2 den första täljaren.
a 3 .a -3 är a 0 = 1, den andra täljaren.
a 3 .a -4 är a -1 , den gemensamma täljaren.
Efter förenkling: a -2 /a -1 och 1/a -1 .

4. Minska exponenterna 2a 4 /5a 3 och 2 /a 4 och ta till en gemensam nämnare.
Svar: 2a 3 /5a 7 och 5a 5 /5a 7 eller 2a 3 /5a 2 och 5/5a 2.

5. Multiplicera (a 3 + b)/b 4 med (a - b)/3.

6. Multiplicera (a 5 + 1)/x 2 med (b 2 - 1)/(x + a).

7. Multiplicera b4/a-2 med h-3/x och a n/y-3.

8. Dividera a 4 /y 3 med a 3 /y 2 . Svar: a/y.

9. Dividera (h 3 - 1)/d 4 med (d n + 1)/h.

Lektionens innehåll

Vad är en examen?

Grad kallas en produkt av flera identiska faktorer. Till exempel:

2 × 2 × 2

Värdet på detta uttryck är 8

2 × 2 × 2 = 8

Den vänstra sidan av denna likhet kan göras kortare - skriv först ner den upprepande faktorn och ange ovanför den hur många gånger den upprepas. Den upprepade multiplikatorn i detta fall är 2. Den upprepas tre gånger. Därför skriver vi en trea ovanför de två:

2 3 = 8

Detta uttryck lyder så här: " två till tredje potens är lika med åtta" eller " Den tredje potensen av 2 är 8."

Den korta formen av notation för att multiplicera identiska faktorer används oftare. Därför måste vi komma ihåg att om ett annat tal skrivs ovanför ett tal, så är detta en multiplikation av flera identiska faktorer.

Till exempel, om uttrycket 5 3 ges, bör man komma ihåg att detta uttryck motsvarar att skriva 5 × 5 × 5.

Numret som upprepas anropas examensbasis. I uttrycket 5 3 är potensens bas talet 5.

Och numret som är skrivet ovanför siffran 5 kallas exponent. I uttrycket 5 3 är exponenten talet 3. Exponenten visar hur många gånger exponentens bas upprepas. I vårt fall upprepas bas 5 tre gånger

Operationen att multiplicera identiska faktorer kallas genom exponentiering.

Till exempel, om du behöver hitta produkten av fyra identiska faktorer, som var och en är lika med 2, så säger de att talet är 2 upphöjd till fjärde makten:

Vi ser att talet 2 till fjärde potensen är talet 16.

Observera att i den här lektionen tittar vi på grader med naturlig exponent. Detta är en typ av grad vars exponent är ett naturligt tal. Kom ihåg att naturliga tal är heltal som är större än noll. Till exempel 1, 2, 3 och så vidare.

I allmänhet ser definitionen av en examen med en naturlig exponent ut så här:

Grad av a med naturlig indikator när ett uttryck för formen en, vilket är lika med produkten n faktorer som var och en är lika a

Exempel:

Du bör vara försiktig när du höjer ett nummer till en makt. Ofta, genom ouppmärksamhet, multiplicerar en person exponentens bas med exponenten.

Till exempel är talet 5 till andra potensen produkten av två faktorer, som var och en är lika med 5. Denna produkt är lika med 25

Föreställ dig nu att vi oavsiktligt multiplicerade bas 5 med exponent 2

Det uppstod ett fel eftersom talet 5 i andra potens inte är lika med 10.

Dessutom bör det nämnas att potensen av ett tal med exponent 1 är själva talet:

Till exempel är siffran 5 till första potensen själva siffran 5

Följaktligen, om ett tal inte har en indikator, måste vi anta att indikatorn är lika med en.

Till exempel ges siffrorna 1, 2, 3 utan en exponent, så deras exponenter blir lika med en. Vart och ett av dessa tal kan skrivas med exponent 1

Och om du höjer 0 till någon makt får du 0. Oavsett hur många gånger du multiplicerar något med sig själv, får du ingenting. Exempel:

Och uttrycket 0 0 är meningslöst. Men i vissa grenar av matematiken, i synnerhet analys och mängdlära, kan uttrycket 0 0 vara vettigt.

För övning, låt oss lösa några exempel på att höja siffror till potenser.

Exempel 1. Höj siffran 3 till andra potensen.

Talet 3 till andra potensen är produkten av två faktorer, som var och en är lika med 3

3 2 = 3 × 3 = 9

Exempel 2. Höj siffran 2 till fjärde potens.

Talet 2 till fjärde potensen är produkten av fyra faktorer, som var och en är lika med 2

2 4 = 2 × 2 × 2 × 2 = 16

Exempel 3. Höj siffran 2 till tredje potens.

Talet 2 till tredje potens är produkten av tre faktorer, som var och en är lika med 2

2 3 = 2 × 2 × 2 = 8

Höjer siffran 10 till makten

För att höja talet 10 till en potens räcker det att efter en addera ett antal nollor lika med exponenten.

Låt oss till exempel höja siffran 10 till andra potens. Först skriver vi ner själva siffran 10 och anger siffran 2 som en indikator

10 2

Nu sätter vi ett likhetstecken, skriver ett och efter detta skriver vi två nollor, eftersom antalet nollor måste vara lika med exponenten

10 2 = 100

Det betyder att talet 10 till andra potensen är talet 100. Detta beror på att talet 10 till andra potensen är produkten av två faktorer som var och en är lika med 10

10 2 = 10 × 10 = 100

Exempel 2. Låt oss höja siffran 10 till tredje potens.

I det här fallet kommer det att finnas tre nollor efter den:

10 3 = 1000

Exempel 3. Låt oss höja siffran 10 till fjärde potens.

I det här fallet kommer det att finnas fyra nollor efter den:

10 4 = 10000

Exempel 4. Låt oss höja siffran 10 till första potensen.

I det här fallet kommer det att finnas en nolla efter den:

10 1 = 10

Representation av siffror 10, 100, 1000 som potenser med bas 10

För att representera talen 10, 100, 1000 och 10000 som en potens med basen 10 måste du skriva ner basen 10 och som exponent ange ett tal lika med antalet nollor i det ursprungliga talet.

Låt oss föreställa oss talet 10 som en potens med basen 10. Vi ser att den har en nolla. Detta betyder att talet 10 som en potens med basen 10 kommer att representeras som 10 1

10 = 10 1

Exempel 2. Låt oss föreställa oss talet 100 som en potens med basen 10. Vi ser att talet 100 innehåller två nollor. Detta betyder att talet 100 som en potens med basen 10 kommer att representeras som 10 2

100 = 10 2

Exempel 3. Låt oss representera talet 1 000 som en potens med basen 10.

1 000 = 10 3

Exempel 4. Låt oss representera talet 10 000 som en potens med basen 10.

10 000 = 10 4

Att höja ett negativt tal till makten

När ett negativt tal höjs till en potens måste det omges inom parentes.

Låt oss till exempel höja det negativa talet −2 till andra potens. Talet −2 i andra potens är produkten av två faktorer, som var och en är lika med (−2)

(−2) 2 = (−2) × (−2) = 4

Om vi ​​inte satte talet −2 inom parentes, skulle det visa sig att vi beräknar uttrycket −2 2, vilket inte jämnlikt 4 . Uttrycket −2² kommer att vara lika med −4. För att förstå varför, låt oss beröra några punkter.

När vi sätter ett minus framför ett positivt tal presterar vi därmed operation att ta det motsatta värdet.

Låt oss säga att du har fått siffran 2 och att du måste hitta dess motsatta nummer. Vi vet att motsatsen till 2 är −2. Med andra ord, för att hitta det motsatta talet för 2, sätt bara ett minus framför detta nummer. Att sätta in ett minus före ett nummer anses redan vara en fullvärdig operation i matematik. Denna operation, som nämnts ovan, kallas operationen att ta det motsatta värdet.

I fallet med uttrycket −2 2 inträffar två operationer: operationen att ta det motsatta värdet och höja det till en potens. Att höja till en makt har högre prioritet än att ta det motsatta värdet.

Därför beräknas uttrycket −2 2 i två steg. Först utförs exponentieringsoperationen. I det här fallet höjdes det positiva talet 2 till andra potensen

Då togs det motsatta värdet. Detta motsatta värde hittades för värdet 4. Och det motsatta värdet för 4 är −4

−2 2 = −4

Parenteser har högsta exekveringsprioritet. Därför, vid beräkning av uttrycket (−2) 2, tas det motsatta värdet först, och sedan höjs det negativa talet −2 till andra potensen. Resultatet är ett positivt svar på 4, eftersom produkten av negativa tal är ett positivt tal.

Exempel 2. Höj talet −2 till tredje potens.

Talet −2 till tredje potens är produkten av tre faktorer, som var och en är lika med (−2)

(−2) 3 = (−2) × (−2) × (−2) = −8

Exempel 3. Höj talet −2 till fjärde potens.

Talet −2 till fjärde potens är produkten av fyra faktorer, som var och en är lika med (−2)

(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16

Det är lätt att se att när man höjer ett negativt tal till en potens kan man få antingen ett positivt eller negativt svar. Svarets tecken beror på den ursprungliga gradens index.

Om exponenten är jämn blir svaret positivt. Om exponenten är udda blir svaret negativt. Låt oss visa detta med exemplet med talet −3

I det första och tredje fallet var indikatorn udda nummer, så blev svaret negativ.

I det andra och fjärde fallet var indikatorn även nummer, så blev svaret positiv.

Exempel 7. Höj −5 till tredje potens.

Talet −5 till tredje potens är produkten av tre faktorer, som var och en är lika med −5. Exponent 3 är ett udda tal, så vi kan säga i förväg att svaret blir negativt:

(−5) 3 = (−5) × (−5) × (−5) = −125

Exempel 8. Höj −4 till fjärde potens.

Talet −4 till fjärde potensen är produkten av fyra faktorer, som var och en är lika med −4. Dessutom är exponent 4 jämn, så vi kan säga i förväg att svaret kommer att vara positivt:

(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256

Hitta uttrycksvärden

När man hittar värdena för uttryck som inte innehåller parenteser, kommer exponentiering att utföras först, följt av multiplikation och division i den ordning de visas, och sedan addition och subtraktion i den ordning de visas.

Exempel 1. Hitta värdet på uttrycket 2 + 5 2

Först utförs exponentiering. I det här fallet höjs siffran 5 till andra potensen - vi får 25. Sedan läggs detta resultat till talet 2

2 + 5 2 = 2 + 25 = 27

Exempel 10. Hitta värdet på uttrycket −6 2 × (−12)

Först utförs exponentiering. Observera att siffran −6 inte står inom parentes, så siffran 6 kommer att höjas till andra potens, sedan kommer ett minus att placeras framför resultatet:

−6 2 × (−12) = −36 × (−12)

Vi kompletterar exemplet genom att multiplicera −36 med (−12)

−6 2 × (−12) = −36 × (−12) = 432

Exempel 11. Hitta värdet på uttrycket −3 × 2 2

Först utförs exponentiering. Sedan multipliceras resultatet med talet −3

−3 × 2 2 = −3 × 4 = −12

Om uttrycket innehåller parenteser måste du först utföra operationerna inom dessa parenteser, sedan exponentiering, sedan multiplikation och division, och sedan addition och subtraktion.

Exempel 12. Hitta värdet på uttrycket (3 2 + 1 × 3) − 15 + 5

Först utför vi åtgärderna inom parentes. Inom parentesen tillämpar vi de tidigare inlärda reglerna, nämligen först höjer vi talet 3 till andra potensen, sedan multiplicerar vi 1 × 3, sedan adderar vi resultatet av att höja siffran 3 till den andra potensen och multiplicera 1 × 3 . Därefter utförs subtraktion och addition i den ordning de visas. Låt oss ordna följande ordning för att utföra åtgärden på det ursprungliga uttrycket:

(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2

Exempel 13. Hitta värdet på uttrycket 2 × 5 3 + 5 × 2 3

Låt oss först höja siffrorna till potenser, multiplicera sedan och lägga till resultaten:

2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290

Identiska makttransformationer

Olika identitetstransformationer kan utföras på befogenheter och därigenom förenkla dem.

Låt oss säga att vi behövde beräkna uttrycket (2 3) 2. I det här exemplet höjs två till tredje potensen till andra potensen. En examen höjs med andra ord till en annan grad.

(2 3) 2 är produkten av två potenser, som var och en är lika med 2 3

Dessutom är var och en av dessa krafter produkten av tre faktorer, som var och en är lika med 2

Vi fick produkten 2 × 2 × 2 × 2 × 2 × 2, vilket är lika med 64. Detta betyder värdet på uttrycket (2 3) 2 eller lika med 64

Detta exempel kan förenklas mycket. För att göra detta kan exponenterna för uttrycket (2 3) 2 multipliceras och denna produkt skrivas över basen 2

Vi fick 26. Två till sjätte potens är produkten av sex faktorer, som var och en är lika med 2. Denna produkt är lika med 64

Den här egenskapen fungerar eftersom 2 3 är produkten av 2 × 2 × 2, som i sin tur upprepas två gånger. Sedan visar det sig att bas 2 upprepas sex gånger. Härifrån kan vi skriva att 2 × 2 × 2 × 2 × 2 × 2 är 2 6

I allmänhet, av någon anledning a med indikatorer m Och n, gäller följande likhet:

(en)m = a n × m

Denna identiska transformation kallas höja en makt till en makt. Det kan läsas så här: "När man höjer en potens till en potens, lämnas basen oförändrad och exponenterna multipliceras" .

Efter att ha multiplicerat indikatorerna får du en annan grad, vars värde kan hittas.

Exempel 2. Hitta värdet på uttrycket (3 2) 2

I det här exemplet är basen 3 och talen 2 och 2 är exponenter. Låt oss använda regeln att höja en makt till en makt. Vi lämnar basen oförändrad och multiplicerar indikatorerna:

Vi fick 34. Och siffran 3 till fjärde potensen är 81

Låt oss överväga de återstående transformationerna.

Multiplicera makter

För att multiplicera potenser måste du separat beräkna varje potens och multiplicera resultaten.

Låt oss till exempel multiplicera 2 2 med 3 3.

2 2 är siffran 4 och 3 3 är siffran 27. Multiplicera siffrorna 4 och 27, vi får 108

2 2 × 3 3 = 4 × 27 = 108

I det här exemplet var examensgrunderna olika. Om baserna är desamma kan du skriva ner en bas och skriva ner summan av indikatorerna för de ursprungliga graderna som en indikator.

Till exempel multiplicera 2 2 med 2 3

I det här exemplet är grunderna för graderna desamma. I det här fallet kan du skriva ner en bas 2 och skriva ner summan av exponenterna för potenserna 2 2 och 2 3 som en exponent. Med andra ord, lämna basen oförändrad och addera indikatorerna för de ursprungliga graderna. Det kommer att se ut så här:

Vi fick 2 5. Siffran 2 till femte potensen är 32

Den här egenskapen fungerar eftersom 2 2 är produkten av 2 × 2 och 2 3 är produkten av 2 × 2 × 2. Då får vi en produkt av fem identiska faktorer, som var och en är lika med 2. Denna produkt kan representeras som 2 5

I allmänhet, för vem som helst a och indikatorer m Och n följande jämlikhet gäller:

Denna identiska transformation kallas grundläggande egenskap av examen. Det kan läsas så här: " PNär potenser multipliceras med samma baser lämnas basen oförändrad och exponenterna adderas." .

Observera att denna transformation kan tillämpas i valfritt antal grader. Huvudsaken är att basen är densamma.

Låt oss till exempel hitta värdet på uttrycket 2 1 × 2 2 × 2 3. Bas 2

I vissa problem kan det vara tillräckligt att utföra lämplig transformation utan att beräkna den slutliga graden. Detta är naturligtvis mycket bekvämt, eftersom det inte är så lätt att beräkna stora effekter.

Exempel 1. Uttryck uttrycket 5 8 × 25 som en potens

I det här problemet måste du se till att du istället för uttrycket 5 8 × 25 får en potens.

Siffran 25 kan representeras som 5 2. Då får vi följande uttryck:

I det här uttrycket kan du tillämpa gradens grundläggande egenskap - lämna basen 5 oförändrad och lägg till exponenterna 8 och 2:

Låt oss kortfattat skriva ner lösningen:

Exempel 2. Uttryck uttrycket 2 9 × 32 som en potens

Siffran 32 kan representeras som 2 5. Då får vi uttrycket 2 9 × 2 5. Därefter kan du tillämpa basegenskapen för graden - lämna bas 2 oförändrad och lägg till exponenterna 9 och 5. Resultatet blir följande lösning:

Exempel 3. Beräkna 3 × 3-produkten med hjälp av den grundläggande egenskapen potenser.

Alla vet väl att tre gånger tre är lika med nio, men problemet kräver att man använder den grundläggande egenskapen grader i lösningen. Hur man gör det?

Vi minns att om ett nummer ges utan en indikator, måste indikatorn anses vara lika med en. Därför kan faktorerna 3 och 3 skrivas som 3 1 och 3 1

3 1 × 3 1

Låt oss nu använda den grundläggande egenskapen grad. Vi lämnar bas 3 oförändrad och lägger ihop indikatorerna 1 och 1:

3 1 × 3 1 = 3 2 = 9

Exempel 4. Beräkna produkten 2 × 2 × 3 2 × 3 3 med hjälp av den grundläggande egenskapen potenser.

Vi ersätter produkten 2 × 2 med 2 1 × 2 1, sedan med 2 1 + 1 och sedan med 2 2. Byt ut produkten 3 2 × 3 3 med 3 2 + 3 och sedan mot 3 5

Exempel 5. Utför multiplikation x × x

Det här är två identiska bokstavsfaktorer med exponenter 1. För tydlighetens skull, låt oss skriva ner dessa exponenter. Nästa är basen x Låt oss lämna det oförändrat och lägga ihop indikatorerna:

När du är på brädan bör du inte skriva ner multiplikationen av potenser med samma baser så detaljerat som här. Sådana beräkningar måste göras i ditt huvud. En detaljerad anteckning kommer med största sannolikhet att irritera läraren och han kommer att sänka betyget för det. Här ges en detaljerad inspelning för att göra materialet så lätt att förstå som möjligt.

Det är lämpligt att skriva lösningen till detta exempel så här:

Exempel 6. Utför multiplikation x 2 × x

Exponenten för den andra faktorn är lika med en. För tydlighetens skull, låt oss skriva ner det. Därefter lämnar vi basen oförändrad och lägger ihop indikatorerna:

Exempel 7. Utför multiplikation y 3 y 2 y

Exponenten för den tredje faktorn är lika med en. För tydlighetens skull, låt oss skriva ner det. Därefter lämnar vi basen oförändrad och lägger ihop indikatorerna:

Exempel 8. Utför multiplikation aa 3 a 2 a 5

Exponenten för den första faktorn är lika med en. För tydlighetens skull, låt oss skriva ner det. Därefter lämnar vi basen oförändrad och lägger ihop indikatorerna:

Exempel 9. Representera potensen 3 8 som en produkt av potenser med samma baser.

I det här problemet måste du skapa en produkt av potenser vars baser kommer att vara lika med 3, och summan av vars exponenter kommer att vara lika med 8. Alla indikatorer kan användas. Låt oss representera potensen 3 8 som produkten av potenserna 3 5 och 3 3

I det här exemplet förlitade vi oss återigen på den grundläggande egenskapen grad. Trots allt kan uttrycket 3 5 × 3 3 skrivas som 3 5 + 3, varav 3 8.

Naturligtvis var det möjligt att representera makten 3 8 som en produkt av andra makter. Till exempel i formen 3 7 × 3 1, eftersom denna produkt också är lika med 3 8

Att representera en examen som en produkt av makter med samma grunder är mest ett kreativt arbete. Därför finns det ingen anledning att vara rädd för att experimentera.

Exempel 10. Skicka in examen x 12 i form av olika produkter av makter med baser x .

Låt oss använda den grundläggande egenskapen för grader. Låt oss föreställa oss x 12 i form av produkter med baser x, och summan av indikatorerna är 12

Konstruktioner med summor av indikatorer registrerades för tydlighetens skull. Oftast kan man hoppa över dem. Då får du en kompakt lösning:

Att höja kraften i en produkt

För att höja en produkt till en potens, måste du höja varje faktor i denna produkt till den angivna effekten och multiplicera resultaten.

Låt oss till exempel höja produkten 2 × 3 till andra potens. Låt oss ta denna produkt inom parentes och ange 2 som en indikator

Låt oss nu höja varje faktor av 2 × 3-produkten till andra potens och multiplicera resultaten:

Funktionsprincipen för denna regel är baserad på definitionen av examen, som gavs i början.

Att höja produkten 2 × 3 till andra potens innebär att du upprepar produkten två gånger. Och om du upprepar det två gånger kan du få följande:

2 × 3 × 2 × 3

Att ordna om platserna för faktorerna förändrar inte produkten. Detta låter dig gruppera liknande faktorer:

2 × 2 × 3 × 3

Upprepande faktorer kan ersättas med korta poster - baser med indikatorer. Produkten 2 × 2 kan ersättas med 2 2 och produkten 3 × 3 kan ersättas med 3 2. Då blir uttrycket 2 × 2 × 3 × 3 uttrycket 2 2 × 3 2.

Låta ab originalverk. Att höja en given produkt till en makt n, måste du multiplicera faktorerna separat a Och b i angiven grad n

Denna egenskap gäller för ett antal faktorer. Följande uttryck är också giltiga:

Exempel 2. Hitta värdet på uttrycket (2 × 3 × 4) 2

I det här exemplet måste du höja produkten 2 × 3 × 4 till andra potens. För att göra detta måste du höja varje faktor av denna produkt till andra potensen och multiplicera resultaten:

Exempel 3. Höj produkten till tredje potens a×b×c

Låt oss omge denna produkt inom parentes och ange siffran 3 som en indikator

Exempel 4. Höj produkten 3 till tredje potens xyz

Låt oss omge denna produkt inom parentes och ange 3 som en indikator

(3xyz) 3

Låt oss höja varje faktor i denna produkt till tredje makten:

(3xyz) 3 = 3 3 x 3 y 3 z 3

Talet 3 till tredje potens är lika med talet 27. Vi lämnar resten oförändrat:

(3xyz) 3 = 3 3 x 3 y 3 z 3 = 27x 3 y 3 z 3

I vissa exempel kan multiplikation av potenser med samma exponent ersättas med produkten av baser med samma exponent.

Låt oss till exempel beräkna värdet på uttrycket 5 2 × 3 2. Låt oss höja varje tal till andra potens och multiplicera resultaten:

5 2 × 3 2 = 25 × 9 = 225

Men du behöver inte beräkna varje grad för sig. Istället kan denna produkt av potenser ersättas med en produkt med en exponent (5 × 3) 2 . Beräkna sedan värdet inom parentes och höj resultatet till andra potens:

5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225

I det här fallet användes återigen regeln om exponentiering av en produkt. När allt kommer omkring, om (a×b)n = a n × b n , Den där a n × b n = (a × b) n. Det vill säga att vänster och höger sida av jämställdheten har bytt plats.

Att höja en grad till en makt

Vi betraktade denna transformation som ett exempel när vi försökte förstå essensen av identiska transformationer av grader.

När man höjer en potens till en potens, lämnas basen oförändrad och exponenterna multipliceras:

(en)m = a n × m

Till exempel är uttrycket (2 3) 2 en potens som höjs till en potens - två till den tredje potensen höjs till den andra potensen. För att hitta värdet på detta uttryck kan basen lämnas oförändrad och exponenterna kan multipliceras:

(2 3) 2 = 2 3 × 2 = 2 6

(2 3) 2 = 2 3 × 2 = 2 6 = 64

Denna regel är baserad på de tidigare reglerna: exponentiering av produkten och gradens grundläggande egenskap.

Låt oss återgå till uttrycket (2 3) 2. Uttrycket inom parentes 2 3 är en produkt av tre identiska faktorer, som var och en är lika med 2. Sedan i uttrycket (2 3) kan 2-potentialen inom parentesen ersättas med produkten 2 × 2 × 2.

(2 × 2 × 2) 2

Och detta är exponentieringen av produkten som vi studerade tidigare. Låt oss komma ihåg att för att höja en produkt till en effekt, måste du höja varje faktor för en given produkt till den angivna effekten och multiplicera de erhållna resultaten:

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2

Nu har vi att göra med den grundläggande egenskapen examen. Vi lämnar basen oförändrad och lägger ihop indikatorerna:

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6

Som tidigare fick vi 2 6. Värdet på denna grad är 64

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64

En produkt vars faktorer också är makter kan också höjas till en makt.

Låt oss till exempel hitta värdet på uttrycket (2 2 × 3 2) 3. Här måste indikatorerna för varje multiplikator multipliceras med den totala indikatorn 3. Hitta sedan värdet på varje grad och beräkna produkten:

(2 2 × 3 2) 3 = 2 2 × 3 × 3 2 × 3 = 2 6 × 3 6 = 64 × 729 = 46656

Ungefär samma sak händer när man höjer en produkt till en makt. Vi sa att när man höjer en produkt till en effekt, höjs varje faktor i denna produkt till den indikerade effekten.

Till exempel, för att höja produkten 2 × 4 till tredje potens, skulle du skriva följande uttryck:

Men tidigare sa det att om ett tal ges utan en indikator, måste indikatorn anses vara lika med en. Det visar sig att faktorerna för produkten 2 × 4 initialt har exponenter lika med 1. Det betyder att uttrycket 2 1 × 4 1 ​​höjdes till tredje potens. Och detta är att höja en grad till en grad.

Låt oss skriva om lösningen med hjälp av regeln för att höja en makt till en makt. Vi borde få samma resultat:

Exempel 2. Hitta värdet på uttrycket (3 3) 2

Vi lämnar basen oförändrad och multiplicerar indikatorerna:

Vi fick 36. Siffran 3 till sjätte potensen är siffran 729

Exempel 3xy)³

Exempel 4. Utför exponentiering i uttrycket ( abc)⁵

Låt oss höja varje faktor i produkten till den femte potensen:

Exempel 5yxa) 3

Låt oss höja varje faktor i produkten till tredje potens:

Eftersom negativt tal −2 höjdes till tredje potens placerades det inom parentes.

Exempel 6. Utför exponentiering i uttryck (10 xy) 2

Exempel 7. Utför exponentiering i uttrycket (−5 x) 3

Exempel 8. Utför exponentiering i uttrycket (-3 y) 4

Exempel 9. Utför exponentiering i uttrycket (−2 abx)⁴

Exempel 10. Förenkla uttrycket x 5×( x 2) 3

Grad x Låt oss lämna 5 oförändrade för nu, och i uttrycket ( x 2) 3 vi utför höjningen av en makt till en makt:

x 5 × (x 2) 3 = x 5 × x 2×3 = x 5 × x 6

Låt oss nu göra multiplikationen x 5 × x 6. För att göra detta kommer vi att använda den grundläggande egenskapen för en grad - basen x Låt oss lämna det oförändrat och lägga ihop indikatorerna:

x 5 × (x 2) 3 = x 5 × x 2×3 = x 5 × x 6 = x 5 + 6 = x 11

Exempel 9. Hitta värdet på uttrycket 4 3 × 2 2 med hjälp av den grundläggande egenskapen makt.

Grundegenskapen för en examen kan användas om grunderna för de ursprungliga graderna är desamma. I det här exemplet är baserna olika, så först måste du modifiera det ursprungliga uttrycket lite, nämligen se till att baserna för potenserna blir desamma.

Låt oss titta närmare på graden 4 3. Basen för denna grad är talet 4, som kan representeras som 2 2. Då kommer det ursprungliga uttrycket att ha formen (2 2) 3 × 2 2. Genom att höja makten till makten i uttrycket (2 2) 3 får vi 2 6. Då kommer det ursprungliga uttrycket att ha formen 2 6 × 2 2, som kan beräknas med hjälp av den grundläggande egenskapen makt.

Låt oss skriva ner lösningen till detta exempel:

Indelning av examina

För att utföra division av potenser måste du hitta värdet på varje potens och sedan dividera vanliga tal.

Låt oss till exempel dividera 4 3 med 2 2.

Låt oss räkna ut 4 3, vi får 64. Beräkna 2 2, få 4. Dela nu 64 med 4, få 16

Om, vid delning av potenserna, baserna visar sig vara desamma, kan basen lämnas oförändrad, och exponenten för divisorn kan subtraheras från exponenten för utdelningen.

Låt oss till exempel hitta värdet på uttrycket 2 3: 2 2

Vi lämnar bas 2 oförändrad och subtraherar exponenten för divisorn från exponenten för utdelningen:

Det betyder att värdet på uttrycket 2 3: 2 2 är lika med 2.

Denna egenskap är baserad på multiplikationen av potenser med samma baser, eller, som vi brukade säga, den grundläggande egenskapen för en potens.

Låt oss återgå till föregående exempel 2 3: 2 2. Här är utdelningen 2 3 och divisor är 2 2.

Att dividera ett tal med ett annat innebär att hitta ett tal som, när det multipliceras med divisorn, kommer att resultera i utdelningen.

I vårt fall innebär att dividera 2 3 med 2 2 att hitta en potens som, när den multipliceras med divisorn 2 2, resulterar i 2 3. Vilken potens kan multipliceras med 2 2 för att få 2 3? Uppenbarligen är bara grad 2 1. Från den grundläggande examensegenskapen har vi:

Du kan verifiera att värdet på uttrycket 2 3: 2 2 är lika med 2 1 genom att direkt beräkna själva uttrycket 2 3: 2 2. För att göra detta hittar vi först värdet på potensen 2 3, vi får 8. Sedan hittar vi värdet på potensen 2 2, vi får 4. Dividera 8 med 4, vi får 2 eller 2 1, eftersom 2 = 2 1.

2 3: 2 2 = 8: 4 = 2

Sålunda, när man delar makter med samma baser, gäller följande likhet:

Det kan också hända att inte bara orsakerna, utan också indikatorerna kan vara desamma. I det här fallet blir svaret ett.

Låt oss till exempel hitta värdet på uttrycket 2 2: 2 2. Låt oss beräkna värdet på varje grad och dividera de resulterande talen:

När du löser exempel 2 2: 2 2 kan du också tillämpa regeln om att dela potenser med samma baser. Resultatet är ett tal med nollpotensen, eftersom skillnaden mellan exponenterna för potenserna 2 2 och 2 2 är lika med noll:

Vi fick reda på ovan varför talet 2 till nollpotensen är lika med ett. Om du beräknar 2 2: 2 2 med den vanliga metoden, utan att använda maktdelningsregeln, får du en.

Exempel 2. Hitta värdet på uttrycket 4 12: 4 10

Låt oss lämna 4 oförändrade och subtrahera exponenten för divisor från exponenten för utdelningen:

4 12: 4 10 = 4 12 − 10 = 4 2 = 16

Exempel 3. Presentera kvoten x 3: x i form av en kraft med en bas x

Låt oss använda maktdelningsregeln. Bas x Låt oss lämna det oförändrat och subtrahera exponenten för divisor från exponenten för utdelningen. Divisorexponenten är lika med ett. För tydlighetens skull, låt oss skriva ner det:

Exempel 4. Presentera kvoten x 3: x 2 som en kraft med en bas x

Låt oss använda maktdelningsregeln. Bas x

Maktsdelning kan skrivas som en bråkdel. Så det tidigare exemplet kan skrivas så här:

Täljaren och nämnaren för ett bråk kan skrivas i expanderad form, nämligen i form av produkter av identiska faktorer. Grad x 3 kan skrivas som x × x × x, och graden x 2 hur x × x. Sedan designen x 3 − 2 kan hoppas över och fraktionen kan reduceras. Det kommer att vara möjligt att reducera två faktorer i täljaren och nämnaren x. Som ett resultat kommer en multiplikator att finnas kvar x

Eller ännu kortare:

Det är också användbart att snabbt kunna reducera bråk som består av potenser. Till exempel kan en bråkdel reduceras med x 2. För att minska en bråkdel med x 2 måste du dividera täljaren och nämnaren för bråket med x 2

Indelningen av examina behöver inte beskrivas i detalj. Ovanstående förkortning kan göras kortare:

Eller ännu kortare:

Exempel 5. Utför division x 12 :x 3

Låt oss använda maktdelningsregeln. Bas x lämna det oförändrat och subtrahera exponenten för divisor från exponenten för utdelningen:

Låt oss skriva lösningen med hjälp av bråkreduktion. Indelning av examina x 12 :x Låt oss skriva 3 i formuläret . Därefter minskar vi denna bråkdel med x 3 .

Exempel 6. Hitta värdet på ett uttryck

I täljaren utför vi multiplikation av potenser med samma baser:

Nu tillämpar vi regeln för att dela potenser med samma baser. Vi lämnar bas 7 oförändrad och subtraherar exponenten för divisorn från exponenten för utdelningen:

Vi kompletterar exemplet genom att beräkna potensen 7 2

Exempel 7. Hitta värdet på ett uttryck

Låt oss höja makten till makten i täljaren. Du måste göra detta med uttrycket (2 3) 4

Låt oss nu multiplicera potenser med samma baser i täljaren.

Addition och subtraktion av potenser

Det är uppenbart att tal med potenser kan adderas som andra storheter , genom att lägga till dem en efter en med sina tecken.

Så summan av a 3 och b 2 är a 3 + b 2.
Summan av a 3 - b n och h 5 -d 4 är a 3 - b n + h 5 - d 4.

Odds lika styrka av identiska variabler kan läggas till eller subtraheras.

Så summan av 2a 2 och 3a 2 är lika med 5a 2.

Det är också uppenbart att om du tar två rutor a, eller tre rutor a, eller fem rutor a.

Men grader olika variabler Och olika grader identiska variabler, måste komponeras genom att lägga till dem med sina tecken.

Så summan av en 2 och en 3 är summan av en 2 + en 3.

Det är uppenbart att kvadraten av a, och kuben av a, inte är lika med två gånger kvadraten av a, utan två gånger kuben av a.

Summan av a 3 b n och 3a 5 b 6 är a 3 b n + 3a 5 b 6.

Subtraktion befogenheter utförs på samma sätt som addition, förutom att subtrahendernas tecken måste ändras i enlighet med detta.

Eller:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Multiplicera makter

Tal med potenser kan multipliceras, precis som andra storheter, genom att skriva dem efter varandra, med eller utan ett multiplikationstecken mellan dem.

Således blir resultatet av att multiplicera a 3 med b 2 a 3 b 2 eller aaabb.

Eller:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Resultatet i det sista exemplet kan beställas genom att lägga till identiska variabler.
Uttrycket kommer att ha formen: a 5 b 5 y 3.

Genom att jämföra flera tal (variabler) med potenser kan vi se att om två av dem multipliceras så blir resultatet ett tal (variabel) med en potens lika med belopp grader av termer.

Så, a 2 .a 3 = aa.aaa = aaaaa = en 5 .

Här är 5 potensen av multiplikationsresultatet, vilket är lika med 2 + 3, summan av termernas potenser.

Så, a n.am = a m+n.

För a n tas a som en faktor lika många gånger som potensen av n;

Och ett m tas som en faktor lika många gånger som graden m är lika med;

Det är därför, potenser med samma baser kan multipliceras genom att addera potensernas exponenter.

Så, a 2 .a 6 = a 2+6 = a 8 . Och x 3 .x 2 .x = x 3+2+1 = x 6 .

Eller:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Multiplicera (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Svar: x 4 - y 4.
Multiplicera (x 3 + x – 5) ⋅ (2x 3 + x + 1).

Denna regel gäller även för tal vars exponenter är negativ.

1. Så, a -2 .a -3 = a -5 . Detta kan skrivas som (1/aa).(1/aaa) = 1/aaaaa.

2. y-n.y-m = y-n-m.

3. a -n .a m = a m-n .

Om a + b multipliceras med a - b, blir resultatet a 2 - b 2: det vill säga

Resultatet av att multiplicera summan eller skillnaden mellan två tal är lika med summan eller skillnaden av deras kvadrater.

Om du multiplicerar summan och skillnaden av två tal upphöjda till fyrkant, blir resultatet lika med summan eller skillnaden av dessa siffror i fjärde grader.

Så, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.

Indelning av examina

Tal med potenser kan delas som andra tal, genom att subtrahera från utdelningen, eller genom att placera dem i bråkform.

Således är a 3 b 2 dividerat med b 2 lika med a 3.

Att skriva 5 dividerat med 3 ser ut som $\frac $. Men detta är lika med en 2 . I en serie siffror
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
vilket tal som helst kan delas med ett annat, och exponenten blir lika med skillnad indikatorer för delbara tal.

När man dividerar grader med samma bas, subtraheras deras exponenter..

Så, y 3:y 2 = y 3-2 = y 1. Det vill säga $\frac = y$.

Och a n+1:a = a n+1-1 = a n . Det vill säga $\frac = a^n$.

Eller:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b +y) n-3

Regeln gäller även för siffror med negativ värden på grader.
Resultatet av att dividera en -5 med en -3 är en -2.
Dessutom, $\frac: \frac = \frac .\frac = \frac = \frac $.

h 2:h -1 = h 2+1 = h 3 eller $h^2:\frac = h^2.\frac = h^3$

Det är nödvändigt att behärska multiplikation och division av potenser mycket väl, eftersom sådana operationer används mycket i algebra.

Exempel på att lösa exempel med bråk som innehåller tal med potenser

1. Minska exponenterna med $\frac $ Svar: $\frac $.

2. Minska exponenter med $\frac$. Svar: $\frac$ eller 2x.

3. Minska exponenterna a 2 /a 3 och a -3 /a -4 och ta till en gemensam nämnare.
a 2 .a -4 är a -2 den första täljaren.
a 3 .a -3 är a 0 = 1, den andra täljaren.
a 3 .a -4 är a -1 , den gemensamma täljaren.
Efter förenkling: a -2 /a -1 och 1/a -1 .

4. Minska exponenterna 2a 4 /5a 3 och 2 /a 4 och ta till en gemensam nämnare.
Svar: 2a 3 /5a 7 och 5a 5 /5a 7 eller 2a 3 /5a 2 och 5/5a 2.

5. Multiplicera (a 3 + b)/b 4 med (a - b)/3.

6. Multiplicera (a 5 + 1)/x 2 med (b 2 - 1)/(x + a).

7. Multiplicera b4/a-2 med h-3/x och a n/y-3.

8. Dividera a 4 /y 3 med a 3 /y 2 . Svar: a/y.

Gradens egenskaper

Vi påminner dig om att i den här lektionen kommer vi att förstå egenskaper hos grader med naturliga indikatorer och noll. Effekter med rationella exponenter och deras egenskaper kommer att diskuteras i lektioner för 8:e klass.

En potens med naturlig exponent har flera viktiga egenskaper som gör att vi kan förenkla beräkningar i exempel med potenser.

Fastighet nr 1
Produkt av makter

När potenser multipliceras med samma baser förblir basen oförändrad, och potensernas exponenter adderas.

a m · a n = a m + n, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Denna egenskap hos makter gäller även produkten av tre eller flera potenser.

• Förenkla uttrycket.
  b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Presentera det som en examen.
  6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
• Presentera det som en examen.
  (0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Observera att i den angivna egenskapen talade vi bara om multiplikation av potenser med samma baser. Det gäller inte deras tillägg.

Du kan inte ersätta summan (3 3 + 3 2) med 3 5. Detta är förståeligt om
beräkna (3 3 + 3 2) = (27 + 9) = 36 och 3 5 = 243

Fastighet nr 2
Partiella examina

När man dividerar potenser med samma baser förblir basen oförändrad, och divisorns exponent subtraheras från exponenten för utdelningen.

• Skriv kvoten som en potens
  (2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
• Beräkna.

11 3 − 2 4 2 − 1 = 11 4 = 44
Exempel. Lös ekvationen. Vi använder egenskapen kvotbefogenheter.
3 8: t = 3 4

Svar: t = 3 4 = 81

Med hjälp av egenskaper nr 1 och nr 2 kan du enkelt förenkla uttryck och utföra beräkningar.

Exempel. Förenkla uttrycket.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Exempel. Hitta värdet på ett uttryck med hjälp av egenskaperna hos exponenter.

2 11 − 5 = 2 6 = 64

Observera att vi i fastighet 2 bara pratade om att dela potenser med samma baser.

Du kan inte ersätta skillnaden (4 3 −4 2) med 4 1. Detta är förståeligt om du beräknar (4 3 −4 2) = (64 − 16) = 48, och 4 1 = 4

Fastighet nr 3
Att höja en grad till en makt

När man höjer en grad till en potens förblir gradens bas oförändrad och exponenterna multipliceras.

(a n) m = a n · m, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Vi påminner om att en kvot kan representeras som en bråkdel. Därför kommer vi att uppehålla oss vid ämnet att höja en bråkdel till en makt mer detaljerat på nästa sida.

Hur man multiplicerar makter

Hur multiplicerar man potenser? Vilka potenser kan multipliceras och vilka kan inte? Hur multiplicerar man ett tal med en potens?

I algebra kan du hitta en produkt av potenser i två fall:

1) om graderna har samma baser;

2) om graderna har samma indikatorer.

När du multiplicerar potenser med samma baser måste basen lämnas densamma och exponenterna måste adderas:

När du multiplicerar grader med samma indikatorer kan den övergripande indikatorn tas ur parentes:

Låt oss titta på hur man multiplicerar potenser med hjälp av specifika exempel.

Enheten skrivs inte i exponenten, men när man multiplicerar potenser tar de hänsyn till:

När du multiplicerar kan det finnas hur många potenser som helst. Det bör komma ihåg att du inte behöver skriva multiplikationstecknet före bokstaven:

I uttryck görs exponentiering först.

Om du behöver multiplicera ett tal med en potens, bör du först utföra exponentieringen, och först därefter multiplikationen:

Multiplicera potenser med samma baser

Denna videohandledning är tillgänglig med prenumeration

Har du redan ett abonnemang? Att komma in

I den här lektionen kommer vi att studera multiplikation av potenser med lika baser. Låt oss först komma ihåg definitionen av grad och formulera en sats om giltigheten av jämlikheten . Sedan kommer vi att ge exempel på dess tillämpning på specifika siffror och bevisa det. Vi kommer också att tillämpa satsen för att lösa olika problem.

Ämne: Kraft med en naturlig exponent och dess egenskaper

Lektion: Multiplicera potenser med samma baser (formel)

1. Grundläggande definitioner

Grundläggande definitioner:

n- exponent,

— n potensen av ett tal.

2. Uttalande av sats 1

Sats 1. För vilket nummer som helst A och alla naturliga n Och k jämställdheten är sann:

Med andra ord: om A- vilket nummer som helst; n Och k naturliga tal, då:

Därav regel 1:

3. Förklarande uppgifter

Slutsats: specialfall bekräftade riktigheten av sats nr 1. Låt oss bevisa det i det allmänna fallet, det vill säga för alla A och alla naturliga n Och k.

4. Bevis för sats 1

Givet ett nummer A– någon; tal n Och k – naturlig. Bevisa:

Beviset bygger på definitionen av examen.

5. Lösa exempel med hjälp av sats 1

Exempel 1: Se det som en examen.

För att lösa följande exempel använder vi sats 1.

och)

6. Generalisering av sats 1

En generalisering som används här:

7. Lösa exempel med hjälp av en generalisering av sats 1

8. Lösa olika problem med hjälp av sats 1

Exempel 2: Beräkna (du kan använda tabellen över grundläggande potenser).

A) (enligt tabellen)

b)

Exempel 3: Skriv det som en potens med bas 2.

A)

Exempel 4: Bestäm tecknet för siffran:

, A - negativ, eftersom exponenten vid -13 är udda.

Exempel 5: Ersätt (·) med en potens av ett tal med en bas r:

Det har vi, alltså.

9. Sammanfattning

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. Algebra 7. 6:e upplagan. M.: Upplysning. 2010

1. Skolassistent (Källa).

1. Presentera som en kraft:

a B C D E)

3. Skriv som en potens med bas 2:

4. Bestäm tecknet för talet:

A)

5. Ersätt (·) med en potens av ett tal med en bas r:

a) r4 · (·) = r 15; b) (·) · r 5 = r 6

Multiplikation och division av potenser med samma exponenter

I den här lektionen kommer vi att studera multiplikation av potenser med lika exponenter. Låt oss först komma ihåg de grundläggande definitionerna och satserna om att multiplicera och dividera potenser med samma baser och höja potenser till potenser. Sedan formulerar och bevisar vi satser om multiplikation och division av potenser med samma exponenter. Och sedan med deras hjälp kommer vi att lösa ett antal typiska problem.

Påminnelse om grundläggande definitioner och satser

Här a- grunden för examen,

— n potensen av ett tal.

Sats 1. För vilket nummer som helst A och alla naturliga n Och k jämställdheten är sann:

När potenser multipliceras med samma baser adderas exponenterna, basen förblir oförändrad.

Sats 2. För vilket nummer som helst A och alla naturliga n Och k, Så att n > k jämställdheten är sann:

När man dividerar grader med samma baser, subtraheras exponenterna, men basen förblir oförändrad.

Sats 3. För vilket nummer som helst A och alla naturliga n Och k jämställdheten är sann:

Alla angivna satser handlade om potenser med samma skäl, i den här lektionen kommer vi att titta på grader med samma indikatorer.

Exempel på att multiplicera potenser med samma exponenter

Tänk på följande exempel:

Låt oss skriva ner uttrycken för att bestämma graden.

Slutsats: Av exemplen kan man se det , men detta måste fortfarande bevisas. Låt oss formulera satsen och bevisa den i det allmänna fallet, det vill säga för vilket som helst A Och b och alla naturliga n.

Formulering och bevis för sats 4

För alla siffror A Och b och alla naturliga n jämställdheten är sann:

Bevis Sats 4 .

Per definition av examen:

Så det har vi bevisat .

För att multiplicera potenser med samma exponenter räcker det att multiplicera baserna och lämna exponenten oförändrad.

Formulering och bevis för sats 5

Låt oss formulera ett teorem för att dividera potenser med samma exponenter.

För vilket nummer som helst A Och b() och alla naturliga n jämställdheten är sann:

Bevis Sats 5 .

Låt oss skriva ner definitionen av examen:

Uttalande av satser i ord

Så det har vi bevisat.

För att dela potenser med samma exponenter i varandra räcker det att dela en bas med en annan och lämna exponenten oförändrad.

Lösa typiska problem med hjälp av sats 4

Exempel 1: Presenteras som en produkt av makter.

För att lösa följande exempel använder vi sats 4.

För att lösa följande exempel, kom ihåg formlerna:

Generalisering av sats 4

Generalisering av sats 4:

Lösa exempel med hjälp av generaliserad sats 4

Att fortsätta lösa typiska problem

Exempel 2: Skriv det som produktens kraft.

Exempel 3: Skriv det som en potens med exponent 2.

Räkneexempel

Exempel 4: Beräkna på det mest rationella sättet.

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. och andra Algebra 7.M.: Upplysning. 2006

2. Skolassistent (Källa).

1. Presentera som en produkt av makter:

A); b) ; V); G);

2. Skriv som en kraft för produkten:

3. Skriv som en potens med exponent 2:

4. Räkna på det mest rationella sättet.

Matematiklektion om ämnet "Multiplikation och maktdelning"

Avsnitt: Matematik

Pedagogiskt mål:

eleven kommer att lära sig skilja mellan egenskaperna för multiplikation och division av potenser med naturliga exponenter; tillämpa dessa egenskaper när det gäller samma baser;

eleven får möjlighet kunna utföra transformationer av grader med olika baser och kunna utföra transformationer i kombinerade uppgifter.

Uppgifter:

organisera elevernas arbete genom att upprepa tidigare studerat material;

säkerställa reproduktionsnivån genom att utföra olika typer av övningar;

organisera en kontroll av elevernas självbedömning genom testning.

Aktivitetsenheter för undervisning: bestämning av grad med en naturlig indikator; examenskomponenter; definition av privat; kombinationslagen för multiplikation.

I. Organisera en demonstration av elevernas behärskning av befintlig kunskap. (steg 1)

a) Uppdatering av kunskap:

2) Formulera en definition av grad med en naturlig exponent.

a n =a a a a … a (n gånger)

b k =b b b b a... b (k gånger) Motivera svaret.

II. Organisation av självbedömning av studentens kunskapsgrad i nuvarande erfarenhet. (steg 2)

Självtest: (enskilt arbete i två versioner.)

A1) Presentera produkten 7 7 7 7 x x x som en potens:

A2) Representera effekten (-3) 3 x 2 som en produkt

A3) Beräkna: -2 3 2 + 4 5 3

Jag väljer antalet uppgifter i provet i enlighet med förberedelsen av klassnivån.

Jag ger dig nyckeln till testet för självtest. Kriterier: godkänt - inget godkänt.

III. Pedagogisk och praktisk uppgift (steg 3) + steg 4. (eleverna ska själva formulera egenskaperna)

beräkna: 2 2 2 3 = ? 3 3 3 2 3 =?

Förenkla: a 2 a 20 = ? b 30 b 10 b 15 = ?

När eleverna löser problem 1) och 2, föreslår eleverna en lösning, och jag som lärare organiserar klassen för att hitta ett sätt att förenkla potenser när man multiplicerar med samma baser.

Lärare: kom på ett sätt att förenkla potenser när du multiplicerar med samma baser.

En post visas i klustret:

Ämnet för lektionen är formulerat. Multiplikation av potenser.

Lärare: kom på en regel för att dela potenser med samma baser.

Resonemang: vilken åtgärd används för att kontrollera division? a 5: a 3 = ? att a 2 a 3 = a 5

Jag återgår till diagrammet - ett kluster och lägger till posten - .. när vi dividerar subtraherar vi och lägger till ämnet för lektionen. ...och uppdelning av grader.

IV. Att förmedla kunskapens gränser till eleverna (som ett minimum och som ett maximum).

Lärare: den minsta uppgiften för dagens lektion är att lära sig att tillämpa egenskaperna för multiplikation och division av potenser med samma baser, och den maximala uppgiften är att tillämpa multiplikation och division tillsammans.

Vi skriver på tavlan : a m a n = a m+n; a m: a n = a m-n

V. Organisation av att studera nytt material. (steg 5)

a) Enligt läroboken: nr 403 (a, c, e) uppgifter med olika formuleringar

Nr 404 (a, d, f) självständigt arbete, sedan organiserar jag en ömsesidig kontroll, ger nycklarna.

b) För vilket värde av m är likheten giltig? a 16 am = a 32; x h x 14 = x 28; x 8 (*) = x 14

Uppgift: kom på liknande exempel för division.

c) nr 417 (a), nr 418 (a) Fällor för studenter: x 3 x n = x 3n; 3 4 3 2 = 9 6; a 16: a 8 = a 2.

VI. Sammanfatta vad som har lärts, utföra diagnostiskt arbete (som uppmuntrar eleverna, och inte läraren, att studera detta ämne) (steg 6)

Diagnostiskt arbete.

Testa(lägg nycklarna på baksidan av degen).

Uppgiftsalternativ: representera kvoten x 15 som en potens: x 3; representera som en effekt produkten (-4) 2 (-4) 5 (-4) 7 ; för vilken m är likheten a 16 a m = a 32 giltig? hitta värdet på uttrycket h 0: h 2 vid h = 0,2; beräkna värdet på uttrycket (5 2 5 0): 5 2 .

Lektionssammanfattning. Reflexion. Jag delar in klassen i två grupper.

Hitta argument i grupp I: till förmån för att känna till gradens egenskaper, och grupp II - argument som säger att du klarar dig utan egenskaper. Vi lyssnar på alla svar och drar slutsatser. I efterföljande lektioner kan du erbjuda statistiska data och kalla rubriken "Det är obegripligt!"

Genomsnittspersonen äter 32 10 2 kg gurkor under sin livstid.

Getingen är kapabel att göra en non-stop flygning på 3,2 10 2 km.

När glas spricker fortplantar sig sprickan med en hastighet av ca 5 10 3 km/h.

En groda äter mer än 3 ton myggor under sitt liv. Använd graden, skriv i kg.

Den mest produktiva anses vara havsfisken - månen (Mola mola), som lägger upp till 300 000 000 ägg med en diameter på cirka 1,3 mm i en lek. Skriv detta nummer med hjälp av en potens.

VII. Läxa.

Historisk referens. Vilka nummer kallas Fermat-nummer.

P.19. nr 403, nr 408, nr 417

Begagnade böcker:

Lärobok "Algebra-7", författarna Yu.N. Makarychev, N.G. Mindyuk et al.

Didaktiskt material för årskurs 7, L.V. Kuznetsova, L.I. Zvavich, S.B. Suvorov.

Encyklopedi av matematik.

Tidningen "Kvant".

Egenskaper för examina, formuleringar, bevis, exempel.

Efter att styrkan av ett tal har bestämts är det logiskt att tala om examensegenskaper. I den här artikeln kommer vi att ge de grundläggande egenskaperna hos ett tals kraft, samtidigt som vi berör alla möjliga exponenter. Här kommer vi att ge bevis på alla egenskaper hos grader, och även visa hur dessa egenskaper används när man löser exempel.

Sidnavigering.

Egenskaper för grader med naturliga exponenter

Per definition av en potens med en naturlig exponent är potensen a n produkten av n faktorer, som var och en är lika med a. Baserat på denna definition, och även använda egenskaper för multiplikation av reella tal, kan vi erhålla och motivera följande gradegenskaper med naturlig exponent:

huvudegenskapen för graden a m ·a n =a m+n, dess generalisering a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +...+n k;

egenskap hos kvotpotenser med identiska baser a m:a n =a m−n ;

egenskapen för graden av en produkt (a·b) n =a n ·b n , dess förlängning (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n ;

egenskap hos kvoten i naturlig grad (a:b) n =a n:b n ;

höja en grad till en potens (a m) n =a m·n, dess generalisering (((a n 1) n 2) …) n k =a n 1 ·n 2 ·…·n k;

jämförelse av grad med noll:

• om a>0, då a n>0 för vilket naturligt tal n som helst;
• om a=0, då är a n=0;
• om a 2·m >0 , om a 2·m−1 n ;
• om m och n är naturliga tal så att m>n, då är för 0m n och för a>0 olikheten a m >a n sann.

Låt oss omedelbart notera att alla skriftliga likheter är det identisk Under de angivna villkoren kan både deras högra och vänstra delar bytas ut. Till exempel, huvudegenskapen för bråket a m ·a n =a m+n med förenkla uttryck används ofta i formen a m+n =a m ·a n .

Låt oss nu titta på var och en av dem i detalj.

Låt oss börja med egenskapen hos produkten av två potenser med samma baser, som kallas examens huvudsakliga egenskap: för alla reella tal a och alla naturliga tal m och n är likheten a m ·a n =a m+n sann.

Låt oss bevisa gradens huvudsakliga egenskap. Genom definitionen av en potens med en naturlig exponent kan produkten av potenser med identiska baser av formen a m ·a n skrivas som produkten . På grund av multiplikationens egenskaper kan det resulterande uttrycket skrivas som , och denna produkt är en potens av talet a med en naturlig exponent m+n, det vill säga en m+n. Detta fullbordar beviset.

Låt oss ge ett exempel som bekräftar gradens huvudegenskap. Låt oss ta grader med samma baser 2 och naturliga potenser 2 och 3, med hjälp av den grundläggande egenskapen för grader kan vi skriva likheten 2 2 ·2 3 =2 2+3 =2 5. Låt oss kontrollera dess giltighet genom att beräkna värdena för uttrycken 2 2 · 2 3 och 2 5 . Genom att utföra exponentiering har vi 2 2 2 3 =(2 2) (2 2 2) = 4 8 = 32 och 2 5 =2 2 2 2 2 = 32 , eftersom vi får lika värden, då är likheten 2 2 ·2 3 =2 5 är korrekt, och det bekräftar gradens huvudegenskap.

Den grundläggande egenskapen för en grad, baserad på multiplikationens egenskaper, kan generaliseras till produkten av tre eller flera potenser med samma baser och naturliga exponenter. Så för vilket tal k som helst av naturliga tal n 1 , n 2 , …, n k är likheten a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +...+n k sann.

Till exempel, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .

Vi kan gå vidare till nästa egenskap hos makter med en naturlig exponent – egendom av kvotbefogenheter med samma baser: för alla reella tal a som inte är noll och godtyckliga naturliga tal m och n som uppfyller villkoret m>n, är likheten a m:a n =a m−n sann.

Innan vi presenterar beviset för denna egenskap, låt oss diskutera innebörden av de ytterligare villkoren i formuleringen. Villkoret a≠0 är nödvändigt för att undvika division med noll, eftersom 0 n =0, och när vi bekantade oss med division var vi överens om att vi inte kan dividera med noll. Villkoret m>n införs för att vi inte ska gå bortom de naturliga exponenterna. Faktum är att för m>n exponenten är a m−n ett naturligt tal, annars blir det antingen noll (vilket händer för m−n) eller ett negativt tal (vilket händer för m m−n ·a n =a (m−n) +n =a m. Av den resulterande likheten a m−n ·a n =a m och av sambandet mellan multiplikation och division följer att en m−n är en kvot av potenser a m och en n. Detta bevisar egenskapen hos potenskvoter med samma baser.

Låt oss ge ett exempel. Låt oss ta två grader med samma baser π och naturliga exponenter 5 och 2, likheten π 5:π 2 =π 5−3 =π 3 motsvarar gradens betraktade egenskap.

Låt oss nu överväga produktkraftsegenskap: den naturliga potensen n av produkten av två reella tal a och b är lika med produkten av potenserna a n och b n , det vill säga (a·b) n =a n ·b n .

I själva verket har vi enligt definitionen av en grad med en naturlig exponent . Baserat på multiplikationens egenskaper kan den sista produkten skrivas om som , vilket är lika med a n · b n .

Här är ett exempel: .

Denna egenskap sträcker sig till produktens kraft av tre eller flera faktorer. Det vill säga egenskapen för naturlig grad n för en produkt av k faktorer skrivs som (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .

För tydlighetens skull kommer vi att visa den här egenskapen med ett exempel. För produkten av tre faktorer i makten 7 har vi .

Följande egendom är egendom av en naturakvot: kvoten av reella tal a och b, b≠0 till den naturliga potensen n är lika med kvoten av potenserna a n och b n, det vill säga (a:b) n =a n:b n.

Beviset kan utföras med den tidigare egenskapen. Så (a:b) n ·b n =((a:b)·b) n =a n , och av likheten (a:b) n ·b n =a n följer att (a:b) n är kvoten av division a n på bn.

Låt oss skriva den här egenskapen med specifika siffror som exempel: .

Låt oss nu uttrycka det egenskapen att höja en makt till en makt: för varje reellt tal a och alla naturliga tal m och n är potensen av a m till potensen av n lika med potensen av talet a med exponent m·n, det vill säga (a m) n =a m·n.

Till exempel, (5 2) 3 =5 2·3 =5 6.

Beviset på egenskapen power-to-degree är följande kedja av likheter: .

Den övervägda fastigheten kan utvidgas i grad till grad till grad m.m. Till exempel, för alla naturliga tal p, q, r och s, är likheten . För större tydlighet, låt oss ge ett exempel med specifika siffror: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10.

Det återstår att uppehålla sig vid egenskaperna för att jämföra grader med en naturlig exponent.

Låt oss börja med att bevisa egenskapen att jämföra noll och makt med en naturlig exponent.

Låt oss först bevisa att a n >0 för valfri a>0.

Produkten av två positiva tal är ett positivt tal, enligt definitionen av multiplikation. Detta faktum och multiplikationens egenskaper tyder på att resultatet av att multiplicera valfritt antal positiva tal också blir ett positivt tal. Och makten för ett tal a med naturlig exponent n, per definition, är produkten av n faktorer, som var och en är lika med a. Dessa argument tillåter oss att hävda att för varje positiv bas a är graden a n ett positivt tal. På grund av den beprövade egenskapen 3 5 >0, (0,00201) 2 >0 och .

Det är ganska uppenbart att för varje naturligt tal n med a=0 är graden av ett n noll. Faktum är att 0n =0·0·…·0=0 . Till exempel, 0 3 =0 och 0 762 =0.

Låt oss gå vidare till negativa gradbaser.

Låt oss börja med fallet när exponenten är ett jämnt tal, låt oss beteckna det som 2·m, där m är ett naturligt tal. Sedan . Enligt regeln för att multiplicera negativa tal är var och en av produkterna av formen a·a lika med produkten av de absoluta värdena av talen a och a, vilket betyder att det är ett positivt tal. Därför kommer produkten också att vara positiv och grad a 2·m. Låt oss ge exempel: (−6) 4 >0 , (−2,2) 12 >0 och .

Slutligen, när basen a är ett negativt tal och exponenten är ett udda tal 2 m−1, då . Alla produkter a·a är positiva tal, produkten av dessa positiva tal är också positiv, och dess multiplikation med det återstående negativa talet a resulterar i ett negativt tal. På grund av denna egenskap (−5) är 3 17 n n produkten av vänster och höger sida av n sanna olikheter a egenskaper hos ojämlikheter, är också en bevisbar olikhet av formen a n n sann. Till exempel, på grund av denna egenskap, ojämlikheterna 3 7 7 och .

Det återstår att bevisa den sista av de listade egenskaperna hos krafter med naturliga exponenter. Låt oss formulera det. Av två potenser med naturliga exponenter och identiska positiva baser mindre än en, är den vars exponent är mindre större; och av två potenser med naturliga exponenter och identiska baser större än en, är den vars exponent är större större. Låt oss gå vidare till beviset för denna egendom.

Låt oss bevisa att för m>n och 0m n . För att göra detta skriver vi ner skillnaden a m − a n och jämför den med noll. Den registrerade skillnaden, efter att ha tagit ett n inom parentes, kommer att ha formen a n ·(a m−n−1) . Den resulterande produkten är negativ som produkten av ett positivt tal a n och ett negativt tal a m−n −1 (a n är positiv som den naturliga potensen av ett positivt tal, och skillnaden a m−n −1 är negativ, eftersom m−n >0 på grund av initialvillkoret m>n, varav det följer att när 0m−n är mindre än enhet). Därför a m −a n m n , vilket är det som behövde bevisas. Som ett exempel ger vi den korrekta ojämlikheten.

Det återstår att bevisa den andra delen av fastigheten. Låt oss bevisa att för m>n och a>1 är a m >a n sant. Skillnaden a m −a n efter att ha tagit ett n inom parentes har formen a n ·(a m−n −1) . Denna produkt är positiv, eftersom graden a n för a>1 är ett positivt tal, och skillnaden a m−n −1 är ett positivt tal, eftersom m−n>0 på grund av initialtillståndet, och för a>1 graden a m−n är större än en . Följaktligen a m −a n >0 och a m >a n , vilket är det som behövde bevisas. Denna egenskap illustreras av ojämlikheten 3 7 >3 2.

Egenskaper för potenser med heltalsexponenter

Eftersom positiva heltal är naturliga tal, så sammanfaller alla egenskaper hos potenser med positiva heltalsexponenter exakt med egenskaperna hos potenser med naturliga exponenter listade och bevisade i föregående stycke.

Vi definierade en grad med en heltals negativ exponent, såväl som en grad med en nollexponent, på ett sådant sätt att alla egenskaper hos grader med naturliga exponenter, uttryckta med likheter, förblev giltiga. Därför är alla dessa egenskaper giltiga för både nollexponenter och negativa exponenter, medan, naturligtvis, potensernas baser skiljer sig från noll.

Så för alla reella och icke-nolltal a och b, såväl som alla heltal m och n, gäller följande: egenskaper hos potenser med heltalsexponenter:

• a m·an =a m+n;
• a m:a n =a m−n;
• (a·b) n =an·bn;
• (a:b) n =a n:bn;
• (a m) n =a m·n;
• om n är ett positivt heltal är a och b positiva tal och a n n och a −n >b −n;
• om m och n är heltal, och m>n, så gäller för 0m n och för a>1 olikheten a m >a n.

När a=0 är potenserna a m och a n vettiga endast när både m och n är positiva heltal, det vill säga naturliga tal. De egenskaper som just skrivits är alltså giltiga för de fall då a=0 och talen m och n är positiva heltal.

Att bevisa var och en av dessa egenskaper är inte svårt; för att göra detta räcker det att använda definitionerna av grader med naturliga och heltalsexponenter, såväl som egenskaperna för operationer med reella tal. Som ett exempel, låt oss bevisa att egenskapen power-to-power gäller för både positiva heltal och icke-positiva heltal. För att göra detta måste du visa att om p är noll eller ett naturligt tal och q är noll eller ett naturligt tal, då är likheterna (a p) q =a p·q, (a −p) q =a (−p) ·q, (a p) −q =a p·(−q) och (a −p) −q =a (−p)·(−q) . Vi gör det.

För positiva p och q bevisades likheten (a p) q =a p·q i föregående stycke. Om p=0 så har vi (a 0) q =1 q =1 och a 0·q =a 0 =1, varav (a 0) q =a 0·q. På liknande sätt, om q=0, då (a p) 0 =1 och a p·0 =a 0 =1, varav (a p) 0 =a p·0. Om både p=0 och q=0, då (a 0) 0 =1 0 =1 och a 0,0 =a 0 =1, varav (a 0) 0 =a 0,0.

Nu bevisar vi att (a −p) q =a (−p)·q . Per definition av en potens med en negativ heltalsexponent, alltså . Genom egenskapen av kvoter till befogenheter vi har . Eftersom 1 p =1·1·…·1=1 och , då . Det sista uttrycket är per definition en potens av formen a −(p·q), som på grund av multiplikationsreglerna kan skrivas som en (−p)·q.

likaså .

OCH .

Med samma princip kan du bevisa alla andra egenskaper hos en grad med en heltalsexponent, skriven i form av likheter.

I den näst sista av de registrerade egenskaperna är det värt att uppehålla sig vid beviset för olikheten a −n >b −n, som gäller för alla negativa heltal −n och alla positiva a och b för vilka villkoret a är uppfyllt. . Låt oss skriva ner och omvandla skillnaden mellan vänster och höger sida av denna ojämlikhet: . Eftersom genom villkor a n n , därför b n −a n >0 . Produkten a n · b n är också positiv som produkten av positiva tal a n och b n . Då är det resulterande bråket positivt som kvoten av de positiva talen b n −a n och a n ·b n . Därför, varifrån a −n >b −n , vilket är det som behövde bevisas.

Den sista egenskapen hos potenser med heltalsexponenter bevisas på samma sätt som en liknande egenskap hos potenser med naturliga exponenter.

Egenskaper hos potenser med rationella exponenter

Vi definierade en grad med en bråkdelsexponent genom att utöka egenskaperna för en grad med en heltalsexponent till den. Potenser med bråkexponenter har med andra ord samma egenskaper som potenser med heltalsexponenter. Nämligen:

1. egenskapen hos produkten av makter med samma baser för a>0, och om och, då för a≥0;
2. egendom av kvotbefogenheter med samma baser för a>0;
3. egenskap hos en produkt till en bråkdel för a>0 och b>0, och om och, då för a≥0 och (eller) b≥0;
4. egenskapen hos en kvot till en bråkpotens för a>0 och b>0, och om, då för a≥0 och b>0;
5. egenskap av grad till grad för a>0, och om och, då för a≥0;
6. egenskapen att jämföra potenser med lika rationella exponenter: för alla positiva tal a och b, a 0 är olikheten a p p sann, och för p p >b p ;
7. egenskapen att jämföra potenser med rationella exponenter och lika baser: för rationella tal p och q, p>q för 0p q, och för a>0 – olikhet a p >a q.

Beviset för egenskaperna hos potenser med bråkexponenter baseras på definitionen av en potens med bråkexponent, på egenskaperna hos den aritmetiska roten av den n:e graden och på egenskaperna hos en potens med en heltalsexponent. Låt oss tillhandahålla bevis.

Per definition av en potens med en bråkdelsexponent och , då . Egenskaperna för den aritmetiska roten gör att vi kan skriva följande likheter. Vidare, genom att använda egenskapen för en grad med en heltalsexponent, får vi , från vilken vi, genom definitionen av en grad med en bråkdelsexponent, har , och indikatorn för den erhållna graden kan omvandlas enligt följande: . Detta fullbordar beviset.

Den andra egenskapen för potenser med bråkexponenter bevisas på ett absolut liknande sätt:


De återstående jämlikheterna bevisas med liknande principer:


Låt oss gå vidare till att bevisa nästa egendom. Låt oss bevisa att för alla positiva a och b, a 0 är olikheten a p p sann, och för p p >b p . Låt oss skriva det rationella talet p som m/n, där m är ett heltal och n är ett naturligt tal. Villkoren p 0 kommer i detta fall att vara ekvivalenta med villkoren m 0, respektive. För m>0 och am m . Från denna olikhet, genom egenskapen rötter, har vi, och eftersom a och b är positiva tal, kan den resulterande olikheten skrivas om till, det vill säga, a p p , baserat på definitionen av en grad med bråkexponent.

På liknande sätt, för m m > b m , varifrån, det vill säga a p > b p .

Det återstår att bevisa den sista av de listade fastigheterna. Låt oss bevisa att för rationella tal p och q, p>q för 0p q, och för a>0 – olikheten a p >a q. Vi kan alltid reducera rationella tal p och q till en gemensam nämnare, även om vi får vanliga bråk och , där m 1 och m 2 är heltal, och n är ett naturligt tal. I detta fall kommer villkoret p>q att motsvara villkoret m 1 >m 2, som följer av regeln för att jämföra vanliga bråk med samma nämnare. Sedan, genom egenskapen att jämföra grader med samma baser och naturliga exponenter, för 0m 1 m 2, och för a>1, olikheten a m 1 >a m 2. Dessa ojämlikheter i egenskaperna hos rötterna kan skrivas om därefter som Och . Och definitionen av en examen med en rationell exponent tillåter oss att gå vidare till ojämlikheter och följaktligen. Härifrån drar vi den slutliga slutsatsen: för p>q och 0p q , och för a>0 – olikheten a p >a q .

Egenskaper hos potenser med irrationella exponenter

Från hur en grad med en irrationell exponent definieras kan vi dra slutsatsen att den har alla egenskaper hos grader med rationella exponenter. Så för alla a>0, b>0 och irrationella tal p och q gäller följande egenskaper hos potenser med irrationella exponenter:

1. a p·aq =a p+q;
2. a p:a q =a p−q;
3. (a·b) p =ap·bp;
4. (a:b) p =a p:bp;
5. (a p) q =a p·q;
6. för alla positiva tal a och b, a 0 är olikheten a p p sann, och för p p >b p ;
7. för irrationella tal p och q, p>q för 0p q, och för a>0 – olikheten a p >a q.

Av detta kan vi dra slutsatsen att potenser med eventuella reella exponenter p och q för a>0 har samma egenskaper.

• Algebra - 10:e klass. Trigonometriska ekvationer Lektion och presentation om ämnet: "Lösa de enklaste trigonometriska ekvationerna" Ytterligare material Kära användare, glöm inte att lämna dina kommentarer, recensioner, förslag! Allt material […]
• En tävling har öppnats för tjänsten "SÄLJARE - KONSULT": Ansvarsområden: försäljning av mobiltelefoner och tillbehör för mobil kommunikation, kundservice för Beeline, Tele2, MTS-abonnenter, anslutning av Beeline och Tele2 tariffplaner och tjänster, MTS-konsulttjänster [... ]
• Parallellepipedformel En parallellepiped är en polyeder med 6 ytor, som var och en är ett parallellogram. En kuboid är en parallellepiped vars sida är en rektangel. Varje parallellepiped kännetecknas av 3 […]
• Society for the Protection of Consumer Rights Astana För att få en pinkod för att komma åt detta dokument på vår webbplats, skicka ett SMS med texten zan till numret Prenumeranter hos GSM-operatörer (Activ, Kcell, Beeline, NEO, Tele2) av skicka ett sms till nummer, […]
• STAVNING N OCH NN I OLIKA DELAR AV TAL S.G. ZELINSKAYA DIDAKTISKT MATERIAL Teoretisk övning 1. När skrivs nn i adjektiv? 2. Nämn undantagen från dessa regler. 3. Hur man skiljer ett verbalt adjektiv med suffixet -n- från ett particip med […]
• Anta en lag om familjegods Anta en federal lag om gratis tilldelning till varje medborgare i Ryska federationen eller en familj av medborgare av en tomt för utveckling av en familjegods på den på följande villkor: 1. Tomten är avsatt för […]
• INSPEKTION AV GOSTEKHNADZOR I BRYANSK REGIONEN Kvitto på betalning av statlig tull (Nedladdning-12,2 kb) Ansökningar om registrering för enskilda (Nedladdning-12 kb) Ansökningar om registrering för juridiska personer (Nedladdning-11,4 kb) 1. Vid registrering av ny bil: 1.ansökan 2.pass […]
• Det var ett tag sedan vi spelade 1v1-turneringar. Och det är förmodligen dags att återuppta denna tradition. Även om vi inte kan organisera en separat stege och turneringar för 1v1-spelare, föreslår vi att du använder dina lagprofiler på sidan. Poäng för spel i matcher kan tas bort eller läggas till [...]

I den tidigare artikeln förklarade vi vad monomialer är. I detta material kommer vi att titta på hur man löser exempel och problem där de används. Här kommer vi att överväga sådana åtgärder som subtraktion, addition, multiplikation, division av monomialer och höja dem till en potens med en naturlig exponent. Vi kommer att visa hur sådana operationer definieras, beskriva de grundläggande reglerna för deras genomförande och vad som bör bli resultatet. Alla teoretiska begrepp kommer som vanligt att illustreras med exempel på problem med beskrivningar av lösningar.

Det är mest bekvämt att arbeta med standardnotationen för monomialer, så vi presenterar alla uttryck som kommer att användas i artikeln i standardform. Om de ursprungligen specificerades annorlunda, rekommenderas att först ta dem till en allmänt accepterad form.

Regler för att addera och subtrahera monomialer

De enklaste operationerna som kan utföras med monomialer är subtraktion och addition. I allmänhet kommer resultatet av dessa åtgärder att vara ett polynom (en monom är möjlig i vissa speciella fall).

När vi adderar eller subtraherar monomer skriver vi först ner motsvarande summa och skillnad i den allmänt accepterade formen och förenklar sedan det resulterande uttrycket. Om det finns liknande termer måste de citeras, och parenteserna ska öppnas. Låt oss förklara med ett exempel.

Exempel 1

Skick: utför tillägget av monomialerna − 3 x och 2, 72 x 3 y 5 z.

Lösning

Låt oss skriva ner summan av de ursprungliga uttrycken. Låt oss lägga till parenteser och sätta ett plustecken mellan dem. Vi kommer att få följande:

(− 3 x) + (2, 72 x 3 y 5 z)

När vi gör parentesexpansionen får vi - 3 x + 2, 72 x 3 y 5 z. Detta är ett polynom, skrivet i standardform, som kommer att vara resultatet av att lägga till dessa monomer.

Svar:(− 3 x) + (2,72 x 3 y 5 z) = − 3 x + 2,72 x 3 y 5 z.

Om vi ​​har tre, fyra eller fler termer utför vi denna åtgärd på exakt samma sätt.

Exempel 2

Skick: utför de angivna operationerna med polynom i rätt ordning

3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c

Lösning

Låt oss börja med att öppna fästena.

3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c

Vi ser att det resulterande uttrycket kan förenklas genom att lägga till liknande termer:

3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = = (3 a 2 + a 2 - 7 a 2) + 4 a c - 2 2 3 a c + 4 9 = = - 3 a 2 + 1 1 3 a c + 4 9

Vi har ett polynom som kommer att bli resultatet av denna åtgärd.

Svar: 3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = - 3 a 2 + 1 1 3 a c + 4 9

I princip kan vi addera och subtrahera två monomialer, med vissa begränsningar, så att vi slutar med en monomial. För att göra detta måste du uppfylla vissa villkor för addends och subtraherade monomialer. Vi kommer att berätta hur detta går till i en separat artikel.

Regler för att multiplicera monomer

Multiplikationsåtgärden lägger inga begränsningar på faktorerna. Monomialerna som multipliceras behöver inte uppfylla några ytterligare villkor för att resultatet ska bli ett monomial.

För att utföra multiplikation av monomialer måste du följa dessa steg:

1. Skriv ner stycket korrekt.
2. Expandera parenteserna i det resulterande uttrycket.
3. Gruppera om möjligt faktorer med samma variabler och numeriska faktorer separat.
4. Utför de nödvändiga operationerna med siffror och använd egenskapen multiplikation av potenser med samma baser på de återstående faktorerna.

Låt oss se hur detta går till i praktiken.

Exempel 3

Skick: multiplicera monomialerna 2 x 4 y z och - 7 16 t 2 x 2 z 11.

Lösning

Låt oss börja med att komponera verket.

Vi öppnar fästena i den och får följande:

2 x 4 y z - 7 16 t 2 x 2 z 11

2 - 7 16 t 2 x 4 x 2 y z 3 z 11

Allt vi behöver göra är att multiplicera siffrorna inom de första parenteserna och tillämpa egenskapen potenser för den andra. Som ett resultat får vi följande:

2 - 7 16 t 2 x 4 x 2 y z 3 z 11 = - 7 8 t 2 x 4 + 2 y z 3 + 11 = = - 7 8 t 2 x 6 y z 14

Svar: 2 x 4 y z - 7 16 t 2 x 2 z 11 = - 7 8 t 2 x 6 y z 14 .

Om vårt villkor innehåller tre eller fler polynom multiplicerar vi dem med exakt samma algoritm. Vi kommer att överväga frågan om att multiplicera monomer mer i detalj i ett separat material.

Regler för att höja en monomial till en makt

Vi vet att en potens med en naturlig exponent är produkten av ett visst antal identiska faktorer. Deras nummer indikeras av siffran i indikatorn. Enligt denna definition är att höja en monomial till en potens likvärdig med att multiplicera det specificerade antalet identiska monomialer. Låt oss se hur det går till.

Exempel 4

Skick: höj monomialen − 2 · a · b 4 till potensen 3 .

Lösning

Vi kan ersätta exponentiering med multiplikation av 3 monomialer − 2 · a · b 4 . Låt oss skriva ner det och få det önskade svaret:

(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12

Svar:(− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .

Men vad händer om graden har en stor indikator? Det är obekvämt att registrera ett stort antal faktorer. Sedan, för att lösa ett sådant problem, måste vi tillämpa egenskaperna hos en examen, nämligen egenskapen hos en produktexamen och egenskapen hos en examen i en examen.

Låt oss lösa problemet vi presenterade ovan med den angivna metoden.

Exempel 5

Skick: höja − 2 · a · b 4 till tredje potens.

Lösning

Genom att känna till egenskapen power-to-degree kan vi gå vidare till ett uttryck av följande form:

(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .

Efter detta höjer vi till makten - 2 och tillämpar maktens egenskap på makter:

(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .

Svar:− 2 · a · b 4 = − 8 · a 3 · b 12 .

Vi ägnade också en separat artikel åt att höja en monomial till en makt.

Regler för att dela monomer

Den sista operationen med monomialer som vi kommer att undersöka i detta material är att dividera ett monomial med ett monomial. Som ett resultat bör vi erhålla en rationell (algebraisk) bråkdel (i vissa fall är det möjligt att få en monomial). Låt oss omedelbart klargöra att division med noll monomial inte är definierad, eftersom division med 0 inte är definierad.

För att utföra division måste vi skriva ner de angivna monomialerna i form av en bråkdel och minska den om möjligt.

Exempel 6

Skick: dividera monomialen − 9 · x 4 · y 3 · z 7 med − 6 · p 3 · t 5 · x 2 · y 2 .

Lösning

Låt oss börja med att skriva monomer i bråkform.

9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2

Denna fraktion kan reduceras. Efter att ha utfört denna åtgärd får vi:

3 x 2 y z 7 2 p 3 t 5

Svar:- 9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2 = 3 x 2 y z 7 2 p 3 t 5 .

De förhållanden under vilka vi, som ett resultat av att dela monomialer, får en monomial, ges i en separat artikel.

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Hur multiplicerar man potenser? Vilka potenser kan multipliceras och vilka kan inte? Hur multiplicerar man ett tal med en potens?

I algebra kan du hitta en produkt av potenser i två fall:

1) om graderna har samma baser;

2) om graderna har samma indikatorer.

När du multiplicerar potenser med samma baser måste basen lämnas densamma och exponenterna måste adderas:

När du multiplicerar grader med samma indikatorer kan den övergripande indikatorn tas ur parentes:

Låt oss titta på hur man multiplicerar potenser med hjälp av specifika exempel.

Enheten skrivs inte i exponenten, men när man multiplicerar potenser tar de hänsyn till:

När du multiplicerar kan det finnas hur många potenser som helst. Det bör komma ihåg att du inte behöver skriva multiplikationstecknet före bokstaven:

I uttryck görs exponentiering först.

Om du behöver multiplicera ett tal med en potens, bör du först utföra exponentieringen, och först därefter multiplikationen:

www.algebraclass.ru

Addition, subtraktion, multiplikation och division av potenser

Addition och subtraktion av potenser

Det är uppenbart att tal med potenser kan adderas som andra storheter , genom att lägga till dem en efter en med sina tecken.

Så summan av a 3 och b 2 är a 3 + b 2.
Summan av a 3 - b n och h 5 -d 4 är a 3 - b n + h 5 - d 4.

Odds lika styrka av identiska variabler kan läggas till eller subtraheras.

Så summan av 2a 2 och 3a 2 är lika med 5a 2.

Det är också uppenbart att om du tar två rutor a, eller tre rutor a, eller fem rutor a.

Men grader olika variabler Och olika grader identiska variabler, måste komponeras genom att lägga till dem med sina tecken.

Så summan av en 2 och en 3 är summan av en 2 + en 3.

Det är uppenbart att kvadraten av a, och kuben av a, inte är lika med två gånger kvadraten av a, utan två gånger kuben av a.

Summan av a 3 b n och 3a 5 b 6 är a 3 b n + 3a 5 b 6.

Subtraktion befogenheter utförs på samma sätt som addition, förutom att subtrahendernas tecken måste ändras i enlighet med detta.

Eller:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Multiplicera makter

Tal med potenser kan multipliceras, precis som andra storheter, genom att skriva dem efter varandra, med eller utan ett multiplikationstecken mellan dem.

Således blir resultatet av att multiplicera a 3 med b 2 a 3 b 2 eller aaabb.

Eller:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Resultatet i det sista exemplet kan beställas genom att lägga till identiska variabler.
Uttrycket kommer att ha formen: a 5 b 5 y 3.

Genom att jämföra flera tal (variabler) med potenser kan vi se att om två av dem multipliceras så blir resultatet ett tal (variabel) med en potens lika med belopp grader av termer.

Så, a 2 .a 3 = aa.aaa = aaaaa = en 5 .

Här är 5 potensen av multiplikationsresultatet, vilket är lika med 2 + 3, summan av termernas potenser.

Så, a n.am = a m+n.

För a n tas a som en faktor lika många gånger som potensen av n;

Och ett m tas som en faktor lika många gånger som graden m är lika med;

Det är därför, potenser med samma baser kan multipliceras genom att addera potensernas exponenter.

Så, a 2 .a 6 = a 2+6 = a 8 . Och x 3 .x 2 .x = x 3+2+1 = x 6 .

Eller:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Multiplicera (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Svar: x 4 - y 4.
Multiplicera (x 3 + x – 5) ⋅ (2x 3 + x + 1).

Denna regel gäller även för tal vars exponenter är negativ.

1. Så, a -2 .a -3 = a -5 . Detta kan skrivas som (1/aa).(1/aaa) = 1/aaaaa.

2. y-n.y-m = y-n-m.

3. a -n .a m = a m-n .

Om a + b multipliceras med a - b, blir resultatet a 2 - b 2: det vill säga

Resultatet av att multiplicera summan eller skillnaden mellan två tal är lika med summan eller skillnaden av deras kvadrater.

Om du multiplicerar summan och skillnaden av två tal upphöjda till fyrkant, blir resultatet lika med summan eller skillnaden av dessa siffror i fjärde grader.

Så, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.

Indelning av examina

Tal med potenser kan delas som andra tal, genom att subtrahera från utdelningen, eller genom att placera dem i bråkform.

Således är a 3 b 2 dividerat med b 2 lika med a 3.

Att skriva 5 dividerat med 3 ser ut som $\frac $. Men detta är lika med en 2 . I en serie siffror
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
vilket tal som helst kan delas med ett annat, och exponenten blir lika med skillnad indikatorer för delbara tal.

När man dividerar grader med samma bas, subtraheras deras exponenter..

Så, y 3:y 2 = y 3-2 = y 1. Det vill säga $\frac = y$.

Och a n+1:a = a n+1-1 = a n . Det vill säga $\frac = a^n$.

Eller:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b +y) n-3

Regeln gäller även för siffror med negativ värden på grader.
Resultatet av att dividera en -5 med en -3 är en -2.
Dessutom, $\frac: \frac = \frac .\frac = \frac = \frac $.

h 2:h -1 = h 2+1 = h 3 eller $h^2:\frac = h^2.\frac = h^3$

Det är nödvändigt att behärska multiplikation och division av potenser mycket väl, eftersom sådana operationer används mycket i algebra.

Exempel på att lösa exempel med bråk som innehåller tal med potenser

1. Minska exponenterna med $\frac $ Svar: $\frac $.

2. Minska exponenter med $\frac$. Svar: $\frac$ eller 2x.

3. Minska exponenterna a 2 /a 3 och a -3 /a -4 och ta till en gemensam nämnare.
a 2 .a -4 är a -2 den första täljaren.
a 3 .a -3 är a 0 = 1, den andra täljaren.
a 3 .a -4 är a -1 , den gemensamma täljaren.
Efter förenkling: a -2 /a -1 och 1/a -1 .

4. Minska exponenterna 2a 4 /5a 3 och 2 /a 4 och ta till en gemensam nämnare.
Svar: 2a 3 /5a 7 och 5a 5 /5a 7 eller 2a 3 /5a 2 och 5/5a 2.

5. Multiplicera (a 3 + b)/b 4 med (a - b)/3.

6. Multiplicera (a 5 + 1)/x 2 med (b 2 - 1)/(x + a).

7. Multiplicera b4/a-2 med h-3/x och a n/y-3.

8. Dividera a 4 /y 3 med a 3 /y 2 . Svar: a/y.

Gradens egenskaper

Vi påminner dig om att i den här lektionen kommer vi att förstå egenskaper hos grader med naturliga indikatorer och noll. Effekter med rationella exponenter och deras egenskaper kommer att diskuteras i lektioner för 8:e klass.

En potens med naturlig exponent har flera viktiga egenskaper som gör att vi kan förenkla beräkningar i exempel med potenser.

Fastighet nr 1
Produkt av makter

När potenser multipliceras med samma baser förblir basen oförändrad, och potensernas exponenter adderas.

a m · a n = a m + n, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Denna egenskap hos makter gäller även produkten av tre eller flera potenser.

Förenkla uttrycket.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Presentera det som en examen.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17

Presentera det som en examen.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Observera att i den angivna egenskapen talade vi bara om multiplikation av potenser med samma baser. Det gäller inte deras tillägg.

Du kan inte ersätta summan (3 3 + 3 2) med 3 5. Detta är förståeligt om
beräkna (3 3 + 3 2) = (27 + 9) = 36 och 3 5 = 243

Fastighet nr 2
Partiella examina

När man dividerar potenser med samma baser förblir basen oförändrad, och divisorns exponent subtraheras från exponenten för utdelningen.

Skriv kvoten som en potens
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Beräkna.

11 3 − 2 4 2 − 1 = 11 4 = 44
Exempel. Lös ekvationen. Vi använder egenskapen kvotbefogenheter.
3 8: t = 3 4

Svar: t = 3 4 = 81

Med hjälp av egenskaper nr 1 och nr 2 kan du enkelt förenkla uttryck och utföra beräkningar.

Exempel. Förenkla uttrycket.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Exempel. Hitta värdet på ett uttryck med hjälp av egenskaperna hos exponenter.

2 11 − 5 = 2 6 = 64

Observera att vi i fastighet 2 bara pratade om att dela potenser med samma baser.

Du kan inte ersätta skillnaden (4 3 −4 2) med 4 1. Detta är förståeligt om du beräknar (4 3 −4 2) = (64 − 16) = 48, och 4 1 = 4

Fastighet nr 3
Att höja en grad till en makt

När man höjer en grad till en potens förblir gradens bas oförändrad och exponenterna multipliceras.

(a n) m = a n · m, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Observera att egenskap nr 4, liksom andra egenskaper för grader, också tillämpas i omvänd ordning.

(a n · b n)= (a · b) n

Det vill säga, för att multiplicera potenser med samma exponenter kan du multiplicera baserna, men lämna exponenten oförändrad.

Exempel. Beräkna.
2 4 5 4 = (2 5) 4 = 10 4 = 10 000

Exempel. Beräkna.
0,5 16 2 16 = (0,5 2) 16 = 1

I mer komplexa exempel kan det finnas fall där multiplikation och division måste utföras över potenser med olika baser och olika exponenter. I det här fallet rekommenderar vi att du gör följande.

Till exempel, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Ett exempel på att höja en decimal till en potens.

4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = 4

Egenskaper 5
Kraften i en kvot (bråkdel)

För att höja en kvot till en potens kan du höja utdelningen och divisorn separat till denna potens och dividera det första resultatet med det andra.

(a: b) n = a n: b n, där "a", "b" är alla rationella tal, b ≠ 0, n - vilket naturligt tal som helst.

Exempel. Presentera uttrycket som en maktkvot.
(5: 3) 12 = 5 12: 3 12

Vi påminner om att en kvot kan representeras som en bråkdel. Därför kommer vi att uppehålla oss vid ämnet att höja en bråkdel till en makt mer detaljerat på nästa sida.

Krafter och rötter

Verksamhet med befogenheter och rötter. Grad med negativ ,

noll och bråk indikator. Om uttryck som inte har någon mening.

Verksamhet med examina.

1. När potenser multipliceras med samma bas, adderas deras exponenter:

en m · a n = a m + n .

2. Vid division av grader med samma bas, deras exponenter dras av .

3. Graden av produkten av två eller flera faktorer är lika med produkten av graderna av dessa faktorer.

4. Graden av ett förhållande (bråk) är lika med förhållandet mellan graderna av utdelningen (täljaren) och divisorn (nämnaren):

(a/b) n = a n/b n .

5. När man höjer en potens till en potens multipliceras deras exponenter:

Alla ovanstående formler läses och exekveras i båda riktningarna från vänster till höger och vice versa.

EXEMPEL (2 3 5 / 15)² = 2² · 3² · 5² / 15² = 900 / 225 = 4 .

Verksamhet med rötter. I alla formlerna nedan betyder symbolen aritmetisk rot(det radikala uttrycket är positivt).

1. Roten av produkten av flera faktorer är lika med produkten av rötterna av dessa faktorer:

2. Roten av ett förhållande är lika med förhållandet mellan utdelningens rötter och divisorn:

3. När man höjer en rot till en makt räcker det att höja till denna makt radikalt nummer:

4. Om du ökar graden av roten med m gånger och samtidigt höjer det radikala talet till m:te potensen, kommer rotens värde inte att ändras:

5. Om du minskar graden av roten med m gånger och samtidigt extraherar den mth roten av radikaltalet, kommer rotens värde inte att ändras:

Utvidgar begreppet grad. Hittills har vi bara betraktat grader med naturliga exponenter; men operationer med befogenheter och rötter kan också leda till negativ, noll Och fraktionerad indikatorer. Alla dessa exponenter kräver ytterligare definition.

En grad med negativ exponent. Potensen för ett visst tal med en negativ (heltals) exponent definieras som en dividerad med potensen av samma tal med en exponent lika med det absoluta värdet av den negativa exponenten:

Nu formeln en m : en = a m - n kan användas inte bara för m, mer än n, men också med m, mindre än n .

EXEMPEL a 4: a 7 = a 4 — 7 = a — 3 .

Om vi ​​vill ha formeln en m : en = en m — n var rättvist när m = n, vi behöver en definition av grad noll.

En grad med nollindex. Potensen för ett tal som inte är noll med exponent noll är 1.

EXEMPEL. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Grad med bråkexponent. För att höja ett reellt tal a till potensen m / n, måste du extrahera den n:te roten av den månte potensen av detta tal a:

Om uttryck som inte har någon mening. Det finns flera sådana uttryck.

Var a ≠ 0 , existerar inte.

Faktum är att om vi antar det xär ett visst antal, så har vi i enlighet med definitionen av divisionsoperationen: a = 0· x, dvs. a= 0, vilket motsäger villkoret: a ≠ 0

— vilket nummer som helst.

Faktum är att om vi antar att detta uttryck är lika med något tal x, då har vi enligt definitionen av divisionsoperationen: 0 = 0 · x. Men denna jämlikhet uppstår när valfritt nummer x, vilket var det som behövde bevisas.

0 0 — vilket nummer som helst.

Lösning. Låt oss överväga tre huvudfall:

1) x = 0 – detta värde uppfyller inte denna ekvation

2) när x> 0 får vi: x/x= 1, dvs. 1 = 1, vilket betyder

Vad x- vilket nummer som helst; men med hänsyn till det i

i vårat fall x> 0, är ​​svaret x > 0 ;

Regler för att multiplicera potenser med olika baser

EXAMEN MED RATIONELL INDIKATOR,

STRÖMFUNKTION IV

§ 69. Multiplikation och division av potenser med samma grunder

Sats 1. För att multiplicera potenser med samma baser räcker det att addera exponenterna och låta basen vara densamma, dvs.

Bevis. Per definition av examen

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

Vi tittade på produkten av två krafter. Faktum är att den beprövade egenskapen gäller för valfritt antal krafter med samma baser.

Sats 2. För att dela potenser med samma baser, när indexet för utdelningen är större än indexet för divisorn, räcker det att subtrahera divisorns index från indexet för utdelningen och lämna basen densamma, dvs. på t > sid

(a =/= 0)

Bevis. Kom ihåg att kvoten för att dividera ett tal med ett annat är det tal som, multiplicerat med divisorn, ger utdelningen. Bevisa därför formeln var a =/= 0, det är samma sak som att bevisa formeln

Om t > sid , sedan numret t - sid kommer att vara naturligt; därför genom sats 1

Sats 2 är bevisat.

Det bör noteras att formeln

vi har bevisat det endast under antagandet att t > sid . Av det som har bevisats är det därför ännu inte möjligt att dra till exempel följande slutsatser:

Dessutom har vi ännu inte övervägt grader med negativa exponenter och vi vet ännu inte vilken innebörd som kan ges till uttryck 3 - 2 .

Sats 3. För att höja en grad till en potens räcker det att multiplicera exponenterna och lämna gradens bas densamma, det är

Bevis. Med hjälp av definitionen av grad och sats 1 i detta avsnitt får vi:

Q.E.D.

Till exempel, (2 3) 2 = 2 6 = 64;

518 (Oral) Bestäm X från ekvationerna:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;

2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .

519. (Set nr.) Förenkla:

520. (Set nr.) Förenkla:

521. Presentera dessa uttryck i form av grader med samma baser:

1) 32 och 64; 3) 8 5 och 16 3; 5) 4 100 och 32 50;

2) -1000 och 100; 4) -27 och -243; 6) 81 75 8 200 och 3 600 4 150.