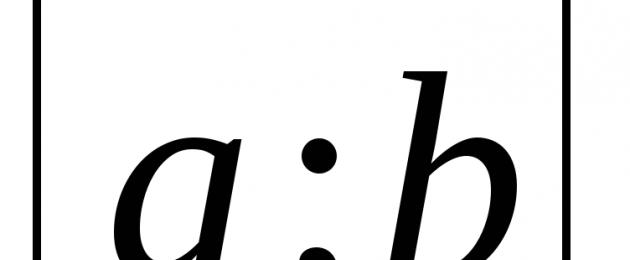В предыдущей главе подробно рассмотрен один из самых распространенных способов приближения функций – интерполирование. Но этот способ не единственный. При решении разнообразных прикладных задач и построении вычислительных схем нередко используют и другие способы. В этой главе мы рассмотрим способы получения среднеквадратических приближений. Название приближений связано с метрическими пространствами, в которых рассматривается задача приближения функции. В главе 1 мы ввели понятия «метрическое линейное нормированное пространство» и «метрическое евклидово пространство» и увидели, что погрешность приближения определяется метрикой пространства, в котором рассматривается задача приближения. В разных пространствах понятие погрешности имеет разный смысл. Рассматривая погрешность интерполяции, мы не акцентировали на этом внимание. А в этой главе нам придется этим вопросом заняться более подробно.

5.1. Приближения тригонометрическими многочленами и многочленами Лежандра Пространство l2

Рассмотрим множество функций , интегрируемых с квадратом по Лебегу на отрезке
, то есть таких, что должен существовать интеграл
.

Поскольку выполняется очевидное неравенство , из интегрируемости с квадратом функций
и
должна следовать и интегрируемость с квадратом любой их линейной комбинации
, (где
и
 любые вещественные числа), а также интегрируемость произведения
.

Введем на множестве функций, интегрируемых с квадратом по Лебегу на отрезке
, операцию скалярного произведения

. (5.1.1)

Из свойств интеграла следует, что введенная операция скалярного произведения обладает почти всеми свойствами скалярного произведения в евклидовом пространстве (см. параграф 1.10, с. 57):

Только первое свойство выполняется не до конца, то есть не будет выполнено условие.

В самом деле, если
, то отсюда не следует, что
на отрезке
. Для того чтобы введенная операция обладала этим свойством, в дальнейшем договоримся не различать (считать эквивалентными) функции
и
, для которых

.

С учетом последнего замечания, мы убедились, что множество интегрируемых с квадратом по Лебегу функций (точнее множество классов эквивалентных функций) образует евклидово пространство, в котором определена операция скалярного произведения по формуле (5.1.1). Это пространство называют пространством Лебега и обозначают
или короче.

Поскольку всякое евклидово пространство автоматически является и нормированным и метрическим, пространство
также является нормированным, и метрическим пространством. Норма (величина элемента) и метрика (расстояние между элементами) в нем обычно вводятся стандартным способом:

(5.1.2)

(5.1.3)

Свойства (аксиомы) нормы и метрики приведены в параграфе 1.10. Элементами пространства
являются не функции, а классы эквивалентных функций. Функции, принадлежащие одному классу, могут иметь разные значения на любом конечном или даже счетном подмножестве
. Поэтому приближения в пространстве
определяются неоднозначно. Эта неприятная особенность пространства
окупается удобствами использования скалярного произведения.

Возьмем полуквадратичную систему координат. Это такая система координат, у которой по оси абсцисс шкала квадратичная, т. е. значения делений откладываются согласно выражению , здесь m – масштаб в каких-либо единицах длины, например, в см.

По оси ординат откладывается линейная шкала в соответствии с выражением

Нанесем на эту систему координат опытные точки. Если точки этого графика располагаются приблизительно по прямой, то это подтверждает наше предположение, что зависимость y от x хорошо выражается функцией вида (4.4). Для отыскания коэффициентов a и b можно теперь применить один из рассмотренных выше способов: способ натянутой нити, способ выбранных точек или способ средней.

Способ натянутой нити применяется также, как и для линейной функции.

Способ выбранных точек можем применить так. На прямолинейном графике возьмем две точки (далекие друг от друга). Координаты этих точек обозначим и (x, y ). Тогда можем записать

Из приведенной системы двух уравнений найдем a и b и подставим их в формулу (4.4) и получим окончательный вид эмпирической формулы.

Можно и не строить прямолинейного графика, а взять числа , (x,y ) прямо из таблицы. Однако полученная при таком выборе точек формула будет менее точна.

Процесс преобразования криволинейного графика в прямолинейный называется выравниванием.

Способ средней . Он применяется аналогично как в случае с линейной зависимостью. Разбиваем опытные точки на две группы с одинаковым (или почти одинаковым) числом точек в каждой группе. Равенство (4.4) перепишем так

Находим сумму невязок для точек первой группы и приравниваем нулю. То же делаем для точек второй группы. Получим два уравнения с неизвестными a и b . Решая систему уравнений, найдем a и b .

Заметим, что при применении этого способа не требуется строить приближающую прямую. Точечный график в полуквадратичной системе координат нужен только для проверки того, что функция вида (4.4) подходит для эмпирической формулы.

Пример. При исследовании влияния температуры на ход хронометра получены следующие результаты:

z	-20	-15,4	-9,0	-5,4	-0,6	+4,8	+9,4
	2,6	2,01	1,34	1,08	0,94	1,06	1,25

При этом нас интересует не сама температура, а ее отклонение от . Поэтому за аргумент примем , где t – температура в градусах Цельсия обычной шкалы.

Нанеся на декартову систему координат соответствующие точки, замечаем, что за приближающую кривую можно принять параболу с осью, параллельной оси ординат (рис.4). Возьмем полуквадратичную систему координат и нанесем на нее опытные точки. Видим, что эти точки достаточно хорошо укладываются на прямой. Значит, эмпирическую формулу

можно искать в виде (4.4).

Определим коэффициенты a и b по методу средней. Для этого разобьем опытные точки на две группы: в первой группе – первые три точки, во второй – остальные четыре точки. Используя равенство (4.5) находим сумму невязок по каждой группе и приравниваем каждую сумму нулю.

Пусть в таблице заданы значения функции, полученные, например, из эксперимента, т. е. измеренные с погрешностью. Тогда приближение с использованием аппарата интерполяции , в основе которого приравнивание значений многочлена в узлах интерполяции табличным значениям, нецелесообразно.

При такой постановке задачи следует выполнить приближение в среднем, т. е. описать таблично заданную функцию некоторой достаточно простой аналитической зависимостью, имеющей небольшое количество параметров. Оптимальный выбор этих параметров и позволит выполнить среднеквадратичное приближение функции, заданной таблицей.

Выбор типа аналитической зависимости следует начинать с нанесения табличных данных на координатную плоскость - так будет сформировано поле экспериментальных точек. Сквозь поле этих точек проводится плавная кривая так, чтобы часть точек легли на эту кривую, часть точек были выше, а часть точек оказались ниже проведённой кривой. По виду этой кривой и следует определить тип аналитической зависимости – линейная ли она, степенная, гиперболическая или какая- либо иная.

Однако по графику на глаз весьма трудно выбрать тип аналитической зависимости. Поэтому был предложен способ ориентировочной оценки и выбора типа аналитической зависимости. Этот способ действительно приблизительный и неточный, так как и кривую можно провести по-разному сквозь поле экспериментальных точек, и в таблице взять разные опорные точки для расчёта да и неизвестна точность предлагаемой методики. Вместе с тем в качестве ориентировочного способа выбора типа зависимости его можно рассмотреть.

Предлагается следующий алгоритм действий.

1. В исходной таблице выбрать две далеко отстоящие друг от друга точки с координатами (x 1 ,y 1) и (x n ,y n) - опорные точки, и для каждой пары координат вычислить среднее арифметическое, среднее геометрическое и среднее гармоническое.

2. На кривой, проведённой через поле экспериментальных точек, найти три ординаты, соответствующие найденным абсциссам x ар,x геом,x гарм:

3. Выполнить сравнение найденных на кривой с вычисленными путём вычисления следующих модулей разностей:

4. Из найденных значений выбирается минимальное:

5. Выводы: если минимальным оказалось

Зависимость линейная

Зависимость показательная

Зависимость дробно-линейная

Зависимость логарифмическая

Зависимость степенная

Зависимость гиперболическая

Зависимость дробно-рациональная

Любую из этих зависимостей можно свести к линейной, выполнив преобразование координат или так называемое выравнивание данных.
Таким образом, первый этап завершается выбором вида аналитической зависимости, параметры которой не определены.

Второй этап состоит в определении наилучших значений коэффициентов выбранной аналитической зависимости. Для этого применяют математический метод наименьших квадратов.

В основе метода – минимизация суммы квадратов отклонений заданных табличных значений () от вычисленных по теоретической зависимости (): .

Пусть выбранная зависимость – прямая линия: . Подставим в функционал : . Тогда минимизируется функционал:

Для нахождения наилучших значений коэффициентов и надо найти частные производные от по и и приравнять их нулю:

После преобразований система уравнений приобретает вид:

Решение этой системы линейных уравнений позволяет найти наилучшие значения коэффициентов и линейной зависимости.

Если выбранной зависимостью является квадратичная парабола:

то минимизируется функционал: .

Парабола имеет три варьируемых коэффициента - , наилучшие значения которых следует найти, приравняв нулю частные производные от минимизируемого функционала по искомым коэффициентам . Это позволяет получить следующую систему трёх линейных уравнений для нахождения коэффициентов :

Пример 1. Определить вид зависимости, заданной следующей таблицей.

X
Y	0,55	0,64	0,78	0,85	0,95	0,98	1,06	1,11

Решение.

На координатную плоскость следует нанести заданные в таблице точки – образуется поле экспериментальных данных. Сквозь это поле проводится гладкая кривая.

По таблице выбираются две опорных точки с координатами (3;0,55) и (10;1,11) и для каждой пары абсцисс и ординат вычисляются среднее арифметическое, геометрическое и гармоническое:

Для трёх вычисленных абсцисс по кривой, проведённой через поле экспериментальных точек, определяются три соответствующих ординаты:

Обратить внимание на ориентировочность проводимых вычислений. Далее определяются семь модулей разности:

Получены три минимальных, близких друг к другу значения

На втором этапе следует для каждой из этих зависимостей определить наилучшие значения коэффициентов, применив метод наименьших квадратов, а затем вычислить среднее квадратичное отклонение от заданных табличных значений.

Окончательный выбор аналитической зависимости выполняют по минимальной величине среднего квадратичного отклонения.

Пример 2. В таблице приведены результаты экспериментальных исследований, которые можно аппроксимировать прямой линией. Найти наилучшие значения коэффициентов прямой, применив метод наименьших квадратов.

Решение.

k	X k	Y k	X k Y k	X k 2	Y k теор	Y k -Y k теор	(Y k -Y k теор) 2
		66,7			67,50	0,20	0,0400
		71,0	284,0		70,98	0,02	0,0004
		76,3	763,0		76,20	0,10	0,0100
		80,6	1209,0		80,55	0,05	0,0025
		85,7	1799,7		85,77	- 0,07	0,0049
		92,9	2694,1		92,73	0,17	0,0289
		99,4	3578,4		98,82	0,58	0,3364
		113,6	5793,6		111,87	1,73	2,9929
		125,1	8506,8		126,66	- 1,56	2,4336
суммы		811,3	24628,6				5,8496

Общее уравнение прямой: .

Система линейных уравнений, из которой следует определять наилучшие значения коэффициентов и , руководствуясь методом наименьших квадратов, имеет вид:

Подставим в систему уравнений вычисленные суммы из 2-го, 3-го, 4-го и 5-го столбцов последней строки таблицы:

Откуда определены коэффициенты линейной зависимости Значит уравнение теоретической прямой имеет вид:

. (*)

В шестом столбце таблицы приведены вычисленные по теоретическому уравнению значений функции для заданных значений аргумента. В седьмом столбце таблицы приведены значения разностей между заданными значениями функции (3-ий столбец) и теоретическими значениями (6-ой столбец), вычисленными по уравнению (*).

В восьмом столбце приведены квадраты отклонений теоретических значений от экспериментальных и определена сумма квадратов отклонений. Теперь можно найти

Пример 3. Пусть данные эксперимента, приведённые в таблице, аппроксимируются квадратичной параболой: Найти наилучшие значения коэффициентов параболы, применив метод наименьших квадратов.

Решение.

k	X k	Y k	X k 2	X k 3	X k 4	X k Y k	X k 2 Y k	Y k теор	Y k -Y k теор
		29,8						29,28	0,52	0,2704
		22,9				45,8	91,6	22,22	0,68	0,4624
		17,1				68,4	273,6	17,60	-0,50	0,2500
		15,1				75,5	377,5	15,56	-0,46	0,2116
		10,7				85,6	684,8	11,53	-0,83	0,6889
		10,1				101,0	1010,0	10,60	-0,50	0,2500
		10,6				127,2	1526,4	11,06	-0,46	0,2116
		15,2				228,0	3420,0	14,38	0,82	0,6724
Сум		122,5				731,5	7383,9			3,0173

Система линейных уравнений для определения коэффициентов параболы имеет вид:

Из последней строки таблицы в систему уравнений подставляют соответствующие суммы:

Решение системы уравнений позволяет определить значения коэффициентов:

Итак, заданная таблицей зависимость на отрезке аппроксимируется квадратичной параболой:

Расчёт по приведённой формуле для заданных значений аргумента позволяет сформировать девятый столбец таблицы, содержащий теоретические значения функции.

Сумма квадратов отклонений теоретических значений от экспериментальных приведена в последней строке 11-го столбца таблицы. Это позволяет определить среднее квадратичное отклонение:

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3

Тема: Методы решения систем уравнений

Метод Гаусса - метод последовательного исключения неизвестных – относится к группе точных методов, и если бы отсутствовала погрешность вычислений, можно было бы получить точное решение.

При ручных расчётах вычисления целесообразно вести в таблице, содержащей столбец контроля. Ниже представлен общий вариант такой таблицы для решения системы линейных уравнений 4-го порядка.

				Свободные члены	Столбец контроля

				Свободные члены	Столбец контроля

Пример 1. Методом Гаусса решить систему уравнений 4-го порядка:

Эти приближённые значения корней можно подставить в исходную систему уравнений и вычислить невязки - , являющиеся разностями между правой и левой частями каждого уравнения системы при подстановке в левую часть найденных корней. Затем подставляются в качестве свободных членов системы невязки и получают поправки

корней - :

Среднеквадратическое приближение функции.

Рассмотрим задачу наилучшего среднеквадратичного приближения функции полиномом
по системе
.

Определение 1.

Обобщенным полиномом порядка m по системе { k } называется линейная комбинация

где C k – произвольные вещественные коэффициенты.

Задача. Найти полином
, наименее уклоняющийся от функции f в метрике L 2 , т.е. удовлетворяющий условию:

Теорема 1.

Если система
линейно независима, то задача наилучшего среднеквадратичного приближения по этой системе однозначно разрешима.

Запишем квадрат расстояния между функцией и полиномом:

(1)

Очевидно, что величина
- неотрицательно определенная квадратичная функция переменных
, а такая функция достигает минимального значения. Таким образом, решение задачи среднеквадратичного приближения существует.

Докажем единственность решения.

Запишем необходимые условия минимума:

, i=0,…,m .

Вычисляя частные производные по c i выражения (1), получим линейную cистему уравнений:

(2)

Система (2) называется нормальной системой .

Выпишем определитель этой системы

(3)

Определитель системы (3) – так называемый определитель Грама системы
. Известно, что если система
- линейно независима, то определитель
0 (легко доказывается от противного). Согласно условию теоремы
0 и система (2) имеет единственное решение.

1.6. Классические ортогональные многочлены и их применение в задачах приближения функций.

Пусть H- гильбертово пространство со скалярным произведением и, соответственно, нормой
. Важным примером такого пространства является так называемое пространство
- пространство функций f(x), для которых конечен интеграл:

(1)

Здесь h(x)- так называемая весовая функция , удовлетворяющая условиям:

Если же =(0,+), то должно выполняться условие:

т.е. должны существовать любые моменты весовой функции.

Определение 1.

Для
определено скалярное произведение:

(2)

и соответственно норма:

согласно условию (1).

Используя неравенство Коши – Буняковского - Шварца, получаем

Поэтому скалярное произведение существует для

Определение 2.

Расстояние между элементами f и g определяется равенством:

.

Возникает вопрос о том, как понимать нулевой элемент. Если норма
, следует ли отсюда, что f=g? Вводится терминология: f=g почти всюду, то есть они могут отличаться в конечном числе точек.

Определение 3.

f и g ортогональны на отрезке с весом h(x), если =0 (кратко пишут
).

Если в гильбертовом пространстве взять любую линейно независимую систему
, i=0,1,2,…, то ее можно ортогонализировать.

Рассмотрим в качестве примера систему:
При
конечный набор степенных функций линейно независим, поэтому на базе этой системы можно построить ортогональные полиномы. Известна следующая рекуррентная процедура ортогонализации (процедура Грама - Шмидта):

(3)

Коэффициенты b k+1,j определяются из условий ортогональности:

Последовательно умножая (3) на
получаем

(4)

Пример 1.

Пусть h(x)1, =[-1,1].

Построить первые три ортогональных полинома по процедуре (3) - (4).

Далее имеем:

следовательно,

Для системы ортогональных многочленов на отрезке [-1,1] с весом h(x)=1 справедлива формула Родрига:

(5)

Из (5) последовательно получаем:

Получаемые таким образом полиномы называются полиномами Лежандра.

Замечание.

Найденные по процедуре (3) – (4) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по явной формуле Родрига (5).

Квадрат нормы у этих полиномов равен:

То есть эти многочлены не нормированы, так как

Для всех классических многочленов существует рекуррентная формула. Для полиномов Лежандра она имеет следующий вид:

Пусть
Рассмотрим среднеквадратичное приближение:

где
- среднеквадратичная ошибка аппроксимации,

- отрезок ряда Фурье для функции f(x) по системе ортогональных многочленов {P k (x)}.

В силу ортогональности многочленов Лежандра, система нормальных уравнений (2) из §1.5 становится диагональной, и ее решение приводит к следующим выражениям для коэффициентов c k:

(7)

то есть обеспечивается минимум нормы в L 2 .

Распишем подробно ошибку аппроксимации

С другой стороны

в силу ортогональности.

Подставляя в (8), получим

. (9)

Пример 2.

Пусть f(x)=|x|.

Аппроксимировать f(x) на [-1,1] в среднеквадратичном многочленом второй степени. Вычислить среднеквадратичную ошибку.

Используем ортогональную систему Лежандра:

Коэффициенты c k находим по формуле (7), учитывая вид полиномов Лежандра:

1.7. Некоторые общие свойства ортогональных полиномов.

Многочлен P n (x) ортогонален любому алгебраическому многочлену m-ой степени M m (x) при m

M m (x) можно единственным образом представить в виде линейной комбинации многочленов Лежандра:

Равенство (10) тождественное, поэтому коэффициенты a k единственным образом вычисляются путем приравнивания коэффициентов при старших степенях. Умножая обе части (10) на P n (x), имеем

в силу ортогональности системы

Полином P n (x) имеет на отрезке [-1,1] ровно n действительных и различных корней.

Заметим, что в силу теоремы Гаусса многочлен P n (x) не может иметь более чем n корней (вообще говоря, комплексных). Пусть P n (x) имеет меньше, чем n простых действительных корней. Обозначим их
По этим точкам построим фундаментальный многочлен

Рассмотрим многочлен:
- многочлен степени (k+n), который имеет нули
четной кратности. Значит, новый многочлен
сохраняет знак при переходе через эти нули, т.е. сохраняет знак на [-1,1]. Отсюда следует, что

Но это противоречит свойству 1, так как P n (x) обязательно должен быть ортогонален M k (x).

Между двумя соседними нулями многочлена P n (x) лежит ровно один нуль многочлена P n-1 (x).

Доказывается по индукции с помощью рекуррентного соотношения (6).

При n- четном многочлен P n (x) – четная функция от x, при n- нечетном, P n (x) – нечетная функция от x.

Наряду с многочленами Лежандра классическими ортогональными многочленами называют следующие системы многочленов (далее (a,b) – промежуток ортогональности, r(x) – весовая функция).

1) Многочлены Якоби {Р п (l ,m) (х )} - при а = -1, b = 1 r(х ) = (1-х ) l (1 + x ) m , l > -1, m > -1. Специальные частные случаи многочленов Якоби соответствуют следующим значениям l и m: l = m- ультрасферические многочлены (их иногда называют многочленами Гегенбауэра); l = m = - 1 / 2 , т. е. -многочлены Чебышева 1-го рода T n (x ); l = m = 1 / 2 , т. е. - многочлены Чебышева 2-го рода U n (x );

2) Многочлены Лагерра L n (x ) - при а = 0, b = + ∞ и r(х ) = е -х (их наз. также многочленами Чебышева - Лагерра) и обобщённые многочлены Лагерра - при . 3) М ногочлены Эрмита Н n (х ) - при а = -∞, b = + ∞ и (их называют также многочленами Чебышева - Эрмита).

Часто значения интерполируемой функции у, у 2 , ..., у„ определяются из эксперимента с некоторыми ошибками, поэтому пользоваться точным приближением в узлах интерполяции неразумно. В этом случае более естественно приближать функцию не по точкам, а в среднем, т. е. в одной из норм L p .

Пространство 1 р - множество функций д(х), определенных на отрезке [а,Ь] и интегрируемых по модулю с р-й степенью, если определена норма

Сходимость в такой норме называется сходимостью в среднем. Пространство 1,2 называется гильбертовым, а сходимость в нем - среднеквадратичной.

Пусть заданы функция Дх) и множество функций ф(х) из некоторого линейного нормированного пространства. В контексте проблемы интерполирования, аппроксимации и приближения можно сформулировать следующие две задачи.

Первая задача - это аппроксимация с заданной точностью, т. е. по заданному е найти такую ф(х), чтобы выполнялось неравенство |[Дх) - ф(х)|| г..

Вторая задача - это поиск наилучшего приближения, т. е. поиск такой функции ф*(х), которая удовлетворяет соотношению:

Определим без доказательства достаточное условие существования наи- лучшего приближения. Для этого в линейном пространстве функций выберем множество, параметризованное выражением

где набор функций ф[(х), ..., ф„(х) будем считать линейно независимым.

Можно показать , что в любом нормированном пространстве при линейной аппроксимации (2.16) наилучшее приближение существует, хотя нс во всяком линейном пространстве оно единственно.

Рассмотрим гильбертово пространство ЬгСр) действительных функций, интегрируемых с квадратом с весом р(х) > 0 на [ , где скалярное произведение (g,h ) определено по

формуле:

Подставляя в условие наилучшего приближения линейную комбинацию (2.16), находим

Приравнивая к нулю производные по коэффициентам (Д, k = 1, ..., П, получим систему линейных уравнений

Определитель системы уравнений (2.17) называется определителем Гра- ма. Определитель Грама отличен от нуля, поскольку считается, что система функций ф[(х), ..., ф„(х) линейно независима.

Таким образом, наилучшее приближение существует и единственно. Для его получения необходимо решить систему уравнений (2.17). Если система функций ф1(х), ..., ф„(х) ортогонализирована, т. е. (ф/,ф,) = 5у, где 5, = 1, 8у = О, Щ, ij = 1, ..., п, то система уравнений может быть решена в виде:

Найденные согласно (2.18) коэффициенты Q, ..., й п называются коэффициентами обобщенного ряда Фурье.

Если набор функций ф t (X), ..., ф„(х),... образует полную систему, то в силу равенства Парсеваля при П -» со норма погрешности неограниченно убывает. Это означает, что наилучшсс приближение среднеквадратично сходится к Дх) с любой заданной точностью.

Отметим, что поиск коэффициентов наилучшего приближения с помощью решения системы уравнений (2.17) практически нсреализуем, поскольку с ростом порядка матрицы Грама ее определитель быстро стремится к нулю, и матрица становится плохо обусловленной. Решение системы линейных уравнений с такой матрицей приведет к значительной потере точности. Проверим это.

Пусть в качестве системы функций ф„ i =1, ..., П, выбираются степени, т. е. ф* = X 1 ", 1 = 1, ..., п, тогда, полагая в качестве отрезка аппроксимации отрезок , находим матрицу Грама

Матрицу Грама вида (2.19) называют еще матрицей Гильберта. Это классический пример так называемой плохо обусловленной матрицы.

С помощью MATLAB рассчитаем определитель матрицы Гильберта в форме (2.19) для некоторых первых значений п. В листинге 2.5 приведен код соответствующей программы.

Листинг 23

%Вычисление определителя матриц Гильберта %очищаем рабочую область clear all;

%выберем максимальное значение порядка %матрицы Гильберта птах =6;

%строим цикл для формирования матриц %Гильберта и вычисления их определителей

for n = 1: птах d(n)=det(hi I b(п)); end

%выводим значения определителей %матриц Гильберта

f о г та t short end

После отработки кода листинга 2.5, в командном окне MATLAB должны появиться значения детерминантов матриц Гильберта для первых шести матриц. В таблице ниже приведены соответствующие численные значения порядков матриц (п) и их определителей (d). Из таблицы отчетливо видно, сколь быстро определитель матрицы Гильберта стремится к нулю при росте порядка и, уже начиная с порядков 5, 6, становится неприемлемо малым.

Таблица значений определителя матриц Гильберта

Численная ортогонализация системы функций ф, i = 1, ..., П также приводит к заметной потере точности, поэтому чтобы учитывать большое число членов в разложении (2.16), необходимо либо проводить ортогонализацию аналитически, т. е. точно, либо пользоваться уже готовой системой ортогональных функций.

Если при интерполяции обычно используют в качестве системы базисных функций степени, то при аппроксимации в среднем в качестве базисных функций выбирают многочлены, ортогональные с заданным весом. Наиболее употребительными из них являются многочлены Якоби, частным случаем которых являются многочлены Лежандра и Чебышева. Используют также полиномы Лагсрра и Эрмита. Более подробно об этих полиномах можно узнать, например, в приложении Ортогональные полиномы книги .