1. Построение отрезка равного данному
Изобразим фигуры, данные в условии: луч ОС и отрезок АВ .
Построение:
Построим окружность радиуса АВ с центром в точке О .
Окружность пересечет луч ОС в некоторой точке D .
Отрезок ОD – искомый.
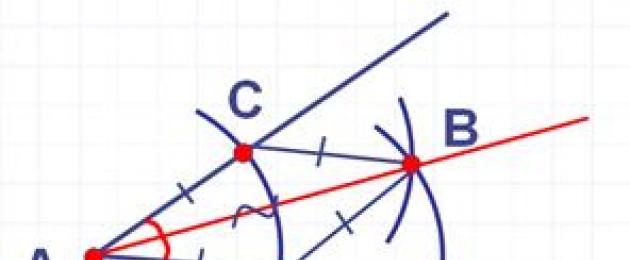
2. Построение угла равного данному
Построить:
Доказательство:
рассмотрим ΔАВС и ΔОDE.
1. АС=ОЕ, как радиусы одной окружности.
2. АВ=ОD, как радиусы одной окружности.
3. ВС=DE, как радиусы одной окружности.
ΔАВС = ΔОDЕ (по трем сторонам) А = О
Построение:
1. Построить произвольный луч.
2. Построить две равные окружности произвольного радиуса и окружность с центрами в начале луча и в вершине данного угла.
3. Найти и обозначить точки пересечения окружностей с лучом и со сторонами угла.
4. Построить окружность с центром в точке пересечения луча и окружности и радиусом, равным расстоянию между точками, построенными на сторонах угла.
5. Найти и обозначить точку пересечения окружностей.
6. Провести новый луч из начала луча через построенную точку пересечения окружностей.
7. Угол, образованный двумя построенными лучами, - искомый.
3. Построение биссектрисы угла
 Дано:
Дано:
Построить:
АВ - биссектриса
Доказательство:
Рассмотрим ∆АСВ и ∆ АDВ
1. АС=АD, как радиусы одной окружности.
2. СВ=DB, как радиусы одной окружности.
3. АВ – общая сторона.
![]() ∆АСВ = ∆ АDВ (по трем сторонам) луч АВ – биссектриса.
∆АСВ = ∆ АDВ (по трем сторонам) луч АВ – биссектриса.
Построение:
1. Построить окружность произвольного радиусас центром в вершине угла.
2. Найти и обозначить точки пересечения окружности со сторонами угла.
3. Построить окружности с центрами в построенных точках и тем же радиусом.
4. Найти иобозначить точку пересечения окружностей.
5. Провести луч с началом в вершине угла через точку пересечения окружностей, - искомая биссектриса угла.
4. Построение перпендикулярных прямых
Случай
 Дано:
Дано:
Построить:
Доказательство:
1.АМ=МВ, как радиусы одной окружности.
2. АР=РВ, как радиусы одной окружности ∆АРВ р/б
3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.
Случай
 Дано:
Дано:
Построить:
Доказательство:
АМ=АN=MB=BN, как равные радиусы.
МN-общая сторона.
∆MВN= ∆MAN (по трем сторонам)
В р/б ∆АМВ отрезок МС является биссектрисой, а значит, и высотой.
Построение:
1. Построить окружность с центром в данной точке и радиусом больше расстояния от данной точки до прямой.
2. Найти и обозначить точки пересечения окружности с прямой.
3. Построить две равные окружности с центрами в построенных на прямой точках радиусом равным длине отрезка.
4. Найти и обозначить точку пересечения окружностей.
5. Провести прямую через данную точку, не лежащую на прямой и точку пересечения окружностей, - искомая прямая.
5.Построение середины отрезка
 Дано:
Дано:
Построить:
О – середина отрезка АВ.
Доказательство:
∆АРQ = ∆ BPQ (по трем сторонам) .
∆ АРВ р/б.
Отрезок РО является биссектрисой, а значит, и медианой.
Тогда, точка О – середина АВ.
Построение:
1. Построить две равные окружности с центрами в концах отрезка и радиусом равным АВ .
2. Обозначить точки пересечения окружностей.
3. Провести прямую через точки пересечения окружностей.
4. Обозначить точку пересечения прямой и отрезка, - искомая точка.
Путивская Юлия
Задача построения середины отрезка, заданного своими концами, с помощью различных инструментов
Скачать:
Предварительный просмотр:
ЗАДАЧА ПОСТРОЕНИЯ СЕРЕДИНЫ ОТРЕЗКА, ЗАДАННОГО СВОИМИ КОНЦАМИ, С ПОМОЩЬЮ РАЗЛИЧНЫХ ИНСТРУМЕНТОВ
Путивская Юлия Олеговна,
ученица 9 класса МОУ «Зинаидинская
основная общеобразовательная школа»
Первые задачи на построение возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древним архитекторам и землемерам приходилось решать простейшие задачи на построение, связанные с их профессией. Решения простейших геометрических задач на построение, которые помогали людям в их хозяйственной жизни, формулировались в виде «практических правил», исходя из наглядных соображений. Именно эти задачи и были основой возникновения наглядной геометрии, нашедшей довольно широкое развитие у древних народов Египта, Вавилона, Индии и др. Геометрические построения привлекли внимание древнегреческих математиков ещё в VI-V вв. до нашей эры. Первым греческим ученым, который занимался решением геометрических задач на построение, был Фалес Милетский (624-547 гг. до н. э.). Ими занимались почти все крупные греческие геометры: Пифагор (VI в. до н. э.) и его ученики, Гиппократ (V в. до н. э.), Евклид, Архимед, Аполлоний (III век до н. э.), Папп (III в. н. э.) и многие другие.
Математики из школы Пифагора уже сумели справиться с такой сравнительно сложной задачей, как построение правильного пятиугольника. В V в. до н. э. возникли знаменитые классические задачи о квадратуре круга, об удвоении куба, о трисекции угла (см. гл. VII). Эти задачи, которые, как оказалось впоследствии, не разрешимы с помощью циркуля и линейки, в течение многих веков вызывали живейший интерес различных исследователей. В IV в. до н. э. греческие мыслители разработали ту общую схему решения геометрической задачи на построение (анализ - построение-доказательство- исследование), которой мы пользуемся и поныне.
Вся история геометрии и некоторых других разделов математики тесно связана с развитием теории геометрических построений. Важнейшие аксиомы геометрии, сформулированные основоположником научной геометрической системы Евклидом около 300г. до н. э., ясно показывают, какую роль сыграли геометрические построения в формировании геометрии. «От всякой точки до всякой точки можно провести прямую линию», «Ограниченную прямую можно непрерывно продолжать», «Из всякого центра и всяким раствором может быть описан круг»-эти постулаты Евклида явно указывают на основное положение конструктивных методов в геометрии древних.
Изучая геометрию в 7 классе, я познакомилась с решением задач на построение с помощью циркуля и линейки. Передо мной возник вопрос: «А возможно ли выполнить решение этих простейших задач с помощью каких-либо других инструментов, и существуют ли они?» Обратившись с этим вопросом к учителю математики, я получила взамен следующую книгу: Геометрические построения на плоскости, Б.И. Аргунов и М.Б.Балк – Учпедгиз, 1955.
Прочитав многие её главы, я узнала, что наиболее употребляемыми инструментами геометрических построений являются: линейка (односторонняя), циркуль, двусторонняя линейка (с параллельными краями), прямой угол и некоторые другие.
Для конструктивной геометрии необходимо располагать точным и для математических целей полным описанием того или иного инструмента. Такое описание даётся в форме аксиом. Эти аксиомы в абстрактной математической форме выражают те свойства реальных чертёжных инструментов, которые используются для геометрических построений.
Сформулирую соответствующие аксиомы.
Аксиома линейки.
Линейка позволяет выполнить следующие геометрические построения:
а) построить отрезок, соединяющий две построенные точки;
б) построить прямую, проходящую через две построенные точки;
в) построить луч, исходящий из построенной точки и проходящий через другую построенную точку.
Аксиома циркуля.
Циркуль позволяет выполнить следующие геометрические построения:
а) построить окружность, если построены центр окружности и концы отрезка, равного радиусу окружности;
б) построить любую из двух дополнительных дуг окружности, если построен центр окружности и концы дуги.
Аксиома двусторонней линейки.
Двусторонняя линейка позволяет:
а) выполнить любое из построений, перечисленных в аксиоме линейки;
б) в каждой из полуплоскостей, определяемых построенной прямой, построить прямую, параллельную данной прямой и проходящую от неё на расстоянии
h,
где
h
- фиксированный для данной линейки отрезок
(ширина линейки);
в) если построены две точки А и В , то установить, будет ли АВ больше некоторого фиксированного отрезка (ширина линейки), и если AB >h, то построить две пары параллельных прямых, проходящих соответственно через точки А и В и отстоящих одна от другой на расстоянии h.
Аксиома прямого угла.
Прямой угол позволяет выполнить следующие геометрические построения:
а) все построения, выполнимые односторонней линейкой;
б) через данную точку плоскости провести прямую, перпендикулярную некоторой построенной прямой;
в) если построены отрезок АВ и некоторая фигура Ф, то установить, содержит ли фигура Ф точку, из которой отрезок виден под прямым углом, и если такая точка существует, то построить такую точку.
Задача на построение состоит в том, что требуется построить наперёд указанными инструментами некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.
Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.
Найти решение задачи на построение - значит свести её к конечному числу основных построений, т. е. указать конечную последовательность основных построений, после выполнения, которых искомая фигура будет уже считаться построенной в силу принятых аксиом конструктивной геометрии. Перечень допустимых основных построений, а, следовательно, и ход решения задачи существенно зависит от того, какие именно инструменты употребляются для построений.
В качестве примера рассмотрю следующую задачу:
Построить середину отрезка, заданного своими концами А и В.
Найдём решение этой задачи с помощью различных инструментов.
1. Циркулем и линейкой
(построение изучается в 7 классе, п.23 Примеры задач на построение)
Пусть АВ - данный отрезок. Построим две окружности с центрами А и В радиуса АВ (). Они пересекаются в точках Р и Q. Проведем прямую PQ. Точка О пересечения этой прямой с отрезком АВ и есть искомая середина отрезка АВ.
В самом деле, треугольники APQ и BPQ равны по трем сторонам, поэтому 1 = 2 ().
Следовательно, отрезок РО - биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. е. точка О - середина отрезка АВ.
2. Циркулем (рисунок ниже описания)
Строим последовательно:
- окружность с центром В радиусом ВА;
- окружность с центром А радиусом АВ;
- общую точку С - точку пересечения окружностей с центром В радиусом ВА и с центром А радиусом АВ;
- окружность с центром С радиусом СА;
- общую точку D - точку пересечения окружностей с центром В радиусом ВА и с центром А радиусом АC, отличную от точки А;
- окружность с центром D радиусом DB;
7) общую точку Е - точку пересечения окружностей с центром В радиусом ВА и с центром D радиусом DB, отличную от точки C;
Заметим, что точки А, В и Е расположены на одной прямой, причём АЕ = 2АВ. Строим далее:
8) окружность с центром Е радиусом ЕА;
9) окружность с центром А радиусом АВ пересекает окружность с центром Е радиусом ЕА в точках M и N
10) окружность с центром M радиусом MA;
11) окружность с центром N радиусом NA;
12) общую точку X - точку пересечения окружностей с центром M радиусом MА и с центром N радиусом NA, отличную от А.
Нетрудно усмотреть, что точка X расположена на прямой.
Кроме того, треугольник АМХ подобен треугольнику АЕМ , так как они равнобедренные и имеют общий угол МАЕ при основании. Поэтому АХ: AM = АМ:АЕ или АХ: АВ = АВ: 2АВ , так что
АХ = АВ и, значит, точка X искомая.
3. Двусторонней линейкой (рисунок ниже описания).
Строим последовательно:
1) прямую АВ;
2) прямую а , параллельную АВ и проходящую на расстоянии h от неё
(h - ширина линейки);
3) прямую b , параллельную а , отстоящую от неё на расстоянии h и отличную от прямой АВ;
4) точку С на прямой b;
5) прямые АС и ВС;
6) точки D – точку пересечения прямых а и АC и Е – точку пересечения прямых а и ВС;
7) прямые АЕ и BD;
8) точку Р – точку пересечения прямых АЕ и ВD;
9) Прямую СР;
10) точку Х - точку пересечения прямых СР и АВ .
Так как DE - средняя линия треугольника АСВ , то АЕ и BD - его медианы, а следовательно, и СР - медиана, так что точка X искомая.
4. Прямым углом (рисунок ниже описания)
1) Строим прямую АВ;
2) проводим прямые АА"
и ВВ", перпендикулярные
прямой АВ;
3) выбираем на АА" произвольную точку С, отличную от А;
4) через точку С
проводим СС"
АС
.
Далее строим последовательно:
5) точку D - точку пересечения прямых CC " и BB" ;
6) прямые AD и ВС;
7) точку P - точку пересечения прямых AD и BC;
Точка X искомая.
Таким образом, рассмотрены различные способы решения одной и той же задачи на построение, с использованием различных инструментов.
Линейка. Наиболее простой и точный метод определения середины отрезка - это измерить его длину с помощью линейки, а затем разделить получившееся значение пополам. В результате можно легко и быстро найти искомый центр с точностью до миллиметра. Однако, помимо такого очевидного метода существует еще один способ того, как построить середину отрезка. Тем не менее без линейки все равно не обойтись. Линейка поможет не только правильно, при необходимости, рассчитать расстояние, но и идеально ровно провести прямую или начертить отрезок, что является необходимым условием любого построения.
Карандаш. В случае построения середины отрезка карандаш вещь действительно незаменимая. Хорошо заточенный он всегда должен быть под рукой если дело касается черчения геометрических фигур линий или отрезков. Сегодня существует большой выбор карандашей любого качества и назначения. Так, для рисования больше подойдет мягкий или твердо-мягкий карандаш, а вот если речь идет о построении, то предпочтение лучше отдать твердому. Удобно, если на конце карандаша имеется хороший ластик.
Циркуль. Для того, что бы именно построить, а не рассчитать или отмерить середину отрезка, необходим циркуль. Вообще подобные знания могут понадобиться не только школьнику, но и, например, студенту при изучении основ начертательной геометрии или инженерной графики. Помимо всего прочего умение отыскать середину может помочь и в ответе на вопрос: как найти середину треугольника. Итак, для построения ставим иглу циркуля на один конец отрезка и отчерчиваем круг, длина диаметра которого равна длине отрезка. Далее, ставим иглу циркуля на второй конец отрезка и делаем такую же окружность.
В результате таких действий мы получаем два одинаковых круга, наложенных друг на друга и пересеченных в двух местах. Отрезок же проходит в центре окружностей и является их радиусом. С помощью линейки проводим прямую через две точки пересечения двух окружностей. В результате чего получаем середину отрезка.Если отрезок находиться в системе координат и возникает вопрос, как найти координаты середины отрезка, действия совершенно идентичные. Так же отчерчиваем два круга или полукруга и, проведя прямую через точки пересечения окружностей или их половин, находим середину отрезка.
После чего строим перпендикуляр от центра отрезка относительно осей координат и получаем координаты. Как правило, такой перпендикуляр наносится пунктиром с помощью линейки и имеет нечеткие очертания.Таким образом, известно не только как найти середину отрезка, но и как вычислить его координаты.Подобные знания могут пригодиться при выполнении различных задач во время учебы в школе, колледже или институте, а также в повседневной жизни, когда обычные способы не пригодны.
Порядок построения следующий (рис.2.2):
1. Из концов отрезка АВ проводят дуги радиусом R, величиной большей, чем половина отрезка.
2. Точки пересечения дуг соединяют прямой линией СD.
Линия CD является перпендикуляром к отрезку АВ, точка О – середина отрезка.
Деление отрезка
Деление отрезка на любое число равных частей
Деление отрезка на 6 равных частей показано на рис. 2.3.
1. Из любого конца отрезка АВ, например, из точки А, проводим луч под острым углом к отрезку.
2. На луче от точки А циркулем откладываем 6 равных отрезков произвольной длины.
3. Конец последнего отрезка, точку 6, соединяем с точкой В.
4. Из всех точек на луче проводим прямые, параллельные 6В, до пересечения с АВ.
Эти прямые разделяют отрезок АВ на шесть равных частей.
Рис.2.3 Рис.2.4
Деление окружности на пять равных частей
(Построение правильного пятиугольника, вписанного в окружность)
Построения показаны на рисунке 2.4.
Из точки С – середины радиуса окружности, как из центра, дугой радиуса СD сделать засечку на диаметре, получим точку М. Отрезок DМ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DМ засечки на окружности, получим точки деления окружности на пять равных частей (вершины вписанного правильного пятиугольника).
Деление окружности на шесть равных частей
(Построение правильного шестиугольника, вписанного в окружность)
Построения показаны на рисунке 2.5.
Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности.
Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

Рис.2.5 Рис.2.6
Определение центра дуги окружности
Построения показаны на рисунке 2.6.
1. Назначить на дуге три произвольные точки А, В и С.
2. Соединить точки прямыми линиями.
3. Через середины полученных хорд АВ и ВС провести перпендикуляры.
Точка О пересечения перпендикуляров является центром дуги.
Сопряжения
Сопряжением называется плавный переход от одной линии к другой.
Роль плавных переходов в очертаниях различных изделий техники огромна. Их обуславливают требования прочности, гидроаэродинамики, промышленной эстетики, технологии. Чаще всего сопряжения осуществляют с помощью дуги окружности.
Из всего многообразия сопряжений различных линий рассмотрим наиболее распространенные:
1. Сопряжение двух прямых линий.
2. Сопряжение прямой линии и окружности.
3. Сопряжение двух окружностей.
Дуги окружностей, при помощи которых выполняется сопряжение, называют дугами сопряжения.
Алгоритм построения
1. Найти центр сопряжения;
2. Найти точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии.
3. Построить дуги сопряжения, значит соединить точки сопряжения заданным радиусом сопряжения.
Сопряжение пересекающихся прямых линий при помощи дуги заданного радиуса.
Пример1 . Сопряжение двух взаимно перпендикулярных прямых а и b дугой заданного радиуса R.
Даны две взаимно перпендикулярные прямые а и b . Задан радиус сопряжения R. (рис.2.7а)
Алгоритм построения
1. Находим центр сопряжения.
Проводим две прямые, параллельные а и b , на расстоянии, равном радиусу R . Эти прямые являются геометрическим местом центров окружностей радиуса R , касательных к данным прямым (рис.2.7б);
Окружность
Окружность - геометрическая фигура, состоящая из всех точек плоскости, которые находятся в заданном расстоянии от данной точки.
Эту точку называют центром окружности, а заданное расстояние - радиусом окружности.
Радиус - это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов и они все имеют одинаковую длину.
Отрезок, который соединяет две точки на окружности, называют хордой .
Если хорда проходит через центр окружности, то её называют диаметром окружности.
Диаметр - самая длинная хорда.
В окружности также можно провести бесконечное количество диаметров.
Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой .
Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.
В рисунке выше можем назвать: дуга \(BDH\), дуга \(ACG\) и другие.
В рисунке ниже нарисованы: дуга \(AxB\) и дуга\(AyB\).
Часть плоскости ограниченная окружностью называется кругом .
Задачи на построение
В задачах, где необходимо выполнить конструкции, используются циркуль и линейка .
Очень важно запомнить, что в этих задачах линейка не используется как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.
Рассмотрим пять основных построений, в которых используем упомянутые действия - построение прямой линии и окружности:
1. На данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
1. На данном луче от его начала отложить отрезок, равный данному
.
См. видео.
Ясно, что таким образом мы получили отрезок, равный с данным. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некой точки (центра окружности).
Если центром служит начальная точка луча \(C\), радиусом - данный отрезок \(AB\), то точка пересечения окружности и луча \(D\) и есть искомая конечная точка отрезка \(CD\), равного с данным отрезком \(AB\).
2. Построение угла, равного данному .
См. видео.
Докажем, что построенный угол \(ECD\) и есть тот искомый угол, равный с данным углом \(AOB\).
Если мы построили окружность с центром \(C\) - начальной точкой луча и таким же радиусом как у окружности с центром \(O\), то\(CD\)\(=\)\(OB\).
Провели луч \(CE\). Очевидно \(OA\)\(=\)\(CE\).
Значит треугольники \(AOB\) и \(ECD\) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол \(ECD\) равен с углом \(AOB\).
3. Построение биссектрисы угла .
См. видео.
Чтобы доказать, что \(OC\) действительно делит угол \(AOB\) пополам, достаточно рассмотреть треугольники \(AOC\) и \(BOC\).