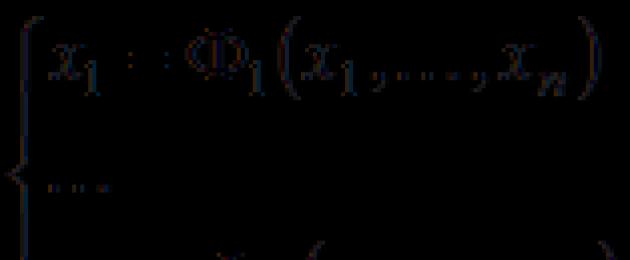The system of nonlinear equations has the form:
Here are unknown variables, and system (7) is called a normal order system if at least one of the functions is nonlinear.
Solving systems of nonlinear equations is one of the difficult problems of computational mathematics. The difficulty is to determine whether the system has a solution, and, if so, how many. Refining solutions in a given area is a simpler task.
Let the functions be defined in areas. Then the area will be the area where a solution can be found. The most common methods for refining the solution are the simple iteration method and Newton's method.
Simple iteration method for solving systems of nonlinear equations
From the original system (7), through equivalent transformations, we move to a system of the form:

Iterative process defined by the formulas

you can start by specifying an initial approximation. A sufficient condition for the convergence of the iterative process is one of two conditions:


Let's write down the first condition:


Let's write down the second condition:


Let us consider one of the ways to reduce system (7) to form (8), allowing convergent iterations.
Let a second-order system of the form:

You need to bring it to this form:

Let's multiply the first equation of the system by an unknown constant, the second by an unknown constant, then add them and add them to both sides of the equation. We obtain the first equation of the transformed system
We determine the unknown constants from sufficient conditions convergence


Let's write these conditions in more detail:

Assuming that the expressions under the modulus sign are equal to zero, we obtain a system of four equations with four unknowns for determining the constants:


With this choice of parameters, the convergence conditions will be met if the partial derivatives of the functions and do not change very quickly in the vicinity of the point.
To solve the system, you need to specify an initial guess and calculate the values of the derivatives and at this point. The calculation is carried out at each iteration step, while
The method of simple iterations is self-correcting, universal and easy to implement on a computer. If the system has a large order, then the application this method, which has a slow convergence rate, is not recommended. In this case, Newton's method is used, which has faster convergence.
Newton's method for solving systems of nonlinear equations
Let it be necessary to solve a system of nonlinear equations of the form (7). Let us assume that the solution exists in some domain in which all functions are continuous and have, according to at least, the first derivative. Newton's method is an iterative process that is carried out according to a certain formula of the following form:

Difficulties in using Newton's method:
is there an inverse matrix?
Doesn't it go beyond the region?
Modified Newton's method makes the first task easier. The modification is that the matrix is not calculated at each point, but only at the initial one. Thus, the modified Newton's method has the following formula:
But the modified Newton method does not answer the second question.
The iterative process according to formulas (8) or (10) ends if the following condition is met
The advantage of Newton's method is its rapid convergence compared to the simple iteration method.
Calculation formula Newton's method has the form:
Where n=0,1,2,..
Geometrically Newton's method means that the next approach to the root is the point of intersection with the OX axis. tangent to the graph of the function y=f(x) at point .
Theorem on the convergence of Newton's method.
Let be a simple root of an equation in some neighborhood of which the function is twice continuously differentiable.
Then there is such a small neighborhood of the root that, with an arbitrary choice of initial approximation from this neighborhood, the iterative sequence of Newton’s method does not go beyond the neighborhood and the estimate is valid
Newton's method(1) sensitive to the choice of initial approximation x 0 .
In practice, for monotonic convergence of the method it is necessary:
1st derivative f(x)
2nd derivative f(x) must be of constant sign on the localization interval [a, b] of the isolated root;
for the initial approach x 0 the boundary of the localization interval is selected at which the product of the function by its 2nd derivative is greater than zero (f(c)f ’’ (c) > 0, where c is one of the boundaries of the interval).
. For a given accuracy >
As indicated in the theorem, Newton’s method has local convergence, that is, the region of its convergence is a small neighborhood of the root .
A poor choice may result in a divergent iteration sequence.
Simple iteration method (method of successive repetitions).
To apply the simple iteration method, the initial equation follows convert to a form convenient for iteration .
This conversion can be done in various ways.
The function is called an iterative function.
The calculation formula for the simple iteration method is:
Where n=0,1,2,..
Theorem on the convergence of the simple iteration method.
Let the function be continuously differentiable in some neighborhood of the root and satisfy the inequality
Where 0 < q < 1 - constant.
Then, regardless of the choice of the initial approximation from the specified neighborhood, the iteration sequence does not leave this neighborhood, the method converges
with the speed of the geometric sequence and the error estimate is valid :
Criterion for ending the iterative process .
For a given accuracy >0, calculations should be carried out until the inequality is satisfied
If the value is , then a simpler criterion for ending iterations can be used:
If in inequality (5) q > 1, then the iterative method (4) diverges.
If in inequality (5) q= 1 , then the iterative method (4) can either converge or diverge.
In case if q > = 1 , then the iterative method (4) diverges and
applies simple iteration method with iteration parameter.
The key point in application is to equivalently transform the equation:
αf(x) = 0
x = x+αf(x), (9)
Where α – iteration parameter (real constant).
Calculation formula simple iteration method with iteration parameter has the form:
x (n+1) = x (n) + αf(x (n) ) , (10)
Where n=0,1,2,..
The iterative process built according to the form (10) converges, If:
1st derivative of a function f(x) is constant in sign and limited over the localization interval of an isolated root;
sign of iterative parameter α opposite sign of the 1st derivative of the function f(x) on the localization interval of an isolated root;
iterative parameter value modulus α is estimated from the inequality
| α | < 2/M , (11)
where M is the maximum modulus of the 1st derivative of the function f(x)
Then, with such a choice of the iteration parameter , method (10) converges for any value of the initial approximation belonging to the interval at the rate of geometric progression with a denominator q equal to
where m is the minimum modulus of the 1st derivative of the function f(x) on the localization interval of an isolated root.
MINISTRY OF EDUCATION AND SCIENCE OF UKRAINE
SUMY STATE UNIVERSITY
Department of Computer Science
COURSE WORK
BY COURSE:
“Iterative methods for solving systems of nonlinear equations”
1. Methods for solving systems of nonlinear equations. general information
2.1 Simple iteration method
2.2 Aitken transformation
2.3 Newton's method
2.3.1 Modifications of Newton's method
2.3.2 Quasi-Newton methods
2.4 Other iterative methods for solving systems of nonlinear equations
2.4.1 Picard method
2.4.2 Gradient descent method
2.4.3 Relaxation method
3. Implementation of iterative methods programmatically and using the Maple mathematical package
3.1 Simple iteration method
3.2 Gradient descent method
3.3 Newton's method
3.4 Modified Newton's method
List of used literature
1. Methods for solving nonlinear equations. General information.
Let us be given a system of equations, where
- some nonlinear operators: (1.1)It can also be represented in matrix form:
(1.1)Its solution is called this value
, for whichA very common computational problem is finding some or all solutions of system (1.1) from n nonlinear algebraic or transcendental equations with n unknown.
Let us denote by X column vector ( X 1 , X 2 ,..., x n)T and write the system of equations in the form of formula (1.2): F(X) = 0, where F=(f 1 ,f 2 ,...,fn)T.
Similar systems of equations can arise directly, for example, when constructing physical systems, or indirectly. So, for example, when solving the problem of minimizing a certain function G(X)it is often necessary to determine those points at which the gradient of this function is zero. Believing F= grad G, we obtain a nonlinear system.
Unlike linear systems algebraic equations, for the solution of which they can be used as straight(or accurate), and iterative(or close) methods, the solution of systems of nonlinear equations can be obtained only by approximate, iterative methods. They allow you to obtain a sequence of approximations
. If the iterative process converges, then the boundary value is a solution to the given system of equations.To complete the understanding of methods for finding a solution to a system, it is necessary to clarify such a concept as “convergence rate”. If for consistency x n, converging to the limit X *, the formula is correct
(k is a positive real number), then k is called the rate of convergence of this sequence.
2. Iterative methods for solving systems of nonlinear equations
2.1 Simple iteration method
The method of simple iterations (successive approximations) is one of the main ones in computational mathematics and is used to solve a wide class of equations. Let us give a description and justification of this method for systems of nonlinear equations of the form
f i (x 1 ,x 2 ,...x n) = 0, i=1,2,..n;
Let us bring the system of equations to a special form:
(2.1)Or in vector form
. (2.2)Moreover, the transition to this system should only be on the condition that
is a contraction mapping.Using some initial approximation X (0) = (x 1 (0) ,x 2 (0) ,...x n (0))
Let's construct an iterative process X (k+1) = (X (k)). Calculations continue until the condition is met
. Then the solution to the system of equations is the fixed point of the mapping.Let us substantiate the method in a certain norm
space.Let us present a convergence theorem, the fulfillment of the conditions of which leads to finding a solution to the system.
Theorem (about convergence). Let
1). The vector function Ф(х) is defined in the region
; condition is met3). Inequality is fair
Then in the iterative process:
, – solution of a system of equations; ,Comment. The inequality of condition 2) is the Lipschitz condition for the vector function Ф(х) in the domain S with constant
(compression condition). It shows that F is the compression operator in the region S, i.e. for equation (2.2) the principle applies compressed mappings. The statements of the theorem mean that equation (2.2) has a solution in the region S, and successive approximations converge to this solution at the rate of a geometric sequence with a denominator q.Proof. Because the
, then for the approximation due to assumption 3) we have . It means that . Let us show that , k=2,3,... and for neighboring approximations inequality (2.3) is satisfiedWe will argue by induction. At
the statement is true, because And . Let us assume that the approximations belong to S, and inequality (2.3) holds for . Since , then for taking into account condition 2) of the theorem we have .By inductive hypothesis
LABORATORY WORK No. 3-4.
Option #5.
Goal of the work: learn to solve systems of nonlinear equations (SNE) using the simple iteration method (SI) and Newton's method using a computer.
1. Study the MPI and Newton’s method for solving systems of nonlinear equations.
2. On specific example to learn the procedure for solving systems of nonlinear equations by the MPI and Newton's method using a computer.
3. Create a program and use it to solve a system of equations with an accuracy of .
EXAMPLE OF WORK PERFORMANCE
Exercise.
1. Solve the SNE analytically:
2. Construct working formulas of the MPI and Newton’s method for the numerical solution of the system at the initial approximation: .
3. Compose a program in any programming language that implements the constructed iterative process.
Solution.
Analytical method.
The analytical solution of the SDE is the points and .
Method of simple iterations (SIM).
To construct working MPI formulas for the numerical solution of the system, it is first necessary to bring it to the form:
To do this, multiply the first equation of the system by an unknown constant, the second by , then add them up and add them to both sides of the equation. We obtain the first equation of the transformed system:
We determine the unknown constants from sufficient conditions for the convergence of the iterative process:
Let's write these conditions in more detail:
Assuming that the expressions under the modulus sign are equal to zero, we obtain a system of linear algebraic equations (SLAE) of 4th order with 4 unknowns:
To solve the system it is necessary to calculate partial derivatives:
Then the SLAE will be written like this:
Note that if the partial derivatives change little in the vicinity of the initial approximation, then:
Then the SLAE will be written like this:
The solution to this system is the points , , , . Then the working formulas of the MPI for solving the SNL will take the form:
For implementation on a computer, the working formulas can be rewritten as follows:
The iterative process can be started by setting the initial approximation x 0 =-2, y 0 =-4. The process ends when two conditions are met simultaneously: and . In this case, the values and are an approximate value of one of the solutions of the SNL.
Newton's method.
To construct working formulas for Newton’s method in the form
where , it is necessary:
1. Find the matrix of partial derivatives:
2. Find the determinant of this matrix:
3. Define inverse matrix:
After making the transformation:
We obtain the working formula of Newton’s method for implementation on a computer:
Block diagram The MPI and Newton's method for solving the SLE are shown in Figure 1.
Fig.1 Schemes of MPI and Newton's method.
Program texts:
Program P3_4; (Iterations)
uses Crt;
var n: integer;
clrscr;
xn:=x-(x-y+2)+(1/2)*(x*y-3);
yn:=y+(2/3)*(x-y+2)+(1/6)*(x*y-3);
writeln (n:3, x:9:5, xn:9:5, (xn-x):9:5, y:9:5, yn:9:5, (yn-y):9:5) ;
n:=n+1;
until (abs(x-zx)<=eps) and (abs(y-zy)<=eps);
readln;
2) Newton's method:
Program P3_4; (Newton)
uses Crt;
var n: integer;
x0,x,xn,y0,y,yn,eps,zx,zy:real;
clrscr;
n:=0; x0:=-2; x:=x0; y0:=-4; y:=y0; eps:=0.001;
writeln(" n x(i) x(i+1) x(i+1)-x(i) y(i) y(i+1) y(i+1)-y(i) ");
xn:=x-(1/(x+y))*(x*x-x*y+2*x+x-y+2);
yn:=y-(1/(x+y))*(x*y*(-y)-3*(-y)+x*y-3);
writeln (n:3, x:9:5, xn:9:5, abs(xn-x):9:5, y:9:5, yn:9:5, abs(yn-y):9: 5);
n:=n+1;
until (abs(x-zx)<=eps) and (abs(y-zy)<=eps);
Results of running the program:
· Fig. 2 – a program working using the method of simple iterations;
· Fig. 3 – a program working according to Newton’s method.
Fig.2 Answer: x(16)≈-3.00023, y(16)≈-1.00001
Fig.3 Answer: x(8)≈-3.00000, y(8)≈-1.00000
The simple iteration method, also called the successive approximation method, is a mathematical algorithm for finding the value of an unknown quantity by gradually refining it. The essence of this method is that, as the name suggests, gradually expressing subsequent ones from the initial approximation, more and more refined results are obtained. This method is used to find the value of a variable in a given function, as well as when solving systems of equations, both linear and nonlinear.
Let us consider how this method is implemented when solving SLAEs. The simple iteration method has the following algorithm:
1. Checking the fulfillment of the convergence condition in the original matrix. Convergence theorem: if the original matrix of the system has diagonal dominance (i.e., in each row, the elements of the main diagonal must be greater in absolute value than the sum of the elements of the secondary diagonals in absolute value), then the simple iteration method is convergent.
2. The matrix of the original system does not always have a diagonal predominance. In such cases, the system can be converted. Equations that satisfy the convergence condition are left untouched, and linear combinations are made with those that do not, i.e. multiply, subtract, add equations to each other until the desired result is obtained.
If in the resulting system there are inconvenient coefficients on the main diagonal, then terms of the form with i * x i are added to both sides of such an equation, the signs of which must coincide with the signs of the diagonal elements.
3. Transformation of the resulting system to normal form:
x - =β - +α*x -
This can be done in many ways, for example, like this: from the first equation, express x 1 in terms of other unknowns, from the second - x 2, from the third - x 3, etc. In this case we use the formulas:
α ij = -(a ij / a ii)
i = b i /a ii
You should again make sure that the resulting system of normal form meets the convergence condition:
∑ (j=1) |α ij |≤ 1, while i= 1,2,...n
4. We begin to apply, in fact, the method of successive approximations itself.
x (0) is the initial approximation, we will express x (1) through it, then we will express x (2) through x (1). The general formula in matrix form looks like this:
x (n) = β - +α*x (n-1)
We calculate until we achieve the required accuracy:
max |x i (k)-x i (k+1) ≤ ε
So, let's put the simple iteration method into practice. Example:
Solve SLAE:
4.5x1-1.7x2+3.5x3=2
3.1x1+2.3x2-1.1x3=1
1.8x1+2.5x2+4.7x3=4 with accuracy ε=10 -3
Let's see whether diagonal elements predominate in modulus.
We see that only the third equation satisfies the convergence condition. Let's transform the first and second, and add the second to the first equation:

7.6x1+0.6x2+2.4x3=3
From the third we subtract the first:
2.7x1+4.2x2+1.2x3=2
We converted the original system into an equivalent one:
7.6x1+0.6x2+2.4x3=3
-2.7x1+4.2x2+1.2x3=2
1.8x1+2.5x2+4.7x3=4
Now let's bring the system to its normal form:
x1=0.3947-0.0789x2-0.3158x3
x2=0.4762+0.6429x1-0.2857x3
x3= 0.8511-0.383x1-0.5319x2
We check the convergence of the iterative process:
0.0789+0.3158=0,3947 ≤ 1
0.6429+0.2857=0.9286 ≤ 1
0.383+ 0.5319= 0.9149 ≤ 1, i.e. the condition is met.
0,3947
Initial guess x(0) = 0.4762
0,8511
Substituting these values into the normal form equation, we obtain the following values:
0,08835
x(1) = 0.486793
0,446639
Substituting new values, we get:
0,215243
x(2) = 0.405396
0,558336
We continue calculations until we approach values that satisfy the given condition.
x(7) = 0.441091
Let's check the correctness of the results obtained:
4,5*0,1880 -1.7*0,441+3.5*0,544=2,0003
3.1*0.1880+2.3*0.441-1.1x*0.544=0.9987
1.8*0,1880+2.5*0,441+4.7*0,544=3,9977
The results obtained by substituting the found values into the original equations fully satisfy the conditions of the equation.
As we can see, the simple iteration method gives fairly accurate results, but to solve this equation we had to spend a lot of time and do cumbersome calculations.
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0