Degree and its properties. Determination of degree

Degree formulas used in the process of reduction and simplification complex expressions, in solving equations and inequalities.

Number c is n-th power of a number a When:

Operations with degrees.

1. By multiplying degrees with the same base, their indicators are added:

a m·a n = a m + n .

2. When dividing degrees with the same base, their exponents are subtracted:

3. Power of the product of 2 or more factors is equal to the product of the powers of these factors:

(abc…) n = a n · b n · c n …

4. The degree of a fraction is equal to the ratio of the degrees of the dividend and the divisor:

(a/b) n = a n /b n .

5. Raising a power to a power, the exponents are multiplied:

(a m) n = a m n .

Each formula above is true in the directions from left to right and vice versa.

For example. (2 3 5/15)² = 2² 3² 5²/15² = 900/225 = 4.

Operations with roots.

1. The root of the product of several factors is equal to the product of the roots of these factors:

2. The root of a ratio is equal to the ratio of the dividend and the divisor of the roots:

3. When raising a root to a power, it is enough to raise the radical number to this power:

4. If you increase the degree of the root in n once and at the same time build into n the th power is a radical number, then the value of the root will not change:

5. If you reduce the degree of the root in n extract the root at the same time n-th power of a radical number, then the value of the root will not change:

A degree with a negative exponent. The power of a certain number with a non-positive (integer) exponent is defined as one divided by the power of the same number with an exponent equal to the absolute value of the non-positive exponent:

Formula a m:a n =a m - n can be used not only for m> n, but also with m< n.

For example. a4:a 7 = a 4 - 7 = a -3.

To formula a m:a n =a m - n became fair when m=n, the presence of zero degree is required.

A degree with a zero index. The power of any number not equal to zero with a zero exponent is equal to one.

For example. 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Degree with a fractional exponent. To raise a real number A to the degree m/n, you need to extract the root n th degree of m-th power of this number A.

If we ignore the eighth power, what do we see here? Let's remember the 7th grade program. So, do you remember? This is the formula for abbreviated multiplication, namely the difference of squares! We get:

Let's look carefully at the denominator. It looks a lot like one of the numerator factors, but what's wrong? The order of the terms is wrong. If they were reversed, the rule could apply.

But how to do that? It turns out that it’s very easy: the even degree of the denominator helps us here.

Magically the terms changed places. This “phenomenon” applies to any expression to an even degree: we can easily change the signs in parentheses.

But it's important to remember: all signs change at the same time!

Let's go back to the example:

And again the formula:

Whole we call the natural numbers, their opposites (that is, taken with the " " sign) and the number.

positive integer, and it is no different from natural, then everything looks exactly like in the previous section.

Now let's look at new cases. Let's start with an indicator equal to.

Any number to the zero power is equal to one:

As always, let us ask ourselves: why is this so?

Let's consider some degree with a base. Take, for example, and multiply by:

So, we multiplied the number by, and we got the same thing as it was - . What number should you multiply by so that nothing changes? That's right, on. Means.

We can do the same with an arbitrary number:

Let's repeat the rule:

Any number to the zero power is equal to one.

But there are exceptions to many rules. And here it is also there - this is a number (as a base).

On the one hand, it must be equal to any degree - no matter how much you multiply zero by itself, you will still get zero, this is clear. But on the other hand, like any number to the zero power, it must be equal. So how much of this is true? The mathematicians decided not to get involved and refused to raise zero to the zero power. That is, now we cannot not only divide by zero, but also raise it to the zero power.

Let's move on. Except natural numbers and numbers to integers include negative numbers. To understand what a negative power is, let’s do as last time: multiply some normal number by the same number to a negative power:

From here it is easy to express what you are looking for:

Now let’s extend the resulting rule to an arbitrary degree:

So, let's formulate a rule:

A number with a negative power is the reciprocal of the same number with a positive power. But at the same time The base cannot be null:(because you can’t divide by).

Let's summarize:

I. The expression is not defined in the case. If, then.

II. Any number to the zero power is equal to one: .

III. A number not equal to zero to a negative power is the inverse of the same number to a positive power: .

Tasks for independent solution:

Well, as usual, examples for independent solutions:

Analysis of problems for independent solution:

I know, I know, the numbers are scary, but on the Unified State Exam you have to be prepared for anything! Solve these examples or analyze their solutions if you couldn’t solve them and you will learn to cope with them easily in the exam!

Let's continue to expand the range of numbers “suitable” as an exponent.

Now let's consider rational numbers. What numbers are called rational?

Answer: everything that can be represented as a fraction, where and are integers, and.

To understand what it is "fractional degree", consider the fraction:

Let's raise both sides of the equation to a power:

Now let's remember the rule about "degree to degree":

What number must be raised to a power to get?

This formulation is the definition of the root of the th degree.

Let me remind you: the root of the th power of a number () is a number that, when raised to a power, is equal to.

That is, the root of the th power is the inverse operation of raising to a power: .

It turns out that. Obviously this special case can be expanded: .

Now we add the numerator: what is it? The answer is easy to obtain using the power-to-power rule:

But can the base be any number? After all, the root cannot be extracted from all numbers.

None!

Let us remember the rule: any number raised to an even power is a positive number. That is, it is impossible to extract even roots from negative numbers!

This means that such numbers cannot be raised to a fractional power with an even denominator, that is, the expression does not make sense.

What about the expression?

But here a problem arises.

The number can be represented in the form of other, reducible fractions, for example, or.

And it turns out that it exists, but does not exist, but these are just two different records of the same number.

Or another example: once, then you can write it down. But if we write down the indicator differently, we will again get into trouble: (that is, we got a completely different result!).

To avoid such paradoxes, we consider only positive base exponent with fractional exponent.

So if:

• - natural number;
• - integer;

Examples:

Rational exponents are very useful for transforming expressions with roots, for example:

5 examples to practice

Analysis of 5 examples for training

1. Don't forget about the usual properties of degrees:

2. . Here we remember that we forgot to learn the table of degrees:

after all - this is or. The solution is found automatically: .

Well, now comes the hardest part. Now we'll figure it out degree with irrational exponent.

All rules and properties of degrees here are exactly the same as for a degree with a rational exponent, with the exception

After all, by definition, irrational numbers are numbers that cannot be represented as a fraction, where and are integers (that is, irrational numbers are all real numbers except rational ones).

When studying degrees with natural, integer and rational exponents, each time we created a certain “image”, “analogy”, or description in more familiar terms.

For example, a degree with a natural exponent is a number multiplied by itself several times;

...number to the zeroth power- this is, as it were, a number multiplied by itself once, that is, they have not yet begun to multiply it, which means that the number itself has not even appeared yet - therefore the result is only a certain “blank number”, namely a number;

...negative integer degree- it’s as if some “reverse process” had occurred, that is, the number was not multiplied by itself, but divided.

By the way, in science a degree with a complex exponent is often used, that is, the exponent is not even a real number.

But at school we don’t think about such difficulties; you will have the opportunity to comprehend these new concepts at the institute.

WHERE WE ARE SURE YOU WILL GO! (if you learn to solve such examples :))

For example:

Decide for yourself:

Analysis of solutions:

1. Let's start with the usual rule for raising a power to a power:

Now look at the indicator. Doesn't he remind you of anything? Let us recall the formula for abbreviated multiplication of difference of squares:

In this case,

It turns out that:

Answer: .

2. We reduce fractions in exponents to the same form: either both decimals or both ordinary ones. We get, for example:

Answer: 16

3. Nothing special, we use the usual properties of degrees:

ADVANCED LEVEL

Determination of degree

A degree is an expression of the form: , where:

• — degree base;
• - exponent.

Degree with natural indicator (n = 1, 2, 3,...)

Raising a number to the natural power n means multiplying the number by itself times:

Degree with an integer exponent (0, ±1, ±2,...)

If the exponent is positive integer number:

Construction to the zero degree:

The expression is indefinite, because, on the one hand, to any degree is this, and on the other hand, any number to the th degree is this.

If the exponent is negative integer number:

(because you can’t divide by).

Once again about zeros: the expression is not defined in the case. If, then.

Examples:

Power with rational exponent

• - natural number;
• - integer;

Examples:

Properties of degrees

To make it easier to solve problems, let’s try to understand: where did these properties come from? Let's prove them.

Let's see: what is and?

A-priory:

So, on the right side of this expression we get the following product:

But by definition it is a power of a number with an exponent, that is:

Q.E.D.

Example : Simplify the expression.

Solution : .

Example : Simplify the expression.

Solution : It is important to note that in our rule Necessarily there must be the same reasons. Therefore, we combine the powers with the base, but it remains a separate factor:

Another important note: this rule - only for product of powers!

Under no circumstances can you write that.

Just as with the previous property, let us turn to the definition of degree:

Let's regroup this work like this:

It turns out that the expression is multiplied by itself times, that is, according to the definition, this is the th power of the number:

In essence, this can be called “taking the indicator out of brackets.” But you can never do this in total: !

Let's remember the abbreviated multiplication formulas: how many times did we want to write? But this is not true, after all.

Power with a negative base.

Up to this point we have only discussed what it should be like index degrees. But what should be the basis? In powers of natural indicator the basis may be any number .

Indeed, we can multiply any numbers by each other, be they positive, negative, or even. Let's think about which signs ("" or "") will have powers of positive and negative numbers?

For example, is the number positive or negative? A? ?

With the first one, everything is clear: no matter how many positive numbers we multiply by each other, the result will be positive.

But the negative ones are a little more interesting. We remember the simple rule from 6th grade: “minus for minus gives a plus.” That is, or. But if we multiply by (), we get - .

And so on ad infinitum: with each subsequent multiplication the sign will change. The following simple rules can be formulated:

1. even degree, - number positive.
2. Negative number raised to odd degree, - number negative.
3. Positive number to any degree is a positive number.
4. Zero to any power is equal to zero.

Determine for yourself what sign the following expressions will have:

1.	2.	3.
4.	5.	6.

Did you manage? Here are the answers:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

In the first four examples, I hope everything is clear? We simply look at the base and exponent and apply the appropriate rule.

In example 5) everything is also not as scary as it seems: after all, it doesn’t matter what the base is equal to - the degree is even, which means the result will always be positive. Well, except when the base is zero. The base is not equal, is it? Obviously not, since (because).

Example 6) is no longer so simple. Here you need to find out which is less: or? If we remember that, it becomes clear that, which means the base is less than zero. That is, we apply rule 2: the result will be negative.

And again we use the definition of degree:

Everything is as usual - we write down the definition of degrees and divide them by each other, divide them into pairs and get:

Before we look at the last rule, let's solve a few examples.

Calculate the expressions:

Solutions :

If we ignore the eighth power, what do we see here? Let's remember the 7th grade program. So, do you remember? This is the formula for abbreviated multiplication, namely the difference of squares!

We get:

Let's look carefully at the denominator. It looks a lot like one of the numerator factors, but what's wrong? The order of the terms is wrong. If they were reversed, rule 3 could apply. But how? It turns out that it’s very easy: the even degree of the denominator helps us here.

If you multiply it by, nothing changes, right? But now it turns out like this:

Magically the terms changed places. This “phenomenon” applies to any expression to an even degree: we can easily change the signs in parentheses. But it's important to remember: All signs change at the same time! You can’t replace it with by changing only one disadvantage we don’t like!

Let's go back to the example:

And again the formula:

So now the last rule:

How will we prove it? Of course, as usual: let’s expand on the concept of degree and simplify it:

Well, now let's open the brackets. How many letters are there in total? times by multipliers - what does this remind you of? This is nothing more than a definition of an operation multiplication: There were only multipliers there. That is, this, by definition, is a power of a number with an exponent:

Example:

Degree with irrational exponent

In addition to information about degrees for the average level, we will analyze the degree with an irrational exponent. All the rules and properties of degrees here are exactly the same as for a degree with a rational exponent, with the exception - after all, by definition, irrational numbers are numbers that cannot be represented as a fraction, where and are integers (that is, irrational numbers are all real numbers except rational numbers).

When studying degrees with natural, integer and rational exponents, each time we created a certain “image”, “analogy”, or description in more familiar terms. For example, a degree with a natural exponent is a number multiplied by itself several times; a number to the zero power is, as it were, a number multiplied by itself once, that is, they have not yet begun to multiply it, which means that the number itself has not even appeared yet - therefore the result is only a certain “blank number”, namely a number; a degree with an integer negative exponent - it’s as if some “reverse process” had occurred, that is, the number was not multiplied by itself, but divided.

It is extremely difficult to imagine a degree with an irrational exponent (just as it is difficult to imagine a 4-dimensional space). It is rather a purely mathematical object that mathematicians created to extend the concept of degree to the entire space of numbers.

By the way, in science a degree with a complex exponent is often used, that is, the exponent is not even a real number. But at school we don’t think about such difficulties; you will have the opportunity to comprehend these new concepts at the institute.

So what do we do if we see an irrational exponent? We are trying our best to get rid of it! :)

For example:

Decide for yourself:

1)

2)

3)

Answers:

1. Let's remember the difference of squares formula. Answer: .
2. We reduce the fractions to the same form: either both decimals or both ordinary ones. We get, for example: .
3. Nothing special, we use the usual properties of degrees:

SUMMARY OF THE SECTION AND BASIC FORMULAS

Degree called an expression of the form: , where:

Degree with an integer exponent

a degree whose exponent is a natural number (i.e., integer and positive).

Power with rational exponent

degree, the exponent of which is negative and fractional numbers.

Degree with irrational exponent

degree whose exponent is infinite decimal or root.

Properties of degrees

Features of degrees.

• Negative number raised to even degree, - number positive.
• Negative number raised to odd degree, - number negative.
• A positive number to any degree is a positive number.
• Zero is equal to any power.
• Any number to the zero power is equal.

NOW YOU HAVE THE WORD...

How do you like the article? Write below in the comments whether you liked it or not.

Tell us about your experience using degree properties.

Perhaps you have questions. Or suggestions.

Write in the comments.

And good luck on your exams!

Lesson topic: Raising to the power of the product, quotient and power

Lesson type: Lesson on generalization and systematization of knowledge

Generated results:

Subject. Strengthen the skills of using the properties of degrees with natural exponents

Personal. Develop the ability to plan your actions in accordance with the educational task

Metasubject. Develop understanding the essence of algebraic prescriptions and the ability to act in accordance with the proposed algorithm

Expected outcomes: Students will learn to use the properties of exponents with natural exponents to calculate the meaning of expressions and convert expressions containing exponents.

Equipment: cards, multimedia projector, signal cards for reflection.

Organizational structure of the lesson:

1 . Organizing time.

Hello, dear guys! I'm very glad to see you. Let's start the math lesson

What difficulties did you have when performing the task?

Reflection.

In front of each student there are mugs of three colors: red, green, blue.

Tell me about your mood using colored circles (red– joyful, I am sure that I will learn a lot of new things in the lesson, I am confident in my knowledge.

Green -calm; I am confident in my knowledge.

Blue– alarming; I'm not sure of myself).

I will cheer you up a little with the words of Poisson: “Life is embellished by two things: doing mathematics and teaching it.”

Let's decorate our lives!

2. Statement of the topic and purpose of the lesson.

Today we will continue to study the topic: “Exponentiation of the product of a quotient and a degree”,

we will consolidate all the learned actions with degrees,

We will learn to reason, think logically and prove our point of view.

3. Blitz survey according to the rules of the topic.

How to multiply powers with the same bases? Give examples.

How to divide degrees with the same bases?

What is the power of a number a, not equal to 0, with a zero exponent?

How to raise a product to a power?

How to raise a degree to a power?

4. Oral counting.

Who owns these words?

“Among all the sciences that open the way for man to understand the laws of nature, the most powerful, the greatest science is mathematics.”

/Sofya Vasilievna Kovalevskaya/

The first woman is a mathematician.

You will learn by completing mental calculation tasks.

K – What is the side of the square if its area is 49 cm 2. (7cm)

O – The square of what number is equal to ? ()

B – x 3 x 4 (x 7)

A – x 6 : x 2 (x 4)

L – (x 3) 3 (x 9)

E -
(m 3 )

IN -
(m 8 )

WITH -
(m 10 )

K – (- 2) 3 (-8)

A - - 2 2 (-4)

I - 2 0 (1)

5. Consolidation of what has been learned.

We repeated the rules for raising a product to a power and a power to a power.

Now let's focus on practical tasks.

Several people will take careresearch. (Slide)

Work in pairs.

1) Prove that the squares of opposite numbers are equal.

2) Prove that the cubes of opposite numbers are opposites.

3) How will the area of ​​a square change if its side is doubled; 3 times; 10 times; n times?

4) How will the volume of a cube change if its edge is doubled; 3 times; 10 times; n times?

6. Reflection: show me your mood.

7. Physical exercise: “I agree - I disagree”

Shake your head if you agree with me or not.

1) (y 2) 3 = y 5 (no)

2) (-3) 3 = -27 (yes)

3) (-x) 2 = -x 2 (no)

4) The graph of the function y = 1.3x passes through the origin. (Yes)

8.

3 · () 2 – 0,5 2

a) -1; b) - 1 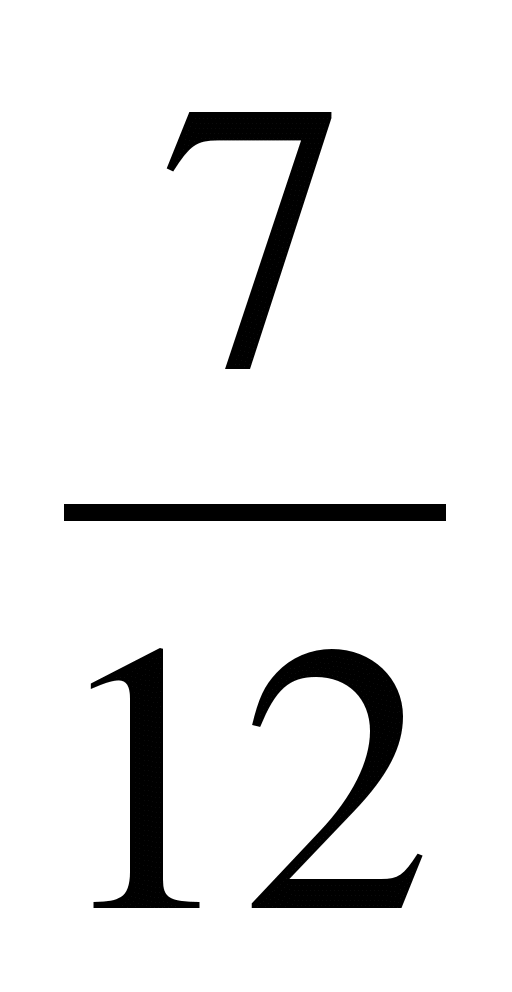; in 1 ; d) 1

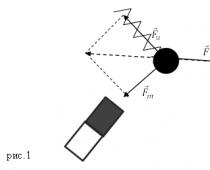
2) Simplify the expression:

a) m 10; b)m 4 ; c) m 2; d) m 8.

3) Calculate:

A) 3; b) 9; c) : d)

4) What expression should be substituted instead of (*) to obtain an identity:

X 8 : (*) = x 4

A) x 4; b) x 2; c) x 8; d) x 12

Checking the slide test:

9. Let's play "Find the mistake!"

1) a 15 : a 3 = a 5

2) –z · z 5 · z 0 = - z 6 - right

3)
=

4)(y 4 y) 2 = y 10 - true

Write down the wrong tasks and solve them correctly.

10. Lesson summary.

What did you learn in the lesson?

11. D/z

No. 458, 457 (slide)

Reports on S.V. Kovalevskaya.

12. Reflection.

Show me how you feel when you leave the lesson?

Slide: Good luck!

FI:

Independent work. (test)

1) Find the meaning of the expression:

3· () 2 – 0.5 2

a) -1; b) - 1 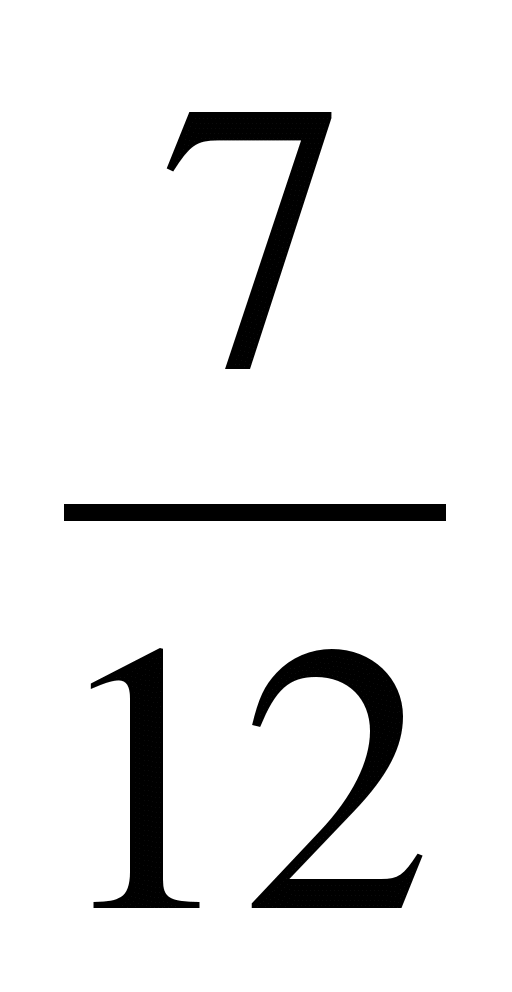; in 1 ; d) 1

2) Simplify the expression:

a) m 10; b)m 4 ; c) m 2; d) m 8.

3) Calculate:

a) 3; b) 9; c) : d)

4) What expression should be substituted instead of (*) to obtain an identity:

x 8 : (*) = x 4

a) x 4; b) x 2; c) x 8; d) x 12

Grade:

Independent work. (test)

1) Find the meaning of the expression:

3· () 2 – 0.5 2

a) -1; b) - 1 ; in 1 ; d) 1

2) Simplify the expression:

primary goal

To familiarize students with the properties of degrees with natural exponents and teach them how to perform operations with degrees.

Topic “Degree and its properties” includes three questions:

• Determination of degree with a natural indicator.
• Multiplication and division of powers.
• Exponentiation of product and degree.

Control questions

1. Formulate the definition of a degree with a natural exponent greater than 1. Give an example.
2. Formulate the definition of degree with exponent 1. Give an example.
3. What is the order of operations when calculating the value of an expression containing powers?
4. Formulate the main property of degree.
5. Give an example.
6. Formulate the rule for multiplying powers with the same bases. Give an example.
7. Formulate a rule for dividing powers with the same bases. Give an example.
8. Formulate the rule for exponentiation of a product. Give an example. Prove the identity (ab) n = a n b n .

Definition of degree.

Power of number a with natural indicator n, greater than 1, is the product of n factors, each of which is equal A. Power of number A with exponent 1 is the number itself A.

Degree with base A and indicator n is written like this: and n. It reads “ A to a degree n”; “ nth power of a number A ”.

By definition of degree:

a 4 = a a a a

. . . . . . . . . . . .

Finding the value of a power is called by exponentiation .

1. Examples of exponentiation:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Find the meanings of the expressions:

a) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

b) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Option 1

a) 0.3 0.3 0.3

c) b b b b b b b

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Present the number as a square:

3. Present the numbers as a cube:

4. Find the meanings of the expressions:

c) -1 4 + (-2) 3

d) -4 3 + (-3) 2

e) 100 - 5 2 4

Multiplication of powers.

For any number a and arbitrary numbers m and n the following holds:

a m a n = a m + n .

Proof:

Rule : When multiplying powers with the same bases, the bases are left the same, and the exponents of the powers are added.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

a) x 5 x 4 = x 5 + 4 = x 9

b) y y 6 = y 1 y 6 = y 1 + 6 = y 7

c) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11

d) 3 4 9 = 3 4 3 2 = 3 6

e) 0.01 0.1 3 = 0.1 2 0.1 3 = 0.1 5

a) 2 3 2 = 2 4 = 16

b) 3 2 3 5 = 3 7 = 2187

Option 1

1. Present as a degree:

a) x 3 x 4 e) x 2 x 3 x 4

b) a 6 a 2 g) 3 3 9

c) y 4 y h) 7 4 49

d) a a 8 i) 16 2 7

e) 2 3 2 4 j) 0.3 3 0.09

2. Present as a degree and find the value from the table:

a) 2 2 2 3 c) 8 2 5

b) 3 4 3 2 d) 27 243

Division of degrees.

For any number a0 and arbitrary natural numbers m and n, such that m>n the following holds:

a m: a n = a m - n

Proof:

a m - n a n = a (m - n) + n = a m - n + n = a m

by definition of quotient:

a m: a n = a m - n .

Rule: When dividing powers with the same base, the base is left the same, and the exponent of the divisor is subtracted from the exponent of the dividend.

Definition: The power of a number a, not equal to zero, with a zero exponent is equal to one:

because a n: a n = 1 at a0.

a) x 4: x 2 = x 4 - 2 = x 2

b) y 8: y 3 = y 8 - 3 = y 5

c) a 7:a = a 7:a 1 = a 7 - 1 = a 6

d) from 5:from 0 = from 5:1 = from 5

a) 5 7:5 5 = 5 2 = 25

b) 10 20:10 17 = 10 3 = 1000

V)

G)

d)

Option 1

1. Present the quotient as a power:

2. Find the meanings of the expressions:

Raising to the power of a product.

For any a and b and an arbitrary natural number n:

(ab) n = a n b n

Proof:

By definition of degree

(ab)n=

Grouping separately the factors a and the factors b, we get:

=

The proven property of the power of a product extends to the power of the product of three or more factors.

For example:

(a b c) n = a n b n c n ;

(a b c d) n = a n b n c n d n .

Rule: When raising a product to a power, each factor is raised to that power and the result is multiplied.

1. Raise to a power:

a) (a b) 4 = a 4 b 4

b) (2 x y) 3 =2 3 x 3 y 3 = 8 x 3 y 3

c) (3 a) 4 = 3 4 a 4 = 81 a 4

d) (-5 y) 3 = (-5) 3 y 3 = -125 y 3

e) (-0.2 x y) 2 = (-0.2) 2 x 2 y 2 = 0.04 x 2 y 2

e) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Find the value of the expression:

a) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000

b) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000

c) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

d) 0.25 11 4 11 = (0.25 4) 11 = 1 11 = 1

d)

Option 1

1. Raise to a power:

b) (2 a c) 4

e) (-0.1 x y) 3

2. Find the value of the expression:

b) (5 7 20) 2

Raising to a power of a power.

For any number a and arbitrary natural numbers m and n:

(a m) n = a m n

Proof:

By definition of degree

(a m) n =

Rule: When raising a power to a power, the base is left the same, and the exponents are multiplied.

1. Raise to a power:

(a 3) 2 = a 6 (x 5) 4 = x 20

(y 5) 2 = y 10 (b 3) 3 = b 9

2. Simplify the expressions:

a) a 3 (a 2) 5 = a 3 a 10 = a 13

b) (b 3) 2 b 7 = b 6 b 7 = b 13

c) (x 3) 2 (x 2) 4 = x 6 x 8 = x 14

d) (y 7) 3 = (y 8) 3 = y 24

A)

b)

Option 1

1. Raise to a power:

a) (a 4) 2 b) (x 4) 5

c) (y 3) 2 d) (b 4) 4

2. Simplify the expressions:

a) a 4 (a 3) 2

b) (b 4) 3 b 5+

c) (x 2) 4 (x 4) 3

d) (y 9) 2

3. Find the meaning of the expressions:

Application

Definition of degree.

Option 2

1st Write the product as a power:

a) 0.4 0.4 0.4

c) a a a a a a a a

d) (-y) (-y) (-y) (-y)

e) (bс) (bс) (bс)

2. Present the number as a square:

3. Present the numbers as a cube:

4. Find the meanings of the expressions:

c) -1 3 + (-2) 4

d) -6 2 + (-3) 2

e) 4 5 2 – 100

Option 3

1. Write the product as a power:

a) 0.5 0.5 0.5

c) with with with with with with with with with

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Present the number as a square: 100; 0.49; .

3. Present the numbers as a cube:

4. Find the meanings of the expressions:

c) -1 5 + (-3) 2

d) -5 3 + (-4) 2

e) 5 4 2 - 100

Option 4

1. Write the product as a power:

a) 0.7 0.7 0.7

c) x x x x x x

d) (-a) (-a) (-a)

e) (bс) (bс) (bс) (bc)

2. Present the number as a square:

3. Present the numbers as a cube:

4. Find the meanings of the expressions:

c) -1 4 + (-3) 3

d) -3 4 + (-5) 2

e) 100 - 3 2 5

Multiplication of powers.

Option 2

1. Present as a degree:

a) x 4 x 5 e) x 3 x 4 x 5

b) a 7 a 3 g) 2 3 4

c) y 5 y h) 4 3 16

d) a a 7 i) 4 2 5

e) 2 2 2 5 j) 0.2 3 0.04

2. Present as a degree and find the value from the table:

a) 3 2 3 3 c) 16 2 3

b) 2 4 2 5 d) 9 81

Option 3

1. Present as a degree:

a) a 3 a 5 f) y 2 y 4 y 6

b) x 4 x 7 g) 3 5 9

c) b 6 b h) 5 3 25

d) y 8 i) 49 7 4

e) 2 3 2 6 j) 0.3 4 0.27

2. Present as a degree and find the value from the table:

a) 3 3 3 4 c) 27 3 4

b) 2 4 2 6 d) 16 64

Option 4

1. Present as a degree:

a) a 6 a 2 e) x 4 x x 6

b) x 7 x 8 g) 3 4 27

c) y 6 y h) 4 3 16

d) x x 10 i) 36 6 3

e) 2 4 2 5 j) 0.2 2 0.008

2. Present as a degree and find the value from the table:

a) 2 6 2 3 c) 64 2 4

b) 3 5 3 2 d) 81 27

Division of degrees.

Option 2

1. Present the quotient as a power:

2. Find the meanings of the expressions:

We remind you that in this lesson we will understand properties of degrees with natural indicators and zero. Degrees with rational indicators

A power with a natural exponent has several important properties that allow us to simplify calculations in examples with powers.

Property No. 1
Product of powers

Remember!

When multiplying powers with the same bases, the base remains unchanged, and the exponents of the powers are added.

a m · a n = a m + n, where “a” is any number, and “m”, “n” are any natural numbers.

This property of powers also applies to the product of three or more powers.

• Simplify the expression.
  b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Present it as a degree.
  6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
• Present it as a degree.
  (0.8) 3 · (0.8) 12 = (0.8) 3 + 12 = (0.8) 15

Important!

Please note that in the indicated property we were only talking about multiplying powers with on the same grounds . It does not apply to their addition.

You cannot replace the sum (3 3 + 3 2) with 3 5. This is understandable if
calculate (3 3 + 3 2) = (27 + 9) = 36, and 3 5 = 243

Property No. 2
Partial degrees

Remember!

When dividing powers with the same base, the base remains unchanged, and the exponent of the divisor is subtracted from the exponent of the dividend.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Example. Solve the equation. We use the property of quotient powers.
3 8: t = 3 4

T = 3 8 − 4

Answer: t = 3 4 = 81

Using properties No. 1 and No. 2, you can easily simplify expressions and perform calculations.

• Example. Simplify the expression.
  4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
• Example. Find the value of an expression using the properties of exponents.
  = = = 2 9 + 2

  2 5

  = 2 11

  2 5

  = 2 11 − 5 = 2 6 = 64

  Important!

  Please note that in Property 2 we were only talking about dividing powers with the same bases.

  You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if you count (4 3 −4 2) = (64 − 16) = 48 , and 4 1 = 4

  Be careful!

  Property No. 3
  Raising a degree to a power

  Remember!

  When raising a degree to a power, the base of the degree remains unchanged, and the exponents are multiplied.

  (a n) m = a n · m, where “a” is any number, and “m”, “n” are any natural numbers.

  
  

  Properties 4
  Product power

  Remember!

  When raising a product to a power, each of the factors is raised to a power. The results obtained are then multiplied.

  (a b) n = a n b n, where “a”, “b” are any rational numbers; "n" is any natural number.

  • Example 1.
    (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 c 1 2 = 36 a 4 b 6 c 2
    
  • Example 2.
    (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6

  Important!

  Please note that property No. 4, like other properties of degrees, is also applied in reverse order.

  (a n · b n)= (a · b) n

  That is, to multiply powers with the same exponents, you can multiply the bases, but leave the exponent unchanged.

  • Example. Calculate.
    2 4 5 4 = (2 5) 4 = 10 4 = 10,000
  • Example. Calculate.
    0.5 16 2 16 = (0.5 2) 16 = 1

  In more complex examples There may be cases when multiplication and division must be performed on powers with different bases and different exponents.

  In this case, we advise you to do the following. For example,
  

  4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

  An example of raising a decimal to a power.

  4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4
  Properties 5

  Remember!

  Power of a quotient (fraction)

  To raise a quotient to a power, you can raise the dividend and the divisor separately to this power, and divide the first result by the second.

  • (a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n is any natural number.
    (5: 3) 12 = 5 12: 3 12

  Example. Present the expression as a quotient of powers.