rotary motion solid body around a fixed axis is called such a movement in which any two points belonging to the body (or invariably associated with it) remain motionless throughout the movement(Fig. 2.2) .
Figure 2.2
passing through fixed points BUT and AT straight line is called axis of rotation. Since the distance between the points of a rigid body must remain unchanged, it is obvious that during rotational motion all points belonging to the axis will be fixed, and all the rest will describe circles whose planes are perpendicular to the axis of rotation, and the centers lie on this axis. To determine the position of a rotating body, we draw through the axis of rotation, along which the axis is directed Az, half plane І - fixed and half-plane ІІ embedded in the body itself and rotating with it. Then the position of the body at any moment of time is uniquely determined by the angle taken with the corresponding sign φ between these planes, which we will call body angle. We will consider the angle φ positive if delayed from a fixed plane in a counterclockwise direction (for an observer looking from the positive end of the axis Az), but negative if clockwise. measure angle φ will be in radians. To know the position of the body at any time, you need to know the dependence of the angle φ from time t, i.e.
|
|
This equation expresses law rotary motion rigid body around a fixed axis.
The main kinematic characteristics of the rotational motion of a rigid body are its angular velocity ω and angular acceleration ε.
9.2.1. Angular velocity and angular acceleration of a body
The value characterizing the rate of change of the angle of rotation φ over time is called the angular velocity.
If for a period of time  body makes a turn
body makes a turn  , then the numerically average angular velocity of the body for this period of time will be
, then the numerically average angular velocity of the body for this period of time will be  . In the limit at
. In the limit at  we get
we get
In this way, the numerical value of the angular velocity of the body at a given moment of time is equal to the first derivative of the angle of rotation with respect to time.
Rule of signs: when the rotation is counterclockwise, ω> 0, and when clockwise, then ω< 0.
 or, since the radian is a dimensionless quantity,
or, since the radian is a dimensionless quantity,  .
.
In theoretical calculations, it is more convenient to use the angular velocity vector  , whose modulus is equal to
, whose modulus is equal to  and which is directed along the axis of rotation of the body in the direction from which the rotation is visible counterclockwise. This vector immediately determines the module of the angular velocity, and the axis of rotation, and the direction of rotation around this axis.
and which is directed along the axis of rotation of the body in the direction from which the rotation is visible counterclockwise. This vector immediately determines the module of the angular velocity, and the axis of rotation, and the direction of rotation around this axis.
The quantity characterizing the rate of change of the angular velocity over time is called the angular acceleration of the body.
If for a period of time  increment of angular velocity is equal to
increment of angular velocity is equal to  , then the ratio
, then the ratio  , i.e. determines the value of the average acceleration of a rotating body over time
, i.e. determines the value of the average acceleration of a rotating body over time  .
.
When striving  we get the value of the angular acceleration at the moment t:
we get the value of the angular acceleration at the moment t:
In this way, the numerical value of the angular acceleration of the body at a given moment of time is equal to the first derivative of the angular velocity or the second derivative of the angle of rotation of the body in time.
The unit of measure is usually  or, which is also
or, which is also  .
.
If the modulus of angular velocity increases with time, the rotation of the body is called accelerated, and if it decreases, - slow. When the quantities ω
and ε
have the same signs, then the rotation will be accelerated, when different - slowed down.  By analogy with angular velocity, angular acceleration can also be represented as a vector
By analogy with angular velocity, angular acceleration can also be represented as a vector  directed along the axis of rotation. Wherein
directed along the axis of rotation. Wherein
 .
.
If the body rotates with an accelerated direction  coincides with
coincides with  , and opposite
, and opposite  during slow rotation.
during slow rotation.
If the angular velocity of the body remains constant during the motion ( ω= const), then the rotation of the body is called uniform.
From  we have
we have  . Hence, assuming that at the initial moment of time
. Hence, assuming that at the initial moment of time  corner
corner  , and taking integrals to the left of
, and taking integrals to the left of  before
before  , and on the right from 0 to t, we finally get
, and on the right from 0 to t, we finally get
|
|
With uniform rotation, when  =0,
=0, and
and  .
.
The speed of uniform rotation is often determined by the number of revolutions per minute, denoting this value as n rpm Let's find the relationship between n rpm and ω 1/s. With one revolution, the body will rotate by 2π, and with n revolutions per 2π n; this turn is done in 1 min, i.e. t= 1min=60s. It follows that
|
|
If the angular acceleration of the body remains constant throughout the motion (ε = const), then the rotation is called equally variable.
At the initial moment of time t=0 angle  , and the angular velocity
, and the angular velocity  (
( - initial angular velocity).
- initial angular velocity).  ;
; =ε
=ε  . Integrating the left side of
. Integrating the left side of  before
before  , and the right one from 0 to t, find
, and the right one from 0 to t, find
Angular velocity ω of this rotation  . If ω and ε have the same signs, the rotation will be uniformly accelerated, and if different equally slow.
. If ω and ε have the same signs, the rotation will be uniformly accelerated, and if different equally slow.
Steering Angle, Angular Velocity and Angular Acceleration
Rotation of a rigid body around a fixed axis is called such a movement in which two points of the body remain motionless during the entire time of movement. In this case, all points of the body located on the straight line passing through its fixed points also remain fixed. This line is called axis of rotation of the body.
If a BUT and AT- fixed points of the body (Fig. 15 ), then the axis of rotation is the axis Oz, which can have any direction in space, not necessarily vertical. One axis direction Oz taken as positive.
Draw a fixed plane through the axis of rotation By and mobile P, attached to a rotating body. Let both planes coincide at the initial moment of time. Then at the time t the position of the moving plane and the rotating body itself can be determined by the dihedral angle between the planes and the corresponding linear angle φ between straight lines located in these planes and perpendicular to the axis of rotation. Corner φ called body angle.
The position of the body relative to the chosen reference system is completely determined in any
point in time if the equation is given φ =f(t) (5)
where f(t)- any, twice differentiable function of time. This equation is called the equation of rotation of a rigid body around a fixed axis.
A body rotating around a fixed axis has one degree of freedom, since its position is determined by setting only one parameter - the angle φ .
Corner φ is considered positive if it is plotted counterclockwise, and negative if it is plotted in the opposite direction when viewed from the positive direction of the axis Oz. The trajectories of the points of the body during its rotation around a fixed axis are circles located in planes perpendicular to the axis of rotation.
To characterize the rotational motion of a rigid body around a fixed axis, we introduce the concepts of angular velocity and angular acceleration. Algebraic angular velocity of the body at any moment in time, the first time derivative of the angle of rotation at this moment is called, i.e. dφ/dt = φ. It is positive when the body rotates counterclockwise, since the angle of rotation increases with time, and negative when the body rotates clockwise, because the angle of rotation decreases.
The modulus of angular velocity is denoted ω. Then ω= ׀dφ/dt׀= ׀φ ׀ (6)
The dimension of the angular velocity is set in accordance with (6)
[ω] = angle/time = rad/s = s -1.
In engineering, angular velocity is the rate of rotation expressed in revolutions per minute. In 1 minute the body will turn through an angle 2πp, if P- number of revolutions per minute. Dividing this angle by the number of seconds in a minute, we get: (7)
Algebraic angular acceleration of the body is called the first time derivative of the algebraic speed, i.e. the second derivative of the angle of rotation d 2 φ / dt 2 \u003d ω. We denote the modulus of angular acceleration ε , then ε=|φ| (8)
The dimension of the angular acceleration is obtained from (8):
[ε ] = angular velocity/time = rad/s 2 = s -2
If a φ’’>0 at φ’>0 , then the algebraic angular velocity increases with time and, consequently, the body rotates acceleratedly at the considered moment of time in positive side(counterclock-wise). At φ’’<0 and φ’<0 the body rotates rapidly in the negative direction. If a φ’’<0 at φ’>0 , then we have a slow rotation in the positive direction. At φ’’>0 and φ’<0 , i.e. slow rotation is in the negative direction. The angular velocity and angular acceleration in the figures are represented by arc arrows around the axis of rotation. The arc arrow for the angular velocity indicates the direction of rotation of the bodies;
For accelerated rotation, arc arrows for angular velocity and angular acceleration have the same directions for slow rotation - their directions are opposite.
Special cases of rotation of a rigid body
A rotation is said to be uniform if ω=const, φ= φ't
The rotation will be uniform if ε=const. φ'= φ' 0 + φ''t and
In general, if φ’’ not always,
![]()
Velocities and accelerations of body points
The equation of rotation of a rigid body around a fixed axis is known φ= f(t)(Fig. 16). Distance s points M in the moving plane P along an arc of a circle (trajectory of a point), counted from a point M oh located in a fixed plane, is expressed through the angle φ addiction s=hφ, where h is the radius of the circle along which the point moves. It is the shortest distance from the point M to the axis of rotation. It is sometimes called the radius of rotation of a point. At each point of the body, the radius of rotation remains unchanged when the body rotates around a fixed axis.
 Algebraic point speed M determined by the formula v τ =s'=hφ Point speed module: v=hω(9)
Algebraic point speed M determined by the formula v τ =s'=hφ Point speed module: v=hω(9)
The velocities of the points of the body during rotation around a fixed axis are proportional to their shortest distances to this axis. The proportionality factor is the angular velocity. The velocities of the points are directed along the tangents to the trajectories and, therefore, are perpendicular to the radii of rotation. Velocities of body points located on a straight line segment OM, in accordance with (9) are distributed according to a linear law. They are mutually parallel, and their ends are located on one straight line passing through the axis of rotation. We decompose the acceleration of a point into tangent and normal components, i.e. a=a τ +a nτ Tangent and normal accelerations are calculated by formulas (10)
since for a circle the radius of curvature p=h(Fig. 17 ). In this way,
 Tangent, normal and full accelerations of points, as well as velocities, are also distributed according to a linear law. They linearly depend on the distances of the points to the axis of rotation. Normal acceleration is directed along the radius of the circle to the axis of rotation. The direction of the tangential acceleration depends on the sign of the algebraic angular acceleration. At φ’>0
and φ’’>0
or φ’<0
and φ’<0
we have an accelerated rotation of the body and the direction of the vectors a τ and v match. If a φ’
and φ’"
have different signs (slow rotation), then a τ and v directed opposite to each other.
Tangent, normal and full accelerations of points, as well as velocities, are also distributed according to a linear law. They linearly depend on the distances of the points to the axis of rotation. Normal acceleration is directed along the radius of the circle to the axis of rotation. The direction of the tangential acceleration depends on the sign of the algebraic angular acceleration. At φ’>0
and φ’’>0
or φ’<0
and φ’<0
we have an accelerated rotation of the body and the direction of the vectors a τ and v match. If a φ’
and φ’"
have different signs (slow rotation), then a τ and v directed opposite to each other.
Denoting α the angle between the full acceleration of a point and its radius of rotation, we have
tanα = | a τ |/a n = ε/ω 2 (11)
since the normal acceleration a p always positive. Corner a the same for all points of the body. It should be postponed from acceleration to the radius of rotation in the direction of the arc arrow of angular acceleration, regardless of the direction of rotation of the rigid body.
Angular velocity and angular acceleration vectors
![]()
Let us introduce the concepts of vectors of angular velocity and angular acceleration of a body. If a To is the unit vector of the axis of rotation, directed in its positive direction, then the vectors of the angular velocity ώ and angular acceleration ε determined by expressions (12)
Because k-vector constant in absolute value and direction, then from (12) it follows that
ε=dώ/dt(13)

At φ’>0 and φ’’>0 vector directions ώ and ε match. They are both directed in the positive direction of the axis of rotation. Oz(Fig. 18.a) If φ’>0 and φ’’<0 , then they are directed in opposite directions (Fig. 18.b ). The angular acceleration vector coincides in direction with the angular velocity vector during accelerated rotation and is opposite to it during slow rotation. Vectors ώ and ε can be drawn at any point on the axis of rotation. They are sliding vectors. This property follows from the vector formulas for the velocities and accelerations of the points of the body.
Complex point movement
Basic concepts
To study some, more complex types of motions of a rigid body, it is advisable to consider the simplest complex motion of a point. In many problems, the motion of a point has to be considered relative to two (or more) frames of reference moving relative to each other. Thus, the motion of a spacecraft moving towards the Moon must be considered both relative to the Earth and relative to the Moon, which is moving relative to the Earth. Any movement of a point can be considered complex, consisting of several movements. For example, the movement of a ship along a river relative to the Earth can be considered complex, consisting of movement on water and along with flowing water.
In the simplest case, the complex motion of a point consists of relative and translational motions. Let's define these movements. Let we have two frames of reference moving relative to each other. If one of these systems O l x 1 y 1 z 1(Fig. 19 ) be taken as the main or fixed one (its movement relative to other frames of reference is not considered), then the second frame of reference Oxyz will move relative to the first. Movement of a point relative to a moving frame of reference Oxyz called relative. The characteristics of this movement, such as trajectory, velocity, and acceleration, are called relative. They are denoted by the index r; for speed and acceleration v r , a r . Movement of a point relative to the main or fixed system of reference O 1 x 1 y 1 z 1 called absolute(or difficult ). It is also sometimes called composite movement. The trajectory, speed and acceleration of this movement are called absolute. The speed and acceleration of absolute motion are denoted by letters v, a without indexes.
 |
The portable movement of a point is the movement that it performs together with a moving reference system, as a point rigidly fastened to this system at the considered moment in time. Due to relative motion, the moving point at different times coincides with different points of the body S, to which the moving frame of reference is attached. Portable speed and portable acceleration are the speed and acceleration of that point of the body S, with which the moving point coincides at the moment. Portable speed and acceleration denote v e , and e.
If the trajectories of all points of the body S, fastened with a moving reference system, depict in the figure (Fig. 20), then we get a family of lines - a family of trajectories of the portable movement of a point M. Due to the relative motion of the point M at each moment of time it is on one of the trajectories of the portable motion. Dot M can coincide with only one point of each of the trajectories of this family of portable trajectories. In this regard, it is sometimes believed that there are no trajectories of translational motion, since it is necessary to consider lines for which only one point is actually a point of the trajectory as trajectories of portable motion.
In the kinematics of a point, the movement of a point relative to any frame of reference was studied, regardless of whether this frame of reference moves relative to other systems or not. Let us supplement this study with consideration of complex motion, in the simplest case consisting of relative and figurative. One and the same absolute motion, choosing different moving frames of reference, can be considered as consisting of different portable and, accordingly, relative motions.
Addition of speeds
 Let us determine the speed of the absolute motion of a point, if the speeds of the relative and figurative motions of this point are known. Let the point make only one, relative motion with respect to the moving frame of reference Oxyz and at time t occupies position M on the trajectory of relative motion (Fig. 20). At the moment of time t+ t due to the relative motion, the point will be in the position M 1 , having moved MM 1 along the trajectory of the relative motion. Let's assume that the point is involved Oxyz and relative trajectory it will move along some curve to MM 2. If a point participates simultaneously in both relative and figurative movements, then in time A; she will move to MM" along the trajectory of absolute motion and at the moment of time t+at takes a position M". If time At small and then pass to the limit at At, tending to zero, then small displacements along the curves can be replaced by segments of chords and taken as displacement vectors. Adding the vector displacements, we get
Let us determine the speed of the absolute motion of a point, if the speeds of the relative and figurative motions of this point are known. Let the point make only one, relative motion with respect to the moving frame of reference Oxyz and at time t occupies position M on the trajectory of relative motion (Fig. 20). At the moment of time t+ t due to the relative motion, the point will be in the position M 1 , having moved MM 1 along the trajectory of the relative motion. Let's assume that the point is involved Oxyz and relative trajectory it will move along some curve to MM 2. If a point participates simultaneously in both relative and figurative movements, then in time A; she will move to MM" along the trajectory of absolute motion and at the moment of time t+at takes a position M". If time At small and then pass to the limit at At, tending to zero, then small displacements along the curves can be replaced by segments of chords and taken as displacement vectors. Adding the vector displacements, we get
![]() In this regard, small quantities of a higher order are discarded, tending to zero at At, tending to zero. Passing to the limit, we have (14)
In this regard, small quantities of a higher order are discarded, tending to zero at At, tending to zero. Passing to the limit, we have (14)
Therefore, (14) takes the form (15)
The so-called velocity addition theorem is obtained: the speed of the absolute motion of a point is equal to the vector sum of the velocities of the portable and relative motions of this point. Since, in the general case, the speeds of translational and relative motions are not perpendicular, then (15 ')
Similar information.
Rotational motion of a rigid body. Rotational is the movement of a rigid body, in which all its points lying on a certain straight line, called the axis of rotation, remain motionless.
During rotational motion, all other points of the body move in planes perpendicular to the axis of rotation and describe circles whose centers lie on this axis.
To determine the position of a rotating body, we draw two half-planes through the z-axis: half-plane I - fixed and half-plane II - connected with a solid body and rotating with it (Fig. 2.4). Then the position of the body at any moment of time will be uniquely determined by the angle j between these half-planes, taken with the corresponding sign, which is called the angle of rotation of the body.
When the body rotates, the angle of rotation j changes depending on time, i.e. it is a function of time t:
This equation is called equation rotational motion of a rigid body.
The main kinematic characteristics of the rotational motion of a rigid body are its angular velocity w and angular acceleration e.
If in time D t= t1 + t the body makes a turn by Dj = j1 –j, then the average angular velocity of the body over this period of time will be equal to
 (1.16)
(1.16)
To determine the value of the angular velocity of the body at a given time t find the limit of the ratio of the rotation angle increment Dj to the time interval D t as the latter tends to zero:
 (2.17)
(2.17)
Thus, the angular velocity of the body at a given moment of time is numerically equal to the first derivative of the angle of rotation with respect to time. The sign of the angular velocity w coincides with the sign of the angle of rotation of the body j: w > 0 for j > 0, and vice versa, if j < 0. then w < 0. The unit of angular velocity is usually 1/s, so the radian is a dimensionless quantity.
The angular velocity can be represented as a vector w , the numerical value of which is equal to dj/dt which is directed along the axis of rotation of the body in the direction from which the rotation is seen to occur counterclockwise.
The change in the angular velocity of the body over time characterizes the angular acceleration e. By analogy with finding the average value of the angular velocity, we find an expression for determining the value of the average acceleration:
 (2.18)
(2.18)
Then the acceleration of the rigid body at a given time is determined from the expression
 (2.19)
(2.19)
i.e., the angular acceleration of the body at a given moment of time is equal to the first derivative of the angular velocity or the second derivative of the angle of rotation of the body with respect to time. The dimension of angular acceleration is 1/s 2 .
The angular acceleration of a rigid body, like the angular velocity, can be represented as a vector. The vector of angular acceleration coincides in direction with the vector of angular velocity during the accelerated motion of a solid top and is directed in the opposite direction during slow motion.
Having established the characteristics of the motion of a rigid body as a whole, let us proceed to the study of the motion of its individual points. Consider some point M a rigid body located at a distance h from the axis of rotation r (Fig. 2.3).
When the body rotates, the point M will describe a circumferential point of radius h centered on the axis of rotation and lying in a plane perpendicular to this axis. If during the time dt an elementary turn of the body occurs at an angle dj , then point M at the same time, it performs an elementary displacement along its trajectory dS = h * dj ,. Then the speed of the point M was determined from the expression
![]() (2.20)
(2.20)
The speed is called the linear or circumferential speed of the point M.
Thus, the linear velocity of a point of a rotating rigid body is numerically equal to the product of the angular velocity of the body and the distance from this point to the axis of rotation. Since for all points of the body the angular velocity w; has the same value, then from the formula for the linear velocity it follows that the linear velocities of the points of the rotating body are proportional to their distances from the axis of rotation. The linear velocity of a point of a rigid body is a vector n directed tangentially to the circle described by the point M.
White is the distance from the axis of rotation of the solid ash to a certain point M considered as the radius vector h of the point M, then the linear velocity vector of the point v can be represented as the vector product of the angular velocity vector w radius vector h:
V = w * h (2/21)
Indeed, the result of the vector product (2.21) is a vector equal in absolute value to the product w * h and directed (Fig. 2.5) perpendicular to the plane in which the two factors lie, in the direction from which the closest combination of the first factor with the second is observed to occur counterclockwise , i.e. tangential to the trajectory of the point M.
Thus, the vector resulting from the cross product (2.21) corresponds in absolute value and in direction to the linear velocity vector of the point M.

Rice. 2.5
To find expression for acceleration a point M we perform time differentiation of expression (2.21) for the speed of the point
 (2.22)
(2.22)
Considering that dj/dt=e, and dh/dt = v, we write expression (2.22) as
where a r and an, respectively, are the tangential and normal components of the total acceleration of the point of the body during rotational motion, determined from the expressions
The tangential component of the full acceleration of the body point (tangential acceleration) at characterizes the change in the velocity vector modulo and is directed tangentially to the trajectory of the body point in the direction of the velocity vector during accelerated motion or in the opposite direction during slow motion. The modulus of the tangential acceleration vector of a point of a body during the rotational motion of a rigid body is determined by the expression
![]() (2,25)
(2,25)
Normal component of full acceleration (normal acceleration) a" arises due to a change in the direction of the velocity vector of a point during dyeing of a solid body. As follows from expression (2.24) for normal acceleration, this acceleration is directed along the radius h to the center of the circle along which the point moves. The modulus of the vector of normal acceleration of a point during the rotational motion of a rigid body is determined, taking into account (2.20), by the expression
In nature and technology, we often encounter the manifestation of the rotational motion of solid bodies, such as shafts and gears. How this type of motion is described in physics, what formulas and equations are used for this, these and other issues are covered in this article.
What is rotation?
Each of us intuitively imagines what kind of movement we are talking about. Rotation is a process in which a body or material point moves along a circular path around some axis. From a geometric point of view, a rigid body is a straight line, the distance to which remains unchanged during the movement. This distance is called the radius of rotation. In what follows, we will denote it by the letter r. If the axis of rotation passes through the center of mass of the body, then it is called its own axis. An example of rotation around its own axis is the corresponding movement of the planets of the solar system.
For rotation to occur, there must be a centripetal acceleration, which arises due to the centripetal force. This force is directed from the center of mass of the body to the axis of rotation. The nature of the centripetal force can be very different. So, on a cosmic scale, its role is played by gravity, if the body is fixed by a thread, then the tension force of the latter will be centripetal. When a body rotates around its own axis, the role of the centripetal force is played by the internal electrochemical interaction between the elements (molecules, atoms) that make up the body.
It must be understood that without the presence of a centripetal force, the body will move in a straight line.
Physical quantities describing rotation

First, these are dynamic characteristics. These include:
- angular momentum L;
- moment of inertia I;
- moment of force M.
Secondly, these are kinematic characteristics. Let's list them:
- rotation angle θ;
- angular velocity ω;
- angular acceleration α.
Let us briefly describe each of these quantities.
The angular momentum is determined by the formula:
Where p is the linear momentum, m is the mass of the material point, v is its linear velocity.
The moment of inertia of a material point is calculated using the expression:
For any body of complex shape, the value of I is calculated as the integral sum of the moments of inertia of material points.
The moment of force M is calculated as follows:
Here F is the external force, d is the distance from the point of its application to the axis of rotation.
The physical meaning of all quantities, in the name of which the word "moment" is present, is similar to the meaning of the corresponding linear quantities. For example, the moment of force shows the possibility of the applied force to inform the system of rotating bodies.
Kinematic characteristics are mathematically defined by the following formulas:
As can be seen from these expressions, the angular characteristics are similar in their meaning to linear ones (velocities v and acceleration a), only they are applicable to a circular trajectory.
Rotation dynamics
In physics, the study of the rotational motion of a rigid body is carried out with the help of two branches of mechanics: dynamics and kinematics. Let's start with dynamics.
Dynamics studies external forces acting on a system of rotating bodies. Let us immediately write down the equation of the rotational motion of a rigid body, and then, we will analyze its constituent parts. So this equation looks like:
Which acts on a system that has a moment of inertia I, causes the appearance of an angular acceleration α. The smaller the value of I, the easier it is with the help of a certain moment M to spin the system up to high speeds in short time intervals. For example, a metal rod is easier to rotate along its axis than perpendicular to it. However, the same rod is easier to rotate about an axis perpendicular to it and passing through the center of mass than through its end.
Law of conservation of L
This quantity was introduced above, it is called the angular momentum. The equation of rotational motion of a rigid body, presented in the previous paragraph, is often written in a different form:
If the moment of external forces M acts on the system during the time dt, then it causes a change in the angular momentum of the system by dL. Accordingly, if the moment of forces is equal to zero, then L = const. This is the law of conservation of the value L. For it, using the relationship between linear and angular velocity, we can write:
L \u003d m * v * r \u003d m * ω * r 2 \u003d I * ω.
Thus, in the absence of the moment of forces, the product of the angular velocity and the moment of inertia is a constant value. This physical law is used by figure skaters in their performances or artificial satellites that need to be rotated around their own axis in outer space.

centripetal acceleration
Above, when studying the rotational motion of a rigid body, this quantity has already been described. The nature of the centripetal forces was also noted. Here we will only supplement this information and give the corresponding formulas for calculating this acceleration. Let's denote it a c .
Since the centripetal force is directed perpendicular to the axis and passes through it, it does not create a moment. That is, this force has absolutely no effect on the kinematic characteristics of rotation. However, it creates a centripetal acceleration. Here are two formulas for its definition:
Thus, the greater the angular velocity and radius, the greater the force must be applied to keep the body on a circular path. A striking example of this physical process is the skidding of a car during a turn. A skid occurs if the centripetal force, the role of which is played by the friction force, becomes less than the centrifugal force (inertial characteristic).

The three main kinematic characteristics were listed above in the article. a solid body is described by the following formulas:
θ = ω*t => ω = const., α = 0;
θ = ω 0 *t + α*t 2 /2 => ω = ω 0 + α*t, α = const.
The first line contains formulas for uniform rotation, which assumes the absence of an external moment of forces acting on the system. The second line contains formulas for uniformly accelerated motion in a circle.

Note that rotation can occur not only with a positive acceleration, but also with a negative one. In this case, in the formulas of the second row, you should put a minus sign in front of the second term.
Problem solution example
A moment of force of 1000 N*m acted on the metal shaft for 10 seconds. Knowing that the moment of inertia of the shaft is 50 kg * m 2, it is necessary to determine the angular velocity that the said moment of force gave to the shaft.

Applying the basic equation of rotation, we calculate the acceleration of the shaft:
Since this angular acceleration acted on the shaft during the time t = 10 seconds, we use the formula for uniformly accelerated motion to calculate the angular velocity:
ω = ω 0 + α*t = M/I*t.
Here ω 0 = 0 (the shaft did not rotate until the moment of forces M).
We substitute the numerical values of the quantities into equality, we get:
ω \u003d 1000/50 * 10 \u003d 200 rad / s.
To translate this number into the usual revolutions per second, you need to divide it by 2 * pi. After completing this action, we get that the shaft will rotate at a frequency of 31.8 rpm.
DEFINITION: Rotational motion of a rigid body we will call such a movement in which all points of the body move along circles whose centers lie on the same straight line, called the axis of rotation.
To study the rotational dynamics, to the known kinematic quantities, we add more two quantities: moment of power(M) and moment of inertia(J).
1. From experience it is known: the acceleration of rotational motion depends not only on the magnitude of the force acting on the body, but also on the distance from the axis of rotation to the line along which the force acts. To characterize this circumstance, a physical quantity called moment of force.
Let's consider the simplest case.
DEFINITION: The moment of force relative to some point “O” is the vector quantity defined by the expression , where is the radius vector drawn from the point “O” to the point of application of the force.
It follows from the definition that is an axial vector. Its direction is chosen so that the rotation of the vector around the point “O” in the direction of the force and the vector form a right-handed system. The modulus of the moment of force is , where a is the angle between the directions of the vectors and , and l= r sin a is the length of the perpendicular dropped from the point “O” to the straight line along which the force acts (called shoulder of strength relative to the point “O”) (Fig. 4.2).
2. Experimental data show that the magnitude of the angular acceleration is influenced not only by the mass of the rotating body, but also by the distribution of mass relative to the axis of rotation. The quantity that takes this circumstance into account is called moment of inertia about the axis of rotation.
DEFINITION: Strictly speaking, moment of inertia body relative to some axis of rotation is called the value of J, equal to the sum of the products of elementary masses by the squares of their distances from the given axis.
The summation is carried out over all elementary masses into which the body was divided. It should be borne in mind that this quantity (J) exists irrespective of rotation (although the concept of the moment of inertia was introduced when considering the rotation of a rigid body).
Each body, regardless of whether it is at rest or rotates, has a certain moment of inertia about any axis, just as a body has mass, regardless of whether it is moving or at rest.
Given that , the moment of inertia can be represented as: . This ratio is approximate and it will be the more accurate, the smaller the elementary volumes and the mass elements corresponding to them. Therefore, the problem of finding the moments of inertia is reduced to integration: . Here, the integration is carried out over the entire volume of the body.
Let us write down the moments of inertia of some bodies of regular geometric shape.
| 1. Homogeneous long rod. | |
| Rice. 4.3 | The moment of inertia about the axis perpendicular to the rod and passing through its middle is equal to |
| 2. Solid cylinder or disk. | |
| Rice. 4.4 | The moment of inertia about the axis coinciding with the geometric axis is . |
| 3. Thin-walled cylinder of radius R. | |
| Rice. 4.5 | |
| 4. Moment of inertia of a ball of radius R about an axis passing through its center | |
| Rice. 4.6 | |
| 5. Moment of inertia of a thin disk (thickness b< | |
| Rice. 4.7 | |
| 6. Moment of inertia of the bar | |
| Rice. 4.8 | |
| 7. Moment of inertia of the ring | |
| Rice. 4.9 |
Calculations of the moment of inertia are quite simple here, because the body is assumed to be homogeneous and symmetrical, and the moment of inertia is determined relative to the axis of symmetry.
To determine the moment of inertia of a body about any axis, you must use the Steiner theorem.
DEFINITION: Moment of inertia J relative to an arbitrary axis is equal to the sum of the moment of inertia J c about an axis parallel to the given one and passing through the center of inertia of the body, and the product of the body mass times the square of the distance between the axes (Fig. 4.10).
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0

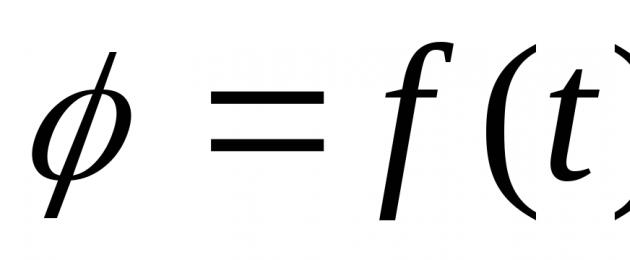
 .
. .
. .
.