Transformaciones de coordenadas afines para tontos. Transformaciones afines usando coordenadas homogéneas.

En coordenadas homogéneas, un punto se escribe como para cualquier factor de escala. Además, si a un punto se le da su representación en coordenadas homogéneas, entonces sus coordenadas cartesianas bidimensionales se pueden encontrar como y.

Significado geométrico coordenadas homogéneas es la siguiente (Fig. 6). punto arbitrario en una recta

Arroz. 6. Interpretación geométrica de coordenadas homogéneas.

Así, se establece una correspondencia uno a uno entre el punto productivo de coordenadas (x, y) y el conjunto de ternas de números de la forma (W×x, W×y, W), W≠0, lo que permite Consideremos los números W×x, W×y, W nuevas coordenadas de este punto. Por tanto, las coordenadas homogéneas se pueden representar como una incrustación de un plano bidimensional escalado por un factor W en el plano z = W (aquí z = 1) en un espacio tridimensional.

El uso de coordenadas homogéneas resulta conveniente a la hora de resolver incluso los problemas más simples.

Si el dispositivo de visualización funciona sólo con números enteros (o si es necesario trabajar sólo con números enteros), entonces para un valor arbitrario de W (por ejemplo, W=1) no se puede representar un punto con coordenadas uniformes (0,5; 0,1; 2,5). representado. Sin embargo, con una elección razonable de W, es posible asegurar que las coordenadas de este punto sean números enteros. En particular, con W=10 para el ejemplo considerado tenemos (5; 1; 25).

Otro caso. Para evitar que los resultados de la transformación conduzcan a un desbordamiento aritmético, para un punto con coordenadas (80000; 40000; 1000), puede tomar, por ejemplo, W=0,001. Como resultado, obtenemos (80; 40; 1).

Sin embargo, la principal aplicación de las coordenadas homogéneas son las transformaciones geométricas, ya que con la ayuda de tripletes de coordenadas homogéneas y matrices de tercer orden se puede describir cualquier transformación afín en el plano. De manera similar, utilizando cuádruples de coordenadas homogéneas y matrices de cuarto orden, se puede describir cualquier transformación en un espacio tridimensional.

Como es sabido, las transformaciones de traslación, escala y rotación en forma matricial se escriben como

P' = P × S;

La traducción se implementa por separado (mediante la suma) del escalado y la rotación (mediante la multiplicación). Si expresamos puntos en coordenadas homogéneas, entonces las tres transformaciones se pueden realizar mediante multiplicaciones. Aquí veremos las transformaciones 2D.

Las ecuaciones de transporte se escriben en forma de matriz de transformación de coordenadas homogéneas de la siguiente manera:

P' = P × T(dx, dy),

.

A veces, estas expresiones se escriben de la siguiente manera:

Consideremos, por ejemplo, la traducción de doble punto. Sea necesario mover el punto P al punto P’ a una distancia (dx1, dy1), y luego a P’’ a una distancia (dx2, dу2). La transferencia total debe ser igual a la distancia (dх1+d2, dу1+dу2). Escribamos los datos en el formulario.

P’ = P × T (dx1, dy1);

P'' = P' × T (dx2, dy2).

Sustituyendo la primera fórmula en la segunda, obtenemos

P’’ = P × (T (dx1, dy1) × T (dx2, dy2)).

El producto matricial T (dx1, dy1) ∙ T (dx2, dy2) es

Por tanto, la transferencia resultante es (dx1+dx2, dy1+dy2), es decir Los acarreos sucesivos son aditivos.

Las ecuaciones de escala en forma matricial usando coordenadas homogéneas se escriben como

,

.

P’ = P’ × S(Sx, Sy).

El producto matricial S(Sx1, Sy1) × S(Sx2, Sy2) es

Por tanto, las escalas sucesivas son multiplicativas.

Finalmente, la ecuación de rotación (en un sistema diestro) se puede representar como

.

Las rotaciones sucesivas son aditivas.

Composición de transformaciones 2D utilizando coordenadas homogéneas.. El producto matricial se llama en diferentes casos. unión, conexión, concatenación Y composición. Usaremos el último de los términos enumerados.

Consideremos, por ejemplo, la rotación de un objeto con respecto a algún punto arbitrario P1. Como sólo sabemos rotar alrededor del origen, dividimos el problema original en tres subproblemas:

Traslación, en la que el punto P1 se desplaza al origen;

Doblar;

Una traslación en la que un punto desde el origen regresa a su posición original P1.

La secuencia de estas transformaciones se muestra en la Fig. 7.1.

Arroz. 7.1. Girar un objeto alrededor de algún punto arbitrario.

La transformación resultante parece

Utilizando un enfoque similar, puede escalar un objeto en relación con un punto arbitrario P1: mueva P1 al origen, escale y muévalo de regreso al punto P1. La transformación resultante en este caso se verá así

Consideremos una transformación más compleja. Supongamos que necesitamos escalar, rotar y posicionar un objeto en la ubicación deseada (la casa en la Fig. 7.2), donde el centro de rotación y escalamiento es el punto P1.

Arroz. 7.2. ejemplo de secuencia de conversión

La secuencia de transformaciones consiste en mover el punto P1 al origen, escalar y rotar, para luego pasar del origen a una nueva posición P2. La estructura de datos del programa de aplicación que contiene esta transformación puede contener los factores de escala, el ángulo de rotación y las cantidades de traslación, o la matriz de transformación resultante puede escribirse:

T (-x1, -y1) × S (Sx, Sy) × R (A) × T (x2, y2).

En general, la multiplicación de matrices no es conmutativa. Si M1 y M2 representan traslación, escalamiento o rotación elemental, la conmutatividad se cumple en los siguientes casos especiales:

M1	M2
Traducir escala Rotar escala (en Sx=Sy)	Traducir Zoom Girar Girar

La composición de la forma más general, formada por las operaciones R, S y T, tiene la matriz

Su parte superior El 2 × 2 es la matriz combinada de rotación y escala, mientras que tx y ty describen la traslación neta. Para calcular P∙M como producto de un vector y una matriz de 3 × 3, se requieren 9 operaciones de multiplicación y 6 operaciones de suma. La estructura de la última columna de la matriz generalizada nos permite simplificar las acciones reales realizadas.

Primero, definamos ¿qué son las transformaciones? Digamos que tenemos un modelo (para simplificar, sea un triángulo). Y tres espacios de coordenadas: espacio de objetos (en el que se describe este triángulo), espacio mundial y espacio de cámara. Entonces, una transformación es una expresión de las coordenadas de un objeto ubicado en un sistema de coordenadas (objeto), utilizando las coordenadas de otro sistema de coordenadas (primero el mundo y luego la cámara).

Como escribí antes, usar diferentes espacios de coordenadas facilita la creación de un mundo virtual. Los objetos se crean en el espacio de objetos y cada objeto tiene su propio espacio de coordenadas. El espacio mundial conecta todos los objetos del mundo virtual y te permite hacer muy simples cosas muy difíciles (por ejemplo, objetos en movimiento). Una vez creada la escena y movidos todos los objetos, las coordenadas mundiales se convierten al espacio de coordenadas de la cámara. Sólo usaremos una cámara, pero en situaciones de la vida real es posible crear varias. Por ejemplo, en el brillante juego Earth 2150: Escape from the blue planet se utilizaron varias cámaras.

Entonces, ¿de qué estoy hablando? Las transformaciones son necesarias para utilizar múltiples espacios de coordenadas.

Primero, recordemos algo sobre los vectores. La siguiente figura nos ayudará con esto:

Qué vemos aquí: el espacio de coordenadas mundial formado por los ejes x, y, z. Vectores unitarios i, j, k se denominan vectores unitarios o vectores base del espacio de coordenadas mundial. Usando la suma de estos vectores, puedes obtener cualquier vector en el espacio de coordenadas mundial.

v- un vector que conecta el origen de las coordenadas mundiales y el origen de las coordenadas del objeto. La longitud del vector v es igual a la distancia entre el origen de las coordenadas mundiales y el origen de las coordenadas del objeto. Considere la forma vectorial v=(5,2,5):

v=x* i+ y* j+z* k = 5*i + 2*j + 5*k

Como escribí anteriormente, con la ayuda de vectores base puedes representar cualquier punto (vector) de un espacio dado, que es lo que demuestra esta ecuación.

Vectores pag,q,r- vectores base del espacio de objetos. Tenga en cuenta que i,j,k no necesariamente será igual pag,q,r.

En esta figura, he omitido una serie de detalles: en el espacio de coordenadas del objeto, se especifican tres puntos que forman un triángulo. Además, no indiqué la cámara, que apunta hacia el triángulo.

Transformaciones de coordenadas lineales usando matrices.

Primero, veamos los vectores unitarios. i,j,k, que en dirección coinciden con los ejes de coordenadas del espacio mundial y se denominan vectores unitarios o vectores base del espacio mundial.

Escribamos estos vectores en forma de coordenadas como matrices:

i= [ yo x yo y yo z ] = [ 1 0 0 ] j= [ j x j y j z ] = [ 0 1 0 ] k= [ k x k y k z ] = [ 0 0 0 ]

Aquí los vectores están representados por matrices de 1x3 (matrices de filas).

Podemos escribir estos vectores base usando una sola matriz:

E incluso, lo que es mucho más importante, podemos escribir estos vectores así:

Como podemos ver, resultó matriz de identidad tamaño 3x3 o 4x4.

Al parecer, ¿qué hay de malo en eso? Piénselo, es posible escribir algunos vectores básicos estúpidos del espacio en una matriz. ¡¡¡Pero no, no “pensarás”!!! Es aquí donde uno de los más terribles secretos programación tridimensional.

Como escribí anteriormente, cualquier punto que esté presente en mundo virtual, se puede escribir en forma vectorial:

v=x* i+ y* j+z* k

Dónde v- punto en el espacio, x,y,z - coordenadas del punto v, A i,j,k- vectores base del espacio. Observe que aquí estamos hablando de un punto, pero estamos mirando un vector. Espero que recuerdes que un vector y un punto son esencialmente lo mismo.

La fórmula anterior se llama forma vectorial de un vector. Hay otro nombre: combinación lineal de vectores. Por cierto, esto es cierto.

Ahora miremos el vector nuevamente. v. Escribámoslo en una matriz de filas: v = [ 5 2 5 ]

Tenga en cuenta que la longitud del vector v es la distancia desde el origen del espacio de coordenadas mundial hasta el origen del espacio de coordenadas del objeto.

Intentemos multiplicar este vector por una matriz en la que están escritos los vectores básicos del espacio mundial (espero que recuerdes la fórmula de multiplicación de matrices):

Como resultado, obtenemos la siguiente ecuación:

v M = [ (xi x + yj x + zk x) (xi y + yj y + zk y) (xi z +yj z + zk z) ]

Tenemos un vector. Aquellos. El resultado de multiplicar un vector por una matriz es un vector. En este caso, el vector no ha cambiado. Pero si los elementos de la matriz no son unos (en la diagonal principal) y ceros (todos los demás elementos), sino algunos otros números, entonces el vector cambiará. Por tanto, podemos decir que la matriz M realiza una transformación de espacios de coordenadas. Considere la fórmula general:

a, b son vectores, M es la matriz de transformación de espacios de coordenadas. La fórmula se puede leer de la siguiente manera: “la matriz M transforma el punto a en el punto b”.

Para mayor claridad, veamos un ejemplo. Necesitamos convertir las coordenadas del espacio de objetos (p,q) al espacio mundial (i,j):

i,j- vectores básicos del espacio mundial, pag,q- vectores base del espacio de objetos. En la imagen puede ver que el espacio de coordenadas del objeto gira -45 grados alrededor del eje z (no es visible en la imagen). Además, los vectores q,pag 1,5 veces más vectores i,j, lo que significa que los objetos definidos en el espacio de objetos se verán una vez y media más pequeños en el espacio mundial.

Para visualizar cómo se verá el modelo de espacio de objetos después de la transformación, puede agregar un marco para vectores. i,j:

Puedes dibujar el mismo marco para pag,q, pero no abarroté el dibujo.

Ahora, digamos que hemos dibujado un triángulo en el espacio de objetos (Fig. a). En el espacio mundial, este triángulo se rotará 45 grados y se reducirá en un tercio (Fig. b):

Ahora recopilemos todos los elementos del rompecabezas: como sabemos, la transformación se puede realizar mediante una matriz. Las filas de las matrices son los vectores base. Las coordenadas de los vectores básicos del espacio de coordenadas mundial en el espacio de objetos son las siguientes:

i = [ 0.473 0.473 ] j = [ -0.473 0.473 ]

¿Cómo descubrimos las coordenadas? Primero, sabemos que los espacios de coordenadas giran 45 grados entre sí. En segundo lugar, los vectores de base espacial de objetos son 1,5 veces más largos que los vectores de base espacial mundial. Sabiendo esto, calculamos fácilmente las coordenadas de los vectores. i,j.

Como resultado, obtenemos la siguiente matriz de transformación (en este caso, rotación o rotación):

O en un espacio tridimensional:

Todos los valores son aproximados.

Esta es una matriz para transformar coordenadas del espacio de objetos al espacio inercial (les recuerdo que los vectores base del espacio inercial coinciden con los vectores base del espacio mundial). Para convertir un triángulo del espacio de objetos al espacio inercial, debes multiplicar todos los puntos (vectores) del triángulo por la matriz de transformación.

En el último ejemplo, encontramos dos transformaciones: rotación y escala. Ambas transformaciones son lineales.

Ahora que hemos visto ejemplos de transformaciones lineales, podemos familiarizarnos con la definición:

Las transformaciones lineales son transformaciones de coordenadas que no distorsionan los espacios. Aquellos. todas las líneas paralelas siguen siendo paralelas (sin embargo, hay una excepción). O simplemente: con transformaciones lineales, un triángulo nunca se convertirá en un círculo o un cuadrado, sino que siempre seguirá siendo un triángulo.

Ahora que entendemos aproximadamente qué son las transformaciones lineales, veamos fórmulas específicas:

Escala

k 1 ,k 2 ,k 3 - factores de escala. Si k 1, los objetos aumentan.

Rotación

Rotación alrededor del eje x:

Rotación alrededor del eje y:

Rotación alrededor del eje z:

Por cierto, es esta matriz (de rotación alrededor del eje z) la que usamos anteriormente.

La rotación puede realizarse no sólo alrededor de los ejes que forman el espacio de coordenadas, sino también alrededor de líneas rectas arbitrarias. La fórmula para girar alrededor de una línea recta arbitraria es bastante compleja y todavía no estamos preparados para considerarla.

Lo más importante que debes recordar de lo anterior es esto: las filas de la matriz de transformación contienen los vectores base del nuevo espacio de coordenadas, expresados ​​en términos de las coordenadas del antiguo espacio de coordenadas. .

Si comprende esto simple (que la matriz contiene los vectores base del nuevo espacio), al observar la matriz de transformación, podrá ver fácilmente el nuevo espacio de coordenadas.

Y lo último:
Las transformaciones lineales no pueden mover objetos. Aquellos. Los objetos se pueden ampliar/reducir, se pueden rotar, pero permanecerán inmóviles.

Transformaciones afines

Las transformaciones afines son transformaciones lineales con traducción. Usando transformaciones afines puedes mover objetos.

La fórmula es muy sencilla:

A = bM + v;

Donde b es el punto de partida, M es la matriz de transformación lineal, a es el punto de transformación y v es el vector que conecta los dos espacios. O dicho de otro modo, es un vector cuya longitud es igual a la distancia entre dos espacios de coordenadas.

En la imagen al comienzo de la lección, lo que se necesita es la transformación afín: primero, una transformación lineal del espacio de objetos al espacio inercial, y luego la transferencia de todos los puntos del espacio de objetos al espacio mundial usando el vector v.

Para simplificar los cálculos en la programación de gráficos 3D, se utilizan vectores 4D, matrices 4x4 y las llamadas coordenadas homogéneas. La cuarta dimensión no juega ningún papel; se introduce sólo para simplificar los cálculos.

Un vector de cuatro dimensiones, como habrás adivinado, utiliza cuatro componentes: x, y, z y w. El cuarto componente del vector se llama coordenada homogénea.

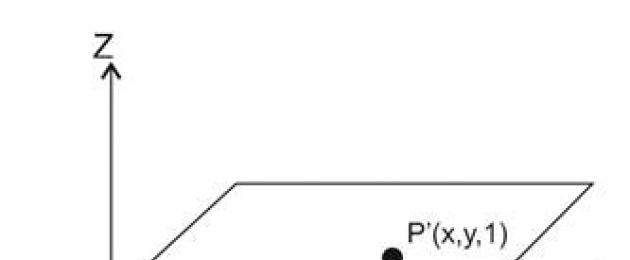
Es muy difícil representar geométricamente una coordenada homogénea. Por tanto, consideraremos un espacio tridimensional homogéneo de coordenadas (x,y,w). Imaginemos que se define un plano bidimensional en el punto w=1. En consecuencia, un punto bidimensional se representa en un espacio homogéneo mediante las siguientes coordenadas (x,y,1). Todos los puntos en el espacio que no están en el plano (están en planos donde w! = 1) se pueden calcular proyectando sobre un plano bidimensional. Para hacer esto, es necesario dividir todos los componentes de este punto en uno homogéneo. Aquellos. si w!=1, en el plano “físico” (donde trabajamos y donde w=1) las coordenadas del punto serán las siguientes: (x/w,y/w,w/w) o (x/w ,año/año ,1). Mira la imagen:

Las coordenadas de los vectores son las siguientes:

V 1 = [ 3 3 3 ] v 2 = [ 3 1 0 ] v 3 = [ 3 -2 -2 ]

Estos vectores se proyectan en el plano "físico" (w=1) de la siguiente manera:

V 1 = [ 1 1 1 ] v 3 = [ -1,5 1 1 ]

La figura muestra tres vectores. Tenga en cuenta que cuando un punto se encuentra en el plano w=0, entonces este punto no se puede proyectar al plano físico (vector v 2).

Para cada punto del plano físico, existe un número infinito de puntos en un espacio homogéneo.

En el espacio de cuatro dimensiones todo es exactamente igual. Trabajamos en un espacio físico donde w = 1: (x,y,z,1). Si, como resultado de los cálculos, w != 1, entonces es necesario dividir todas las coordenadas del punto en una homogénea: (x/w,y/w,z/w,w/w) o (x/ w,y/w,z/w,1). También hay un caso especial cuando w = 0. Lo veremos más adelante.

Ahora pasemos a la práctica: ¿por qué diablos necesitamos una coordenada homogénea?

Como ya hemos descubierto, una matriz de 3x3 representa una transformación lineal, es decir no contiene transferencia (movimiento). Se utiliza un vector separado para la transferencia (y esta es una transformación afín):

V = aM + b

Aquellos. multiplicamos todos los puntos (vectores) del objeto por la matriz de transformación M para ir al sistema de coordenadas inercial (cuyos vectores base coinciden con los vectores base del sistema de coordenadas mundial), y luego llegamos al espacio mundial usando el vector b. . Permítanme recordarles que el vector b conecta el comienzo del espacio de objetos y el comienzo del espacio mundial.

Entonces, usando cuatro dimensiones, puedes agrupar tanto transformaciones lineales (rotación, escalamiento) como traslación en una sola matriz.

Imaginemos que el cuarto componente es siempre igual a uno (aunque ya hemos descubierto que no es así). Ahora la transformación lineal se puede representar usando una matriz de 4x4:

Veamos la fórmula para multiplicar vectores por una matriz de transformación en un espacio de cuatro dimensiones:

V x = (xi x + yj x + zk x + w*0) v y = (xi y + yj y + zk y + w*0) v z = (xi z + yj z + zk z + w*0) v w = (x*0 + y*0 + z*0 + w*1) Como podemos ver, las componentes del vector transformado usando una matriz de 4x4 son iguales a las componentes del vector transformado usando una matriz de 3x3. El cuarto componente, como acordamos, siempre será igual a uno, por lo que simplemente podemos descartarlo. Por tanto, podemos decir que las transformaciones realizadas por matrices de tamaño 3x3 y 3x4 son equivalentes.

Ahora veamos la matriz de transferencia:

Multiplique cualquier vector del espacio de objetos (vea la figura al comienzo de la lección) por esta matriz y podrá expresar este vector en el espacio de coordenadas mundial (esto es si los vectores base de los espacios de objetos y mundo son iguales).

Tenga en cuenta que esta también es una transformación lineal, solo que en un espacio de cuatro dimensiones.

Usando el producto matricial podemos combinar la matriz de rotación y la matriz de traslación:

Esta última matriz es exactamente la que necesitábamos desde el principio. Debe comprender bien qué significan exactamente todos sus elementos (con excepción de la cuarta columna).

Inglés: Wikipedia está haciendo que el sitio sea más seguro. Eres utilizando un navegador web antiguo que no podrá conectarse a Wikipedia en el futuro. Actualice su dispositivo o comuníquese con su administrador de TI.

中文: 维基百科正在使网站更加安全。您正在使用旧的浏览器，请更新IT ）。

Español: Wikipedia está haciendo el sitio más seguro. Usted está utilizando un navegador web antiguo que no podrá conectarse a Wikipedia en el futuro. Actualice su dispositivo o contacte a su administrador informático. Más abajo hay una actualización más larga y más técnica en inglés.

ﺎﻠﻋﺮﺒﻳﺓ: ويكيبيديا تسعى لتأمين الموقع أكثر من ذي قبل. أنت تستخدم متصفح وب قديم لن يتمكن من الاتصال بموقع ويكيبيديا في المستقبل. يرجى تحديث جهازك أو الاتصال بغداري تقنية المعلومات الخاص بك. يوجد تحديث فني أطول ومغرق في التقنية باللغة الإنجليزية تاليا.

Francés: Wikipédia va bientôt aumenta la seguridad de su sitio. Actualmente utiliza un navegador web antiguo, que no podrá conectarse a Wikipédia cuando lo haga. Merci de mettre à jour su aparato o de contactar su administrador informático à este fin. Hay información complementaria y técnicas en inglés disponibles aquí.

日本語: ? ??? IT情報は以下に英語で提供しています.

Alemán: Wikipedia contiene la seguridad del sitio web. Du benutzt einen alten Webbrowser, der in Zukunft nicht mehr auf Wikipedia zugreifen zugreifen wird. Bitte actualisiere dein Gerät oder sprich deinen IT-Administrator an. Ausführlichere (und technisch Detailliertere) Hinweise findest Du unten in englischer Sprache.

Italiano: Wikipedia está rendendo el sitio más seguro. Siga usando un navegador web que no será capaz de conectarse a Wikipedia en el futuro. Por favor, actualice su dispositivo o comuníquese con su administrador informático. Más en bajo está disponible un aggiornamento más detallado y técnico en inglés.

Magiar: Biztonságosabb lesz en Wikipédia. A böngésző, amit használsz, nem lesz képes kapcsolódni a jövőben. Használj modernebb szoftvert vagy jelezd a problémát a rendszergazdádnak. Alább olvashatod a részletesebb magyarázatot (angolul).

Svenská: Wikipedia gör sidan mer säker. Du använder en äldre webbläsare som inte kommer att kunna läsa Wikipedia i framtiden. Actualícese desde cualquier lugar o póngase en contacto con el administrador de TI. Det finns en langre och mer teknisk förklaring på engelska langre ned.

हिन्दी: विकिपीडिया साइट को और अधिक सुरक्षित बना रहा है। आप एक पुराने वेब ब्राउज़र का उपयोग कर रहे हैं जो भविष्य में विकिपीडिया से कनेक्ट नहीं हो पाएगा। कृपया अपना डिवाइस अपडेट करें या अपने आईटी व्यवस्थापक से संपर्क करें। नीचे अंग्रेजी में एक लंबा और अधिक तकनीकी अद्यतन है।

Estamos eliminando la compatibilidad con versiones inseguras del protocolo TLS, específicamente TLSv1.0 y TLSv1.1, en las que se basa el software de su navegador para conectarse a nuestros sitios. Esto suele deberse a navegadores obsoletos o teléfonos inteligentes Android más antiguos. O podría ser interferencia del software de "seguridad web" personal o corporativo, que en realidad degrada la seguridad de la conexión.

Debe actualizar su navegador web o solucionar este problema para acceder a nuestros sitios. Este mensaje permanecerá hasta el 1 de enero de 2020. Después de esa fecha, su navegador no podrá establecer una conexión con nuestros servidores.

M 1 =(x 1,y 1), M=(x,y). Dado que el punto M divide el segmento M 0 M 1 en relación con λ, entonces

; (1)

Con esta transformación afín, los puntos M 0,M 1,M irán a los puntos M 0 ′,M 1 ′, M′ con las mismas coordenadas que los puntos M 0,M 1,M, pero solo en la O" e sistema de coordenadas " 1 e" 2. Estas coordenadas todavía están conectadas por las relaciones (1), de lo que se deduce que M′ divide el segmento M 0 ′M 1 ′ con relación a λ. Esto demuestra el teorema.

3. Expresión analítica de transformaciones afines (fórmulas de transición).

Tarea:¿Cómo, conociendo los parámetros de un sistema en relación con otro, se puede determinar la posición de un punto en ambos sistemas de coordenadas (es decir, cómo encontrar fórmulas para la transición de un sistema (antiguo) a otro? nuevo sistema.

Consideremos los casos de transformación para sistemas de coordenadas afines.

1) Sea el sistema R = (O, (e 1, e 2)) y sea M = (x,y) R, sean O (0,0) R las coordenadas del origen. e 1 (1,0) R, e 2 (0,1) R – coordenadas de los vectores base.

2) Dejemos que se dé el segundo sistema de coordenadas R′=(O, (e 1 ′, e 2 ′)) y se conozcan los parámetros que definen la nueva base y el nuevo origen a través del antiguo sistema de coordenadas, es decir, O′(x 0 ,y 0) R , mi 1 ′(C 11 ,C 12) R , mi 2 ′(C 12 ,C 22) R

Establezcamos la tarea de encontrar las coordenadas del punto M en el nuevo sistema de coordenadas (M(x′,y′) R ′). Denotamos las coordenadas desconocidas del punto M(x′,y′).

Para tres puntos O,O′,M: O′M=O′O +OM. О′М – vector de radio del punto M en el nuevo sistema de coordenadas, lo que significa que sus coordenadas coincidirán con las coordenadas del vector О′М en el sistema R′ (О′М↔М R ′)=>О′М( x′,y′) R ′ => О′М=x′e 1 ′+y′e 2 ′ (1) ; О′О - vector de radio del punto О′ en el sistema R′, es decir sus coordenadas coincidirán con las coordenadas de О′О↔ О′ R => О′О(x 0 ,y 0) R => О′О= x 0 e 1 +y 0 e 2 (2) ; OM↔ M R => OM=xe 1 +ye 2 (3). Eso. el vector О′М=ОМ −ОО′ después de la sustitución en este vector por la igualdad de desarrollo (1), (2) y (3) tendrá la forma:

x′e 1 ′+y′e 2 ′= xe 1 +ye 2 −(x 0 e 1 +y 0 e 2) (4); porque en la condición se especifican parámetros que determinan las coordenadas de los nuevos vectores base a través de la base anterior, obtenemos las siguientes igualdades vectoriales para los nuevos vectores base:

mi 1 ′(C 11,C 12) R => mi 1 ′= C 11 mi 1 +C 21 mi 2;

mi 2 ′(C 12,C 22) R => mi 2 ′= C 12 mi 1 +C 22 mi 2; (5)

Sustituyamos (5) en el lado izquierdo de (4) y agrupemos con respecto a los vectores base e 1 y e 2.

x′(C 11 e 1 +C 21 e 2)+y′(C 12 e 1 +C 22 e 2)- xe 1 -xe 2 +x 0 e 1 -ye 2 +x 0 e 1 +y 0 e 2 = 0.
(x′C 11 + y′C 12 e 1 -x+x 0)e 1 + (x′C 21 +y′ C 22 -y+y 0)e 2 =0.

Porque (e 1, e 2) forman una base, entonces este es un sistema linealmente independiente para el cual se satisface la última igualdad vectorial siempre que todos los coeficientes del lado izquierdo sean iguales a cero, es decir dado que

(6);

(6) - fórmulas para la transición del antiguo sistema R al nuevo sistema R′ para las variables x′ e y′.

Dado que las columnas del determinante son las coordenadas de los vectores base e 1 ′ y e 2 ′, este determinante nunca desaparece, es decir El sistema (6) tiene solución única con respecto a las variables x′ e y′, lo que siempre permite encontrar una fórmula para la transición inversa de R′ a R.

Para las fórmulas (6) hay dos casos especiales

1. sustitución de la base;

2. transferencia del inicio.

1. Sistema R′ obtenido del sistema R reemplazando la base manteniendo el mismo origen R=(O, (e 1 , e 2))→ R′=(O, (e 1 ′, e 2 ′)), t .mi. O′(x 0 ,y 0)=O(0,0)=>x 0 =y 0 =0, entonces las fórmulas de reemplazo de bases tomarán la forma:

(7)

2. Sea el sistema R′ el que se obtiene a partir de R trasladando el inicio del punto O al punto O′ manteniendo la misma base:
R=(O, (e 1, e 2))→ R′=(O′, (e 1, e 2))=> e 1 ′(1.0), e 2 ′(0.1),t .O. las fórmulas tomarán la forma.