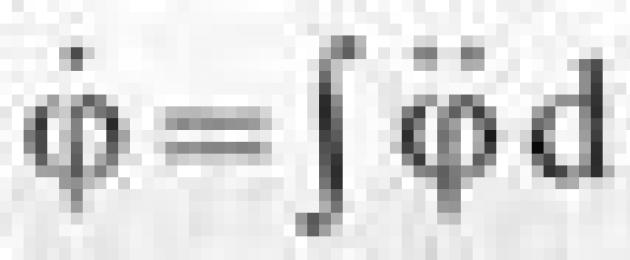Movimiento de rotación de un cuerpo alrededor de un eje. Movimiento de rotación de un cuerpo rígido.

y Saveliev.

Con el movimiento de traslación del cuerpo (§ 60 en el libro de texto de E. M. Nikitin), todos sus puntos se mueven a lo largo de las mismas trayectorias y en cada este momento tienen velocidades iguales y aceleraciones iguales.

Por lo tanto, el movimiento de traslación del cuerpo lo determina el movimiento de cualquier punto, generalmente el movimiento del centro de gravedad.

Considerando en cualquier problema el movimiento de un carro (problema 147) o una locomotora (problema 141), en realidad consideramos el movimiento de sus centros de gravedad.

El movimiento de rotación de un cuerpo (E. M. Nikitin, § 61) no puede identificarse con el movimiento de ninguno de sus puntos. El eje de cualquier cuerpo giratorio (volante diesel, rotor de motor eléctrico, husillo de máquina, aspas de ventilador, etc.) en el proceso de movimiento ocupa el mismo lugar en el espacio en relación con los cuerpos fijos circundantes.

Movimiento de un punto material o movimiento hacia adelante Los cuerpos se caracterizan dependiendo del tiempo. cantidades lineales s (recorrido, distancia), v (velocidad) y a (aceleración) con sus componentes a t y a n .

movimiento de rotación cuerpos en función del tiempo t caracterizar valores angulares: φ (ángulo de rotación en radianes), ω (velocidad angular en rad/s) y ε (aceleración angular en rad/s 2).

La ley del movimiento de rotación de un cuerpo se expresa mediante la ecuación
φ = f(t).

Velocidad angular- el valor que caracteriza la velocidad de rotación del cuerpo, se define en el caso general como la derivada del ángulo de rotación con respecto al tiempo
ω \u003d dφ / dt \u003d f "(t).

Aceleración angular- el valor que caracteriza la tasa de cambio de la velocidad angular, se define como la derivada de la velocidad angular
ε = dω/dt = f"" (t).

Al comenzar a resolver problemas para el movimiento de rotación de un cuerpo, debe tenerse en cuenta que en los cálculos y problemas técnicos, por regla general, el desplazamiento angular no se expresa en radianes φ, sino en revoluciones φ rev.

Por lo tanto, es necesario poder cambiar del número de revoluciones a la medida del desplazamiento angular en radianes y viceversa.

Dado que una revolución completa corresponde a 2π rad, entonces
φ = 2πφ rev y φ rev = φ/(2π).

La velocidad angular en los cálculos técnicos a menudo se mide en revoluciones producidas por minuto (rpm), por lo que debe entenderse claramente que ω rad / seg y n rpm expresan el mismo concepto: la velocidad de rotación del cuerpo (velocidad angular), pero en diferentes unidades - en rad / seg o en rpm.

La transición de una unidad de velocidad angular a otra se realiza según las fórmulas
ω = πn/30 y n = 30ω/π.

Durante el movimiento de rotación del cuerpo, todos sus puntos se mueven a lo largo de círculos, cuyos centros están ubicados en una línea recta fija (el eje del cuerpo en rotación). Al resolver los problemas presentados en este capítulo, es muy importante comprender claramente la relación entre las cantidades angulares φ, ω y ε, que caracterizan el movimiento de rotación del cuerpo, y las cantidades lineales s, v, at y an, que caracterizan el movimiento. de varios puntos de este cuerpo (Fig. 205).

Si R es la distancia desde el eje geométrico del cuerpo giratorio a cualquier punto A (en la Fig. 205 R=OA), entonces la relación entre φ - el ángulo de rotación del cuerpo y s - la distancia recorrida por el punto de el cuerpo en el mismo tiempo, se expresa de la siguiente manera:
s = φR.

La relación entre la velocidad angular de un cuerpo y la velocidad de un punto en un momento dado se expresa mediante la igualdad
v = ωR.

La aceleración tangencial de un punto depende de aceleración angular y está determinada por la fórmula
a t = εR.

La aceleración normal de un punto depende de la velocidad angular del cuerpo y está determinada por la dependencia
un norte = ω 2 R.

Al resolver el problema presentado en este capítulo, es necesario comprender claramente que la rotación se llama movimiento. cuerpo solido, no puntos. tomado por separado punto material no gira, sino que se mueve en círculo: hace un movimiento curvilíneo.

§ 33. Movimiento de rotación uniforme

Si la velocidad angular ω=const, entonces el movimiento de rotación se llama uniforme.

La ecuación de rotación uniforme tiene la forma
φ = φ 0 + ωt.

En un caso particular, cuando el ángulo inicial de rotación φ 0 =0,
φ = ωt.

Velocidad angular de un cuerpo que gira uniformemente
ω = φ/t
también se puede expresar así:
ω = 2π/T,
donde T es el período de rotación del cuerpo; φ=2π - ángulo de rotación para un período.

§ 34. Movimiento de rotación igualmente variable

El movimiento de rotación con velocidad angular variable se denomina no uniforme (ver § 35 a continuación). Si la aceleración angular ε=const, entonces el movimiento de rotación se llama igualmente variable. Por lo tanto, la rotación uniforme del cuerpo - caso especial movimiento de rotación irregular.

Ecuación de rotación de igual variable
(1) φ = φ 0 + ω 0 t + εt 2 /2
y una ecuación que expresa la velocidad angular del cuerpo en cualquier momento,
(2) ω = ω 0 + εt
representan un conjunto de fórmulas básicas para el movimiento rotacional uniforme de un cuerpo.

Estas fórmulas incluyen solo seis cantidades: tres constantes para este problema φ 0 , ω 0 y ε y tres variables φ, ω y t. Por tanto, la condición de cada problema para rotación igualmente variable debe contener al menos cuatro valores dados.

Por conveniencia de resolver algunos problemas, las ecuaciones (1) y (2) pueden usarse para obtener dos fórmulas auxiliares más.

Excluyamos de (1) y (2) la aceleración angular ε:
(3) φ = φ 0 + (ω + ω 0)t/2.

Excluyamos de (1) y (2) el tiempo t:
(4) φ = φ 0 + (ω 2 - ω 0 2)/(2ε).

En el caso particular de la rotación uniformemente acelerada, que parte de un estado de reposo, φ 0 =0 y ω 0 =0. Por lo tanto, las fórmulas principal y auxiliar anteriores toman la siguiente forma:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

§ 35. Movimiento de rotación desigual

Considere un ejemplo de resolución de un problema en el que se da un movimiento de rotación no uniforme de un cuerpo.

Ángulo de dirección, velocidad angular y aceleración angular

Rotación de un cuerpo rígido alrededor de un eje fijo Se denomina movimiento a tal movimiento en el que dos puntos del cuerpo permanecen inmóviles durante todo el tiempo del movimiento. En este caso, todos los puntos del cuerpo ubicados en la línea recta que pasa por sus puntos fijos también permanecen fijos. Esta línea se llama eje de rotación del cuerpo.

Si PERO Y EN- puntos fijos del cuerpo (Fig. 15 ), entonces el eje de rotación es el eje Onz, que puede tener cualquier dirección en el espacio, no necesariamente vertical. Dirección de un eje Onz tomado como positivo.

Dibuja un plano fijo a través del eje de rotación. Por y móvil PAGS, unido a un cuerpo giratorio. Que ambos planos coincidan en el momento inicial del tiempo. Entonces en ese momento t la posición del plano en movimiento y el propio cuerpo giratorio se puede determinar por el ángulo diedro entre los planos y el ángulo lineal correspondiente φ entre rectas situadas en estos planos y perpendiculares al eje de giro. Inyección φ llamado ángulo del cuerpo

La posición del cuerpo en relación con el sistema de referencia elegido está completamente determinada en cualquier

punto en el tiempo si se da la ecuación φ =pie) (5)

donde pie)- cualquier función del tiempo dos veces diferenciable. Esta ecuación se llama la ecuación de rotación de un cuerpo rígido alrededor de un eje fijo.

Un cuerpo que gira alrededor de un eje fijo tiene un grado de libertad, ya que su posición se determina ajustando solo un parámetro: el ángulo φ .

Inyección φ se considera positivo si se grafica en sentido antihorario y negativo si se grafica en la dirección opuesta cuando se ve desde la dirección positiva del eje Onz. Las trayectorias de los puntos del cuerpo durante su rotación alrededor de un eje fijo son círculos ubicados en planos perpendiculares al eje de rotación.

Para caracterizar el movimiento de rotación de un cuerpo rígido alrededor de un eje fijo, presentamos los conceptos de velocidad angular y aceleración angular. Velocidad angular algebraica del cuerpo. en cualquier momento en el tiempo, la primera derivada temporal del ángulo de rotación en ese momento se llama, es decir, dφ/dt = φ. Es un valor positivo cuando el cuerpo gira en sentido contrario a las agujas del reloj, ya que el ángulo de rotación aumenta con el tiempo, y negativo, cuando el cuerpo gira en el sentido de las agujas del reloj, porque el ángulo de rotación disminuye.

El módulo de velocidad angular se denota ω. Luego ω= ׀dφ/dt׀= ׀φ ׀ (6)

La dimensión de la velocidad angular se establece de acuerdo con (6)

[ω] = ángulo/tiempo = rad/s = s -1.

En ingeniería, la velocidad angular es la tasa de rotación expresada en revoluciones por minuto. En 1 minuto el cuerpo girará en un ángulo 2πp, si PAGS- número de revoluciones por minuto. Dividiendo este ángulo por el número de segundos en un minuto, obtenemos: (7)

aceleración angular algebraica del cuerpo se llama la primera derivada temporal de la velocidad algebraica, es decir la segunda derivada del ángulo de rotación re 2 φ / dt 2 \u003d ω. Denotamos el módulo de aceleración angular ε , luego ε=|φ| (8)

La dimensión de la aceleración angular se obtiene de (8):

[ε ] = velocidad angular/tiempo = rad/s 2 = s -2

Si φ’’>0 en φ’>0 , entonces la velocidad angular algebraica aumenta con el tiempo y, en consecuencia, el cuerpo gira aceleradamente en el momento de tiempo considerado en lado positivo(en sentido anti-horario). En φ’’<0 Y φ’<0 el cuerpo gira rápidamente en la dirección negativa. Si φ’’<0 en φ’>0 , entonces tenemos una rotación lenta en la dirección positiva. En φ’’>0 Y φ’<0 , es decir. la rotación lenta es en la dirección negativa. La velocidad angular y la aceleración angular en las figuras están representadas por flechas de arco alrededor del eje de rotación. La flecha de arco para la velocidad angular indica la dirección de rotación de los cuerpos;

Para la rotación acelerada, las flechas de arco para la velocidad angular y la aceleración angular tienen las mismas direcciones para la rotación lenta; sus direcciones son opuestas.

Casos especiales de rotación de un cuerpo rígido

Se dice que una rotación es uniforme si ω=const, φ= φ't

La rotación será uniforme si ε=const. φ'= φ' 0 + φ''t y

En general, si φ’’ no siempre,

Velocidades y aceleraciones de los puntos del cuerpo.

Se conoce la ecuación de rotación de un cuerpo rígido alrededor de un eje fijo φ= f(t)(Figura 16). Distancia s puntos METRO en el plano en movimiento PAGS a lo largo de un arco de círculo (trayectoria de un punto), contado desde un punto M-oh ubicado en un plano fijo, se expresa a través del ángulo φ adiccion s=hφ, donde h es el radio del círculo a lo largo del cual se mueve el punto. Es la distancia más corta desde el punto. METRO al eje de giro. A veces se le llama el radio de rotación de un punto. En cada punto del cuerpo, el radio de rotación permanece sin cambios cuando el cuerpo gira alrededor de un eje fijo.

velocidad de punto algebraico METRO determinado por la fórmula vτ =s'=hφ Módulo de velocidad de punto: v=hω(9)

Las velocidades de los puntos del cuerpo durante la rotación alrededor de un eje fijo son proporcionales a sus distancias más cortas a este eje. El factor de proporcionalidad es la velocidad angular. Las velocidades de los puntos están dirigidas a lo largo de las tangentes a las trayectorias y, por lo tanto, son perpendiculares a los radios de rotación. Velocidades de los puntos del cuerpo ubicados en un segmento de línea recta OM, de acuerdo con (9) se distribuyen de acuerdo con una ley lineal. Son paralelos entre sí y sus extremos están ubicados en una línea recta que pasa por el eje de rotación. Descomponemos la aceleración de un punto en sus componentes tangente y normal, es decir a=a τ +a nτ Las aceleraciones tangente y normal se calculan mediante fórmulas (10)

ya que para un círculo el radio de curvatura pag = h(Figura 17 ). De este modo,

Las aceleraciones tangentes, normales y completas de los puntos, así como las velocidades, también se distribuyen de acuerdo con una ley lineal. Dependen linealmente de las distancias de los puntos al eje de rotación. La aceleración normal se dirige a lo largo del radio del círculo hacia el eje de rotación. La dirección de la aceleración tangencial depende del signo de la aceleración angular algebraica. En φ’>0 Y φ’’>0 o φ’<0 Y φ’<0 tenemos una rotación acelerada del cuerpo y la dirección de los vectores un τ Y v partido. Si φ’ Y φ’" tienen diferentes signos (rotación lenta), entonces un τ Y v dirigidos uno frente al otro.

denotar α el ángulo entre la aceleración total de un punto y su radio de rotación, tenemos

tanα = | un τ |/un norte = ε/ω 2 (11)

ya que la aceleración normal una p siempre positivo. Inyección pero lo mismo para todos los puntos del cuerpo. Debe posponerse desde la aceleración hasta el radio de rotación en la dirección de la flecha del arco de la aceleración angular, independientemente de la dirección de rotación del cuerpo rígido.

Vectores de velocidad angular y aceleración angular

Introduzcamos los conceptos de vectores de velocidad angular y aceleración angular de un cuerpo. Si PARA es el vector unitario del eje de rotación, dirigido en su dirección positiva, entonces los vectores de la velocidad angular ώ y aceleración angular ε determinado por expresiones (12)

Porque k-vector constante en valor absoluto y dirección, entonces de (12) se sigue que

ε=dώ/dt(13)

En φ’>0 Y φ’’>0 direcciones vectoriales ώ Y ε partido. Ambos están dirigidos en la dirección positiva del eje de rotación. Onz(Fig. 18.a) Si φ’>0 Y φ’’<0 , luego se dirigen en direcciones opuestas (Fig. 18.b ). El vector de aceleración angular coincide en dirección con el vector de velocidad angular durante la rotación acelerada y es opuesto a él durante la rotación lenta. Vectores ώ Y ε se puede dibujar en cualquier punto del eje de rotación. Son vectores deslizantes. Esta propiedad se sigue de las fórmulas vectoriales para las velocidades y aceleraciones de los puntos del cuerpo.

Movimiento de punto complejo

Conceptos básicos

Para estudiar algunos tipos de movimientos más complejos de un cuerpo rígido, es recomendable considerar el movimiento complejo más simple de un punto. En muchos problemas, el movimiento de un punto debe considerarse en relación con dos (o más) marcos de referencia que se mueven entre sí. Por lo tanto, el movimiento de una nave espacial que se mueve hacia la Luna debe considerarse tanto en relación con la Tierra como en relación con la Luna, que se mueve en relación con la Tierra. Cualquier movimiento de un punto puede considerarse complejo, que consta de varios movimientos. Por ejemplo, el movimiento de un barco a lo largo de un río en relación con la Tierra puede considerarse complejo, y consiste en el movimiento sobre el agua y junto con el agua que fluye.

En el caso más simple, el movimiento complejo de un punto consta de movimientos relativos y de traslación. Definamos estos movimientos. Tengamos dos marcos de referencia que se mueven uno respecto al otro. Si uno de estos sistemas O l x 1 y 1 z 1(Figura 19 ) ser tomado como el principal o fijo (no se considera su movimiento relativo a otros marcos de referencia), entonces el segundo marco de referencia Oxyz se moverá con respecto al primero. Movimiento de un punto relativo a un marco de referencia en movimiento Oxyz llamado relativo. Las características de este movimiento, como la trayectoria, la velocidad y la aceleración, se denominan relativo. Se denotan por el índice r; para velocidad y aceleración v r , a r . Movimiento de un punto relativo al sistema de referencia principal o fijo O 1 x 1 y 1 z 1 llamado absoluto(o difícil ). A veces también se le llama compuesto movimiento. La trayectoria, la velocidad y la aceleración de este movimiento se denominan absolutas. La velocidad y la aceleración del movimiento absoluto se denotan con letras v, un sin índices.

El movimiento portátil de un punto es el movimiento que realiza junto con un sistema de referencia en movimiento, como un punto rígidamente sujeto a este sistema en el momento considerado. Debido al movimiento relativo, el punto en movimiento en diferentes momentos coincide con diferentes puntos del cuerpo. S, al que se une el marco de referencia móvil. La velocidad portátil y la aceleración portátil son la velocidad y la aceleración de ese punto del cuerpo. S, con el que coincide el punto móvil en ese momento. La velocidad portátil y la aceleración denotan v e y e.

Si las trayectorias de todos los puntos del cuerpo S, fijado con un sistema de referencia en movimiento, representado en la figura (Fig. 20), luego obtenemos una familia de líneas, una familia de trayectorias del movimiento portátil de un punto METRO. Debido al movimiento relativo del punto. METRO en cada instante de tiempo se encuentra en una de las trayectorias del movimiento portátil. Punto METRO puede coincidir con un solo punto de cada una de las trayectorias de esta familia de trayectorias portátiles. En este sentido, a veces se cree que no existen trayectorias de movimiento de traslación, ya que es necesario considerar líneas en las que solo un punto es en realidad un punto de la trayectoria como trayectorias de movimiento portátil.

En la cinemática de un punto se estudia el movimiento de un punto con respecto a cualquier marco de referencia, independientemente de que este marco de referencia se mueva con respecto a otros sistemas o no. Complementemos este estudio con la consideración del movimiento complejo, en el caso más simple consistente en relativo y figurativo. Un mismo movimiento absoluto, eligiendo diferentes marcos móviles de referencia, puede considerarse como consistente en diferentes movimientos portátiles y, en consecuencia, relativos.

Adición de velocidades

Determinemos la velocidad del movimiento absoluto de un punto, si se conocen las velocidades de los movimientos relativo y figurativo de este punto. Deje que el punto realice solo un movimiento relativo con respecto al marco móvil de referencia Oxyz, y en el tiempo t ocupa la posición M en la trayectoria del movimiento relativo (Fig. 20). En el instante de tiempo t+ t debido al movimiento relativo, el punto estará en la posición M 1 , habiéndose movido MM 1 a lo largo de la trayectoria del movimiento relativo. Supongamos que el punto está involucrado Oxyz y trayectoria relativa se moverá a lo largo de alguna curva para mm 2. Si un punto participa simultáneamente en movimientos relativos y figurativos, entonces en el tiempo A; ella se mudará a milímetro" a lo largo de la trayectoria del movimiento absoluto y en el momento del tiempo t+en toma una posición METRO". si el tiempo En pequeño y luego pasar al límite en En, tendiendo a cero, entonces los pequeños desplazamientos a lo largo de las curvas pueden reemplazarse por segmentos de cuerdas y tomarse como vectores de desplazamiento. Sumando los desplazamientos vectoriales, obtenemos

En este sentido, se descartan pequeñas cantidades de orden superior, con tendencia a cero en En, tendiendo a cero. Pasando al límite, tenemos (14)

Por lo tanto, (14) toma la forma (15)

Se obtiene el llamado teorema de la suma de velocidades: la velocidad del movimiento absoluto de un punto es igual a la suma vectorial de las velocidades de los movimientos portátil y relativo de este punto. Dado que, en el caso general, las velocidades de los movimientos de traslación y relativo no son perpendiculares, entonces (15 ')

Información similar.

En la naturaleza y la tecnología, a menudo encontramos la manifestación del movimiento de rotación de cuerpos sólidos, como ejes y engranajes. Cómo se describe este tipo de movimiento en física, qué fórmulas y ecuaciones se usan para esto, estos y otros temas se tratan en este artículo.

¿Qué es la rotación?

Cada uno de nosotros imagina intuitivamente de qué tipo de movimiento estamos hablando. La rotación es un proceso en el que un cuerpo o punto material se mueve a lo largo de una trayectoria circular alrededor de algún eje. Desde un punto de vista geométrico, un cuerpo rígido es una línea recta, cuya distancia permanece constante durante el movimiento. Esta distancia se llama radio de rotación. En lo que sigue, lo denotaremos con la letra r. Si el eje de rotación pasa por el centro de masa del cuerpo, entonces se llama su propio eje. Un ejemplo de rotación alrededor de su propio eje es el correspondiente movimiento de los planetas del sistema solar.

Para que ocurra la rotación, debe haber una aceleración centrípeta, que surge debido a la fuerza centrípeta. Esta fuerza se dirige desde el centro de masa del cuerpo al eje de rotación. La naturaleza de la fuerza centrípeta puede ser muy diferente. Entonces, en una escala cósmica, su papel lo juega la gravedad, si el cuerpo está sujeto por un hilo, entonces la fuerza de tensión de este último será centrípeta. Cuando un cuerpo gira alrededor de su propio eje, el papel de la fuerza centrípeta lo juega la interacción electroquímica interna entre los elementos (moléculas, átomos) que componen el cuerpo.

Debe entenderse que sin la presencia de una fuerza centrípeta, el cuerpo se moverá en línea recta.

Magnitudes físicas que describen la rotación

Primero, estas son características dinámicas. Éstos incluyen:

• momento angular L;
• momento de inercia I;
• momento de fuerza m

En segundo lugar, estas son características cinemáticas. Vamos a enumerarlos:

• ángulo de rotación θ;
• velocidad angular ω;
• aceleración angular α.

Describamos brevemente cada una de estas cantidades.

El momento angular está determinado por la fórmula:

Donde p es el momento lineal, m es la masa del punto material, v es su velocidad lineal.

El momento de inercia de un punto material se calcula mediante la expresión:

Para cualquier cuerpo de forma compleja, el valor de I se calcula como la suma integral de los momentos de inercia de los puntos materiales.

El momento de la fuerza M se calcula de la siguiente manera:

Aquí F es la fuerza externa, d es la distancia desde el punto de su aplicación hasta el eje de rotación.

El significado físico de todas las cantidades, en cuyo nombre está presente la palabra "momento", es similar al significado de las cantidades lineales correspondientes. Por ejemplo, el momento de la fuerza muestra la posibilidad de que la fuerza aplicada informe al sistema de cuerpos en rotación.

Las características cinemáticas se definen matemáticamente mediante las siguientes fórmulas:

Como puede verse en estas expresiones, las características angulares son similares en su significado a las lineales (velocidades v y aceleración a), solo que son aplicables a una trayectoria circular.

Dinámica de rotación

En física, el estudio del movimiento de rotación de un cuerpo rígido se realiza con la ayuda de dos ramas de la mecánica: la dinámica y la cinemática. Comencemos con la dinámica.

La dinámica estudia las fuerzas externas que actúan sobre un sistema de cuerpos en rotación. Inmediatamente escribiremos la ecuación del movimiento de rotación de un cuerpo rígido y luego analizaremos sus partes constituyentes. Así que esta ecuación se ve como:

El que actúa sobre un sistema que tiene un momento de inercia I, provoca la aparición de una aceleración angular α. Cuanto menor sea el valor de I, más fácil será, con la ayuda de un cierto momento M, hacer girar el sistema a altas velocidades en intervalos cortos de tiempo. Por ejemplo, es más fácil girar una barra de metal a lo largo de su eje que perpendicularmente a él. Sin embargo, la misma barra es más fácil de girar alrededor de un eje perpendicular a ella y que pasa por el centro de masa que por su extremo.

Ley de conservación de L

Esta cantidad se introdujo anteriormente, se llama momento angular. La ecuación del movimiento de rotación de un cuerpo rígido, presentada en el párrafo anterior, a menudo se escribe en una forma diferente:

Si el momento de las fuerzas externas M actúa sobre el sistema durante el tiempo dt, provoca un cambio en el momento angular del sistema de dL. En consecuencia, si el momento de las fuerzas es igual a cero, entonces L = const. Esta es la ley de conservación del valor L. Para ello, usando la relación entre velocidad lineal y angular, podemos escribir:

L \u003d metro * v * r \u003d metro * ω * r 2 \u003d yo * ω.

Así, en ausencia del momento de las fuerzas, el producto de la velocidad angular y el momento de inercia es un valor constante. Esta ley física es utilizada por patinadores artísticos en sus actuaciones o satélites artificiales que necesitan rotar alrededor de su propio eje en el espacio exterior.

aceleración centrípeta

Arriba, al estudiar el movimiento de rotación de un cuerpo rígido, ya se ha descrito esta cantidad. También se señaló la naturaleza de las fuerzas centrípetas. Aquí solo complementaremos esta información y daremos las fórmulas correspondientes para calcular esta aceleración. Lo denotaremos como c.

Dado que la fuerza centrípeta se dirige perpendicularmente al eje y lo atraviesa, no crea un momento. Es decir, esta fuerza no tiene absolutamente ningún efecto sobre las características cinemáticas de rotación. Sin embargo, crea una aceleración centrípeta. Aquí hay dos fórmulas para su definición:

Por lo tanto, cuanto mayor sea la velocidad angular y el radio, mayor será la fuerza que se debe aplicar para mantener el cuerpo en una trayectoria circular. Un ejemplo sorprendente de este proceso físico es el derrape de un automóvil durante un giro. Se produce un derrape si la fuerza centrípeta, cuyo papel desempeña la fuerza de fricción, se vuelve menor que la fuerza centrífuga (característica de inercia).

Las tres características cinemáticas principales se enumeraron anteriormente en el artículo. un cuerpo sólido se describe mediante las siguientes fórmulas:

θ = ω*t => ω = constante, α = 0;

θ = ω 0 *t + α*t 2 /2 => ω = ω 0 + α*t, α = const.

La primera línea contiene fórmulas para la rotación uniforme, que supone la ausencia de un momento externo de fuerzas que actúan sobre el sistema. La segunda línea contiene fórmulas para el movimiento uniformemente acelerado en un círculo.

Tenga en cuenta que la rotación puede ocurrir no solo con una aceleración positiva, sino también con una negativa. En este caso, en las fórmulas de la segunda fila, debes poner un signo menos delante del segundo término.

Ejemplo de solucion de problema

Un momento de fuerza de 1000 N*m actuó sobre el eje de metal durante 10 segundos. Sabiendo que el momento de inercia del eje es de 50 kg * m 2 , es necesario determinar la velocidad angular que dicho momento de fuerza le dio al eje.

Aplicando la ecuación básica de rotación, calculamos la aceleración del eje:

Dado que esta aceleración angular actuó sobre el eje durante el tiempo t = 10 segundos, usamos la fórmula para el movimiento uniformemente acelerado para calcular la velocidad angular:

ω = ω 0 + α*t = M/I*t.

Aquí ω 0 = 0 (el eje no giró hasta el momento de las fuerzas M).

Sustituimos los valores numéricos de las cantidades en igualdad, obtenemos:

ω \u003d 1000/50 * 10 \u003d 200 rad / s.

Para traducir este número a las revoluciones por segundo habituales, debe dividirlo por 2 * pi. Después de realizar esta acción, obtenemos que el eje girará a una frecuencia de 31,8 rpm.

DEFINICIÓN: Movimiento de rotación de un cuerpo rígido. llamaremos eje de rotación a un movimiento en el que todos los puntos del cuerpo se mueven a lo largo de círculos cuyos centros se encuentran en la misma línea recta.

Para estudiar la dinámica rotacional, a las cantidades cinemáticas conocidas, agregamos más dos cantidades: momento de poder(M) y momento de inercia(J).

1. Se sabe por experiencia que la aceleración del movimiento de rotación depende no solo de la magnitud de la fuerza que actúa sobre el cuerpo, sino también de la distancia desde el eje de rotación hasta la línea a lo largo de la cual actúa la fuerza. Para caracterizar esta circunstancia, una cantidad física llamada momento de fuerza.

Consideremos el caso más simple.

DEFINICIÓN: El momento de la fuerza relativo a algún punto “O” es la cantidad vectorial definida por la expresión , donde es el radio vector dibujado desde el punto “O” hasta el punto de aplicación de la fuerza.

De la definición se deduce que es un vector axial. Su dirección se elige de modo que la rotación del vector alrededor del punto "O" en la dirección de la fuerza y ​​el vector formen un sistema de mano derecha. El módulo del momento de la fuerza es , donde a es el ángulo entre las direcciones de los vectores y , y yo= r pecado a es la longitud de la perpendicular que cae desde el punto “O” hasta la línea recta a lo largo de la cual actúa la fuerza (llamada hombro de fuerza con respecto al punto “O”) (Fig. 4.2).

2. Los datos experimentales muestran que la magnitud de la aceleración angular se ve afectada no solo por la masa del cuerpo giratorio, sino también por la distribución de la masa en relación con el eje de rotación. La cantidad que tiene en cuenta esta circunstancia se llama momento de inercia sobre el eje de giro.

DEFINICIÓN: En sentido estricto, momento de inercia cuerpo con respecto a algún eje de rotación se llama el valor de J, igual a la suma de los productos de las masas elementales por los cuadrados de sus distancias desde el eje dado.

La sumatoria se realiza sobre todas las masas elementales en que se dividió el cuerpo. Debe tenerse en cuenta que esta cantidad (J) existe independientemente de la rotación (aunque el concepto de momento de inercia se introdujo al considerar la rotación de un cuerpo rígido).

Cada cuerpo, independientemente de si está en reposo o gira, tiene un cierto momento de inercia alrededor de cualquier eje, al igual que un cuerpo tiene masa, independientemente de si está en movimiento o en reposo.

Dado que , el momento de inercia se puede representar como: . Esta relación es aproximada y será tanto más exacta cuanto menores sean los volúmenes elementales y los elementos de masa correspondientes a ellos. Por lo tanto, el problema de encontrar los momentos de inercia se reduce a la integración: . Aquí, la integración se lleva a cabo en todo el volumen del cuerpo.

Escribamos los momentos de inercia de algunos cuerpos de forma geométrica regular.

1. Varilla larga homogénea.
Arroz. 4.3	El momento de inercia con respecto al eje perpendicular a la barra y que pasa por su centro es igual a
2. Cilindro o disco macizo.
Arroz. 4.4	El momento de inercia con respecto al eje que coincide con el eje geométrico es .
3. Cilindro de pared delgada de radio R.
Arroz. 4.5
4. Momento de inercia de una bola de radio R alrededor de un eje que pasa por su centro
Arroz. 4.6
5. Momento de inercia de un disco delgado (espesor b<
Arroz. 4.7
6. Momento de inercia de la barra
Arroz. 4.8
7. Momento de inercia del anillo
Arroz. 4.9

Los cálculos del momento de inercia son bastante simples aquí, porque se supone que el cuerpo es homogéneo y simétrico, y el momento de inercia se determina en relación con el eje de simetría.

Para determinar el momento de inercia de un cuerpo con respecto a cualquier eje, debe usar el teorema de Steiner.

DEFINICIÓN: Momento de inercia J relativo a un eje arbitrario es igual a la suma del momento de inercia J c alrededor de un eje paralelo al dado y que pasa por el centro de inercia del cuerpo, y el producto de la masa del cuerpo por el cuadrado de la distancia entre los ejes (Fig. 4.10).

traslacional Se llama movimiento de un cuerpo rígido a tal movimiento en el que cualquier línea recta, invariablemente asociada con este cuerpo, permanece paralela a su posición inicial.

Teorema. En el movimiento de traslación de un cuerpo rígido, todos sus puntos describen las mismas trayectorias y en cualquier momento tienen velocidades y aceleraciones iguales en magnitud y dirección.

Prueba. Pase por dos puntos y , segmento de cuerpo en movimiento traslacional
y considere el movimiento de este segmento en la posición
. Al mismo tiempo, el punto describe la trayectoria
, y el punto – trayectoria
(Figura 56).

Teniendo en cuenta que el segmento
se mueve paralelo a sí mismo, y su longitud no cambia, se puede establecer que las trayectorias de los puntos Y será lo mismo. Por tanto, la primera parte del teorema queda demostrada. Determinaremos la posición de los puntos. Y de forma vectorial con respecto al origen fijo . Al mismo tiempo, estos radios - vectores dependen de
. Porque. ni la longitud ni la dirección del segmento
no cambia cuando el cuerpo se mueve, entonces el vector

. Se procede a la determinación de las velocidades según la dependencia (24):

, obtenemos
.

Se procede a la determinación de aceleraciones según dependencia (26):

, obtenemos
.

Del teorema probado se sigue que el movimiento de traslación de un cuerpo estará completamente determinado si se conoce el movimiento de uno solo de algunos puntos. Por tanto, el estudio del movimiento de traslación de un cuerpo rígido se reduce al estudio del movimiento de uno de sus puntos, es decir al problema de la cinemática puntual.

Tema 11. Movimiento de rotación de un cuerpo rígido

rotacional Es un movimiento de un cuerpo rígido en el que dos de sus puntos permanecen inmóviles durante todo el tiempo del movimiento. La recta que pasa por estos dos puntos fijos se llama eje de rotación.

Cada punto del cuerpo que no se encuentra sobre el eje de rotación, durante tal movimiento, describe un círculo, cuyo plano es perpendicular al eje de rotación, y su centro se encuentra sobre este eje.

Dibujamos a través del eje de rotación un plano fijo I y un plano móvil II, invariablemente conectados con el cuerpo y girando con él (Fig. 57). La posición del plano II y, en consecuencia, de todo el cuerpo, con respecto al plano I en el espacio, está completamente determinada por el ángulo . Cuando un cuerpo gira alrededor de un eje este ángulo es una función del tiempo continua y de un solo valor. Por lo tanto, conociendo la ley de cambio de este ángulo con el tiempo, podemos determinar la posición del cuerpo en el espacio:

- ley de rotación del cuerpo. (43)

En este caso supondremos que el ángulo contado desde el plano fijo en el sentido contrario a las agujas del reloj cuando se ve desde el extremo positivo del eje . Dado que la posición de un cuerpo que gira alrededor de un eje fijo está determinada por un parámetro, se dice que dicho cuerpo tiene un grado de libertad.

Velocidad angular

El cambio en el ángulo de rotación del cuerpo con el tiempo se llama ángulo velocidad del cuerpo y denotado
(omega):

.(44)

La velocidad angular, como la velocidad lineal, es una cantidad vectorial, y este vector construido sobre el eje de rotación del cuerpo. Está dirigido a lo largo del eje de rotación en esa dirección de modo que, mirando desde su extremo hasta su comienzo, se puede ver la rotación del cuerpo en sentido antihorario (Fig. 58). El módulo de este vector está determinado por la dependencia (44). Punto de aplicación en el eje se puede elegir arbitrariamente, ya que el vector se puede trasladar a lo largo de su línea de acción. Si denotamos el orto-vector del eje de rotación a través de , entonces obtenemos la expresión vectorial de la velocidad angular:

. (45)

Aceleración angular

La tasa de cambio en la velocidad angular de un cuerpo con el tiempo se llama aceleración angular cuerpos y se denota (épsilon):

. (46)

La aceleración angular es una cantidad vectorial, y este vector construido sobre el eje de rotación del cuerpo. Está dirigido a lo largo del eje de rotación en esa dirección, de modo que, mirando desde su extremo hasta su comienzo, se puede ver la dirección de rotación del épsilon en el sentido contrario a las agujas del reloj (Fig. 58). El módulo de este vector está determinado por la dependencia (46). Punto de aplicación en el eje se puede elegir arbitrariamente, ya que el vector se puede trasladar a lo largo de su línea de acción.

Si denotamos el orto-vector del eje de rotación a través de , entonces obtenemos la expresión vectorial de la aceleración angular:

. (47)

Si la velocidad angular y la aceleración son del mismo signo, entonces el cuerpo gira acelerado, y si es diferente - lentamente. Un ejemplo de rotación lenta se muestra en la fig. 58.

Considere casos especiales de movimiento de rotación.

1. Rotación uniforme:

,
.

,
,
,

,
. (48)

2. Rotación de variables iguales:

.

,
,
,
,
,
,
,
,

,
,
.(49)

Relación entre parámetros lineales y angulares

Considere el movimiento de un punto arbitrario
cuerpo giratorio. En este caso, la trayectoria del punto será un círculo, radio
, ubicado en un plano perpendicular al eje de rotación (Fig. 59, pero).

Supongamos que en ese momento el punto está en posición
. Supongamos que el cuerpo gira en la dirección positiva, es decir en la dirección del ángulo creciente . en el momento
el punto tomará posición
. Denota el arco
. Por lo tanto, durante un período de tiempo
el punto ha pasado el camino
. Su velocidad promedio , y cuando
,
. Pero, de la Fig. 59, B, está claro que
. Luego. Finalmente obtenemos

. (50)

Aquí - velocidad lineal del punto
. Como se obtuvo anteriormente, esta velocidad está dirigida tangencialmente a la trayectoria en un punto dado, es decir tangente al círculo.

Así, el módulo de velocidad lineal (circunferencial) de un punto de un cuerpo en rotación es igual al producto del valor absoluto de la velocidad angular por la distancia de este punto al eje de rotación.

Ahora conectemos los componentes lineales de la aceleración del punto con los parámetros angulares.

,
. (51)

El módulo de aceleración tangencial de un punto de un cuerpo rígido que gira alrededor de un eje fijo es igual al producto de la aceleración angular del cuerpo por la distancia de este punto al eje de rotación.

,
. (52)

El módulo de aceleración normal de un punto de un cuerpo rígido que gira alrededor de un eje fijo es igual al producto del cuadrado de la velocidad angular del cuerpo por la distancia de este punto al eje de rotación.

Entonces la expresión para la aceleración total del punto toma la forma

. (53)

Direcciones vectoriales ,,se muestra en la figura 59, en.

movimiento plano Un cuerpo rígido es un movimiento en el que todos los puntos del cuerpo se mueven paralelos a un plano fijo. Ejemplos de tal movimiento:

El movimiento de cualquier cuerpo cuya base se desliza a lo largo de un plano fijo dado;

Rueda rodando a lo largo de una sección recta de la vía (carril).

Obtenemos las ecuaciones del movimiento plano. Para hacer esto, considere una figura plana que se mueve en el plano de la hoja (Fig. 60). Referimos este movimiento a un sistema de coordenadas fijo
, y con la figura misma asociaremos un sistema de coordenadas en movimiento
, que se mueve con él.

Obviamente, la posición de una figura en movimiento en un plano fijo está determinada por la posición de los ejes en movimiento
relativo a ejes fijos
. Esta posición está determinada por la posición del origen móvil. , es decir. coordenadas ,y ángulo de rotación , un sistema de coordenadas móvil con respecto al fijo, que se contará a partir del eje en sentido antihorario.

En consecuencia, el movimiento de una figura plana en su plano estará completamente determinado si se conocen los valores para cada instante de tiempo ,,, es decir. ecuaciones de la forma:

,
,
. (54)

Las ecuaciones (54) son ecuaciones de movimiento plano de un cuerpo rígido, ya que si se conocen estas funciones, entonces para cada momento de tiempo es posible encontrar a partir de estas ecuaciones, respectivamente ,,, es decir. determinar la posición de la figura en movimiento en un momento dado.

Considere casos especiales:

1.

, entonces el movimiento del cuerpo será de traslación, ya que los ejes móviles se desplazan permaneciendo paralelos a su posición inicial.

2.

,

. Con este movimiento, solo cambia el ángulo de rotación. , es decir. el cuerpo rotará alrededor de un eje que pasa perpendicular al plano de la figura a través del punto .

Descomposición del movimiento de una figura plana en traslacional y rotacional

Considere dos posiciones consecutivas Y
ocupado por el cuerpo a veces Y
(Figura 61). cuerpo fuera de posicion en posición
se puede transferir de la siguiente manera. Primero movamos el cuerpo progresivamente. Al mismo tiempo, el segmento
se mueve paralelo a sí mismo a la posición
, y luego demos vuelta cuerpo alrededor de un punto (polo) en la esquina
hasta que los puntos coincidan Y .

Como consecuencia, cualquier movimiento plano se puede representar como la suma del movimiento de traslación junto con el polo elegido y el movimiento de rotación, sobre este polo.

Consideremos los métodos por los cuales es posible determinar las velocidades de los puntos de un cuerpo que realiza un movimiento plano.

1. Método de polos. Este método se basa en la descomposición resultante del movimiento plano en traslación y rotación. La velocidad de cualquier punto de una figura plana se puede representar como dos componentes: traslacional, con una velocidad igual a la velocidad de un punto elegido arbitrariamente -postes , y rotacional alrededor de este polo.

Considere un cuerpo plano (Fig. 62). Las ecuaciones de movimiento son:
,
,
.

Determinamos a partir de estas ecuaciones la velocidad del punto (como con el método de ajuste de coordenadas)

,
,
.

Entonces la velocidad del punto - el valor es conocido. Tomamos este punto como un polo y determinamos la velocidad de un punto arbitrario
cuerpo.

Velocidad
estará compuesto por el componente traslacional , al moverse junto con el punto y rotacional
, cuando se gira el punto
relativo al punto . Velocidad de punto mover al punto
paralelo a sí mismo, ya que en el movimiento de traslación las velocidades de todos los puntos son iguales tanto en magnitud como en dirección. Velocidad
determinado por la dependencia (50)
, y este vector está dirigido perpendicularmente al radio
en la dirección de rotación
. Vector
estará dirigido a lo largo de la diagonal de un paralelogramo construido sobre los vectores Y
, y su módulo está determinado por la dependencia:

, .(55)

2. El teorema de las proyecciones de las velocidades de dos puntos del cuerpo.

Las proyecciones de las velocidades de dos puntos de un cuerpo rígido sobre la línea recta que une estos puntos son iguales entre sí.

Considere dos puntos del cuerpo. Y (Figura 63). Tomando un punto por polo, determine la dirección por dependencia (55):
. Proyectamos esta igualdad vectorial sobre la recta
y considerando que
perpendicular
, obtenemos

3. Centro instantáneo de velocidades.

Centro instantáneo de velocidades(MCS) es un punto cuya velocidad en un momento dado es cero.

Demostremos que si el cuerpo no se mueve hacia adelante, entonces tal punto existe en cada momento del tiempo y, además, es único. Deja en el momento puntos Y cuerpos yacen en la sección , tiene velocidades Y , no paralelos entre sí (Fig. 64). Entonces el punto
, situada en la intersección de las perpendiculares a los vectores Y , y habrá un MCS, ya que
.

En efecto, si asumimos que
, entonces por el teorema (56), el vector
debe ser perpendicular
Y
, lo cual es imposible. Se puede ver del mismo teorema que ningún otro punto de sección en este momento no puede tener una velocidad igual a cero.

Aplicando el método del polo
- polo, determinar la velocidad del punto (55): desde
,
. (57)

Se puede obtener un resultado similar para cualquier otro punto del cuerpo. Por tanto, la velocidad de cualquier punto del cuerpo es igual a su velocidad de rotación relativa al MCS:

,
,
, es decir. las velocidades de los puntos del cuerpo son proporcionales a sus distancias al MCS.

De los tres métodos considerados para determinar las velocidades de los puntos de una figura plana, se puede ver que el MCS es preferible, ya que aquí la velocidad se determina inmediatamente tanto en valor absoluto como en la dirección de un componente. Sin embargo, este método puede usarse si conocemos o podemos determinar la posición del MCS para el cuerpo.

Determinación de la posición del MCS

1. Si conocemos para una posición dada del cuerpo las direcciones de las velocidades de dos puntos del cuerpo, entonces el MCC será el punto de intersección de las perpendiculares a estos vectores de velocidad.

2. Las velocidades de dos puntos del cuerpo son antiparalelas (Fig. 65, pero). En este caso, la perpendicular a las velocidades será común, es decir El MCC está ubicado en algún lugar de esta perpendicular. Para determinar la posición del MCC, es necesario conectar los extremos de los vectores de velocidad. El punto de intersección de esta recta con la perpendicular será el MCS deseado. En este caso, el MCS se encuentra entre estos dos puntos.

3. Las velocidades de dos puntos del cuerpo son paralelas, pero no iguales en magnitud (Fig. 65, B). El procedimiento para obtener una MDS es similar al descrito en el párrafo 2.

d) Las velocidades de dos puntos son iguales tanto en magnitud como en dirección (Fig. 65, en). Obtenemos el caso del movimiento de traslación instantáneo, en el que las velocidades de todos los puntos del cuerpo son iguales. Por lo tanto, la velocidad angular del cuerpo en esta posición es cero:

4. Definimos el MCC para una rueda que rueda sin deslizar sobre una superficie fija (Fig. 65, GRAMO). Dado que el movimiento ocurre sin deslizamiento, entonces en el punto de contacto de la rueda con la superficie, la velocidad será la misma e igual a cero, ya que la superficie está estacionaria. Por tanto, el punto de contacto de la rueda con una superficie fija será el MCC.

Determinación de aceleraciones de puntos de una figura plana

Al determinar las aceleraciones de los puntos de una figura plana, se puede trazar una analogía con los métodos para determinar las velocidades.

1. Método de polos. Así como en la determinación de velocidades, tomamos como polo un punto arbitrario del cuerpo, cuya aceleración conocemos, o podemos determinarla. Luego la aceleración de cualquier punto de una figura plana es igual a la suma de las aceleraciones del polo y la aceleración en el movimiento de rotación alrededor de este polo:

Al mismo tiempo, el componente
determina la aceleración de un punto mientras gira alrededor del polo . Al girar, la trayectoria del punto será curvilínea, lo que significa
(Figura 66).

Entonces la dependencia (58) toma la forma
. (59)

Teniendo en cuenta las dependencias (51) y (52), obtenemos
,
.

2. Centro instantáneo de aceleración.

Centro de aceleración instantánea(MCC) es un punto cuya aceleración en un momento dado es cero.

Demostremos que tal punto existe en cualquier momento dado. Tomamos un punto como polo , cuya aceleración
sabemos. Encontrar un ángulo , acostado dentro
, y cumpliendo la condición
. Si
, luego
y viceversa, es decir inyección se deposita en la dirección . Aparte del punto en un angulo al vector
sección
(Figura 67). El punto obtenido por tales construcciones
será MCU.

De hecho, la aceleración de un punto
igual a la suma de las aceleraciones
postes y aceleración
en rotación alrededor del polo :
.

,
. Luego
. Por otro lado, la aceleración
formas con la dirección del segmento
inyección
, que satisface la condición
. El signo menos se coloca delante de la tangente del ángulo. , ya que la rotación
relativo al polo en sentido antihorario y el ángulo
se deposita en el sentido de las agujas del reloj. Luego
.

Como consecuencia,
y luego
.

Casos especiales de determinación del MCC

1.
. Luego
y, por lo tanto, la MCU no existe. En este caso, el cuerpo se mueve hacia adelante, es decir, las velocidades y aceleraciones de todos los puntos del cuerpo son iguales.

2.
. Luego
,
. Esto significa que la MCU se encuentra en la intersección de las líneas de acción de las aceleraciones de los puntos del cuerpo (Fig. 68, pero).

3.
. Luego,
,
. Esto significa que el MCC se encuentra en la intersección de las perpendiculares a las aceleraciones de los puntos del cuerpo (Fig. 68, B).

4.
. Luego
,

. Esto significa que la MCU se encuentra en la intersección de los rayos dibujados con las aceleraciones de los puntos del cuerpo en un ángulo (fig. 68, en).

De los casos especiales considerados, podemos concluir: si tomamos el punto
por polo, entonces la aceleración de cualquier punto de una figura plana está determinada por la aceleración en el movimiento de rotación alrededor del MCC:

. (60)

Movimiento de puntos complicado Se denomina movimiento a tal movimiento en el que el punto participa simultáneamente en dos o más movimientos. Con tal movimiento, la posición del punto se determina con respecto al móvil y con respecto a los sistemas de referencia fijos.

El movimiento de un punto relativo a un marco de referencia en movimiento se llama movimiento relativo de un punto . Denotemos los parámetros del movimiento relativo
.

El movimiento de aquel punto del marco de referencia móvil, con el cual el punto móvil coincide en un momento dado con respecto al marco de referencia fijo, se denomina punto de movimiento . Denotemos los parámetros del movimiento portátil.
.

El movimiento de un punto relativo a un marco fijo de referencia se llama absoluto (complejo) punto de movimiento . Denotemos los parámetros del movimiento absoluto
.

Como ejemplo de un movimiento complejo, podemos considerar el movimiento de una persona en un vehículo en movimiento (tranvía). En este caso, el movimiento de una persona está relacionado con un sistema de coordenadas en movimiento, un tranvía, y con un sistema de coordenadas fijo, la tierra (carretera). Entonces, según las definiciones anteriores, el movimiento de una persona con respecto al tranvía es relativo, el movimiento junto con el tranvía con respecto al suelo es figurativo y el movimiento de una persona con respecto al suelo es absoluto.

Determinaremos la posición del punto.
radios - vectores relativos al movimiento
e inmóvil
sistemas de coordenadas (Fig. 69). Introduzcamos la notación: - radio vector que define la posición del punto
en relación con el sistema de coordenadas en movimiento
,
;- radio vector que determina la posición del origen del sistema de coordenadas en movimiento (puntos ) (puntos );- radio - un vector que define la posición de un punto
relativo al sistema de coordenadas fijo
;
,.

Obtengamos condiciones (restricciones) correspondientes a movimientos relativos, figurativos y absolutos.

1. Al considerar el movimiento relativo, supondremos que el punto
se mueve en relación con el sistema de coordenadas en movimiento
, y el propio sistema de coordenadas en movimiento
relativo al sistema de coordenadas fijo
no se mueve.

Entonces las coordenadas del punto
cambiará en movimiento relativo, y los orto-vectores del sistema de coordenadas en movimiento no cambiarán de dirección:

,

,

.

2. Al considerar el movimiento portátil, supondremos que las coordenadas del punto
con respecto al sistema de coordenadas en movimiento son fijos, y el punto se mueve con el sistema de coordenadas en movimiento
relativamente inmóvil
:

,

,

,.

3. Con movimiento absoluto, el punto también se mueve relativamente
y junto con el sistema de coordenadas
relativamente inmóvil
:

Entonces las expresiones para las velocidades, teniendo en cuenta (27), tienen la forma

,
,

Comparando estas dependencias, obtenemos una expresión para la velocidad absoluta:
. (61)

Hemos obtenido un teorema sobre la suma de las velocidades de un punto en un movimiento complejo: la velocidad absoluta de un punto es igual a la suma geométrica de las componentes relativa y portátil de la velocidad.

Usando la dependencia (31), obtenemos expresiones para aceleraciones:

,

Comparando estas dependencias, obtenemos una expresión para la aceleración absoluta:
.

Se encontró que la aceleración absoluta de un punto no es igual a la suma geométrica de las componentes relativas y portátiles de las aceleraciones. Definamos la componente de aceleración absoluta, que está entre paréntesis, para casos especiales.

1. Movimiento de traslación del punto
. En este caso, los ejes del sistema de coordenadas en movimiento
se mueven todo el tiempo paralelos a ellos mismos, entonces.

,

,

,
,
,
, luego
. Finalmente obtenemos

. (62)

Si el movimiento portátil del punto es de traslación, entonces la aceleración absoluta del punto es igual a la suma geométrica de las componentes relativa y portátil de la aceleración.

2. El movimiento portátil del punto no es traslacional. Entonces, en este caso, el sistema de coordenadas en movimiento
gira alrededor del eje instantáneo de rotación con velocidad angular (Figura 70). Denote el punto al final del vector al otro lado de . Luego, usando el método vectorial de especificar (15), obtenemos el vector velocidad de este punto
.

Por otro lado,
. Igualando las partes derechas de estas igualdades vectoriales, obtenemos:
. Procediendo de manera similar, para el resto de los vectores vectoriales, obtenemos:
,
.

En el caso general, la aceleración absoluta de un punto es igual a la suma geométrica de las componentes relativas y portátiles de la aceleración más dos veces el producto vectorial del vector de la velocidad angular del movimiento portátil por el vector de la velocidad lineal de el movimiento relativo.

El producto vectorial duplicado del vector de velocidad angular del movimiento portátil por el vector de la velocidad lineal del movimiento relativo se llama Aceleración de Coriolis y denotado

. (64)

La aceleración de Coriolis caracteriza el cambio en la velocidad relativa en movimiento portátil y el cambio en la velocidad portátil en movimiento relativo.

reenviado
según la regla del producto vectorial. El vector aceleración de Coriolis siempre está dirigido perpendicularmente al plano formado por los vectores Y , de modo que, mirando desde el final del vector
, ver turno para , a través del ángulo más pequeño, en sentido antihorario.

El módulo de aceleración de Coriolis es igual a.