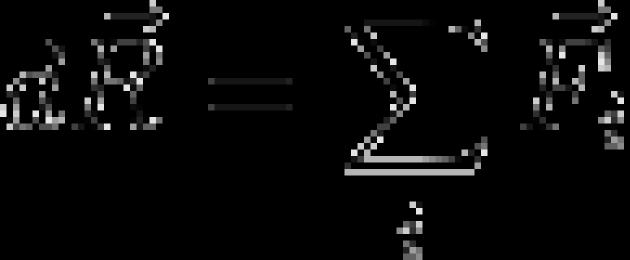Vista: este artículo ha sido leído 14066 veces
Pdf Seleccionar idioma... Ruso Ucraniano Inglés
Todo el material se descarga arriba, luego de seleccionar el idioma.
Cantidad de movimiento
Momento de un punto material - una cantidad vectorial igual al producto de la masa de un punto por su vector velocidad.
La unidad de medida del impulso es (kg m/s).
Cantidad de movimiento sistema mecánico - cantidad vectorial igual a suma geométrica(vector principal) del momento de un sistema mecánico es igual al producto de la masa de todo el sistema por la velocidad de su centro de masa.
Cuando un cuerpo (o sistema) se mueve de modo que su centro de masa esté estacionario, entonces la cantidad de movimiento del cuerpo es igual a cero (por ejemplo, la rotación del cuerpo alrededor eje fijo pasando por el centro de masa del cuerpo).
En el caso de un movimiento complejo, la cantidad de movimiento del sistema no caracterizará la parte rotacional del movimiento cuando gira alrededor del centro de masa. Es decir, la cantidad de movimiento caracteriza únicamente el movimiento de traslación del sistema (junto con el centro de masa).
fuerza de impulso
El impulso de una fuerza caracteriza la acción de una fuerza durante un determinado período de tiempo.
Impulso de fuerza durante un período de tiempo finito. se define como la suma integral de los impulsos elementales correspondientes.
Teorema sobre el cambio de impulso de un punto material
(en formas diferenciales mi ):
La derivada temporal del momento de un punto material es igual a la suma geométrica de las fuerzas que actúan sobre los puntos.
(V forma integral ):
El cambio en el impulso de un punto material durante un cierto período de tiempo es igual a la suma geométrica de los impulsos de fuerzas aplicadas al punto durante este período de tiempo.
Teorema sobre el cambio de momento de un sistema mecánico
(en forma diferencial ):
La derivada con respecto al tiempo del momento del sistema es igual a la suma geométrica de todos Fuerzas externas, actuando sobre el sistema.
(en forma integral ):
El cambio en el impulso de un sistema durante un cierto período de tiempo es igual a la suma geométrica de los impulsos de las fuerzas externas que actúan sobre el sistema durante este período de tiempo.
El teorema permite excluir de la consideración fuerzas internas obviamente desconocidas.
El teorema sobre el cambio de momento de un sistema mecánico y el teorema sobre el movimiento del centro de masa son dos formas diferentes del mismo teorema.
Ley de conservación del impulso de un sistema.
- Si la suma de todas las fuerzas externas que actúan sobre el sistema es igual a cero, entonces el vector del impulso del sistema será constante en dirección y magnitud.
- Si la suma de las proyecciones de todas las fuerzas externas que actúan sobre cualquier eje arbitrario es igual a cero, entonces la proyección del impulso sobre este eje es un valor constante.
conclusiones:
- Las leyes de conservación indican que las fuerzas internas no pueden cambiar la cantidad total de movimiento del sistema.
- El teorema sobre el cambio de momento de un sistema mecánico no caracteriza el movimiento de rotación de un sistema mecánico, sino sólo el de traslación.
Se da un ejemplo: determine el momento de un disco de cierta masa si se conocen su velocidad angular y su tamaño.
Ejemplo de cálculo de un engranaje recto
Un ejemplo de cálculo de un engranaje recto. Se ha realizado la elección del material, cálculo de tensiones admisibles, cálculo de resistencia de contacto y de flexión.
Un ejemplo de resolución de un problema de flexión de una viga.
En el ejemplo, los diagramas se construyen. fuerzas cortantes y momentos de flexión, se encontró una sección peligrosa y se seleccionó una viga en I. El problema analizó la construcción de diagramas utilizando dependencias diferenciales, realizado análisis comparativo diferentes secciones transversales de la viga.
Un ejemplo de resolución de un problema de torsión de eje.
La tarea consiste en probar la resistencia de un eje de acero con un diámetro, un material y una tensión admisible determinados. Durante la solución, se construyen diagramas de pares, esfuerzos cortantes y ángulos de torsión. No se tiene en cuenta el peso propio del eje.
Un ejemplo de resolución de un problema de tensión-compresión de una varilla.
La tarea consiste en probar la resistencia de una barra de acero ante tensiones permitidas específicas. Durante la solución se construyen diagramas de fuerzas longitudinales, tensiones normales y desplazamientos. No se tiene en cuenta el propio peso de la caña.
Aplicación del teorema sobre la conservación de la energía cinética.
Un ejemplo de resolución de un problema utilizando el teorema de conservación de la energía cinética de un sistema mecánico.
Determinar la velocidad y la aceleración de un punto usando ecuaciones de movimiento dadas.
Un ejemplo de resolución de un problema para determinar la velocidad y la aceleración de un punto utilizando ecuaciones de movimiento dadas.
Determinación de velocidades y aceleraciones de puntos de un cuerpo rígido durante el movimiento plano paralelo.
Un ejemplo de resolución de un problema para determinar las velocidades y aceleraciones de puntos. sólido en movimiento plano paralelo
Determinación de fuerzas en las barras de una armadura plana.
Un ejemplo de resolución del problema de determinar las fuerzas en las varillas de una armadura plana utilizando el método de Ritter y el método de corte de nodos.
Aplicación del teorema sobre el cambio de momento angular
Un ejemplo de resolución de un problema utilizando el teorema del cambio. momento cinético para determinar la velocidad angular de un cuerpo que gira alrededor de un eje fijo.
El sistema discutido en el teorema puede ser cualquier sistema mecánico formado por cualquier cuerpo.
Declaración del teorema
La cantidad de movimiento (impulso) de un sistema mecánico es una cantidad igual a la suma de las cantidades de movimiento (impulsos) de todos los cuerpos incluidos en el sistema. El impulso de las fuerzas externas que actúan sobre los cuerpos del sistema es la suma de los impulsos de todas las fuerzas externas que actúan sobre los cuerpos del sistema.
( kgm/s)
El teorema sobre el cambio de impulso de un sistema establece
El cambio en el impulso del sistema durante un cierto período de tiempo es igual al impulso de las fuerzas externas que actúan sobre el sistema durante el mismo período de tiempo.
Ley de conservación del impulso de un sistema.
Si la suma de todas las fuerzas externas que actúan sobre el sistema es cero, entonces la cantidad de movimiento (momento) del sistema es una cantidad constante.
,
obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma diferencial:
Habiendo integrado ambos lados de la igualdad resultante durante un período de tiempo arbitrariamente tomado entre algunos y , obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma integral:
Ley de conservación del impulso. (Ley de conservación del impulso.) afirma que la suma vectorial de los impulsos de todos los cuerpos del sistema es un valor constante si la suma vectorial de las fuerzas externas que actúan sobre el sistema es igual a cero.
(momento de impulso m 2 kg s −1)
Teorema sobre el cambio del momento angular con respecto al centro.
la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier centro fijo es igual al momento de fuerza que actúa sobre el punto con respecto al mismo centro.
dk 0 /dt = M 0 (F ) .
Teorema sobre el cambio del momento angular con respecto a un eje
la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier eje fijo es igual al momento de la fuerza que actúa sobre este punto con respecto al mismo eje.
dk X /dt = M X (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) .
Consideremos punto material METRO masa metro , moviéndose bajo la influencia de la fuerza. F (Figura 3.1). Anotemos y construyamos el vector del momento angular (momento cinético) METRO 0 punto material relativo al centro oh :
Diferenciamos la expresión del momento angular (momento cinético k 0) por tiempo:
Porque dr. /dt = V , entonces el producto vectorial V ⊗ metro ⋅ V (vectores colineales V Y metro ⋅ V ) es igual a cero. Al mismo tiempo re(m) ⋅ V) /dt = F según el teorema del impulso de un punto material. Por lo tanto entendemos que
dk 0 /dt = r ⊗F , (3.3)
Dónde r ⊗F = METRO 0 (F ) – vector-momento de fuerza F relativo a un centro fijo oh . Vector k 0 ⊥ plano ( r , metro ⊗V ), y el vector METRO 0 (F ) ⊥ avión ( r ,F ), finalmente tenemos
dk 0 /dt = M 0 (F ) . (3.4)
La ecuación (3.4) expresa el teorema sobre el cambio en el momento angular (momento angular) de un punto material con respecto al centro: la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier centro fijo es igual al momento de fuerza que actúa sobre el punto con respecto al mismo centro.
Proyectando la igualdad (3.4) sobre los ejes de coordenadas cartesianas, obtenemos
dk X /dt = M X (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) . (3.5)
Las igualdades (3.5) expresan el teorema sobre el cambio en el momento angular (momento cinético) de un punto material con respecto al eje: la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier eje fijo es igual al momento de la fuerza que actúa sobre este punto con respecto al mismo eje.
Consideremos las consecuencias que se derivan de los teoremas (3.4) y (3.5).
Corolario 1. Considere el caso cuando la fuerza F durante todo el movimiento el punto pasa por el centro estacionario oh (caso de fuerza central), es decir Cuando METRO 0 (F ) = 0. Entonces del teorema (3.4) se deduce que k 0 = constante ,
aquellos. en el caso de una fuerza central, el momento angular (momento cinético) de un punto material con respecto al centro de esta fuerza permanece constante en magnitud y dirección (Figura 3.2).
Figura 3.2
De la condición k 0 = constante de ello se deduce que la trayectoria de un punto en movimiento es una curva plana, cuyo plano pasa por el centro de esta fuerza.
Corolario 2. Dejar METRO z (F ) = 0, es decir fuerza cruza el eje z o paralelo a él. En este caso, como se puede ver en la tercera de las ecuaciones (3.5), k z = constante ,
aquellos. Si el momento de fuerza que actúa sobre un punto con respecto a cualquier eje fijo es siempre cero, entonces el momento angular (momento cinético) del punto con respecto a este eje permanece constante.
Prueba del teorema sobre el cambio de impulso.
Sea el sistema formado por puntos materiales con masas y aceleraciones. Dividimos todas las fuerzas que actúan sobre los cuerpos del sistema en dos tipos:
Las fuerzas externas son fuerzas que actúan desde cuerpos no incluidos en el sistema considerado. La resultante de fuerzas externas que actúan sobre un punto material con número i vamos a denotar
Las fuerzas internas son aquellas fuerzas con las que los cuerpos del propio sistema interactúan entre sí. La fuerza con la que sobre el punto con el número. i el punto con el número es válido k, denotaremos , y la fuerza de influencia i punto en kº punto - . Obviamente, cuando, entonces
Usando la notación introducida, escribimos la segunda ley de Newton para cada uno de los puntos materiales considerados en la forma
Teniendo en cuenta que 
y sumando todas las ecuaciones de la segunda ley de Newton, obtenemos:
La expresión representa la suma de todas las fuerzas internas que actúan en el sistema. Según la tercera ley de Newton, en esta suma, a cada fuerza le corresponde una fuerza tal que, por tanto, se cumple 
Dado que toda la suma consta de esos pares, la suma misma es cero. Así, podemos escribir
Usando la notación para el momento del sistema, obtenemos
Al introducir en consideración el cambio en el impulso de las fuerzas externas 
, obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma diferencial:
Así, cada una de las últimas ecuaciones obtenidas nos permite afirmar: un cambio en el impulso del sistema se produce sólo como resultado de la acción de fuerzas externas, y las fuerzas internas no pueden tener ninguna influencia sobre este valor.
Habiendo integrado ambos lados de la igualdad resultante en un intervalo de tiempo arbitrariamente tomado entre algunos y , obtenemos la expresión del teorema sobre el cambio en el impulso del sistema en forma integral:
donde y son los valores de la cantidad de movimiento del sistema en momentos de tiempo y, respectivamente, y es el impulso de fuerzas externas durante un período de tiempo. De acuerdo con lo dicho anteriormente y las notaciones introducidas,
Dejar que un punto material se mueva bajo la influencia de una fuerza. F. Se requiere determinar el movimiento de este punto en relación con el sistema en movimiento. Oxyz(ver movimiento complejo de un punto material), que se mueve de forma conocida en relación con un sistema estacionario oh 1 X 1 y 1 z 1 .
Ecuación básica de dinámica en un sistema estacionario.
Escribamos la aceleración absoluta de un punto usando el teorema de Coriolis.
Dónde a abdominales– aceleración absoluta;
a rel– aceleración relativa;
a carril– aceleración portátil;
a centro– Aceleración de Coriolis.
Reescribamos (25) teniendo en cuenta (26)
Introduzcamos la notación 
- fuerza de inercia portátil, 
- Fuerza de inercia de Coriolis. Entonces la ecuación (27) toma la forma
La ecuación básica de la dinámica para estudiar el movimiento relativo (28) está escrita de la misma manera que para el movimiento absoluto, solo a las fuerzas que actúan sobre un punto se deben sumar las fuerzas de inercia de transferencia y de Coriolis.
Teoremas generales sobre la dinámica de un punto material.
Al resolver muchos problemas, puede utilizar espacios en blanco prefabricados obtenidos según la segunda ley de Newton. Estos métodos de resolución de problemas se combinan en esta sección.
Teorema sobre el cambio de impulso de un punto material
Introduzcamos las siguientes características dinámicas:
1. Momento de un punto material– cantidad vectorial igual al producto de la masa de un punto por su vector velocidad
.
(29)
2. Impulso de fuerza
Impulso elemental de fuerza.– cantidad vectorial igual al producto del vector de fuerza por un intervalo de tiempo elemental
(30).
Entonces impulso completo
.
(31)
En F=constante obtenemos S=Pie.
El impulso total durante un período de tiempo finito se puede calcular sólo en dos casos, cuando la fuerza que actúa sobre un punto es constante o depende del tiempo. En otros casos, es necesario expresar la fuerza en función del tiempo.
La igualdad de las dimensiones de impulso (29) y momento (30) nos permite establecer una relación cuantitativa entre ellos.
Consideremos el movimiento de un punto material M bajo la acción fuerza arbitraria F siguiendo una trayectoria arbitraria.
ACERCA DE 
UD: 
.
(32)
Separamos las variables en (32) e integramos
.
(33)
Como resultado, teniendo en cuenta (31), obtenemos
.
(34)
La ecuación (34) expresa el siguiente teorema.
Teorema: El cambio en el impulso de un punto material durante un cierto período de tiempo es igual al impulso de la fuerza que actúa sobre el punto durante el mismo intervalo de tiempo.
Al resolver problemas, la ecuación (34) debe proyectarse sobre los ejes de coordenadas.
Este teorema es conveniente de utilizar cuando entre las cantidades dadas y desconocidas se encuentran la masa de un punto, su velocidad inicial y final, fuerzas y tiempo de movimiento.
Teorema sobre el cambio de momento angular de un punto material
METRO 
momento de impulso de un punto material con respecto al centro es igual al producto del módulo del momento del punto y el hombro, es decir la distancia más corta (perpendicular) desde el centro a la línea que coincide con el vector velocidad
,
(36)
.
(37)
La relación entre el momento de fuerza (causa) y el momento de impulso (efecto) se establece mediante el siguiente teorema.
Sea el punto M de una masa dada metro se mueve bajo la influencia de la fuerza F.
,
,
,
(38)
.
(39)
Calculemos la derivada de (39)
.
(40)
Combinando (40) y (38), finalmente obtenemos
.
(41)
La ecuación (41) expresa el siguiente teorema.
Teorema: La derivada temporal del vector del momento angular de un punto material con respecto a algún centro es igual al momento de la fuerza que actúa sobre el punto con respecto al mismo centro.
Al resolver problemas, la ecuación (41) debe proyectarse sobre los ejes de coordenadas.
En las ecuaciones (42), los momentos de impulso y fuerza se calculan en relación con los ejes de coordenadas.
De (41) se sigue Ley de conservación del momento angular (ley de Kepler).
Si el momento de fuerza que actúa sobre un punto material con respecto a cualquier centro es cero, entonces el momento angular del punto con respecto a este centro conserva su magnitud y dirección.
Si 
, Eso 
.
El teorema y la ley de conservación se utilizan en problemas que involucran movimiento curvilíneo, especialmente bajo la acción de fuerzas centrales.
Consideremos un sistema formado por puntos materiales. Compongamos para este sistema. ecuaciones diferenciales movimientos (13) y sumarlos término por término. Entonces obtenemos
La última suma, debido a la propiedad de las fuerzas internas, es igual a cero. Además,
finalmente encontramos
La ecuación (20) expresa el teorema sobre el cambio en el momento del sistema en forma diferencial: la derivada temporal del momento del sistema es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema. En proyecciones sobre ejes de coordenadas voluntad:
Encontremos otra expresión para el teorema. Deje que en ese momento la cantidad de movimiento del sistema sea igual y en ese momento sea igual a . Luego, multiplicando ambos lados de la igualdad (20) por e integrando, obtenemos
ya que las integrales de la derecha dan impulsos de fuerzas externas.
La ecuación (21) expresa el teorema sobre el cambio en el momento del sistema en forma integral: el cambio en el momento del sistema durante un cierto período de tiempo es igual a la suma de los impulsos que actúan sobre el sistema de fuerzas externas durante el mismo periodo de tiempo.
En proyecciones sobre ejes de coordenadas habrá:
Señalemos la conexión entre el teorema demostrado y el teorema sobre el movimiento del centro de masa. Ya que , entonces, sustituyendo este valor en la igualdad (20) y teniendo en cuenta que obtenemos , es decir, la ecuación (16).
En consecuencia, el teorema sobre el movimiento del centro de masa y el teorema sobre el cambio en el momento del sistema son esencialmente dos Diferentes formas el mismo teorema. En los casos en que se estudia el movimiento de un cuerpo rígido (o sistema de cuerpos), cualquiera de estas formas se puede usar igualmente y la ecuación (16) suele ser más conveniente de usar. Para un medio continuo (líquido, gas), al resolver problemas, se suele utilizar el teorema del cambio en el impulso del sistema. Este teorema también tiene aplicaciones importantes en la teoría del impacto (ver Capítulo XXXI) y en el estudio del movimiento de un chorro (ver § 114).
Ecuación diferencial de movimiento de un punto material bajo la influencia de una fuerza. F se puede representar en la siguiente forma vectorial:
Dado que la masa de un punto metro se acepta como constante, entonces se puede ingresar bajo el signo de derivada. Entonces
La fórmula (1) expresa el teorema sobre el cambio en el momento de un punto en forma diferencial: la primera derivada con respecto al tiempo del momento de un punto es igual a la fuerza que actúa sobre el punto.
En proyecciones sobre ejes de coordenadas (1) se puede representar como
Si ambos lados (1) se multiplican por dt, luego obtenemos otra forma del mismo teorema: el teorema del momento en forma diferencial:
aquellos. el diferencial del momento de un punto es igual al impulso elemental de la fuerza que actúa sobre el punto.
Proyectando ambas partes de (2) sobre los ejes de coordenadas, obtenemos
Integrando ambas partes de (2) desde cero hasta t (Fig. 1), tenemos
¿Dónde está la velocidad del punto en este momento? t; - velocidad a t = 0;
S- impulso de fuerza en el tiempo t.
Una expresión en la forma (3) a menudo se denomina teorema del momento en forma finita (o integral): el cambio en el impulso de un punto durante cualquier período de tiempo es igual al impulso de la fuerza durante el mismo período de tiempo.
En proyecciones sobre ejes de coordenadas, este teorema se puede representar de la siguiente forma:
Para un punto material, el teorema sobre el cambio de momento en cualquiera de sus formas no difiere esencialmente de las ecuaciones diferenciales de movimiento de un punto.
Teorema sobre el cambio de impulso de un sistema
La cantidad de movimiento del sistema se llamará cantidad vectorial. q, igual a la suma geométrica (vector principal) de las cantidades de movimiento de todos los puntos del sistema.
Considere un sistema que consta de norte puntos materiales. Compongamos ecuaciones diferenciales de movimiento para este sistema y sumémoslas término por término. Entonces obtenemos:
La última suma, debido a la propiedad de las fuerzas internas, es igual a cero. Además,
Finalmente encontramos:
La ecuación (4) expresa el teorema sobre el cambio de momento del sistema en forma diferencial: la derivada temporal del impulso del sistema es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema.
Encontremos otra expresión para el teorema. Deja entrar el momento t= 0 la cantidad de movimiento del sistema es P 0, y en el momento del tiempo t 1 se vuelve igual Pregunta 1. Luego, multiplicando ambos lados de la igualdad (4) por dt e integrando obtenemos:
O donde:
(S-impulso de fuerza)
dado que las integrales de la derecha dan impulsos de fuerzas externas,
La ecuación (5) expresa el teorema sobre el cambio en el momento del sistema en forma integral: el cambio en el impulso del sistema durante un cierto período de tiempo es igual a la suma de los impulsos de las fuerzas externas que actúan sobre el sistema durante el mismo período de tiempo.
En proyecciones sobre los ejes de coordenadas tendremos:
Ley de conservación del impulso.
Del teorema sobre el cambio de momento de un sistema, se pueden obtener los siguientes corolarios importantes:
1. Sea la suma de todas las fuerzas externas que actúan sobre el sistema igual a cero:
Entonces de la ecuación (4) se deduce que en este caso Q = constante.
De este modo, Si la suma de todas las fuerzas externas que actúan sobre el sistema es igual a cero, entonces el vector del momento del sistema será constante en magnitud y dirección.
2.01Sean las fuerzas externas que actúan sobre el sistema tales que la suma de sus proyecciones sobre algún eje (por ejemplo Ox) sea igual a cero:
Entonces de las ecuaciones (4`) se deduce que en este caso Q = constante.
De este modo, Si la suma de las proyecciones de todas las fuerzas externas que actúan sobre cualquier eje es igual a cero, entonces la proyección de la cantidad de movimiento del sistema sobre este eje es un valor constante.
Estos resultados expresan Ley de conservación del momento de un sistema. De ellos se deduce que las fuerzas internas no pueden cambiar la cantidad total de movimiento del sistema.
Veamos algunos ejemplos:
· Fenómeno de devolución del rollo. Si consideramos el rifle y la bala como un solo sistema, entonces la presión de los gases de la pólvora durante el disparo será una fuerza interna. Esta fuerza no puede cambiar el impulso total del sistema. Pero dado que los gases de pólvora, al actuar sobre la bala, le imparten una cierta cantidad de movimiento hacia adelante, deben impartir simultáneamente al rifle la misma cantidad de movimiento en dirección hacia adelante. direccion contraria. Esto hará que el rifle se mueva hacia atrás, es decir. el llamado retorno. Un fenómeno similar ocurre al disparar un arma (retroceso).
· Funcionamiento de la hélice (hélice). La hélice imparte movimiento a una determinada masa de aire (o agua) a lo largo del eje de la hélice, devolviendo esta masa hacia atrás. Si consideramos la masa lanzada y el avión (o barco) como un solo sistema, entonces las fuerzas de interacción entre la hélice y el medio ambiente, como internas, no pueden cambiar la cantidad total de movimiento de este sistema. Por lo tanto, cuando se expulsa una masa de aire (agua), el avión (o el barco) recibe una velocidad de avance correspondiente tal que la cantidad total de movimiento del sistema considerado sigue siendo igual a cero, ya que era cero antes de que comenzara el movimiento. .
Un efecto similar se consigue mediante la acción de remos o ruedas de paletas.
· Propulsión R e c t i v e. En un cohete (cohete), los productos gaseosos de la combustión del combustible son expulsados a gran velocidad por el orificio situado en la cola del cohete (desde la tobera del motor a reacción). Las fuerzas de presión que actúan en este caso serán fuerzas internas y no pueden cambiar el momento total del sistema de gases de pólvora del cohete. Pero como los gases que se escapan tienen un cierto movimiento dirigido hacia atrás, el cohete recibe una velocidad de avance correspondiente.
Teorema de los momentos respecto de un eje.
Considere el punto de masa material. metro, moviéndose bajo la influencia de la fuerza. F. Encontremos para ello la relación entre el momento de los vectores. mV Y F en relación con algún eje Z fijo.
m z (F) = xF - yF (7)
Lo mismo ocurre con el valor metro(mV), si se saca metro Estará fuera de paréntesis
metro z (mV) = m(xV - yV)(7`)
Tomando las derivadas con respecto al tiempo de ambos lados de esta igualdad, encontramos
En el lado derecho de la expresión resultante, el primer paréntesis es igual a 0, ya que dx/dt=V y dу/dt = V, el segundo paréntesis según la fórmula (7) es igual a
mz(F), ya que según la ley básica de la dinámica:
Finalmente tendremos (8)
La ecuación resultante expresa el teorema de los momentos con respecto al eje: la derivada temporal del momento de impulso de un punto con respecto a cualquier eje es igual al momento fuerza actuante sobre el mismo eje. Un teorema similar se cumple para momentos con respecto a cualquier centro O.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0
