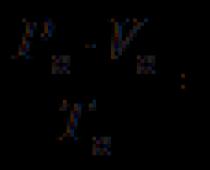Calcular el área de una figura Este es quizás uno de los problemas más difíciles de la teoría de áreas. En la geometría escolar se les enseña a encontrar las áreas de formas geométricas básicas como, por ejemplo, un triángulo, un rombo, un rectángulo, un trapezoide, un círculo, etc. Sin embargo, a menudo hay que lidiar con el cálculo de las áreas de figuras más complejas. Es en la resolución de tales problemas que es muy conveniente utilizar el cálculo integral.
Definición.
Trapecio curvilíneo se llama alguna figura G, acotada por las rectas y = f(x), y = 0, x = a y x = b, y la función f(x) es continua en el segmento [a; b] y no cambia su signo en él (Figura 1). El área de un trapezoide curvilíneo se puede denotar por S(G).
La integral definida ʃ a b f(x)dx para la función f(x), que es continua y no negativa en el segmento [a; b], y es el área del trapezoide curvilíneo correspondiente.
Es decir, para encontrar el área de la figura G, delimitada por las líneas y \u003d f (x), y \u003d 0, x \u003d a y x \u003d b, es necesario calcular el integral definida ʃ abf (x) dx.
De este modo, S(G) = ʃ a b f(x)dx.
Si la función y = f(x) no es positiva en [a; b], entonces el área del trapezoide curvilíneo se puede encontrar mediante la fórmula S(G) = -ʃ a b f(x)dx.
Ejemplo 1
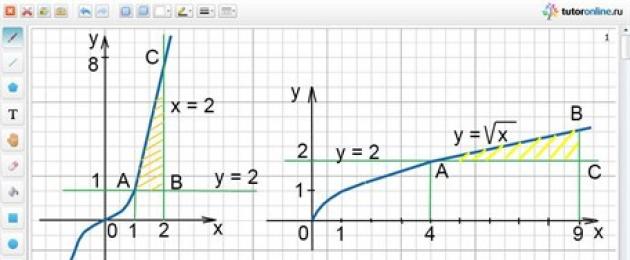
Calcule el área de la figura delimitada por las líneas y \u003d x 3; y = 1; x = 2
Solución.
Las líneas dadas forman la figura ABC, que se muestra sombreada en arroz. 2.
El área deseada es igual a la diferencia entre las áreas del trapezoide curvilíneo DACE y el cuadrado DABE.
Usando la fórmula S = ʃ a b f(x)dx = S(b) – S(a), encontramos los límites de integración. Para ello, resolvemos un sistema de dos ecuaciones:
(y \u003d x 3,
(y = 1.
Por lo tanto, tenemos x 1 \u003d 1 - el límite inferior y x \u003d 2 - el límite superior.
Entonces, S = S DACE - S DABE = ʃ 1 2 x 3 dx - 1 = x 4 /4| 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (unidades cuadradas).
Respuesta: 11/4 m2 unidades

Ejemplo 2
Calcule el área de la figura delimitada por líneas y \u003d √x; y = 2; x = 9.
Solución.
Las rectas dadas forman la figura ABC, que está acotada superiormente por la gráfica de la función
y \u003d √x, y desde abajo el gráfico de la función y \u003d 2. La figura resultante se muestra sombreada en arroz. 3.
El área deseada es igual a S = ʃ a b (√x - 2). Encontremos los límites de integración: b = 9, para encontrar a, resolvemos el sistema de dos ecuaciones:
(y = √x,
(y = 2.
Así, tenemos que x = 4 = a es el límite inferior.
Entonces, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 - 2x| 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (unidades cuadradas).
Respuesta: S = 2 2/3 cuadrados. unidades
Ejemplo 3
Calcule el área de la figura delimitada por las líneas y \u003d x 3 - 4x; y = 0; x ≥ 0.
Solución.
Tracemos la función y \u003d x 3 - 4x para x ≥ 0. Para hacer esto, encontramos la derivada y ':
y’ = 3x 2 – 4, y’ = 0 en х = ±2/√3 ≈ 1.1 son puntos críticos.
Si representamos los puntos críticos sobre el eje real y colocamos los signos de la derivada, obtenemos que la función decrece de cero a 2/√3 y crece de 2/√3 a más infinito. Entonces x = 2/√3 es el punto mínimo, el valor mínimo de la función y es min = -16/(3√3) ≈ -3.
Determinemos los puntos de intersección del gráfico con los ejes de coordenadas:
si x \u003d 0, entonces y \u003d 0, lo que significa que A (0; 0) es el punto de intersección con el eje Oy;
si y \u003d 0, entonces x 3 - 4x \u003d 0 o x (x 2 - 4) \u003d 0, o x (x - 2) (x + 2) \u003d 0, de donde x 1 \u003d 0, x 2 \u003d 2, x 3 \u003d -2 (no adecuado, porque x ≥ 0).
Los puntos A(0; 0) y B(2; 0) son los puntos de intersección de la gráfica con el eje Ox.
Las líneas dadas forman la figura OAB, que se muestra sombreada en arroz. 4.
Dado que la función y \u003d x 3 - 4x toma (0; 2) un valor negativo, entonces
S = |ʃ 0 2 (x 3 – 4x)dx|.
Tenemos: ʃ 0 2 (x 3 - 4x)dx = (x 4 /4 - 4x 2 /2)| 0 2 \u003d -4, desde donde S \u003d 4 metros cuadrados. unidades
Respuesta: S = 4 cuadrados. unidades

Ejemplo 4
Encuentre el área de la figura delimitada por la parábola y \u003d 2x 2 - 2x + 1, las líneas rectas x \u003d 0, y \u003d 0 y la tangente a esta parábola en el punto con la abscisa x 0 \u003d 2.
Solución.
Primero, componemos la ecuación de la tangente a la parábola y \u003d 2x 2 - 2x + 1 en el punto con la abscisa x₀ \u003d 2.
Como la derivada y' = 4x - 2, entonces para x 0 = 2 obtenemos k = y'(2) = 6.
Encuentra la ordenada del punto de contacto: y 0 = 2 2 2 – 2 2 + 1 = 5.
Por lo tanto, la ecuación tangente tiene la forma: y - 5 \u003d 6 (x - 2) o y \u003d 6x - 7.
Construyamos una figura delimitada por líneas:
y \u003d 2x 2 - 2x + 1, y \u003d 0, x \u003d 0, y \u003d 6x - 7.
Г y \u003d 2x 2 - 2x + 1 - parábola. Puntos de intersección con los ejes de coordenadas: A(0; 1) - con el eje Oy; con el eje Ox - no hay puntos de intersección, porque la ecuación 2x 2 - 2x + 1 = 0 no tiene solución (D< 0). Найдем вершину параболы:
x b \u003d 2/4 \u003d 1/2;
y b \u003d 1/2, es decir, el vértice del punto de parábola B tiene las coordenadas B (1/2; 1/2).
Entonces, la figura cuya área se va a determinar se muestra sombreada en arroz. cinco.
Tenemos: S O A B D \u003d S OABC - S ADBC.
Encuentre las coordenadas del punto D a partir de la condición:
6x - 7 = 0, es decir x \u003d 7/6, luego DC \u003d 2 - 7/6 \u003d 5/6.
Encontramos el área del triángulo DBC usando la fórmula S ADBC = 1/2 · DC · BC. De este modo,
S ADBC = 1/2 5/6 5 = 25/12 cuadrados. unidades
S OABC = ʃ 0 2 (2x 2 - 2x + 1)dx = (2x 3 /3 - 2x 2 /2 + x)| 0 2 \u003d 10/3 (unidades cuadradas).
Finalmente obtenemos: S O A B D \u003d S OABC - S ADBC \u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (unidades cuadradas).
Respuesta: S = 1 1/4 pies cuadrados. unidades
Hemos revisado ejemplos encontrar las áreas de figuras limitadas por líneas dadas. Para resolver con éxito tales problemas, debe poder construir líneas y gráficos de funciones en un plano, encontrar los puntos de intersección de las líneas, aplicar una fórmula para encontrar el área, lo que implica la capacidad y las habilidades para calcular ciertas integrales.
sitio, con copia total o parcial del material, se requiere un enlace a la fuente.
En esta lección aprenderemos a calcular áreas de figuras planas, que se llaman trapecios curvilíneos .
Ejemplos de tales figuras se encuentran en la siguiente figura.
Por un lado, encontrar el área de una figura plana mediante una integral definida es sumamente sencillo. Estamos hablando del área de la figura, que está limitada desde arriba por una cierta curva, desde abajo, por el eje de abscisas ( Buey), y a la izquierda y a la derecha hay algunas líneas rectas. La sencillez es que la integral definida de la función a la que se le da la curva, y ahí está el área de tal figura(trapecio curvilíneo).
Para calcular el área de una figura necesitamos:
- Integral definida de la función que define la curva , que limita el trapezoide curvilíneo desde arriba. Y aquí viene el primer matiz significativo: un trapezoide curvilíneo puede estar limitado por una curva no solo desde arriba, sino también desde abajo . ¿Cómo actuar en este caso? Simple pero importante de recordar: la integral en este caso se toma con signo menos .
- Límites de integración a Y B, que encontramos a partir de las ecuaciones de las rectas que limitan la figura por la izquierda y la derecha: X = a , X = B, donde a Y B- numeros
Por separado, algunos matices más..
La curva que limita el trapezoide curvilíneo desde arriba (o desde abajo) debe ser gráfico de una función continua y no negativa y = F(X) .
Los valores de X deben pertenecer al segmento [a, B] . Es decir, por ejemplo, no se tienen en cuenta las líneas como una sección de un hongo, en el que la pierna encaja perfectamente en este segmento y el sombrero es mucho más ancho.
Los segmentos laterales pueden degenerar en puntos . Si viste una figura así en el dibujo, esto no debería confundirte, ya que este punto siempre tiene su propio valor en el eje x. Entonces todo está en orden con los límites de la integración.
Ahora puede pasar a fórmulas y cálculos. Entonces el área s trapezoide curvilíneo se puede calcular mediante la fórmula
Si F(X) ≤ 0 (la gráfica de la función se encuentra debajo del eje Buey), luego área de un trapezoide curvo se puede calcular con la formula
También hay casos en los que los límites superior e inferior de la figura son funciones, respectivamente y = F(X) Y y = φ (X) , entonces el área de dicha figura se calcula mediante la fórmula
![]() . (3)
. (3)
Resolvemos problemas juntos
Comencemos con los casos en los que el área de una figura se puede calcular usando la fórmula (1).
Ejemplo 1Buey) y directo X = 1 , X = 3 .

Solución. Porque y = 1/X> 0 en el segmento , entonces el área del trapezoide curvilíneo se encuentra por la fórmula (1):
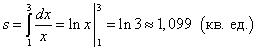 .
.
Ejemplo 2 Halla el área de la figura acotada por la gráfica de la función, recta X= 1 y el eje x ( Buey ).

Solución. El resultado de aplicar la fórmula (1):
![]()
si entonces s= 1/2; si entonces s= 1/3, etc
Ejemplo 3 Encuentra el área de la figura acotada por la gráfica de la función, el eje x ( Buey) y directo X = 4 .

Solución. La figura correspondiente a la condición del problema es un trapezoide curvilíneo, en el que el segmento izquierdo ha degenerado en un punto. Los límites de integración son 0 y 4. Ya que, según la fórmula (1), encontramos el área del trapezoide curvilíneo:
 .
.
Ejemplo 4 Halla el área de la figura delimitada por las rectas , , y ubicada en el 1er cuarto.

Solución. Para usar la fórmula (1), representamos el área de la figura dada por las condiciones del ejemplo como la suma de las áreas de un triángulo OAB y trapecio curvilíneo A B C. Al calcular el área de un triángulo. OAB los límites de integración son las abscisas de los puntos O Y A, y para la figura A B C- abscisas de puntos A Y C (A es el punto de intersección de la recta OA y parábolas, y C- punto de intersección de la parábola con el eje Buey). Resolviendo conjuntamente (como sistema) las ecuaciones de una recta y una parábola, obtenemos (la abscisa del punto A) y (la abscisa de otro punto de intersección de la recta y la parábola, que no es necesaria para la solución). Análogamente, obtenemos , (abscisas de los puntos C Y D). Ahora tenemos todo para encontrar el área de la figura. Encontramos:

Ejemplo 5 Encuentra el área de un trapezoide curvilíneo ACDB, si la ecuación de la curva discos compactos y abscisa A Y B respectivamente 1 y 2.

Solución. Esta ecuación de la curva la expresamos a través de Y: El área del trapezoide curvilíneo se encuentra mediante la fórmula (1):
 .
.
Pasemos a los casos en los que el área de una figura se puede calcular usando la fórmula (2).
Ejemplo 6 Encuentra el área de la figura delimitada por la parábola y el eje x ( Buey ).

Solución. Esta figura se encuentra debajo del eje x. Por lo tanto, para calcular su área, usamos la fórmula (2). Los límites de integración son las abscisas y los puntos de intersección de la parábola con el eje Buey. Como consecuencia,

Ejemplo 7 Encuentre el área entre el eje x ( Buey) y dos ondas sinusoidales vecinas.

Solución. El área de esta figura se puede encontrar mediante la fórmula (2):
![]() .
.
Encontremos cada término por separado:
 .
.
 .
.
Finalmente encontramos el área:
![]() .
.
Ejemplo 8 Encuentra el área de la figura encerrada entre la parábola y la curva.

Solución. Expresemos las ecuaciones de las rectas en términos de Y:
El área según la fórmula (2) se obtendrá como
![]() ,
,
donde a Y B- abscisas de puntos A Y B. Los encontramos resolviendo las ecuaciones juntas:

Finalmente encontramos el área:

Y, finalmente, hay casos en que el área de una figura se puede calcular usando la fórmula (3).
Ejemplo 9 Halla el área de la figura encerrada entre las parábolas ![]() Y .
Y .
Calcular el área de una figura delimitada por rectas.
Solución.
Hallamos los puntos de intersección de las rectas dadas. Para ello, resolvemos el sistema de ecuaciones:
Para encontrar las abscisas de los puntos de intersección de las rectas dadas, resolvemos la ecuación:
Encontramos: X 1 = -2, X 2 = 4.
Entonces, estas líneas, que son una parábola y una línea recta, se cortan en los puntos A(-2; 0), B(4; 6).

Estas líneas forman una figura cerrada, cuyo área se calcula utilizando la fórmula anterior:



De acuerdo con la fórmula de Newton-Leibniz, encontramos:



Encuentra el área de un área limitada por una elipse.
Solución.

De la ecuación de la elipse para el cuadrante I tenemos . De aquí, según la fórmula, obtenemos
Apliquemos la sustitución X = a pecado t, dx = a porque t dt. Nuevos límites de integración t = α Y t = β se determinan a partir de las ecuaciones 0 = a pecado t, a = a pecado t. se puede poner α = 0 y β = π /2.
Encontramos un cuarto del área requerida
![]()
De aquí S = pab.
Hallar el área de una figura delimitada por rectasy = - X 2 + X + 4 yy = - X + 1.
Solución.
Encuentra los puntos de intersección de las rectas y = -X 2 + X + 4, y = -X+ 1, igualando las ordenadas de las rectas: - X 2 + X + 4 = -X+ 1 o X 2 - 2X- 3 = 0. Encuentra las raíces X 1 = -1, X 2 = 3 y sus correspondientes ordenadas y 1 = 2, y 2 = -2.

Usando la fórmula del área de la figura, obtenemos
Encuentre el área encerrada por la parábolay = X 2 + 1 y directoX + y = 3.
Solución.
Resolviendo el sistema de ecuaciones
encontrar las abscisas de los puntos de intersección X 1 = -2 y X 2 = 1.

Asumiendo y 2 = 3 - X Y y 1 = X 2 + 1, según la fórmula que obtenemos
Calcular el área contenida dentro de la lemniscata de Bernoullir 2 = a 2 porque 2 φ .
Solución.

En el sistema de coordenadas polares, el área de la figura delimitada por el arco de la curva r = F(φ ) y dos radios polares φ 1 = ʅ Y φ 2 = ʆ , se expresa por la integral
Debido a la simetría de la curva, primero determinamos un cuarto del área deseada
Por lo tanto, el área total es S = a 2 .
Calcular la longitud de arco de un astroideX 2/3 + y 2/3 = a 2/3 .
Solución.

Escribimos la ecuación de la astroide en la forma
(X 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .
Pongamos X 1/3 = a 1/3 porque t, y 1/3 = a 1/3 pecado t.
De aquí obtenemos las ecuaciones paramétricas de la astroide
X = a porque 3 t, y = a pecado 3 t, (*)
donde 0 ≤ t ≤ 2π .
Dada la simetría de la curva (*), basta encontrar un cuarto de la longitud del arco L correspondiente al cambio de parámetro t de 0 a π /2.
Obtenemos
dx = -3a porque 2 t pecado t dt, dy = 3a pecado 2 t porque t dt.
A partir de aquí encontramos
![]()
Integrando la expresión resultante en el rango de 0 a π /2, obtenemos
![]()
![]()
De aquí L = 6a.
Encuentre el área delimitada por la espiral de Arquímedesr = aφ y dos radios vectores que corresponden a ángulos polaresφ 1 Yφ 2 (φ 1 < φ 2 ).
Solución.

Area delimitada por una curva r = F(φ ) se calcula mediante la fórmula , donde α Y β - límites de cambio del ángulo polar.
Así, obtenemos

 (*)
(*)
De (*) se sigue que el área delimitada por el eje polar y la primera vuelta de la espiral de Arquímedes ( φ 1 = 0; φ 2 = 2π ):
De manera similar, encontramos el área delimitada por el eje polar y la segunda vuelta de la espiral de Arquímedes ( φ 1 = 2π ; φ 2 = 4π ):
![]()
El área requerida es igual a la diferencia de estas áreas
Calcular el volumen de un cuerpo obtenido por rotación alrededor de un ejeBuey figura limitada por parábolasy = X 2 YX = y 2 .
Solución.

Resolvamos el sistema de ecuaciones
y obten X 1 = 0, X 2 = 1, y 1 = 0, y 2 = 1, de donde los puntos de intersección de las curvas O(0; 0), B(once). Como puede verse en la figura, el volumen deseado del cuerpo de revolución es igual a la diferencia entre los dos volúmenes formados por la rotación alrededor del eje Buey trapecios curvilíneos OBA Y ODBA:

Calcular el área delimitada por el ejeBuey y sinusoidey = pecadoX en segmentos: a); B) .
Solución.

a) Sobre el segmento, la función sen X conserva el signo, y por lo tanto por la fórmula , asumiendo y= pecado X, encontramos


b) Sobre el segmento , función sen X cambia de signo. Para la correcta solución del problema, es necesario dividir el segmento en dos y [ π , 2π ], en cada uno de los cuales la función conserva su signo.
Según la regla de los signos, en el segmento [ π , 2π ] área se toma con un signo menos.
Como resultado, el área deseada es igual a
![]()
![]()
![]()
![]()
![]()
Determinar el volumen del cuerpo acotado por la superficie obtenida a partir de la rotación de la elipsealrededor del eje mayora .
Solución.

Dado que la elipse es simétrica respecto a los ejes de coordenadas, basta encontrar el volumen formado por la rotación alrededor del eje Bueyárea OAB, igual a un cuarto del área de la elipse, y el doble del resultado.
Denotemos el volumen del cuerpo de revolución a través de V X; entonces, con base en la fórmula, tenemos , donde 0 y a- abscisas de puntos B Y A. De la ecuación de la elipse encontramos . De aquí
Por lo tanto, el volumen requerido es igual a . (Cuando la elipse gira alrededor del eje menor B, el volumen del cuerpo es )
Encuentre el área delimitada por parábolasy 2 = 2 píxeles YX 2 = 2 py .
Solución.

Primero, encontramos las coordenadas de los puntos de intersección de las parábolas para determinar el intervalo de integración. Transformando las ecuaciones originales, obtenemos y . Igualando estos valores, obtenemos o X 4 - 8pags 3 X = 0.
X 4 - 8pags 3 X = X(X 3 - 8pags 3) = X(X - 2pags)(X 2 + 2píxeles + 4pags 2) = 0.
Encontramos las raíces de las ecuaciones:
![]()
![]()
Teniendo en cuenta el hecho de que el punto A la intersección de las parábolas está en el primer cuarto, entonces los límites de integración X= 0 y X = 2pags.
El área deseada se encuentra mediante la fórmula
pero)
Solución.
El primer y más importante momento de la decisión es la construcción de un dibujo..
Hagamos un dibujo:
La ecuacion y=0 establece el eje x;
- x=-2 Y x=1 - recto, paralelo al eje UNED;
- y \u003d x 2 +2 - una parábola cuyas ramas están dirigidas hacia arriba, con un vértice en el punto (0;2).
Comentario. Para construir una parábola, basta encontrar los puntos de su intersección con los ejes de coordenadas, es decir poniendo x=0 encontrar la intersección con el eje UNED y resolviendo la ecuación cuadrática correspondiente, encuentre la intersección con el eje Oh .
El vértice de una parábola se puede encontrar usando las fórmulas:
Puede dibujar líneas y punto por punto.
En el intervalo [-2;1] la gráfica de la función y=x 2 +2 situado sobre el eje Buey , es por eso:
Responder: S \u003d 9 unidades cuadradas
Una vez completada la tarea, siempre es útil mirar el dibujo y averiguar si la respuesta es real. En este caso, "a ojo" contamos la cantidad de celdas en el dibujo; bueno, se escribirán alrededor de 9, parece ser cierto. Está bastante claro que si tuviéramos, digamos, la respuesta: 20 unidades cuadradas, entonces, obviamente, se cometió un error en alguna parte: 20 celdas claramente no encajan en la cifra en cuestión, como máximo una docena. Si la respuesta resultó ser negativa, entonces la tarea también se resolvió incorrectamente.
Qué hacer si se encuentra el trapezoide curvilíneo debajo del eje ¿Oh?
B) Calcular el área de una figura delimitada por rectas y=-e x , x=1 y ejes de coordenadas.
Solución.
Hagamos un dibujo.
Si un trapezoide curvilíneo completamente debajo del eje Oh , entonces su área se puede encontrar por la fórmula:
Responder: S=(e-1) unidad cuadrada" 1.72 unidad cuadrada
¡Atención! No confundas los dos tipos de tareas.:
1) Si se le pide que resuelva solo una integral definida sin ningún significado geométrico, entonces puede ser negativa.
2) Si se le pide que encuentre el área de una figura usando una integral definida, ¡entonces el área siempre es positiva! Por eso aparece el signo menos en la fórmula que acabamos de considerar.
En la práctica, la mayoría de las veces la figura se ubica tanto en el semiplano superior como en el inferior.
desde) Encuentra el área de una figura plana delimitada por rectas y \u003d 2x-x 2, y \u003d -x.
Solución.
Primero necesitas hacer un dibujo. En términos generales, cuando construimos un dibujo en problemas de área, estamos más interesados en los puntos de intersección de las líneas. Encontremos los puntos de intersección de la parábola y la recta, esto se puede hacer de dos maneras. La primera forma es analítica.
Resolvemos la ecuación:
Entonces el límite inferior de integración un=0 , el límite superior de integración b=3 .
|
Construimos las líneas dadas: 1. Parábola - vértice en el punto (1;1); intersección del eje Oh - puntos(0;0) y (0;2). 2. Línea recta: la bisectriz de los ángulos de coordenadas segundo y cuarto. Y ahora ¡Atención! Si en el intervalo [ a;b] alguna función continua f(x) mayor o igual que alguna función continua g(x), entonces el área de la figura correspondiente se puede encontrar mediante la fórmula: . Y no importa dónde se encuentre la figura, sobre el eje o debajo del eje, pero es importante qué gráfico está MÁS ALTO (en relación con otro gráfico) y cuál está ABAJO. En el ejemplo en consideración, es obvio que en el segmento la parábola se encuentra por encima de la línea recta y, por lo tanto, es necesario restar de |
Es posible construir líneas punto por punto, mientras que los límites de integración se descubren como "por sí mismos". Sin embargo, el método analítico para encontrar los límites todavía tiene que usarse a veces si, por ejemplo, el gráfico es lo suficientemente grande o la construcción enhebrada no reveló los límites de integración (pueden ser fraccionarios o irracionales).
La figura deseada está limitada por una parábola desde arriba y una línea recta desde abajo.
Sobre el segmento , según la fórmula correspondiente:
Responder: S \u003d 4.5 unidades cuadradas
De hecho, para encontrar el área de una figura, no necesita tanto conocimiento de la integral indefinida y definida. La tarea "calcular el área usando una integral definida" siempre involucra la construcción de un dibujo, por lo que tus conocimientos y habilidades de dibujo serán un tema mucho más relevante. En este sentido, es útil para refrescar la memoria de los gráficos de las principales funciones elementales y, como mínimo, poder construir una línea recta y una hipérbola.
Un trapezoide curvilíneo es una figura plana limitada por un eje, líneas rectas y una gráfica de una función continua en un segmento que no cambia de signo en este intervalo. Que esta figura se ubique no menos abscisa:
Luego el área de un trapezoide curvilíneo es numéricamente igual a cierta integral. Cualquier integral definida (que existe) tiene un muy buen significado geométrico.
En términos de geometría, la integral definida es el ÁREA.
Es decir, la integral definida (si existe) corresponde geométricamente al área de alguna figura. Por ejemplo, considere la integral definida . El integrando define una curva en el plano que se encuentra arriba del eje (los que lo deseen pueden completar el dibujo), y la propia integral definida es numéricamente igual al área del trapezoide curvilíneo correspondiente.
Ejemplo 1
Esta es una declaración de tarea típica. El primer y más importante momento de la decisión es la construcción de un dibujo.. Además, el dibujo debe construirse CORRECTO.
Al construir un plano, recomiendo el siguiente orden: en primer lugar es mejor construir todas las líneas (si las hay) y solo Luego- parábolas, hipérbolas, gráficas de otras funciones. Los gráficos de funciones son más rentables para construir puntualmente
En este problema, la solución podría verse así.
Hagamos un dibujo (nótese que la ecuación define el eje):
En el segmento se encuentra la gráfica de la función sobre el eje, es por eso:
Responder:
Una vez completada la tarea, siempre es útil mirar el dibujo y averiguar si la respuesta es real. En este caso, "a ojo" contamos la cantidad de celdas en el dibujo; bueno, se escribirán alrededor de 9, parece ser cierto. Está bastante claro que si tuviéramos, digamos, la respuesta: 20 unidades cuadradas, entonces, obviamente, se cometió un error en alguna parte: 20 celdas claramente no encajan en la cifra en cuestión, como máximo una docena. Si la respuesta resultó ser negativa, entonces la tarea también se resolvió incorrectamente.
Ejemplo 3
Calcula el área de la figura delimitada por líneas y ejes de coordenadas.
Solución: Hagamos un dibujo:
Si el trapezoide curvilíneo se encuentra debajo del eje(o al menos no más alto eje dado), entonces su área se puede encontrar mediante la fórmula:
En este caso:
¡Atención! No confundas los dos tipos de tareas.:
1) Si se le pide que resuelva solo una integral definida sin ningún significado geométrico, entonces puede ser negativa.
2) Si se le pide que encuentre el área de una figura usando una integral definida, ¡entonces el área siempre es positiva! Por eso aparece el signo menos en la fórmula que acabamos de considerar.
En la práctica, la mayoría de las veces la figura se ubica tanto en el semiplano superior como en el inferior y, por lo tanto, desde los problemas escolares más simples, pasamos a ejemplos más significativos.
Ejemplo 4
Encuentra el área de una figura plana delimitada por rectas, .
Solución: Primero necesitas completar el dibujo. En términos generales, cuando construimos un dibujo en problemas de área, estamos más interesados en los puntos de intersección de las líneas. Encontremos los puntos de intersección de la parábola y la recta. Esto se puede hacer de dos maneras. La primera forma es analítica. Resolvemos la ecuación:
Por lo tanto, el límite inferior de integración, el límite superior de integración.
Es mejor no usar este método si es posible..
Es mucho más rentable y rápido construir las líneas punto por punto, mientras que los límites de integración se van descubriendo como “por sí mismos”. Sin embargo, el método analítico para encontrar los límites todavía tiene que usarse a veces si, por ejemplo, el gráfico es lo suficientemente grande o la construcción enhebrada no reveló los límites de integración (pueden ser fraccionarios o irracionales). Y también consideraremos tal ejemplo.
Volvemos a nuestra tarea: es más racional construir primero una línea recta y luego una parábola. Hagamos un dibujo:
Y ahora la fórmula de trabajo: Si hay alguna función continua en el intervalo mayor que o igual alguna función continua, entonces el área de la figura limitada por los gráficos de estas funciones y líneas rectas, se puede encontrar mediante la fórmula:
Aquí ya no es necesario pensar dónde se encuentra la figura: sobre el eje o debajo del eje y, en términos generales, importa qué gráfico está ARRIBA(relativo a otro gráfico), y cual esta ABAJO.
En el ejemplo en consideración, es obvio que en el segmento la parábola se encuentra por encima de la línea recta y, por lo tanto, es necesario restar de
La finalización de la solución podría verse así:
La figura deseada está limitada por una parábola desde arriba y una línea recta desde abajo.
Sobre el segmento , según la fórmula correspondiente:
Responder:
Ejemplo 4
Calcula el área de la figura delimitada por las rectas , , , .
Solución: Primero hagamos un dibujo:
La figura cuya área necesitamos encontrar está sombreada en azul.(Mire cuidadosamente la condición, ¡cómo la figura es limitada!). Pero en la práctica, debido a la falta de atención, a menudo ocurre un "fallo", ¡que necesita encontrar el área de la figura que está sombreada en verde!
Este ejemplo también es útil porque en él el área de la figura se calcula utilizando dos integrales definidas.
En realidad:
1) En el segmento sobre el eje hay un gráfico de línea recta;
2) En el segmento sobre el eje hay un gráfico de hipérbola.
Es bastante obvio que las áreas pueden (y deben) agregarse, por lo tanto:
Cómo calcular el volumen de un cuerpo de revoluciónutilizando una integral definida?
Imagina una figura plana en el plano de coordenadas. Ya hemos encontrado su área. Pero, además, esta figura también se puede girar, y girar de dos formas:
Alrededor del eje x;
Alrededor del eje y .
En este artículo se discutirán ambos casos. El segundo método de rotación es especialmente interesante, causa las mayores dificultades, pero de hecho la solución es casi la misma que en la rotación más común alrededor del eje x.
Comencemos con el tipo de rotación más popular.
- En contacto con 0
- Google+ 0
- OK 0
- Facebook 0