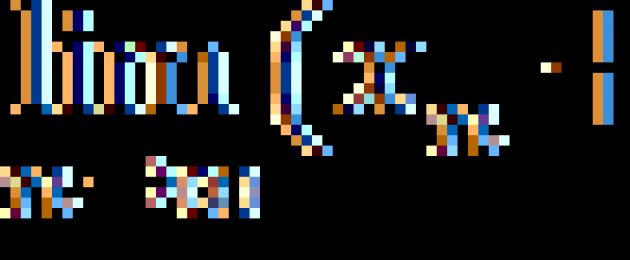Dé la definición de una función infinitesimal en un punto. Funciones infinitesimales y sus propiedades básicas.

Función y=f(x) llamado infinitesimal en x→a o cuando X→∞, si o , es decir una función infinitesimal es una función cuyo límite en un punto dado es cero.

Ejemplos.

1. Función f(x)=(X-1) 2 es infinitesimal en X→1, ya que (ver figura).

2. Función f(x)= tg X– infinitesimal en X→0.

3. f(x)= iniciar sesión(1+ X) – infinitesimal en X→0.

4. f(x) = 1/X– infinitesimal en X→∞.

Establezcamos la siguiente relación importante:

Teorema. Si la función y=f(x) representable con x→a como suma de un número constante b y magnitud infinitesimal α(x): f (x)=b+ α(x) Eso .

Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a.

Prueba.

1. Probemos la primera parte del enunciado. Desde la igualdad f(x)=b+a(x) debería |f(x) – b|=| α|. Pero desde hacha) es infinitesimal, entonces para ε arbitrario hay δ – una vecindad del punto a, en frente de todos X de donde, valores hacha) satisfacer la relación |α(x)|< ε. Entonces |f(x) – b|< ε. Y esto significa que.

2. Si , entonces para cualquier ε >0 para todos X desde algún δ - vecindad de un punto a voluntad |f(x) – b|< ε. Pero si denotamos f(x) – b= α, Eso |α(x)|< ε, lo que significa que a– infinitesimal.

Consideremos las propiedades básicas de las funciones infinitesimales.

Teorema 1. La suma algebraica de dos, tres y en general cualquier número finito de infinitesimales es una función infinitesimal.

Prueba. Demos una prueba para dos términos. Dejar f(x)=α(x)+β(x), dónde y . Necesitamos demostrar que para cualquier ε pequeño y arbitrario > 0 encontrado δ> 0, tal que para X, satisfaciendo la desigualdad |x – a|<δ , realizado |f(x)|< ε.

Entonces, arreglemos un número arbitrario ε > 0. Dado que según las condiciones del teorema a(x) es una función infinitesimal, entonces existe tal δ 1 > 0, que es |x – a|< δ 1 tenemos |α(x)|< ε / 2. Asimismo, desde β(x) es infinitesimal, entonces existe tal δ 2 > 0, que es |x – a|< δ 2 tenemos | β(x)|< ε / 2.

Echemos δ=mín(δ 1 , δ2 } .Luego en las cercanías del punto a radio δ cada una de las desigualdades será satisfecha |α(x)|< ε / 2 y | β(x)|< ε / 2. Por lo tanto, en este barrio habrá

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

aquellos. |f(x)|< ε, que es lo que había que demostrar.

Teorema 2. Producto de una función infinitesimal hacha) para una función limitada f(x) en x→a(o cuando x→∞) es una función infinitesimal.

Prueba. Desde la función f(x) es limitado, entonces hay un número METRO tal que para todos los valores X desde algún barrio de un punto a|f(x)|≤M. Es más, desde hacha) es una función infinitesimal en x→a, entonces para un ε arbitrario > 0 hay una vecindad del punto a, en el que se mantendrá la desigualdad |α(x)|< ε /METRO. Luego, en el más pequeño de estos barrios tenemos | αf|< ε /METRO= ε. Y esto significa que af– infinitesimal. Para la ocasión x→∞ la prueba se realiza de manera similar.

Del teorema probado se sigue:

Corolario 1. Si y, entonces.

Corolario 2. Si c= constante, entonces.

Teorema 3. Razón de una función infinitesimal a(x) por función f(x), cuyo límite es distinto de cero, es una función infinitesimal.

Prueba. Dejar . Entonces 1 /f(x) hay una función limitada. Por tanto, una fracción es el producto de una función infinitesimal y una función limitada, es decir la función es infinitesimal.

Definición función numérica. Métodos para especificar funciones.

Sea D un conjunto en la recta numérica R. Si cada x perteneciente a D está asociada con un solo número y=f(x), entonces decimos que se da una función f.

Métodos para especificar funciones:

1) tabular: para funciones definidas en un conjunto finito.

2) analítico

3) gráfico

2 y 3 – para funciones definidas en un conjunto infinito.

El concepto de función inversa.

Si la función y=f(x) es tal que diferentes valores del argumento x corresponden a diferentes valores de la función, entonces la variable x se puede expresar como una función de la variable y: x=g(y ). La función g se llama inversa de f y se denota por f^(-1).

El concepto de función compleja.

Complejo función-función, cuyo argumento es cualquier otra función.

Sean dadas las funciones f(x) y g(x). Hagamos dos funciones complejas con ellas. Considerando que la función f es externa (principal) y la función g es interna, obtenemos una función compleja u(x)=f(g(x)).

Determinación del límite de secuencia.

Un número a se llama límite de una secuencia (xn) si para cualquier positivo hay un número n0, a partir del cual todos los términos de la secuencia difieren de a en módulo en menos de ε (es decir, caen en la vecindad ε del punto a):

Reglas para calcular los límites de sucesiones convergentes.

1. Toda secuencia convergente tiene un solo límite. 2. Si todos los elementos de la secuencia (x n) son iguales a C (constante), entonces el límite de la secuencia (x n) también es igual a C. 3. ; 4. ; 5. .

Definición secuencia limitada.

La secuencia (x n) se llama acotada si el conjunto de números X=(x n) está acotado: .

Definición de una secuencia infinitesimal.

Se dice que una secuencia (x n) es infinitesimal si para cualquier (no importa cuán pequeño) >0 existe un número n 0 tal que para cualquier n>n 0 la desigualdad |x n |< .

Definición de una secuencia infinitamente grande.

Se dice que una secuencia es infinitamente grande si para cualquier número (sin importar cuán grande) A>0 existe un número n 0 tal que para cada número n>n 0 se cumple la desigualdad |x n |>A.

Definición de secuencias monótonas.

Secuencias monótonas: 1) aumentando six n x n +1 para todo n, 4) no creciente si x n x n +1 para todo n.

Determinación del límite de una función en un punto.

El límite de la función y=f(x) en el punto x 0 (o en x x 0) es el número a si para cualquier secuencia (x n) valores del argumento que convergen a x 0 (todos x n x 0), El La secuencia de valores (f(x n)) de la función converge al límite a.

Definición de una función infinitesimal.

F-iya Se dice que f(x) es infinitesimal cuando x→A si .

Definición de una función infinitamente grande.

F-iya Se dice que f(x) es infinitamente grande para x→A si .

Definiciones y propiedades de funciones infinitesimales e infinitamente grandes en un punto. Pruebas de propiedades y teoremas. Relación entre funciones infinitesimales e infinitamente grandes.

Contenido

Ver también: Secuencias infinitesimales: definición y propiedades
Propiedades de secuencias infinitamente grandes.

Definición de funciones infinitesimales y infinitesimales

sea ​​x 0 es un punto finito o infinito: ∞, -∞ o +∞.

Definición de una función infinitesimal
Función α (X) llamado infinitesimal cuando x tiende a x 0 0 , y es igual a cero:
.

Definición de una función infinitamente grande
Función f (X) llamado infinitamente grande cuando x tiende a x 0 , si la función tiene un límite como x → x 0 , y es igual a infinito:
.

Propiedades de funciones infinitesimales

Propiedad de la suma, diferencia y producto de funciones infinitesimales

Suma, diferencia y producto número finito de funciones infinitesimales cuando x → x 0 es una función infinitesimal como x → x 0 .

Esta propiedad es una consecuencia directa de las propiedades aritméticas de los límites de una función.

Teorema del producto función limitada a infinitesimal

Producto de una función acotada en alguna vecindad perforada del punto x 0 , a infinitesimal, como x → x 0 , es una función infinitesimal como x → x 0 .

La propiedad de representar una función como la suma de una constante y una función infinitesimal.

Para que la función f (X) tenía un límite finito, es necesario y suficiente que
,
donde es una función infinitesimal cuando x → x 0 .

Propiedades de funciones infinitamente grandes

Teorema sobre la suma de una función acotada y una función infinitamente grande

La suma o diferencia de una función acotada en alguna vecindad perforada del punto x 0 , y una función infinitamente grande, como x → x 0 , es una función infinitamente grande cuando x → x 0 .

Teorema sobre la división de una función acotada por una infinitamente grande

Si la función f (X) es infinitamente grande como x → x 0 , y la función g (X)- está limitado por alguna vecindad perforada del punto x 0 , Eso
.

Teorema sobre la división de una función acotada inferiormente por una infinitesimal

Si la función, en alguna vecindad perforada del punto, está acotada desde abajo en valor absoluto numero positivo:
,
y la función es infinitesimal cuando x → x 0 :
,
y hay una vecindad perforada del punto en el que, entonces
.

Propiedad de desigualdades de funciones infinitamente grandes.

Si la función es infinitamente grande en:
,
y las funciones y , en alguna vecindad perforada del punto satisfacen la desigualdad:
,
entonces la función también es infinitamente grande en:
.

Esta propiedad tiene dos casos especiales.

Sean, en alguna vecindad perforada del punto , las funciones y satisfacen la desigualdad:
.
Entonces si, entonces y.
Si, entonces y.

Relación entre funciones infinitamente grandes e infinitesimales

De las dos propiedades anteriores se desprende la conexión entre funciones infinitamente grandes e infinitesimales.

Si una función es infinitamente grande en , entonces la función es infinitesimal en .

Si una función es infinitesimal para , y , entonces la función es infinitamente grande para .

La relación entre una función infinitesimal y una función infinitamente grande se puede expresar simbólicamente:
, .

Si una función infinitesimal tiene cierto signo en , es decir, es positiva (o negativa) en alguna vecindad perforada del punto , entonces podemos escribirla así:
.
De la misma manera, si una función infinitamente grande tiene un cierto signo en , entonces escriben:
, o .

Entonces, la conexión simbólica entre funciones infinitamente pequeñas e infinitamente grandes se puede complementar con las siguientes relaciones:
, ,
, .

Se pueden encontrar fórmulas adicionales relacionadas con los símbolos de infinito en la página
"Puntos al infinito y sus propiedades".

Prueba de propiedades y teoremas.

Demostración del teorema sobre el producto de una función acotada y una infinitesimal

Para demostrar este teorema usaremos . También usamos la propiedad de las sucesiones infinitesimales, según la cual

Sea la función infinitesimal en y esté acotada en alguna vecindad perforada del punto:
en .

Como hay un límite, hay una vecindad perforada del punto en el que se define la función. Que haya una intersección de barrios y . Luego las funciones y están definidas en él.

.
,
una secuencia es infinitesimal:
.

Aprovechemos que el producto de una secuencia acotada y una secuencia infinitesimal es una secuencia infinitesimal:
.
.

El teorema ha sido demostrado.

Prueba de la propiedad de representar una función como la suma de una constante y una función infinitesimal

Necesidad. Sea la función un límite finito en un punto
.
Considere la función:
.
Usando la propiedad del límite de la diferencia de funciones, tenemos:
.
Es decir, existe una función infinitesimal en .

Adecuación. Déjalo ser. Apliquemos la propiedad del límite de la suma de funciones:
.

La propiedad ha sido probada.

Demostración del teorema sobre la suma de una función acotada y una función infinitamente grande

Para demostrar el teorema, usaremos la definición de Heine del límite de una función.

en .

Como hay un límite, hay una vecindad perforada del punto en el que se define la función. Que haya una intersección de barrios y . Luego las funciones y están definidas en él.

Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia es limitada:
,
una secuencia es infinitamente grande:
.

Dado que la suma o diferencia de una secuencia limitada y una infinitamente grande
.
Entonces, según la definición del límite de una secuencia según Heine,
.

El teorema ha sido demostrado.

Prueba del teorema sobre el cociente de división de una función acotada por una infinitamente grande

Para demostrar esto, usaremos la definición de Heine del límite de una función. También utilizamos la propiedad de las sucesiones infinitamente grandes, según la cual es una sucesión infinitesimal.

Sea la función infinitamente grande en y esté acotada en alguna vecindad perforada del punto:
en .

Dado que la función es infinitamente grande, existe una vecindad perforada del punto donde está definida y no desaparece:
en .
Que haya una intersección de barrios y . Luego las funciones y están definidas en él.

Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia es limitada:
,
una secuencia es infinitamente grande con diferentes de cero miembros:
, .

Dado que el cociente de dividir una secuencia limitada por una infinitamente grande es una secuencia infinitesimal, entonces
.
Entonces, según la definición del límite de una secuencia según Heine,
.

El teorema ha sido demostrado.

Prueba del teorema del cociente para dividir una función acotada inferiormente por una infinitesimal

Para demostrar esta propiedad, usaremos la definición de Heine del límite de una función. También utilizamos la propiedad de las secuencias infinitamente grandes, según la cual es una secuencia infinitamente grande.

Sea la función infinitesimal para , y dejemos que la función esté limitada en valor absoluto desde abajo por un número positivo, en alguna vecindad perforada del punto:
en .

Por condición, existe una vecindad perforada del punto en el que se define la función y no desaparece:
en .
Que haya una intersección de barrios y . Luego las funciones y están definidas en él. Además, y .

Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia está limitada a continuación:
,
y la secuencia es infinitesimal con términos distintos de cero:
, .

Dado que el cociente de dividir una secuencia acotada debajo por una infinitesimal es una secuencia infinitamente grande, entonces
.
Y que haya una vecindad perforada del punto en el que
en .

Tomemos una secuencia arbitraria que converge a . Entonces, a partir de algún número N, los elementos de la secuencia pertenecerán a esta vecindad:
en .
Entonces
en .

Según la definición del límite de una función según Heine,
.
Entonces, por la propiedad de las desigualdades de secuencias infinitamente grandes,
.
Dado que la secuencia es arbitraria y converge a , entonces, por la definición del límite de una función según Heine,
.

La propiedad ha sido probada.

Referencias:
L.D. Kudryavtsev. Bien Análisis matemático. Volumen 1. Moscú, 2003.

Ver también:

Funciones infinitesimales

La función %%f(x)%% se llama infinitesimal(b.m.) con %%x \to a \in \overline(\mathbb(R))%%, si con esta tendencia del argumento el límite de la función es igual a cero.

El concepto de b.m. La función está indisolublemente ligada a instrucciones para cambiar su argumento. Podemos hablar de b.m. funciona en %%a \to a + 0%% y en %%a \to a - 0%%. Generalmente b.m. las funciones se indican con las primeras letras del alfabeto griego %%\alpha, \beta, \gamma, \ldots%%

Ejemplos

1. La función %%f(x) = x%% es b.m. en %%x \to 0%%, ya que su límite en el punto %%a = 0%% es cero. Según el teorema sobre la conexión entre el límite bilateral y el límite unilateral, esta función es b.m. tanto con %%x \to +0%% como con %%x \to -0%%.
2. Función %%f(x) = 1/(x^2)%% - b.m. en %%x \to \infty%% (así como en %%x \to +\infty%% y en %%x \to -\infty%%).

Un número constante distinto de cero, por pequeño que sea en valor absoluto, no es una b.m. función. Para números constantes, la única excepción es el cero, ya que la función %%f(x) \equiv 0%% tiene un límite cero.

Teorema

La función %%f(x)%% tiene en el punto %%a \in \overline(\mathbb(R))%% de la recta numérica extendida un límite final igual al número %%b%% si y sólo si esta función es igual a la suma de este número %%b%% y b.m. funciones %%\alpha(x)%% con %%x \to a%%, o $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$

Propiedades de funciones infinitesimales

De acuerdo con las reglas de paso al límite con %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, se siguen las siguientes afirmaciones:

1. La suma del número final de b.m. funciones para %%x \to a%% es b.m. en %%x \a un%%.
2. El producto de cualquier número b.m. funciones para %%x \to a%% es b.m. en %%x \a un%%.

Producto b.m. funciones en %%x \to a%% y una función limitada en algún vecindario perforado %%\stackrel(\circ)(\text(U))(a)%% del punto a, hay b.m. en %%x \a una función%%.

Está claro que el producto de una función constante y b.m. en %%x \to a%% hay b.m. funcionar en %%x \to a%%.

Funciones infinitesimales equivalentes

Las funciones infinitesimales %%\alpha(x), \beta(x)%% para %%x \to a%% se llaman equivalente y escribe %%\alpha(x) \sim \beta(x)%%, si

$$ \lim\limits_(x \a a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \a a)(\frac(\beta(x) )(\alfa(x))) = 1. $$

Teorema sobre la sustitución de b.m. funciones equivalentes

Sea %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m. funciones para %%x \to a%%, y %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, entonces $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ límites_(x \a a)(\frac(\alpha_1(x))(\beta_1(x))). $$

Equivalente b.m. funciones.

Sea %%\alpha(x)%% b.m. funcionar en %%x \to a%%, entonces

1. %%\sin(\alpha(x)) \sim \alpha(x)%%
2. %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
3. %%\tan \alpha(x) \sim \alpha(x)%%
4. %%\arcsin\alpha(x) \sim \alpha(x)%%
5. %%\arctan\alpha(x) \sim \alpha(x)%%
6. %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
7. %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
8. %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%

Ejemplo

$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(matriz) $$

Funciones infinitamente grandes

La función %%f(x)%% se llama infinitamente grande(b.b.) con %%x \to a \in \overline(\mathbb(R))%%, si con esta tendencia del argumento la función tiene límite infinito.

Similar a b.m. concepto de funciones b.b. La función está indisolublemente ligada a instrucciones para cambiar su argumento. Podemos hablar de b.b. funciones para %%x \to a + 0%% y %%x \to a - 0%%. El término "infinitamente grande" no se refiere al valor absoluto de la función, sino a la naturaleza de su cambio en las proximidades del punto en cuestión. Ningún número constante, por grande que sea en valor absoluto, es infinitamente grande.

Ejemplos

1. Función %%f(x) = 1/x%% - b.b. en %%x \a 0%%.
2. Función %%f(x) = x%% - b.b. en %%x \to \infty%%.

Si la definición condiciona $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(array) $$

luego hablan de positivo o negativo cama y desayuno. en la función %%a%%.

Ejemplo

Función %%1/(x^2)%% - positivo b.b. en %%x \a 0%%.

La conexión entre b.b. y b.m. funciones

Si %%f(x)%% es b.b. con %%x \a una función%%, luego %%1/f(x)%% - b.m.

en %%x \a un%%. Si %%\alpha(x)%% - b.m. para %%x \to a%% es una función distinta de cero en alguna vecindad perforada del punto %%a%%, entonces %%1/\alpha(x)%% es b.b. en %%x \a un%%.

Propiedades de funciones infinitamente grandes

Presentemos varias propiedades del b.b. funciones. Estas propiedades se derivan directamente de la definición de b.b. funciones y propiedades de funciones que tienen límites finitos, así como del teorema sobre la conexión entre b.b. y b.m. funciones.

1. El producto de un número finito de b.b. funciones para %%x \to a%% es b.b. funcionar en %%x \to a%%. De hecho, si %%f_k(x), k = \overline(1, n)%% - b.b. funcionar en %%x \to a%%, luego en alguna vecindad perforada del punto %%a%% %%f_k(x) \ne 0%%, y por el teorema de conexión b.b. y b.m. funciones %%1/f_k(x)%% - b.m. funcionar en %%x \to a%%. Resulta %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - función b.m para %%x \to a%%, y %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funcionar en %%x \to a%%.
2. Producto b.b. funciones para %%x \to a%% y una función que en alguna vecindad perforada del punto %%a%% en valor absoluto es mayor que una constante positiva es b.b. funcionar en %%x \to a%%. En particular, el producto b.b. una función con %%x \to a%% y una función que tiene un límite finito distinto de cero en el punto %%a%% será b.b. funcionar en %%x \to a%%.

La suma de una función acotada en alguna vecindad perforada del punto %%a%% y b.b. funciones con %%x \to a%% es b.b. funcionar en %%x \to a%%.

Por ejemplo, las funciones %%x - \sin x%% y %%x + \cos x%% son b.b. en %%x \to \infty%%.

3. La suma de dos b.b. funciones en %%x \to a%% hay incertidumbre. Dependiendo del signo de los términos, la naturaleza del cambio en dicha suma puede ser muy diferente.

   Ejemplo

   Sean dadas las funciones %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. funciona en %%x \to \infty%%. Entonces:

   • %%f(x) + g(x) = 3x%% - b.b. función en %%x \to \infty%%;
   • %%f(x) + h(x) = 0%% - b.m. función en %%x \to \infty%%;
   • %%h(x) + v(x) = \sin x%% no tiene límite en %%x \to \infty%%.

Cálculo de infinitesimales y grandes.

Cálculo infinitesimal- cálculos realizados con cantidades infinitesimales, en los que el resultado obtenido se considera como una suma infinita de infinitesimales. El cálculo infinitesimal es concepto general para el cálculo diferencial e integral, que forman la base de las matemáticas superiores modernas. El concepto de cantidad infinitesimal está estrechamente relacionado con el concepto de límite.

Infinitesimal

Subsecuencia a norte llamado infinitesimal, Si . Por ejemplo, una secuencia de números es infinitesimal.

La función se llama infinitesimal en la proximidad de un punto X 0 si .

La función se llama infinitesimal en el infinito, Si o .

También infinitesimal es una función que es la diferencia entre una función y su límite, es decir, si , Eso F(X) − a = α( X) , .

Cantidad infinitamente grande

Subsecuencia a norte llamado infinitamente grande, Si .

La función se llama infinitamente grande en las proximidades de un punto X 0 si .

La función se llama infinitamente grande en el infinito, Si o .

En todos los casos, se supone que el infinito a la derecha de la igualdad tiene un signo determinado (ya sea “más” o “menos”). Esta es, por ejemplo, la función X pecado X no es infinitamente grande en .

Propiedades de infinitamente pequeño e infinitamente grande.

Comparación de cantidades infinitesimales

¿Cómo comparar cantidades infinitesimales?
La proporción de cantidades infinitesimales forma la llamada incertidumbre.

Definiciones

Supongamos que tenemos valores infinitesimales α( X) y β( X) (o, lo que no es importante para la definición, secuencias infinitesimales).

Para calcular dichos límites es conveniente utilizar la regla de L'Hopital.

Ejemplos de comparación

Usando ACERCA DE-simbolismo, los resultados obtenidos se pueden escribir de la siguiente forma X 5 = oh(X 3). En este caso, las siguientes entradas son verdaderas: 2X 2 + 6X = oh(X) Y X = oh(2X 2 + 6X).

Valores equivalentes

Definición

Si , entonces las cantidades infinitesimales α y β se llaman equivalente ().
Es obvio que las cantidades equivalentes son un caso especial de cantidades infinitesimales del mismo orden de pequeñez.

Cuando sean válidas las siguientes relaciones de equivalencia: , , .

Teorema

El límite del cociente (ratio) de dos cantidades infinitesimales no cambiará si una de ellas (o ambas) se reemplaza por una cantidad equivalente..

Este teorema tiene importancia práctica a la hora de encontrar límites (ver ejemplo).

Ejemplo de uso

Reemplazo sinorte 2X valor equivalente 2 X, obtenemos

Bosquejo histórico

El concepto de "infinitesimal" se discutió en la antigüedad en relación con el concepto de átomos indivisibles, pero no se incluyó en las matemáticas clásicas. Revivió nuevamente con la llegada del "método de los indivisibles" en el siglo XVI, dividiendo la figura en estudio en secciones infinitesimales.

En el siglo XVII se produjo la algebraización del cálculo infinitesimal. Comenzaron a definirse como cantidades numéricas que son menores que cualquier cantidad finita (distinta de cero) y, sin embargo, no iguales a cero. El arte del análisis consistía en trazar una relación que contuviera infinitesimales (diferenciales) y luego integrarla.

Los matemáticos de la vieja escuela ponen a prueba el concepto infinitesimal duras críticas. Michel Rolle escribió que el nuevo cálculo es “ conjunto de errores ingeniosos"; Voltaire señaló cáusticamente que el cálculo es el arte de calcular y medir con precisión cosas cuya existencia no se puede probar. Incluso Huygens admitió que no entendía el significado de los diferenciales de órdenes superiores.

Como una ironía del destino, se puede considerar el surgimiento a mediados de siglo de un análisis no estándar, que demostró que el punto de vista original, los infinitesimales reales, también era consistente y podía usarse como base para el análisis.

ver también

Fundación Wikimedia. 2010.

Vea qué es "Infinitamente grande" en otros diccionarios:

La cantidad variable Y es la inversa de la cantidad infinitesimal X, es decir, Y = 1/X... Gran diccionario enciclopédico

La variable y es la inversa del infinitesimal x, es decir, y = 1/x. * * * INFINITAMENTE GRANDE, INFINITAMENTE GRANDE, cantidad variable Y, la inversa del valor infinitesimal X, es decir, Y = 1/X... diccionario enciclopédico

En matemáticas, cantidad variable que, en un proceso de cambio dado, se vuelve y sigue siendo mayor en valor absoluto que cualquier número predeterminado. Estudio de B. b. Las cantidades se pueden reducir al estudio de los infinitesimales (Ver... ... Gran enciclopedia soviética