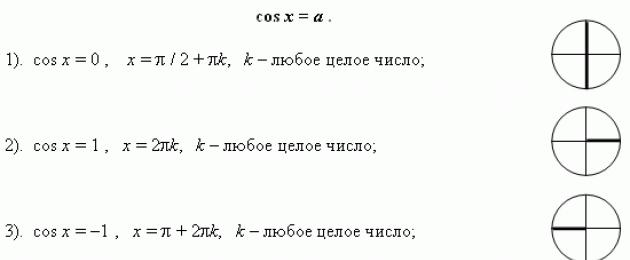La tabla de ecuaciones trigonométricas más simple. Ecuaciones trigonométricas: fórmulas, soluciones, ejemplos

Ecuaciones trigonométricas .

Las ecuaciones trigonométricas más simples. .

Métodos para resolver ecuaciones trigonométricas.

Ecuaciones trigonométricas. Una ecuación que contiene una incógnita bajo el signo de la función trigonométrica se llama trigonométrico.

Las ecuaciones trigonométricas más simples.

Métodos para resolver ecuaciones trigonométricas. Resolver una ecuación trigonométrica consta de dos etapas: transformación de ecuación para hacerlo más simple tipo (ver arriba) y soluciónel resultado más simple ecuación trigonométrica. Hay siete Métodos básicos para resolver ecuaciones trigonométricas.

1. Método algebraico. Este método nos resulta bien conocido por el álgebra.

(método de sustitución y sustitución de variables).

2. Factorización. Veamos este método con ejemplos.

Ejemplo 1. Resuelve la ecuación: pecado X+porque X = 1 .

Solución. Movamos todos los términos de la ecuación hacia la izquierda:

Pecado X+porque X – 1 = 0 ,

Transformemos y factoricemos la expresión en

Lado izquierdo de la ecuación:

Ejemplo 2. Resuelve la ecuación: porque 2 X+ pecado X porque X = 1.

Solución: cos 2 X+ pecado X porque X– pecado 2 X– porque 2 X = 0 ,

Pecado X porque X– pecado 2 X = 0 ,

Pecado X· (porque X– pecado X ) = 0 ,

Ejemplo 3. Resuelve la ecuación: porque 2 X–cos 8 X+ porque 6 X = 1.

Solución: cos 2 X+ porque 6 X= 1 + porque 8 X,

2 porque 4 X porque 2 X= 2cos² 4 X ,

porque 4 X · (porque 2 X– porque 4 X) = 0 ,

porque 4 X · 2 pecado 3 X pecado X = 0 ,

1). porque 4 X= 0, 2). pecado 3 X= 0, 3). pecado X = 0 ,

3.

Llevando a ecuación homogénea. La ecuacion llamado homogéneo de acerca de pecado Y porque , Si todo ello términos del mismo grado en relación con pecado Y porque mismo ángulo. Para resolver una ecuación homogénea, necesitas: A) mover todos sus miembros hacia el lado izquierdo; b) sacar todos los factores comunes entre paréntesis; V) igualar todos los factores y paréntesis a cero; GRAMO) paréntesis igual a cero dan ecuación homogénea de menor grado, que debe dividirse en porque(o pecado) en el grado superior; d) resuelve el resultado ecuación algebraica relativamentebroncearse . EJEMPLO Resolver ecuación: 3 pecado 2 X+ 4 pecado X porque X+ 5cos 2 X = 2. Solución: 3 pecado 2 X+ 4 pecado X porque X+ 5 porque 2 X= 2 pecado 2 X+ 2cos 2 X , Pecado 2 X+ 4 pecado X porque X+ 3 porque 2 X = 0 , Bronceado 2 X+ 4 bronceado X + 3 = 0 , de aquí y 2 + 4y +3 = 0 , Las raíces de esta ecuación son:y 1 = - 1, y 2 = - 3, por lo tanto 1) bronceado X= –1, 2) bronceado X = –3,

4. Transición a medio ángulo. Veamos este método usando un ejemplo:

EJEMPLO Resolver ecuación: 3 pecado X– 5 porque X = 7.

Solución: 6 pecado ( X/ 2) porque ( X/ 2) – 5 cos² ( X/ 2) + 5 sen² ( X/ 2) =

7 pecado² ( X/ 2) + 7 cos² ( X/ 2) ,

2 pecado² ( X/ 2) – 6 pecado ( X/ 2) porque ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

bronceado²( X/ 2) – 3 bronceado ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introducción de un ángulo auxiliar. Considere una ecuación de la forma:

a pecado X + b porque X = C ,

Dónde a, b, C– coeficientes;X- desconocido.

Ahora los coeficientes de la ecuación tienen las propiedades del seno y el coseno, a saber: módulo (valor absoluto) de cada uno

Clase: 10

"Las ecuaciones durarán para siempre".

A. Einstein

Objetivos de la lección:

• Educativo:
  • profundizar la comprensión de los métodos para resolver ecuaciones trigonométricas;
  • Desarrollar las habilidades para distinguir y seleccionar correctamente métodos de resolución de ecuaciones trigonométricas.
• Educativo:
  • fomentar el interés cognitivo en el proceso educativo;
  • desarrollar la capacidad de analizar una tarea determinada;
  • Contribuir a mejorar el clima psicológico en el aula.
• De desarrollo:
  • promover el desarrollo de la habilidad de adquirir conocimientos de forma independiente;
  • promover la capacidad de los estudiantes para argumentar su punto de vista;

Equipo: cartel con fórmulas trigonométricas básicas, computadora, proyector, pantalla.

1 lección

I. Actualización de conocimientos de referencia

Resuelve las ecuaciones oralmente:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) pecado2x = 0;
5) senx = –;
6) senx = ;
7) tgx = ;
8) cos 2 x – sen 2 x = 0

1)x = 2k;
2) x = ± + 2k;
3) x =± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = +k;
8) x = + k; a Z.

II. Aprendiendo nuevo material

– Hoy veremos más complejos. ecuaciones trigonométricas. Veamos 10 formas de resolverlos. A continuación habrá dos lecciones para la consolidación y para la siguiente lección habrá una prueba. En el stand "Para la lección" hay tareas publicadas que son similares a las que estarán en el examen, debes resolverlas antes del examen; (El día antes de la prueba, publicar en el stand las soluciones a estas tareas).

Entonces, pasemos a considerar formas de resolver ecuaciones trigonométricas. Algunos de estos métodos probablemente te parecerán difíciles, mientras que otros te parecerán fáciles, porque... Ya conoces algunas técnicas para resolver ecuaciones.

Cuatro estudiantes de la clase recibieron una tarea individual: comprender y mostrarte 4 formas de resolver ecuaciones trigonométricas.

(Los estudiantes que hablan han preparado diapositivas con anticipación. El resto de la clase escribe los pasos principales para resolver ecuaciones en un cuaderno).

1 estudiante: 1 vía. Resolver ecuaciones factorizando

pecado 4x = 3 porque 2x

Para resolver la ecuación, usamos la fórmula del seno del ángulo doble sin 2 = 2 sin cos
2 sen 2x porque 2x – 3 porque 2x = 0,
cos 2x (2 sin 2x – 3) = 0. El producto de estos factores es igual a cero si al menos uno de los factores es igual a cero.

2x = + k, k Z o sen 2x = 1,5 – no hay soluciones, porque | pecado| 1
x = +k; a Z.
Respuesta: x = + k, k Z.

2 estudiante. Método 2. Resolver ecuaciones convirtiendo la suma o diferencia de funciones trigonométricas en un producto

cos 3x + sen 2x – sen 4x = 0.

Para resolver la ecuación usamos la fórmula sin– sin = 2 sin сos

cos 3x + 2 sen cos = 0,

cos 3x – 2 sen x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. La ecuación resultante es equivalente a un conjunto de dos ecuaciones:

El conjunto de soluciones de la segunda ecuación está completamente incluido en el conjunto de soluciones de la primera ecuación. Medio

Respuesta:

3 estudiante. 3 vías. Resolver ecuaciones convirtiendo el producto de funciones trigonométricas en una suma.

sen 5x cos 3x = sen 6x cos2x.

Para resolver la ecuación usamos la fórmula

Respuesta:

4 estudiante. 4 maneras. Resolver ecuaciones que se reducen a ecuaciones cuadráticas.

3 pecado x – 2 porque 2 x = 0,
3 pecado x – 2 (1 – pecado 2 x) = 0,
2 pecado 2 x + 3 pecado x – 2 = 0,

Sea sen x = t, donde | t|. Obtenemos ecuación cuadrática 2t 2 + 3t – 2 = 0,

D = 9 + 16 = 25.

De este modo . no cumple la condición | t|.

Entonces sen x = . Es por eso .

Respuesta:

III. Consolidación de lo aprendido en el libro de texto de A. N. Kolmogorov

1. N° 164 (a), 167 (a) (ecuación cuadrática)
2. N° 168 (a) (factorización)
3. No. 174 (a) (conversión de una suma en un producto)
4. (convertir producto en suma)

(Al final de la lección, muestre la solución de estas ecuaciones en la pantalla para su verificación)

№ 164 (A)

2 sen 2 x + sen x – 1 = 0.
Sea sen x = t, | t | 1. Entonces
2 t 2 + t – 1 = 0, t = – 1, t= . Dónde

Respuesta: - .

№ 167 (A)

3 tg 2 x + 2 tg x – 1 = 0.

Sea tg x = 1, entonces obtenemos la ecuación 3 t 2 + 2 t – 1 = 0.

Respuesta:

№ 168 (A)

Respuesta:

№ 174 (A)

Resuelve la ecuación:

Respuesta:

Lección 2 (lección-conferencia)

IV. Aprendiendo nuevo material(continuación)

– Entonces, sigamos estudiando formas de resolver ecuaciones trigonométricas.

5 vías. Resolver ecuaciones trigonométricas homogéneas.

Ecuaciones de la forma a sen x + b porque x = 0, donde a y b son algunos números, se denominan ecuaciones homogéneas de primer grado con respecto a sen x o cos x.

Considere la ecuación

pecado x – porque x = 0. Dividamos ambos lados de la ecuación por cos x. Esto se puede hacer; no se producirá la pérdida de raíces, porque , Si porque x = 0, Eso pecado x = 0. Pero esto contradice la identidad trigonométrica básica. pecado 2 x+cos 2 x = 1.

Obtenemos tan x – 1 = 0.

bronceado x = 1,

Ecuaciones de la forma como en 2 x + b cos 2 x + c sen x porque x = 0 , Dónde a B C - algunos números se llaman ecuaciones homogéneas de segundo grado con respecto a sen x o cos x.

Considere la ecuación

sen 2 x – 3 sen x cos x + 2 cos 2 = 0. Dividamos ambos lados de la ecuación por cos x, y la raíz no se perderá, porque porque x = 0 no es la raíz de esta ecuación.

tg 2 x – 3tg x + 2 = 0.

Sea tg x = t. D = 9 – 8 = 1.

Entonces, por lo tanto, tg x = 2 o tg x = 1.

Como resultado, x = arctan 2 + , x =

Respuesta: arctg 2 +,

Considere otra ecuación: 3 sen 2 x – 3 sen x cos x + 4 cos 2 x = 2.
transformemos lado derecho ecuaciones en la forma 2 = 2 · 1 = 2 · (sen 2 x + cos 2 x). Entonces obtenemos:
3sen 2 x – 3sen x cos x + 4cos 2 x = 2 (sen 2 x + cos 2 x),
3sen 2 x – 3sen x porque x + 4cos 2 x – 2sen 2 x – 2 porque 2 x = 0,
sen 2 x – 3sin x cos x + 2cos 2 x = 0. (Obtuvimos la segunda ecuación, que ya hemos analizado).

Respuesta: arctan 2 + k,

6 vías. Resolver ecuaciones trigonométricas lineales

Una ecuación trigonométrica lineal es una ecuación de la forma a pecado x + b porque x = c, donde a, b, c son algunos números.

Considere la ecuación pecado x + porque x= – 1.
Reescribamos la ecuación como:

Considerando eso y, obtenemos:

Respuesta:

7 vías. Introduciendo un argumento adicional

Expresión a cos x + b sen x se puede convertir:

(ya hemos usado esta transformación al simplificar expresiones trigonométricas)

Introduzcamos un argumento adicional: el ángulo es tal que

Entonces

Considere la ecuación: 3 senx + 4 cosx = 1. =

Tarea: Núms. 164-170 (c, d).

Métodos para resolver ecuaciones trigonométricas.

Resolver una ecuación trigonométrica consta de dos etapas: transformación de ecuación para hacerlo más simple tipo (ver arriba) y soluciónel resultado más simple ecuación trigonométrica. Hay siete Métodos básicos para resolver ecuaciones trigonométricas.

1. Método algebraico.

(método de sustitución y sustitución de variables).

2. Factorización.

Ejemplo 1. Resuelve la ecuación: pecado X+porque X = 1 .

Solución. Movamos todos los términos de la ecuación hacia la izquierda:

Pecado X+porque X – 1 = 0 ,

Transformemos y factoricemos la expresión en

Lado izquierdo de la ecuación:

Ejemplo 2. Resuelve la ecuación: porque 2 X+ pecado X porque X = 1.

Solución: cos 2 X+ pecado X porque X– pecado 2 X– porque 2 X = 0 ,

Pecado X porque X– pecado 2 X = 0 ,

Pecado X· (porque X– pecado X ) = 0 ,

Ejemplo 3. Resuelve la ecuación: porque 2 X–cos 8 X+ porque 6 X = 1.

Solución: cos 2 X+ porque 6 X= 1 + porque 8 X,

2 porque 4 X porque 2 X= 2cos² 4 X ,

porque 4 X · (porque 2 X– porque 4 X) = 0 ,

porque 4 X · 2 pecado 3 X pecado X = 0 ,

1). porque 4 X= 0, 2). pecado 3 X= 0, 3). pecado X = 0 ,

3. Reducción a ecuación homogénea. La ecuacion llamado homogéneo de acerca de pecado Y porque , Si todo ello términos del mismo grado en relación con pecado Y porque mismo ángulo. Para resolver una ecuación homogénea, necesitas: A) mover todos sus miembros hacia el lado izquierdo; b) sacarlo todo factores comunes más allá de los corchetes; V) igualar todos los factores y paréntesis a cero; GRAMO) paréntesis igual a cero dan ecuación homogénea de menor grado, que debe dividirse en porque(o pecado) en el grado superior; d) resuelve la ecuación algebraica resultante con respecto abroncearse . pecado 2 X+ 4 pecado X porque X+ 5cos 2 X = 2. Solución: 3 pecado 2 X+ 4 pecado X porque X+ 5 porque 2 X= 2 pecado 2 X+ 2cos 2 X , Pecado 2 X+ 4 pecado X porque X+ 3 porque 2 X = 0 , Bronceado 2 X+ 4 bronceado X + 3 = 0 , de aquí y 2 + 4y +3 = 0 , Las raíces de esta ecuación son:y 1 = - 1, y 2 = - 3, por lo tanto 1) bronceado X= –1, 2) bronceado X = –3,

4. Transición a medio ángulo.

Veamos este método usando un ejemplo:

EJEMPLO Resolver ecuación: 3 pecado X– 5 porque X = 7.

Solución: 6 pecado ( X/ 2) porque ( X/ 2) – 5 cos² ( X/ 2) + 5 sen² ( X/ 2) =

7 pecado² ( X/ 2) + 7 cos² ( X/ 2) ,

2 pecado² ( X/ 2) – 6 pecado ( X/ 2) porque ( X/ 2) + 12 cos² ( X/ 2) = 0 ,

bronceado²( X/ 2) – 3 bronceado ( X/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Introducción de un ángulo auxiliar.

Considere una ecuación de la forma:

a pecado X + b porque X = C ,

Dónde a, b, C– coeficientes;X- desconocido.

Ahora los coeficientes de la ecuación tienen las propiedades del seno y el coseno, a saber: módulo (valor absoluto) de cada uno de los cuales no más de 1, y la suma de sus cuadrados es 1. Entonces podemos denotar ellos en consecuencia Cómo cos y pecado (aquí - llamado ángulo auxiliar), Ytoma nuestra ecuación

puedes ordenar solución detallada¡¡¡tu tarea!!!

Una igualdad que contiene una incógnita bajo el signo de una función trigonométrica (`sin x, cos x, tan x` o `ctg x`) se llama ecuación trigonométrica, y son sus fórmulas las que consideraremos más a fondo.

Las ecuaciones más simples son `sin x=a, cos x=a, tg x=a, ctg x=a`, donde `x` es el ángulo que se va a encontrar, `a` es cualquier número. Anotemos las fórmulas raíz de cada uno de ellos.

1. Ecuación `sen x=a`.

Para `|a|>1` no tiene soluciones.

Cuando `|a| \leq 1` tiene un número infinito de soluciones.

Fórmula raíz: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Ecuación `cos x=a`

Para `|a|>1` - como en el caso del seno, no tiene soluciones entre los números reales.

Cuando `|a| \leq 1` tiene un número infinito de soluciones.

Fórmula raíz: `x=\pm arccos a + 2\pi n, n \in Z`

Casos especiales de seno y coseno en gráficas.

3. Ecuación `tg x=a`

Tiene un número infinito de soluciones para cualquier valor de "a".

Fórmula raíz: `x=arctg a + \pi n, n \in Z`

4. Ecuación `ctg x=a`

También tiene un número infinito de soluciones para cualquier valor de "a".

Fórmula raíz: `x=arcctg a + \pi n, n \in Z`

Fórmulas para las raíces de ecuaciones trigonométricas en la tabla.

Para seno:
Para coseno:
Para tangente y cotangente:
Fórmulas para resolver ecuaciones que contienen inversas. funciones trigonométricas:

Métodos para resolver ecuaciones trigonométricas.

Resolver cualquier ecuación trigonométrica consta de dos etapas:

• con la ayuda de transformarlo al más simple;
• resuelva la ecuación más simple obtenida usando las fórmulas de raíz y las tablas escritas arriba.

Veamos los principales métodos de solución mediante ejemplos.

Método algebraico.

Este método implica reemplazar una variable y sustituirla en una igualdad.

Ejemplo. Resuelve la ecuación: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

haga un reemplazo: `cos(x+\frac \pi 6)=y`, luego `2y^2-3y+1=0`,

encontramos las raíces: `y_1=1, y_2=1/2`, de lo que se siguen dos casos:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Respuesta: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Factorización.

Ejemplo. Resuelve la ecuación: `sen x+cos x=1`.

Solución. Movamos todos los términos de la igualdad hacia la izquierda: `sin x+cos x-1=0`. Usando , transformamos y factorizamos el lado izquierdo:

`pecado x — 2pecado^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sen x/2 (cos x/2-sen x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sen x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Respuesta: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Reducción a una ecuación homogénea

Primero, necesitas reducir esta ecuación trigonométrica a una de dos formas:

`a sin x+b cos x=0` (ecuación homogénea de primer grado) o `a sin^2 x + b sin x cos x +c cos^2 x=0` (ecuación homogénea de segundo grado).

Luego divide ambas partes por `cos x \ne 0` - para el primer caso, y por `cos^2 x \ne 0` - para el segundo. Obtenemos ecuaciones para `tg x`: `a tg x+b=0` y `a tg^2 x + b tg x +c =0`, que deben resolverse utilizando métodos conocidos.

Ejemplo. Resuelve la ecuación: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Solución. Escribamos el lado derecho como `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`pecado^2 x+pecado x cos x — 2 cos^2 x=0`.

Esta es una ecuación trigonométrica homogénea de segundo grado, dividimos sus lados izquierdo y derecho por `cos^2 x \ne 0`, obtenemos:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2x+tgx — 2=0`. Introduzcamos el reemplazo `tg x=t`, lo que resulta en `t^2 + t - 2=0`. Las raíces de esta ecuación son `t_1=-2` y `t_2=1`. Entonces:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.

Respuesta. `x_1=arctg (-2)+\pi n`, `n \en Z`, `x_2=\pi/4+\pi n`, `n \en Z`.

Moviéndose a medio ángulo

Ejemplo. Resuelve la ecuación: `11 sen x - 2 cos x = 10`.

Solución. Apliquemos las fórmulas de los ángulos dobles, lo que da como resultado: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Aplicando el método algebraico descrito anteriormente, obtenemos:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Respuesta. `x_1=2 arctg 2+2\pi n, n \en Z`, `x_2=arctg 3/4+2\pi n`, `n \en Z`.

Introducción del ángulo auxiliar.

En la ecuación trigonométrica `a sin x + b cos x =c`, donde a,b,c son coeficientes y x es una variable, divide ambos lados por `sqrt (a^2+b^2)`:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`.

Los coeficientes del lado izquierdo tienen las propiedades del seno y el coseno, es decir, la suma de sus cuadrados es igual a 1 y sus módulos no son mayores que 1. Denotémoslos de la siguiente manera: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, entonces:

`cos \varphi sin x + sin \varphi cos x =C`.

Echemos un vistazo más de cerca al siguiente ejemplo:

Ejemplo. Resuelve la ecuación: `3 sen x+4 cos x=2`.

Solución. Dividiendo ambos lados de la igualdad por `sqrt (3^2+4^2)`, obtenemos:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`

`3/5 sen x+4/5 porque x=2/5`.

Denotemos `3/5 = cos \varphi`, `4/5=sin \varphi`. Dado que `sin \varphi>0`, `cos \varphi>0`, entonces tomamos `\varphi=arcsin 4/5` como ángulo auxiliar. Luego escribimos nuestra igualdad en la forma:

`cos \varphi sin x+sin \varphi cos x=2/5`

Aplicando la fórmula para la suma de ángulos del seno, escribimos nuestra igualdad de la siguiente forma:

`pecado (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcosen 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcosin 2/5-` `arcossin 4/5+ \pi n`, `n \in Z`.

Respuesta. `x=(-1)^n arcosin 2/5-` `arcossin 4/5+ \pi n`, `n \in Z`.

Ecuaciones trigonométricas racionales fraccionarias

Se trata de igualdades con fracciones cuyos numeradores y denominadores contienen funciones trigonométricas.

Ejemplo. Resuelve la ecuación. `\frac (sin x)(1+cos x)=1-cos x`.

Solución. Multiplica y divide el lado derecho de la igualdad por `(1+cos x)`. Como resultado obtenemos:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin^2 x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin^2 x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Considerando que el denominador no puede ser igual a cero, obtenemos `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.

Igualemos el numerador de la fracción a cero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Entonces `sin x=0` o `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \en Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Dado que ` x \ne \pi+2\pi n, n \in Z`, las soluciones son `x=2\pi n, n \in Z` y `x=\pi /2+2\pi n` , `n\en Z`.

Respuesta. `x=2\pi n`, `n \en Z`, `x=\pi /2+2\pi n`, `n \en Z`.

La trigonometría, y las ecuaciones trigonométricas en particular, se utilizan en casi todas las áreas de la geometría, la física y la ingeniería. Los estudios comienzan en el décimo grado, siempre hay tareas para el Examen Estatal Unificado, así que trate de recordar todas las fórmulas de ecuaciones trigonométricas: ¡definitivamente le serán útiles!

Sin embargo, ni siquiera es necesario memorizarlos, lo principal es comprender la esencia y poder deducirla. No es tan difícil como parece. Compruébalo tú mismo viendo el vídeo.

Concepto de resolución de ecuaciones trigonométricas.

• Para resolver una ecuación trigonométrica, conviértala en una o más ecuaciones trigonométricas básicas. En última instancia, resolver una ecuación trigonométrica se reduce a resolver las cuatro ecuaciones trigonométricas básicas.

Resolver ecuaciones trigonométricas básicas.

• Hay 4 tipos de ecuaciones trigonométricas básicas:
• pecado x = a; porque x = a
• tanx = a; ctg x = a
• Resolver ecuaciones trigonométricas básicas implica considerar las diferentes posiciones de "x" en circulo unitario y usando una tabla de conversión (o calculadora).
• Ejemplo 1. sen x = 0,866. Usando una tabla de conversión (o calculadora) obtendrás la respuesta: x = π/3. El círculo unitario da otra respuesta: 2π/3. Recuerde: todas las funciones trigonométricas son periódicas, es decir, sus valores se repiten. Por ejemplo, la periodicidad de sen x y cos x es 2πn, y la periodicidad de tg x y ctg x es πn. Por lo tanto la respuesta se escribe de la siguiente manera:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Ejemplo 2. cos x = -1/2. Usando una tabla de conversión (o calculadora) obtendrás la respuesta: x = 2π/3. El círculo unitario da otra respuesta: -2π/3.
• x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
• Ejemplo 3. tg (x - π/4) = 0.
• Respuesta: x = π/4 + πn.
• Ejemplo 4. ctg 2x = 1,732.
• Respuesta: x = π/12 + πn.

Transformaciones utilizadas en la resolución de ecuaciones trigonométricas.

• Para transformar ecuaciones trigonométricas se utilizan transformaciones algebraicas (factorización, reducción miembros homogéneos etc.) e identidades trigonométricas.
• Ejemplo 5: Usando identidades trigonométricas, la ecuación sin x + sin 2x + sin 3x = 0 se convierte en la ecuación 4cos x*sin (3x/2)*cos (x/2) = 0. Por lo tanto, las siguientes ecuaciones trigonométricas básicas necesita ser resuelto: cos x = 0; pecado(3x/2) = 0; porque(x/2) = 0.

• Encontrar ángulos usando valores de funciones conocidas.

  • Antes de aprender a resolver ecuaciones trigonométricas, debes aprender a encontrar ángulos utilizando valores de funciones conocidas. Esto se puede hacer usando una tabla de conversión o una calculadora.
  • Ejemplo: cos x = 0,732. La calculadora dará la respuesta x = 42,95 grados. El círculo unitario dará ángulos adicionales, cuyo coseno también es 0,732.

• Reserva la solución en el círculo unitario.

  • Puedes trazar soluciones a una ecuación trigonométrica en el círculo unitario. Las soluciones de una ecuación trigonométrica en el círculo unitario son los vértices de un polígono regular.
  • Ejemplo: Las soluciones x = π/3 + πn/2 en el círculo unitario representan los vértices del cuadrado.
  • Ejemplo: Las soluciones x = π/4 + πn/3 en el círculo unitario representan los vértices de un hexágono regular.

• Métodos para resolver ecuaciones trigonométricas.

  • Si una ecuación trigonométrica determinada contiene solo una función trigonométrica, resuelva esa ecuación como una ecuación trigonométrica básica. Si una ecuación dada incluye dos o más funciones trigonométricas, entonces existen 2 métodos para resolver dicha ecuación (según la posibilidad de su transformación).
    • Método 1.
  • Transforma esta ecuación en una ecuación de la forma: f(x)*g(x)*h(x) = 0, donde f(x), g(x), h(x) son las ecuaciones trigonométricas básicas.
  • Ejemplo 6. 2cos x + sen 2x = 0. (0< x < 2π)
  • Solución. Usando la fórmula del doble ángulo sin 2x = 2*sin x*cos x, reemplaza sin 2x.
  • 2cos x + 2*sin x*cos x = 2cos x*(sen x + 1) = 0. Ahora resuelve las dos ecuaciones trigonométricas básicas: cos x = 0 y (sen x + 1) = 0.
  • Ejemplo 7. cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Solución: Usando identidades trigonométricas, transforma esta ecuación en una ecuación de la forma: cos 2x(2cos x + 1) = 0. Ahora resuelve las dos ecuaciones trigonométricas básicas: cos 2x = 0 y (2cos x + 1) = 0.
  • Ejemplo 8. sen x - sen 3x = cos 2x. (0< x < 2π)
  • Solución: Usando identidades trigonométricas, transforma esta ecuación en una ecuación de la forma: -cos 2x*(2sin x + 1) = 0. Ahora resuelve las dos ecuaciones trigonométricas básicas: cos 2x = 0 y (2sin x + 1) = 0 .
    • Método 2.
  • Convierta la ecuación trigonométrica dada en una ecuación que contenga solo una función trigonométrica. Luego reemplace esta función trigonométrica con alguna desconocida, por ejemplo, t (sen x = t; cos x = t; cos 2x = t, tan x = t; tg (x/2) = t, etc.).
  • Ejemplo 9. 3sin^2 x - 2cos^2 x = 4sin x + 7 (0< x < 2π).
  • Solución. En esta ecuación, reemplace (cos^2 x) con (1 - sin^2 x) (según la identidad). La ecuación transformada es:
  • 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Reemplaza sen x con t. Ahora la ecuación se ve así: 5t^2 - 4t - 9 = 0. Esta es una ecuación cuadrática que tiene dos raíces: t1 = -1 y t2 = 9/5. La segunda raíz t2 no satisface el rango de función (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Ejemplo 10. tg x + 2 tg^2 x = ctg x + 2
  • Solución. Reemplace tg x con t. Reescribe la ecuación original de la siguiente manera: (2t + 1)(t^2 - 1) = 0. Ahora encuentra t y luego encuentra x para t = tan x.

• Ecuaciones trigonométricas especiales.

  • Hay varias ecuaciones trigonométricas especiales que requieren transformaciones específicas. Ejemplos:
  • a*sen x+ b*cos x = c ; a(sen x + cos x) + b*cos x*sen x = c;
  • a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0

• Periodicidad de funciones trigonométricas.

  • Como se mencionó anteriormente, todas las funciones trigonométricas son periódicas, lo que significa que sus valores se repiten después de un cierto período. Ejemplos:
    • El período de la función f(x) = sen x es 2π.
    • El período de la función f(x) = tan x es igual a π.
    • El período de la función f(x) = sen 2x es igual a π.
    • El período de la función f(x) = cos (x/2) es 4π.
  • Si se especifica un período en el problema, calcule el valor de "x" dentro de ese período.
  • Nota: Resolver ecuaciones trigonométricas no es una tarea fácil y, a menudo, genera errores. Por lo tanto, revisa tus respuestas cuidadosamente. Para hacer esto, puedes usar una calculadora gráfica para representar gráficamente la ecuación dada R(x) = 0. En tales casos, las soluciones se presentarán como decimales(es decir, π se reemplaza por 3.14).