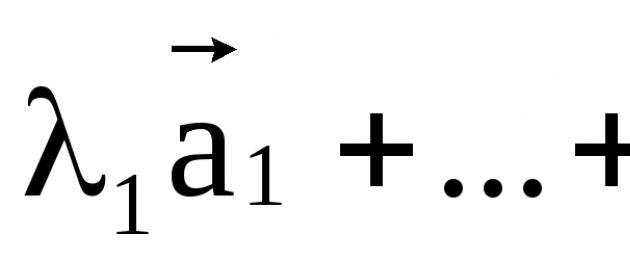Aluse leidmine. Vektorite lineaarne sõltuvus

Artiklis n-mõõtmeliste vektorite kohta jõudsime n-mõõtmeliste vektorite komplekti poolt genereeritud lineaarse ruumi mõisteni. Nüüd peame arvestama sama oluliste mõistetega, nagu vektorruumi mõõde ja alus. Need on otseselt seotud lineaarselt sõltumatu vektorite süsteemi kontseptsiooniga, seega on lisaks soovitatav meelde tuletada selle teema põhitõed.

Tutvustame mõningaid määratlusi.

Definitsioon 1

Vektorruumi mõõde– arv, mis vastab maksimaalsele lineaarselt sõltumatute vektorite arvule selles ruumis.

2. definitsioon

Vektorruumi alus– lineaarselt sõltumatute vektorite kogum, mis on järjestatud ja arvult võrdne ruumi mõõtmega.

Vaatleme teatud n -vektorite ruumi. Selle mõõde on vastavalt võrdne n-ga. Võtame n-ühikuliste vektorite süsteemi:

e (1) = (1, 0, . . . . 0) e (2) = (0, 1, . . . , 0) e (n) = (0, 0, . . . , 1)

Me kasutame neid vektoreid maatriksi A komponentidena: see on ühikmaatriks mõõtmetega n korda n. Selle maatriksi auaste on n. Seetõttu on vektorsüsteem e (1) , e (2) , . . . , e(n) on lineaarselt sõltumatu. Sel juhul on võimatu süsteemile lisada ühte vektorit, ilma et see rikuks selle lineaarset sõltumatust.

Kuna vektorite arv süsteemis on n, siis n-mõõtmeliste vektorite ruumi mõõde on n ja ühikvektoriteks on e (1), e (2), . . . , e (n) on määratud ruumi aluseks.

Saadud definitsioonist võime järeldada: iga n-mõõtmeliste vektorite süsteem, milles vektorite arv on väiksem kui n, ei ole ruumi baas.

Kui vahetame esimese ja teise vektori, saame vektorite süsteemi e (2) , e (1) , . . . , e (n) . See on ka n-mõõtmelise vektorruumi aluseks. Koostame maatriksi, võttes selle ridadeks saadud süsteemi vektorid. Maatriksi saab identiteedimaatriksist, kui vahetada kaks esimest rida, selle järjestus on n. Süsteem e (2) , e (1) , . . . , e(n) on lineaarselt sõltumatu ja on n-mõõtmelise vektorruumi aluseks.

Teisi vektoreid algses süsteemis ümber paigutades saame teise aluse.

Võime võtta lineaarselt sõltumatu mitteühikvektorite süsteemi ja see esindab ka n-mõõtmelise vektorruumi alust.

3. definitsioon

Vektorruumil mõõtmega n on nii palju aluseid, kui on lineaarselt sõltumatuid arvu n n-mõõtmeliste vektorite süsteeme.

Tasapind on kahemõõtmeline ruum - selle aluseks on mis tahes kaks mittekollineaarset vektorit. Kolmemõõtmelise ruumi aluseks on mis tahes kolm mittetasatasandilist vektorit.

Vaatleme selle teooria rakendamist konkreetsete näidete abil.

Näide 1

Algandmed: vektorid

a = (3 , - 2 , 1) b = (2 , 1 , 2) c = (3 , - 1 , - 2)

On vaja kindlaks teha, kas määratud vektorid on kolmemõõtmelise vektorruumi aluseks.

Lahendus

Ülesande lahendamiseks uurime antud lineaarse sõltuvuse vektorite süsteemi. Koostame maatriksi, kus read on vektorite koordinaadid. Määrame maatriksi auastme.

A = 3 2 3 - 2 1 - 1 1 2 - 2 A = 3 - 2 1 2 1 2 3 - 1 - 2 = 3 1 (- 2) + (- 2) 2 3 + 1 2 · (- 1) - 1 · 1 · 3 - (- 2) · 2 · (- 2) - 3 · 2 · (- 1) = = - 25 ≠ 0 ⇒ R a n k (A) = 3

Järelikult on ülesande tingimusega määratud vektorid lineaarselt sõltumatud ning nende arv võrdub vektorruumi mõõtmega - need on vektorruumi aluseks.

Vastus: näidatud vektorid on vektorruumi aluseks.

Näide 2

Algandmed: vektorid

a = (3, - 2, 1) b = (2, 1, 2) c = (3, - 1, - 2) d = (0, 1, 2)

Tuleb kindlaks teha, kas antud vektorite süsteem saab olla kolmemõõtmelise ruumi aluseks.

Lahendus

Ülesande püstituses määratud vektorite süsteem on lineaarselt sõltuv, sest lineaarselt sõltumatute vektorite maksimaalne arv on 3. Seega ei saa näidatud vektorite süsteem olla aluseks kolmemõõtmelisele vektorruumile. Kuid tasub märkida, et algsüsteemi alamsüsteem a = (3, - 2, 1), b = (2, 1, 2), c = (3, - 1, - 2) on aluseks.

Vastus: näidatud vektorite süsteem ei ole aluseks.

Näide 3

Algandmed: vektorid

a = (1, 2, 3, 3) b = (2, 5, 6, 8) c = (1, 3, 2, 4) d = (2, 5, 4, 7)

Kas need võivad olla neljamõõtmelise ruumi aluseks?

Lahendus

Koostame maatriksi, kasutades ridadena etteantud vektorite koordinaate

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

Gaussi meetodi abil määrame maatriksi auastme:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7 ~ 1 2 3 3 0 1 0 2 0 1 - 1 1 0 1 - 2 1 ~ ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 - 2 - 1 ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 0 1 ⇒ ⇒ R a n k (A) = 4

Järelikult on antud vektorite süsteem lineaarselt sõltumatu ja nende arv võrdub vektorruumi mõõtmega - need on neljamõõtmelise vektorruumi aluseks.

Vastus: antud vektorid on neljamõõtmelise ruumi aluseks.

Näide 4

Algandmed: vektorid

a (1) = (1, 2, - 1, - 2) a (2) = (0, 2, 1, - 3) a (3) = (1, 0, 0, 5)

Kas need moodustavad 4. mõõtmega ruumi aluse?

Lahendus

Algne vektorite süsteem on lineaarselt sõltumatu, kuid vektorite arv selles ei ole piisav, et saada neljamõõtmelise ruumi aluseks.

Vastus: ei, nad ei tee seda.

Vektori dekomponeerimine baasiks

Oletame, et suvalised vektorid e (1) , e (2) , . . . , e (n) on n-mõõtmelise vektorruumi aluseks. Lisame neile teatud n-mõõtmelise vektori x →: saadud vektorite süsteem muutub lineaarselt sõltuvaks. Lineaarse sõltuvuse omadused väidavad, et vähemalt ühte sellise süsteemi vektoritest saab teiste kaudu lineaarselt väljendada. Selle väite ümbersõnastamisel võime öelda, et vähemalt ühte lineaarselt sõltuva süsteemi vektoritest saab laiendada ülejäänud vektoriteks.

Seega jõudsime kõige olulisema teoreemi sõnastamiseni:

4. definitsioon

Iga n-mõõtmelise vektorruumi vektori saab unikaalselt lagundada baasiks.

Tõendid 1

Tõestame selle teoreemi:

paneme n-mõõtmelise vektorruumi aluse - e (1) , e (2) , . . . , e (n) . Muudame süsteemi lineaarselt sõltuvaks, lisades sellele n-mõõtmelise vektori x →. Seda vektorit saab lineaarselt väljendada algsete vektoritega e:

x = x 1 · e (1) + x 2 · e (2) + . . . + x n · e (n) , kus x 1 , x 2 , . . . , x n - mõned arvud.

Nüüd tõestame, et selline lagunemine on ainulaadne. Oletame, et see pole nii ja on veel üks sarnane lagunemine:

x = x ~ 1 e (1) + x 2 ~ e (2) + . . . + x ~ n e (n) , kus x ~ 1 , x ~ 2 , . . . , x ~ n - mõned arvud.

Lahutame selle võrrandi vasakust ja paremast poolest vastavalt võrrandi x = x 1 · e (1) + x 2 · e (2) + vasak ja parem pool. . . + x n · e (n) . Saame:

0 = (x ~ 1 - x 1) · e (1) + (x ~ 2 - x 2) · e (2) + . . . (x ~ n - x n) e (2)

Alusvektorite süsteem e (1) , e (2) , . . . , e(n) on lineaarselt sõltumatu; vektorite süsteemi lineaarse sõltumatuse definitsiooni järgi on ülaltoodud võrdsus võimalik ainult siis, kui kõik koefitsiendid on (x ~ 1 - x 1) , (x ~ 2 - x 2) , . . . , (x ~ n - x n) on võrdne nulliga. Millest see on õiglane: x 1 = x ~ 1, x 2 = x ~ 2, . . . , x n = x ~ n . Ja see tõestab ainsat võimalust vektori baasiks lagundamiseks.

Sel juhul on koefitsiendid x 1, x 2, . . . , x n nimetatakse vektori x → koordinaatideks aluses e (1) , e (2) , . . . , e (n) .

Tõestatud teooria teeb selgeks avaldise "antud n-mõõtmelise vektori x = (x 1 , x 2 , . . . , x n)": vaadeldakse vektorit x → n-mõõtmelist vektorruumi ja selle koordinaadid määratakse a. teatud alus. Samuti on selge, et samal vektoril n-mõõtmelise ruumi teises aluses on erinevad koordinaadid.

Vaatleme järgmist näidet: oletame, et n-mõõtmelise vektorruumi mõnes aluses on antud n lineaarselt sõltumatust vektorist koosnev süsteem

ja samuti on antud vektor x = (x 1 , x 2 , . . . , x n).

Vektorid e 1 (1) , e 2 (2) , . . . , e n (n) on antud juhul ka selle vektorruumi aluseks.

Oletame, et on vaja määrata vektori x → koordinaadid aluses e 1 (1) , e 2 (2) , . . . , e n (n) , tähistatud kui x ~ 1 , x ~ 2 , . . . , x ~ n.

Vektor x → esitatakse järgmiselt:

x = x ~ 1 e (1) + x ~ 2 e (2) + . . . + x ~ n e (n)

Kirjutame selle avaldise koordinaatide kujul:

(x 1 , x 2 , . . . , x n) = x ~ 1 (e (1) 1, e (1) 2, . . , e (1) n) + x ~ 2 (e (2) 1, e (2) 2, ..., e (2) n) + . . . + + x ~ n · (e (n) 1, e (n) 2, ..., e (n) n) = = (x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + ... + x ~ n e 1 (n), x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + + .. + x ~ n e 2 (n), ..., x ~ 1 e n (1) + x ~ 2 e n (2) + ... + x ~ n e n (n))

Saadud võrdsus on samaväärne n lineaarse algebralise avaldise süsteemiga n tundmatu lineaarse muutujaga x ~ 1, x ~ 2, . . . , x ~ n:

x 1 = x ~ 1 e 1 1 + x ~ 2 e 1 2 + . . . + x ~ n e 1 n x 2 = x ~ 1 e 2 1 + x ~ 2 e 2 2 + . . . + x ~ n e 2 n ⋮ x n = x ~ 1 e n 1 + x ~ 2 e n 2 + . . . + x ~ n e n n

Selle süsteemi maatriks on järgmisel kujul:

e 1 (1) e 1 (2) ⋯ e 1 (n) e 2 (1) e 2 (2) ⋯ e 2 (n) ⋮ ⋮ ⋮ ⋮ e n (1) e n (2) ⋯ e n (n)

Olgu selleks maatriks A ja selle veerud on lineaarselt sõltumatu vektorisüsteemi e 1 (1), e 2 (2), vektoriteks. . . , e n (n) . Maatriksi auaste on n ja selle determinant on nullist erinev. See näitab, et võrrandisüsteemil on ainulaadne lahendus, mis määratakse mis tahes mugava meetodiga: näiteks Crameri meetod või maatriksmeetod. Nii saame määrata koordinaadid x ~ 1, x ~ 2, . . . , x ~ n vektor x → baasis e 1 (1) , e 2 (2) , . . . , e n (n) .

Rakendame vaadeldavat teooriat konkreetse näite puhul.

Näide 6

Algandmed: vektorid määratakse kolmemõõtmelise ruumi alusel

e (1) = (1, - 1, 1) e (2) = (3, 2, -5) e (3) = (2, 1, - 3) x = (6, 2, -7)

On vaja kinnitada tõsiasja, et vektorite süsteem e (1), e (2), e (3) toimib ka antud ruumi alusena, ning määrata ka vektori x koordinaadid antud aluses.

Lahendus

Vektorite süsteem e (1), e (2), e (3) on kolmemõõtmelise ruumi aluseks, kui see on lineaarselt sõltumatu. Selgitame selle võimaluse välja, määrates maatriksi A astme, mille ridadeks on antud vektorid e (1), e (2), e (3).

Kasutame Gaussi meetodit:

A = 1 - 1 1 3 2 - 5 2 1 - 3 ~ 1 - 1 1 0 5 - 8 0 3 - 5 ~ 1 - 1 1 0 5 - 8 0 0 - 1 5

R a n k (A) = 3 . Seega on vektorite süsteem e (1), e (2), e (3) lineaarselt sõltumatu ja on aluseks.

Olgu vektoril x → baasis koordinaadid x ~ 1, x ~ 2, x ~ 3. Nende koordinaatide vaheline seos määratakse võrrandiga:

x 1 = x ~ 1 e 1 (1) + x ~ 2 e 1 (2) + x ~ 3 e 1 (3) x 2 = x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + x ~ 3 e 2 (3) x 3 = x ~ 1 e 3 (1) + x ~ 2 e 3 (2) + x ~ 3 e 3 (3)

Kasutame väärtusi vastavalt probleemi tingimustele:

x ~ 1 + 3 x ~ 2 + 2 x ~ 3 = 6 - x ~ 1 + 2 x ~ 2 + x ~ 3 = 2 x ~ 1 - 5 x ~ 2 - 3 x 3 = - 7

Lahendame võrrandisüsteemi Crameri meetodi abil:

∆ = 1 3 2 - 1 2 1 1 - 5 - 3 = - 1 ∆ x ~ 1 = 6 3 2 2 2 1 - 7 - 5 - 3 = - 1 , x ~ 1 = ∆ x ~ 1 ∆ = - 1 - 1 = 1 ∆ x ~ 2 = 1 6 2 - 1 2 1 1 - 7 - 3 = - 1 , x ~ 2 = ∆ x ~ 2 ∆ = - 1 - 1 = 1 ∆ x ~ 3 = 1 3 6 - 1 2 2 1 - 5 - 7 = - 1 , x ~ 3 = ∆ x ~ 3 ∆ = - 1 - 1 = 1

Seega vektor x → baasis e (1), e (2), e (3) on koordinaatidega x ~ 1 = 1, x ~ 2 = 1, x ~ 3 = 1.

Vastus: x = (1, 1, 1)

Aluste vaheline seos

Oletame, et mingis n-mõõtmelise vektorruumi baasis on antud kaks lineaarselt sõltumatut vektorisüsteemi:

c (1) = (c 1 (1), c 2 (1) , . . . , c n (1)) c (2) = (c 1 (2), c 2 (2) , . . . , c n (2)) ⋮ c (n) = (c 1 (n) , e 2 (n) , . . . , c n (n))

e (1) = (e 1 (1) , e 2 (1) , . . ., e n (1)) e (2) = (e 1 (2), e 2 (2) , ..., e n (2)) ⋮ e (n) = (e 1 (n) , e 2 (n) , . . . , e n (n))

Need süsteemid on ka antud ruumi alused.

Olgu c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1) - vektori c (1) koordinaadid baasis e (1) , e (2) , . . . , e (3) , siis antakse koordinaatide seos lineaarvõrrandisüsteemiga:

c 1 (1) = c ~ 1 (1) e 1 (1) + c ~ 2 (1) e 1 (2) +. . . + c ~ n (1) e 1 (n) c 2 (1) = c ~ 1 (1) e 2 (1) + c ~ 2 (1) e 2 (2) +. . . + c ~ n (1) e 2 (n) ⋮ c n (1) = c ~ 1 (1) e n (1) + c ~ 2 (1) e n (2) + . . . + c ~ n (1) e n (n)

Süsteemi saab esitada maatriksina järgmiselt:

(c 1 (1) , c 2 (1) , . . . , c n (1)) = (c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

Teeme analoogia põhjal sama kirje vektori c (2) jaoks:

(c 1 (2) , c 2 (2) , . . . , c n (2)) = (c ~ 1 (2) , c ~ 2 (2) , . . . , c ~ n (2)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

(c 1 (n) , c 2 (n) , ... , c n (n)) = (c ~ 1 (n) , c ~ 2 (n) , . . . , c ~ n (n)) e 1 (1) e 2 (1) … e n (1) e 1 (2) e 2 (2) … e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) … e n (n)

Kombineerime maatriksi võrdsused üheks avaldiseks:

c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n) c 2 (n) ⋯ c n (n) = c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n ) e 2 (n) ⋯ e n (n)

See määrab seose kahe erineva aluse vektorite vahel.

Sama printsiipi kasutades on võimalik väljendada kõiki baasvektoreid e(1), e(2), . . . , e (3) läbi aluse c (1) , c (2) , . . . , c (n) :

e 1 (1) e 2 (1) ⋯ e n (1) e 1 (2) e 2 (2) ⋯ e n (2) ⋮ ⋮ ⋮ ⋮ e 1 (n) e 2 (n) ⋯ e n (n) = e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) c 1 (1) c 2 (1) ⋯ c n (1) c 1 (2) c 2 (2) ⋯ c n (2) ⋮ ⋮ ⋮ ⋮ c 1 (n ) c 2 (n) ⋯ c n (n)

Anname järgmised määratlused:

Definitsioon 5

Maatriks c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) on üleminekumaatriks baasist e (1) , e (2) , . . . , e (3)

alusele c (1) , c (2) , . . . , c (n) .

Definitsioon 6

Maatriks e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) on üleminekumaatriks alustest c (1) , c (2) , . . . , c(n)

alusele e (1) , e (2) , . . . , e (3) .

Nendest võrdsustest on ilmne, et

c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 e ~ 1 (1) e ) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n ) · c ~ 1 (1) c ~ 2 (1) ⋯ c ~ n (1) c ~ 1 (2) c ~ 2 (2) ⋯ c ~ n (2) ⋮ ⋮ ⋮ ⋮ c ~ 1 (n) c ~ 2 (n) ⋯ c ~ n (n) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1

need. üleminekumaatriksid on vastastikused.

Vaatame teooriat konkreetse näite abil.

Näide 7

Algandmed: baasist on vaja leida üleminekumaatriks

c (1) = (1, 2, 1) c (2) = (2, 3, 3) · c (3) = (3, 7, 1)

e (1) = (3, 1, 4) e (2) = (5, 2, 1) e (3) = (1, 1, -6)

Samuti tuleb näidata suvalise vektori x → koordinaatide vaheline seos antud alustes.

Lahendus

1. Olgu T üleminekumaatriks, siis on võrdus tõene:

3 1 4 5 2 1 1 1 1 = T 1 2 1 2 3 3 3 7 1

Korrutage võrdsuse mõlemad pooled arvuga

1 2 1 2 3 3 3 7 1 - 1

ja saame:

T = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1

2. Määratlege üleminekumaatriks:

T = 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 = = 3 1 4 5 2 1 1 1 - 6 · - 18 5 3 7 - 2 - 1 5 - 1 - 1 = - 27 9 4 - 71 20 12 - 41 9 8

3. Defineerime vektori x → koordinaatide vahelise seose:

Oletame, et aluses c (1) , c (2) , . . . , c (n) vektoril x → on koordinaadid x 1 , x 2 , x 3 , siis:

x = (x 1, x 2, x 3) 1 2 1 2 3 3 3 7 1,

ja aluses e (1) , e (2) , . . . , e (3) koordinaadid on x ~ 1, x ~ 2, x ~ 3, siis:

x = (x ~ 1, x ~ 2, x ~ 3) 3 1 4 5 2 1 1 1 - 6

Sest Kui nende võrduste vasakpoolsed küljed on võrdsed, saame võrdsustada ka paremad pooled:

(x 1, x 2, x 3) · 1 2 1 2 3 3 3 7 1 = (x ~ 1, x ~ 2, x ~ 3) · 3 1 4 5 2 1 1 1 - 6

Korrutage mõlemad parempoolsed küljed arvuga

1 2 1 2 3 3 3 7 1 - 1

ja saame:

(x 1, x 2, x 3) = (x ~ 1, x ~ 2, x ~ 3) · 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 ⇔ ⇔ ( x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) T ⇔ ⇔ (x 1 , x 2 , x 3 ) = (x ~ 1 , x ~ 2 , x ~ 3 ) · - 27 9 4 - 71 20 12 - 41 9 8

Teisel pool

(x ~ 1, x ~ 2, x ~ 3) = (x 1, x 2, x 3) · - 27 9 4 - 71 20 12 - 41 9 8

Viimased võrdsused näitavad seost vektori x → koordinaatide vahel mõlemas aluses.

Vastus:üleminekumaatriks

27 9 4 - 71 20 12 - 41 9 8

Vektori x → koordinaadid antud alustes on seotud seosega:

(x 1, x 2, x 3) = (x ~ 1, x ~ 2, x ~ 3) · - 27 9 4 - 71 20 12 - 41 9 8

(x ~ 1, x ~ 2, x ~ 3) = (x 1, x 2, x 3) · - 27 9 4 - 71 20 12 - 41 9 8 - 1

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Lineaarne vektorite kombinatsioon on vektor
, kus λ 1, ..., λ m on suvalised koefitsiendid.

Vektorsüsteem
nimetatakse lineaarseks sõltuvaks, kui selle lineaarne kombinatsioon on võrdne , millel on vähemalt üks nullist erinev koefitsient.

Vektorsüsteem
nimetatakse lineaarselt sõltumatuks, kui mõnes selle lineaarses kombinatsioonis on võrdne , kõik koefitsiendid on nullid.

Vektorsüsteemi alus
kutsutakse välja selle mittetühi lineaarselt sõltumatu alamsüsteem, mille kaudu saab väljendada süsteemi mis tahes vektorit.

Näide 2. Leidke vektorite süsteemi alus = (1, 2, 2, 4),= (2, 3, 5, 1),= (3, 4, 8, -2),= (2, 5, 0, 3) ja väljenda ülejäänud vektorid aluse kaudu.

Lahendus: koostame maatriksi, milles nende vektorite koordinaadid on paigutatud veergudesse. Toome selle astmelisele kujule.

~
~
~
.

Selle süsteemi aluse moodustavad vektorid ,,, mis vastavad ringidena esile tõstetud joonte juhtivatele elementidele. Vektori väljendamiseks lahendage võrrand x 1 +x 2 + x 4 =. See taandub lineaarsete võrrandite süsteemiks, mille maatriks saadakse veeru algsest permutatsioonist, mis vastab , vabade tingimuste veeru asemel. Seetõttu kasutame süsteemi lahendamiseks saadud maatriksit astmelisel kujul, tehes selles vajalikud ümberkorraldused.

Leiame järjekindlalt:

x 1 + 4 = 3, x 1 = -1;

= -+2.

Märkus 1. Kui aluse kaudu on vaja väljendada mitut vektorit, siis igaühele neist koostatakse vastav lineaarvõrrandisüsteem. Need süsteemid erinevad ainult tasuta liikmete veergudes. Seetõttu saate nende lahendamiseks luua ühe maatriksi, millel on mitu vaba termini veergu. Pealegi lahendatakse iga süsteem teistest sõltumatult.

Märkus 2. Mis tahes vektori väljendamiseks piisab, kui kasutada ainult sellele eelneva süsteemi baasvektoreid. Sel juhul pole vaja maatriksit ümber vormindada, piisab vertikaalse joone õigesse kohta asetamisest.

Ülesanne 2. Leidke vektorite süsteemi alus ja väljendage ülejäänud vektorid aluse kaudu:

A) = (1, 3, 2, 0),= (3, 4, 2, 1),= (1, -2, -2, 1),= (3, 5, 1, 2);

b) = (2, 1, 2, 3),= (1, 2, 2, 3),= (3, -1, 2, 2),= (4, -2, 2, 2);

V) = (1, 2, 3),= (2, 4, 3),= (3, 6, 6),= (4, -2, 1);= (2, -6, -2).

3. Fundamentaalne lahenduste süsteem

Lineaarvõrrandisüsteemi nimetatakse homogeenseks, kui kõik selle vabad liikmed on võrdsed nulliga.

Homogeense lineaarvõrrandisüsteemi põhilahenduste süsteem on selle lahenduste hulga aluseks.

Olgu meile antud ebahomogeenne lineaarvõrrandisüsteem. Antud süsteemiga seotud homogeenne süsteem on süsteem, mis saadakse antud süsteemist, asendades kõik vabad liikmed nullidega.

Kui ebahomogeenne süsteem on järjekindel ja määramatu, siis on selle suvaline lahend kujul f n +  1 f o1 + ... +  k f o k, kus f n on ebahomogeense süsteemi konkreetne lahend ja f o1, ... , f o k on seotud homogeense süsteemi fundamentaalsed süsteemilahendused.

Näide 3. Leidke näite 1 ebahomogeensele süsteemile konkreetne lahendus ja sellega seotud homogeense süsteemi põhilahenduste süsteem.

Lahendus. Kirjutame näites 1 saadud lahendi vektori kujul ja lagundame saadud vektori selles sisalduvate vabade parameetrite ja fikseeritud arvväärtuste summaks:

= (x 1 , x 2 , x 3 , x 4) = (–2a + 7b – 2, a, –2b + 1, b) = (–2a, a, 0, 0) + (7b, 0, – 2b, b) + +(– 2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (– 2, 0, 1, 0 ).

Saame f n = (– 2, 0, 1, 0), f o1 = (-2, 1, 0, 0), f o2 = (7, 0, -2, 1).

Kommenteeri. Sarnaselt lahendatakse ka homogeensele süsteemile fundamentaalse lahendussüsteemi leidmise probleem.

Ülesanne 3.1 Leidke homogeense süsteemi põhilahenduste süsteem:

c) 2x 1 – x 2 +3x 3 = 0.

Harjutus 3.2. Leidke ebahomogeensele süsteemile konkreetne lahendus ja sellega seotud homogeense süsteemi põhilahenduste süsteem:

Leidke vektorite ja baasi mittekuuluvate vektorite süsteemi alus, laiendage neid vastavalt alusele:

A 1 = {5, 2, -3, 1}, A 2 = {4, 1, -2, 3}, A 3 = {1, 1, -1, -2}, A 4 = {3, 4, -1, 2}, A 5 = {13, 8, -7, 4}.

Lahendus. Vaatleme homogeenset lineaarvõrrandisüsteemi

A 1 X 1 + A 2 X 2 + A 3 X 3 + A 4 X 4 + A 5 X 5 = 0

või laiendatud kujul.

Lahendame selle süsteemi Gaussi meetodil, ridu ja veerge vahetamata ning lisaks valides põhielemendi mitte vasakus ülanurgas, vaid kogu rea ulatuses. Väljakutse on vali teisendatud vektorite süsteemi diagonaalosa.

~ ~

~ ~ ~ .

Algse vektorite lubatud süsteemil on vorm

A 1 1 X 1 + A 2 1 X 2 + A 3 1 X 3 + A 4 1 X 4 + A 5 1 X 5 = 0 ,

Kus A 1 1 = , A 2 1 = , A 3 1 = , A 4 1 = , A 5 1 = . (1)

Vektorid A 1 1 , A 3 1 , A 4 1 moodustavad diagonaalsüsteemi. Seetõttu vektorid A 1 , A 3 , A 4 moodustavad vektorsüsteemi aluse A 1 , A 2 , A 3 , A 4 , A 5 .

Laiendame nüüd vektoreid A 2 Ja A 5 alusel A 1 , A 3 , A 4 . Selleks laiendame esmalt vastavaid vektoreid A 2 1 Ja A 5 1 diagonaalsüsteem A 1 1 , A 3 1 , A 4 1, pidades silmas, et vektori piki diagonaalsüsteemi laienemise koefitsiendid on selle koordinaadid x i.

Alates (1) on meil:

A 2 1 = A 3 1 · (-1) + A 4 1 0 + A 1 1 · 1 => A 2 1 = A 1 1 – A 3 1 .

A 5 1 = A 3 1 0 + A 4 1 1 + A 1 1 · 2 => A 5 1 = 2A 1 1 + A 4 1 .

Vektorid A 2 Ja A 5 on laiendatud A 1 , A 3 , A 4 samade koefitsientidega kui vektorid A 2 1 Ja A 5 1 diagonaalsüsteem A 1 1 , A 3 1 , A 4 1 (need koefitsiendid x i). Seega

A 2 = A 1 – A 3 , A 5 = 2A 1 + A 4 .

Ülesanded. 1.Leia vektorite ja baasi mittekuuluvate vektorite süsteemi alus, laiendada neid vastavalt alusele:

1. a 1 = { 1, 2, 1 }, a 2 = { 2, 1, 3 }, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4 }.

2. a 1 = { 1, 1, 2 }, a 2 = { 0, 1, 2 }, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0 }.

3. a 1 = { 1, -2, 3 }, a 2 = { 0, 1, -1 }, a 3 = { 1, 3, 0 }, a 4 = { 0, -7, 3 }, a 5 = { 1, 1, 1 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

2. Leia kõik vektorsüsteemi alused:

1. a 1 = { 1, 1, 2 }, a 2 = { 3, 1, 2 }, a 3 = { 1, 2, 1 }, a 4 = { 2, 1, 2 }.

2. a 1 = { 1, 1, 1 }, a 2 = { -3, -5, 5 }, a 3 = { 3, 4, -1 }, a 4 = { 1, -1, 4 }.

Vormi väljendamine helistas vektorite lineaarne kombinatsioon A 1, A 2,...,A n koefitsientidega λ 1, λ 2,...,λ n.

Vektorite süsteemi lineaarse sõltuvuse määramine

Vektorsüsteem A 1, A 2,...,A n helistas lineaarselt sõltuv, kui on nullist erinev arvude hulk λ 1, λ 2,...,λ n, milles vektorite lineaarne kombinatsioon λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n võrdne nullvektoriga, see tähendab võrrandisüsteemi: on nullist erinev lahendus.
Numbrite komplekt λ 1, λ 2,...,λ n on nullist erinev, kui vähemalt üks arvudest λ 1, λ 2,...,λ n nullist erinev.

Vektorite süsteemi lineaarse sõltumatuse määramine

Vektorsüsteem A 1, A 2,...,A n helistas lineaarselt sõltumatu, kui nende vektorite lineaarne kombinatsioon λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n võrdne nullvektoriga ainult nullarvude hulga puhul λ 1, λ 2,...,λ n , see tähendab võrrandisüsteemi: A 1 x 1 +A 2 x 2 +...+A n x n =Θ omab ainulaadset nulllahendust.

Näide 29.1

Kontrollige, kas vektorite süsteem on lineaarselt sõltuv

Lahendus:

1. Koostame võrrandisüsteemi:

2. Lahendame selle Gaussi meetodil. Süsteemi Jordanano teisendused on toodud tabelis 29.1. Arvutamisel süsteemi paremaid külgi üles ei kirjutata, kuna need on võrdsed nulliga ega muutu Jordani teisenduste käigus.

3. Tabeli kolmest viimasest reast kirjutage üles lahendatud süsteem, mis on samaväärne algse süsteemiga süsteem:

4. Saame süsteemi üldlahenduse:

5. Olles määranud vaba muutuja väärtuse x 3 =1 oma äranägemise järgi, saame konkreetse nullist erineva lahenduse X=(-3,2,1).

Vastus: Seega nullist erineva arvude hulga (-3,2,1) korral võrdub vektorite lineaarne kombinatsioon nullvektoriga -3A 1 +2A 2 +1A 3 =Θ. Seega vektorsüsteem lineaarselt sõltuv.

Vektorsüsteemide omadused

Vara (1)
Kui vektorite süsteem on lineaarselt sõltuv, siis vähemalt ühte vektorit laiendatakse teiste suhtes ja vastupidi, kui vähemalt ühte süsteemi vektoritest laiendatakse teiste suhtes, siis vektorite süsteem on lineaarselt sõltuv.

Vara (2)
Kui mis tahes vektorite alamsüsteem on lineaarselt sõltuv, siis on lineaarselt sõltuv kogu süsteem.

Vara (3)
Kui vektorite süsteem on lineaarselt sõltumatu, siis on iga selle alamsüsteem lineaarselt sõltumatu.

Kinnistu (4)
Iga nullvektorit sisaldav vektorite süsteem on lineaarselt sõltuv.

Kinnisvara (5)
M-mõõtmeliste vektorite süsteem on alati lineaarselt sõltuv, kui vektorite arv n on suurem kui nende mõõde (n>m)

Vektorsüsteemi alused

Vektorsüsteemi alus A 1 , A 2 ,..., A sellist alamsüsteemi B 1 , B 2 ,...,B r nimetatakse(iga vektorid B 1, B 2,..., B r on üks vektoritest A 1, A 2,..., A n), mis vastab järgmistele tingimustele:
1. B 1 ,B 2 ,...,B r lineaarselt sõltumatu vektorite süsteem;
2. mis tahes vektor A j Süsteemi A 1 , A 2 ,..., A n väljendatakse lineaarselt läbi vektorite B 1 , B 2 ,..., B r

r— baasis sisalduvate vektorite arv.

Teoreem 29.1 Vektorite süsteemi ühiku alusel.
Kui m-mõõtmeliste vektorite süsteem sisaldab m erinevat ühikvektorit E 1 E 2 ,..., E m , siis moodustavad need süsteemi aluse.

Algoritm vektorite süsteemi aluse leidmiseks

Vektorite süsteemi A 1 ,A 2 ,...,A n aluse leidmiseks on vaja:

Loo homogeenne vektorisüsteemile vastav võrrandisüsteem A 1 x 1 +A 2 x 2 +...+A n x n =Θ
Tooge see süsteem

Loengud algebrast ja geomeetriast. 1. semester.

Loeng 9. Vektorruumi alused.

Kokkuvõte: vektorite süsteem, vektorite süsteemi lineaarne kombinatsioon, vektorite süsteemi lineaarse kombinatsiooni koefitsiendid, alus joonel, tasapinnal ja ruumis, vektoriruumide mõõtmed sirgel, tasapinnal ja ruumis, dekomponeerimine vektor piki baasi, vektori koordinaadid baasi suhtes, võrdusteoreem kaks vektorit, lineaartehted vektoritega koordinaatide tähistuses, vektorite ortonormaalne kolmik, vektorite parem- ja vasakkolmik, ortonormaalne alus, vektori algebra põhiteoreem.

Peatükk 9. Vektorruumi alused ja vektori lagunemine baasi suhtes.

punkt 1. Alusel sirgjoonel, tasapinnal ja ruumis.

Definitsioon. Igasugust lõplikku vektorite hulka nimetatakse vektorite süsteemiks.

Definitsioon. Väljend kus
nimetatakse vektorite süsteemi lineaarseks kombinatsiooniks
ja numbrid
nimetatakse selle lineaarse kombinatsiooni koefitsientideks.

Olgu L, P ja S vastavalt sirgjoon, tasapind ja punktide ruum ning
. Siis
– vektorite vektorruumid suunatud lõikudena vastavalt sirgel L, tasapinnal P ja ruumis S.

kutsutakse mis tahes nullist erinevat vektorit
, st. mis tahes nullist erinev vektor, mis on sirge L suhtes kollineaarne:
Ja
.

Aluse määramine
:
- alus
.

Definitsioon. Vektorruumi alused
on mis tahes järjestatud mittekollineaarsete vektorite paar ruumis
.

, Kus
,
- alus
.

Definitsioon. Vektorruumi alused
on ruumi mis tahes järjestatud kolmik mitte-tasapinnaliste vektorite (st ei asu samal tasapinnal)
.

- alus
.

Kommenteeri. Vektorruumi alus ei saa sisaldada nullvektorit: ruumis
määratluse järgi ruumis
kaks vektorit on ruumis kollineaarsed, kui vähemalt üks neist on null
kolm vektorit on tasapinnalised, st nad asuvad samal tasapinnal, kui vähemalt üks kolmest vektorist on null.

punkt 2. Vektori lagunemine baasi järgi.

Definitsioon. Lase - suvaline vektor,
– suvaline vektorite süsteem. Kui võrdsus kehtib

siis nad ütlevad, et vektor esitatakse antud vektorite süsteemi lineaarse kombinatsioonina. Kui antud vektorite süsteem
on vektorruumi alus, siis võrdsust (1) nimetatakse vektori lagunemiseks alusel
. Lineaarsed kombinatsiooni koefitsiendid
nimetatakse sel juhul vektori koordinaatideks aluse suhtes
.

Teoreem. (Vektori lagunemise kohta aluse suhtes.)

Iga vektorruumi vektorit saab laiendada selle baasiks ja pealegi ainulaadsel viisil.

Tõestus. 1) Olgu L suvaline sirge (või telg) ja
- alus
. Võtame suvalise vektori
. Kuna mõlemad vektorid Ja kollineaarne samale sirgele L, siis
. Kasutame teoreemi kahe vektori kollineaarsuse kohta. Sest
, siis on (olemas) selline arv
, Mida
ja seega saime vektori lagunemise alusel
vektorruum
.

Nüüd tõestame sellise lagunemise unikaalsust. Oletame vastupidist. Olgu vektoril kaks dekompositsiooni alusel
vektorruum
:

Ja
, Kus
. Siis
ja jaotusseadust kasutades saame:

Sest
, siis viimasest võrdsusest järeldub, et
, jne.

2) Olgu nüüd P suvaline tasapind ja
- alus
. Lase
selle tasandi suvaline vektor. Joonistame kõik kolm vektorit selle tasandi mis tahes punktist. Ehitame 4 sirget. Teeme otse , millel vektor asub , sirge
, millel vektor asub . Läbi vektori otsa tõmmake vektoriga paralleelne sirgjoon ja vektoriga paralleelne sirge . Need 4 sirget nikerdavad rööpküliku. Vaata allpool joon. 3. Rööpkülikureegli järgi
, Ja
,
,
- alus ,
- alus
.

Nüüd, selle tõestuse esimeses osas juba tõestatu kohaselt on sellised arvud olemas
, Mida

Ja
. Siit saame:

ja baasi laiendamise võimalus on tõestatud.

Nüüd tõestame laienduse unikaalsust aluse osas. Oletame vastupidist. Olgu vektoril kaks dekompositsiooni alusel
vektorruum
:
Ja
. Saame võrdsuse

Kust see tuleb?
. Kui
, See
, ja sellepärast
, See
ja laienduskoefitsiendid on võrdsed:
,
. Las see nüüd
. Siis
, Kus
. Kahe vektori kollineaarsuse teoreemist järeldub, et
. Oleme saanud vastuolu teoreemi tingimustega. Seega
Ja
, jne.

3) Lase
- alus
lase sel minna
suvaline vektor. Teostame järgmised konstruktsioonid.

Jätame kõrvale kõik kolm baasvektorit
ja vektor ühest punktist ja konstrueerida 6 tasapinda: tasapind, millel asuvad baasvektorid
, lennuk
ja lennuk
; edasi läbi vektori otsa Joonistame kolm tasandit paralleelselt kolme äsja konstrueeritud tasapinnaga. Need 6 tasapinda nikerdavad rööptahuka:

Kasutades vektorite liitmise reeglit, saame võrdsuse:

. (1)

Ehituse järgi
. Siit kahe vektori kollineaarsuse teoreemi põhjal järeldub, et on olemas arv
, selline, et
. Samamoodi
Ja
, Kus
. Nüüd, asendades need võrdsused (1), saame:

ja baasi laiendamise võimalus on tõestatud.

Tõestame sellise lagunemise unikaalsust. Oletame vastupidist. Olgu vektoril kaks dekompositsiooni alusel
:

JA . Siis

Pange tähele, et tingimuse järgi vektorid
mittekoplanaarsed, seega on nad paarikaupa mittekollineaarsed.

Võimalikud on kaks juhtumit:
või
.

a) Lase
, siis võrdsusest (3) järeldub:

. (4)

Võrdusest (4) järeldub, et vektor laieneb vastavalt alusele
, st. vektor asub vektortasandil
ja seega ka vektorid
koplanaarne, mis on tingimusega vastuolus.

b) Juhtum jääb alles
, st.
. Siis võrdsusest (3) saame või

Sest
on tasapinnas asuvate vektorite ruumi alus ja me oleme juba tõestanud tasandi vektorite baasi laienemise unikaalsust, siis võrdsusest (5) järeldub, et
Ja
, jne.

Teoreem on tõestatud.

Tagajärg.

1) Vektorruumi vektorite hulga vahel on üks-ühele vastavus
ja reaalarvude hulk R.

2) Vektorruumi vektorite hulga vahel on üks-ühele vastavus
ja Descartes'i väljak

3) Vektorruumi vektorite hulga vahel on üks-ühele vastavus
ja Descartes'i kuubik
reaalarvude komplekt R.

Tõestus. Tõestame kolmandat väidet. Kaks esimest on tõestatud sarnasel viisil.

Valige ja fikseerige ruumis
mingi alus
ja korraldada väljapanek
vastavalt järgmisele reeglile:

need. Seostame iga vektori selle koordinaatide järjestatud hulgaga.

Kuna kindlal alusel on igal vektoril üks koordinaatide komplekt, on reegliga (6) määratud vastavus tõepoolest vastendus.

Teoreemi tõestusest järeldub, et erinevatel vektoritel on sama aluse suhtes erinevad koordinaadid, s.t. kaardistamine (6) on süstimine.

Lase
suvaline järjestatud reaalarvude hulk.

Mõelge vektorile
. Sellel konstruktsiooni vektoril on koordinaadid
. Järelikult on kaardistamine (6) surjektsioon.

Kaardistus, mis on nii injektiivne kui ka sürjektiivne, on bijektiivne, st. üks-ühele jne.

Uurimine on tõestatud.

Teoreem. (Kahe vektori võrdsuse kohta.)

Kaks vektorit on võrdsed siis ja ainult siis, kui nende koordinaadid sama aluse suhtes on võrdsed.

Tõestus tuleneb vahetult eelmisest järeldusest.

punkt 3. Vektorruumi mõõde.

Definitsioon. Vektorruumi baasil olevate vektorite arvu nimetatakse selle dimensiooniks.

Määramine:
– vektorruumi V mõõde.

Seega on meil vastavalt sellele ja eelmistele määratlustele:

1)
– sirge L vektorite vektorruum.

- alus
,
,
,
– vektori lagunemine
alusel
,
– vektori koordinaat aluse suhtes
.

2)
– tasandi R vektorite vektorruum.

- alus
,
,
,
– vektori lagunemine
alusel
,
- vektori koordinaadid aluse suhtes
.

3)
– vektorite vektorruum punktide S ruumis.

- alus
,
,
– vektori lagunemine
alusel
,
- vektori koordinaadid aluse suhtes
.

Kommenteeri. Kui
, See
ja saate valida aluse
ruumi
Niisiis
- alus
Ja
- alus
. Siis
, Ja
, .

Seega saab mistahes sirge L, tasandi P ja ruumi S vektorit alusele laiendada
:

Määramine. Vektorite võrdsuse teoreemi alusel saame identifitseerida mis tahes vektori, millel on järjestatud reaalarvude kolmik, ja kirjutada:

See on võimalik ainult siis, kui alus
fikseeritud ja pole ohtu sassi minna.

Definitsioon. Vektori kirjutamist reaalarvude järjestatud kolmiku kujul nimetatakse vektori kirjutamise koordinaatvormiks:
.

punkt 4. Lineaartehted vektoritega koordinaatide tähistuses.

Lase
– ruumi alus
Ja
on kaks selle suvalist vektorit. Lase
Ja
– nende vektorite salvestamine koordinaatide kujul. Lase edasi,
on suvaline reaalarv. Seda tähistust kasutades kehtib järgmine teoreem.

Teoreem. (Koordinaadikujuliste vektoritega lineaarsete operatsioonide kohta.)

2)
.

Teisisõnu, kahe vektori liitmiseks tuleb lisada neile vastavad koordinaadid ja vektori korrutamiseks arvuga tuleb antud vektori iga koordinaat antud arvuga korrutada.

Tõestus. Kuna vastavalt teoreemi tingimustele, siis kasutades vektorruumi aksioome, mis juhivad vektorite liitmise ja vektori arvuga korrutamise toiminguid, saame:

See tähendab.

Teine võrdsus on tõestatud sarnaselt.

Teoreem on tõestatud.

punkt 5. Ortogonaalsed vektorid. Ortonormaalne alus.

Definitsioon. Kaht vektorit nimetatakse ortogonaalseteks, kui nendevaheline nurk on võrdne täisnurgaga, s.t.
.

Määramine:
- vektorid Ja ortogonaalne.

Definitsioon. Vektorite troika
nimetatakse ortogonaalseks, kui need vektorid on paarikaupa üksteise suhtes ortogonaalsed, st.
,
.

Definitsioon. Vektorite troika
nimetatakse ortonormaalseks, kui see on ortogonaalne ja kõigi vektorite pikkused on võrdsed ühega:
.

Kommenteeri. Definitsioonist järeldub, et vektorite ortogonaalne ja seega ka ortonormaalne kolmik on mittetasapinnaline.

Definitsioon. Järjestatud mittekoplanaarne vektorkolmik
ühest punktist joonistatud nimetatakse paremale (paremale orienteeritud), kui vaadeldakse kolmanda vektori lõpust tasapinnale, millel asuvad kaks esimest vektorit Ja , esimese vektori lühim pöörlemine teisele toimub vastupäeva. Vastasel juhul nimetatakse vektorite kolmikut vasakpoolseks (vasakule orienteeritud).