Vaba trapets. Ristkülikukujuline trapets: kõik valemid ja näidisülesanded Trapetsi lahendamine mutriga a ja

Et mõista, kuidas trapetsikujulisi probleeme lahendada, on kasulik meeles pidada kolme põhilahendust.

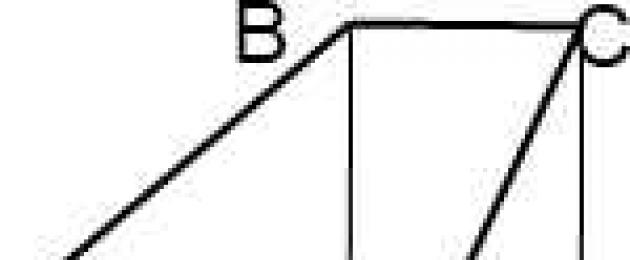
I. Joonista kaks kõrgust.

Ia. Nelinurk BCKF on ristkülik (kuna selle kõik nurgad on täisnurgad). Seega FK=BC.

AD=AF+FK+KD, seega AD=AF+BC+KD.

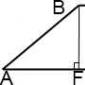
Kolmnurgad ABF ja DCK on täisnurksed kolmnurgad.

(Arvesse tuleks võtta ka teist võimalust:

Ib.

Sel juhul AD=AF+FD=AF+FK-DK=AF+BC-DK.)

Ic. Kui trapets on võrdhaarne, on ülesande lahendus lihtsustatud:

Sel juhul on täisnurksed kolmnurgad ABF ja DCK võrdsed näiteks piki jalga ja hüpotenuusi (tingimuse järgi AB=CD, trapetsi kõrgusena BF=CK). Kolmnurkade võrdsusest järeldub, et vastavad küljed on võrdsed:

AF=KD=(AD-FK):2=(AD-BC):2.

II. Joonistage küljega paralleelne sirgjoon.

IIa. BM∥CD. Kuna BC∥ AD (nagu trapetsi alused), siis BCDM on rööpkülik. Seetõttu MD=BC, BM=CD, AM=AD-BC.

IIb. Eelkõige võrdhaarse trapetsi puhul

BM∥ CD. Kuna CD=AB, siis BM=AB. See tähendab, et saame võrdhaarse kolmnurga ABM ja rööpküliku BCDM.

III. Jätkake külgi ja saage kolmnurk.

Sirged AB ja CD ristuvad punktis P.

Kolmnurgad APD ja BPC on kahes nurgas sarnased (nurk P on ühine, ∠ PAD= ∠ PBC vastab BC∥ AD ja sekant AP-le).

Seetõttu on nende küljed proportsionaalsed:

Need kolm lähenemist trapetsiprobleemide lahendamisele on peamised. Peale nende on veel palju muid viise. Mõned neist on sellel saidil üle vaadatud. Näiteks kuidas lahendada ülesandeid trapetsiga, mille diagonaalid on risti.

Selles artiklis on teie jaoks tehtud veel üks valik trapetsi probleeme. Tingimused on kuidagi seotud selle keskjoonega. Ülesande tüübid on võetud tüüpiliste ülesannete avatud pangast. Soovi korral saate värskendada oma teoreetilisi teadmisi. Blogis on juba käsitletud ülesandeid, mille tingimused on seotud, samuti. Lühidalt keskmisest reast:

Trapetsi keskjoon ühendab külgmiste külgede keskpunkte. See on paralleelne alustega ja võrdne nende poolsummaga.

Enne probleemide lahendamist vaatame teoreetilist näidet.

Antud trapets ABCD. Keskjoonega lõikuv diagonaal AC moodustab punkti K, diagonaal BD punkti L. Tõesta, et lõik KL võrdub poolega aluste erinevusest.

Märgime esmalt tõsiasja, et trapetsi keskjoon poolitab iga lõigu, mille otsad asuvad selle alustel. See järeldus viitab iseenesest. Kujutage ette segmenti, mis ühendab kahte aluse punkti; see jagab selle trapetsi kaheks teiseks. Selgub, et trapetsi alustega paralleelne ja külje keskosa läbiv segment läbib teise külje keskosa.

See põhineb ka Thalese teoreemil:

Kui ühele kahest sirgest on paigutatud järjest mitu võrdset lõiku ja nende otstest tõmmatakse paralleelsed jooned, mis lõikuvad teise joonega, siis lõikavad nad teiselt sirgelt võrdsed lõigud.

See tähendab, et antud juhul on K AC ja L BD keskpunkt. Seetõttu on EK kolmnurga ABC keskjoon, LF kolmnurga DCB keskjoon. Vastavalt kolmnurga keskjoone omadusele:

Nüüd saame segmenti KL väljendada aluste kaudu:

Tõestatud!

See näide on toodud põhjusega. Iseseisva lahenduse ülesannetes on just selline ülesanne. Ainult see ei ütle, et diagonaalide keskpunkte ühendav segment asub keskjoonel. Vaatleme ülesandeid:

27819. Leidke trapetsi keskjoon, kui selle alused on 30 ja 16.

Arvutame järgmise valemi abil:

27820. Trapetsi keskjoon on 28 ja väiksem alus on 18. Leia trapetsi suurem alus.

Väljendame suuremat alust:

Seega:

27836. Nürinurga tipust võrdhaarse trapetsi suuremale alusele langetatud risti jagab selle osadeks, mille pikkus on 10 ja 4. Leidke selle trapetsi keskjoon.

Keskjoone leidmiseks peate teadma aluseid. Alus AB on kergesti leitav: 10+4=14. Leiame DC.

Ehitame teise risti DF:

Segmendid AF, FE ja EB on vastavalt 4, 6 ja 4. Miks?

Võrdhaarse trapetsi puhul jagavad suuremale alusele langetatud ristid selle kolmeks segmendiks. Kaks neist, mis on äralõigatud täisnurksete kolmnurkade jalad, on üksteisega võrdsed. Kolmas segment on võrdne väiksema alusega, kuna näidatud kõrguste ehitamisel moodustub ristkülik ja ristküliku vastasküljed on võrdsed. Selles ülesandes:

Seega DC=6. Arvutame:

27839. Trapetsi alused on vahekorras 2:3 ja keskjoon on 5. Leia väiksem alus.

Tutvustame proportsionaalsuskoefitsienti x. Siis AB = 3x, DC = 2x. Võime kirjutada:

Seetõttu on väiksem alus 2∙2=4.

27840. Võrdhaarse trapetsi ümbermõõt on 80, selle keskjoon on võrdne külgküljega. Leidke trapetsi külg.

Tingimuse põhjal võime kirjutada:

Kui tähistame keskmist joont läbi väärtuse x, saame:

Teise võrrandi saab juba kirjutada järgmiselt:

27841. Trapetsi keskjoon on 7 ja üks selle alustest on teisest 4 võrra suurem. Leia trapetsi suurem alus.

Tähistame väiksemat alust (DC) kui x, siis suurem (AB) võrdub x+4-ga. Võime selle üles kirjutada

Leidsime, et väiksem baas on varajane viis, mis tähendab, et suurem on 9.

27842. Trapetsi keskjoon on 12. Üks diagonaalidest jagab selle kaheks lõiguks, mille vahe on 2. Leia trapetsi suurem alus.

Leiame lihtsalt trapetsi suurema aluse, kui arvutame välja lõigu EO. See on kolmnurga ADB keskjoon ja AB=2∙EO.

Mis meil on? Öeldakse, et keskjoon võrdub 12-ga ning lõikude EO ja ОF vahe on 2. Võime kirjutada kaks võrrandit ja lahendada süsteemi:

On selge, et sel juhul saate valida arvudepaari ilma arvutusteta, need on 5 ja 7. Kuid siiski lahendame süsteemi:

Seega EO=12–5=7. Seega on suurem alus võrdne AB=2∙EO=14.

27844. Võrdhaarse trapetsi diagonaalid on risti. Trapetsi kõrgus on 12. Leia selle keskjoon.

Märgime kohe, et läbi võrdhaarse trapetsi diagonaalide lõikepunkti tõmmatud kõrgus asub sümmeetriateljel ja jagab trapetsi kaheks võrdseks ristkülikukujuliseks trapetsiks, st selle kõrguse alused jagatakse pooleks.

Näib, et keskjoone arvutamiseks peame leidma põhjused. Siin tekib väike tupik... Kuidas kõrgust teades antud juhul aluseid arvutada? Pole võimalik! Selliseid fikseeritud kõrgusega ja 90 kraadise nurga all ristuvate diagonaalidega trapetse on palju. Mida ma peaksin tegema?

Vaadake trapetsi keskjoone valemit. Lõppude lõpuks ei pea me teadma põhjuseid endid, piisab, kui teada nende summat (või poolsummat). Me suudame seda teha.

Kuna diagonaalid lõikuvad täisnurga all, moodustatakse võrdhaarsed täisnurksed kolmnurgad kõrgusega EF:

Eeltoodust järeldub, et FO=DF=FC ja OE=AE=EB. Nüüd kirjutame üles, millega võrdub kõrgus, väljendatuna segmentide DF ja AE kaudu:

Nii et keskmine joon on 12.

*Üldiselt on see probleem, nagu te aru saate, peast arvutamisel. Kuid olen kindel, et esitatud üksikasjalik selgitus on vajalik. Ja nii... Kui joonist vaadata (eeldusel, et ehitamisel jälgitakse diagonaalide vahelist nurka), hakkab kohe silma võrdsus FO=DF=FC, ja OE=AE=EB.

Prototüüpide hulka kuuluvad ka trapetsidega ülesannete tüübid. See on ehitatud ruudukujulisele paberilehele ja peate leidma keskmise joone; lahtri külg on tavaliselt võrdne 1-ga, kuid see võib olla erinev väärtus.

27848. Leia trapetsi keskjoon ABCD, kui ruudukujuliste lahtrite küljed on võrdsed 1-ga.

See on lihtne, me arvutame alused lahtrite kaupa ja kasutame valemit: (2+4)/2=3

Kui alused on ehitatud rakuvõrgu suhtes nurga all, siis on kaks võimalust. Näiteks!

Kõigil lõpetajatel, kes valmistuvad sooritama ühtset matemaatika riigieksamit, on kasulik värskendada mälu teemal “Vaba trapets”. Nagu paljude aastate praktika on näidanud, põhjustavad selle jaotise planimeetrilised probleemid paljudele keskkooliõpilastele teatud raskusi. Samas on nii sertifitseerimistesti põhi- kui ka profiilitaseme läbimisel vajalik ühtse riigieksami ülesannete lahendamine teemal “Vaba trapets”. Seetõttu peaksid kõik lõpetajad selliste harjutustega hakkama saama.

Kuidas valmistuda eksamiks?

Enamik planimeetrilisi probleeme lahendatakse klassikaliste konstruktsioonidega. Kui ühtse riigieksami ülesandes on vaja leida näiteks joonisel kujutatud trapetsi pindala, tasub kõik teadaolevad parameetrid joonisele märkida. Pärast seda pidage meeles nendega seotud põhiteoreeme. Neid rakendades leiate õige vastuse.

Eksamiks valmistumise tõeliselt tõhusaks muutmiseks vaadake Shkolkovo haridusportaali. Siit leiate kogu algmaterjali teemadel “Tasuta trapets ehk mis aitab edukalt sooritada ühtse riigieksami. Joonise, valemite ja teoreemide peamised omadused on kogutud jaotisesse "Teoreetiline teave".

Lõpetajad saavad ka meie matemaatikaportaalis oma probleemide lahendamise oskusi täiendada. Jaotises "Kataloog" on esitatud suur valik erineva raskusastmega asjakohaseid harjutusi. Meie spetsialistid ajakohastavad ja täiendavad regulaarselt ülesannete nimekirja.

Moskva ja teiste linnade õpilased saavad harjutusi järjepidevalt veebis sooritada. Vajadusel saab mis tahes ülesande salvestada jaotisesse “Lemmikud” ja hiljem selle juurde tagasi pöörduda, et õpetajaga arutada.

Eelmise aasta ühtse riigieksami ja riigieksami praktika näitab, et geomeetriaprobleemid valmistavad raskusi paljudele koolilastele. Nendega saate hõlpsalt hakkama, kui õpite pähe kõik vajalikud valemid ja harjutate ülesannete lahendamist.

Selles artiklis näete trapetsi pindala leidmise valemeid, samuti näiteid probleemidest lahendustega. KIM-ides võite sertifitseerimiseksamitel või olümpiaadidel kohata neid samu. Seetõttu käsitlege neid hoolikalt.

Mida peate trapetsi kohta teadma?

Alustuseks meenutagem seda trapetsikujuline nimetatakse nelinurgaks, mille kaks vastaskülge, mida nimetatakse ka alusteks, on paralleelsed ja ülejäänud kaks mitte.

Trapetsis saab ka kõrgust (alusega risti) langetada. Joonistatakse keskmine joon - see on sirgjoon, mis on alustega paralleelne ja võrdne poolega nende summast. Nagu ka diagonaalid, mis võivad ristuda, moodustades terav- ja nürinurki. Või mõnel juhul täisnurga all. Lisaks, kui trapets on võrdhaarne, saab sellesse kirjutada ringi. Ja kirjeldage ringi selle ümber.

Trapetsi pindala valemid

Esiteks vaatame standardseid valemeid trapetsi pindala leidmiseks. Allpool käsitleme võrdkülgsete ja kõverjooneliste trapetside pindala arvutamise viise.

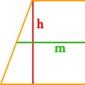
Kujutage ette, et teil on trapets alustega a ja b, mille kõrgus h on langetatud suuremale alusele. Figuuri pindala arvutamine on sel juhul sama lihtne kui pirnide koorimine. Peate lihtsalt aluste pikkuste summa jagama kahega ja korrutama tulemuse kõrgusega: S = 1/2(a + b)*h.

Võtame teise juhtumi: oletame, et trapetsis on lisaks kõrgusele ka keskjoon m. Teame keskjoone pikkuse leidmise valemit: m = 1/2(a + b). Seetõttu võime õigustatult lihtsustada trapetsi pindala valemit järgmisele kujule: S = m*h. Teisisõnu, trapetsi pindala leidmiseks peate keskjoone korrutama kõrgusega.

Vaatleme teist võimalust: trapets sisaldab diagonaale d 1 ja d 2, mis ei ristu täisnurga α all. Sellise trapetsi pindala arvutamiseks peate jagama diagonaalide korrutise kahega ja korrutama tulemuse nendevahelise nurga patuga: S = 1/2d 1 d 2 *sinα.

Mõelge nüüd trapetsi pindala leidmise valemile, kui selle kohta pole midagi teada, välja arvatud selle kõigi külgede pikkused: a, b, c ja d. See on tülikas ja keeruline valem, kuid see on kasulik igaks juhuks meeles pidada: S = 1/2 (a + b) * √c 2 – ((1/2 (b – a)) * ((b – a) 2 + c 2 – d 2)) 2.

Muide, ülaltoodud näited kehtivad ka juhul, kui vajate ristkülikukujulise trapetsi pindala valemit. See on trapets, mille külg külgneb alustega täisnurga all.

Võrdhaarne trapets

Võrdhaarseks nimetatakse trapetsi, mille küljed on võrdsed. Vaatleme võrdhaarse trapetsi pindala valemi jaoks mitmeid võimalusi.

Esimene võimalus: juhuks, kui ring raadiusega r on kantud võrdhaarse trapetsi sisse ning külg ja suurem alus moodustavad teravnurga α. Ringi saab kirjutada trapetsi, kui selle aluste pikkuste summa on võrdne külgede pikkuste summaga.

Võrdhaarse trapetsi pindala arvutatakse järgmiselt: korrutage sisse kirjutatud ringi raadiuse ruut neljaga ja jagage see kõik sinα-ga: S = 4r2/sina. Teine pindalavalem on erijuhtum valiku puhul, kui suure aluse ja külje vaheline nurk on 30 0: S = 8r2.

Teine variant: seekord võtame võrdhaarse trapetsi, kuhu on lisaks joonistatud diagonaalid d 1 ja d 2 ning kõrgus h. Kui trapetsi diagonaalid on üksteisega risti, on kõrgus pool aluste summast: h = 1/2(a + b). Seda teades on lihtne teisendada teile juba tuttav trapetsi pindala valem järgmisele kujule: S = h 2.

Kumera trapetsi pindala valem

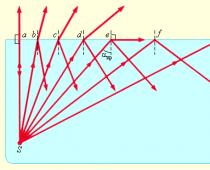
Alustuseks selgitame välja, mis on kõver trapets. Kujutage ette koordinaatide telge ja pideva ja mittenegatiivse funktsiooni f graafikut, mis ei muuda märki x-telje antud segmendis. Kõverjoonelise trapetsi moodustab funktsiooni y = f(x) graafik - ülaosas on x-telg all (segment) ja külgedel - punktide a ja b vahele tõmmatud sirged ning graafik funktsiooni.

Sellise mittestandardse kujundi pindala on ülaltoodud meetodite abil võimatu arvutada. Siin peate rakendama matemaatilist analüüsi ja kasutama integraali. Nimelt: Newtoni-Leibnizi valem - S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a). Selles valemis on F meie funktsiooni antiderivaat valitud segmendis. Ja kõverjoonelise trapetsi pindala vastab antud segmendi antiderivaadi juurdekasvule.

Näidisprobleemid

Et kõiki neid valemeid oleks teie peas lihtsam mõista, on siin mõned näited trapetsi pindala leidmise probleemidest. Kõige parem on, kui proovite esmalt probleeme ise lahendada ja alles siis võrrelda saadud vastust valmislahendusega.

Ülesanne nr 1: Antud trapets. Selle suurem põhi on 11 cm, väiksem 4 cm. Trapetsil on diagonaalid, üks 12 cm pikk, teine ​​9 cm.

Lahendus: konstrueerige trapetsikujuline AMRS. Joonistage sirge РХ läbi tipu P nii, et see oleks paralleelne diagonaaliga MC ja lõikub sirgega AC punktis X. Saad kolmnurga APХ.

Vaatleme kahte nende manipulatsioonide tulemusena saadud joonist: kolmnurk APX ja rööpkülik CMRX.

Tänu rööpkülikule saame teada, et PX = MC = 12 cm ja CX = MR = 4 cm. Kust saame arvutada kolmnurga ARX külje AX: AX = AC + CX = 11 + 4 = 15 cm.

Samuti saame tõestada, et kolmnurk APX on täisnurkne (selleks rakendage Pythagorase teoreemi - AX 2 = AP 2 + PX 2). Ja arvutage selle pindala: S APX = 1/2 (AP * PX) = 1/2 (9 * 12) = 54 cm 2.

Järgmisena peate tõestama, et kolmnurgad AMP ja PCX on pindalalt võrdsed. Aluseks saab poolte MR ja CX võrdsus (eespool juba tõestatud). Ja ka kõrgused, mida nendel külgedel alandate - need on võrdsed AMRS-i trapetsi kõrgusega.

Kõik see võimaldab teil öelda, et S AMPC = S APX = 54 cm 2.

Ülesanne nr 2: Trapets KRMS on antud. Selle külgmistel külgedel on punktid O ja E, samas kui OE ja KS on paralleelsed. Samuti on teada, et trapetsi ORME ja OKSE pindalad on vahekorras 1:5. RM = a ja KS = b. Peate leidma OE.

Lahendus: tõmmake läbi punkti M joonega RK paralleelne sirge ja määrake selle lõikepunkt OE-ga kui T. A on läbi punkti E joonestatud sirge, mis on tõmmatud läbi punkti E paralleelselt alusega KS, lõikepunkt.

Tutvustame veel ühte tähistust – OE = x. Ja ka kolmnurga TME kõrgus h 1 ja kolmnurga AEC kõrgus h 2 (saate iseseisvalt tõestada nende kolmnurkade sarnasust).

Eeldame, et b > a. Trapetside ORME ja OKSE pindalad on vahekorras 1:5, mis annab meile õiguse luua järgmine võrrand: (x + a) * h 1 = 1/5(b + x) * h 2. Teisendame ja saame: h 1 / h 2 = 1/5 * ((b + x)/(x + a)).

Kuna kolmnurgad TME ja AEC on sarnased, on meil h 1 / h 2 = (x – a)/(b – x). Kombineerime mõlemad kirjed ja saame: (x – a)/(b – x) = 1/5 * ((b + x)/(x + a)) ↔ 5(x – a)(x + a) = ( b + x)(b – x) ↔ 5 (x 2 – a 2) = (b 2 – x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √(5a 2 + b 2)/6.

Seega OE = x = √(5a 2 + b 2)/6.

Järeldus

Geomeetria ei ole loodusteadustest kõige lihtsam, kuid eksamiküsimustega saad kindlasti hakkama. Piisab, kui näidata ettevalmistusel pisut visadust. Ja muidugi pidage meeles kõiki vajalikke valemeid.

Püüdsime koguda kõik trapetsi pindala arvutamise valemid ühte kohta, et saaksite neid kasutada eksamiteks valmistumisel ja materjali läbivaatamisel.

Rääkige sellest artiklist kindlasti oma klassikaaslastele ja sõpradele sotsiaalvõrgustikes. Olgu rohkem ühtse riigieksami ja riigieksamite häid hindeid!

veebisaidil, materjali täielikul või osalisel kopeerimisel on vajalik link allikale.