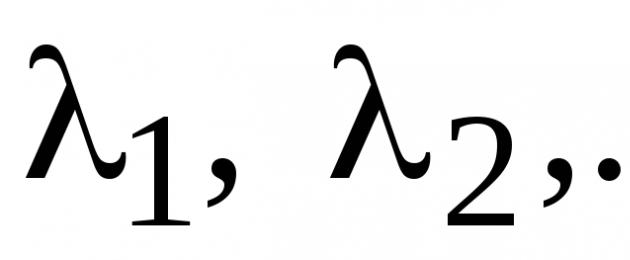Являются ли вектора линейно зависимыми. Линейно зависимые и линейно независимые вектора

Линейная зависимость векторов

При решении различных задач, как правило, приходится иметь дело не с одним вектором, а с некоторой совокупностью векторов одной и той же размерности. Такие совокупности называют системой векторов и обозначают

Определение. Линейной комбинацией векторов называется вектор вида

где - любые действительные числа. Также говорят, что вектор линейно выражается через векторы или разлагается по этим векторам.

Например, пусть даны три вектора: , , . Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор

Определение. Множество всевозможных линейных комбинаций системы векторов называется линейной оболочкой этой системы.

Определение. Система ненулевых векторов называется линейно зависимой , если существуют такие числа , не равные одновременно нулю, что линейная комбинация данной системы с указанными числами равна нулевому вектору:

Если же последнее равенство для данной системы векторов возможно лишь при , то эта система векторов называется линейно независимой .

Например, система двух векторов , линейно независима; система двух векторов и линейно зависима, так как .

Пусть система векторов (19) линейно зависима. Выберем в сумме (20) слагаемое, в котором коэффициент , и выразим его через остальные слагаемые:

Как видно из этого равенства, один из векторов линейно зависимой системы (19) оказался выраженным через другие векторы этой системы (или разлагается по остальным ее векторам).

Свойства линейно зависимой системы векторов

1. Система, состоящая из одного ненулевого вектора, линейно независима.

2. Система, содержащая нулевой вектор, всегда линейно зависима.

3. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди ее векторов содержится, по крайней мере, один вектор, который линейно выражается через остальные.

Геометрический смысл линейной зависимости в случае двухмерных векторов на плоскости: когда один вектор выражается через другой, мы имеем , т.е. эти векторы коллинеарны, или что то же самое, находятся на параллельных прямых.

В пространственном случае линейной зависимости трех векторов они параллельны одной плоскости, т.е. компланарны . Достаточно «подправить» соответствующими сомножителями длины этих векторов, чтобы один из них стал суммой двух других или выражался через них.

Теорема. В пространстве любая система, содержащая векторов, линейно зависима при .

Пример. Выяснить, являются ли векторы линейно зависимыми.

Решение . Составим векторное равенство . Записывая в виде вектор-столбцов, получаем

Таким образом, задача свелась к решению системы

Решим систему методом Гаусса:

В результате получим систему уравнений:

которая имеет бесконечное множество решений, среди которых обязательно найдется одно ненулевое, следовательно, векторы линейно зависимые.

В данной статье мы расскажем:

что такое коллинеарные векторы;
какие существуют условия коллинеарности векторов;
какие существуют свойства коллинеарных векторов;
что такое линейная зависимость коллинеарных векторов.

Определение 1

Коллинеарные векторы - это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Пример 1

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

условие 1 . Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
условие 2 . Векторы a и b коллинеарны при равном отношении координат:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

условие 3 . Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:

a ∥ b ⇔ a , b = 0

Замечание 1

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Замечание 2

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Пример 1

Исследуем векторы а = (1 ; 3) и b = (2 ; 1) на коллинеарность.

Как решить?

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ : a | | b

Пример 2

Какое значение m вектора a = (1 ; 2) и b = (- 1 ; m) необходимо для коллинеарности векторов?

Как решить?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Отсюда видно, что m = - 2 .

Ответ: m = - 2 .

Критерии линейной зависимости и линейной независимости систем векторов

Теорема

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Доказательство

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Обозначим:

A k - 1 a m , где m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

В таком случае:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Достаточность

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен - 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

Следствие:

Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Свойства линейно зависимых векторов

Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора - коллинеарны. Два коллинеарных вектора - линейно зависимы.
Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора - компланарны. (3 компланарных вектора - линейно зависимы).
Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.

Примеры решения задач на линейную зависимость или линейную независимость векторов

Пример 3

Проверим векторы a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Пример 4

Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Решаем эту систему при помощи метода Гаусса:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Из 2-ой строки вычитаем 1-ю, из 3-ей - 1-ю:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Определение 1 . Линейной комбинацией векторовназывается сумма произведений этих векторов на скаляры
:

Определение 2 . Система векторов
называется линейно зависимой системой, если линейная комбинация их (2.8) обращается в нуль:

причем среди чисел
существует хотя бы одно, отличное от нуля.

Определение 3 . Векторы
называются линейно независимыми, если их линейная комбинация (2.8) обращается в нуль лишь в случае, когда все числа.

Из этих определений можно получить следующие следствия.

Следствие 1 . В линейно зависимой системе векторов хотя бы один вектор может быть выражен как линейная комбинация остальных.

Доказательство . Пусть выполнено (2.9) и пусть для определенности, коэффициент
. Имеем тогда:
. Заметим, что справедливо и обратное утверждение.

Следствие 2. Если система векторов
содержит нулевой вектор, то эта система (обязательно) линейно зависима – доказательство очевидно.

Следствие 3 . Если средиn векторов
какие либоk (
) векторов линейно зависимы, то и всеn векторов линейно зависимы (опустим доказательство).

2 0 . Линейные комбинации двух, трех и четырех векторов . Рассмотрим вопросы линейной зависимости и независимости векторов на прямой, плоскости и в пространстве. Приведем соответствующие теоремы.

Теорема 1 . Для того чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Необходимость . Пусть векторыилинейно зависимы. Это означает, что их линейная комбинация
=0 и (ради определенности)
. Отсюда следует равенство
, и (по определению умножения вектора на число) векторыиколлинеарны.

Достаточность . Пусть векторыиколлинеарны (║) (предполагаем, что они отличны от нулевого вектора; иначе их линейная зависимость очевидна).

По теореме (2.7) (см. §2.1,п.2 0) тогда
такое, что
, или
– линейная комбинация равна нулю, причем коэффициент приравен 1 – векторыилинейно зависимы.

Из этой теоремы вытекает следующее следствие.

Следствие . Если векторыине коллинеарны, то они линейно независимы.

Теорема 2 . Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Необходимость . Пусть векторы,илинейно зависимы. Покажем, что они компланарны.

Из определения линейной зависимости векторов следует существование чисел
итаких, что линейная комбинация
, и при этом (для определенности)
. Тогда из этого равенства можно выразить вектор:=
, то есть векторравен диагонали параллелограмма, построенного на векторах, стоящих в правой части этого равенства (рис.2.6). Это означает, что векторы,илежат в одной плоскости.

Достаточность . Пусть векторы,икомпланарны. Покажем, что они линейно зависимы.

Исключим случай коллинеарности какой либо пары векторов (ибо тогда эта пара линейно зависима и по следствию 3 (см.п.1 0) все три вектора линейно зависимы). Заметим, что такое предположение исключает также существование нулевого вектора среди указанных трех.

Перенесем три компланарных вектора в одну плоскость и приведем их к общему началу. Через конец вектора проведем прямые, параллельные векторами; получим при этом векторыи(рис.2.7) – их существование обеспечено тем, что векторыине коллинеарные по предположению векторы. Отсюда следует, что вектор=+. Переписав это равенство в виде (–1)++=0, заключаем, что векторы,илинейно зависимы.

Из доказанной теоремы вытекает два следствия.

Следствие 1 . Пустьине коллинеарные векторы, вектор– произвольный, лежащий в плоскости, определяемой векторамии, вектор. Существуют тогда числаитакие, что

=+. (2.10)

Следствие 2 . Если векторы,ине компланарны, то они линейно независимы.

Теорема 3 . Любые четыре вектора линейно зависимы.

Доказательство опустим; с некоторыми изменениями оно копирует доказательство теоремы 2. Приведем следствие из этой теоремы.

Следствие . Для любых некомпланарных векторов,,и любого вектора
итакие, что

. (2.11)

Замечание . Для векторов в (трехмерном) пространстве понятия линейной зависимости и независимости имеют, как это следует из приведенных выше теорем 1-3, простой геометрический смысл.

Пусть имеются два линейно зависимых вектора и. В таком случае один из них является линейной комбинацией второго, то есть просто отличается от него численным множителем (например,
). Геометрически это означает, что оба вектора находятся на общей прямой; они могут иметь одинаковое или противоположное направления (рис.2.8 хх).

Если же два вектора расположены под углом друг к другу (рис.2.9 хх), то в этом случае нельзя получить один из них умножением другого на число – такие векторы линейно независимы. Следовательно, линейная независимость двух векторов иозначает, что эти векторы не могут быть уложены на одну прямую.

Выясним геометрический смысл линейной зависимости и независимости трех векторов.

Пусть векторы ,илинейно зависимы и пусть (для определенности) векторявляется линейной комбинацией векторови, то есть расположен в плоскости, содержащей векторыи. Это означает, что векторы,илежат в одной плоскости. Справедливо и обратное утверждение: если векторы,илежат в одной плоскости, то они линейно зависимы.

Таким образом, векторы ,илинейно независимы в том и только в том случае, если они не лежат в одной плоскости.

3 0 . Понятие базиса . Одним из важнейших понятий линейной и векторной алгебры является понятие базиса. Введем определения.

Определение 1 . Пара векторов называется упорядоченной, если указано, какой вектор этой пары считается первым, а какой вторым.

Определение 2. Упорядоченная пара,неколлинеарных векторов называется базисом на плоскости, определяемой заданными векторами.

Теорема 1 . Всякий векторна плоскости может быть представлен как линейная комбинация базисной системы векторов,:

(2.12)

и это представление единственно.

Доказательство . Пусть векторыиобразуют базис. Тогда любой векторможно представить в виде
.

Для доказательства единственности предположим, что имеется еще одно разложение
. Имеем тогда=0, причем хотя бы одна из разностей отлична от нуля. Последнее означает, что векторыилинейно зависимы, то есть коллинеарны; это противоречит утверждению, что они образуют базис.

Но тогда – разложение единственно.

Определение 3 . Тройка векторов называется упорядоченной, если указано, какой вектор ее считается первым, какой вторым, а какой третьим.

Определение 4 . Упорядоченная тройка некомпланарных векторов называется базисом в пространстве.

Здесь также справедлива теорема разложения и единственности.

Теорема 2 . Любой векторможет быть представлен как линейная комбинация базисной системы векторов,,:

(2.13)

и это представление единственно (опустим доказательство теоремы).

В разложениях (2.12) и (2.13) величины называются координатами векторав заданном базисе (точнее, аффинными координатами).

При фиксированном базисе
и
можно писать
.

Например, если задан базис
и дано, что
, то это означает, что имеет место представление (разложение)
.

4 0 . Линейные операции над векторами в координатной форме . Введение базиса позволяет линейные операции над векторами заменить обычными линейными операциями над числами – координатами этих векторов.

Пусть задан некоторый базис
. Очевидно, задание координат вектора в этом базисе полностью определяет сам вектор. Имеют место следующие предложения:

а) два вектора
и
равны тогда и только тогда, когда равны их соответственные координаты:

б) при умножении вектора
на числоего координаты умножаются на это число:

; (2.15)

в) при сложении векторов складываются их соответственные координаты:

Доказательства этих свойств опустим; докажем лишь для примера свойство б). Имеем

Замечание . В пространстве (на плоскости) можно выбрать бесконечно много базисов.

Приведем пример перехода от одного базиса к другому, установим соотношения между координатами вектора в различных базисах.

Пример 1 . В базисной системе
заданы три вектора:
,
и
. В базисе,,векторимеет разложение. Найти координаты векторав базисе
.

Решение . Имеем разложения:
,
,
; следовательно,
=
+2
+
= =
, то есть
в базисе
.

Пример 2 . Пусть в некотором базисе
четыре вектора заданы своими координатами:
,
,
и
.

Выяснить, образуют ли векторы
базис; в случае положительного ответа найти разложение векторав этом базисе.

Решение . 1) векторы образуют базис, если они линейно независимы. Составим линейную комбинацию векторов
(
) и выясним, при каких
иона обращается в нуль:
=0. Имеем:

=
+
+
=

По определению равенства векторов в координатной форме получим следующую систему (линейных однородных алгебраических) уравнений:
;
;
, определитель которой
=1
, то есть система имеет (лишь) тривиальное решение
. Это означает линейную независимость векторов
и, следовательно, они образуют базис.

2) разложим вектор в этом базисе. Имеем:=
или в координатной форме.

Переходя к равенству векторов в координатной форме, получим систему линейных неоднородных алгебраических уравнений:
;
;
. Решая ее (например, по правилу Крамера), получим:
,
,
и (
)
. Имеем разложение векторав базисе
:=.

5 0 . Проекция вектора на ось. Свойства проекций. Пусть имеется некоторая осьl , то есть прямая с выбранным на ней направлением и пусть задан некоторый вектор.Определим понятие проекции векторана осьl .

Определение . Проекцией векторана осьl называется произведение модуля этого вектора на косинус угла между осьюl и вектором (рис.2.10):

. (2.17)

Следствием этого определения является утверждение о том, что равные векторы имеют равные проекции (на одну и ту же ось).

Отметим свойства проекций.

1) проекция суммы векторов на некоторую ось l равна сумме проекций слагаемых векторов на ту же ось:

2) проекция произведения скаляра на вектор равна произведению этого скаляра на проекцию вектора на ту же ось:

=
. (2.19)

Следствие . Проекция линейной комбинации векторов на ось равна линейной комбинации их проекций:

Доказательства свойств опустим.

6 0 . Прямоугольная декартова система координат в пространстве .Разложение вектора по ортам осей. Пусть в качестве базиса выбраны три взаимно перпендикулярных орта; для них вводим специальные обозначения
. Поместив их начала в точкуO , направим по ним (в соответствии с ортами
) координатные осиOx ,Oy иOz (ось с выбранным на ней положительным направлением, началом отсчета и единицей длины называется координатной осью).

Определение . Упорядоченная система трех взаимно перпендикулярных координатных осей с общим началом и общей единицей длины называется прямоугольной декартовой системой координат в пространстве.

Ось Ox называется осью абсцисс,Oy – осью ординат иOz – осью аппликат.

Займемся разложением произвольного вектора по базису
. Из теоремы (см.§2.2,п.3 0 , (2.13)) следует, что
может быть и единственным образом разложен по базису
(здесь вместо обозначения координат
употребляют
):

. (2.21)

В (2.21)
суть (декартовы прямоугольные) координаты вектора. Смысл декартовых координат устанавливает следующая теорема.

Теорема . Декартовы прямоугольные координаты
вектораявляются проекциями этого вектора соответственно на осиOx ,Oy иOz .

Доказательство. Поместим векторв начало системы координат – точкуO . Тогда его конец будет совпадать с некоторой точкой
.

Проведем через точку
три плоскости, параллельные координатным плоскостямOyz ,Oxz иOxy (рис.2.11 хх). Получим тогда:

. (2.22)

В (2.22) векторы
и
называются составляющими вектора
по осямOx ,Oy иOz .

Пусть через
иобозначены соответственно углы, образованные векторомс ортами
. Тогда для составляющих получим следующие формулы:

=
=
,
=
=
,
=
=
(2.23)

Из (2.21), (2.22) (2.23) находим:

=
=
;=
=
;=
=
(2.23)

– координаты
вектораесть проекции этого вектора на координатные осиOx ,Oy иOz соответственно.

Замечание . Числа
называются направляющими косинусами вектора.

Модуль вектора (диагональ прямоугольного параллелепипеда) вычисляется по формуле:

. (2.24)

Из формул (2.23) и (2.24) следует, что направляющие косинусы могут быть вычислены по формулам:

=
;
=
;
=
. (2.25)

Возводя обе части каждого из равенств в (2.25) и складывая почленно левые и правые части полученных равенств, придем к формуле:

– не любые три угла образуют некоторое направление в пространстве, но лишь те, косинусы которых связаны соотношением (2.26).

7 0 . Радиус-вектор и координаты точки .Определение вектора по его началу и концу . Введем определение.

Определение . Радиусом-вектором (обозначается) называется вектор, соединяющий начало координатO с этой точкой (рис.2.12 хх):

. (2.27)

Любой точке пространства соответствует определенный радиус-вектор (и обратно). Таким образом, точки пространства представляются в векторной алгебре их радиус-векторами.

Очевидно, координаты
точкиM являются проекциями ее радиус-вектора
на координатные оси:

(2.28’)

и, таким образом,

(2.28)

– радиус-вектор точки есть вектор, проекции которого на оси координат равны координатам этой точки. Отсюда следует две записи:
и
.

Получим формулы для вычисления проекций вектора
по координатам его начала – точке
и конца – точке
.

Проведем радиус-векторы
и вектор
(рис.2.13). Получим, что

=
=(2.29)

– проекции вектора на координатные орты равны разностям соответствующих координат конца и начала вектора.

8 0 . Некоторые задачи на декартовы координаты .

1) условия коллинеарности векторов . Из теоремы (см.§2.1,п.2 0 , формула (2.7)) следует, что для коллинеарности векторовинеобходимо и достаточно, чтобы выполнялось соотношение:=. Из этого векторного равенства получаем три в координатной форме равенства:, откуда следует условие коллинеарности векторов в координатной форме:

(2.30)

– для коллинеарности векторов инеобходимо и достаточно, чтобы их соответствующие координаты были пропорциональны.

2) расстояние между точками . Из представления (2.29) следует, что расстояние
между точками
и
определяется формулой

=
=. (2.31)

3) деление отрезка в данном отношении . Пусть даны точки
и
и отношение
. Нужно найти
– координаты точкиM (рис.2.14).

Имеем из условия коллинеарности векторов:
, откуда
и

. (2.32)

Из (2.32) получим в координатной форме:

Из формул (2.32’) можно получить формулы для вычисления координат середины отрезка
, полагая
:

Замечание . Будем считать отрезки
и
положительными или отрицательными в зависимости от того, совпадает их направление с направлением от начала
отрезка к концу
, или не совпадает. Тогда по формулам (2.32) – (2.32”) можно находить координат точки, делящей отрезок
внешним образом, то есть так, что делящая точкаM находится на продолжении отрезка
, а не внутри его. При этом конечно,
.

4) уравнение сферической поверхности . Составим уравнение сферической поверхности – геометрического места точек
, равноудаленных на расстояниеот некоторого фиксированного центра – точки
. Очевидно, что в данном случае
и с учетом формулы (2.31)

Уравнение (2.33) и есть уравнение искомой сферической поверхности.

Введенные нами линейные операции над векторами дают возможность составлять различные выражения для векторных величин и преобразовывать их при помощи установленных для этих операций свойств.

Исходя из заданного набора векторов а 1 , ..., а n , можно составить выражение вида

где а 1 , ..., а n - произвольные действительные числа. Это выражение называют линейной комбинацией векторов а 1 , ..., а n . Числа α i , i = 1, n , представляют собой коэффициенты линейной комбинации . Набор векторов называют еще системой векторов .

В связи с введенным понятием линейной комбинации векторов возникает задача описания множества векторов, которые могут быть записаны в виде линейной комбинации данной системы векторов а 1 , ..., а n . Кроме того, закономерны вопросы об условиях, при которых существует представление вектора в виде линейной комбинации, и о единственности такого представления.

Определение 2.1. Векторы а 1 , ..., а n называют линейно зависимыми , если существует такой набор коэффициентов α 1 , ... , α n , что

α 1 a 1 + ... + α n а n = 0 (2.2)

и при этом хотя бы один из этих коэффициентов ненулевой. Если указанного набора коэффициентов не существует, то векторы называют линейно независимыми .

Если α 1 = ... = α n = 0, то, очевидно, α 1 а 1 + ... + α n а n = 0. Имея это в виду, можем сказать так: векторы а 1 , ..., а n линейно независимы, если из равенства (2.2) вытекает, что все коэффициенты α 1 , ... , α n равны нулю.

Следующая теорема поясняет, почему новое понятие названо термином "зависимость" (или "независимость"), и дает простой критерий линейной зависимости.

Теорема 2.1. Для того чтобы векторы а 1 , ..., а n , n > 1, были линейно зависимы, необходимо и достаточно, чтобы один из них являлся линейной комбинацией остальных.

◄ Необходимость. Предположим, что векторы а 1 , ..., а n линейно зависимы. Согласно определению 2.1 линейной зависимости, в равенстве (2.2) слева есть хотя бы один ненулевой коэффициент, например α 1 . Оставив первое слагаемое в левой части равенства, перенесем остальные в правую часть, меняя, как обычно, у них знаки. Разделив полученное равенство на α 1 , получим

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

т.е. представление вектора a 1 в виде линейной комбинации остальных векторов а 2 , ..., а n .

Достаточность. Пусть, например, первый вектор а 1 можно представить в виде линейной комбинации остальных векторов: а 1 = β 2 а 2 + ... + β n а n . Перенеся все слагаемые из правой части в левую, получим а 1 - β 2 а 2 - ... - β n а n = 0, т.е. линейную комбинацию векторов а 1 , ..., а n с коэффициентами α 1 = 1, α 2 = - β 2 , ..., α n = - β n , равную нулевому вектору. В этой линейной комбинации не все коэффициенты равны нулю. Согласно определению 2.1, векторы а 1 , ..., а n линейно зависимы.

Определение и критерий линейной зависимости сформулированы так, что подразумевают наличие двух или более векторов. Однако можно также говорить о линейной зависимости одного вектора. Чтобы реализовать такую возможность, нужно вместо "векторы линейно зависимы" говорить "система векторов линейно зависима". Нетрудно убедиться, что выражение "система из одного вектора линейно зависима" означает, что этот единственный вектор является нулевым (в линейной комбинации имеется только один коэффициент, и он не должен равняться нулю).

Понятие линейной зависимости имеет простую геометрическую интерпретацию. Эту ин-терпретацию проясняют следующие три утверждения.

Теорема 2.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

◄ Если векторы а и b линейно зависимы, то один из них, например а, выражается через другой, т.е. а = λb для некоторого действительного числа λ. Согласно определению 1.7 произведения вектора на число, векторы а и b являются коллинеарными.

Пусть теперь векторы а и b коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их линейная комбинация равна нулевому вектору. Пусть один из этих векторов не равен 0, например вектор b. Обозначим через λ отношение длин векторов: λ = |а|/|b|. Коллинеарные векторы могут быть однонаправленными или противоположно направленными . В последнем случае у λ изменим знак. Тогда, проверяя определение 1.7, убеждаемся, что а = λb. Согласно теореме 2.1, векторы а и b линейно зависимы.

Замечание 2.1. В случае двух векторов, учитывая критерий линейной зависимости, доказанную теорему можно переформулировать так: два вектора коллинеарны тогда и только тогда, когда один из них представляется как произведение другого на число. Это является удобным критерием коллинеарности двух векторов.

Теорема 2.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны .

◄ Если три вектора а, Ь, с линейно зависимы, то, согласно теореме 2.1, один из них, например а, является линейной комбинацией остальных: а = βb + γс. Совместим начала векторов b и с в точке A. Тогда векторы βb, γс будут иметь общее начало в точке A и по правилу параллелограмма их сумма, т.е. вектор а, будет представлять собой вектор с началом A и концом , являющимся вершиной параллелограмма, построенного на векторах-слагаемых. Таким образом, все векторы лежат в одной плоскости, т. е. компланарны.

Пусть векторы а, b, с компланарны. Если один из этих векторов является нулевым, то очевидно, что он будет линейной комбинацией остальных. Достаточно все коэффициенты линейной комбинации взять равными нулю. Поэтому можно считать, что все три вектора не являются нулевыми. Совместим начала этих векторов в общей точке O. Пусть их концами будут соот-ветственно точки A, B, C (рис. 2.1). Через точку C проведем прямые, параллельные прямым, проходящим через пары точек O, A и O, B. Обозначив точки пересечения через A" и B", получим параллелограмм OA"CB", следовательно, OC" = OA" + OB" . Вектор OA" и ненулевой вектор а= OA коллинеарны, а потому первый из них может быть получен умножением второго на действительное число α:OA" = αOA . Аналогично OB" = βOB , β ∈ R. В результате получаем,что OC" = α OA + βOB , т.е. вектор с является линейной комбинацией векторов а и b. Согласно теореме 2.1, векторы a, b, с являются линейно зависимыми.

Теорема 2.4. Любые четыре вектора линейно зависимы.

◄ Доказательство проводим по той же схеме, что и в теореме 2.3. Рассмотрим произвольные четыре вектора a, b, с и d. Если один из четырех векторов является нулевым, либо среди них есть два коллинеарных вектора, либо три из четырех векторов компланарны, то эти четыре вектора линейно зависимы. Например, если векторы а и b коллинеарны, то мы можем составить их линейную комбинацию αa + βb = 0 с ненулевыми коэффициентами, а затем в эту комбинацию добавить оставшиеся два вектора, взяв в качестве коэффициентов нули. Получим равную 0 линейную комбинацию четырех векторов, в которой есть ненулевые коэффициенты.

Таким образом, мы можем считать, что среди выбранных четырех векторов нет нулевых, никакие два не коллинеарны и никакие три не являются компланарными. Выберем в качестве их общего начала точку О. Тогда концами векторов a, b, с, d будут некоторые точки A, B, С, D (рис. 2.2). Через точку D проведем три плоскости, параллельные плоскостям ОВС, OCA, OAB, и пусть A", B", С" - точки пересечения этих плоскостей с прямыми OA, OB, ОС соответственно. Мы получаем параллелепипед OA"C"B"C"B"DA", и векторы a, b, с лежат на его ребрах, выходящих из вершины О. Так как четырехугольник OC"DC" является параллелограммом, то OD = OC" + OC" . В свою очередь, отрезок ОС" является диагональю параллелограмма OA"C"B", так что OC" = OA" + OB" , а OD = OA" + OB" + OC" .

Остается заметить, что пары векторов OA ≠ 0 и OA" , OB ≠ 0 и OB" , OC ≠ 0 и OC" коллинеарны, и, следовательно, можно подобрать коэффициенты α, β, γ так, что OA" = αOA , OB" = βOB и OC" = γOC . Окончательно получаем OD = αOA + βOB + γOC . Следовательно, вектор OD выражается через остальные три вектора, а все четыре вектора, согласно теореме 2.1, линейно зависимы.

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Р е ш е н и е. Ищем общее решение системы уравнений

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

методом Гаусса. Для этого запишем эту однородную систему по координатам:

Матрица системы

Разрешенная система имеет вид: (r A = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2 – свободная переменная): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . Наличие ненулевого частного решения, например, , говорит о том, векторы a 1 , a 2 , a 3 линейно зависимы.

Пример 2.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Р е ш е н и е. Рассмотрим однородную систему уравнений a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.

Проверяем систему на вырожденность:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.