Formula di compressione eccentrica. Compressione o tensione eccentrica

Molti elementi delle strutture edili (colonne, cremagliere, supporti) sono sotto l'influenza di forze di compressione applicate non al centro di gravità della sezione. Nella fig. La Figura 12.9 mostra la colonna su cui poggia la trave del solaio. Come si vede la forza agisce rispetto all'asse della colonna con eccentricità e, e quindi, in una sezione arbitraria Ah ah colonne insieme alla forza longitudinale N = -R si verifica un momento flettente, la cui grandezza è uguale a Rif. La tensione eccentrica (compressione) di un'asta rappresenta un tipo di deformazione in cui le risultanti forze esterne agire lungo una retta parallela all'asse dell'asta. Nel seguito considereremo principalmente problemi di compressione eccentrica. Con la tensione eccentrica in tutte le formule di calcolo fornite, il segno davanti alla forza dovrebbe essere cambiato R al contrario.

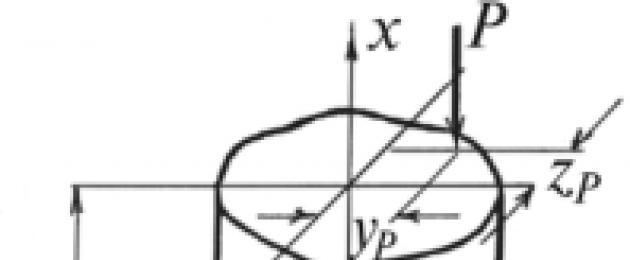
Lasciamo che un'asta di sezione trasversale arbitraria (Fig. 12.10) sia caricata all'estremità con una forza di compressione applicata eccentricamente R, parallelo all'asse OH. Accettiamo il positivo

direzioni degli assi principali di inerzia della sezione UO E Oz in modo che il punto di applicazione della forza R era nel primo quarto degli assi coordinati. Indichiamo le coordinate del punto di applicazione della forza R Attraverso sì r E zP-

Le forze interne in una sezione arbitraria dell'asta sono uguali

I segni negativi dei momenti flettenti sono dovuti al fatto che nel primo quarto degli assi coordinati questi momenti provocano compressione. L'entità delle forze interne in questo esempio non cambia lungo la lunghezza dell'asta, e quindi la distribuzione delle sollecitazioni in sezioni sufficientemente distanti dal luogo di applicazione del carico sarà la stessa.

Sostituendo la (12.11) nella (12.1), otteniamo la formula per le tensioni normali sotto compressione eccentrica:

Questa formula può essere convertita nel modulo

Dove io, io- principali raggi di inerzia della sezione. In cui

Ponendo o = 0 nella (12.12), otteniamo l'equazione linea zero:

Ecco y 0 e z0 - coordinate dei punti della linea zero (Fig. 12.11). L'equazione (12.14) è l'equazione di una retta che non passa per il baricentro della sezione. Per disegnare la linea zero, troviamo i punti della sua intersezione con gli assi delle coordinate. Assumendo in (12.14) in sequenza y 0 = 0 e z0= 0, di conseguenza troviamo

Dove una z E e tu - segmenti tagliati dalla linea zero sugli assi delle coordinate (Fig. 12.11).

Stabiliamo le caratteristiche della posizione della linea zero durante la compressione eccentrica.

• 1. Dalle formule (12.15) segue che e sì E una z hanno rispettivamente segni opposti ai segni sì r E zP- Pertanto, la linea zero passa attraverso quei quarti degli assi delle coordinate che non contengono il punto di applicazione della forza (Fig. 12.12).
• 2. Quando si avvicina il punto di applicazione della forza R in linea retta al centro di gravità delle coordinate della sezione di questo punto sì r E zP stanno diminuendo. Dalla (12.15) segue che i valori assoluti delle lunghezze dei segmenti e sì E una z aumento, cioè la linea dello zero si allontana dal centro di gravità, rimanendo parallela a se stessa (Fig. 12.13). Nel limite a Z P = y P = 0 (forza applicata al baricentro) la linea dello zero si sposta all'infinito. In questo caso le tensioni nella sezione trasversale saranno costanti e pari a o = -P/F.
• 3. Se il punto di applicazione della forza R si trova su uno degli assi principali, la linea dello zero è parallela all'altro asse. Infatti, inserendo (12.15), ad esempio, sì r= 0, lo otteniamo e sì= cioè la linea dello zero non interseca l'asse UO(Fig. 12.14).
• 4. Se il punto di applicazione della forza si muove lungo una linea retta che non passa per il centro di gravità, la linea zero ruota attorno a un certo punto. Dimostriamo questa proprietà. Punti di applicazione della forza Rx E R2, situate sugli assi delle coordinate corrispondono alle linee zero 1 - 1 e 2-2, parallele agli assi (Fig. 12.15), che si intersecano nel punto D. Poiché questo punto appartiene a due linee zero, le sollecitazioni in questo punto provengono da forze applicate simultaneamente Rx E R2 sarà uguale a zero. Poiché qualsiasi forza R3, il cui punto di applicazione si trova su una linea retta R(R2, Potere

decomporre in due componenti parallele applicate nei punti Pj e R2, quindi ne consegue che lo stress sul punto D dall'azione della forza R3 sono anch'essi uguali a zero. Pertanto, la linea zero è 3-3, corrispondente alla forza R3, passa per un punto D.

In altre parole, a un insieme di punti R, situato su una linea retta R(R2, corrisponde ad un fascio di rette passanti per un punto D.È vero anche il contrario: quando la linea dello zero ruota attorno ad un certo punto, il punto di applicazione della forza si sposta lungo una linea retta che non passa per il baricentro.

Se la linea zero interseca la sezione, la divide in zone di compressione e tensione. Lo stesso che con la flessione obliqua, dall'ipotesi sezioni piane ne consegue che le sollecitazioni raggiungono i loro valori maggiori nei punti più lontani dalla linea dello zero. La natura del diagramma delle sollecitazioni in questo caso è mostrata in Fig. 12.16, UN.

Se la linea zero si trova all'esterno della sezione, in tutti i punti della sezione le tensioni avranno lo stesso segno (Fig. 12.16, B).

Esempio 12.3. Costruiamo un diagramma delle tensioni normali in una sezione arbitraria di una colonna compressa eccentricamente di sezione trasversale rettangolare con dimensioni B X H(Fig. 12.17). I raggi quadrati di inerzia della sezione secondo la (12.22) sono uguali

I segmenti tagliati dalla linea zero sugli assi delle coordinate sono determinati dalle formule (12.15):

Sostituendo sequenzialmente nella (12.12) le coordinate dei punti C più lontani dalla linea dello zero IN(Fig. 12.18)

troveremo

Il diagramma o è mostrato in Fig. 12.18. Le sollecitazioni di compressione più elevate in valore assoluto sono quattro volte superiori ai valori di sollecitazione che esisterebbero nel caso di un'applicazione centrale della forza. Inoltre, nella sezione sono apparse significative sollecitazioni di trazione. Si noti che dalla (12.12) segue che al centro di gravità (y = z= 0) le tensioni sono pari a o = -P/F.

Esempio 12.4. La striscia ritagliata è sottoposta a una forza di trazione R(Fig. 12.19, UN). Confrontiamo le sollecitazioni nella sezione LV, sufficientemente distante dall'estremità e dalla posizione del ritaglio, con sollecitazioni nella sezione CD nella posizione del ritaglio.

In sezione trasversale AB(Fig. 12.19, B) forza R provoca tensione centrale e sollecitazioni pari a a = P/F = P/bh.

In sezione trasversale CD(Fig. 12.19, V) linea di forza R non passa per il baricentro della sezione e quindi si verifica una tensione eccentrica. Cambiando la formula di accesso (12.12) al contrario e accettando sì r= 0, otteniamo per questa sezione

Prendendo

Linea zero nella sezione CD parallelo all'asse UO e interseca l'asse Oz sulla distanza un =-i 2 y /z P- B/ 12. Nei punti della sezione più lontani dalla linea dello zero C(z - -b/ 4) e D(z - b/ 4) le tensioni secondo (12.16) sono uguali

Diagrammi di sollecitazione normale per le sezioni LW E CD mostrato in Fig. 12.19, avanti Cristo.

Pertanto, nonostante il fatto che la sezione CD ha un'area due volte più piccola della sezione trasversale AB, A causa dell'applicazione eccentrica della forza, le sollecitazioni di trazione nella sezione indebolita aumentano non di due, ma di otto volte. Inoltre, in questa sezione compaiono notevoli sollecitazioni di compressione.

È opportuno notare che il calcolo sopra riportato non tiene conto delle ulteriori sollecitazioni locali che si originano in prossimità del punto C a causa della presenza di una rientranza. Tali sollecitazioni dipendono dal raggio della scanalatura (al diminuire del raggio aumentano) e possono superare notevolmente il valore riscontrato e con = 8P/bh. In questo caso, la natura del diagramma delle sollecitazioni vicino al punto C differirà significativamente da quello lineare. La determinazione delle sollecitazioni locali (concentrazione delle sollecitazioni) è discussa nel Capitolo 18.

Molti materiali da costruzione (cemento, muratura, ecc.) hanno una scarsa resistenza alla trazione. La loro resistenza alla trazione è molte volte inferiore alla loro resistenza alla compressione. Pertanto, la comparsa di tensioni di trazione negli elementi strutturali realizzati con tali materiali è indesiderabile. Affinché questa condizione sia soddisfatta, la linea dello zero deve trovarsi all'esterno della sezione. Altrimenti, la linea zero intersecherà la sezione e in essa appariranno tensioni di trazione. Se la linea zero è tangente al contorno della sezione, la posizione corrispondente del punto di applicazione della forza è limitante. Secondo la proprietà 2 della linea zero, se il punto di applicazione della forza si avvicina al baricentro della sezione, la linea zero si allontanerà da esso. Il luogo geometrico dei punti limite corrispondenti alle diverse tangenti al contorno della sezione è il confine kernel della sezione. Il nucleo della sezione è un'area convessa attorno al baricentro, che ha la seguente proprietà: se il punto di applicazione della forza si trova all'interno o sul confine di quest'area, allora in tutti i punti della sezione le sollecitazioni hanno lo stesso segno. Il nucleo della sezione è una figura convessa, poiché le linee zero devono toccare l'involucro del contorno della sezione e non intersecarlo.

Attraverso il punto UN(Fig. 12.20) puoi disegnare innumerevoli tangenti (linee zero); in questo caso solo tangente ACè tangente all'inviluppo e ad esso deve corrispondere un certo punto sul contorno del nucleo della sezione. Allo stesso tempo, ad esempio, è impossibile tracciare una tangente all'area AB contorno della sezione perché interseca la sezione.

Costruiamo un nucleo di sezione per il rettangolo (Fig. 12.21). Per la tangente 1 - 1 a7 - b/ 2; UN= . Dalla (12.15) troviamo per il punto 1 corrispondente a questa tangente, z P = -i 2 y / a 7 = -b/6; sì r - 0. Per la tangente 2-2 ay - k/ 2; a 7 =°°, e le coordinate del punto 2 saranno uguali AR- -h/6; zP- 0. Secondo la proprietà 4 della linea zero, i punti di applicazione della forza corrispondenti a varie tangenti al punto d'angolo inferiore destro della sezione si trovano sulla retta 1-2. La posizione dei punti 3 e 4 è determinata dalle condizioni di simmetria. Pertanto, il nucleo della sezione trasversale di un rettangolo è un rombo con le diagonali B/3 e DA.

Per costruire un nucleo di sezione per un cerchio, è sufficiente disegnare una tangente (Fig. 12.22). In cui un = R; UN= °o.

"UU^^

Considerandolo per un cerchio io y - J y /F - R / 4, dalla (12.15) si ottiene

Pertanto, il nucleo della sezione trasversale di un cerchio è un cerchio con un raggio R/4.

Nella fig. 12.23, un, 6 vengono mostrati i nuclei in sezione trasversale per la trave a I e il canale. La presenza di quattro punti d'angolo del nucleo della sezione in ciascuno di questi esempi è dovuta al fatto che il contorno dell'inviluppo sia della trave a I che del canale è un rettangolo.

La tensione eccentrica (compressione) è causata da una forza parallela all'asse della trave, ma non coincidente con esso (Fig. 9.4).

La proiezione del punto di applicazione della forza sulla sezione trasversale è detta polo o punto di forza, e la retta che passa per il polo e il centro della sezione è detta linea di forza.

La tensione eccentrica (compressione) può essere ridotta a tensione assiale (compressione) e flessione obliqua se la forza P viene trasferita al centro di gravità della sezione. Pertanto, la forza P, indicata in Fig. 9.4 con un trattino G causerà una tensione assiale della trave, e una coppia di forze contrassegnate con due trattini causerà una flessione obliqua.

Basandosi sul principio di indipendenza dell'azione delle forze di sollecitazione nei punti della sezione trasversale durante la tensione eccentrica (compressione), sono determinati dalla formula

In questa formula, la forza assiale, i momenti flettenti, nonché le coordinate del punto della sezione trasversale in cui viene determinata la sollecitazione, devono essere sostituiti con i loro segni. Per i momenti flettenti accetteremo la stessa regola dei segni della flessione obliqua e la forza assiale sarà considerata positiva quando provoca tensione.

Se le coordinate del polo sono indicate con , allora assume la forma la Formula del momento (9.5).

Da questa equazione è chiaro che le estremità dei vettori di sollecitazione nei punti della sezione trasversale si trovano sul piano. La linea di intersezione del piano di sollecitazione con il piano della sezione trasversale è una linea neutra, la cui equazione si trova eguagliando lato destro uguaglianza (9.6) a zero. Dopo la riduzione di P otteniamo

Pertanto, la linea neutra durante la tensione eccentrica (compressione) non passa per il baricentro della sezione e non è perpendicolare al piano d'azione del momento flettente. La linea neutra taglia i segmenti sugli assi delle coordinate

Rappresentiamo i momenti di inerzia come il prodotto dell'area della sezione trasversale e il quadrato del corrispondente raggio di inerzia

Allora le espressioni (9.8) possono essere scritte come segue:

Dalle formule (9.8) è chiaro che il polo e la linea neutra si trovano sempre su lati opposti rispetto al baricentro della sezione, e la posizione della linea neutra è determinata dalle coordinate del polo.

Quando il polo si avvicina al baricentro della sezione lungo la linea di forza, la linea neutra si allontanerà dal centro, rimanendo parallela alla sua direzione originaria. Nel limite a, la linea neutra va all'infinito. In questo caso si verificherà una tensione centrale (compressione) della trave.

Su una linea di forza puoi sempre trovare una posizione del polo in cui la linea neutra toccherà il contorno della sezione senza intersecarla da nessuna parte. Se disegniamo tutte le possibili linee neutre in modo che tocchino il contorno della sezione senza intersecarla da nessuna parte e troviamo i poli corrispondenti, si scopre che i poli si troveranno su una linea chiusa completamente specifica per ciascuna sezione. L'area delimitata da questa linea è chiamata nucleo della sezione. In una sezione trasversale circolare, ad esempio, il nucleo è un cerchio con un diametro 4 volte inferiore al diametro della sezione trasversale, e nelle sezioni rettangolare e ad I il nucleo ha la forma di un parallelogramma (Fig. 9.5).

Dalla costruzione stessa del nucleo della sezione consegue che finché il polo è all'interno del nucleo, la linea neutra non intersecherà il contorno della sezione e le tensioni nell'intera sezione saranno dello stesso segno. Se il polo si trova all'esterno del nucleo, la linea neutra intersecherà il contorno della sezione e quindi le tensioni agiranno nella sezione segno diverso. Questa circostanza deve essere presa in considerazione quando si calcola la compressione decentrata di cremagliere realizzate con materiali fragili. Poiché i materiali fragili non sopportano bene i carichi di trazione, è consigliabile applicare forze esterne al palo in modo che su tutta la sezione trasversale agiscano solo sollecitazioni di compressione. Per fare ciò, il punto di applicazione delle forze esterne risultanti che comprimono il puntone deve essere situato all'interno del nucleo della sezione.

I calcoli della resistenza per la tensione e la compressione eccentrica vengono eseguiti allo stesso modo della flessione obliqua, in base alla sollecitazione nel punto pericoloso della sezione trasversale. Il punto pericoloso è il punto di sezione più lontano dalla sua linea neutra. Tuttavia, nei casi in cui in questo punto agisce la sollecitazione di compressione e il materiale del supporto è fragile, il punto in cui agisce la massima sollecitazione di trazione può essere pericoloso.

Il diagramma delle sollecitazioni è costruito su un asse perpendicolare alla linea neutra della sezione ed è limitato da una linea retta (vedi Fig. 9.4).

La condizione di forza sarà scritta come segue.

Riso. 12.3. Tensione eccentrica della trave

Le sollecitazioni in un punto arbitrario della sezione trasversale con coordinate (x, y) basate sul principio di indipendenza delle forze possono essere calcolate come segue (somma algebrica)

La loro equazione (12.4) segue che il diagramma delle tensioni nella sezione in esame forma un piano. L'equazione della linea neutra, nei cui punti le tensioni normali sono pari a zero, si ottiene dalla (12.4), eguagliando l'espressione a zero, cioè

(12.5)

Dall'equazione risultante segue che la linea neutra non passa per il baricentro della sezione, che coincide con l'origine delle coordinate. Inoltre, se le coordinate del punto di applicazione della forza (x 0 , y 0) sono positive, allora almeno una delle coordinate x o y dell'equazione (12.4) deve essere negativa e quindi, se il punto di applicazione della forza è nel primo quadrante, allora la linea neutra deve passare per i quadranti 2,3 e 4 (Fig. 12.4) .

È noto (geometria analitica) che se una retta è data da un'equazione della forma

quindi la distanza dall'origine alla retta sarà uguale a

Nel caso in esame (12.5) otteniamo (Fig. 12.4)

(12.5a)

Dall'espressione risultante segue che quando il punto di applicazione della forza P si avvicina al baricentro della sezione, cioè al diminuire del valore delle coordinate x 0 , y 0 aumenta la distanza ρ dal baricentro della sezione alla linea neutra.

σC

X

sì

UN

Figura 12.4. Distribuzione degli sforzi sotto tensione eccentrica

Nel limite in x 0 =y 0 =0, cioè quando la forza P è applicata al baricentro della sezione, la linea neutra è all'infinito. In questo caso si verifica una semplice tensione o compressione (centrale), tutte le tensioni nella sezione sono dello stesso segno e sono uguali tra loro.

Se la linea neutra interseca la sezione, su un lato di essa appare una zona di tensione e sull'altro una zona di compressione (Fig. 12.4). Tracciando linee parallele alla linea neutra e tangenti al contorno della sezione, è possibile trovare i punti più distanti dalla linea neutra in cui le tensioni normali raggiungono il loro massimo valori massimi. Nel caso considerato si tratta dei punti C e D.

Scriviamo le condizioni di forza in questi punti del modulo

dove x C, y C, x D, y D sono le coordinate dei punti pericolosi. I segni dei termini nelle formule (12.6) vengono selezionati sulla base di un'analisi delle direzioni di azione dei momenti flettenti e delle forze normali. Se la linea neutra non interseca la sezione trasversale, tutte le tensioni normali avranno lo stesso segno.

La zona in prossimità del baricentro della sezione, che ha la proprietà che applicando una forza P all'interno di tale zona, le tensioni in tutti i punti della sezione saranno dello stesso segno, è detta nucleo della sezione.

Alcuni materiali (cemento, mattoni, ghisa grigia) resistono alla tensione molto peggio della compressione. Per le strutture corrispondenti è importante che nel materiale non si creino tensioni di trazione, il che significa che devono essere applicate forze di compressione all'interno del nucleo della sezione.

Se una forza durante la tensione eccentrica (compressione) viene applicata al confine del nucleo della sezione, la linea neutra tocca il contorno della sezione. Questa condizione viene utilizzata per determinare le dimensioni del nucleo della sezione. Ad esempio, per una trave a sezione circolare, dalla condizione di simmetria geometrica ne consegue che il nucleo della sezione dovrebbe avere la forma di un cerchio (Fig. 12.5). Sia il punto di applicazione della forza P situato sull'asse Oy ad una distanza dall'origine delle coordinate pari a r (le coordinate del punto di applicazione della forza sono x 0 =0, y 0 =r). L'equazione della linea neutra in questo caso assume la forma (vedi formula 12.5)

Questa è l'equazione di una linea parallela all'asse del Bue. Poiché il nucleo della sezione è un cerchio di raggio r, la linea neutra deve toccare il contorno nel punto A (Fig. 12.5). La distanza dall'origine delle coordinate alla linea neutra è uguale al raggio del cerchio della sezione trasversale della trave R. Quindi, tenendo conto dell'espressione (12.5a), troviamo

Quindi r=R/4, cioè il nucleo di una trave di sezione circolare di raggio R è un cerchio di raggio R/4.

Compressione eccentrica. Costruzione kernel della sezione. Flessione con torsione. Calcoli della resistenza in stati tensionali complessi.

La compressione eccentrica è un tipo di deformazione in cui la forza longitudinale nella sezione trasversale dell'asta non è applicata al baricentro. A compressione eccentrica, oltre alla forza longitudinale (N), si creano due momenti flettenti ( e ).

Si presuppone che l'asta abbia un'elevata rigidità alla flessione per trascurare la flessione dell'asta sotto compressione eccentrica.

Trasformiamo la formula dei momenti sottoposti a compressione eccentrica sostituendo i valori dei momenti flettenti: .

Indichiamo le coordinate di un certo punto della linea zero sotto compressione eccentrica e sostituiamole nella formula per le sollecitazioni normali sotto compressione eccentrica. Considerando che le tensioni nei punti della linea zero sono pari a zero, dopo aver ridotto di , otteniamo l'equazione della linea zero per la compressione eccentrica: .

La linea zero della compressione eccentrica e il punto di applicazione del carico si trovano sempre su lati opposti del baricentro della sezione.

I segmenti tagliati dalla linea dello zero dagli assi delle coordinate, indicati con e , possono essere facilmente trovati dall'equazione della linea dello zero sotto compressione eccentrica. Se prima prendi e poi accettare , quindi troviamo i punti di intersezione della linea zero durante la compressione eccentrica con gli assi centrali principali:

La linea zero durante la compressione eccentrica dividerà la sezione trasversale in due parti. In una parte le sollecitazioni saranno di compressione, nell'altra di trazione. I calcoli della resistenza, come nel caso della flessione obliqua, vengono eseguiti utilizzando le sollecitazioni normali derivanti nel punto pericoloso della sezione trasversale (il più lontano dalla linea zero).

Il nucleo della sezione è una piccola area attorno al baricentro della sezione trasversale, caratterizzata dal fatto che qualsiasi forza longitudinale di compressione applicata all'interno del nucleo provoca sollecitazioni di compressione in tutti i punti della sezione trasversale.

Esempi di nuclei di sezione per sezioni trasversali rettangolari e circolari di un'asta.

Flessione con torsione. Gli alberi delle macchine e dei meccanismi sono spesso soggetti a tali carichi (azione simultanea di momenti torsionali e flettenti). Per calcolare il legname è necessario innanzitutto stabilire le sezioni pericolose. A questo scopo vengono costruiti diagrammi dei momenti flettenti e torcenti.

Utilizzando il principio di indipendenza dell'azione delle forze, determineremo le sollecitazioni derivanti nella trave separatamente per torsione e flessione.

Durante la torsione, si verificano tensioni tangenziali nelle sezioni trasversali della trave, raggiungendo valore più alto nei punti del contorno della sezione Durante la flessione si verificano tensioni normali nelle sezioni trasversali della trave, che raggiungono il loro valore massimo nelle fibre esterne della trave .

Consideriamo un'asta diritta caricata all'estremità con forze dirette parallelamente all'asse OH. La risultante di queste forze F applicato al punto CON. In un sistema di coordinate locale destrorso yOz, coincidenti con gli assi centrali principali della sezione, le coordinate del punto CON pari UN E B(Fig. 5.18).

Sostituiamo il carico applicato con un sistema staticamente equivalente di forze e momenti. Per fare ciò, trasferiamo la forza risultante F al baricentro della sezione DI e caricare l'asta con due momenti flettenti pari al prodotto della forza T^ esercitata dai suoi bracci rispetto agli assi coordinati: Mff = Fa E Mz = Fb.

Si noti che secondo la regola del sistema di coordinate destrorso per il punto C situato nel primo quarto, i momenti flettenti saranno formalmente i seguenti:

Riso. 5.18.Asta diritta caricata all'estremità con forze dirette parallelamente all'asseOH

segni che soffiano: M y = Fa e M7= -Fb. In questo caso, nella zona elementare giacente nel primo quarto, entrambi i momenti provocano tensioni di trazione.

Utilizzando il principio di indipendenza dell'azione delle forze, determiniamo le tensioni nel punto corrente della sezione con coordinate A E z da ciascun fattore di potenza separatamente. La tensione totale si ottiene sommando tutte e tre le componenti della tensione:

Determiniamo la posizione dell'asse neutro. Per fare ciò, secondo la formula (5.69), equiparamo a zero il valore della tensione normale nel punto corrente:

Come risultato di semplici trasformazioni, otteniamo l'equazione della linea neutra

Dove io sì E i z - raggi di inerzia principali, determinato dalle formule (3.14).

Pertanto, nel caso di tensione-compressione eccentrica, la linea neutra non passa per il baricentro della sezione (Fig. 5.19), come indicato dalla presenza nell'equazione (5.70) di un termine libero diverso da zero.

Le sollecitazioni massime si verificano nei punti della sezione trasversale UN E IN, più lontano dalla linea neutra. Stabiliamo la relazione tra le coordinate del punto di applicazione della forza e la posizione della linea neutra. Per fare ciò, determiniamo i punti di intersezione di questa linea di assi coordinati:

Riso. 5.19.

Le formule risultanti mostrano che la coordinata del punto di applicazione della forza UN e la coordinata del punto in cui la linea neutra interseca l'asse delle coordinate Oz(punto r 0) hanno segni opposti. Lo stesso si può dire delle quantità B E e0. Pertanto, il punto di applicazione della forza risultante e la linea neutra si trovano su lati opposti rispetto all'origine.

Secondo le formule ottenute, man mano che il punto di applicazione della forza si avvicina al baricentro della sezione, la linea neutra si allontana da zona centrale. Nel caso limite (a = b = 0) arriviamo al caso di tensione-compressione centrale.

È interessante determinare in quale zona di applicazione della forza le tensioni nella sezione avranno lo stesso segno. In particolare, per materiali che presentano scarsa resistenza a trazione, è razionale applicare la forza di compressione proprio in questa zona, in modo che nella sezione agiscano solo sforzi di compressione. Questa zona attorno al baricentro della sezione viene chiamata nucleo della sezione.

Se la forza viene applicata al centro della sezione, la linea neutra non interseca la sezione. Se viene applicata una forza lungo il confine del nucleo della sezione, la linea neutra tocca il contorno della sezione. Per determinare il nucleo della sezione trasversale, è possibile utilizzare la formula (5.71).

Se la linea neutra è rappresentata come tangente al contorno della sezione e si considerano tutte le possibili posizioni della tangente e i punti di applicazione della forza corrispondenti a queste posizioni, allora i punti di applicazione della forza delineeranno il nucleo della sezione .

Riso. 5.20.

UN - ellisse; 6 - rettangolo