Iniziamo a considerare il processo effettivo di calcolo dell'integrale doppio e a familiarizzare con il suo significato geometrico.

Il doppio integrale è numericamente uguale all'area di una figura piatta (regione di integrazione). Questa è la forma più semplice dell'integrale doppio, quando la funzione di due variabili è uguale a una: .

Consideriamo innanzitutto il problema in termini generali. Ora rimarrai sorpreso da quanto sia davvero semplice! Calcoliamo l'area di una figura piatta delimitata da linee. Per certezza, assumiamo che sull'intervallo . L'area di questa figura è numericamente uguale a:

Descriviamo l'area nel disegno:

Scegliamo il primo modo per aggirare l'area:

In questo modo:

E subito un importante accorgimento tecnico: gli integrali iterati possono essere considerati separatamente. Prima l'integrale interno, poi l'integrale esterno. Questo metodo è altamente raccomandato per i principianti nell'argomento teiere.

1) Calcolare l'integrale interno, mentre l'integrazione avviene sulla variabile "y":

L'integrale indefinito qui è il più semplice, e quindi viene utilizzata la formula banale di Newton-Leibniz, con l'unica differenza che i limiti dell'integrazione non sono i numeri, ma le funzioni. In primo luogo, abbiamo sostituito il limite superiore nella "y" (funzione antiderivativa), quindi il limite inferiore

2) Il risultato ottenuto nel primo comma deve essere sostituito nell'integrale esterno:

Una notazione più compatta per l'intera soluzione si presenta così:

La formula risultante è esattamente la formula di lavoro per calcolare l'area di una figura piatta utilizzando l'integrale definito "ordinario"! Vedi lezione Calcolo dell'area utilizzando un integrale definito, eccola a ogni angolo!

Cioè, il problema del calcolo dell'area utilizzando un integrale doppio poco diverso dal problema di trovare l'area usando un integrale definito! In effetti, sono la stessa cosa!

Di conseguenza, non dovrebbero sorgere difficoltà! Non prenderò in considerazione molti esempi, poiché tu, in effetti, hai riscontrato ripetutamente questo problema.

Esempio 9

Soluzione: Descriviamo l'area nel disegno:

Scegliamo il seguente ordine di attraversamento della regione:

Qui e sotto, non entrerò in come attraversare un'area perché il primo paragrafo era molto dettagliato.

In questo modo:

Come ho già notato, è meglio per i principianti calcolare gli integrali iterati separatamente, aderirò allo stesso metodo:

1) Innanzitutto, usando la formula di Newton-Leibniz, trattiamo l'integrale interno:

2) Il risultato ottenuto al primo passo è sostituito nell'integrale esterno:

Il punto 2 sta effettivamente trovando l'area di una figura piatta usando un integrale definito.

Risposta:

Ecco un compito così stupido e ingenuo.

Un curioso esempio di soluzione indipendente:

Esempio 10

Usando l'integrale doppio, calcola l'area di una figura piana delimitata dalle linee , ,

Un esempio di soluzione finale alla fine della lezione.

Negli Esempi 9-10, è molto più vantaggioso utilizzare il primo metodo per aggirare l'area; lettori curiosi, tra l'altro, possono modificare l'ordine del bypass e calcolare le aree nel secondo modo. Se non si commette un errore, naturalmente si ottengono gli stessi valori dell'area.

Ma in alcuni casi, il secondo modo per aggirare l'area è più efficace e, a conclusione del corso del giovane nerd, diamo un'occhiata a un altro paio di esempi su questo argomento:

Esempio 11

Usando l'integrale doppio, calcola l'area di una figura piana delimitata da linee.

Soluzione: aspettiamo due parabole con una brezza che giacciono dalla loro parte. Non c'è bisogno di sorridere, spesso si incontrano cose simili in più integrali.

Qual è il modo più semplice per fare un disegno?

Rappresentiamo la parabola come due funzioni:
- ramo superiore e - ramo inferiore.

Allo stesso modo, rappresentiamo la parabola come i rami superiore e inferiore.

L'area della figura viene calcolata utilizzando il doppio integrale secondo la formula:

Cosa succede se scegliamo il primo modo per aggirare l'area? Innanzitutto, quest'area dovrà essere divisa in due parti. E in secondo luogo, osserveremo questa triste immagine: . Gli integrali, ovviamente, non sono di un livello supercomplesso, ma... c'è un vecchio detto matematico: chi è amico delle radici non ha bisogno di una compensazione.

Pertanto, dall'equivoco che è dato nella condizione, esprimiamo le funzioni inverse:

Le funzioni inverse in questo esempio hanno il vantaggio di impostare immediatamente l'intera parabola senza foglie, ghiande, rami e radici.

Secondo il secondo metodo, l'attraversamento dell'area sarà il seguente:

In questo modo:

Come si suol dire, senti la differenza.

1) Trattiamo l'integrale interno:

Sostituiamo il risultato nell'integrale esterno:

L'integrazione sulla variabile "y" non dovrebbe essere imbarazzante, se ci fosse una lettera "zyu" - sarebbe fantastico integrarla su di essa. Anche se chi ha letto il secondo paragrafo della lezione Come calcolare il volume di un corpo di rivoluzione, non prova più il minimo imbarazzo con l'integrazione su "y".

Prestare attenzione anche al primo passaggio: l'integrando è pari e il segmento di integrazione è simmetrico rispetto a zero. Pertanto, il segmento può essere dimezzato e il risultato può essere raddoppiato. Questa tecnica è commentata in dettaglio nella lezione. Metodi efficienti per il calcolo dell'integrale definito.

Cosa aggiungere…. Qualunque cosa!

Risposta:

Per testare la tua tecnica di integrazione, puoi provare a calcolare . La risposta dovrebbe essere esattamente la stessa.

Esempio 12

Usando l'integrale doppio, calcola l'area di una figura piana delimitata da linee

Questo è un esempio fai da te. È interessante notare che se si tenta di utilizzare il primo modo per aggirare l'area, la figura non sarà più divisa in due, ma in tre parti! E, di conseguenza, otteniamo tre coppie di integrali iterati. Qualche volta succede.

La master class è giunta al termine ed è ora di passare al livello da grande maestro - Come calcolare l'integrale doppio? Esempi di soluzioni. Cercherò di non essere così maniacale nel secondo articolo =)

Ti auguro successo!

Soluzioni e risposte:

Esempio 2:Soluzione: Disegna un'area sul disegno:

Scegliamo il seguente ordine di attraversamento della regione:

In questo modo:
Passiamo alle funzioni inverse:


In questo modo:
Risposta:

Esempio 4:Soluzione: Passiamo alle funzioni dirette:


Eseguiamo il disegno:

Cambiamo l'ordine di attraversamento dell'area:

Risposta:

Ordine di attraversamento dell'area:

In questo modo:

1)
2)

Risposta:

Integrale definito. Come calcolare l'area di una figura

Passiamo ora alla considerazione delle applicazioni del calcolo integrale. In questa lezione analizzeremo un compito tipico e più comune. Come utilizzare un integrale definito per calcolare l'area di una figura piana. Infine, coloro che cercano un significato nella matematica superiore, possano trovarlo. Non si sa mai. Nella vita reale, dovrai approssimare un cottage estivo con funzioni elementari e trovare la sua area usando un certo integrale.

Per padroneggiare con successo il materiale, devi:

1) Comprendere l'integrale indefinito almeno a un livello intermedio. Pertanto, i manichini dovrebbero prima leggere la lezione Non.

2) Saper applicare la formula di Newton-Leibniz e calcolare l'integrale definito. Puoi stabilire relazioni amichevoli amichevoli con determinati integrali sulla pagina Integrale definito. Esempi di soluzioni.

Infatti, per trovare l'area di una figura, non è necessaria tanta conoscenza dell'integrale indefinito e definito. Il compito "calcolare l'area utilizzando un integrale definito" comporta sempre la costruzione di un disegno, quindi le tue conoscenze e abilità di disegno saranno una questione molto più rilevante. A questo proposito è utile rinfrescare la memoria dei grafici delle principali funzioni elementari e, come minimo, poter costruire una retta, una parabola e un'iperbole. Questo può essere fatto (molti ne hanno bisogno) con l'aiuto di materiale metodologico e un articolo sulle trasformazioni geometriche dei grafici.

In realtà, tutti hanno familiarità con il problema di trovare l'area utilizzando un integrale definito fin dalla scuola, e andremo un po' più avanti rispetto al curriculum scolastico. Questo articolo potrebbe non esistere affatto, ma il fatto è che il problema si verifica in 99 casi su 100, quando uno studente è tormentato con entusiasmo da una torre odiata mentre padroneggia un corso di matematica superiore.

I materiali di questo workshop sono presentati in modo semplice, dettagliato e con un minimo di teoria.

Iniziamo con un trapezio curvilineo.

Trapezio curvilineo detta figura piatta delimitata dall'asse , dalle rette e dal grafico di una funzione continua su un segmento che non cambia segno in questo intervallo. Lascia che questa figura sia localizzata non meno ascissa:

Quindi l'area di un trapezio curvilineo è numericamente uguale a un certo integrale. Qualsiasi integrale definito (che esiste) ha un significato geometrico molto buono. Sulla lezione Integrale definito. Esempi di soluzioni Ho detto che un integrale definito è un numero. E ora è il momento di affermare un altro fatto utile. Dal punto di vista della geometria, l'integrale definito è l'AREA.

Cioè, l'integrale definito (se esiste) corrisponde geometricamente all'area di qualche figura. Si consideri ad esempio l'integrale definito. L'integrando definisce una curva sul piano che si trova sopra l'asse (chi lo desidera può completare il disegno), e l'integrale definito stesso è numericamente uguale all'area del corrispondente trapezio curvilineo.

Esempio 1

Questa è una tipica dichiarazione di attività. Il primo e più importante momento della decisione è la costruzione di un disegno. Inoltre, il disegno deve essere costruito GIUSTO.

Quando si costruisce un progetto, consiglio il seguente ordine: All'inizioè meglio costruire tutte le linee (se presenti) e solo Quindi- parabole, iperboli, grafici di altre funzioni. I grafici delle funzioni sono più redditizi da costruire punto per punto, con la tecnica della costruzione puntuale si trovano nel materiale di riferimento Grafici e proprietà delle funzioni elementari. Lì puoi anche trovare materiale molto utile in relazione alla nostra lezione: come costruire rapidamente una parabola.

In questo problema, la soluzione potrebbe essere simile a questa.
Facciamo un disegno (notare che l'equazione definisce l'asse):

Non tratterò un trapezio curvilineo, è ovvio di quale area stiamo parlando qui. La soluzione continua così:

Sul segmento si trova il grafico della funzione oltre l'asse, Ecco perché:

Risposta:

Chi ha difficoltà a calcolare l'integrale definito e ad applicare la formula di Newton-Leibniz , fare riferimento alla lezione Integrale definito. Esempi di soluzioni.

Dopo che l'attività è stata completata, è sempre utile guardare il disegno e capire se la risposta è reale. In questo caso, "a occhio" contiamo il numero di celle nel disegno - beh, ne verranno digitate circa 9, sembra essere vero. È abbastanza chiaro che se avessimo, diciamo, la risposta: 20 unità quadrate, allora, ovviamente, è stato commesso un errore da qualche parte: 20 celle ovviamente non rientrano nella cifra in questione, al massimo una dozzina. Se la risposta si è rivelata negativa, anche il compito è stato risolto in modo errato.

Esempio 2

Calcola l'area della figura delimitata dalle linee , , e l'asse

Questo è un esempio fai da te. Soluzione completa e risposta alla fine della lezione.

Cosa fare se si trova il trapezio curvilineo sotto l'asse?

Esempio 3

Calcola l'area della figura delimitata da linee e assi coordinati.

Soluzione: Facciamo un disegno:

Se si trova il trapezio curvilineo sotto l'asse(o quantomeno non superiore asse dato), allora la sua area può essere trovata dalla formula:
In questo caso:

Attenzione! Non confondere i due tipi di attività:

1) Se ti viene chiesto di risolvere solo un integrale definito senza alcun significato geometrico, allora può essere negativo.

2) Se ti viene chiesto di trovare l'area di una figura usando un integrale definito, allora l'area è sempre positiva! Ecco perché nella formula appena considerata compare il meno.

In pratica, il più delle volte la figura si trova sia nel semipiano superiore che in quello inferiore, e quindi, dai problemi scolastici più semplici, si passa ad esempi più significativi.

Esempio 4

Trova l'area di una figura piatta delimitata da linee , .

Soluzione: Per prima cosa devi completare il disegno. In generale, quando si costruisce un disegno in problemi di area, siamo più interessati ai punti di intersezione delle linee. Troviamo i punti di intersezione della parabola e della retta. Questo può essere fatto in due modi. Il primo modo è analitico. Risolviamo l'equazione:

Quindi, il limite inferiore di integrazione, il limite superiore di integrazione.
È meglio non utilizzare questo metodo, se possibile..

È molto più proficuo e veloce costruire le linee punto per punto, mentre i limiti dell'integrazione si scoprono come “da soli”. La tecnica di costruzione punto per punto per vari grafici è discussa in dettaglio nella guida Grafici e proprietà delle funzioni elementari. Tuttavia, il metodo analitico per trovare i limiti a volte deve essere utilizzato se, ad esempio, il grafo è sufficientemente grande o la costruzione filettata non ha rivelato i limiti di integrazione (possono essere frazionari o irrazionali). E considereremo anche un tale esempio.

Torniamo al nostro compito: è più razionale costruire prima una retta e solo dopo una parabola. Facciamo un disegno:

Ripeto che con la costruzione puntuale i limiti dell'integrazione si scoprono il più delle volte “automaticamente”.

Ed ora la formula di lavoro: Se è presente una funzione continua sull'intervallo Maggiore o uguale qualche funzione continua, quindi l'area della figura delimitata dai grafici di queste funzioni e dalle rette, può essere trovata dalla formula:

Qui non è più necessario pensare a dove si trova la figura - sopra l'asse o sotto l'asse e, grosso modo, importa quale grafico è SOPRA(relativo a un altro grafico), e quale è SOTTO.

Nell'esempio in esame è ovvio che sul segmento la parabola si trova al di sopra della retta, e quindi è necessario sottrarre da

Il completamento della soluzione potrebbe essere simile a questo:

La figura desiderata è delimitata da una parabola dall'alto e da una retta dal basso.
Sul segmento , secondo la formula corrispondente:

Risposta:

In effetti, la formula della scuola per l'area di un trapezio curvilineo nel semipiano inferiore (vedi semplice esempio n. 3) è un caso speciale della formula . Poiché l'asse è dato dall'equazione e si trova il grafico della funzione non superiore assi, quindi

E ora un paio di esempi per una soluzione indipendente

Esempio 5

Esempio 6

Trova l'area della figura racchiusa dalle linee , .

Nel corso della risoluzione dei problemi per il calcolo dell'area utilizzando un determinato integrale, a volte accade un incidente divertente. Il disegno è stato eseguito correttamente, i calcoli erano corretti, ma a causa della disattenzione ... trovato l'area della figura sbagliata, è così che il tuo obbediente servitore ha sbagliato diverse volte. Ecco un caso reale:

Esempio 7

Calcola l'area della figura delimitata dalle linee , , , .

Soluzione: Facciamo prima un disegno:

…Eh, il disegno è uscito di merda, ma tutto sembra essere leggibile.

La figura di cui dobbiamo trovare l'area è ombreggiata in blu.(guarda attentamente la condizione: come la cifra è limitata!). Ma in pratica, a causa della disattenzione, si verifica spesso un "glitch", che è necessario trovare l'area della figura che è ombreggiata in verde!

Questo esempio è utile anche in quanto in esso l'area della figura viene calcolata utilizzando due integrali definiti. Veramente:

1) Sul segmento sopra l'asse c'è un grafico a linea retta;

2) Sul segmento sopra l'asse c'è un grafico dell'iperbole.

È abbastanza ovvio che le aree possono (e dovrebbero) essere aggiunte, quindi:

Risposta:

Passiamo a un altro compito significativo.

Esempio 8

Calcola l'area di una figura delimitata da linee,
Presentiamo le equazioni in una forma "scuola" ed eseguiamo un disegno punto per punto:

Si può vedere dal disegno che il nostro limite superiore è “buono”: .
Ma qual è il limite inferiore? È chiaro che questo non è un numero intero, ma cosa? Forse ? Ma dov'è la garanzia che il disegno sia realizzato con perfetta accuratezza, potrebbe benissimo scoprirlo. O radice. E se non avessimo ottenuto il grafico giusto?

In questi casi, è necessario dedicare ulteriore tempo e affinare analiticamente i limiti dell'integrazione.

Troviamo i punti di intersezione della retta e della parabola.
Per fare ciò, risolviamo l'equazione:


,

Veramente, .

L'ulteriore soluzione è banale, l'importante è non confondersi in sostituzioni e segni, i calcoli qui non sono dei più facili.

Sul segmento , secondo la formula corrispondente:

Risposta:

Bene, a conclusione della lezione, considereremo due compiti più difficili.

Esempio 9

Calcola l'area della figura delimitata da linee , ,

Soluzione: Disegna questa figura nel disegno.

Accidenti, ho dimenticato di firmare il programma e di rifare la foto, scusa, non hotz. Non un disegno, insomma oggi è il giorno =)

Per la costruzione punto per punto è necessario conoscere l'aspetto della sinusoide (e in generale è utile conoscere grafici di tutte le funzioni elementari), oltre ad alcuni valori sinusoidali, possono essere trovati in tavola trigonometrica. In alcuni casi (come in questo caso) è consentito costruire un disegno schematico, sul quale devono essere visualizzati in linea di principio correttamente grafici e limiti di integrazione.

Non ci sono problemi con i limiti di integrazione qui, seguono direttamente dalla condizione: - "x" cambia da zero a "pi". Prendiamo un'ulteriore decisione:

Sul segmento il grafico della funzione si trova sopra l'asse, quindi:

In questa lezione impareremo a calcolare aree di figure piatte, che sono chiamati trapezi curvilinei .

Esempi di tali figure sono nella figura seguente.

Da un lato, trovare l'area di una figura piatta utilizzando un integrale definito è estremamente semplice. Stiamo parlando dell'area della figura, che è limitata dall'alto da una certa curva, dal basso - dall'asse delle ascisse ( Bue), e a sinistra e a destra ci sono alcune linee rette. La semplicità è quella l'integrale definito della funzione a cui è data la curva, e c'è l'area di tale figura(trapezio curvilineo).

Per calcolare l'area di una figura, abbiamo bisogno di:

1. Integrale definito della funzione che definisce la curva , che limita il trapezio curvilineo dall'alto. Ed ecco che arriva la prima sfumatura significativa: un trapezio curvilineo può essere limitato da una curva non solo dall'alto, ma anche dal basso . Come agire in questo caso? Semplice ma importante da ricordare: l'integrale in questo caso è preso con un segno meno .
2. Limiti di integrazione un e B, che troviamo dalle equazioni delle rette che delimitano la figura a sinistra e a destra: X = un , X = B, dove un e B- numeri.

Separatamente, alcune sfumature in più.

La curva che limita il trapezio curvilineo dall'alto (o dal basso) deve essere grafico di una funzione continua e non negativa y = F(X) .

I valori X devono appartenere al segmento [un, B] . Cioè, ad esempio, le linee come una sezione di un fungo non vengono prese in considerazione, in cui la gamba si adatta perfettamente a questo segmento e il cappello è molto più largo.

I segmenti laterali possono degenerare in punti . Se hai visto una figura del genere nel disegno, questo non dovrebbe confonderti, poiché questo punto ha sempre il suo valore sull'asse x. Quindi tutto è in ordine con i limiti dell'integrazione.

Ora puoi passare a formule e calcoli. Quindi la zona S il trapezio curvilineo può essere calcolato con la formula

Se F(X) ≤ 0 (il grafico della funzione si trova sotto l'asse Bue), poi area di un trapezio curvo può essere calcolato con la formula

Ci sono anche casi in cui entrambi i limiti superiore e inferiore della figura sono rispettivamente funzioni y = F(X) e y = φ (X) , quindi l'area di tale cifra viene calcolata dalla formula

. (3)

Risolviamo i problemi insieme

Iniziamo con i casi in cui l'area di una figura può essere calcolata utilizzando la formula (1).

Esempio 1Bue) e diretto X = 1 , X = 3 .

Soluzione. Perché y = 1/X> 0 sul segmento , quindi l'area del trapezio curvilineo si trova dalla formula (1):

.

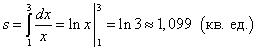Esempio 2 Trova l'area della figura delimitata dal grafico della funzione, linea retta X= 1 e l'asse x ( Bue ).

Soluzione. Il risultato dell'applicazione della formula (1):

Se poi S= 1/2; se poi S= 1/3, ecc.

Esempio 3 Trova l'area della figura delimitata dal grafico della funzione, l'asse x ( Bue) e diretto X = 4 .

Soluzione. La figura corrispondente alla condizione del problema è un trapezio curvilineo, in cui il segmento sinistro è degenerato in un punto. I limiti di integrazione sono 0 e 4. Poiché, secondo la formula (1), troviamo l'area del trapezio curvilineo:

.

Esempio 4 Trova l'area della figura delimitata dalle linee , , e situata nel 1° quarto.

Soluzione. Per usare la formula (1), rappresentiamo l'area della figura data dalle condizioni dell'esempio come somma delle aree di un triangolo OAB e trapezio curvilineo ABC. Quando si calcola l'area di un triangolo OAB i limiti dell'integrazione sono le ascisse dei punti o e UN, e per la figura ABC- ascisse di punti UN e C (UNè il punto di intersezione della retta OA e parabole, e C- punto di intersezione della parabola con l'asse Bue). Risolvendo congiuntamente (come sistema) le equazioni di una retta e di una parabola, otteniamo (l'ascissa del punto UN) e (l'ascissa di un altro punto di intersezione della retta e la parabola, che non serve per la soluzione). Allo stesso modo, otteniamo , (ascisse di punti C e D). Ora abbiamo tutto per trovare l'area della figura. Noi troviamo:

Esempio 5 Trova l'area di un trapezio curvilineo ACDB, se l'equazione della curva cd e ascisse UN e B rispettivamente 1 e 2.

Soluzione. Esprimiamo questa equazione della curva attraverso Y: L'area del trapezio curvilineo è trovata dalla formula (1):

.

Passiamo ai casi in cui l'area di una figura può essere calcolata utilizzando la formula (2).

Esempio 6 Trova l'area della figura delimitata dalla parabola e dall'asse x ( Bue ).

Soluzione. Questa figura si trova sotto l'asse x. Pertanto, per calcolare la sua area, utilizziamo la formula (2). I limiti di integrazione sono le ascisse ei punti di intersezione della parabola con l'asse Bue. Di conseguenza,

Esempio 7 Trova l'area tra l'asse x ( Bue) e due sinusoidi adiacenti.

Soluzione. L'area di questa figura può essere trovata dalla formula (2):

.

Troviamo ogni termine separatamente:

.

.

Infine troviamo la zona:

.

Esempio 8 Trova l'area della figura racchiusa tra la parabola e la curva.

Soluzione. Esprimiamo le equazioni delle rette in termini di Y:

L'area secondo la formula (2) sarà ottenuta come

,

dove un e B- ascisse di punti UN e B. Li troviamo risolvendo insieme le equazioni:

Infine troviamo la zona:

E, infine, ci sono casi in cui l'area di una figura può essere calcolata utilizzando la formula (3).

Esempio 9 Trova l'area della figura racchiusa tra le parabole E .

Abbiamo scoperto come trovare l'area di un trapezio curvilineo G. Ecco le formule risultanti:
per una funzione continua e non negativa y=f(x) sul segmento ,
per una funzione continua e non positiva y=f(x) sul segmento .

Tuttavia, quando si risolvono problemi di reperimento del territorio, si ha spesso a che fare con figure più complesse.

In questo articolo parleremo del calcolo dell'area delle figure i cui confini sono esplicitamente specificati da funzioni, cioè come y=f(x) o x=g(y) , e analizzeremo in dettaglio la soluzione di esempi tipici .

Navigazione della pagina.

Formula per calcolare l'area di una figura delimitata dalle linee y=f(x) o x=g(y) .

Teorema.

Lascia che le funzioni e siano definite e continue sul segmento, e per qualsiasi valore x da . Quindi area della figura G, delimitata da linee x=a , x=b e viene calcolato dalla formula .

Una formula simile è valida per l'area della figura delimitata dalle linee y \u003d c, y \u003d d e: .

Prova.

Mostriamo la validità della formula per tre casi:

Nel primo caso, quando entrambe le funzioni sono non negative, per la proprietà di additività dell'area, la somma dell'area della figura originaria G e del trapezio curvilineo è uguale all'area della figura. Di conseguenza,

Ecco perché, . L'ultima transizione è possibile grazie alla terza proprietà dell'integrale definito.

Allo stesso modo, nel secondo caso, l'uguaglianza è vera. Ecco un'illustrazione grafica:

Nel terzo caso, quando entrambe le funzioni sono non positive, abbiamo . Illustriamo questo:

Ora possiamo passare al caso generale in cui le funzioni e incrociano l'asse Ox.

Indichiamo i punti di intersezione. Questi punti dividono il segmento in n parti, dove . La figura G può essere rappresentata dall'unione delle figure . È ovvio che sul suo intervallo ricade in uno dei tre casi considerati in precedenza, quindi le loro aree si trovano come

Di conseguenza,

L'ultima transizione è valida per la quinta proprietà dell'integrale definito.

Illustrazione grafica del caso generale.

Quindi la formula provato.

È ora di passare alla risoluzione di esempi per trovare l'area delle figure delimitata dalle linee y=f(x) e x=g(y) .

Esempi di calcolo dell'area di una figura delimitata dalle linee y=f(x) o x=g(y) .

Inizieremo la soluzione di ogni problema costruendo una figura su un piano. Questo ci permetterà di rappresentare una figura complessa come unione di figure più semplici. In caso di difficoltà con la costruzione, fare riferimento agli articoli:; E .

Esempio.

Calcola l'area di una figura delimitata da una parabola e rette , x=1 , x=4 .

Soluzione.

Costruiamo queste linee sull'aereo.

Ovunque sul segmento, il grafico di una parabola sopra dritto. Pertanto, applichiamo la formula precedentemente ottenuta per l'area e calcoliamo l'integrale definito usando la formula di Newton-Leibniz:

Complichiamo un po' l'esempio.

Esempio.

Calcola l'area della figura delimitata da linee.

Soluzione.

In che modo è diverso dagli esempi precedenti? In precedenza, avevamo sempre due rette parallele all'asse x e ora solo una x=7 . Sorge subito la domanda: dove prendere il secondo limite di integrazione? Diamo un'occhiata al disegno per questo.

È diventato chiaro che il limite inferiore di integrazione quando si trova l'area della figura è l'ascissa del punto di intersezione del grafico della retta y \u003d x e della semiparabola. Troviamo questa ascissa dall'uguaglianza:

Pertanto, l'ascissa del punto di intersezione è x=2 .

Nota.

Nel nostro esempio e nel disegno si può notare che le linee e y=x si intersecano nel punto (2;2) ei calcoli precedenti sembrano ridondanti. Ma in altri casi, le cose potrebbero non essere così ovvie. Pertanto, si consiglia di calcolare sempre analiticamente le ascisse e le ordinate dei punti di intersezione delle rette.

Ovviamente il grafico della funzione y=x si trova sopra il grafico della funzione sull'intervallo . Applichiamo la formula per calcolare l'area:

Complichiamo ancora di più il compito.

Esempio.

Calcola l'area della figura delimitata dai grafici delle funzioni e .

Soluzione.

Costruiamo un grafico di proporzionalità inversa e una parabola .

Prima di applicare la formula per trovare l'area di una figura, bisogna decidere i limiti di integrazione. Per fare ciò, troviamo le ascisse dei punti di intersezione delle rette eguagliando le espressioni e .

Per valori di x diversi da zero, l'uguaglianza equivalente all'equazione di terzo grado con coefficienti interi. Puoi fare riferimento alla sezione per richiamare l'algoritmo per risolverlo.

È facile verificare che x=1 è la radice di questa equazione: .

Dividendo l'espressione al binomio x-1 , abbiamo:

Pertanto, le radici rimanenti si trovano dall'equazione :

Ora dal disegno è risultato chiaro che la figura G è racchiusa sopra la linea blu e sotto la linea rossa nell'intervallo . Pertanto, l'area richiesta sarà uguale a

Diamo un'occhiata a un altro esempio tipico.

Esempio.

Calcola l'area di una figura delimitata da curve e l'asse delle ascisse.

Soluzione.

Facciamo un disegno.

Questa è una normale funzione di potenza con un esponente di un terzo, il grafico della funzione può essere ottenuto dal grafico visualizzandolo simmetricamente rispetto all'asse x e sollevandolo di uno.

Trova i punti di intersezione di tutte le linee.

L'asse x ha l'equazione y=0 .

I grafici delle funzioni e y=0 si intersecano nel punto (0;0) poiché x=0 è l'unica vera radice dell'equazione.

Grafici delle funzioni e y=0 si intersecano in (2;0) , poiché x=2 è l'unica radice dell'equazione .

Grafici di funzione e intersecano nel punto (1;1) poiché x=1 è l'unica radice dell'equazione . Questa affermazione non è del tutto ovvia, ma è una funzione strettamente crescente, e - in senso stretto, quindi, l'equazione ha al massimo una radice.

Unica osservazione: in questo caso, per trovare l'area, dovrai utilizzare una formula del form . Cioè, le linee di delimitazione devono essere rappresentate come funzioni dell'argomento y, ma con una linea nera.

Definiamo i punti di intersezione delle rette.

Iniziamo con i grafici delle funzioni e:

Troviamo il punto di intersezione dei grafici delle funzioni e :

Resta da trovare il punto di intersezione delle rette e :

Come puoi vedere, i valori corrispondono.

Riassumere.

Abbiamo analizzato tutti i casi più comuni di trovare l'area di una figura delimitata da linee esplicitamente date. Per fare ciò, devi essere in grado di costruire linee su un piano, trovare i punti di intersezione delle linee e applicare la formula per trovare l'area, il che implica la capacità di calcolare determinati integrali.

Esempio 1 . Calcola l'area della figura delimitata da linee: x + 2y - 4 = 0, y = 0, x = -3 e x = 2

Costruiamo una figura (vedi Fig.) Costruiamo una linea retta x + 2y - 4 \u003d 0 lungo due punti A (4; 0) e B (0; 2). Esprimendo y in termini di x, otteniamo y \u003d -0,5x + 2. Secondo la formula (1), dove f (x) \u003d -0,5x + 2, a \u003d -3, b \u003d 2, noi trovare

S \u003d \u003d [-0,25 \u003d 11,25 mq. unità

Esempio 2 Calcola l'area della figura delimitata da linee: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 e y \u003d 0.

Soluzione. Costruiamo una figura.

Costruiamo una retta x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Costruiamo una retta x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Trova il punto di intersezione delle rette risolvendo il sistema di equazioni:

x = 2, y = 3; M(2; 3).

Per calcolare l'area richiesta, dividiamo il triangolo AMC in due triangoli AMN e NMC, poiché quando x cambia da A a N, l'area è limitata da una retta e quando x cambia da N a C, è una retta

Per il triangolo AMN abbiamo: ; y \u003d 0,5x + 2, ovvero f (x) \u003d 0,5x + 2, a \u003d - 4, b \u003d 2.

Per il triangolo NMC abbiamo: y = - x + 5, cioè f(x) = - x + 5, a = 2, b = 5.

Calcolando l'area di ciascuno dei triangoli e sommando i risultati, troviamo:

mq unità

mq unità

9 + 4, 5 = 13,5 mq. unità Verifica: = 0,5 AC = 0,5 mq. unità

Esempio 3 Calcola l'area di una figura delimitata da linee: y = x 2 , y = 0, x = 2, x = 3.

In questo caso occorre calcolare l'area di un trapezio curvilineo delimitato da una parabola y = x 2 , rette x \u003d 2 e x \u003d 3 e l'asse Ox (vedi Fig.) Secondo la formula (1), troviamo l'area di un trapezio curvilineo

= = 6kv. unità

Esempio 4 Calcola l'area di una figura delimitata da linee: y \u003d - x 2 + 4 e y = 0

Costruiamo una figura. L'area desiderata è racchiusa tra la parabola y \u003d - x 2 + 4 e asse Oh.

Trova i punti di intersezione della parabola con l'asse x. Supponendo y \u003d 0, troviamo x \u003d Poiché questa cifra è simmetrica rispetto all'asse Oy, calcoliamo l'area della figura situata a destra dell'asse Oy e raddoppiamo il risultato: \u003d + 4x] quadrato. unità 2 = 2 mq. unità

Esempio 5 Calcola l'area di una figura delimitata da linee: y 2 = x, yx = 1, x = 4

Qui è necessario calcolare l'area del trapezio curvilineo delimitata dal ramo superiore della parabola y 2 \u003d x, l'asse Ox e le linee rette x \u003d 1x \u003d 4 (vedi Fig.)

Secondo la formula (1), dove f(x) = a = 1 e b = 4, abbiamo = (= unità quadrate

Esempio 6 . Calcola l'area della figura delimitata da linee: y = sinx, y = 0, x = 0, x= .

L'area desiderata è limitata da una sinusoide a semionda e dall'asse Ox (vedi Fig.).

Abbiamo - cosx \u003d - cos \u003d 1 + 1 \u003d 2 metri quadrati. unità

Esempio 7 Calcola l'area della figura delimitata da linee: y \u003d - 6x, y \u003d 0 e x \u003d 4.

La figura si trova sotto l'asse Ox (vedi Fig.).

Pertanto, la sua area è trovata dalla formula (3)

= =

Esempio 8 Calcola l'area della figura delimitata dalle linee: y \u003d e x \u003d 2. Costruiremo la curva y \u003d per punti (vedi figura). Pertanto, l'area della figura è trovata dalla formula (4)

Esempio 9 .

X 2 + y 2 = R 2 .

Qui devi calcolare l'area delimitata dal cerchio x 2 + y 2 = R 2 , cioè l'area di una circonferenza di raggio r centrata nell'origine. Troviamo la quarta parte di quest'area, prendendo i limiti di integrazione da 0

dor; noi abbiamo: 1 = = [

Di conseguenza, 1 =

Esempio 10 Calcola l'area della figura delimitata da linee: y \u003d x 2 e y = 2x

Questa cifra è limitata dalla parabola y \u003d x 2 e retta y \u003d 2x (vedi Fig.) Per determinare i punti di intersezione delle linee date, risolviamo il sistema di equazioni: x 2 – 2x = 0x = 0 ex = 2

Usando la formula (5) per trovare l'area, otteniamo

= }