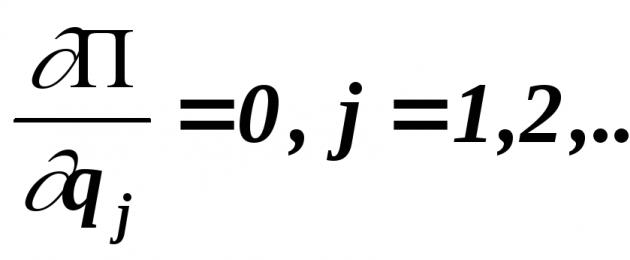Condizioni per l'equilibrio statico di un sistema meccanico. Statica

Un caso importante di moto dei sistemi meccanici è il loro moto oscillatorio. Le oscillazioni sono movimenti ripetuti di un sistema meccanico rispetto ad alcune delle sue posizioni, che si verificano più o meno regolarmente nel tempo. Il lavoro del corso considera il moto oscillatorio di un sistema meccanico rispetto alla posizione di equilibrio (relativa o assoluta).

Un sistema meccanico può oscillare per un periodo di tempo sufficientemente lungo solo in prossimità di una posizione di equilibrio stabile. Pertanto, prima di compilare le equazioni del moto oscillatorio, è necessario trovare le posizioni di equilibrio e studiarne la stabilità.

5.1. Condizioni di equilibrio per sistemi meccanici

Secondo il principio degli spostamenti possibili (l'equazione di base della statica), affinché un sistema meccanico, su cui sono imposti vincoli ideali, stazionari, confinanti e olonomi, sia in equilibrio, è necessario e sufficiente che tutte le forze generalizzate in questo sistema è uguale a zero:

dove Q j è la forza generalizzata corrispondente a j- oh coordinata generalizzata;

S - il numero di coordinate generalizzate nel sistema meccanico.

Se per il sistema in esame sono state compilate equazioni differenziali del moto sotto forma di equazioni di Lagrange del secondo tipo, per determinare le possibili posizioni di equilibrio è sufficiente eguagliare a zero le forze generalizzate e risolvere le equazioni risultanti rispetto a le coordinate generalizzate.

Se il sistema meccanico è in equilibrio in un campo di forze potenziali, dalle equazioni (5.1) otteniamo le seguenti condizioni di equilibrio:

(5.2)

Pertanto, nella posizione di equilibrio, l'energia potenziale ha un valore estremo. Non tutti gli equilibri definiti dalle formule di cui sopra possono essere realizzati nella pratica. A seconda del comportamento del sistema quando devia dalla posizione di equilibrio, si parla di stabilità o instabilità di questa posizione.

5.2. Stabilità dell'equilibrio

La definizione del concetto di stabilità di una posizione di equilibrio fu data alla fine del XIX secolo nelle opere dello scienziato russo A. M. Lyapunov. Diamo un'occhiata a questa definizione.

Per semplificare i calcoli, concorderemo ulteriormente sulle coordinate generalizzate q 1 , q 2 ,..., q S contare dalla posizione di equilibrio del sistema:

, dove

Una posizione di equilibrio si dice stabile se per un numero arbitrariamente piccolo  > 0 puoi trovare un altro numero  (  ) > 0 , che nel caso in cui i valori iniziali delle coordinate e delle velocità generalizzate non superino  :

i valori di coordinate e velocità generalizzate durante l'ulteriore movimento del sistema non supereranno 

.

In altre parole, la posizione di equilibrio del sistema q 1 = q 2 = ...= q S = 0 chiamato sostenibile, se è sempre possibile trovare valori iniziali così sufficientemente piccoli
, in cui il movimento del sistema
non lascerà alcun dato intorno arbitrariamente piccolo della posizione di equilibrio
. Per un sistema con un grado di libertà, il moto stabile del sistema può essere visualizzato nel piano delle fasi (Fig. 5.1). Per una posizione di equilibrio stabile, il movimento del punto rappresentativo, a partire dall'area [-  ,  ] , non andrà oltre la regione [-  ,  ] .

Viene chiamata la posizione di equilibrio stabile asintoticamente , se nel tempo il sistema si avvicinerà alla posizione di equilibrio, cioè

Determinare le condizioni per la stabilità di una posizione di equilibrio è un problema piuttosto complicato [4], quindi ci limitiamo al caso più semplice: lo studio della stabilità dell'equilibrio dei sistemi conservativi.

Condizioni sufficienti per la stabilità delle posizioni di equilibrio per tali sistemi sono determinate da Teorema di Lagrange - Dirichlet : la posizione di equilibrio di un sistema meccanico conservativo è stabile se, nella posizione di equilibrio, l'energia potenziale del sistema ha un minimo isolato .

L'energia potenziale di un sistema meccanico è determinata fino a una costante. Scegliamo questa costante in modo che nella posizione di equilibrio l'energia potenziale sia uguale a zero:

P(0)=0.

Allora, per un sistema con un grado di libertà, condizione sufficiente per l'esistenza di un minimo isolato, insieme alla condizione necessaria (5.2), è la condizione

Poiché nella posizione di equilibrio l'energia potenziale ha un minimo isolato e P(0) = 0 , quindi in qualche quartiere finito di questa posizione

Ï(q) > 0 .

Le funzioni che hanno un segno costante e sono uguali a zero solo per i valori zero di tutti i loro argomenti sono dette segno-definito. Pertanto, affinché la posizione di equilibrio di un sistema meccanico sia stabile, è necessario e sufficiente che, in prossimità di tale posizione, l'energia potenziale sia una funzione definita positivamente di coordinate generalizzate.

Per i sistemi lineari e per i sistemi che possono essere ridotti a lineari per piccoli scostamenti dalla posizione di equilibrio (linearizzati), l'energia potenziale può essere rappresentata come una forma quadratica di coordinate generalizzate [2, 3, 9]

(5.3)

dove - coefficienti di rigidità generalizzati.

Coefficienti generalizzati sono numeri costanti che possono essere determinati direttamente dall'espansione dell'energia potenziale in una serie o dai valori delle derivate seconde dell'energia potenziale rispetto alle coordinate generalizzate nella posizione di equilibrio:

(5.4)

Dalla formula (5.4) segue che i coefficienti di rigidezza generalizzati sono simmetrici rispetto agli indici

Affinché le condizioni sufficienti per la stabilità della posizione di equilibrio siano soddisfatte, l'energia potenziale deve essere una forma quadratica definita positiva delle sue coordinate generalizzate.

In matematica c'è Il criterio di Silvestro , che fornisce condizioni necessarie e sufficienti per la definitività positiva delle forme quadratiche: la forma quadratica (5.3) è definita positiva se il determinante composto dai suoi coefficienti e tutte le sue principali diagonali minori sono positive, cioè se i coefficienti c ij soddisferà le condizioni

D 1 = c 11 > 0,

D 2 =
> 0 ,

D S =
> 0,

In particolare, per un sistema lineare a due gradi di libertà, l'energia potenziale e le condizioni del criterio di Silvestro avranno la forma

P = (),

In modo simile, si possono studiare le posizioni di equilibrio relativo se, al posto dell'energia potenziale, viene introdotta l'energia potenziale del sistema ridotto [4].

Si consideri un punto materiale il cui moto è limitato in modo tale da avere un solo grado di libertà.

Ciò significa che la sua posizione può essere determinata utilizzando un unico valore, come la coordinata x. Un esempio è una sfera che scorre senza attrito lungo un filo fisso, immobile, piegato su un piano verticale (Fig. 26.1, a).

Un altro esempio è una sfera fissata all'estremità della molla, che scorre senza attrito sulla guida orizzontale (Fig. 26.2, a).

Sulla palla agisce una forza conservativa: nel primo caso è la forza di gravità, nel secondo è la forza elastica della molla deformata. I grafici dell'energia potenziale sono mostrati in fig. 26.1b e 26.2b.

Poiché le palline si muovono lungo il filo senza attrito, la forza con cui il filo agisce sulla palla è in entrambi i casi perpendicolare alla velocità della palla e, quindi, non agisce sulla palla. Pertanto, c'è una conservazione dell'energia:

Dalla (26.1) segue che l'energia cinetica può aumentare solo riducendo l'energia potenziale. Pertanto, se la palla è in uno stato tale che la sua velocità è zero e l'energia potenziale ha un valore minimo, senza influenza esterna non sarà in grado di muoversi, cioè sarà in equilibrio.

I minimi di U corrispondono ai valori sui grafici che sono uguali (in Fig. 26.2 c'è la lunghezza della squadra non deformata) La condizione per l'energia potenziale minima ha la forma

In accordo con t (22.4), la condizione (26.2) è equivalente al fatto che

(nel caso in cui U sia funzione di una sola variabile, ). Pertanto, la posizione corrispondente all'energia potenziale minima ha la proprietà che la forza che agisce sul corpo è zero.

Nel caso mostrato in Fig. 26.1, sono soddisfatte anche le condizioni (26.2) e (26.3) per x pari a (cioè per il massimo di U). Anche la posizione della palla determinata da questo valore sarà in equilibrio. Tuttavia, questo equilibrio, in contrasto con l'equilibrio a volontà, è instabile: è sufficiente spostare leggermente la palla fuori da questa posizione, poiché sorge una forza che rimuoverà la palla dalla posizione. Le forze che si generano quando la palla viene spostata dalla posizione di equilibrio stabile (per cui ) sono dirette in modo tale da tendere a riportare la palla nella posizione di equilibrio.

Conoscendo la forma t della funzione che esprime l'energia potenziale, si possono trarre alcune conclusioni sulla natura del moto della particella. Spieghiamo questo utilizzando il grafico mostrato in Fig. 26.1, b. Se l'energia totale ha il valore indicato in figura, la particella può spostarsi da verso o da verso l'infinito. La particella non può penetrare nella regione, poiché l'energia potenziale non può diventare maggiore dell'energia totale (se ciò accadesse, l'energia cinetica diventerebbe negativa). Pertanto, la regione è una barriera potenziale attraverso la quale la particella non può penetrare, avendo una data quantità di energia totale. L'area è chiamata pozzo potenziale.

Se una particella non può andare all'infinito durante il suo movimento, il movimento è chiamato finito. Se la particella può andare arbitrariamente lontano, il moto è chiamato infinito. Una particella in un pozzo di potenziale compie un moto finito. Anche il moto di una particella con un'energia totale negativa nel campo centrale delle forze attrattive sarà finito (si presume che l'energia potenziale svanisca all'infinito).

Come segue dall'esempio di studio del moto oscillatorio di un punto materiale, il moto proprio del sistema è causato da una forza elastica. In precedenza è stato dimostrato che la forza elastica appartiene al campo di forza potenziale. Pertanto, procedendo allo studio dei moti oscillatori naturali dei sistemi meccanici, si deve supporre che tali moti siano causati dalle forze del campo potenziale. Quindi, se il sistema ha s gradi di libertà, le sue forze generalizzate saranno scritte in termini di funzione di forza U o energia potenziale П nella forma:

Come risulta dallo studio del moto di un punto, le sue oscillazioni avvengono attorno alla posizione di equilibrio. Il moto oscillatorio del sistema avverrà anche vicino alla posizione del suo equilibrio, che è caratterizzato da condizioni.

Queste condizioni indicano che i moti oscillatori del sistema possono verificarsi in prossimità di posizioni caratterizzate da un estremo relativo della funzione di forza o energia potenziale del sistema. Tuttavia, il movimento oscillatorio del sistema non è possibile vicino a nessuna posizione di equilibrio.

Determinazione di una posizione di equilibrio stabile di un sistema meccanico

Lascia che il sistema meccanico sia costituito da punti materiali che sono in equilibrio sotto l'azione delle forze ad essi applicate. Diamo ai punti di questo sistema piccole deviazioni dalla posizione di equilibrio e piccole velocità iniziali. Quindi il sistema inizierà a muoversi. Se per tutto il tempo successivo alla violazione dell'equilibrio, i punti del sistema rimangono in prossimità della loro posizione di equilibrio, allora questa posizione è chiamata stabile. In caso contrario, l'equilibrio del sistema è detto instabile. Si può parlare di oscillazioni del sistema solo nel caso in cui queste oscillazioni avvengano in prossimità della posizione di equilibrio stabile. Se la posizione del sistema è instabile, cioè se, con una piccola deviazione dalla posizione di equilibrio e basse velocità, il sistema si allontana ulteriormente da essa, allora non si può parlare di oscillazioni del sistema vicino a questa posizione. Pertanto, lo studio delle oscillazioni del sistema dovrebbe iniziare con la definizione di un criterio per la stabilità dell'equilibrio di un sistema meccanico.

Criterio di stabilità dell'equilibrio per un sistema meccanico conservativo

Il criterio di stabilità per l'equilibrio di un sistema conservativo è stabilito dal teorema di Lagrange-Dirichlet, che è il seguente: se un sistema meccanico ha vincoli stazionari ed è conservativo, e se nella posizione di equilibrio di questo sistema la sua energia potenziale ha un minimo (cioè, la funzione di forza ha un massimo), quindi l'equilibrio del sistema è stabile.

Dimostriamo questo teorema. Lascia che la posizione del sistema meccanico sia determinata da coordinate generalizzate che vengono misurate dalla posizione di equilibrio. Allora in questa posizione avremo:

Le quantità possono essere considerate come coordinate di un punto nello spazio -dimensionale. Quindi ogni posizione del sistema corrisponderà a un certo punto di questo spazio. In particolare, l'origine delle coordinate O corrisponderà alla posizione di equilibrio.

L'energia potenziale P sarà contata dalla posizione di equilibrio, assumendo che in questa posizione ciò non violi la generalità del ragionamento, poiché l'energia potenziale è determinata fino a una costante arbitraria.

Prendiamo un numero positivo e descriviamo dal punto O una sfera di raggio . La regione delimitata da questa sfera sarà indicata con Il numero sarà considerato arbitrario, ma sufficientemente piccolo. Quindi, per qualsiasi punto sul confine della regione D, vale la seguente disuguaglianza:

poiché nel punto O la funzione P è uguale a zero e ha un minimo.

Sia il valore più piccolo di П sul confine della regione D uguale a Р. Quindi per qualsiasi punto appartenente a questo confine, avremo

Portiamo ora fuori equilibrio il sistema dando ai suoi punti deviazioni iniziali così piccole e velocità iniziali così piccole che valgono le disuguaglianze:

dove sono i valori iniziali di energia potenziale e cinetica. Allora avremo:

Ma con un ulteriore movimento del sistema, dovuto alla legge di conservazione dell'energia meccanica, che vale per i sistemi conservativi con vincoli stazionari, l'uguaglianza sarà soddisfatta.

È noto che per l'equilibrio di un sistema con vincoli ideali è necessario e sufficiente che o. (7)

Poiché le variazioni delle coordinate generalizzate sono indipendenti tra loro e, nel caso generale, non sono uguali a zero, è necessario che
,
,…,
.

Per l'equilibrio di un sistema con vincoli olonomi confinanti, stazionari, ideali, è necessario e sufficiente che tutte le forze generalizzate corrispondenti alle coordinate generalizzate scelte siano uguali a zero.

Il caso delle forze potenziali:

Se il sistema è in un campo di forza potenziale, allora

,
,…,

,
,…,

Cioè, le posizioni di equilibrio del sistema possono essere solo per quei valori di coordinate generalizzate per cui la forza funziona u ed energia potenziale P avere valori estremi ( max o min).

Il concetto di stabilità di equilibrio.

Determinate le posizioni in cui il sistema può trovarsi in equilibrio, è possibile determinare quali di queste posizioni sono realizzabili e quali irrealizzabili, cioè determinare quale posizione è stabile e quale instabile.

In generale, il necessario segno di stabilità dell'equilibrio secondo Lyapunov può essere formulato come segue:

Portiamo il sistema fuori dalla posizione di equilibrio riportando piccoli valori di modulo delle coordinate generalizzate e le loro velocità. Se, dopo un'ulteriore considerazione del sistema, le coordinate generalizzate e le loro velocità rimangono piccoli valori di modulo, cioè il sistema non devia molto dalla posizione di equilibrio, allora tale posizione di equilibrio è stabile.

Condizione sufficiente per la stabilità di un equilibrio il sistema è determinato Teorema di Lagrange-Dirichl :

Se nella posizione di equilibrio di un sistema meccanico con connessioni ideali l'energia potenziale ha un valore minimo, allora tale posizione di equilibrio è stabile.

,
- sostenibile.

DEFINIZIONE

equilibrio sostenibile- questo è un equilibrio in cui il corpo, sbilanciato e abbandonato a se stesso, ritorna nella sua posizione precedente.

Ciò accade se, con un leggero spostamento del corpo in qualsiasi direzione dalla posizione iniziale, la risultante delle forze agenti sul corpo diventa diversa da zero e si dirige verso la posizione di equilibrio. Ad esempio, una palla che giace sul fondo di una cavità sferica (Fig. 1a).

DEFINIZIONE

Equilibrio instabile- questo è un equilibrio in cui il corpo, tolto dalla posizione di equilibrio e lasciato a se stesso, si discosterà ancora di più dalla posizione di equilibrio.

In questo caso, con un piccolo spostamento del corpo dalla posizione di equilibrio, la risultante delle forze applicate ad esso è diversa da zero ed è diretta dalla posizione di equilibrio. Un esempio è una palla situata alla sommità di una superficie sferica convessa (Fig. 1 b).

DEFINIZIONE

Equilibrio indifferente- questo è un equilibrio in cui il corpo, sbilanciato e abbandonato a se stesso, non cambia posizione (stato).

In questo caso, con piccoli spostamenti del corpo dalla sua posizione originaria, la risultante delle forze applicate al corpo rimane uguale a zero. Ad esempio, una palla che giace su una superficie piana (Fig. 1, c).

Fig. 1. Diversi tipi di equilibrio corporeo su un supporto: a) equilibrio stabile; b) equilibrio instabile; c) equilibrio indifferente.

Equilibrio statico e dinamico dei corpi

Se, a causa dell'azione delle forze, il corpo non riceve accelerazione, può essere fermo o muoversi uniformemente in linea retta. Si può quindi parlare di equilibrio statico e dinamico.

DEFINIZIONE

Equilibrio statico- questo è un tale equilibrio quando, sotto l'azione delle forze applicate, il corpo è a riposo.

equilibrio dinamico- questo è un tale equilibrio quando, sotto l'azione delle forze, il corpo non cambia il suo movimento.

In uno stato di equilibrio statico è una lanterna sospesa su cavi, qualsiasi struttura edilizia. Come esempio di equilibrio dinamico, possiamo considerare una ruota che rotola su una superficie piana in assenza di forze di attrito.