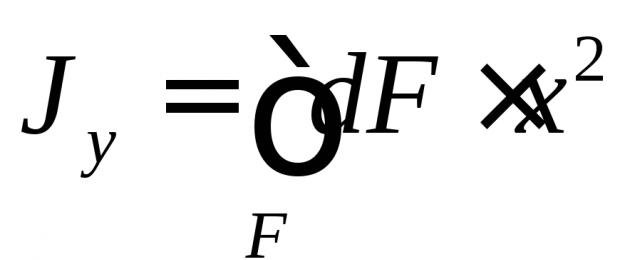Momento d'inerzia misto. Momento d'inerzia centrifugo

Momento d'inerzia assiale pari alla somma prodotti di aree elementari per il quadrato della distanza dall'asse corrispondente.

(8)

Il segno è sempre "+".

Non può essere uguale a 0.

Proprietà: Assume il valore minimo quando si trova il punto di intersezione assi coordinati coincide con il baricentro della sezione.

Il momento d'inerzia assiale di una sezione viene utilizzato nei calcoli di resistenza, rigidità e stabilità.

1.3. Momento d'inerzia polare della sezione Jρ

(9)

Relazione tra momento d'inerzia polare e assiale:

(10)

(11)

Il momento d'inerzia polare della sezione è pari alla somma momenti assiali.

Proprietà:

quando gli assi vengono ruotati in qualsiasi direzione, uno dei momenti d'inerzia assiali aumenta e l'altro diminuisce (e viceversa). La somma dei momenti d'inerzia assiali rimane costante.

1.4. Momento d'inerzia centrifugo della sezione Jxy

Il momento d'inerzia centrifugo della sezione è pari alla somma dei prodotti delle aree elementari e delle distanze dai due assi

(12)

Unità di misura [cm 4 ], [mm 4 ].

Segno "+" o "-".

, se gli assi delle coordinate sono assi di simmetria (esempio - trave a I, rettangolo, cerchio), o uno degli assi delle coordinate coincide con l'asse di simmetria (esempio - canale).

Pertanto, per le figure simmetriche il momento d'inerzia centrifugo è 0.

Assi coordinati tu E v , passanti per il baricentro della sezione, attorno alla quale il momento centrifugo è pari a zero, vengono chiamati i principali assi centrali di inerzia della sezione. Sono detti principali perché il momento centrifugo ad essi relativo è nullo, e centrali perché passano per il baricentro della sezione.

Per sezioni non simmetriche rispetto agli assi X O sì , ad esempio, all'angolo, non sarà uguale a zero. Per queste sezioni viene determinata la posizione degli assi tu E v calcolando l'angolo di rotazione degli assi X E sì

(13)

Momento centrifugo rispetto agli assi tu E v -

Formula per determinare i momenti di inerzia assiale rispetto agli assi centrali principali tu E v :

(14)

Dove
- momenti di inerzia assiale rispetto agli assi centrali,

- momento d'inerzia centrifugo rispetto agli assi centrali.

1.5. Momento d'inerzia attorno ad un asse parallelo a quello centrale (teorema di Steiner)

Teorema di Steiner:

Il momento d'inerzia attorno ad un asse parallelo a quello centrale è uguale al momento d'inerzia assiale centrale più il prodotto dell'area dell'intera figura e il quadrato della distanza tra gli assi.

(15)

Dimostrazione del teorema di Steiner.

Secondo la fig. 5 distanza A al sito elementare dF

Sostituendo il valore A nella formula otteniamo:

Termine
, poiché il punto C è il baricentro della sezione (vedi proprietà dei momenti statici della sezione rispetto agli assi centrali).

Per un rettangolo con altezzaH e larghezzaB :

Momento d'inerzia assiale:

Momento flettente:

il momento resistente a flessione è pari al rapporto tra il momento d'inerzia e la distanza della fibra più distante dalla linea neutra:

Perché
, Quello

Per un cerchio:

Momento d'inerzia polare:

Momento d'inerzia assiale:

Momento torcente:

Perché
, Quello

Momento flettente:

Esempio 2. Determinare il momento di inerzia di una sezione trasversale rettangolare attorno all'asse centrale CON X .

Soluzione. Dividiamo l'area del rettangolo in rettangoli elementari con dimensioni B (larghezza) e dy (altezza). Quindi l'area di tale rettangolo (ombreggiata in Fig. 6) è uguale a dF=amico. Calcoliamo il valore del momento d'inerzia assiale J X

Per analogia scriviamo

- momento d'inerzia assiale della sezione rispetto alla centrale

Momento d'inerzia centrifugo

, poiché gli assi CON X e C sì sono assi di simmetria.

Esempio 3. Determinare il momento d'inerzia polare di una sezione trasversale circolare.

Soluzione. Dividiamo il cerchio in anelli di spessore infinitamente sottili
raggio , l'area di tale anello
. Sostituendo il valore
Integrando nell'espressione del momento d'inerzia polare, otteniamo

Tenendo conto dell'uguaglianza dei momenti assiali di una sezione circolare
E

, otteniamo

I momenti di inerzia assiale dell'anello sono uguali

Con– il rapporto tra il diametro dell'apertura e il diametro esterno dell'albero.

Lezione n. 2 “Assi principali epunti principaliinerzia

Consideriamo come cambiano i momenti di inerzia quando gli assi delle coordinate vengono ruotati. Supponiamo che siano dati i momenti di inerzia di una certa sezione rispetto agli assi 0 X, 0A(non necessariamente centrale) - ,- momenti d'inerzia assiale della sezione. È necessario determinare ,- momenti assiali relativi agli assi tu,v, ruotato rispetto al primo sistema di un angolo
(Fig. 8)

Poiché la proiezione della linea spezzata OABC è uguale alla proiezione della linea finale, troviamo:

(15)

Escludiamo u e v nelle espressioni dei momenti di inerzia:

(18)

Consideriamo le prime due equazioni. Sommandoli termine per termine, otteniamo

Pertanto, la somma dei momenti di inerzia assiale attorno a due assi reciprocamente perpendicolari non dipende dall'angolo
e rimane costante quando gli assi vengono ruotati. Notiamo allo stesso tempo che

Dove - distanza dall'origine delle coordinate al sito elementare (vedi Fig. 5). Così

Dove - il già familiare momento di inerzia polare:

Determiniamo il momento d'inerzia assiale del cerchio rispetto al diametro.

Poiché a causa della simmetria
ma, come sai,

Pertanto, per un cerchio

Con una modifica dell'angolo di rotazione degli assi
valori del momento E cambia, ma l’importo rimane lo stesso. Pertanto esiste un tale significato
, in cui uno dei momenti d'inerzia raggiunge il suo valore massimo, mentre l'altro momento assume un valore minimo. Differenziare l'espressione per angolo
e uguagliando la derivata a zero, troviamo

(19)

A questo valore dell'angolo
uno dei momenti assiali sarà il più grande e l'altro sarà il più piccolo. Allo stesso tempo, il momento d'inerzia centrifugo
nulla, cosa che può essere facilmente verificata uguagliando a zero la formula del momento d'inerzia centrifugo
.

Vengono chiamati assi attorno ai quali il momento d'inerzia centrifugo è zero e i momenti assiali assumono valori estremi principaleassi. Se sono anche centrali (il punto di origine coincide con il baricentro della sezione), allora si chiamano assi centrali principali (tu; v). Si chiamano momenti assiali di inerzia rispetto agli assi principali principali momenti di inerzia -E

E il loro valore è determinato dalla seguente formula:

(20)

Il segno più corrisponde al momento d'inerzia massimo, il segno meno al minimo.

C'è un'altra caratteristica geometrica: raggio di rotazione sezioni. Questo valore viene spesso utilizzato nelle conclusioni teoriche e nei calcoli pratici.

Ad esempio, il raggio di rotazione della sezione rispetto a un determinato asse 0 X , si chiama quantità , determinato dall’uguaglianza

(21)

F – area della sezione trasversale,

- momento d'inerzia assiale della sezione,

Dalla definizione segue che il raggio di rotazione è uguale alla distanza dall'asse 0 X al punto in cui l'area della sezione trasversale F dovrebbe essere concentrata (condizionatamente) in modo che il momento di inerzia di questo punto sia uguale al momento di inerzia dell'intera sezione. Conoscendo il momento d'inerzia della sezione e la sua area, si può ricavare il raggio di rotazione relativo all'asse 0 X:

(22)

Vengono chiamati i raggi di rotazione corrispondenti agli assi principali raggi d’inerzia principali e sono determinati dalle formule

(23)

Lezione 3. Torsione di aste di sezione circolare.

Se tracciamo gli assi coordinati passanti per il punto O, allora rispetto a questi assi i momenti d'inerzia centrifughi (o prodotti di inerzia) sono le quantità definite dalle uguaglianze:

dove sono le masse dei punti; - le loro coordinate; è ovvio che ecc.

Per i corpi solidi, le formule (10), per analogia con la (5), assumono la forma

A differenza di quelli assiali, i momenti d'inerzia centrifughi possono essere quantità sia positive che negative e, in particolare, con un certo modo di scegliere gli assi, possono diventare nulli.

Assi principali di inerzia. Consideriamo un corpo omogeneo avente un asse di simmetria. Disegniamo gli assi delle coordinate Oxyz in modo che l'asse sia diretto lungo l'asse di simmetria (Fig. 279). Quindi, per simmetria, ad ogni punto di un corpo con massa mk e coordinate corrisponderà un punto con indice diverso, ma con la stessa massa e con coordinate pari a . Di conseguenza, otteniamo che poiché in queste somme tutti i termini sono a due a due identici in grandezza e opposti in segno; da qui, tenendo conto delle uguaglianze (10), troviamo:

Pertanto, la simmetria nella distribuzione delle masse rispetto all'asse z è caratterizzata dall'annullamento di due momenti di inerzia centrifughi. L'asse Oz, per il quale i momenti d'inerzia centrifughi che contengono il nome di questo asse nei loro indici sono pari a zero, è chiamato asse d'inerzia principale del corpo per il punto O.

Da quanto sopra ne consegue che se un corpo ha un asse di simmetria, allora questo asse è l'asse di inerzia principale del corpo per uno qualsiasi dei suoi punti.

L'asse principale di inerzia non è necessariamente l'asse di simmetria. Consideriamo un corpo omogeneo che abbia un piano di simmetria (nella Fig. 279 il piano di simmetria del corpo è il piano ). Disegniamo alcuni assi e un asse ad essi perpendicolare in questo piano. Quindi, per simmetria, ogni punto con massa e coordinate corrisponderà a un punto con la stessa massa e coordinate pari a . Di conseguenza, come nel caso precedente, troviamo che o da dove segue che l'asse è l'asse di inerzia principale per il punto O. Pertanto, se un corpo ha un piano di simmetria, allora qualsiasi asse perpendicolare a questo piano sarà l'asse principale di inerzia del corpo per il punto O, in cui l'asse interseca il piano.

Le uguaglianze (11) esprimono le condizioni secondo cui l'asse è l'asse principale di inerzia del corpo per il punto O (origine).

Allo stesso modo, se allora l'asse Oy sarà l'asse d'inerzia principale per il punto O. Pertanto, se tutti i momenti di inerzia centrifughi sono uguali a zero, cioè

quindi ciascuno degli assi delle coordinate è l'asse di inerzia principale del corpo per il punto O (origine).

Ad esempio, nella Fig. 279 tutti e tre gli assi sono gli assi principali di inerzia per il punto O (l'asse è l'asse di simmetria e gli assi Ox e Oy sono perpendicolari ai piani di simmetria).

I momenti di inerzia di un corpo rispetto agli assi di inerzia principali sono chiamati momenti di inerzia principali del corpo.

Gli assi principali di inerzia costruiti per il centro di massa del corpo sono chiamati assi centrali principali di inerzia del corpo. Da quanto sopra dimostrato ne consegue che se un corpo ha un asse di simmetria, allora questo asse è uno dei principali assi centrali di inerzia del corpo, poiché su questo asse giace il centro di massa. Se il corpo ha un piano di simmetria, allora l'asse perpendicolare a questo piano e passante per il centro di massa del corpo sarà anche uno dei principali assi centrali di inerzia del corpo.

Negli esempi forniti sono stati considerati corpi simmetrici, il che è sufficiente per risolvere i problemi che incontreremo. Tuttavia si può dimostrare che attraverso qualsiasi punto di qualsiasi corpo si può tracciare, secondo almeno, tre assi reciprocamente perpendicolari per i quali saranno soddisfatte le uguaglianze (11), ovvero quali saranno gli assi di inerzia principali del corpo per questo punto.

Gioca il concetto degli assi principali di inerzia ruolo importante nella dinamica del corpo rigido. Se gli assi delle coordinate Oxyz sono diretti lungo di essi, tutti i momenti d'inerzia centrifughi diventano zero e le equazioni o formule corrispondenti vengono notevolmente semplificate (vedere § 105, 132). A questo concetto si associa anche la soluzione di problemi sull'equazione dinamica dei corpi rotanti (vedi § 136), sul centro d'urto (vedi § 157), ecc.

Il momento d'inerzia centrifugo attorno a due assi coordinati è chiamato la somma dei prodotti della massa di ciascun punto del corpo e delle coordinate lungo gli assi corrispondenti.

Se un corpo ha un asse di simmetria, allora il momento d'inerzia centrifugo del corpo è zero e gli assi y e x sono i principali

17. Teorema di Huygens-Steiner sul calcolo dei momenti rispetto ad assi paralleli.

Momento di inerzia solido relativo ad un asse non passante per il baricentro è pari alla somma dei momenti d'inerzia relativi all'asse centrale passante per il baricentro e parallelo a quello dato e il prodotto della massa corporea per il quadrato della distanza tra gli assi.

JC è il momento d'inerzia noto attorno ad un asse passante per il centro di massa del corpo,

J è il momento di inerzia desiderato rispetto all'asse parallelo,

m - peso corporeo,

d è la distanza tra gli assi indicati.

18. Calcolo dei momenti d'inerzia di corpi omogenei: lastra sottile, asta sottile, anello, cilindro, cono.

Asta sottile: Cilindro sottile:

Piatto sottile: Cono:

Anello sottile: Palla:

Calcolo dei momenti di inerzia attorno ad assi arbitrari.

Permette di trovare il momento di inerzia relativo a qualsiasi asse passante per gli assi coordinati e i componenti del carbone

Con questi assi, attraverso i valori dei momenti di inerzia assiale e centrifugo di questi assi.

Ellissoide d'inerzia. Assi centrali di inerzia. Proprietà estreme dei momenti di inerzia.

Il centro dell'ellissoide è nell'origine.

I 3 assi di simmetria dell'ellissoide sono chiamati assi di inerzia principali, i momenti di inerzia attorno agli assi principali sono chiamati momenti di inerzia principali.

Se prendiamo gli assi di inerzia principali come assi delle coordinate, i momenti di inerzia centrifughi attorno a questi assi saranno pari a zero.

ELLISSOIDE D'INERZIA - una superficie che caratterizza la distribuzione dei momenti di inerzia di un corpo rispetto a un raggio di assi che passa attraverso un punto fisso O. E. e. come geom. la posizione delle estremità dei segmenti OK = 1/ disposti lungo Ol dal punto O, dove Ol è qualsiasi asse passante per il punto O; Il è il momento di inerzia del corpo rispetto a questo asse (Fig.). Centro E. e. coincide con il punto O e la sua equazione negli assi coordinati disegnati arbitrariamente Oxyz ha la forma

dove Ix, Iy, Iz sono assiali e Ixу, Iyz, Lzx sono i momenti di inerzia centrifughi del corpo rispetto agli assi coordinati indicati. A sua volta, conoscendo E. e. per il punto O, puoi trovare il momento d'inerzia attorno a qualsiasi asse Ol passante per questo punto dall'uguaglianza Il = 1/R2, misurando la distanza R = OK nelle unità corrispondenti.

Sentiamo spesso le espressioni: “è inerte”, “si muove per inerzia”, “momento di inerzia”. IN significato figurato la parola “inerzia” può essere interpretata come mancanza di iniziativa e di azione. A noi interessa il significato diretto.

Cos'è l'inerzia

Secondo definizione inerzia in fisica è la capacità dei corpi di mantenere uno stato di quiete o di movimento in assenza di forze esterne.

Se tutto è chiaro con il concetto stesso di inerzia a livello intuitivo, allora momento di inerzia– una domanda separata. D'accordo, è difficile immaginare nella tua mente di cosa si tratta. In questo articolo imparerai come risolvere i problemi di base sull'argomento "Momento di inerzia".

Determinazione del momento d'inerzia

Dal corso scolastico lo si sa massa: misura dell'inerzia di un corpo. Se spingiamo due carri di massa diversa, sarà più difficile fermare quello più pesante. Cioè, maggiore è la massa, maggiore è l'influenza esterna necessaria per modificare il movimento del corpo. Quanto considerato si applica al movimento traslatorio, quando il carrello dell'esempio si muove in linea retta.

Per analogia con massa e movimento in avanti il momento d'inerzia è una misura dell'inerzia di un corpo durante il movimento rotatorio attorno ad un asse.

Momento di inerzia– scalare quantità fisica, una misura dell'inerzia di un corpo quando ruota attorno ad un asse. Indicato con la lettera J e nel sistema SI misurato in chilogrammi per metro quadrato.

Come calcolare il momento di inerzia? Mangiare formula generale, che viene utilizzato in fisica per calcolare il momento di inerzia di qualsiasi corpo. Se un corpo viene spezzato in pezzi infinitesimali dotati di massa dm , allora il momento d'inerzia sarà uguale alla somma dei prodotti di queste masse elementari per il quadrato della distanza dall'asse di rotazione.

Questa è la formula generale del momento d'inerzia in fisica. Per punto materiale masse M , ruotando attorno ad un asse a distanza R da esso, questa formula assume la forma:

Il teorema di Steiner

Da cosa dipende il momento di inerzia? Dalla massa, posizione dell'asse di rotazione, forma e dimensione del corpo.

Il teorema di Huygens-Steiner è un teorema molto importante che viene spesso utilizzato nella risoluzione dei problemi.

A proposito! Per i nostri lettori ora c'è uno sconto del 10% su qualsiasi tipo di lavoro

Il teorema di Huygens-Steiner afferma:

Il momento di inerzia di un corpo rispetto a un asse arbitrario è uguale alla somma del momento di inerzia del corpo rispetto a un asse passante per il centro di massa parallelo a un asse arbitrario e il prodotto della massa corporea per il quadrato della distanza tra gli assi.

Per coloro che non vogliono integrarsi costantemente nella risoluzione dei problemi relativi alla ricerca del momento di inerzia, presentiamo un disegno che indica i momenti di inerzia di alcuni corpi omogenei che si incontrano spesso nei problemi:

Un esempio di risoluzione di un problema per trovare il momento di inerzia

Diamo un'occhiata a due esempi. Il primo compito è trovare il momento di inerzia. Il secondo compito è utilizzare il teorema di Huygens-Steiner.

Problema 1. Trova il momento d'inerzia di un disco omogeneo di massa me raggio R. L'asse di rotazione passa per il centro del disco.

Soluzione:

Dividiamo il disco in anelli infinitamente sottili, il cui raggio varia da 0 A R e considera uno di questi anelli. Sia il suo raggio R, e massa – dm. Allora il momento di inerzia dell'anello è:

La massa dell'anello può essere rappresentata come:

Qui dz– altezza dell'anello. Sostituiamo nella formula il momento d'inerzia con la massa e integriamo:

Il risultato fu una formula per il momento di inerzia di un disco o cilindro assolutamente sottile.

Problema 2. Sia ancora un disco di massa me raggio R. Ora dobbiamo trovare il momento d'inerzia del disco rispetto all'asse passante per il centro di uno dei suoi raggi.

Soluzione:

Il momento d'inerzia del disco rispetto all'asse passante per il centro di massa è noto dal problema precedente. Applichiamo il teorema di Steiner e troviamo:

A proposito, sul nostro blog puoi trovare altri materiali utili sulla fisica e sulla risoluzione dei problemi.

Ci auguriamo che troverai qualcosa di utile per te nell'articolo. Se sorgono difficoltà nel processo di calcolo del tensore d'inerzia, non dimenticare il servizio agli studenti. I nostri specialisti ti consiglieranno su qualsiasi problema e ti aiuteranno a risolverlo in pochi minuti.

Se m = 1, n = 1, otteniamo la caratteristica

che si chiama momento d'inerzia centrifugo.

Momento d'inerzia centrifugo rispetto agli assi coordinati – la somma dei prodotti delle aree elementari dA alle loro distanze da questi assi, prese su tutta l'area della sezione trasversale UN.

Se almeno uno degli assi sì O zè l'asse di simmetria della sezione, il momento d'inerzia centrifugo di tale sezione rispetto a tali assi è pari a zero (poiché in questo caso ogni valore positivo z·y·dA possiamo mettere in corrispondenza esattamente uguale, ma negativa, dall'altra parte dell'asse di simmetria della sezione, vedi figura).

Consideriamo ulteriori caratteristiche geometriche che possono essere ricavate da quelle principali elencate e che vengono spesso utilizzate anche nei calcoli di resistenza e rigidezza.

Momento d'inerzia polare

Momento d'inerzia polare Jp nominare la caratteristica

D'altra parte,

Momento d'inerzia polare(relativo ad un dato punto) – la somma dei prodotti delle aree elementari dA dai quadrati delle loro distanze a questo punto, occupata l'intera area della sezione trasversale UN.

La dimensione dei momenti di inerzia è m 4 in SI.

Momento di resistenza

Momento di resistenza rispetto ad un asse - un valore pari al momento di inerzia rispetto allo stesso asse diviso per la distanza ( ymax O zmassimo) al punto più distante da questo asse

La dimensione dei momenti resistenti è m 3 in SI.

Raggio di inerzia

Raggio di inerzia sezione relativa ad un certo asse è chiamata valore determinato dalla relazione:

I raggi di rotazione sono espressi in unità SI di m.

Commento: le sezioni trasversali degli elementi delle strutture moderne rappresentano spesso una certa composizione di materiali con diversa resistenza alla deformazione elastica, caratterizzata, come noto da un corso di fisica, dal modulo di Young E. Nel caso più generale di una sezione d'urto disomogenea, il modulo di Young è funzione continua coordinate dei punti della sezione, cioè E = E(z, y). Pertanto, la rigidezza di una sezione disomogenea nelle proprietà elastiche è caratterizzata da caratteristiche più complesse delle caratteristiche geometriche di una sezione omogenea, cioè quelle elastico-geometriche della forma

2.2. Calcolo delle caratteristiche geometriche di figure semplici

Sezione rettangolare

Determiniamo il momento d'inerzia assiale del rettangolo rispetto all'asse z. Dividiamo l'area del rettangolo in aree elementari con dimensioni B(larghezza) e dy(altezza). Quindi l'area di un rettangolo così elementare (ombreggiato) è uguale a dA = bdy. Sostituendo il valore dA nella prima formula, otteniamo

Per analogia, scriviamo il momento assiale attorno all'asse A:

Momenti resistenti assiali di un rettangolo:

;

In modo simile si possono ottenere caratteristiche geometriche per altre figure semplici.

Sezione rotonda

È conveniente trovarlo prima momento d'inerzia polare J p .

Quindi, dato che per un cerchio J z = J y, UN J p = J z + J y, troveremo Jz =Jy = Jp / 2.

Dividiamo il cerchio in anelli infinitesimi di spessore dρ e raggio ρ ; area di un tale anello dA = 2 ∙ π ∙ ρ ∙ dρ. Sostituendo l'espressione con dA in un'espressione per Jp e integrando, otteniamo

2.3. Calcolo dei momenti d'inerzia rispetto ad assi paralleli

z E sì:

È necessario determinare i momenti di inerzia di questa sezione rispetto ai “nuovi” assi z1 E sì 1, paralleli a quelli centrali e distanziati da essi a distanza UN E B rispettivamente:

Coordinate di qualsiasi punto nel “nuovo” sistema di coordinate z101y1 può essere espresso tramite coordinate nei “vecchi” assi z E sì COSÌ:

Dagli assi z E sì– momento centrale, quindi statico Sz = 0.

Infine possiamo scrivere le formule di “transizione” per il trasferimento parallelo degli assi:

Tieni presente che le coordinate UN E B devono essere sostituiti tenendo conto del loro segno (nel sistema di coordinate z101y1).

2.4. Calcolo dei momenti di inerzia durante la rotazione degli assi delle coordinate

Siano noti i momenti di inerzia di una sezione arbitraria rispetto agli assi centrali z, y:

; ;

Giriamo gli assi z, sì ad angolo α in senso antiorario, considerando positivo l'angolo di rotazione degli assi in questa direzione.

È necessario determinare i momenti di inerzia relativi ai “nuovi” assi (ruotati). z1 E sì 1:

Coordinate del sito elementare dA nel “nuovo” sistema di coordinate z10y1 può essere espresso tramite coordinate nei “vecchi” assi come questo:

Sostituiamo questi valori nelle formule per i momenti di inerzia nei “nuovi” assi e integriamo termine per termine:

Dopo aver effettuato trasformazioni simili con le restanti espressioni, annoteremo finalmente le formule di “transizione” durante la rotazione degli assi delle coordinate:

Nota che se aggiungiamo le prime due equazioni, otteniamo

cioè il momento polare di inerzia è la quantità invariante(in altre parole, invariato durante la rotazione degli assi delle coordinate).

2.5. Assi principali e momenti principali di inerzia

Finora abbiamo considerato le caratteristiche geometriche delle sezioni in sistema arbitrario coordinate, tuttavia, di maggiore interesse pratico è il sistema di coordinate in cui la sezione è descritta dal minor numero di caratteristiche geometriche. Questo sistema di coordinate “speciale” è specificato dalla posizione degli assi principali della sezione. Introduciamo i concetti: assi principali E principali momenti di inerzia.

Assi principali– due assi tra loro perpendicolari, rispetto ai quali il momento d’inerzia centrifugo è nullo, mentre i momenti d’inerzia assiali assumono valori estremi (massimo e minimo).

Vengono chiamati gli assi principali passanti per il baricentro della sezione assi centrali principali.

I momenti d'inerzia rispetto agli assi principali si chiamano principali momenti di inerzia.

Gli assi centrali principali sono solitamente indicati da lettere tu E v; principali momenti di inerzia – J u E Jv(per definizione Juv = 0).

Deriviamo le espressioni che ci permettono di trovare la posizione degli assi principali e l'entità dei principali momenti di inerzia. Sapendolo Juv= 0, usiamo l'equazione (2.3):

Angolo α 0 definisce la posizione degli assi principali rispetto agli eventuali assi centrali z E sì. Angolo α 0 depositato tra l'asse z e asse tu ed è considerato positivo in senso antiorario.

Si noti che se una sezione ha un asse di simmetria, allora, in conformità con la proprietà del momento d'inerzia centrifugo (vedere sezione 2.1, paragrafo 4), tale asse sarà sempre l'asse principale della sezione.

Angolo escluso α nelle espressioni (2.1) e (2.2) utilizzando (2.4), otteniamo formule per determinare i principali momenti di inerzia assiale:

Scriviamo la regola: l'asse massimo forma sempre un angolo minore con quello degli assi (zoy) rispetto ai quali il momento d'inerzia ha valore maggiore.

2.6. Forme razionali delle sezioni trasversali

Tensioni normali in un punto arbitrario nella sezione trasversale di una trave curva dritta sono determinati dalla formula:

, (2.5)

Dove M– momento flettente nella sezione trasversale considerata; A– la distanza dal punto considerato all'asse centrale principale perpendicolare al piano d'azione del momento flettente; Jx– il momento d’inerzia centrale principale della sezione.

Le maggiori sollecitazioni normali di trazione e compressione in una data sezione trasversale si verificano nei punti più lontani dall'asse neutro. Sono determinati dalle formule:

; ,

Dove alle 1 E alle 2– distanze dall’asse centrale principale X alle fibre stirate e compresse più distanti.

Per travi in ​​materiali plastici, quando [σ p ] = [σ c ] ([σ p ], [σ c ] sono le tensioni ammissibili per il materiale della trave rispettivamente in trazione e compressione), le sezioni simmetriche rispetto all'asse centrale vengono utilizzati gli assi In questo caso la condizione di forza ha la forma:

≤ [σ], (2.6)

Dove L x = J x / y max– momento resistente della sezione trasversale della trave rispetto all'asse centrale principale; ymax = h/2(H– altezza della sezione); M massimo– il momento flettente maggiore in valore assoluto; [σ] – sollecitazione di flessione ammissibile del materiale.

Oltre alla condizione di resistenza, la trave deve soddisfare anche la condizione di economia. Le più economiche sono quelle forme di sezione trasversale per le quali si ottiene il momento resistente maggiore con la minima quantità di materiale (o con la sezione trasversale più piccola). Affinché la forma della sezione sia razionale è necessario, se possibile, distribuire la sezione lontano dall'asse centrale principale.

Ad esempio, una trave a I standard è circa sette volte più resistente e trenta volte più rigida di una trave quadrata della stessa sezione trasversale realizzata con lo stesso materiale.

Si tenga presente che quando cambia la posizione della sezione rispetto al carico agente, la resistenza della trave cambia significativamente, pur mantenendo invariata l'area della sezione trasversale. Di conseguenza la sezione deve essere posizionata in modo che la linea di forza coincida con quella degli assi principali rispetto ai quali il momento d'inerzia è minimo. Dovresti sforzarti di garantire che la curvatura della trave avvenga nel piano della sua massima rigidità.