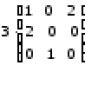
Uno degli argomenti più difficili per gli studenti è risolvere equazioni contenenti una variabile sotto il segno del modulo. Vediamo per cominciare a cosa è collegato? Perché, ad esempio, le equazioni quadratiche la maggior parte dei bambini fa clic come matti, ma con un concetto così lontano dal più complesso come modulo ha così tanti problemi?
A mio avviso, tutte queste difficoltà sono associate alla mancanza di regole chiaramente formulate per risolvere equazioni con un modulo. Quindi, quando si risolve un'equazione quadratica, lo studente sa per certo che deve prima applicare la formula discriminante e poi le formule per le radici dell'equazione quadratica. Ma cosa succede se si incontra un modulo nell'equazione? Cercheremo di descrivere chiaramente il piano d'azione necessario nel caso in cui l'equazione contenga un'incognita sotto il segno del modulo. Diamo diversi esempi per ogni caso.
Ma prima, ricordiamo definizione del modulo. Quindi, il modulo del numero UN il numero stesso si chiama if UN non negativo e -UN se il numero UN meno di zero. Puoi scriverlo così:
|un| = a se a ≥ 0 e |a| = -a se a< 0
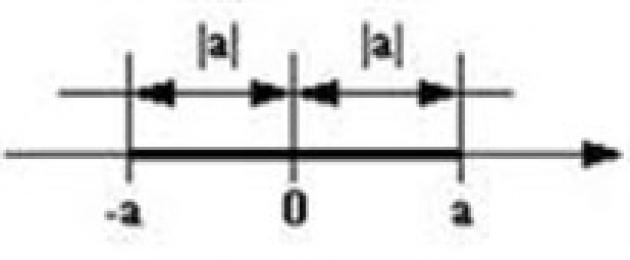
Parlando del significato geometrico del modulo, va ricordato che ogni numero reale corrisponde a un certo punto sull'asse dei numeri - è a 
coordinata. Quindi, il modulo o il valore assoluto di un numero è la distanza da questo punto all'origine dell'asse numerico. La distanza è sempre data come un numero positivo. Pertanto, il modulo di qualsiasi numero negativo è un numero positivo. A proposito, anche in questa fase, molti studenti iniziano a confondersi. Qualsiasi numero può essere nel modulo, ma il risultato dell'applicazione del modulo è sempre un numero positivo.
Passiamo ora alla risoluzione delle equazioni.
1. Consideriamo un'equazione della forma |x| = c, dove c è un numero reale. Questa equazione può essere risolta usando la definizione del modulo.
Dividiamo tutti i numeri reali in tre gruppi: quelli maggiori di zero, quelli minori di zero e il terzo gruppo è il numero 0. Scriviamo la soluzione sotto forma di diagramma:
(±c se c > 0
Se |x| = c, allora x = (0 se c = 0
(senza radici se con< 0
1) |x| = 5, perché 5 > 0, allora x = ±5;
2) |x| = -5, perché -5< 0, то уравнение не имеет корней;
3) |x| = 0, quindi x = 0.
2. Un'equazione della forma |f(x)| = b, dove b > 0. Per risolvere questa equazione, è necessario eliminare il modulo. Facciamo così: f(x) = bo f(x) = -b. Ora è necessario risolvere separatamente ciascuna delle equazioni ottenute. Se nell'equazione originale b< 0, решений не будет.
1) |x + 2| = 4, perché 4 > 0, quindi
x + 2 = 4 o x + 2 = -4
2) |x 2 – 5| = 11, perché 11 > 0, quindi
x 2 - 5 = 11 o x 2 - 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 senza radici
3) |x 2 – 5x| = -8 , perché -8< 0, то уравнение не имеет корней.
3. Un'equazione della forma |f(x)| = g(x). Secondo il significato del modulo, tale equazione avrà soluzioni se il suo lato destro è maggiore o uguale a zero, cioè g(x) ≥ 0. Allora abbiamo:
f(x) = g(x) O f(x) = -g(x).
1) |2x – 1| = 5x - 10. Questa equazione avrà radici se 5x - 10 ≥ 0. È qui che inizia la soluzione di tali equazioni.
1. O.D.Z. 5x – 10 ≥ 0
2. Soluzione:
2x - 1 = 5x - 10 o 2x - 1 = -(5x - 10)
3. Combina O.D.Z. e la soluzione, otteniamo:
La radice x \u003d 11/7 non si adatta secondo O.D.Z., è inferiore a 2 e x \u003d 3 soddisfa questa condizione.
Risposta: x = 3
2) |x – 1| \u003d 1 - x 2.
1. O.D.Z. 1 - x 2 ≥ 0. Risolviamo questa disuguaglianza usando il metodo dell'intervallo:
(1 – x)(1 + x) ≥ 0
2. Soluzione:
x - 1 \u003d 1 - x 2 o x - 1 \u003d - (1 - x 2)
x 2 + x - 2 = 0 x 2 - x = 0
x = -2 o x = 1 x = 0 o x = 1
3. Combina soluzione e O.D.Z.:
Solo le radici x = 1 e x = 0 sono adatte.
Risposta: x = 0, x = 1.
4. Un'equazione della forma |f(x)| = |g(x)|. Tale equazione è equivalente alle seguenti due equazioni f(x) = g(x) o f(x) = -g(x).
1) |x 2 - 5x + 7| = |2x – 5|. Questa equazione è equivalente alle due seguenti:
x 2 - 5x + 7 = 2x - 5 o x 2 - 5x +7 = -2x + 5
x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0
x = 3 o x = 4 x = 2 o x = 1
Risposta: x = 1, x = 2, x = 3, x = 4.
5. Equazioni risolte con il metodo della sostituzione (cambio di variabile). Questo metodo di soluzione è più facile da spiegare con un esempio specifico. Quindi, sia data un'equazione quadratica con un modulo:
x 2 – 6|x| + 5 = 0. Per la proprietà del modulo x 2 = |x| 2 , quindi l'equazione può essere riscritta come segue:
|x| 2–6|x| + 5 = 0. Facciamo la modifica |x| = t ≥ 0, allora avremo:
t 2 - 6t + 5 \u003d 0. Risolvendo questa equazione, otteniamo che t \u003d 1 o t \u003d 5. Torniamo alla sostituzione:
|x| = 1 o |x| = 5
x = ±1 x = ±5
Risposta: x = -5, x = -1, x = 1, x = 5.
Diamo un'occhiata a un altro esempio:
x 2 + |x| – 2 = 0. Per la proprietà del modulo x 2 = |x| 2, così
|x| 2 + |x| – 2 = 0. Facciamo la modifica |x| = t ≥ 0, allora:
t 2 + t - 2 \u003d 0. Risolvendo questa equazione, otteniamo t \u003d -2 o t \u003d 1. Torniamo alla sostituzione:
|x| = -2 o |x| = 1
Nessuna radice x = ± 1
Risposta: x = -1, x = 1.
6. Un altro tipo di equazioni sono le equazioni con un modulo "complesso". Tali equazioni includono equazioni che hanno "moduli all'interno di un modulo". Equazioni di questo tipo possono essere risolte utilizzando le proprietà del modulo.
1) |3 – |x|| = 4. Agiremo allo stesso modo delle equazioni del secondo tipo. Perché 4 > 0, otteniamo due equazioni:
3 – |x| = 4 o 3 – |x| = -4.
Ora esprimiamo il modulo x in ogni equazione, quindi |x| = -1 o |x| = 7.
Risolviamo ciascuna delle equazioni risultanti. Non ci sono radici nella prima equazione, perché -1< 0, а во втором x = ±7.
Rispondere x = -7, x = 7.
2) |3 + |x + 1|| = 5. Risolviamo questa equazione in modo simile:
3 + |x + 1| = 5 o 3 + |x + 1| = -5
|x+1| = 2 |x + 1| = -8
x + 1 = 2 o x + 1 = -2. Non ci sono radici.
Risposta: x = -3, x = 1.
Esiste anche un metodo universale per risolvere le equazioni con un modulo. Questo è il metodo di spaziatura. Ma lo considereremo ulteriormente.
site, con copia integrale o parziale del materiale, è richiesto il link alla fonte.
Il modulo di numero introduce un nuovo concetto in matematica. Analizziamo in dettaglio cos'è il modulo di un numero e come lavorarci?
Considera un esempio:
Siamo usciti di casa per il negozio. Sono passati 300 m, matematicamente questa espressione può essere scritta come +300, il significato del numero 300 dal segno “+” non cambierà. La distanza o modulo di un numero in matematica è la stessa e può anche essere scritta così: |300|=300. Il segno del modulo di un numero è indicato da due linee verticali.
E poi nella direzione opposta abbiamo camminato per 200 metri. Matematicamente, possiamo scrivere il percorso di ritorno come -200. Ma non diciamo così “siamo andati meno duecento metri”, anche se siamo tornati, perché la distanza come quantità rimane positiva. Per questo, in matematica è stato introdotto il concetto di modulo. Puoi scrivere la distanza o il modulo di -200 come segue: |-200|=200.
Proprietà del modulo.
Definizione:
Modulo di un numero o valore assoluto di un numeroè la distanza dal punto di partenza alla destinazione.
Il modulo di un intero diverso da zero è sempre un numero positivo.
Il modulo è scritto così:
1. Il modulo di un numero positivo è uguale al numero stesso.
|
a|=UN
2. Il modulo di un numero negativo è uguale al numero opposto.
|-
a|=UN
3. Modulo di zero, uguale a zero.
|0|=0
4. I moduli di numeri opposti sono uguali.
|
a|=|-a|=UN
Domande correlate:
Qual è il modulo di un numero?
Risposta: Il modulo è la distanza dal punto di partenza alla destinazione.
Se metti un segno "+" davanti a un numero intero, cosa succede?
Risposta: il numero non cambierà il suo significato, per esempio, 4=+4.
Se metti un segno "-" davanti a un numero intero, cosa succede?
Risposta: il numero cambierà ad esempio in 4 e -4.
Quali numeri hanno lo stesso modulo?
Risposta: i numeri positivi e zero avranno lo stesso modulo. Ad esempio, 15=|15|.
Quali numeri hanno il modulo - il numero opposto?
Risposta: per i numeri negativi, il modulo sarà uguale al numero opposto. Ad esempio, |-6|=6.
Esempio 1:
Trova il modulo dei numeri: a) 0 b) 5 c) -7?
Soluzione:
a) |0|=0
b) |5|=5
c)|-7|=7
Esempio #2:
Ci sono due numeri distinti i cui moduli sono uguali?
Soluzione:
|10|=10
|-10|=10
I moduli di numeri opposti sono uguali.
Esempio #3:
Quali due numeri opposti hanno modulo 9?
Soluzione:
|9|=9
|-9|=9
Risposta: 9 e -9.
Esempio #4:
Procedere come segue: a) |+5|+|-3| b) |-3|+|-8| c)|+4|-|+1|
Soluzione:
a) |+5|+|-3|=5+3=8
b) |-3|+|-8|=3+8=11
c)|+4|-|+1|=4-1=3
Esempio #5:
Trova: a) modulo del numero 2 b) modulo del numero 6 c) modulo del numero 8 d) modulo del numero 1 e) modulo del numero 0.
Soluzione:
a) il modulo del numero 2 è indicato come |2| o |+2| È lo stesso.
|2|=2
b) il modulo del numero 6 è indicato come |6| o |+6| È lo stesso.
|6|=6
c) il modulo del numero 8 è indicato come |8| o |+8| È lo stesso.
|8|=8
d) il modulo del numero 1 è indicato come |1| o |+1| È lo stesso.
|1|=1
e) il modulo del numero 0 è indicato come |0|, |+0| o |-0| È lo stesso.
|0|=0
A è calcolato secondo le seguenti regole:
Per brevità, usa |un|. Così, |10| = 10; - 1/3 = | 1/3 |; | -100| =100 ecc.
Qualsiasi dimensione X corrisponde a un valore abbastanza preciso | X|. E questo significa identità A= |X| stabilisce A come alcuni funzione argomento X.
Programma Questo funzioni presentato di seguito.
Per X > 0 |X| = X, e per X< 0 |X|= -X; in connessione con questa linea y = | X| A X> 0 è allineato con la linea y=x(bisettrice del primo angolo di coordinate) e quando X< 0 - с прямой y = -x(bisettrice del secondo angolo di coordinate).
Separato equazioni includere sconosciuti sotto il segno modulo.
Esempi arbitrari di tali equazioni - | X— 1| = 2, |6 — 2X| =3X+ 1 ecc.
Risoluzione di equazioni contenente l'ignoto sotto il segno del modulo si basa sul fatto che se il valore assoluto del numero sconosciuto x è uguale al numero positivo a, allora questo numero x stesso è uguale a a o -a.
Per esempio: se | X| = 10, poi o X=10, o X = -10.
Prendere in considerazione soluzione di singole equazioni.
Analizziamo la soluzione dell'equazione | X- 1| = 2.
Apriamo il modulo poi la differenza X- 1 può essere uguale a + 2 o - 2. Se x - 1 = 2, allora X= 3; Se X- 1 = - 2, quindi X= - 1. Facciamo una sostituzione e otteniamo che entrambi questi valori soddisfano l'equazione.
Risposta. Questa equazione ha due radici: X 1 = 3, X 2 = - 1.
Analizziamo soluzione dell'equazione | 6 — 2X| = 3X+ 1.
Dopo espansione del modulo otteniamo: o 6 - 2 X= 3X+ 1 o 6 - 2 X= - (3X+ 1).
Nel primo caso X= 1, e nel secondo X= - 7.
Visita medica. A X= 1 |6 — 2X| = |4| = 4, 3X+ 1 = 4; segue dal tribunale X = 1 - radice b dato equazioni.
A X = - 7 |6 — 2X| = |20| = 20, 3X+1=-20; poiché 20 ≠ -20, allora X= - 7 non è la radice di questa equazione.
Risposta. A le equazioni hanno una sola radice: X = 1.
Equazioni di questo tipo possono risolvere e graficamente.
Quindi decidiamo Per esempio, graficamente equazione | X- 1| = 2.
Costruiamo prima grafico delle funzioni A = |X— 1|. Disegniamo prima il grafico della funzione. A=X- 1:
Quella parte di esso arti grafiche, che si trova sopra l'asse X non cambieremo. Per lei X- 1 > 0 e quindi | X-1|=X-1.
La parte del grafico che si trova sotto l'asse X, raffigurare simmetricamente attorno a questo asse. Perché per questa parte X - 1 < 0 и соответственно |X - 1|= - (X - 1). Formato come risultato linea(linea continua) e volontà grafico delle funzioni y = | X—1|.
Questa linea si intersecherà con Dritto A= 2 in due punti: M 1 con ascissa -1 e M 2 con ascissa 3. E, di conseguenza, l'equazione | X- 1| =2 avrà due radici: X 1 = - 1, X 2 = 3.
Non scegliamo la matematica la sua professione, e lei ci sceglie.
Il matematico russo Yu.I. Manin
Modulo Equazioni
I problemi più difficili da risolvere nella matematica scolastica sono le equazioni contenenti variabili sotto il segno del modulo. Per risolvere con successo tali equazioni, è necessario conoscere la definizione e le proprietà di base del modulo. Naturalmente, gli studenti dovrebbero avere le capacità per risolvere equazioni di questo tipo.
Concetti base e proprietà
Modulo (valore assoluto) di un numero reale denotato ed è definito come segue:
Le proprietà semplici del modulo includono le seguenti relazioni:
Nota, che le ultime due proprietà valgono per ogni grado pari.
Inoltre, se , dove , allora e
Proprietà del modulo più complesse, che può essere efficacemente utilizzato per risolvere equazioni con moduli, sono formulati mediante i seguenti teoremi:
Teorema 1.Per tutte le funzioni analitiche E la disuguaglianza
Teorema 2. L'uguaglianza è uguale alla disuguaglianza.
Teorema 3. Uguaglianza equivale alla disuguaglianza.
Considera esempi tipici di risoluzione di problemi sull'argomento “Equazioni, contenente variabili sotto il segno del modulo.
Risoluzione di equazioni con modulo
Il metodo più comune nella matematica scolastica per risolvere equazioni con un modulo è il metodo, basato sull'espansione del modulo. Questo metodo è generico, tuttavia, nel caso generale, la sua applicazione può portare a calcoli molto macchinosi. A questo proposito, gli studenti dovrebbero anche essere consapevoli di altro, metodi e tecniche più efficienti per risolvere tali equazioni. In particolare, bisogno di avere le competenze per applicare i teoremi, dato in questo articolo.
Esempio 1 Risolvi l'equazione. (1)
Soluzione. L'equazione (1) sarà risolta con il metodo "classico" - il metodo di espansione del modulo. Per fare ciò, rompiamo l'asse numerico punti e intervalli e considerare tre casi.
1. Se , allora , , , e l'equazione (1) assume la forma . Ne consegue da qui. Tuttavia, qui , quindi il valore trovato non è la radice dell'equazione (1).
2. Se , quindi dall'equazione (1) otteniamo O .
Da allora la radice dell'equazione (1).
3. Se , quindi l'equazione (1) assume la forma O . Notare che .
Risposta: , .
Quando risolviamo le seguenti equazioni con un modulo, utilizzeremo attivamente le proprietà dei moduli per aumentare l'efficienza della risoluzione di tali equazioni.
Esempio 2 risolvere l'equazione.
Soluzione. Da e quindi segue dall'equazione. A questo proposito, , , e l'equazione diventa. Da qui arriviamo. Tuttavia , quindi l'equazione originale non ha radici.
Risposta: nessuna radice.
Esempio 3 risolvere l'equazione.
Soluzione. Da allora . Se poi , e l'equazione diventa.
Da qui otteniamo.
Esempio 4 risolvere l'equazione.
Soluzione.Riscriviamo l'equazione in forma equivalente. (2)
L'equazione risultante appartiene a equazioni del tipo .
Tenendo conto del Teorema 2, possiamo affermare che l'equazione (2) è equivalente alla disuguaglianza . Da qui otteniamo.
Risposta: .
Esempio 5 Risolvi l'equazione.
Soluzione. Questa equazione ha la forma. Ecco perché , secondo il Teorema 3, qui abbiamo la disuguaglianza O .
Esempio 6 risolvere l'equazione.
Soluzione. Supponiamo che. Perché , quindi l'equazione data assume la forma di un'equazione quadratica, (3)
Dove . Poiché l'equazione (3) ha una sola radice positiva poi . Da qui otteniamo due radici dell'equazione originale: E .
Esempio 7 risolvere l'equazione. (4)
Soluzione. Poiché l'equazioneè equivalente alla combinazione di due equazioni: E , quindi quando si risolve l'equazione (4) è necessario considerare due casi.
1. Se , allora o .
Da qui otteniamo , e .
2. Se , allora o .
Da allora .
Risposta: , , , .
Esempio 8risolvere l'equazione . (5)
Soluzione. Da allora e , poi . Da qui e dall'equazione (5) segue che e , cioè qui abbiamo un sistema di equazioni
Tuttavia, questo sistema di equazioni è incoerente.
Risposta: nessuna radice.
Esempio 9 risolvere l'equazione. (6)
Soluzione. Se designiamo e dall'equazione (6) otteniamo
O . (7)
Poiché l'equazione (7) ha la forma , questa equazione è equivalente alla disuguaglianza . Da qui otteniamo. Poiché , allora o .
Risposta: .
Esempio 10risolvere l'equazione. (8)
Soluzione.Secondo il Teorema 1, possiamo scrivere
(9)
Tenendo conto dell'equazione (8), concludiamo che entrambe le disuguaglianze (9) si trasformano in uguaglianze, ad es. esiste un sistema di equazioni
Tuttavia, per il Teorema 3, il suddetto sistema di equazioni è equivalente al sistema di disequazioni
(10)
Risolvendo il sistema di disequazioni (10) si ottiene . Poiché il sistema di disuguaglianze (10) è equivalente all'equazione (8), l'equazione originale ha un'unica radice .
Risposta: .
Esempio 11. risolvere l'equazione. (11)
Soluzione. Sia e , allora l'equazione (11) implica l'uguaglianza .
Da ciò segue che e . Quindi, qui abbiamo un sistema di disuguaglianze
La soluzione a questo sistema di disuguaglianze sono E .
Risposta: , .
Esempio 12.risolvere l'equazione. (12)
Soluzione. L'equazione (12) sarà risolta con il metodo dell'espansione successiva dei moduli. Per fare ciò, considera diversi casi.
1. Se , allora .
1.1. Se , allora e , .
1.2. Se poi . Tuttavia , quindi, in questo caso, l'equazione (12) non ha radici.
2. Se , allora .
2.1. Se , allora e , .
2.2. Se , allora e .
Risposta: , , , , .
Esempio 13risolvere l'equazione. (13)
Soluzione. Poiché il lato sinistro dell'equazione (13) è non negativo, allora e . A questo proposito, , e l'equazione (13)
assume la forma o .
È noto che l'equazione equivale alla combinazione di due equazioni E , soluzione che otteniamo, . Perché , allora l'equazione (13) ha una radice.
Risposta: .
Esempio 14 Risolvere un sistema di equazioni (14)
Soluzione. Da e , poi e . Pertanto, dal sistema di equazioni (14) otteniamo quattro sistemi di equazioni:
Le radici dei suddetti sistemi di equazioni sono le radici del sistema di equazioni (14).
Risposta: ,, , , , , , .
Esempio 15 Risolvere un sistema di equazioni (15)
Soluzione. Da allora . A questo proposito, dal sistema di equazioni (15) si ottengono due sistemi di equazioni
Le radici del primo sistema di equazioni sono e , e dal secondo sistema di equazioni otteniamo e .
Risposta: , , , .
Esempio 16 Risolvere un sistema di equazioni (16)
Soluzione. Dalla prima equazione del sistema (16) segue che .
Da allora . Considera la seconda equazione del sistema. Perché il, Quello , e l'equazione diventa, , O .
Se sostituiamo il valorenella prima equazione del sistema (16), quindi , o .
Risposta: , .
Per uno studio più approfondito dei metodi di problem solving, relativo alla soluzione di equazioni, contenente variabili sotto il segno del modulo, puoi consigliare tutorial dall'elenco della letteratura consigliata.
1. Raccolta di compiti di matematica per i candidati alle università tecniche / Ed. MI. Scanavi. - M .: Mondo ed educazione, 2013. - 608 pag.
2. Suprun V.P. Matematica per studenti delle scuole superiori: compiti di maggiore complessità. - M.: KD "Librocom" / URSS, 2017. - 200 pag.
3. Suprun V.P. Matematica per studenti delle scuole superiori: metodi non standard per la risoluzione dei problemi. - M.: KD "Librocom" / URSS, 2017. - 296 pag.
Avete domande?
Per ottenere l'aiuto di un tutor - registrati.
site, con copia integrale o parziale del materiale, è richiesto il link alla fonte.
In questo articolo, analizzeremo in dettaglio il valore assoluto di un numero. Daremo varie definizioni del modulo di un numero, introdurremo la notazione e forniremo illustrazioni grafiche. In questo caso, consideriamo vari esempi di come trovare il modulo di un numero per definizione. Successivamente, elenchiamo e giustifichiamo le proprietà principali del modulo. Alla fine dell'articolo parleremo di come viene determinato e trovato il modulo di un numero complesso.
Navigazione della pagina.
Modulo di numero - definizione, notazione ed esempi
Per prima cosa introduciamo designazione del modulo. Il modulo del numero a sarà scritto come , cioè a sinistra ea destra del numero metteremo delle linee verticali che formano il segno del modulo. Facciamo un paio di esempi. Ad esempio, modulo -7 può essere scritto come ; il modulo 4.125 è scritto come , e il modulo è scritto come .
La seguente definizione del modulo si riferisce a, e quindi, a, ea numeri interi, ea numeri razionali e irrazionali, come alle parti costitutive dell'insieme dei numeri reali. Parleremo del modulo di un numero complesso in.
Definizione.
Modulo di aè o il numero a stesso, se a è un numero positivo, o il numero −a, l'opposto del numero a, se a è un numero negativo, o 0, se a=0 .
La definizione sonora del modulo di un numero è spesso scritta nella forma seguente 
, questa notazione significa che se a>0 , se a=0 e se a<0
.
Il record può essere rappresentato in una forma più compatta 
. Questa notazione significa che se (a è maggiore o uguale a 0 ) e se a<0
.
C'è anche un record 
. Qui, il caso in cui a=0 dovrebbe essere spiegato separatamente. In questo caso abbiamo , ma −0=0 , poiché zero è considerato un numero opposto a se stesso.
Portiamo esempi di trovare il modulo di un numero con una data definizione. Ad esempio, troviamo i moduli dei numeri 15 e . Cominciamo con la ricerca. Poiché il numero 15 è positivo, il suo modulo è, per definizione, uguale a questo numero stesso, cioè . Qual è il modulo di un numero? Poiché è un numero negativo, il suo modulo è uguale al numero opposto al numero, cioè al numero 
. Così, .
In conclusione di questo paragrafo, diamo una conclusione, che è molto comoda da applicare nella pratica quando si trova il modulo di un numero. Dalla definizione del modulo di un numero segue che il modulo di un numero è uguale al numero sotto il segno del modulo, indipendentemente dal suo segno, e dagli esempi discussi sopra, questo è molto chiaramente visibile. L'affermazione sonora spiega perché viene chiamato anche il modulo di un numero il valore assoluto del numero. Quindi il modulo di un numero e il valore assoluto di un numero sono la stessa cosa.
Modulo di un numero come distanza
Geometricamente, il modulo di un numero può essere interpretato come distanza. Portiamo determinazione del modulo di un numero in termini di distanza.
Definizione.
Modulo di aè la distanza dall'origine sulla linea delle coordinate al punto corrispondente al numero a.
Questa definizione è coerente con la definizione del modulo di un numero fornita nel primo paragrafo. Spieghiamo questo punto. La distanza dall'origine al punto corrispondente a un numero positivo è uguale a questo numero. Zero corrisponde al punto di riferimento, quindi la distanza dal punto di riferimento al punto con coordinata 0 è uguale a zero (non è necessario alcun segmento singolo e nessun segmento che costituisca una frazione di un singolo segmento per andare dal punto O al punto con coordinata 0). La distanza dall'origine a un punto con coordinata negativa è uguale al numero opposto alla coordinata del punto dato, poiché è uguale alla distanza dall'origine al punto la cui coordinata è il numero opposto.
Ad esempio, il modulo del numero 9 è 9, poiché la distanza dall'origine al punto con coordinate 9 è nove. Facciamo un altro esempio. Il punto con coordinata −3.25 si trova a una distanza di 3.25 dal punto O, quindi 
.
La definizione suonata del modulo di un numero è un caso speciale di definizione del modulo della differenza di due numeri.
Definizione.
Modulo di differenza di due numeri a e b è uguale alla distanza tra i punti della linea di coordinate con coordinate a e b .
Cioè, se vengono dati i punti sulla linea di coordinate A(a) e B(b), allora la distanza dal punto A al punto B è uguale al modulo della differenza tra i numeri a e b. Se prendiamo il punto O (punto di riferimento) come punto B, otterremo la definizione del modulo del numero dato all'inizio di questo paragrafo.
Determinazione del modulo di un numero attraverso la radice quadrata aritmetica
A volte trovato determinazione del modulo mediante la radice quadrata aritmetica.
Ad esempio, calcoliamo i moduli dei numeri −30 e in base a questa definizione. Abbiamo . Allo stesso modo, calcoliamo il modulo di due terzi: 
.
Anche la definizione del modulo di un numero in termini di radice quadrata aritmetica è coerente con la definizione data nel primo paragrafo di questo articolo. Dimostriamolo. Sia a un numero positivo e sia −a negativo. Poi 
E 
, se a=0 , allora 
.
Proprietà del modulo
Il modulo ha una serie di risultati caratteristici: proprietà del modulo. Ora daremo il principale e il più comunemente usato di loro. Nel convalidare queste proprietà, faremo affidamento sulla definizione del modulo di un numero in termini di distanza.
Iniziamo con la proprietà del modulo più ovvia - il modulo di un numero non può essere un numero negativo. In forma letterale, questa proprietà ha la forma per qualsiasi numero a . Questa proprietà è molto facile da giustificare: il modulo di un numero è la distanza, e la distanza non può essere espressa come numero negativo.
Passiamo alla proprietà successiva del modulo. Il modulo di un numero è uguale a zero se e solo se questo numero è zero. Il modulo di zero è zero per definizione. Lo zero corrisponde all'origine, nessun altro punto sulla linea delle coordinate corrisponde a zero, poiché ogni numero reale è associato a un singolo punto sulla linea delle coordinate. Per lo stesso motivo, qualsiasi numero diverso da zero corrisponde a un punto diverso dall'origine. E la distanza dall'origine a qualsiasi punto diverso dal punto O non è uguale a zero, poiché la distanza tra due punti è uguale a zero se e solo se questi punti coincidono. Il ragionamento di cui sopra dimostra che solo il modulo di zero è uguale a zero.
Andare avanti. I numeri opposti hanno moduli uguali, cioè per ogni numero a . Infatti, due punti sulla linea delle coordinate, le cui coordinate sono numeri opposti, sono alla stessa distanza dall'origine, il che significa che i moduli di numeri opposti sono uguali.
La prossima proprietà del modulo è: il modulo del prodotto di due numeri è uguale al prodotto dei moduli di questi numeri, questo è, . Per definizione, il modulo del prodotto dei numeri a e b è o a b se , o −(a b) se . Dalle regole di moltiplicazione dei numeri reali segue che il prodotto dei moduli dei numeri a e b è uguale a a b , , o −(a b) , se , il che dimostra la proprietà considerata.
Il modulo del quoziente di divisione di a per b è uguale al quoziente di divisione del modulo di a per il modulo di b, questo è, . Giustifichiamo questa proprietà del modulo. Poiché il quoziente è uguale al prodotto, allora . In virtù della proprietà precedente, abbiamo 
. Resta solo da usare l'uguaglianza , che è valida per la definizione del modulo del numero.
La seguente proprietà del modulo è scritta come una disuguaglianza: 
, a , b e c sono numeri reali arbitrari. La disuguaglianza scritta non è altro che disuguaglianza triangolare. Per chiarire questo, prendiamo i punti A(a) , B(b) , C(c) sulla retta delle coordinate, e consideriamo il triangolo degenere ABC, i cui vertici giacciono sulla stessa retta. Per definizione, il modulo della differenza è uguale alla lunghezza del segmento AB, - alla lunghezza del segmento AC, e - alla lunghezza del segmento CB. Poiché la lunghezza di qualsiasi lato di un triangolo non supera la somma delle lunghezze degli altri due lati, la disuguaglianza 
, quindi vale anche la disuguaglianza.
La disuguaglianza appena dimostrata è molto più comune nella forma 
. La disuguaglianza scritta è solitamente considerata come una proprietà separata del modulo con la formulazione: “ Il modulo della somma di due numeri non supera la somma dei moduli di questi numeri". Ma la disuguaglianza segue direttamente dalla disuguaglianza , se mettiamo −b invece di b in essa, e prendiamo c=0 .
Modulo dei numeri complessi
Diamo determinazione del modulo di un numero complesso. Lasciamoci dare numero complesso, scritto in forma algebrica , dove x e y sono dei numeri reali, che rappresentano, rispettivamente, la parte reale e immaginaria di un dato numero complesso z, ed è un'unità immaginaria.
- In contatto con 0
- Google Plus 0
- OK 0
- Facebook 0
