Trascrizione
1 Funzioni reciprocamente inverse Due funzioni f e g si dicono reciprocamente inverse se le formule y=f(x) e x=g(y) esprimono la stessa relazione tra le variabili x e y, cioè se l'uguaglianza y=f(x) è vera se e solo se l'uguaglianza x=g(y) è vera: y=f(x) x=g(y) Se due funzioni f e g sono mutuamente inverse, allora g è detta funzione inversa di f e, viceversa, f è la funzione inversa di g. Ad esempio, y=10 x e x=lgy sono funzioni reciprocamente inverse. Condizione per l'esistenza di una funzione mutuamente inversa Una funzione f è inversa se, dalla relazione y=f(x), la variabile x può essere espressa univocamente tramite y. Ci sono funzioni per le quali è impossibile esprimere in modo inequivocabile l'argomento attraverso il valore dato della funzione. Ad esempio: 1. y= x. Per un dato numero positivo y, ci sono due valori dell'argomento x tali che x = y. Ad esempio, se y=2, allora x=2 oppure x= - 2. Ciò significa che è impossibile esprimere x in modo inequivocabile tramite y. Pertanto, questa funzione non ha reciproco. 2. y=x 2. x=, x= - 3. y=sinx. Per un dato valore di y (y 1), ci sono infiniti valori di x tali che y=sinx. La funzione y=f(x) ha inversa se ogni retta y=y 0 interseca il grafico della funzione y=f(x) in non più di un punto (potrebbe non intersecare affatto il grafico se y 0 lo fa non appartengono all'intervallo di valori della funzione f). Questa condizione può essere formulata diversamente: l'equazione f(x)=y 0 per ogni y 0 ha al più una soluzione. La condizione che una funzione abbia un inverso è certamente soddisfatta se la funzione è strettamente crescente o strettamente decrescente. Se f è strettamente crescente, allora per due diversi valori dell'argomento assume valori diversi, poiché a un valore maggiore dell'argomento corrisponde un valore maggiore della funzione. Di conseguenza, l'equazione f(x)=y per una funzione strettamente monotona ha al più una soluzione. La funzione esponenziale y=a x è strettamente monotona, quindi ha una funzione logaritmica inversa. Molte funzioni non hanno inverse. Se per qualche b l'equazione f(x)=b ha più di una soluzione, allora la funzione y=f(x) non ha inversa. Su un grafico, ciò significa che la linea y=b interseca il grafico della funzione in più di un punto. Ad esempio, y=x 2 ; y=sinx; y=tgx.
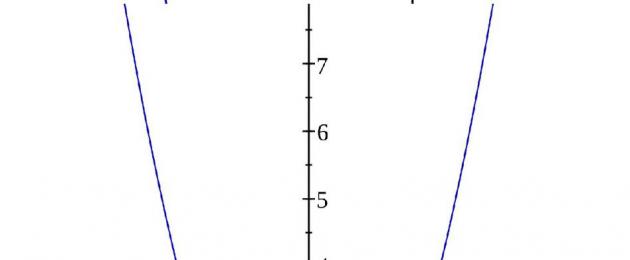
2 L'ambiguità della soluzione dell'equazione f(x) = b può essere risolta riducendo il dominio di definizione della funzione f in modo che il suo intervallo di valori non cambi, ma in modo che assuma ciascun valore una volta. Ad esempio, y=x 2, x 0; y=sinx, ; y=tgx,. La regola generale per trovare la funzione inversa di una funzione: 1. risolvendo l'equazione per x, troviamo; 2. Cambiando le designazioni della variabile x in y e y in x, otteniamo la funzione inversa di quella data. Proprietà delle funzioni mutuamente inverse Identità Siano feg funzioni mutuamente inverse. Ciò significa che le uguaglianze y=f(x) e x=g(y) sono equivalenti: f(g(y))=y e g(f(x))=x. Ad esempio, 1. Sia f una funzione esponenziale e g una funzione logaritmica. Otteniamo: i. 2. Le funzioni y=x2, x0 e y= sono reciprocamente inverse. Abbiamo due identità: e per x 0. Dominio di definizione Siano feg funzioni reciprocamente inverse. Il dominio della funzione f coincide con il dominio della funzione g, e, viceversa, il dominio della funzione f coincide con il dominio della funzione g. Esempio. Il dominio di definizione della funzione esponenziale è l'intero asse numerico R, e il suo intervallo di valori è l'insieme di tutti i numeri positivi. Per una funzione logaritmica è il contrario: il dominio di definizione è l'insieme di tutti i numeri positivi e l'intervallo di valori è l'intero insieme di R. Monotonia Se una delle funzioni mutuamente inverse è strettamente crescente, allora l'altra è strettamente crescente. Prova. Siano x 1 e x 2 due numeri che giacciono nel dominio di definizione della funzione g, e x 1 3 Grafici di funzioni mutuamente inverse Teorema. Siano f e g funzioni reciprocamente inverse. I grafici delle funzioni y=f(x) e x=g(y) sono tra loro simmetrici rispetto alla bisettrice dell'angolo how. Prova. Per la definizione di funzioni mutuamente inverse, le formule y=f(x) e x=g(y) esprimono la stessa dipendenza tra le variabili x e y, il che significa che questa dipendenza è rappresentata dallo stesso grafico di una curva C. La curva C è un grafico di funzioni y=f(x). Prendiamo un punto arbitrario P(a; b) C. Ciò significa che b=f(a) e allo stesso tempo a=g(b). Costruiamo un punto Q simmetrico al punto P rispetto alla bisettrice dell'angolo xy. Il punto Q avrà coordinate (b; a). Poiché a=g(b), allora il punto Q appartiene al grafico della funzione y=g(x): infatti, per x=b, il valore di y=a è uguale a g(x). Tutti i punti simmetrici ai punti della curva C rispetto alla retta indicata giacciono quindi sul grafico della funzione y=g(x). Esempi di funzioni i cui grafici sono reciprocamente inversi: y=e x e y=lnx; y=x 2 (x 0) e y= ; y=2x4 e y= +2. 4 Derivata di una funzione inversa Siano feg funzioni reciprocamente inverse. I grafici delle funzioni y=f(x) e x=g(y) sono tra loro simmetrici rispetto alla bisettrice dell'angolo how. Prendiamo il punto x=a e calcoliamo il valore di una delle funzioni in questo punto: f(a)=b. Quindi, per definizione della funzione inversa, g(b)=a. I punti (a; f(a))=(a; b) e (b; g(b))=(b; a) sono simmetrici rispetto alla retta l. Poiché le curve sono simmetriche, le tangenti ad esse sono simmetriche rispetto alla retta l. Dalla simmetria, l'angolo di una delle linee con l'asse x è uguale all'angolo dell'altra linea con l'asse y. Se una retta forma un angolo α con l'asse x, allora il suo coefficiente angolare è pari a k 1 =tgα; allora la seconda retta ha coefficiente angolare k 2 =tg(α)=ctgα=. Pertanto, i coefficienti angolari delle linee simmetriche rispetto alla retta l sono reciprocamente inversi, cioè k 2 =, oppure k 1 k 2 = 1. Passando alle derivate e tenendo conto che la pendenza della tangente è il valore della derivata nel punto di contatto, concludiamo: I valori delle derivate di funzioni mutuamente inverse nei punti corrispondenti sono mutuamente inversi, cioè Esempio 1. Dimostrare che la funzione f(x) = x 3, reversibile. Soluzione. y=f(x)=x 3. La funzione inversa sarà la funzione y=g(x)=. Troviamo la derivata della funzione g:. Quelli. =. Compito 1. Dimostrare che la funzione data dalla formula è invertibile 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 5 Esempio 2. Trova la funzione inversa della funzione y=2x+1. Soluzione. La funzione y=2x+1 è crescente, quindi ha un inverso. Esprimiamo x tramite y: otteniamo... Passando alle notazioni generalmente accettate, Risposta: Attività 2. Trova funzioni inverse per queste funzioni 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Lezione 20 TEOREMA SULLA FUNZIONE COMPLESSA DERIVATA. Sia y = f(u) e u= u(x). Otteniamo una funzione y in funzione dell'argomento x: y = f(u(x)). L'ultima funzione è chiamata funzione da una funzione o funzione complessa. Capitolo 9 Gradi Grado con esponente intero. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Se è pari, allora ()< (). Например, () 0 = 0 < 0 = = () 0. Если нечетно, то () >(). Ad esempio, () = > = = (), quindi Cosa studieremo: Lezione sul tema: Studio di una funzione per monotonicità. Funzioni decrescenti e crescenti. Relazione tra derivata e monotonicità di una funzione. Due importanti teoremi sulla monotonia. Esempi. Ragazzi, noi L'equazione lineare a x = b ha: un'unica soluzione, per a 0; un insieme infinito di soluzioni, con a = 0, b = 0; non ha soluzioni, per a = 0, b 0. L'equazione quadratica ax 2 + bx + c = 0 ha: due diversi 6 Problemi che portano al concetto di derivata Lasciamo che un punto materiale si muova lungo una linea retta in una direzione secondo la legge s f (t), dove t è il tempo e s è il percorso percorso dal punto nel tempo t. un certo punto Banca di compiti sull'argomento MATEMATICA “DERIVATA” Grado 11 (base) Gli studenti dovrebbero conoscere/capire: Il concetto di derivata. Definizione di derivato. Teoremi e regole per trovare le derivate di una somma, differenza, prodotto Significato geometrico della derivata Consideriamo il grafico della funzione y=f(x) e la tangente nel punto P 0 (x 0 ; f(x 0)). Troviamo a questo punto la pendenza della tangente al grafico. Angolo di inclinazione della tangente P 0 Funzione quadratica in vari problemi Dikhtyar MB Informazioni di base Una funzione quadratica (trinomio quadratico) è una funzione della forma y ax bx c, dove abc, dati numeri e Funzioni quadratiche y IL CONCETTO DI FUNZIONE DERIVATA Sia una funzione definita su un insieme X e sia un punto X un punto interno di quei punti per i quali esiste un intorno X. Prendiamo un punto qualsiasi e lo denotiamo con chiamato Lezione 5 Derivate di funzioni elementari di base Abstract: Vengono fornite interpretazioni fisiche e geometriche della derivata di una funzione di una variabile, vengono considerati esempi di differenziazione di funzioni e regole. 1 SA Lavrenchenko Lezione 12 Funzioni inverse 1 Il concetto di funzione inversa Definizione 11 Una funzione si dice biunivoca se non assume alcun valore più di una volta, quelli che seguono quando Dipartimento di Matematica e Informatica Elementi di Matematica Superiore Complesso didattico e metodologico per gli studenti della formazione professionale secondaria che studiano utilizzando le tecnologie a distanza Modulo Calcolo differenziale A cura di: Capitolo 5 Studio delle funzioni utilizzando la formula di Taylor Estremo locale di una funzione Definizione Funzione = f (raggiunge un massimo (minimo) locale nel punto c, se è possibile specificare un δ > tale che il suo incremento MODULO “Applicazione della continuità e della derivata. Applicazione della derivata allo studio delle funzioni." Applicazione della continuità.. Metodo dell'intervallo.. Tangente al grafico. La formula di Lagrange. 4. Applicazione del derivato Lezione 9. Derivati e differenziali di ordine superiore, loro proprietà. Punti estremi della funzione. Teoremi di Fermat e Rolle. Sia la funzione y differenziabile su un intervallo [b]. In questo caso è la derivata Dipartimento di Matematica e Informatica Analisi matematica Complesso didattico e metodologico per gli studenti delle scuole superiori che studiano utilizzando le tecnologie a distanza Modulo 4 Applicazioni derivate A cura di: Professore Associato Capitolo 1. Limiti e continuità 1. Insiemi di numeri 1 0. Numeri reali Dalla matematica scolastica conosci gli N interi naturali Z i numeri razionali Q e i numeri reali R Numeri naturali e interi Lezione 19 LA DERIVATA E LE SUE APPLICAZIONI. DEFINIZIONE DI DERIVATO. Diamo una funzione y=f(x), definita su un certo intervallo. Per ogni valore dell'argomento x da questo intervallo, la funzione y=f(x) Calcolo differenziale Concetti e formule di base Definizione 1 La derivata di una funzione in un punto è il limite del rapporto tra l'incremento della funzione e l'incremento dell'argomento, a condizione che l'incremento dell'argomento Argomento 8. Funzioni esponenziali e logaritmiche. 1. Funzione esponenziale, suo grafico e proprietà In pratica vengono spesso utilizzate le funzioni y=2 x,y=10 x,y=(1 2x),y=(0,1) x, ecc., cioè la funzione di la forma y=a x, 44 Esempio Trova la derivata totale di una funzione complessa = sin v cos w dove v = ln + 1 w= 1 Usando la formula (9) d v w v w = v w d sin cos + cos cos + 1 sin sin 1 Ora trova il differenziale totale del complesso funzione f Compiti per una soluzione indipendente. Trova il dominio della funzione 6x. Trova la tangente dell'angolo di inclinazione rispetto all'asse x della tangente che passa per il punto M (;) del grafico della funzione. Trova la tangente dell'angolo Argomento Funzione numerica, sue proprietà e grafico Concetto di funzione numerica Dominio di definizione e insieme di valori di una funzione Sia dato un insieme numerico X Una regola che associa ogni numero X a un unico Lezione 23 CONVESSO E CONCAVITÀ DEL GRAFICO DI UNA FUNZIONE DI PUNTO DI FLESSIONE Il grafico della funzione y=f(x) si dice convesso sull'intervallo (a; b) se si trova al di sotto di una qualsiasi delle sue tangenti su tale intervallo. Grafico Argomento Teoria dei limiti Lezione pratica Sequenze numeriche Definizione di una sequenza numerica Sequenze limitate e illimitate Sequenze monotone Infinitesimi Funzioni numeriche e sequenze numeriche D. V. Lytkina NPP, I semestre D. V. Lytkina (SibGUTI) analisi matematica della NPP, I semestre 1 / 35 Contenuti 1 Funzione numerica Concetto di funzione Funzioni numeriche. Banca di compiti sull'argomento MATEMATICA “DERIVATA” classe (profilo) Gli studenti dovrebbero conoscere/capire: Il concetto di derivata. Definizione di derivato. Teoremi e regole per trovare le derivate di una somma, differenza, prodotto UN. UN. MISURAZIONE DEL PERICOLO: IL QUADRO DEL QUADRO. MANUALE DIDATTICO RIPRESA PER SPO - edizione, corretta e integrata dall'Accademia russa delle scienze AV. Matematica Zemlyanko. Algebra e principi di analisi Voronezh INDICE ARGOMENTO 1. PROPRIETÀ FONDAMENTALI DI UNA FUNZIONE... 6 1.1. Funzione numerica... 6 1.2. Grafico di una funzione... 9 1.3. Conversione dei grafici delle funzioni... Soggetto. Funzione. Modalità di assegnazione. Funzione implicita. Funzione inversa. Classificazione delle funzioni Elementi di teoria degli insiemi. Concetti di base Uno dei concetti di base della matematica moderna è il concetto di insieme. Sia dato un insieme numerico D R. Se ogni numero x D è associato a un solo numero y, allora diciamo che sull'insieme D è data una funzione numerica: y = f (x), x D. L'insieme D si chiama Funzioni di più variabili 11. Definizione di funzione di più variabili. Limite e continuità della FNP 1. Definizione di una funzione di più variabili DEFINIZIONE. Sia X = ( 1 n i X i R ) U R. Funzione MATEMATICA PER TUTTI Y.L. Kalinovsky Contenuto 1 Grafici di funzioni. Parte I.................................... 5 1.1 Introduzione 5 1.1.1 Il concetto di insieme.. .................................... 5 1.1. Lavoro pratico 6 Argomento: “Studio completo delle funzioni. Tracciare grafici" Scopo del lavoro: imparare a esplorare le funzioni secondo uno schema generale e costruire grafici. A seguito del completamento del lavoro, lo studente dovrà: Capitolo 8 Funzioni e grafici Variabili e dipendenze tra loro. Due quantità sono dette direttamente proporzionali se il loro rapporto è costante, cioè se =, dove è un numero costante che non cambia al variare LEZIONE 2. Operazioni con sottospazi, numero di basi, numero di basi e numero di sottospazi di dimensione k. Principali risultati della Lezione 2. 1) U V, U + V, dim(u + V). 2) Contare il numero di aerei in F 4 2. Domanda 5. Funzione, modalità di assegnazione. Esempi di funzioni elementari e loro grafica. Siano dati due insiemi arbitrari X e Y. Una funzione è una regola mediante la quale è possibile trovare ciascun elemento dell'insieme X Lezione 4 FUNZIONI NUMERICHE DI UNA VARIABILE REALE Concetto di funzione Metodi per specificare una funzione Proprietà di base delle funzioni Funzione complessa 4 Funzione inversa Concetto di funzione Metodi per specificare una funzione Sia D Lezioni Capitolo Funzioni di più variabili Concetti di base Alcune funzioni di più variabili sono ben note Facciamo alcuni esempi Per calcolare l'area di un triangolo è nota la formula S di Erone Continuità delle funzioni Continuità di una funzione in un punto Limiti unilaterali Definizione Un numero A è detto limite di una funzione f(x) da sinistra poiché x tende ad a se per qualsiasi numero esiste tale numero Lavoro di ricerca Matematica “Applicazione delle proprietà estreme di una funzione per risolvere equazioni” Completato da: Elena Gudkova, studentessa dell'11° grado “G” MBOU della scuola secondaria “Anninsky Lyceum” insediamento urbano. Anna Testa: Agenzia federale per l'istruzione ----- UNIVERSITÀ POLITECNICA STATALE DI SAN PIETROBURGO AI Surygin EF Izotova OA Novikova TA Chaikina MATEMATICA Funzioni elementari e loro grafici Didattica FUNZIONI DI PIÙ VARIABILI Le funzioni di una variabile indipendente non coprono tutte le dipendenze che esistono in natura. Pertanto, è naturale espandere il noto concetto di dipendenza funzionale e introdurlo Funzione Concetto di funzione Metodi per specificare una funzione Caratteristiche di una funzione Funzione inversa Limite di una funzione Limite di una funzione in un punto Limiti unilaterali Limite di una funzione in x Funzione infinitamente grande 4 Lezione Sezione Calcolo differenziale di funzioni di una o più variabili Funzione di argomento reale I numeri reali Gli interi positivi sono chiamati numeri naturali Somma a numeri naturali Sergey A Belyaev pagina 1 Minimo matematico Parte 1 Teorico 1 La definizione è corretta? Il minimo comune multiplo di due interi è il più piccolo numero divisibile per ciascuno dei numeri dati Sezione 2 Teoria dei limiti Argomento Sequenze numeriche Definizione di una sequenza numerica 2 Successioni limitate e illimitate 3 Successioni monotone 4 Infinitesimi e Differenziazione di una funzione data implicitamente Considera la funzione (,) = C (C = cost) Questa equazione definisce la funzione implicita () Supponiamo di aver risolto questa equazione e di aver trovato l'espressione esplicita = () Ora possiamo Compiti di prova per la preparazione all'ESAME nella disciplina "Matematica" per studenti di corrispondenza. La derivata della funzione y=f() si chiama: f A) B) f C) f f Se in qualche intorno di un punto la funzione VARIABILI E QUANTITÀ COSTANTI Come risultato della misurazione delle quantità fisiche (tempo, area, volume, massa, velocità, ecc.), vengono determinati i loro valori numerici. La matematica si occupa di quantità, distrattamente Analisi matematica Sezione: Introduzione all'analisi Argomento: concetto di funzione (definizioni di base, classificazione, caratteristiche di base del comportamento) Docente Rozhkova S.V. Letteratura 2012 Piskunov N.S. Differenziale Lezione 7 Teoremi della media. Regola di L'Hôpital 7. Teoremi sulla media I teoremi sulla media sono tre teoremi: Rolle, Lagrange e Cauchy, ciascuno dei quali generalizza il precedente. Questi teoremi sono anche chiamati Lezione preparata dal Professore Associato Musina MV Continuità di una funzione Sia definita la funzione y = f(x) nel punto x e in qualche intorno di questo punto La funzione y = f(x) si dice continua nel punto x se è esiste DIFFERENZIAZIONE DI FUNZIONI DI UNA VARIABILE Il concetto di derivata, il suo significato geometrico e fisico Problemi che portano al concetto di derivata Determinazione della Tangente S alla retta y f (x) nel punto A x; F ( 13. Derivate parziali di ordine superiore Sia = avere e sono definite su D O. Le funzioni e sono anche chiamate derivate parziali del primo ordine di una funzione o derivate parziali prime di una funzione. e in generale Ministero dell'Istruzione della Repubblica di Bielorussia ISTITUZIONE EDUCATIVA "UNIVERSITÀ STATALE DI GRODNO CHE DÀ IL NOME A YANKA KUPALA" Yu.Yu. Gnezdovsky, V.N. Gorbuzov, P.F. Pronevich ESPONENZIALE E LOGARITMICO Capitolo lezione Insiemi e operazioni su di essi Il concetto di insieme Il concetto di insieme si riferisce ai concetti più elementari della matematica che non sono definiti attraverso concetti più semplici.Un insieme è inteso come una raccolta Lezione 8 Differenziazione di una funzione complessa Considera una funzione complessa t t t f dove ϕ t t t t t t t f t t t t t t t t t Teorema Lascia che le funzioni siano differenziabili in un punto N t t t e la funzione f sia differenziabile Lezione 3 Estremo di una funzione di più variabili Sia definita una funzione di più variabili u = f (x, x) nel dominio D, e a questo dominio appartiene il punto x (x, x) = La funzione u = f ( x, x) ha Domanda. Disuguaglianze, sistema di disuguaglianze lineari Consideriamo le espressioni che contengono un segno di disuguaglianza e una variabile:. >, - +x sono disuguaglianze lineari con una variabile x.. 0 è una disuguaglianza quadratica. SEZIONE PROBLEMI CON I PARAMETRI Commento I problemi con i parametri sono tradizionalmente compiti complessi nella struttura dell'Esame di Stato Unificato, che richiedono al richiedente non solo di padroneggiare tutti i metodi e le tecniche per risolvere vari 2.2.7. Applicazione del differenziale a calcoli approssimati. Il differenziale della funzione y = dipende da x ed è la parte principale dell'incremento di x. Puoi anche usare la formula: dy d Quindi l'errore assoluto è: Capitolo 6 Calcolo differenziale di una funzione di una variabile Problemi che portano al concetto di derivata Problema sulla velocità del movimento rettilineo non uniforme S - la legge del movimento rettilineo non uniforme Retta su un piano Equazione generale della retta. Prima di introdurre l'equazione generale della retta su un piano, introduciamo la definizione generale di retta. Definizione. Un'equazione della forma F(x,y)=0 (1) è detta equazione della retta L COMITATO PER L’ISTRUZIONE GENERALE E PROFESSIONALE DELLA REGIONE DI LENINGRADO BILANCIO DELLO STATO ISTITUTO EDUCATIVO PROFESSIONALE DELLA REGIONE DI LENINGRADO “VOLKHOV ALUMINIUM COLLEGE” Metodologico Regole di derivazione e differenziazione Lascia che la funzione y = f riceva un incremento y f 0 f 0 corrispondente all'incremento dell'argomento 0 Definizione Se esiste un limite al rapporto tra l'incremento della funzione y e il chiamante Università tecnica statale di Mosca intitolata a N.E. Bauman Facoltà di Scienze Fondamentali Dipartimento di Modellazione Matematica A.N. Kaviakovykov, A.P. Kremenko FUNZIONI INVERSE Problemi in cui sono coinvolte funzioni inverse si trovano in vari rami della matematica e nelle sue applicazioni.Un'area importante della matematica sono i problemi inversi nella teoria degli integrali Sistema di problemi sull'argomento "Equazione tangente" Determinare il segno della pendenza della tangente disegnata sul grafico della funzione y f (), nei punti con ascisse a, b, c a) b) Indicare i punti in cui la derivata Espressioni corrispondenti che si invertono. Per capire cosa significa, vale la pena guardare un esempio specifico. Diciamo che abbiamo y = cos(x). Se prendi il coseno dall'argomento, puoi trovare il valore di y. Ovviamente, per questo è necessario avere X. Ma cosa succederebbe se il gioco fosse stato inizialmente regalato? È qui che si arriva al nocciolo della questione. Per risolvere il problema è necessario utilizzare la funzione inversa. Nel nostro caso è l'arcocoseno. Dopo tutte le trasformazioni otteniamo: x = arccos(y). Cioè, per trovare una funzione inversa a una data, è sufficiente esprimere semplicemente un argomento da essa. Ma questo funziona solo se il risultato risultante ha un unico significato (ne parleremo più avanti). In termini generali, questo fatto può essere scritto come segue: f(x) = y, g(y) = x. Sia f una funzione il cui dominio è l'insieme X e il cui dominio è l'insieme Y. Allora, se esiste una g i cui domini svolgono compiti opposti, allora f è invertibile. Inoltre, in questo caso g è unico, il che significa che esiste esattamente una funzione che soddisfa questa proprietà (né più né meno). Allora si chiama funzione inversa, e per iscritto si denota come segue: g(x) = f -1 (x). In altre parole, possono essere pensati come una relazione binaria. La reversibilità si verifica solo quando un elemento dell'insieme corrisponde a un valore di un altro. La funzione inversa non esiste sempre. Per fare ciò, ogni elemento y є Y deve corrispondere al più a un x є X. Allora f è detta biunivoca o iniezione. Se f -1 appartiene a Y, allora ogni elemento di questo insieme deve corrispondere a qualche x ∈ X. Le funzioni con questa proprietà sono chiamate suriezioni. Vale per definizione se Y è un'immagine di f, ma non è sempre così. Per essere inversa, una funzione deve essere sia un'iniezione che una suriezione. Tali espressioni sono chiamate biiezioni. La funzione è definita su )
Definizione
Esempio: funzioni quadrata e radice