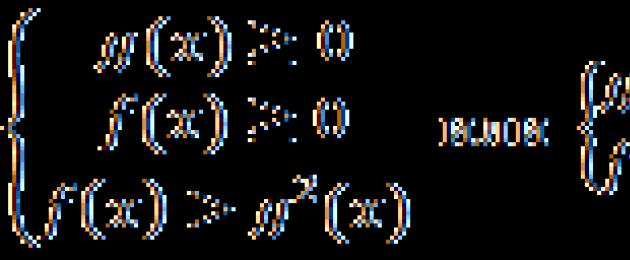Неравенства с квадратным корнем. Решение иррациональных неравенств

В данном уроке мы рассмотрим решение иррациональных неравенств, приведем различные примеры.

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Иррациональные неравенства

При решении иррациональных неравенств довольно часто необходимо возводить обе части неравенства в некоторую степень, это довольно ответственная операция. Напомним особенности.

Обе части неравенства можно возвести в квадрат, если обе они неотрицательны, только тогда мы получаем из верного неравенства верное неравенство.

Обе части неравенства можно возвести куб в любом случае, если исходное неравенство было верным, то при возведении в куб мы получим верное неравенство.

Рассмотрим неравенство вида:

Подкоренное выражение должно быть неотрицательным. Функция может принимать любые значения, необходимо рассмотреть два случая.

В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) больше отрицательного выражения, значит, неравенство выполняется всегда.

Итак, имеем следующую схему решения:

В первой системе мы не защищаем отдельно подкоренное выражение, т. к. при выполнении второго неравенства системы подкоренное выражение автоматически должно быть положительно.

Пример 1 - решить неравенство:

Согласно схеме, переходим к эквивалентной совокупности двух систем неравенств:

Проиллюстрируем:

Рис. 1 - иллюстрация решения примера 1

Как мы видим, при избавлении от иррациональности, например, при возведении в квадрат, получаем совокупность систем. Иногда эту сложную конструкцию можно упростить. В полученной совокупности мы имеем право упростить первую систему и получить эквивалентную совокупность:

В качестве самостоятельного упражнения необходимо доказать эквивалентность данных совокупностей.

Рассмотрим неравенство вида:

Аналогично предыдущему неравенству, рассматриваем два случая:

В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) меньше отрицательного выражения, значит, неравенство противоречиво. Вторую систему рассматривать не нужно.

Имеем эквивалентную систему:

Иногда иррациональное неравенство можно решить графическим методом. Данный способ применим, когда соответствующие графики можно достаточно легко построить и найти их точки пересечения.

Пример 2 - решить неравенства графически:

а)

б)

Первое неравенство мы уже решали и знаем ответ.

Чтобы решить неравенства графически, нужно построить график функции, стоящей в левой части, и график функции, стоящей в правой части.

Рис. 2. Графики функций и

Для построения графика функции необходимо преобразовать параболу в параболу (зеркально отобразить относительно оси у), полученную кривую сместить на 7 единиц вправо. График подтверждает, что данная функция монотонно убывает на своей области определения.

График функции - это прямая, ее легко построить. Точка пересечения с осью у - (0;-1).

Первая функция монотонно убывает, вторая монотонно возрастает. Если уравнение имеет корень, то он единственный, по графику легко его угадать: .

Когда значение аргумента меньше корня, парабола находится выше прямой. Когда значение аргумента находится в пределах от трех до семи, прямая проходит выше параболы.

Имеем ответ:

Эффективным методом решения иррациональных неравенств является метод интервалов.

Пример 3 - решить неравенства методом интервалов:

а)

б)

согласно методу интервалов, необходимо временно отойти от неравенства. Для этого перенести в заданном неравенстве все в левую часть (получить справа ноль) и ввести функцию, равную левой части:

теперь необходимо изучить полученную функцию.

ОДЗ:

Данное уравнение мы уже решали графически, поэтому не останавливаемся на определении корня.

Теперь необходимо выделить интервалы знакопостоянства и определить знак функции на каждом интервале:

Рис. 3. Интервалы знакопостоянства к примеру 3

Напомним, что для определения знаков на интервале необходимо взять пробную точку и подставить ее в функцию, полученный знак функция будет сохранять на всем интервале.

Проверим значение в граничной точке:

Очевиден ответ:

Рассмотрим следующий тип неравенств:

Сначала запишем ОДЗ:

Корни существуют, они неотрицательны, обе части можем возвести в квадрат. Получаем:

Получили эквивалентную систему:

Полученную систему можно упростить. При выполнении второго и третьего неравенств первое истинно автоматически. Имеем::

Пример 4 - решить неравенство:

Действуем по схеме - получаем эквивалентную систему.

Всякое неравенство, в состав которого входит функция, стоящая под корнем, называется иррациональным . Существует два типа таких неравенств:

В первом случае корень меньше функции g (x ), во втором - больше. Если g (x ) - константа , неравенство резко упрощается. Обратите внимание: внешне эти неравенства очень похожи, но схемы решения у них принципиально различаются.

Сегодня научимся решать иррациональные неравенства первого типа - они самые простые и понятные. Знак неравенства может быть строгим или нестрогим. Для них верно следующее утверждение:

Теорема. Всякое иррациональное неравенство вида

Равносильно системе неравенств:

Неслабо? Давайте рассмотрим, откуда берется такая система:

1. f (x ) ≤ g 2 (x ) - тут все понятно. Это исходное неравенство, возведенное в квадрат;
2. f (x ) ≥ 0 - это ОДЗ корня. Напомню: арифметический квадратный корень существует только из неотрицательного числа;
3. g (x ) ≥ 0 - это область значений корня. Возводя неравенство в квадрат, мы сжигаем минусы. В результате могут возникнуть лишние корни. Неравенство g (x ) ≥ 0 отсекает их.

Многие ученики «зацикливаются» на первом неравенстве системы: f (x ) ≤ g 2 (x ) - и напрочь забывают два других. Результат предсказуем: неправильное решение, потерянные баллы.

Поскольку иррациональные неравенства - достаточно сложная тема, разберем сразу 4 примера. От элементарных до действительно сложных. Все задачи взяты из вступительных экзаменов МГУ им. М. В. Ломоносова.

Примеры решения задач

Задача. Решите неравенство:

Перед нами классическое иррациональное неравенство : f (x ) = 2x + 3; g (x ) = 2 - константа. Имеем:

Из трех неравенств к концу решения осталось только два. Потому что неравенство 2 ≥ 0 выполняется всегда. Пересечем оставшиеся неравенства:

Итак, x ∈ [−1,5; 0,5]. Все точки закрашены, поскольку неравенства нестрогие .

Задача. Решите неравенство:

Применяем теорему:

Решаем первое неравенство. Для этого раскроем квадрат разности. Имеем:

2x 2 − 18x + 16 < (x − 4) 2 ;
2x 2 − 18x + 16 < x 2 − 8x + 16:
x 2 − 10x < 0;
x (x − 10) < 0;
x ∈ (0; 10).

Теперь решим второе неравенство. Там тоже квадратный трехчлен :

2x 2 − 18x + 16 ≥ 0;
x 2 − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪}