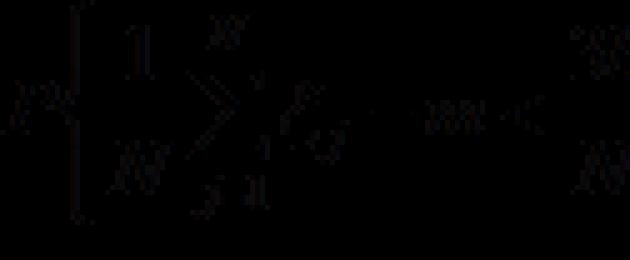Метод Монте-Карло относится к методам __________ моделирования. Метод монте карло Метод монте карло в физических процессах пример

Лекция 5.

Метод Монте-Карло

Тема 3. Процессы массового обслуживания в экономических системах

1. Вводные замечания. 1

2. Общая схема метода Монте-Карло. 2

3. Пример расчета системы массового обслуживания методом Монте-Карло. 4

Контрольные вопросы.. 5

1. Вводные замечания

Метод статистического моделирования на ЭВМ - основной метод получения результатов с помощью имитационных моделей стохастических систем, использующий в качестве теоретической базы предельные теоремы теории вероятностей. Основа - метод статистических испытаний Монте-Карло.

Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Как правило, предполагается, что моделирование осуществляется с помощью электронных вычислительных машин (ЭВМ), хотя в некоторых случаях можно добиться успеха, используя приспособления типа рулетки, карандаша и бумаги.

Термин "метод Монте-Карло" (предложенный Дж. Фон Нейманом и в 1940-х) относится к моделированию процессов с использованием генератора случайных чисел. Термин Монте-Карло (город, широко известный своими казино) произошел от того факта, что "число шансов" (методы моделирования Монте-Карло) было использовано с целью нахождения интегралов от сложных уравнений при разработке первых ядерных бомб (интегралы квантовой механики). С помощью формирования больших выборок случайных чисел из, например, нескольких распределений, интегралы этих (сложных) распределений могут быть аппроксимированы из (сгенерированных) данных.

Возникновение идеи использования случайных явлений в области приближенных вычислений принято относить к 1878 г., когда появилась работа Холла об определении чисел p с помощью случайных бросаний иглы на разграфленную параллельными линиями бумагу. Существо дела заключается в том, чтобы экспериментально воспроизвести событие, вероятность которого выражается через число p, и приближенно оценить эту вероятность.

Отечественные работы по методу Монте-Карло появились в гг. За два десятилетия накопилась обширная библиография по методу Монте-Карло, которая насчитывает более 2000 названий. При этом даже беглый просмотр названий работ позволяет сделать вывод о применимости методы Монте-Карло для решения прикладных задач из большого числа областей науки и техники.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались мало пригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию. К разделам науки, где все в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.

Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие метода вычислительной математики (например, развитие методов численного интегрирования) и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественностью получения ответа с некоторой заданной вероятностью в задачах с вероятным содержанием, так и существенным упрощением процедуры решения. Трудность решения той или иной задачи на ЭВМ определятся в значительной мере трудностью переложения ее на «язык» машины. Создание языков автоматического программирования существенно упростило один из этапов этой работы. Наиболее сложными этапами поэтому в настоящее время являются: математическое описание исследуемого явления, необходимые упрощения задачи, выбор подходящего численного метода, исследование его погрешности и запись алгоритма. В тех случаях, когда имеется теоретико-вероятностное описание задачи, использование метода Монте-Карло может существенно упростить упомянутые промежуточные этапы. Впрочем, как будет следовать из дальнейшего, во многих случаях полезно и для задач строго детерминированных строить вероятностную модель (рандомизовать исходную задачу) с тем, чтобы далее использовать метод Монте-Карло.

2. Общая схема метода Монте-Карло

Предположим, что нам требуется вычислить некоторую неизвестную величину m, и мы хотим сделать это, рассматривая случайную величину такую, что ее математическое ожидание М, = m. Пусть при этом дисперсия данной случайной величины D = b.

Рассмотрим N случайных независимых величин,,…, распределения которых совпадают с распределением рассматриваемой случайной величины ξ..gif" width="247" height="48">

Последнее соотношение можно переписать в виде

Полученная формула дает метод расчета т и оценку погрешности этого метода.

Сущность применения метода Монте-Карло заключается в определении результатов на основании статистики, полу чаемой к моменту принятия некоторого решения.

Например. Пусть Е1 и Е2 - две единственно возможные реализации некоторого случайного процесса, причем p1 - - вероятность исхода Е1, а р2 = 1 – p1 - вероятность исхода Е2. Чтобы определить, какое из двух событий, e1 или Е2, имеет место в данном случае, возьмем в интервале между 0 и 1 случайное число и, равномерно распределенное в интервале (0, 1), и произведем испытание. Исход Е1 будет иметь место, если , а исход Е2 - в противном случае.

Таким образом, достоверность результатов, получаемых при использовании метода Монте-Карло, решающим образом определяется качеством генератора случайных чисел.

Для получения случайных чисел на ЭВМ используются способы генерирования, которые обычно основаны на много кратном повторении некоторой операции. Полученной таким образом последовательности более соответствует название псевдослучайных чисел, поскольку генерируемая последовательность является периодичной и, начиная с некоторого момента, числа начнут повторяться. Это следует из того, что в коде ЭВМ можно записать лишь конечное число различных чисел. Следовательно, в конце концов одно из генерируемых чисел γ1, совпадет с одним из предыдущих членов последовательности γL. А поскольку генерация осуществляется по формуле вида

γк+1 = F(γk),

с этого момента будут повторяться и остальные члены последовательности.

Использование равномерно распределенных случайных чисел составляет основу моделирования с помощью метода Монте-Карло. Можно сказать, что если некоторая случайная величина была определена с помощью метода Монте-Карло, то для ее вычисления использовалась последовательность равномерно распределенных случайных чисел.

Равномерно распределенные случайные числа заключены в интервале от 0 до 1 и выбираются случайным образом в соответствии с функцией распределения

F(x) = Рr{Х< х} = х, .

При этом распределении одинаково правдоподобно по явление любых значений случайной величины в интервале (0, 1). Здесь Рг{Х< х} - вероятность того, что случайная величина X примет значение меньше х.

Основным методом получения случайных чисел является их генерация по модулю. Пусть m, a, с, х0 - целые числа, такие, что m > х0 и а, с, х0 > 0. Псевдослучайное число хi из последовательности {хi} получается с помощью рекуррентного соотношения

xi = а xi-1 + с (mod m).

Стохастические характеристики генерируемых чисел решающим образом зависят от выбора m, а и с. Их неудачный выбор приводит к ошибочным результатам при моделировании методом Монте-Карло.

Для численного моделирования часто требуется большое количество случайных чисел. Следовательно, период последовательности генерируемых случайных чисел, после которого последовательность начинает повторяться, должен быть достаточно большим. Он должен быть существенно больше требуемого для моделирования количества случайных чисел, иначе получаемые результаты будут искажены.

Большинство компьютеров и программных оболочек содержат генератор случайных чисел. Однако большинство статистических тестов показывает коррелированность между получаемыми случайными числами.

Существует быстрый тест, с помощью которого необходимо проверять каждый генератор. Качество генератора случайных чисел можно продемонстрировать, заполняя полностью d-мерную решетку (например, двух - или трехмерную). Хороший генератор должен заполнить все пространство гиперкуба.

Другой приближенный способ проверки равномерности распределения N случайных чисел хi состоит в вычислении их математического ожидания и дисперсии. Согласно этому критерию, для равномерного распределения должны выполняться условия

Существует множество статистических критериев, которые можно использовать для проверки того, будет ли последовательность случайной. Наиболее точным считается спектральный критерий. Например, очень распространенный критерий, называемый КС-критерием, или критерием Колмогорова-Смирнова. Проверка показывает, что, например, генератор случайных чисел в электронных таблицах Excel не удовлетворяет данному критерию.

На практике главной проблемой является построение простого и надежного генератора случайных чисел, который можно использовать в своих программах. Для этого предлагается следующая процедура.

В начале программы целой переменной X присваивается некоторое значение Х0. Затем случайные числа генерируются по правилу

X = (аХ + с) mod m. (1)

Выбор параметров следует осуществлять, пользуясь следующими основными принципами.

1. Начальное число Х0 можно выбрать произвольно. Если программа используется несколько раз и каждый раз требуются различные источники случайных чисел, можно, например, присвоить Х0 значение X, полученное последним на предыдущем прогоне.

2.Число m должно быть большим, например, 230 (поскольку именно это число определяет период генерируемой псевдослучайной последовательности).

3.Если m - степень двойки, выбирают а таким, чтобы a mod8 = 5. Если m - степень десяти, выбирают а таким, чтобы a mod10 = 21. Такой выбор гарантирует, что генератор случайных чисел будет вырабатывать все m возможных значений, прежде чем они начнут повторяться.

4.Множитель а предпочтительнее выбирать лежащим между 0.01m и 0.99m, и его двоичные или десятичные цифры не должны иметь простую регулярную структуру. Множитель должен пройти спектральный критерий и, желательно, еще несколько критериев.

5.Если a - хороший множитель, значение с не существен но, за исключением того, что с не должно иметь общего множителя с m, если m - размер компьютерного слова. Можно, например, выбрать с = 1 или с = а.

6. Можно генерировать не больше m/1000 случайных чисел. После этого должна использоваться новая схема, например, новый множитель а .

Перечисленные правила, главным образом, относятся к машинному языку программирования. Для языка программирования высокого уровня, например С++, часто используют другой вариант (1): выбирается простое число m, близкое к наибольшему легко вычисляемому целому числу, значение а полагается равным первообразному корню из m, а с берется равным нулю. Например, можно принять a = 48271 и т =

3. Пример расчета системы массового обслуживания методом Монте-Карло

Рассмотрим простейшую систему массового обслуживания (СМО), которая состоит из n линий (иначе называемых каналами или пунктами обслуживания). В случайные моменты времени в систему поступают заявки. Каждая заявка поступает на линию № 1. Если в момент поступления за явки Тк эта линия свободна, заявка обслуживается время t3 (время занятости линии). Если линия занята, заявка мгновенно передается на линию № 2 и т. д. Если все n линий в данный момент заняты, то система выдает отказ.

Естественной является задача определения характеристик данной системы, по которым можно оценить ее эффективность: среднее время ожидания обслуживания, доля времени простоя системы, среднюю длину очереди и т. д.

Для подобных систем практически единственным методом расчета является метод Монте-Карло.

https://pandia.ru/text/78/241/images/image013_34.gif" width="373" height="257">

Для получения случайных чисел на ЭВМ используются алгоритмы, поэтому такие последовательности, являющиеся по сути детерминированными, называются псевдослучайными. ЭВМ оперирует n-разрядными числами, поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2n случайных чисел того же интервала - закон распределения такой дискретной последовательности называется квазиравномерны распределением.

Требования к идеальному генератору случайных чисел:

1. Последовательность должна состоять из квазиравномерно распределенных чисел.

2. Числа должны быть независимыми.

3. Последовательности случайных чисел должны быть воспроизводимыми.

4. Последовательности должны иметь неповторяющиеся числа.

5. Последовательности должны получаться с минимальными затратами вычислительных ресурсов.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных числе находят алгоритмы вида:

представляющие собой реккурентные соотношения первого порядка.

Например. x0 = 0,2152 , (x0)2=0, x1 = 0,6311 , (x1)2=0, x2=0,8287 и т. д.

Недостаток подобных методов - наличие коррелляции между числами последовательности, а иногда случайность вообще отсутствует, например:

x0 = 0,4500 , (x0)2=0, x1 = 0,2500 , (x1)2=0, x2=0,2500 и т. д.

Широкое применение получили конгруэнтные процедуры генерации псевдослучайных последовательностей.

Два целых числа a и b конгруэнтны (сравнимы) по модулю m, где m - целое число, тогда и только тогда, когда существует такое целое число k, что a-b=km.

1984º4 (mod 10), 5008º8 (mod 103).

Большинство конгруэнтных процедур генерации случайных чисел основаны на следующей формуле:

где - неотрицательные целые числа.

По целым числам последовательности {Xi} можно построить последовательность {xi}={Xi/M} рациональных чисел из единичного интервала (0,1).

Применяемые генераторы случайных чисел перед моделированием должны пройти тщательное предварительное тестирование на равномерность, стохастичность и независимость получаемых последовательностей случайных чисел.

Методы улучшения качества последовательностей случайных чисел:

1. Использование рекуррентных формул порядка r:

Но применение этого способа приводит к увеличению затрат вычислительных ресурсов на получение чисел.

2. Метод возмущений:

.

5. Моделирование случайных воздействий на системы

1. Необходимо реализовать случайное событие А, наступающее с заданной вероятностью p. Определим А как событие, состоящее в том, что выбранное значение xi равномерно распределенной на интервале (0,1) случайной величины удовлетворяет неравенству:

Тогда вероятность события А будет https://pandia.ru/text/78/241/images/image019_31.gif" width="103" height="25">,

Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел xi со значениями lr. Если условие выполняется, исходом испытания оказывается событие Аm.

3. Рассмотрим независимые события А и В с вероятностями наступления рА и рВ. Возможными исходами совместных испытаний в этом случае будут события АВ, с вероятностями рАрВ, (1-рА)рВ, рА(1-рВ), (1-рА)(1-рВ). Для моделирования совместных испытаний можно использовать два варианта процедуры:

Последовательное выполнение процедуры, рассмотренной в п.1.

Определение одного из исходов АВ, по жребию с соответствующими вероятностями, т. е. процедура, рассмотренная в п.2.

Первый вариант потребует двух чисел xi и двух сравнений. При втором варианте можно обойтись одним числом xi, но сравнений может потребоваться больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и памяти ЭВМ более предпочтителен первый вариант.

4. События А и В являются зависимыми и наступают с вероятностями pА и pВ. Обозначим через pА(В) условную вероятность наступления события В при условии, что событие А произошло.

Контрольные вопросы

1) Как можно определить метод Монте-Карло?

2) Практическое значение метода Монте-Карло.

3) Общая схема метода Монте-Карло.

4) Пример расчета системы массового обслуживания методом Монте-Карло.

5) Способы генерации случайных чисел.

6) Каковы требования к идеальному генератору случайных чисел?

7) Методы улучшения качества последовательностей случайных чисел.

Различные методы и приборы для определения параметров и характеристик случайных процессов можно объединить в две группы. Первую группу составляют приборы для определения корреляционных функций (корреляторы), спектральных плотностей (спектрометры), математических ожиданий, дисперсий, законов распределения и прочих случайных процессов и величин.

Все приборы первой группы можно разделить на две подгруппы. Одни определяют характеристики записанных случайных сигналов за достаточно большое время, намного превышающее время реализации самого случайного процесса. Другие (они в последнее время вызывают наибольший интерес) позволяют получать характеристики случайного процесса оперативно, в такт с поступлением информации при натурных испытаниях новых систем управления, так как, пользуясь их показаниями, можно непосредственно изменять процесс управления и в ходе эксперимента наблюдать за результатами этих изменений.

Вторая группа содержит методы и приборы, предназначенные для исследования случайных процессов и главным образом систем управления, в которых присутствуют случайные сигналы, на универсальных цифровых и аналоговых вычислительных машинах. Иногда для таких исследований приходится создавать специализированные вычислительные машины цифрового, аналогового или чаще всего аналого-цифрового (гибридного) типа, так как существующие типовые машины не приспособлены для решения некоторых задач.

Широко применяется на практике метод Монте-Карло (метод статических испытаний). Его основная идея чрезвычайно проста и заключается по существу в математическом моделировании на вычислительной машине тех случайных процессов и преобразований с ними, которые имеют место в реальной системе управления. Этот метод в основном реализуется на цифровых и, реже, на аналоговых вычислительных машинах.

Можно утверждать, что метод Монте-Карло остаётся чистым методом моделирования случайных процессов, чистым математическим экспериментом, в известном смысле лишённым ограничений, свойственным другим методам. Рассмотрим данный метод применительно к решению различных задач управления.

Общая характеристика метода Монте-Карло

Как уже указывалось, идея метода Монте-Карло (или метода статистического моделирования) очень проста и заключается в том, что в вычислительной машине создаётся процесс преобразования цифровых данных, аналогичный реальному процессу. Вероятностные характеристики обоих процессов (реального и смоделированного) совпадают с какой-то точностью.

Допустим, необходимо вычислить математическое ожидание случайной величины X, подчиняющейся некоторому закону распределения F(x). Для этого в машине реализуют датчик случайных чисел, имеющий данное распределение F(x), и по формуле, которую легко запрограммировать, определяют оценку математического ожидания:

Каждое значение случайной величины x i представляется в машине двоичным числом, которое поступает с выхода датчика случайных чисел на сумматор. Для статистического моделирования рассматриваемой задачи требуется N-кратное повторение решения.

Рассмотрим ещё один пример. Производится десять независимых выстрелов по мишени. Вероятность попадания при одном выстреле задана и равна p. Требуется определить вероятность того, что число попаданий будет чётным, т.е. 0, 2, 4, 6, 8, 10. Вероятность того, что число попаданий будет 2k, равна:

откуда искомая вероятность

Если эта формула известна, то можно осуществить физический эксперимент, произведя несколько партий выстрелов (по десять в каждой) по реальной мишени. Но проще выполнить математический эксперимент на вычислительной машине следующим образом. Датчик случайных чисел выдаст в цифровом виде значение случайной величины?, подчиняющейся равномерному закону распределения в интервале . Вероятность неравенства?

Для пояснения целесообразно обратиться к рис. 1, на котором весь набор случайных чисел представляется в виде точек отрезка . Вероятность попадания случайной величины?, имеющей равномерное распределение в интервале , в интервал (где) равна длине этого отрезка, т.е. p. Поэтому на каждом такте моделирования полученное число? сравнивают с заданной вероятностью p. Если?

Различают две области применения метода Монте-Карло. Во-первых, для исследования на вычислительных машинах таких случайных явлений и процессов, как прохождение элементарных ядерных частиц (нейтронов, протонов и пр.) через вещество, системы массового обслуживания (телефонная сеть, система парикмахерских, система ПВО и пр.), надёжность сложных систем, в которых выход из строя элементов и устранения неисправностей являются случайными процессами, статистическое распознавание образов. Это - применение статистического моделирования к изучению так называемых вероятностных систем управления.

Этот метод широко применяется и для исследования дискретных систем управления, когда используются кибернетические модели в виде вероятностного графа (например, сетевое планирование с?-распределением времени выполнением работ) или вероятностного автомата.

Если динамика системы управления описывается дифференциальными или разностными уравнениями (случай детерминированных систем управления) и на систему, например угловую следящую систему радиолокационной станции воздействуют случайные сигналы, то статическое моделирование также позволяет получить необходимые точностные характеристики. В данном случае с успехом применяются как аналоговые, так и цифровые вычислительные машины. Однако, учитывая более широкое применение при статистическом моделировании цифровых машин, рассмотрим в данном разделе вопросы, связанные только с этим типом машин.

Вторая область применения метода Монте-Карло охватывает чисто детерминированные, закономерные задачи, например нахождение значений определённых одномерных и многомерных интегралов. Особенно проявляется преимущество этого метода по сравнению с другими численными методами в случае кратных интегралов.

При решении алгебраических уравнений методом Монте-Карло число операций пропорционально числу уравнений, а при их решении детерминированными численными методами это число пропорционально кубу числа уравнений. Такое же приблизительно преимущество сохраняется вообще при выполнении различных вычислений с матрицами и особенно в операции обращения матрицы. Надо заметить, что универсальные вычислительные машины не приспособлены для матричных вычислений и метод Монте-Карло, применённый на этих машинах, лишь несколько улучшает процесс решения, но особенно преимущества вероятностного счёта проявляются при использовании специализированных вероятностных машин. Основной идеей, которая используется при решении детерминированных задач методом Монте-Карло, является замена детерминированной задачи эквивалентной статистической задачей, к которой можно применять этот метод. Естественно, что при такой замене вместо точного решения задачи получается приближённое решение, погрешность которого уменьшается с увеличением числа испытаний.

Эта идея используется в задачах дискретной оптимизации, которые возникают при управлении. Часто эти задачи сводятся к перебору большого числа вариантов, исчисляемого комбинаторными числами вида N=. Так, задача распределения n видов ресурсов между отраслями для n>3 не может быть точно решена на существующих цифровых вычислительных машинах (ЦВМ) и ЦВМ ближайшего будущего из-за большого объёма перебора вариантов. Однако таких задач возникает очень много в кибернетике, например синтез конечных автоматов. Если искусственно ввести вероятностную модель-аналог, то задача существенно упростится, правда, решение будет приближённым, но его можно получить с помощью современных вычислительных машин за приемлемое время счёта.

При обработке больших массивов информации и управлении сверхбольшими системами, которые насчитывают свыше 100 тыс. компонентов (например, видов работ, промышленных изделий и пр.), встаёт задача укрупнения или эталонизации, т.е. сведения сверхбольшого массива к 100-1000 раз меньшему массиву эталонов. Это можно выполнить с помощью вероятностной модели. Считается, что каждый эталон может реализоваться или материализоваться в виде конкретного представителя случайным образом с законом вероятности, определяемым относительной частотой появления этого представителя. Вместо исходной детерминированной системы вводится эквивалентная вероятностная модель, которая легче поддаётся расчёту. Можно построить несколько уровней, строя эталоны эталонов. Во всех этих вероятностных моделях с успехом применяется метод Монте-Карло. Очевидно, что успех и точность статистического моделирования зависит в основном от качества последовательности случайных чисел и выбора оптимального алгоритма моделирования.

Задача получения случайных чисел обычно разбивается на две. Вначале получают последовательность случайных чисел, имеющих равномерное распределение в интервале . Затем из неё получают последовательность случайных чисел, имеющих произвольный закон распределения. Один из способов такого преобразования состоит в использовании нелинейных преобразований. Пусть имеется случайная величина X, функция распределения вероятности для которой

Если y является функцией x, т.е. y=F(x), то и поэтому. Таким образом, для получения последовательности случайных чисел, имеющих заданную функцию распределения F(x), необходимо каждое число y с выхода датчика случайных чисел, который формирует числа с равномерным законом распределения в интервале , подать на нелинейное устройство (аналоговое или цифровое), в котором реализуется функция, обратная F(x), т.е.

Полученная таким способом случайная величина X будет иметь функцию распределения F(x). Рассмотренная выше процедура может быть использована для графического способа получения случайных чисел, имеющих заданный закон распределения. Для этого на миллиметровой бумаге строится функция F(x) и вводится в рассмотрение другая случайная величина Y, которая связана со случайной величиной X соотношением (2) (рис. 2).

Так как любая функция распределения монотонно неубывающая, то

Отсюда следует, что величина Y имеет равномерный закон распределения в интервале , т. к. её функция распределения равна самой величине

Плотность распределения вероятности для Y

Для получения значения X берётся число из таблиц случайных чисел, имеющих равномерное распределение, которое откладывается на оси ординат (рис. 2), и на оси абсцисс считывается соответствующее число X. Повторив неоднократно эту процедуру, получим набор случайных чисел, имеющих закон распределения F(x). Таким образом, основная проблема заключается в получении равномерно распределённых в интервале случайных чисел. Один из методов, который используется при физическом способе получения случайных чисел для ЭВМ, состоит в формировании дискретной случайной величины, которая может принимать только два значения: 0 или 1 с вероятностями

Можно доказать, что случайная величина? * , заключённая в интервале , имеет равномерный закон распределения

В цифровой вычислительной машине имеется конечное число разрядов k. Поэтому максимальное количество несовпадающих между собой чисел равно 2 k . В связи с этим в машине можно реализовать дискретную совокупность случайных чисел, т.е. конечное множество чисел, имеющих равномерный закон распределения. Такое распределение называется квазиравномерным. Возможные значения реализации дискретного псевдослучайного числа в вычислительной машине с k разрядами будут иметь вид:

Вероятность каждого значения (3) равна 2 -k . Эти значения можно получить следующим образом

Случайная величина имеет математическое ожидание

Учитывая, что

и выражение для конечной суммы геометрической прогрессии

получаем:

Аналогично можно определить дисперсию величины:

или, используя формулу (4), получаем:

Согласно формуле (5) оценка величины?* получается смещённой при конечном k. Это смещение особенно сказывается при малом k. Поэтому вместо вводят оценку

Очевидно, что случайная величина? в соответствии с соотношением (3) может принимать значения

I=0,1,2,…, 2 k -1

с вероятностью p=1/2 k .

Математическое ожидание и дисперсию величины? можно получить из соотношений (5) и (6), если учесть (7). Действительно,

Отсюда получаем выражение для среднеквадратичного значения в виде

Напомним, что для равномерно распределённой в интервале величины x имеем

Из формулы (8) следует, что при среднеквадратичное отклонение? квазиравномерной совокупности стремится к. Ниже приведены значения отношения среднеквадратичных значений двух величин? и? в зависимости от числа разрядов, причём величина? имеет равномерное распределение в интервале (табл. 1).

Таблица 1

Из табл. 1 видно, что при k>10 различие в дисперсиях несущественно.

На основании вышеизложенного задача получения совокупности квазиравномерных чисел сводится к получению последовательности независимых случайных величин z i (i=1,2,…, k), каждая из которых принимает значение 0 или 1 с вероятностью 1/2. Различают два способа получения совокупности этих величин: физический способ генерирования и алгоритмическое получение так называемых псевдослучайных чисел. В первом случае требуется специальная электронная приставка к цифровой вычислительной машине, во втором случае загружаются блоки машины.

При физическом генерировании чаще всего используются радиоактивные источники или шумящие электронные устройства. В первом случае радиоактивные частицы, излучаемые источником, поступают на счётчик частиц. Если показание счётчика чётное, то z i =1, если нечётное, то z i =0. Определим вероятность того, что z i =1. Число частиц k, которое испускается за время?t, подчиняются закону Пуассона:

Вероятность чётного числа частиц

Таким образом, при больших??t вероятность P{Z i =1} близка к 1/2.

Второй способ получения случайных чисел z i более удобен и связан с собственными шумами электронных ламп. При усилении этих шумов получается напряжение u(t), которое является случайным процессом. Если брать его значения, достаточно отстоящие друг от друга, так чтобы они были некоррелированы, то величины u(t i) образуют последовательность независимых случайных величин. Обычно выбирают уровень отсечки a и полагают

причём уровень a следует выбрать так, чтобы

Также применяется более сложная логика образования чисел z i . В первом варианте используют два соседних значения u(t i) и u(t i+1), и величина Z i строится по такому правилу:

Если пара u(t i) - a и u(t i+1) - a одного знака, то берётся следующая пара. Требуется определить вероятность при заданной логике. Будем считать, что P {u(t i)>a}=W и постоянная для всех t i . Тогда вероятность события равна по формуле событий A 1 H v . Здесь H v - это вероятность того, что v раз появилась пара одинакового знака

u(t i) - a; u(t i+1) - a. (9)

Поэтому вероятность события A 1 H v

P{A 1 H v }=W (1-W) v .

Это - вероятность того, что после v пар вида (9) появилось событие A 1 . Оно может появиться сразу с вероятностью W (1-W), оно может появиться и после одной пары вида (9) с вероятностью

W (1-W)

и т.д. В результате

Отсюда следует, что если W=const, то логика обеспечивает хорошую последовательность случайных чисел. Второй способ формирования чисел zi состоит в следующем:

W=P {u(t i)>a}=1/2+?.

P{Z i =1}=2W (1-W)=1/2-2? 2 .

Чем меньше?, тем ближе вероятность P{Z i =1} к величине 1/2.

Для получения случайных чисел алгоритмическим путём с помощью специальных программ на вычислительной машине разработано большое количество методов. Так как на ЦВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно набрать конечное множество чисел, такие последовательности называются псевдослучайными. На самом деле повторяемость или периодичность в последовательности псевдослучайных чисел наступает значительно раньше и обусловливается спецификой алгоритма получения случайных чисел. Точные аналитические методы определения периодичности, как правило, отсутствуют, и величина периода последовательности псевдослучайных чисел определяется экспериментально на ЦВМ. Большинство алгоритмов получается эвристически и уточняется в процессе экспериментальной проверки. Рассмотрение начнём с так называемого метода усечений. Пусть задана произвольная случайная величина u, изменяющаяся в интервале , т.е. . Образуем из неё другую случайную величину

u n =u , (10)

где u используется для определения операции получения остатка от деления числа u на 2 -n . Можно доказать, что величины u n в пределе при имеют равномерное распределение в интервале .

По существу с помощью формулы (10) осуществляется усечение исходного числа со стороны старших разрядов. При оставлении далёких младших разрядов естественно исключается закономерность в числах и они более приближаются к случайным. Рассмотрим это на примере.

Пример 1. Пусть u = 0,10011101… = 1?1/2 + 0?1/2 2 + 0?1/2 3 + 1?1/2 4 + 1?1/2 5 + 1?1/2 6 + 0?1/2 7 + 1?1/2 8 + …

Выберем для простоты n=4. Тогда {u mod 2 -4 } = 0,1101…

Из рассмотренного свойства ясно, что существует большое количество алгоритмов получения псевдослучайных чисел. При этом после операции усечения со стороны младших разрядов применяется стандартная процедура нормализации числа в цифровой вычислительной машине. Так, если усечённое слева число не умещается по длине в машине, то производится усечение числа справа.

При проверке качества псевдослучайных чисел прежде всего интересуются длиной отрезка апериодичности и длиной периода (рис. 3). Под длиной отрезка апериодичности L понимается совокупность последовательно полученных случайных чисел? 1 , …, ? L таких, что? i ? j при, но? L+1 равно одному из? k ().

Под длиной периода последовательности псевдослучайных чисел понимается T=L-i+1. Начиная с некоторого номера i числа будут периодически повторяться с этим периодом (рис. 3).

Как правило, эти два параметра (длины апериодичности и периода) определяются экспериментально. Качество совпадения закона распределения случайных чисел с равномерным законом проверяется с помощью критериев согласия.

Точность метода Монте-Карло

Метод Монте-Карло применяется там, где не требуется высокой точности. Например, если определяют вероятность поражения мишени при стрельбе, то разница между p 1 =0,8 и p 2 =0,805 несущественна. Обычно считается, что метод Монте-Карло позволяет получить точность примерно 0,01-0,05 максимального значения определяемой величины.

Получим некоторые рабочие формулы. Определим по методу Монте-Карло вероятность пребывания системы в некотором состоянии. Эта вероятность оценивается отношением

где M - число пребываний системы в этом состоянии в результате N моделирований. Учитывая выражение для дисперсии величины M/N

и неравенство Чебышёва

Величина

есть ни что иное, как ошибка моделирования по методу Монте-Карло. С помощью формулы (11) можно написать следующую формулу для величины (12):

где p 0 - вероятность невыполнения этой оценки. С помощью частоты M/N может быть получена оценка математического ожидания m x некоторой случайной величины X. Ошибка этой оценки

находится с помощью соотношения

Отсюда видно, что ошибка моделирования находится в квадратичной зависимости от числа реализаций, т.е.

Пример 2. Допустим, что определяется математическое ожидание ошибки x поражения мишени. Процесс стрельбы и поражения моделируется на ЦВМ по методу Монте-Карло. Требуется точность моделирования? = 0,1 м с вероятностью p = 1-p 0 = 0,9 при заданной дисперсии? x = 1 м. Необходимо определить количество моделирований N. По формуле (13) получаем:

При таком количестве реализаций обеспечивается?=0,1 м с вероятностью p=0,9.

Методы Монте-Карло используются в основном для вычисления кратных интегралов. В принципе такие интегралы можно вычислить и повторным применением выше изложенных методов. Однако с повышением кратности интеграла резко возрастает объем вычислительной работы. Методы статистических испытаний (методы Монте-Карло) свободны от этого недостатка, хотя и обеспечивают сравнительно невысокую точность. Существует большое количество вариантов этих методов. Рассмотрим два из них.

Первый из них можно интерпретировать как статистический вариант метода прямоугольников, когда в качестве узла берется случайное число, равномерно распределенное в интервале интегрирования
. Вследствие случайности узла погрешность также будет носить случайный характер. Проведя вычислений с такими случайными узлами, усредняем результат, который и принимаем за приближенное значение интеграла,

. (5.48)

Погрешность вычисления будет уменьшаться с ростом числа используемых узлов расчета функции по закону
. Графическая иллюстрация метода представлена на рисунке 5.5

Рисунок 5.5. Статистический вариант метода прямоугольников

Формула (5.48) обобщается на случай кратных интегралов

Здесь
– -мерный объем области интегрирования . Число узлов, в которых необходимо вычислять подынтегральную функцию, будет пропорционально
.

Во втором варианте метода Монте-Карло интеграл приводится к виду

,(5.50)

где
находится в интервале . Тогда две случайные величины и
можно рассматривать как координаты точек в единичном квадрате (рисунок 5.8). При равномерном распределении точек в квадрате за приближенное значение интеграла принимается отношение количества точек , попавших под кривую
, к общему числу испытаний

.(5.51)

Этот алгоритм также обобщается на кратные интегралы.

Метод наименьших квадратов

Будем рассматривать систему линейных алгебраических уравнений вида

. (6.1)

Из курса линейной алгебры известно, что в том случае, когда
и число уравнений равно числу неизвестных система имеет единственное решение. На практике часто встречаются задачи, в которых либо число уравнений не совпадает с числом неизвестных, либо матрица или вектор заданы не полностью или не точно. Решение таких задач строится методом наименьших квадратов (МНК).

6.1. Решение пере- и недоопределенных слау

Задача наименьших квадратов в разных дисциплинах называется по-разному. Например, математически это есть задача отыскания для заданной точки функционального пространства ближайшей точки в заданном подпространстве. Статистика вводит в свою постановку задачи вероятностные распределения и оперирует терминами типа регрессионный анализ. Инженерный подход к решению проблемы анализа сложных систем приводит к задачам оценивания параметров или фильтрации.

Главное состоит в том, что все эти задачи содержат в себе одну и ту же центральную проблему, а именно последовательность линейных задач наименьших квадратов. Эту проблему можно сформулировать следующим образом. Пусть дана действительная
-матрица ранга
и действительный -вектор . Задача наименьших квадратов состоит в нахождении действительного -вектора , минимизирующий евклидову длину (норму) вектора невязки
.

Здесь не выдвигается никаких предположений относительно сравнительной величины параметров и , поэтому удобно все многообразие разделить на шесть случаев (рис.6.1).

В основе решения задач такого типа лежит представление
-матрицы в виде произведения
, где
и
– ортогональные матрицы. Напомним, что матрица
называется ортогональной, если
( – единичная матрица), из единственности обратной матрицы следует, что и
. Любое разложение
-матрицы такого типа называется его ортогональным разложением. Важным свойством ортогональных матриц является сохранение евклидовой длины при умножении. Это значит, что для любого -вектора и любой ортогональной
-матрицы

.(6.2)

В контексте решения задачи наименьших квадратов минимизации евклидовой нормы имеем

для произвольной ортогональной
-матрицы
и -вектора .

Использование такого разложение позволяет сформулировать задачу метода наименьших квадратов в следующем виде. Пусть – ортогональная
-матрица ранга , представленная в виде

,(6.4)

где
и
– ортогональные матрицы размерности соответственно
и
, а –
-матрица вида

,(6.5)

где
–
-матрица ранга.

Рисунок 6.1. Шесть случаев задачи МНК в соответствии со сравнительной характеристикой величин , и ранга .

Определим вектор

(6.6)

и новую переменную

(6.7)

Определим как единственное решение системы
.

, где

–произвольно. (6.8)

.(6.9)

Для нормы вектора невязки справедливо

Единственным решением минимальной длины является вектор

.(6.11)

Заменим согласно формуле (4) и получим

из уравнений (6.6)-(6.11) следует, что

для всех . Очевидно, что правая часть (6.13) имеет минимальное значение
, если

.(6.14)

Это уравнение допускает единственное решение , так как ранг
равен . Общее решение выражается формулой

,(6.15)

где произвольно. Для вектора из (6.11) имеем

, (6.16)

что устанавливает равенство (6.9). Среди векторов вида (6.15) наименьшую длину (норму) будет иметь тот, для которого
, поэтому из (6.8) получим

,(6.17)

что доказывает (6.11).

В случае
или
величины с размерностями
и
отсутствуют. В частности, при
решение задачи наименьших квадратов единственно. Отметим, что решение минимальной длины (нормы), множество всех решений и минимальное значение для нормы вектора невязки определяются единственным образом и не зависят от вида конкретного ортогонального разложения.

Для дальнейшего ограничимся несколькими утверждениями, приведенными без доказательств.

,(6.18)

где – верхняя треугольная
-матрица ранга . При этом для
-подматрицы
существует ортогональная матрица
такая, что

,

где – нижняя треугольная матрица ранга .

Первое утверждение дает возможность построить разложение матрицы в случаях
и
, где
. Действительно,
( – единичная
-матрица). Для случая
(
) запишем
или
( – единичная
-матрица). Второе утверждение дает возможность построить разложения
для случаев
-
При этом матрица представима в виде

,(6.20)

где
– невырожденная треугольная
-матрица.

Данный метод родился в 1949 благодаря усилиям американских ученых Дж. Неймана и Стива Улана в городе Монте-Карло (княжество Монако).

Метод Монте-Карло - численный метод решения математических задач при помощи моделирования случайных чисел.

Суть метода заключается в том, что посредствам специальной программы на ЭВМ производится последовательность псевдослучайных чисел с равномерным законом распределения от 0 до1. Затем данные числа с помощью специальных программ преобразуются в числа, распределенные по закону Эрланга, Пуассона, Релея и т.д.

Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию) получить распределение доходности проекта.

Блок-схема, представленная на рисунке отражает укрупненную схему работы с моделью.

Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.

Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое и принимают x в качестве оценки (приближённого значения) a* искомого числа a:

Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.

Применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master) , в то время, как метод сценариев может быть реализован даже при помощи обыкновенного калькулятора.

Как уже отмечалось, анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой “воссоединение” методов анализа чувствительности и анализа сценариев на базе теории вероятностей.

Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения NPV<0).

Упоминаемый ранее программный пакет Risk-Master позволяет в диалоговом режиме осуществить процедуру подготовки информации к анализу рисков инвестиционного проекта по методу Монте-Карло и провести сами расчеты.

Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая оказывает влияние на формирование потока наличности. Как правило, предполагается, что функция распределения являются нормальной, и, следовательно, для того, чтобы задать ее необходимо определить только два момента (математическое ожидание и дисперсию).

Как только функция распределения определена, можно применять процедуру Монте-Карло.

Алгоритм метода имитации Монте-Карло

Шаг 1.Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения значение переменной, которая является одним из параметров определения потока наличности.

Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными используется при подсчете чистой приведенной стоимости проекта.

Шаги 1 и 2 повторяются большое количество раз, например 1000, и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.

Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе методом сценариев.

Теперь необходимо определить минимальное и максимальное значения критической переменной, а для переменной с пошаговым распределением помимо этих двух еще и остальные значения, принимаемые ею. Границы варьирования переменной определяются, просто исходя из всего спектра возможных значений.

По прошлым наблюдениям за переменной можно установить частоту, с которой та принимает соответствующие значения. В этом случае вероятностное распределение есть то же самое частотное распределение, показывающее частоту встречаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из определенного интервала. В соответствии с заданным распределением модель оценки рисков будет выбирать произвольные значения переменной. До рассмотрения рисков мы подразумевали, что переменная принимает одно определенное нами значение с вероятностью 1. И через единственную итерацию расчетов мы получали однозначно определенный результат. В рамках модели вероятностного анализа рисков проводится большое число итераций, позволяющих установить, как ведет себя результативный показатель (в каких пределах колеблется, как распределен) при подстановке в модель различных значений переменной в соответствии с заданным распределением.

Задача аналитика, занимающегося анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть следующими: нормальное, постоянное, треугольное, пошаговое. Эксперт присваивает переменной вероятностное распределение, исходя из своих количественных ожиданий и делает выбор из двух категорий распределений: симметричных (например, нормальное, постоянное, треугольное) и несимметричных (например, пошаговое распределение).

Существование коррелированных переменных в проектном анализе вызывает порой проблему, не рассмотреть которую означало бы заранее обречь себя на неверные результаты. Ведь без учета коррелированности, скажем, двух переменных - компьютер, посчитав их полностью независимыми, генерирует нереалистичные проектные сценарии. Допустим цена и количество проданного продукта есть две отрицательно коррелированные переменные. Если не будет уточнена связь между переменными (коэффициент корреляции), то возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной продукции будут вместе либо высоки, либо низки, что естественно негативно отразится на результате.

Проведение расчетных итераций является полностью компьютеризированная часть анализа рисков проекта. 200-500 итераций обычно достаточно для хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, NPV). И так далее, от итерации к итерации.

Завершающая стадия анализа проектных рисков - интерпретация результатов, собранных в процессе итерационных расчетов. Результаты анализа рисков можно представить в виде профиля риска. На нем графически показывается вероятность каждого возможного случая (имеются в виду вероятности возможных значений результативного показателя).

Часто при сравнении вариантов капиталовложений удобнее пользоваться кривой, построенной на основе суммы вероятностей (кумулятивный профиль риска). Такая кривая показывает вероятности того, что результативный показатель проекта будет больше или меньше определенного значения. Проектный риск, таким образом, описывается положением и наклоном кумулятивного профиля риска.

Кумулятивный (интегральный, накопленный) профиль риска, показывает кумулятивное вероятностное распределение чистой текущей стоимости (NPV) с точки зрения банкира, предпринимателя и экономиста на определенный проект. Вероятность того, что NPV < 0 с точки зрения экономиста - около 0.4, в то время как для предпринимателя эта вероятность менее 0.2. С точки зрения банкира проект кажется совсем безопасным, так как вероятность того, что NPV > 0, около 95%.

Будем исходить из того, что проект подлежит рассмотрению и считается выгодным, в случае, если NPV > 0. При сравнении нескольких одноцелевых проектов выбирается тот, у которого NPV больше при соблюдении сказанного в предыдущем предложении.

Рассмотрим 5 иллюстративных случаев на Рис.3 принятия решений (см. учебные материалы Института экономического развития Всемирного банка). Случаи 1-3 имеют дело с решением инвестировать в отдельно взятый проект, тогда как два последних случая (4, 5) относятся к решению-выбору из альтернативных проектов. В каждом случае рассматривается как кумулятивный, так и некумулятивный профили риска для сравнительных целей. Кумулятивный профиль риска более полезен в случае выбора наилучшего проекта из представленных альтернатив, в то время как некумулятивный профиль риска лучше индуцирует вид распределения и показателен для понимания концепций, связанных с определением математического ожидания. Анализ базируется на показателе чистой текущей стоимости.

Случай 1: Минимальное возможное значение NPV выше, чем нулевое (см. Рис.3а,кривая 1).

Вероятность отрицательного NPV равна 0, так как нижний конец кумулятивного профиля риска лежит справа от нулевого значения NPV. Так как данный проект имеет положительное значение NPV во всех случаях, ясно, что проект принимается.

Случай 2: Максимальное возможное значение NPV ниже нулевого(см. Рис.3а, кривая 2).

Вероятность положительного NPV равна 0 (см. следующий рисунок)., так как верхний конец кумулятивного профиля риска лежит слева от нулевого значения NPV. Так как данный проект имеет отрицательное значение NPV во всех случаях, ясно, что проект не принимается.

Случай 3: Максимальное значение NPV больше, а минимальное меньше нулевого (см. Рис3а, кривая 3).

Вероятность нулевого NPV больше, чем 0, но меньше, чем 1, так как вертикаль нулевого NPV пересекает кумулятивный профиль рисков. Так как NPV может быть как отрицательным, так и положительным, решение будет зависеть от предрасположенности к риску инвестора. По-видимому, если математическое ожидание NPV меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику) проект должен отклоняться от дальнейшего рассмотрения.

Случай 4: Непересекающиеся кумулятивные профили рисков альтернативных (взаимоисключающих) проектов (см. Рис.3б).

При фиксированной вероятности отдача проекта В всегда выше, нежели у проекта А. Профиль рисков также говорит о том, что при фиксированной NPV вероятность, с которой та будет достигнута, начиная с некоторого уровня будет выше для проекта В, чем для проекта А. Таким образом, мы подошли к правилу 1.

Правило 1: Если кумулятивные профили рисков двух альтернативных проектов не пересекаются ни в одной точке, тогда следует выбирать тот проект, чей профиль рисков расположен правее.

Случай 5: Пересекающиеся кумулятивные профили рисков альтернативных проектов. (см. Рис.3в).

Склонные к риску инвесторы предпочтут возможность получения высокой прибыли и, таким образом, выберут проект А. Несклонные к риску инвесторы предпочтут возможность нести низкие потери и, вероятно, выберут проект В.

Правило 2: Если кумулятивные профили риска альтернативных проектов пересекаются в какой-либо точке, то решение об инвестировании зависит от склонности к риску инвестора.

Ожидаемая стоимость агрегирует информацию, содержащуюся в вероятностном распределении. Она получается умножением каждого значения результативного показателя на соответствующую вероятность и последующего суммирования результатов. Сумма всех отрицательных значений показателя, перемноженных на соответствующие вероятности есть ожидаемый убыток. Ожидаемый выигрыш - сумма всех положительных значений показателя, перемноженных на соответствующие вероятности. Ожидаемая стоимость есть, конечно, их сумма.

В качестве индикатора риска ожидаемая стоимость может выступать как надежная оценка только в ситуациях, где операция, связанная с данным риском, может быть повторена много раз. Хорошим примером такого риска служит риск, страхуемый страховыми компаниями, когда последние предлагают обычно одинаковые контракты большому числу клиентов. В инвестиционном проектировании мера ожидаемой стоимости должна всегда применяться в комбинации с мерой вариации, такой как стандартное отклонение.

Инвестиционное решение не должно базироваться лишь на одном значении ожидаемой стоимости, потому что индивид не может быть равнодушен к различным комбинациям значения показателя отдачи и соответствующей вероятности, из которых складывается ожидаемая стоимость.