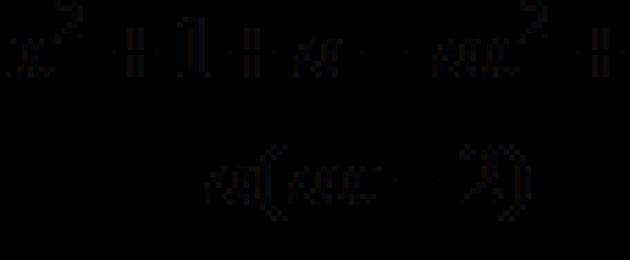Ibland i ekvationer är vissa koefficienter inte givna av specifika numeriska värden, utan anges med bokstäver.
Exempel: axe+b=c.
I denna ekvation X- okänd, a, b, c– koefficienter som kan anta olika numeriska värden. Koefficienterna som anges på detta sätt kallas parametrar.
En ekvation med parametrar definierar många ekvationer (för alla möjliga parametervärden).
Exempel: –5 X+10=– 1;
x+4y= 0;
–102–1000y=; etc.
dessa är alla ekvationer som specificeras av ekvationen med parametrar axe+b=c.
Att lösa en ekvation med parametrar innebär:
1. Ange vid vilka parametervärden ekvationen har rötter och hur många det finns för olika parametervärden.
2. Hitta alla uttryck för rötterna och ange för var och en av dem de parametervärden där detta uttryck bestämmer roten till ekvationen.
Låt oss gå över till den redan givna ekvationen med parametrar axe+b=c och vi löser det.
Om A¹0, sedan https://pandia.ru/text/80/014/images/image002_67.gif" width="63" height="41">;
på a=0 Och b=c, x– valfritt reellt tal;
på a=0 Och b¹ c, ekvationen har inga rötter.
I processen att lösa denna ekvation isolerade vi värdet på parametern a=0, vid vilken en kvalitativ förändring i ekvationen inträffar, kommer vi vidare att kalla detta värde på parametern "kontroll". Beroende på vilken ekvation vi har, hittas parameterns "kontroll"-värden annorlunda. Låt oss titta på olika typer av ekvationer och ange hur man hittar parameterns "kontrollvärden".
I. Linjära ekvationer med en parameter och ekvationer som kan reduceras till linjära
I sådana ekvationer är "kontroll"-värdena för parametrarna som regel de värden som gör koefficienterna till noll X.
Exempel 1. : 2A(A–2)x=a– 2
1. "Control"-värden är värden som uppfyller villkoret:
2A(A–2)=0
Låt oss lösa denna ekvation för variabeln A.
2a= 0 eller A–2= 0, varifrån a= 0, a= 2.
2. Låt oss lösa den initiala ekvationen för "kontroll"-värden för parametern.
På a= 0 vi har 0× x=– 2, men detta är inte fallet för några verkliga värden X, det vill säga i detta fall har ekvationen inga rötter.
På a= 2 vi har 0× x= 0, detta är sant för alla värden X, vilket betyder att roten av ekvationen är ett valfritt reellt tal X.
3. Låt oss lösa den ursprungliga ekvationen i fallet när A¹ 0 och A¹ 2 sedan 2 A(A–2)¹ 0 och båda sidor av ekvationen kan delas med 2 A(A–2), får vi:
Därför att A¹ 2, då kan fraktionen reduceras med ( A–2), då har vi .
Svar: på a= 0, inga rötter;
på a= 2, rot – valfritt reellt tal;
på A¹ 0, A¹ 2, .
Man kan tänka sig en algoritm för att lösa denna typ av ekvationer.
1. Bestäm "kontroll"-värdena för parametern.
2. Lös ekvationen för X, vid kontrollparametervärden.
3. Lös ekvationen för X, vid värden som skiljer sig från "kontroll".
4. Skriv svaret i formuläret:
Svar: 1) för parametervärden... har ekvationen rötter...;
2) för parametervärden... har ekvationen rötter...;
3) för värden på parametern..., har ekvationen inga rötter.
Exempel 2. Lös ekvation med parameter
(A 2–2A+1)x=a 2+2A- 3
1. Hitta kontrollvärdena för parametern
A 2–2A+1=0 Û ( A–1)2=0 Û A=1
2. Lös ekvationen för a= 1
0× x=(1+2×1–3) Û 0× x= 0 Þ X– valfritt reellt tal.
3. Lös ekvationen för A¹ 1
A 2–2A+1¹ 0 Þ https://pandia.ru/text/80/014/images/image006_39.gif" width="115" height="45 src=">
därför att A¹ 1, kan fraktionen reduceras
https://pandia.ru/text/80/014/images/image007_35.gif" width="64" height="41 src=">.
Exempel 3. Lös ekvation med parameter
https://pandia.ru/text/80/014/images/image009_29.gif" width="72" height="41 src=">.
4. Svar: 1) kl a= 2, inga rötter;
2) när A¹ 0,A¹ 2, ;
3) när a= 0-ekvationen är inte vettig.
Exempel 4. Lös ekvation med parameter
https://pandia.ru/text/80/014/images/image011_28.gif" width="135" height="45 src=">
https://pandia.ru/text/80/014/images/image013_25.gif" width="175" height="45 src=">
därför att X¹ 0 och A¹ – 2 är ekvationen ekvivalent med ekvationen
(A+3)x= 2A–1
låt oss hitta parameterns kontrollvärden
A+3= 0 Þ a=– 3.
2. Lös ekvationen för a=– 3.
0× x=– 7
vid någon X det finns ingen jämlikhet
3. Lös ekvationen för A¹ – 3, a+ 3¹ 0.
https://pandia.ru/text/80/014/images/image015_21.gif" width="69" height="41 src="> Û ,
därför, för att ekvationen ska vara vettig https://pandia.ru/text/80/014/images/image016_21.gif" width="40" height="41 src=">, finns det inga rötter;
2) när A¹ – 2, A¹ – 3, , .
II. Andragradsekvationer med en parameter och ekvationer som kan reduceras till andragradsekvationer
I sådana ekvationer tas värdena på parametern som gör koefficienten till noll noll vanligtvis som "kontroll" X 2, eftersom ekvationen i detta fall blir linjär, liksom värdet på parametern, vilket gör att ekvationens diskriminant försvinner, eftersom antalet reella rötter av andragradsekvationen beror på diskriminantens värde.
Exempel 5. Lös ekvation med parameter
(A–1)X 2+2(2A+1)X+(4A+3)= 0
1. Låt oss hitta parametervärdena som gör koefficienten till noll X
A- 1=0 Û a= 1
2. Lös ekvationen för a= 1
0× X 2+2(2×1+1) X+4×1+3=0 Û 6 X+7=0 Û .
3. Låt oss hitta värdena för parametern som får ekvationens diskriminant att försvinna
D=(2(2A+1))2–4(A–1)(4A+3)=(4A+1)2–(4A–4)(4A+3)=4(5A+4)
4(5A+4)=0 Û.
4. Låt oss lösa ekvationen för , i det här fallet kommer ekvationen att ha en riktig rot
https://pandia.ru/text/80/014/images/image021_15.gif" width="133" height="41"> Û
9X 2+6X+1=0 Û (3 X+1)2=0 Û https://pandia.ru/text/80/014/images/image023_15.gif" width="51" height="41 src=">. I det här fallet D<0, поэтому уравнение действительных корней не имеет.
6. Lös ekvationen för A Nr 1, https://pandia.ru/text/80/014/images/image025_12.gif" width="341" height="49 src=">
7. Svar: 1) med https://pandia.ru/text/80/014/images/image022_14.gif" width="51" height="41 src=">;
2) när a= 1, ;
3) för , det finns inga riktiga rötter;
4) vid och A Nr 1, https://pandia.ru/text/80/014/images/image027_10.gif" width="144" height="44 src=">
1. Sedan Aär i bråkets nämnare, då är ekvationen vettig endast när A#0. Nämnaren innehåller också uttrycken a2x– 2A och 2- Åh, som också måste vara icke-noll
a2x– 2A¹0 Û A(Åh–2)¹0 Û A¹0, Åh–2¹0 Û A¹0, ;
2–Åh¹0 Û https://pandia.ru/text/80/014/images/image028_9.gif" width="41" height="41 src=">.
2. Lös ekvationen för A¹0, https://pandia.ru/text/80/014/images/image029_9.gif" width="169" height="47 src="> Û ![]() Û
Û
(1–A)X 2+2X+1+A=0 ...................(*)
3. Låt oss hitta parametervärdena som gör koefficienten till noll X 2
1–A=0 Û A=1
4. Lös ekvation (*) för A=1
0× X 2+2X+2=0 Û 2 x=– 2 Û x=–1
Låt oss genast kolla om det stämmer X från https://pandia.ru/text/80/014/images/image032_8.gif" width="72" height="41 src=">, vilket betyder att när A=1, x=– 1.
Mål:
- upprepa lösning av linjära ekvationssystem med två variabler
- definiera ett system av linjära ekvationer med parametrar
- kommer att lära dig hur man löser system av linjära ekvationer med parametrar.
Under lektionerna
- Att organisera tid
- Upprepning
- Förklaring av ett nytt ämne
- Konsolidering
- Lektionssammanfattning
- Läxa
2. Upprepning:
I. Linjär ekvation med en variabel:
1. Definiera en linjär ekvation med en variabel
[En ekvation av formen ax=b, där x är en variabel, a och b är några tal, kallas en linjär ekvation med en variabel]
2. Hur många rötter kan en linjär ekvation ha?
[- Om a=0, b0, så har ekvationen inga lösningar, x
Om a=0, b=0, då x R
Om a0, så har ekvationen en unik lösning, x =
3. Ta reda på hur många rötter ekvationen har (enligt alternativ)
II. Linjär ekvation med 2 variabler och system av linjära ekvationer med 2 variabler.
1. Definiera en linjär ekvation i två variabler. Ge ett exempel.
[En linjär ekvation med två variabler är en ekvation av formen ax + by = c, där x och y är variabler, a, b och c är några tal. Till exempel, x-y=5]
2. Vad kallas att lösa en ekvation med två variabler?
[En lösning på en ekvation med två variabler är ett par av värden av variabler som förvandlar ekvationen till en sann likhet.]
3. Är värdeparet för variablerna x = 7, y = 3 en lösning på ekvationen 2x + y = 17?
4. Vad kallas grafen för en ekvation i två variabler?
[Grafen för en ekvation med två variabler är mängden av alla punkter på koordinatplanet vars koordinater är lösningar till denna ekvation.]
5. Ta reda på vad ekvationens graf är:
[Låt oss uttrycka variabeln y till x: y=-1,5x+3
Formeln y=-1,5x+3 är en linjär funktion, vars graf är en rät linje. Eftersom ekvationerna 3x+2y=6 och y=-1,5x+3 är ekvivalenta, är denna linje också en graf över ekvationen 3x+2y=6]
6. Vilken är grafen för ekvationen ax+by=c med variablerna x och y, där a0 eller b0?
[Grafen för en linjär ekvation med två variabler där åtminstone en av koefficienterna för variablerna inte är noll är en rät linje.]
7. Vad kallas att lösa ett ekvationssystem med två variabler?
[En lösning på ett ekvationssystem med två variabler är ett par av värden av variabler som förvandlar varje ekvation i systemet till en sann likhet]
8. Vad innebär det att lösa ett ekvationssystem?
[Att lösa ett ekvationssystem innebär att hitta alla dess lösningar eller bevisa att det inte finns några lösningar.]
9. Ta reda på om ett sådant system alltid har lösningar och i så fall hur många (grafiskt).
10. Hur många lösningar kan ett system med två linjära ekvationer med två variabler ha?
[Den enda lösningen är om linjerna skär varandra; har inga lösningar om linjerna är parallella; oändligt många om raderna sammanfaller]
11. Vilken ekvation brukar definiera en rät linje?
12. Upprätta ett samband mellan vinkelkoefficienter och fria termer:
Alternativ I:
k 1 = k 2 , b 1 b 2, inga lösningar; |
Alternativ II:
k1k2, en lösning; |
Alternativ III:
k 1 = k 2, b 1 = b 2, många lösningar. |
Slutsats:
- Om vinkelkoefficienterna för linjerna som är grafer för dessa funktioner är olika, så skärs dessa linjer och systemet har en unik lösning.
- Om linjernas vinkelkoefficienter är desamma och skärningspunkterna med y-axeln är olika, så är linjerna parallella och systemet har inga lösningar.
- Om vinkelkoefficienterna och skärningspunkterna med y-axeln är desamma, så sammanfaller linjerna och systemet har oändligt många lösningar.
På tavlan finns en tabell som läraren och eleverna efter hand fyller i.
III. Förklaring av ett nytt ämne.
Definition: View system
- A1x+B1y=C
- A2x+B2y=C2
där A 1, A 2, B 1, B 2, C 1 C 2 är uttryck beroende på parametrarna, och x och y är okända, kallas ett system av två linjära algebraiska ekvationer med två okända i parametrarna.
Följande fall är möjliga:
1) Om , då har systemet en unik lösning
2) Om , så har systemet inga lösningar
3) Om , så har systemet oändligt många lösningar.
IV. Konsolidering
Exempel 1.
Vid vilka värden av parameter a gör systemet
- 2x - 3y = 7
- ah - 6y = 14
a) har ett oändligt antal lösningar;
b) har en unik lösning
Svar:
a) om a=4 så har systemet ett oändligt antal lösningar;
b) om a4, då finns det bara en lösning.
Exempel 2.
Lös ekvationssystemet
- x+(m+l)y=1
- x+2y=n
Lösning: a) , dvs. för m1 har systemet en unik lösning.

b), dvs. för m=1 (2=m+1) och n1 har det ursprungliga systemet inga lösningar
c) , för m=1 och n=1 har systemet oändligt många lösningar.
Svar: a) om m=1 och n1, så finns det inga lösningar
b) m=1 och n=1, då är lösningen en oändlig mängd
- y - någon
- x=n-2y
c) om m1 och n är några, då
Exempel 3.
- akh-3ау=2а+3
- x+ay=1
Lösning: Från ekvation II finner vi x = 1-аy och ersätter ekvation I med ekvation
а(1-ау)-3ау=2а+3
a-a 2 y-3ау=2а+3
A 2 y-3ау=а+3
A(a+3)y=a+3
Möjliga fall:
1) a=0. Då ser ekvationen ut som 0*y=3 [y]
Därför har systemet inga lösningar för a=0
2) a=-3. Sedan 0*y=0.
Därför, y. I detta fall x=1-ау=1+3у
3) aO och a-3. Då y=-, x=1-a(-=1+1=2
Svar:
1) om a=0, då (x; y)
2) om a=-3, då x=1+3y, y
3) om a0 och a?-3, sedan x=2, y=-
Låt oss överväga den andra metoden för att lösa systemet (1).
Låt oss lösa system (1) med den algebraiska additionsmetoden: multiplicera först den första ekvationen i systemet med B 2, den andra med B 1 och addera dessa ekvationer term för term, vilket eliminerar variabeln y:

Därför att AiB2-A2B10, sedan x =
Låt oss nu eliminera variabeln x. För att göra detta, multiplicera den första ekvationen i system (1) med A 2 och den andra med A 1 och addera båda ekvationerna term för term:
- A 1 A 2 x + A 2 B 1 y=A 2 C 1
- -A 1 A 2 x-A 1 B 2 y=-A 1 C 2
- y(A 2 B 1 -A 1 B 2) = A 2 C 1 - A 1 C 2
därför att A2Bi-AiB20y = ![]()
För att underlätta lösningssystemet (1) introducerar vi följande notation:
![]() - huvudsaklig bestämningsfaktor
- huvudsaklig bestämningsfaktor

Nu kan lösningen till system (1) skrivas med hjälp av determinanter:
De givna formlerna kallas Cramers formler.
Om , då har system (1) en unik lösning: x=; y=
Om , eller , så har system (1) inga lösningar
Om , , , , så har system (1) ett oändligt antal lösningar.
I det här fallet behöver systemet utredas ytterligare. I detta fall reduceras den som regel till en linjär ekvation. I det här fallet är det ofta bekvämt att studera systemet på följande sätt: genom att lösa ekvationen hittar vi specifika värden på parametrarna eller uttrycker en av parametrarna i termer av de andra och ersätter dessa parametervärden med systemet. Då får vi ett system med specifika numeriska koefficienter eller med ett mindre antal parametrar, som måste studeras.
Om koefficienterna A 1 , A 2 , B 1 , B 2 i systemet beror på flera parametrar, är det lämpligt att studera systemet med hjälp av systemets determinanter.
Exempel 4.
För alla värden av parameter a, lös ekvationssystemet
- (a+5)x+(2a+3)y=3a+2
- (3a+10)x+(5a+6)y=2a+4
Lösning: Låt oss hitta bestämningsfaktorn för systemet:
![]() = (a+5)(5a+6) – (3a+10) (2a+3)= 5a 2 +31a+30-6a 2 -29a-30=-a 2 +2a=a(2-a)
= (a+5)(5a+6) – (3a+10) (2a+3)= 5a 2 +31a+30-6a 2 -29a-30=-a 2 +2a=a(2-a)
= (3a+2) (5a+6) –(2a+4)(2a+3)=15a 2 +28a+12-4a 2 -14a-12=11a 2 +14a=a(11a+14)
![]() =(a+5) (2a+4)-(3a+10)(3a+2)=2a 2 +14a+20-9a 2 -36a-20=-7a 2 -22a=-a(7a+22)
=(a+5) (2a+4)-(3a+10)(3a+2)=2a 2 +14a+20-9a 2 -36a-20=-7a 2 -22a=-a(7a+22)
Låt oss lösa ett ekvationssystem med en parameter (A. Larin, alternativ 98)
Hitta alla värden för parametern, för var och en av dem systemet

har exakt en lösning.
Låt oss ta en närmare titt på systemet. I systemets första ekvation är den vänstra sidan , och den högra är inte beroende av parametern. Det vill säga, vi kan betrakta denna ekvation som ekvationen för funktionen

och vi kan plotta denna funktion.
Systemets andra ekvation
![]()
beror på parametern, och genom att välja en hel kvadrat på vänster sida av ekvationen får vi ekvationen för en cirkel.
Så det är vettigt att rita grafer för varje ekvation och se vid vilket värde av parametern dessa grafer har en skärningspunkt.
Låt oss börja med den första ekvationen. Låt oss först öppna modulerna. För att göra detta likställer vi varje submodulärt uttryck till noll för att hitta de punkter där tecknet ändras.
Det första submodulära uttrycket ändrar tecken vid , det andra - vid .
Låt oss plotta dessa punkter på koordinatlinjen och hitta tecknen för varje submodulärt uttryck på varje intervall:
Observera att för och ekvationen inte är vettig, så vi punkterar dessa punkter.

Låt oss nu utöka modulerna för varje intervall. (Kom ihåg: om ett submodulärt uttryck är större än eller lika med noll, expanderar vi modulen med samma tecken, och om mindre än noll, då med motsatt tecken.)
Båda submodulära uttrycken är negativa, därför expanderar vi båda modulerna med motsatt tecken:

![]()
Det vill säga när den ursprungliga funktionen har formen
På detta intervall är det första submodulära uttrycket negativt och det andra är positivt, därför får vi:

![]() - funktionen finns inte på detta intervall.
- funktionen finns inte på detta intervall.
3. title="x>2">!}
På detta intervall är båda submodulära uttryck positiva; vi expanderar båda modulerna med samma tecken. Vi får:

![]()
Det vill säga med title="x>2"> исходная функция имеет вид !}
Så vi fick grafen för funktionen 

Låt oss nu titta på den andra ekvationen:
![]()
Låt oss välja en komplett kvadrat på vänster sida av ekvationen; för att göra detta, lägg till siffran 4 på båda sidor av ekvationen:
![]()
![]()
För ett specifikt värde på parametern är grafen för denna ekvation en cirkel med ett centrum i en punkt med koordinater, vars radie är 5. För olika värden har vi en serie cirklar:

Vi kommer att flytta cirkeln från botten till toppen tills den vidrör den vänstra sidan av grafen för den första funktionen. På bilden är denna cirkel röd. Mitten av denna cirkel är punkten, dess koordinater är (-2;-3). Vidare, när den rör sig uppåt, har cirkeln en skärningspunkt med den vänstra sidan av funktionsgrafen, det vill säga systemet har en unik lösning.
Vi fortsätter att flytta cirkeln uppåt tills den vidrör den högra sidan av grafen för den första funktionen. Detta kommer att hända när cirkelns mittpunkt är vid punkten med koordinaterna (-2;0) - i figuren är denna cirkel blå.
När du rör dig längre uppåt kommer cirkeln att skära både vänster och höger del av grafen för den första funktionen, det vill säga cirkeln kommer att ha två skärningspunkter med grafen för den första funktionen, och systemet kommer att ha två lösningar. Denna situation fortsätter tills cirkelns mittpunkt är vid punkten med koordinaterna (-2; 5) - denna cirkel är grön. Vid denna punkt rör cirkeln den vänstra sidan av grafen och skär den högra. Det vill säga att systemet har en lösning.
Så, systemet har en unik lösning när(-3;0); om värdena för parameter a är fler än ett, kommer ekvationen att ha två rötter.
Har du fortfarande frågor? Vet du inte hur man löser ekvationer med en parameter?
För att få hjälp av en handledare -.
Första lektionen är gratis!
blog.site, vid kopiering av material helt eller delvis krävs en länk till originalkällan.
1. System av linjära ekvationer med en parameter
System av linjära ekvationer med en parameter löses med samma grundläggande metoder som vanliga ekvationssystem: substitutionsmetoden, metoden att addera ekvationer och den grafiska metoden. Kunskap om den grafiska tolkningen av linjära system gör det enkelt att svara på frågan om antalet rötter och deras existens.
Exempel 1.
Hitta alla värden för parameter a som ekvationssystemet inte har några lösningar för.
(x + (a 2 – 3)y = a,
(x + y = 2.
Lösning.
Låt oss titta på flera sätt att lösa denna uppgift.
1 sätt. Vi använder egenskapen: systemet har inga lösningar om förhållandet mellan koefficienterna framför x är lika med förhållandet mellan koefficienterna framför y, men inte lika med förhållandet mellan de fria termerna (a/a 1 = b /b1 ≠ c/c 1). Då har vi:
1/1 = (a 2 – 3)/1 ≠ a/2 eller system
(och 2 – 3 = 1,
(a ≠ 2.
Från den första ekvationen a 2 = 4, därför, med hänsyn till villkoret att a ≠ 2, får vi svaret.
Svar: a = -2.
Metod 2. Vi löser genom substitutionsmetod.
(2 – y + (a 2 – 3)y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
Efter att ha tagit den gemensamma faktorn y ur parentes i den första ekvationen får vi:
((a 2 – 4)y = a – 2,
(x = 2 – y.
Systemet har inga lösningar om den första ekvationen inte har några lösningar, det vill säga
(och 2 – 4 = 0,
(a – 2 ≠ 0.
Uppenbarligen är a = ±2, men med hänsyn till det andra villkoret kommer svaret bara med ett minussvar.
Svar: a = -2.
Exempel 2.
Hitta alla värden för parameter a för vilken ekvationssystemet har ett oändligt antal lösningar.
(8x + ay = 2,
(ax + 2y = 1.
Lösning.
Enligt egenskapen, om förhållandet mellan koefficienterna för x och y är detsamma och är lika med förhållandet mellan de fria medlemmarna i systemet, så har det ett oändligt antal lösningar (dvs a/a 1 = b/ b 1 = c/c 1). Därför 8/a = a/2 = 2/1. När vi löser var och en av de resulterande ekvationerna finner vi att a = 4 är svaret i detta exempel.
Svar: a = 4.
2. System av rationella ekvationer med en parameter
Exempel 3.
(3|x| + y = 2,
(|x| + 2y = a.
Lösning.
Låt oss multiplicera den första ekvationen i systemet med 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Subtraherar vi den andra ekvationen från den första får vi 5|x| = 4 – a. Denna ekvation kommer att ha en unik lösning för a = 4. I andra fall kommer denna ekvation att ha två lösningar (för en< 4) или ни одного (при а > 4).
Svar: a = 4.
Exempel 4.
Hitta alla värden för parametern a som ekvationssystemet har en unik lösning för.
(x + y = a,
(y – x 2 = 1.
Lösning.
Vi kommer att lösa detta system med den grafiska metoden. Sålunda är grafen för systemets andra ekvation en parabel som höjs längs Oy-axeln uppåt med ett enhetssegment. Den första ekvationen specificerar en uppsättning linjer parallella med linjen y = -x (bild 1). Det framgår tydligt av figuren att systemet har en lösning om den räta linjen y = -x + a tangerar parabeln i en punkt med koordinater (-0,5, 1,25). Genom att ersätta dessa koordinater i den räta linjeekvationen istället för x och y, hittar vi värdet på parameter a: 
1,25 = 0,5 + a;
Svar: a = 0,75.
Exempel 5.
Med hjälp av substitutionsmetoden, ta reda på vilket värde av parametern a, systemet har en unik lösning.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Lösning.
Från den första ekvationen uttrycker vi y och ersätter den med den andra:
(y = axe – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.
Låt oss reducera den andra ekvationen till formen kx = b, som kommer att ha en unik lösning för k ≠ 0. Vi har:
ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
Vi representerar det kvadratiska trinomiet a 2 + 3a + 2 som en produkt av parenteser
(a + 2)(a + 1), och till vänster tar vi x från parentes:
(a2 + 3a)x = 2 + (a + 2)(a + 1).
Uppenbarligen bör a 2 + 3a inte vara lika med noll, därför
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, vilket betyder a ≠ 0 och ≠ -3.
Svar: a ≠ 0; ≠ -3.
Exempel 6.
Använd den grafiska lösningsmetoden, bestäm till vilket värde av parametern som systemet har en unik lösning.
(x 2 + y 2 = 9,
(y – |x| = a.
Lösning.
Baserat på villkoret konstruerar vi en cirkel med ett centrum i origo och en radie på 3 enhetssegment; detta är vad som specificeras av systemets första ekvation
x 2 + y 2 = 9. Systemets andra ekvation (y = |x| + a) är en streckad linje. Genom att använda figur 2 Vi överväger alla möjliga fall av dess plats i förhållande till cirkeln. Det är lätt att se att a = 3. 
Svar: a = 3.
Har du fortfarande frågor? Vet du inte hur man löser ekvationssystem?
För att få hjälp av en handledare -.
Första lektionen är gratis!
blog.site, vid kopiering av material helt eller delvis krävs en länk till originalkällan.
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0