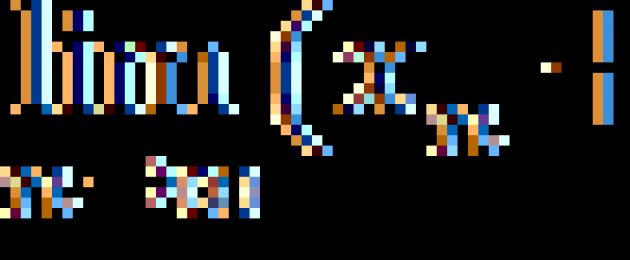Ge definitionen av en infinitesimal funktion vid en punkt. Infinitesimala funktioner och deras grundläggande egenskaper

Fungera y=f(x) kallad oändligt liten på x→a eller när x→∞, om eller , dvs. en infinitesimal funktion är en funktion vars gräns vid en given punkt är noll.

Exempel.

1. Funktion f(x)=(x-1) 2 är oändligt liten vid x→1, sedan (se figur).

2. Funktion f(x)= tg x– oändligt liten kl x→0.

3. f(x)= log(1+ x) – oändligt vid x→0.

4. f(x) = 1/x– oändligt liten kl x→∞.

Låt oss upprätta följande viktiga relation:

Sats. Om funktionen y=f(x) representerbar med x→a som summan av ett konstant tal b och oändlig storlek α(x): f (x)=b+ α(x) Den där .

Omvänt, om , då f (x)=b+α(x), Var yxa)– oändligt liten kl x→a.

Bevis.

1. Låt oss bevisa den första delen av påståendet. Från jämlikhet f(x)=b+α(x) skall |f(x) – b|=| α|. Men eftersom yxa)är oändligt liten, då finns det för godtycklig ε δ – en grannskap av punkten a, inför alla x från vilka, värden yxa) tillfredsställa relationen |α(x)|< ε. Sedan |f(x) – b|< ε. Och detta betyder att.

2. Om , då för alla ε >0 för alla X från någon δ – grannskap av en punkt a kommer |f(x) – b|< ε. Men om vi betecknar f(x) – b= α, Den där |α(x)|< ε, vilket betyder att a– oändligt liten.

Låt oss överväga de grundläggande egenskaperna hos infinitesimala funktioner.

Sats 1. Den algebraiska summan av två, tre och i allmänhet vilket ändligt antal infinitesimals som helst är en infinitesimal funktion.

Bevis. Låt oss ge ett bevis för två termer. Låta f(x)=α(x)+β(x), var och . Vi måste bevisa det för alla godtyckliga små ε > 0 hittade δ> 0, så att för x, som tillfredsställer ojämlikheten |x – a|<δ , genomförde |f(x)|< ε.

Så låt oss fixa ett godtyckligt nummer ε > 0. Eftersom enligt satsens villkor α(x)är en infinitesimal funktion, så finns det en sådan δ 1 > 0, vilket är |x – a|< δ 1 vi har |α(x)|< ε / 2. Likaså sedan β(x)är oändligt liten, så finns det sådan δ 2 > 0, vilket är |x – a|< δ 2 har vi | β(x)|< ε / 2.

Låt oss ta δ=min(δ 1 , 52 } .Då i närheten av punkten a radie δ var och en av ojämlikheterna kommer att tillfredsställas |α(x)|< ε / 2 och | β(x)|< ε / 2. Därför kommer det att finnas i det här området

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

de där. |f(x)|< ε, vilket är det som behövde bevisas.

Sats 2. Produkt av en oändlig funktion yxa) för en begränsad funktion f(x) på x→a(eller när x→∞) är en infinitesimal funktion.

Bevis. Sedan funktionen f(x)är begränsad, så finns det ett antal M sådan för alla värden x från något område av en punkt a|f(x)|≤M. Dessutom sedan yxa)är en oändlig funktion vid x→a, sedan för en godtycklig ε > 0 finns det ett område till punkten a, där ojämlikheten kommer att hålla |α(x)|< ε /M. Sedan i det mindre av dessa kvarter vi har | αf|< ε /M= ε. Och detta betyder det af– oändligt liten. För tillfället x→∞ bevisningen utförs på liknande sätt.

Från den beprövade satsen följer:

Följd 1. Om och, då.

Följd 2. Om c= const, alltså.

Sats 3. Förhållandet mellan en infinitesimal funktion α(x) per funktion f(x), vars gräns skiljer sig från noll, är en infinitesimal funktion.

Bevis. Låt . Sedan 1 /f(x) det finns en begränsad funktion. Därför är en bråkdel produkten av en infinitesimal funktion och en begränsad funktion, d.v.s. funktionen är oändlig.

Definition numerisk funktion. Metoder för att specificera funktioner.

Låt D vara en mängd på tallinjen R. Om varje x som hör till D är associerat med ett enda tal y=f(x), så säger vi att en funktion f ges.

Metoder för att specificera funktioner:

1) tabell – för funktioner definierade på en finit uppsättning.

2) analytisk

3) grafik

2 och 3 – för funktioner definierade på en oändlig uppsättning.

Konceptet med en omvänd funktion.

Om funktionen y=f(x) är sådan att olika värden på x-argumentet motsvarar olika värden på funktionen, så kan variabeln x uttryckas som en funktion av variabeln y: x=g(y ). Funktionen g kallas inversen av f och betecknas med f^(-1).

Konceptet med en komplex funktion.

Komplex funktion-funktion, vars argument är någon annan funktion.

Låt funktionerna f(x) och g(x) ges. Låt oss göra två komplexa funktioner av dem. Om man betraktar funktionen f som extern (huvud) och funktionen g som intern, får vi en komplex funktion u(x)=f(g(x)).

Bestämning av sekvensgränsen.

Ett tal a kallas gränsen för en sekvens (xn) om det för något positivt finns ett tal n0, från vilket alla termer i sekvensen skiljer sig från a i modul med mindre än ε (dvs. de faller i ε-grannskapet av punkten a):

Regler för beräkning av gränserna för konvergerande sekvenser.

1. Varje konvergent sekvens har bara en gräns. 2. Om alla element i sekvensen (x n) är lika med C (konstant), så är gränsen för sekvensen (x n) också lika med C. 3. ; 4. ; 5. .

Definition begränsad sekvens.

Sekvensen (x n) kallas avgränsad om mängden tal X=(x n) är begränsad: .

Definition av en infinitesimal sekvens.

En sekvens (x n) sägs vara infinitesimal om det för någon (oavsett hur liten) >0 det finns ett tal n 0 så att för vilken som helst n>n 0 olikheten |x n |< .

Definition av en oändligt stor sekvens.

En sekvens sägs vara oändligt stor om det för något (oavsett hur stort) tal A>0 som helst finns ett tal n 0 så att för varje tal n>n 0 gäller olikheten |x n |>A.

Definition av monotona sekvenser.

Monotona sekvenser: 1) öka ifx n x n +1 för alla n, 4) icke-ökande om x n x n +1 för alla n.

Bestämning av gränsen för en funktion vid en punkt.

Gränsen för funktionen y=f(x) vid punkten x 0 (eller vid x x 0) är talet a if för alla sekvensvärden (x n) av argumentet som konvergerar till x 0 (alla x n x 0), sekvens av (f(x n)) värden för funktionen konvergerar till gränsen a.

Definition av en infinitesimal funktion.

F-iya f(x) sägs vara infinitesimal som x→A om .

Definition av en oändligt stor funktion.

F-iya f(x) sägs vara oändligt stor för x→A om .

Definitioner och egenskaper för infinitesimala och oändligt stora funktioner i en punkt. Bevis på egenskaper och satser. Samband mellan oändligt små och oändligt stora funktioner.

Innehåll

Se även: Infinitesimala sekvenser - definition och egenskaper
Egenskaper för oändligt stora sekvenser

Definition av infinitesimala och infinitesimala funktioner

Låt x 0 är en ändlig eller oändlig punkt: ∞, -∞ eller +∞.

Definition av en infinitesimal funktion
Funktion α (x) kallad oändligt liten som x tenderar till x 0 0 , och det är lika med noll:
.

Definition av en oändligt stor funktion
Funktion f (x) kallad oändligt stor som x tenderar till x 0 , om funktionen har en gräns som x → x 0 , och det är lika med oändlighet:
.

Egenskaper för infinitesimala funktioner

Egenskapen för summan, skillnaden och produkten av infinitesimala funktioner

Summa, skillnad och produktändligt antal infinitesimala funktioner som x → x 0 är en infinitesimal funktion som x → x 0 .

Denna egenskap är en direkt följd av de aritmetiska egenskaperna för gränserna för en funktion.

Produktsats begränsad funktion till oändligt liten

Produkt av en funktion begränsad på något punkterat område av punkt x 0 , till oändligt, som x → x 0 , är en infinitesimal funktion som x → x 0 .

Egenskapen att representera en funktion som summan av en konstant och en infinitesimal funktion

För att funktionen f (x) hade en ändlig gräns, är det nödvändigt och tillräckligt att
,
där är en infinitesimal funktion som x → x 0 .

Egenskaper för oändligt stora funktioner

Sats om summan av en begränsad funktion och en oändligt stor

Summan eller skillnaden av en begränsad funktion på någon punkterad grannskap av punkten x 0 , och en oändligt stor funktion, som x → x 0 , är en oändligt stor funktion som x → x 0 .

Sats om divisionen av en begränsad funktion med en oändligt stor

Om funktion f (x)är oändligt stor som x → x 0 och funktionen g (x)- är avgränsad till någon punkterad grannskap av punkt x 0 , Den där
.

Sats om divisionen av en funktion som avgränsas nedan av en infinitesimal

Om funktionen, på någon punkterad grannskap av punkten, är avgränsad underifrån i absolut värde Positivt nummer:
,
och funktionen är infinitesimal som x → x 0 :
,
och det finns en punkterad grannskap av punkten där
.

Egenskapen för ojämlikheter av oändligt stora funktioner

Om funktionen är oändligt stor vid:
,
och funktionerna och , på någon punkterad grannskap av punkten uppfyller ojämlikheten:
,
då är funktionen också oändligt stor vid:
.

Denna fastighet har två specialfall.

Låt, på någon punkterad grannskap av punkten, funktionerna och tillfredsställa ojämlikheten:
.
Sedan om , då och .
Om , då och .

Samband mellan oändligt stora och oändligt små funktioner

Av de två föregående egenskaperna följer sambandet mellan oändligt stora och oändligt små funktioner.

Om en funktion är oändligt stor vid , då är funktionen oändligt liten vid .

Om en funktion är oändligt liten för , och , då är funktionen oändligt stor för .

Relationen mellan en infinitesimal och en oändligt stor funktion kan uttryckas symboliskt:
, .

Om en infinitesimal funktion har ett visst tecken vid , det vill säga den är positiv (eller negativ) på någon punkterad omgivning av punkten , då kan vi skriva det så här:
.
På samma sätt, om en oändligt stor funktion har ett visst tecken vid , så skriver de:
, eller .

Sedan kan det symboliska sambandet mellan oändligt små och oändligt stora funktioner kompletteras med följande relationer:
, ,
, .

Ytterligare formler för oändlighetssymboler finns på sidan
"Pekar på oändligheten och deras egenskaper."

Bevis på egenskaper och satser

Bevis för satsen om produkten av en begränsad funktion och en infinitesimal

För att bevisa detta teorem kommer vi att använda . Vi använder också egenskapen för infinitesimala sekvenser, enligt vilken

Låt funktionen vara oändlig vid , och låt funktionen avgränsas i någon punkterad omgivning av punkten:
kl.

Eftersom det finns en gräns finns det en punkterad grannskap till den punkt där funktionen definieras. Låt det bli en korsning av kvarter och . Sedan definieras funktionerna och på den.

.
,
en sekvens är oändlig:
.

Låt oss dra fördel av det faktum att produkten av en bunden sekvens och en infinitesimal sekvens är en infinitesimal sekvens:
.
.

Teoremet har bevisats.

Bevis på egenskapen att representera en funktion som summan av en konstant och en infinitesimal funktion

Nödvändighet. Låt funktionen ha en ändlig gräns vid en punkt
.
Tänk på funktionen:
.
Genom att använda egenskapen för gränsen för skillnaden mellan funktioner har vi:
.
Det vill säga, det finns en oändligt liten funktion vid .

Lämplighet. Låt det vara. Låt oss tillämpa egenskapen för gränsen för summan av funktioner:
.

Fastigheten är bevisad.

Bevis för satsen om summan av en begränsad funktion och en oändligt stor

För att bevisa satsen kommer vi att använda Heines definition av gränsen för en funktion

kl.

Eftersom det finns en gräns finns det en punkterad grannskap till den punkt där funktionen definieras. Låt det bli en korsning av kvarter och . Sedan definieras funktionerna och på den.

Låt det finnas en godtycklig sekvens som konvergerar till , vars element tillhör grannskapet:
.
Sedan definieras sekvenserna och. Dessutom är sekvensen begränsad:
,
en sekvens är oändligt stor:
.

Eftersom summan eller skillnaden av en begränsad sekvens och en oändligt stor
.
Sedan, enligt definitionen av gränsen för en sekvens enligt Heine,
.

Teoremet har bevisats.

Bevis för satsen om kvoten för division av en begränsad funktion med en oändligt stor

För att bevisa detta kommer vi att använda Heines definition av gränsen för en funktion. Vi använder också egenskapen för oändligt stora sekvenser, enligt vilken är en oändligt liten sekvens.

Låt funktionen vara oändligt stor vid , och låt funktionen avgränsas i någon punkterad omgivning av punkten:
kl.

Eftersom funktionen är oändligt stor, finns det en punkterad omgivning till den punkt där den definieras och försvinner inte:
kl.
Låt det bli en korsning av kvarter och . Sedan definieras funktionerna och på den.

Eftersom kvoten för att dividera en begränsad sekvens med en oändligt stor är en oändligt liten sekvens, då
.
Sedan, enligt definitionen av gränsen för en sekvens enligt Heine,
.

Teoremet har bevisats.

Bevis på kvotsatsen för att dividera en funktion som begränsas nedan med en infinitesimal etta

För att bevisa denna egenskap kommer vi att använda Heines definition av gränsen för en funktion. Vi använder också egenskapen för oändligt stora sekvenser, enligt vilken är en oändligt stor sekvens.

Låt funktionen vara infinitesimal för , och låt funktionen avgränsas i absolut värde underifrån av ett positivt tal, på någon punkterad grannskap av punkten:
kl.

Tillståndet innebär att det finns en punkterad omgivning till punkten där funktionen definieras och försvinner inte:
kl.
Låt det bli en korsning av kvarter och . Sedan definieras funktionerna och på den. Dessutom, och.

Låt det finnas en godtycklig sekvens som konvergerar till , vars element tillhör grannskapet:
.
Sedan definieras sekvenserna och. Dessutom är sekvensen avgränsad nedan:
,
och sekvensen är oändlig med termer som inte är noll:
, .

Eftersom kvoten för att dividera en sekvens som avgränsas nedan med en oändligt liten etta är en oändligt stor sekvens, så
.
Och låt det finnas en punkterad grannskap av den punkt på vilken
kl.

Låt oss ta en godtycklig sekvens som konvergerar till . Sedan, med början från något nummer N, kommer elementen i sekvensen att tillhöra denna stadsdel:
kl.
Sedan
kl.

Enligt definitionen av gränsen för en funktion enligt Heine,
.
Sedan, genom egenskapen ojämlikheter i oändligt stora sekvenser,
.
Eftersom sekvensen är godtycklig, konvergerande till , då, enligt definitionen av gränsen för en funktion enligt Heine,
.

Fastigheten är bevisad.

Referenser:
L.D. Kudryavtsev. Väl matematisk analys. Volym 1. Moskva, 2003.

Se även:

Infinitesimala funktioner

Funktionen %%f(x)%% anropas oändligt liten(b.m.) med %%x \to a \in \overline(\mathbb(R))%%, om med denna tendens av argumentet gränsen för funktionen är lika med noll.

Begreppet b.m. funktion är oupplösligt kopplad till instruktioner för att ändra dess argument. Vi kan prata om b.m. fungerar vid %%a \to a + 0%% och vid %%a \to a - 0%%. Vanligtvis b.m. funktioner betecknas med de första bokstäverna i det grekiska alfabetet %%\alpha, \beta, \gamma, \ldots%%

Exempel

Funktionen %%f(x) = x%% är b.m. vid %%x \till 0%%, eftersom dess gräns vid punkten %%a = 0%% är noll. Enligt satsen om sambandet mellan den tvåsidiga gränsen och den ensidiga gränsen är denna funktion b.m. både med %%x \till +0%% och med %%x \till -0%%.
Funktion %%f(x) = 1/(x^2)%% - b.m. vid %%x \to \infty%% (liksom vid %%x \to +\infty%% och vid %%x \to -\infty%%).

Ett annat konstant tal än noll, oavsett hur litet det är i absolut värde, är inte ett b.m. fungera. För konstanta tal är det enda undantaget noll, eftersom funktionen %%f(x) \equiv 0%% har en nollgräns.

Sats

Funktionen %%f(x)%% har vid punkten %%a \in \overline(\mathbb(R))%% av den utökade talraden en slutgräns lika med talet %%b%% om och endast om denna funktion är lika med summan av detta tal %%b%% och b.m. funktioner %%\alpha(x)%% med %%x \to a%%, eller $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$

Egenskaper för infinitesimala funktioner

Enligt reglerna för passage till gränsen med %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, följer följande påståenden:

Summan av det slutliga antalet b.m. funktioner för %%x \till a%% är b.m. vid %%x \till a%%.
Produkten av valfritt antal b.m. funktioner för %%x \till a%% är b.m. vid %%x \till a%%.

Produkt b.m. fungerar vid %%x \to a%% och en funktion avgränsad i något punkterat område %%\stackrel(\circ)(\text(U))(a)%% av punkt a, det finns b.m. vid %%x \till en %% funktion.

Det är tydligt att produkten av en konstant funktion och b.m. vid %%x \till a%% finns b.m. funktion vid %%x \till a%%.

Ekvivalenta infinitesimala funktioner

Infinitesimala funktioner %%\alpha(x), \beta(x)%% för %%x \to a%% kallas likvärdig och skriv %%\alpha(x) \sim \beta(x)%%, if

$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$

Sats om ersättning av b.m. funktioner motsvarande

Låt %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% vara b.m. funktioner för %%x \to a%%, och %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, sedan $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limits_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$

Motsvarande b.m. funktioner.

Låt %%\alpha(x)%% vara b.m. funktion vid %%x \till a%%, sedan

%%\sin(\alpha(x)) \sim \alpha(x)%%
%%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
%%\tan \alpha(x) \sim \alpha(x)%%
%%\arcsin\alpha(x) \sim \alpha(x)%%
%%\arctan\alpha(x) \sim \alpha(x)%%
%%\ln(1 + \alpha(x)) \sim \alpha(x)%%
%%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
%%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%

Exempel

$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \till 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \till 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(array) $$

Oändligt stora funktioner

Funktionen %%f(x)%% anropas oändligt stor(b.b.) med %%x \to a \in \overline(\mathbb(R))%%, om med denna tendens av argumentet har funktionen en oändlig gräns.

Liknar b.m. funktioner koncept b.b. funktion är oupplösligt kopplad till instruktioner för att ändra dess argument. Vi kan prata om b.b. fungerar för %%x \to a + 0%% och %%x \to a - 0%%. Termen "oändligt stor" talar inte om funktionens absoluta värde, utan om arten av dess förändring i närheten av punkten i fråga. Inget konstant tal, oavsett hur stort det är i absolut värde, är oändligt stort.

Exempel

Funktion %%f(x) = 1/x%% - b.b. vid %%x \till 0%%.
Funktion %%f(x) = x%% - b.b. vid %%x \till \infty%%.

Om definitionsvillkoren $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(array) $$

då pratar de om positiv eller negativ b.b. vid %%a%% funktion.

Exempel

Funktion %%1/(x^2)%% - positiv b.b. vid %%x \till 0%%.

Sambandet mellan b.b. och b.m. funktioner

Om %%f(x)%% är b.b. med %%x \till a%% funktion, sedan %%1/f(x)%% - b.m.

vid %%x \till a%%. Om %%\alpha(x)%% - b.m. för %%x är \till a%% en funktion som inte är noll i någon punkterad omgivning av punkten %%a%%, då är %%1/\alpha(x)%% b.b. vid %%x \till a%%.

Egenskaper för oändligt stora funktioner

Låt oss presentera flera egenskaper hos b.b. funktioner. Dessa egenskaper följer direkt av definitionen av b.b. funktioner och egenskaper hos funktioner som har ändliga gränser, samt från satsen om sambandet mellan b.b. och b.m. funktioner.

Produkten av ett ändligt antal b.b. funktioner för %%x \till a%% är b.b. funktion vid %%x \till a%%. Faktum är att om %%f_k(x), k = \overline(1, n)%% - b.b. funktion vid %%x \to a%%, sedan i någon punkterad omgivning av punkten %%a%% %%f_k(x) \ne 0%%, och genom sambandssatsen b.b. och b.m. funktioner %%1/f_k(x)%% - b.m. funktion vid %%x \till a%%. Det visar sig %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m-funktion för %%x \to a%%, och %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funktion vid %%x \till a%%.
Produkt b.b. funktioner för %%x \to a%% och en funktion som i någon punkterad omgivning av punkten %%a%% i absolut värde är större än en positiv konstant är b.b. funktion vid %%x \till a%%. I synnerhet produkten b.b. en funktion med %%x \to a%% och en funktion som har en ändlig icke-nollgräns vid punkten %%a%% kommer att vara b.b. funktion vid %%x \till a%%.

Summan av en funktion avgränsad i någon punkterad omgivning av punkten %%a%% och b.b. funktioner med %%x \till a%% är b.b. funktion vid %%x \till a%%.

Till exempel är funktionerna %%x - \sin x%% och %%x + \cos x%% b.b. vid %%x \till \infty%%.

Summan av två b.b. fungerar vid %%x \till a%% finns det osäkerhet. Beroende på villkorens tecken kan karaktären av förändringen i en sådan summa vara mycket olika.

Exempel
Låt funktionerna %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% ges. fungerar vid %%x \till \infty%%. Sedan:
- %%f(x) + g(x) = 3x%% - b.b. funktion vid %%x \till \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funktion vid %%x \till \infty%%;
- %%h(x) + v(x) = \sin x%% har ingen gräns vid %%x \to \infty%%.

Kalkyl av infinitesimals och larges

Infinitesimal kalkyl- beräkningar utförda med infinitesimala storheter, där det härledda resultatet betraktas som en oändlig summa av infinitesimaler. Infinitesimal kalkyl är allmänt begrepp för differential- och integralkalkyl, som ligger till grund för modern högre matematik. Begreppet en oändlig storhet är nära besläktat med begreppet gräns.

Oändligt liten

Efterföljd a n kallad oändligt liten, Om . Till exempel är en talföljd oändlig.

Funktionen kallas oändligt liten i närheten av en punkt x 0 om .

Funktionen kallas oändligt till oändligt, Om eller .

Också infinitesimal är en funktion som är skillnaden mellan en funktion och dess gräns, det vill säga om , Den där f(x) − a = α( x) , .

Oändligt stor mängd

Efterföljd a n kallad oändligt stor, Om .

Funktionen kallas oändligt stor i närheten av en punkt x 0 om .

Funktionen kallas oändligt stor i oändlighet, Om eller .

I alla fall antyds oändligheten till rätten till jämlikhet att ha ett visst tecken (antingen "plus" eller "minus"). Det är till exempel funktionen x synd xär inte oändligt stor vid .

Egenskaper av oändligt litet och oändligt stort

Jämförelse av oändliga mängder

Hur jämför man oändligt små mängder?
Förhållandet mellan infinitesimala storheter bildar den så kallade osäkerheten.

Definitioner

Anta att vi har oändliga värden α( x) och β( x) (eller, vilket inte är viktigt för definitionen, infinitesimala sekvenser).

För att beräkna sådana gränser är det bekvämt att använda L'Hopitals regel.

Jämförelseexempel

Använder sig av HANDLA OM-symbolik, de erhållna resultaten kan skrivas i följande form x 5 = o(x 3). I det här fallet är följande poster sanna: 2x 2 + 6x = O(x) Och x = O(2x 2 + 6x).

Motsvarande värden

Definition

Om , då de infinitesimala storheterna α och β kallas likvärdig ().
Det är uppenbart att ekvivalenta kvantiteter är ett specialfall av infinitesimala kvantiteter av samma storleksordning.

När följande ekvivalensrelationer är giltiga: , , .

Sats

Gränsen för kvoten (kvoten) av två infinitesimala storheter kommer inte att ändras om en av dem (eller båda) ersätts med en motsvarande kvantitet.

Denna sats har praktisk betydelse när man ska hitta gränser (se exempel).

Användningsexempel

Byter ut sin 2x motsvarande värde 2 x, vi får

Historisk skiss

Begreppet "oändligt" diskuterades redan i antiken i samband med begreppet odelbara atomer, men ingick inte i klassisk matematik. Det återupplivades igen med tillkomsten av "metoden för odelbara" på 1500-talet - uppdelning av figuren som studeras i oändliga sektioner.

På 1600-talet ägde algebraiseringen av infinitesimalkalkyl rum. De började definieras som numeriska storheter som är mindre än någon ändlig (icke-noll) kvantitet och ändå inte lika med noll. Analyskonsten bestod i att rita upp en relation innehållande infinitesimals (differentialer) och sedan integrera den.

Gamla skolans matematiker satte konceptet på prov oändligt liten hård kritik. Michel Rolle skrev att den nya kalkylen är " uppsättning geniala misstag"; Voltaire påpekade kaustiskt att kalkyl är konsten att beräkna och noggrant mäta saker vars existens inte kan bevisas. Även Huygens medgav att han inte förstod innebörden av differentialer av högre ordning.

Som en ödets ironi kan man betrakta framväxten i mitten av seklet av icke-standardiserad analys, som bevisade att den ursprungliga synvinkeln - faktiska infinitesimals - också var konsekvent och kunde användas som grund för analys.

se även

Wikimedia Foundation. 2010.

Se vad "oändligt stort" är i andra ordböcker:

Den variabla kvantiteten Y är inversen av den infinitesimala storheten X, det vill säga Y = 1/X... Stor encyklopedisk ordbok

Variabeln y är inversen av infinitesimal x, det vill säga y = 1/x. * * * OÄNDLIGT STORT OÄNDLIGT STORT, varierande mängd Y, inversen av det infinitesimala värdet X, det vill säga Y = 1/X ... encyklopedisk ordbok

Inom matematiken en variabel storhet som i en given förändringsprocess blir och förblir större i absolut värde än något förutbestämt tal. Studie av B. b. kvantiteter kan reduceras till studiet av infinitesimals (Se... ... Stora sovjetiska encyklopedien

Total:0
I kontakt med 0
Google+ 0
OK 0
Facebook 0