Roterande rörelse fast runt en fast axel är en rörelse där två punkter som tillhör kroppen (eller alltid associerade med den) förblir orörliga under hela rörelsen(Fig. 2.2) .
Figur 2.2
Passerar genom fasta punkter A Och I den räta linjen kallas rotationsaxel. Eftersom avståndet mellan punkterna i en stel kropp måste förbli oförändrat, är det uppenbart att under rotationsrörelse kommer alla punkter som hör till axeln att vara orörliga, och alla andra kommer att beskriva cirklar, vars plan är vinkelräta mot rotationsaxeln, och mittpunkterna ligger på denna axel. För att bestämma positionen för en roterande kropp, ritar vi genom rotationsaxeln längs vilken axeln är riktad Az, halvplan І – fast och halvplan ІІ inbäddad i själva kroppen och roterande med den. Då bestäms kroppens position vid varje tidpunkt unikt av vinkeln som tas med motsvarande tecken φ mellan dessa plan, som vi kallar kroppsrotationsvinkel. Vi kommer att överväga vinkeln φ positivt om det är försenat från ett fast plan i moturs riktning (för en observatör som tittar från den positiva änden av axeln Az), och negativ om medurs. Mät vinkel φ Vi kommer att vara i radianer. För att känna till en kropps position när som helst i tiden måste du känna till vinkelns beroende φ från tid t, dvs.
|
|
Denna ekvation uttrycker lag rotationsrörelse stel kropp runt en fast axel.
De huvudsakliga kinematiska egenskaperna för rotationsrörelsen hos en stel kropp är dess vinkelhastighet ω och vinkelacceleration ε.
9.2.1. En kropps vinkelhastighet och vinkelacceleration
Den kvantitet som kännetecknar förändringshastigheten i rotationsvinkeln φ över tiden kallas vinkelhastighet.
Om under en tid  kroppen roterar i en vinkel
kroppen roterar i en vinkel  , då kommer kroppens numeriskt genomsnittliga vinkelhastighet under denna tidsperiod att vara
, då kommer kroppens numeriskt genomsnittliga vinkelhastighet under denna tidsperiod att vara  . I gränsen kl
. I gränsen kl  vi får
vi får
Således, det numeriska värdet av en kropps vinkelhastighet vid en given tidpunkt är lika med den första derivatan av rotationsvinkeln i förhållande till tiden.
Teckenregel: När rotation sker moturs, ω> 0, och när medurs, då ω< 0.
 eller eftersom radian är en dimensionslös storhet,
eller eftersom radian är en dimensionslös storhet,  .
.
I teoretiska beräkningar är det bekvämare att använda vinkelhastighetsvektorn  , vars modul är lika med
, vars modul är lika med  och som är riktad längs kroppens rotationsaxel i den riktning från vilken rotationen är synlig moturs. Denna vektor bestämmer omedelbart storleken på vinkelhastigheten, rotationsaxeln och rotationsriktningen runt denna axel.
och som är riktad längs kroppens rotationsaxel i den riktning från vilken rotationen är synlig moturs. Denna vektor bestämmer omedelbart storleken på vinkelhastigheten, rotationsaxeln och rotationsriktningen runt denna axel.
Den kvantitet som kännetecknar förändringshastigheten i vinkelhastighet över tiden kallas kroppens vinkelacceleration.
Om under en tid  ökningen i vinkelhastighet är lika med
ökningen i vinkelhastighet är lika med  , sedan relationen
, sedan relationen  , dvs. bestämmer värdet på den genomsnittliga accelerationen för en roterande kropp över tiden
, dvs. bestämmer värdet på den genomsnittliga accelerationen för en roterande kropp över tiden  .
.
När man strävar  vi erhåller storleken på vinkelaccelerationen för tillfället t:
vi erhåller storleken på vinkelaccelerationen för tillfället t:
Således, det numeriska värdet av en kropps vinkelacceleration vid en given tidpunkt är lika med den första derivatan av vinkelhastigheten eller den andra derivatan av kroppens rotationsvinkel i tid.
Måttenheten används vanligtvis  eller, vilket också är,
eller, vilket också är,  .
.
Om vinkelhastighetsmodulen ökar med tiden kallas kroppens rotation accelererad, och om det minskar, - långsam När värdena ω
Och ε
har samma tecken, då kommer rotationen att accelereras, när de är olika, kommer den att saktas ner.  I analogi med vinkelhastighet kan vinkelacceleration också representeras som en vektor
I analogi med vinkelhastighet kan vinkelacceleration också representeras som en vektor  , riktad längs rotationsaxeln. Vart i
, riktad längs rotationsaxeln. Vart i
 .
.
Om en kropp roterar i en accelererad riktning  sammanfaller med
sammanfaller med  , och mitt emot
, och mitt emot  med långsam rotation.
med långsam rotation.
Om en kropps vinkelhastighet förblir konstant under rörelse ( ω= konst), så kallas kroppens rotation enhetlig.
Från  vi har
vi har  . Därför, med tanke på det i det första ögonblicket
. Därför, med tanke på det i det första ögonblicket  hörn
hörn  , och ta integralerna till vänster om
, och ta integralerna till vänster om  innan
innan  , och till höger från 0 till t, får vi äntligen
, och till höger från 0 till t, får vi äntligen
|
|
Med enhetlig rotation, när  =0,
=0, Och
Och  .
.
Hastigheten för enhetlig rotation bestäms ofta av antalet varv per minut, vilket anger detta värde med n rpm Låt oss hitta förhållandet mellan n rpm och ω 1/s. Med ett varv kommer kroppen att rotera med 2π, och med n rpm vid 2π n; denna sväng är gjord på 1 minut, d.v.s. t= 1min=60s. Det följer att
|
|
Om en kropps vinkelacceleration förblir konstant under hela dess rörelse (ε = konst), så kallas rotationen lika varierande.
I det första ögonblicket t=0 vinkel  och vinkelhastigheten
och vinkelhastigheten  (
( - initial vinkelhastighet).
- initial vinkelhastighet).  ;
; =ε
=ε  . Integrering av vänster sida av
. Integrering av vänster sida av  innan
innan  , och den högra från 0 till t, vi hittar
, och den högra från 0 till t, vi hittar
Vinkelhastigheten ω för denna rotation  . Om ω och ε har samma tecken blir rotationen jämnt accelererat, och om olika - lika långsamt.
. Om ω och ε har samma tecken blir rotationen jämnt accelererat, och om olika - lika långsamt.
Rotationsvinkel, vinkelhastighet och vinkelacceleration
Rotation av en stel kropp runt en fast axel Det kallas en sådan rörelse där två punkter på kroppen förblir orörliga under hela rörelsetiden. I detta fall förblir alla punkter på kroppen som ligger på en rät linje som passerar genom dess fasta punkter också orörliga. Denna linje kallas kroppens rotationsaxel.
Om A Och I- kroppens fasta punkter (bild 15 ), då är rotationsaxeln axeln Uns, som kan ha vilken riktning som helst i rymden, inte nödvändigtvis vertikalt. En axelriktning Uns tas som positivt.
Vi ritar ett fast plan genom rotationsaxeln Förbi och mobil P, fäst vid en roterande kropp. Låt båda planen sammanfalla i det första ögonblicket. Då vid ett ögonblick i tiden t positionen för det rörliga planet och den roterande kroppen själv kan bestämmas av den dihedriska vinkeln mellan planen och motsvarande linjära vinkel φ mellan raka linjer belägna i dessa plan och vinkelräta mot rotationsaxeln. Hörn φ kallad kroppsrotationsvinkel.
Kroppens position i förhållande till det valda referenssystemet är helt bestämt i varje
ögonblick i tiden, om ekvationen ges φ =med) (5)
Var med)- vilken som helst två gånger differentierbar funktion av tiden. Denna ekvation kallas ekvation för rotationen av en stel kropp runt en fast axel.
En kropp som roterar runt en fast axel har en frihetsgrad, eftersom dess position bestäms genom att endast specificera en parameter - vinkeln φ .
Hörn φ anses positivt om det ritas moturs och negativt i motsatt riktning sett från axelns positiva riktning Uns. Banorna för en kropps punkter under dess rotation runt en fast axel är cirklar placerade i plan vinkelräta mot rotationsaxeln.
För att karakterisera rotationsrörelsen hos en stel kropp runt en fast axel introducerar vi begreppen vinkelhastighet och vinkelacceleration. Algebraisk vinkelhastighet hos kroppen vid varje ögonblick i tiden kallas den första derivatan med avseende på tiden av rotationsvinkeln i detta ögonblick, dvs. dφ/dt = φ. Det är en positiv kvantitet när kroppen roterar moturs, eftersom rotationsvinkeln ökar med tiden, och negativ när kroppen roterar medurs, eftersom rotationsvinkeln minskar.
Vinkelhastighetsmodulen betecknas med ω. Sedan ω= ׀dφ/dt׀= ׀φ ׀ (6)
Dimensionen på vinkelhastigheten ställs in i enlighet med (6)
[ω] = vinkel/tid = rad/s = s -1.
Inom teknik är vinkelhastigheten rotationshastigheten uttryckt i varv per minut. På 1 minut kommer kroppen att rotera i en vinkel 2πп, Om P- antal varv per minut. Om vi dividerar denna vinkel med antalet sekunder i en minut får vi: (7)
Algebraisk vinkelacceleration av kroppen kallas förstaderivatan med avseende på tiden av den algebraiska hastigheten, dvs. andra derivatan av rotationsvinkeln d 2 φ/dt 2 = ω. Låt oss beteckna vinkelaccelerationsmodulen ε , Då ε=|φ| (8)
Dimensionen för vinkelaccelerationen erhålls från (8):
[ε ] = vinkelhastighet/tid = rad/s 2 = s -2
Om φ’’>0 på φ’>0 , då ökar den algebraiska vinkelhastigheten med tiden och därför roterar kroppen accelererat vid det aktuella ögonblicket i positiva sidan(moturs). På φ’’<0 Och φ’<0 kroppen roterar snabbt i negativ riktning. Om φ’’<0 på φ’>0 , då har vi långsam rotation i positiv riktning. På φ’’>0 Och φ’<0 , dvs. långsam rotation sker i negativ riktning. Vinkelhastighet och vinkelacceleration i figurerna avbildas med bågspilar runt rotationsaxeln. Bågpilen för vinkelhastighet anger kropparnas rotationsriktning;
För accelererad rotation har bågpilarna för vinkelhastighet och vinkelacceleration samma riktningar; för långsam rotation är deras riktningar motsatta.
Specialfall av rotation av en stel kropp
Rotation sägs vara enhetlig om ω=const, φ= φ’t
Rotationen blir enhetlig om ε=konst. φ’= φ’ 0 + φ’’t och
I allmänhet, om φ’’ inte alltid,
![]()
Hastigheter och accelerationer av kroppspunkter
Ekvationen för rotationen av en stel kropp runt en fast axel är känd φ= f(t)(Fig. 16). Distans s poäng M i ett rörligt plan P längs en cirkelbåge (punktbana), mätt från punkten M o, belägen i ett fast plan, uttryckt genom vinkeln φ missbruk s=hφ, Var h-radien för den cirkel längs vilken punkten rör sig. Det är det kortaste avståndet från en punkt M till rotationsaxeln. Detta kallas ibland rotationsradien för en punkt. Vid varje punkt av kroppen förblir rotationsradien oförändrad när kroppen roterar runt en fast axel.
 Algebraisk hastighet för en punkt M bestäms av formeln v τ =s’=hφ Punkthastighetsmodul: v=hω(9)
Algebraisk hastighet för en punkt M bestäms av formeln v τ =s’=hφ Punkthastighetsmodul: v=hω(9)
Hastigheterna för kroppspunkter när de roterar runt en fast axel är proportionella mot deras kortaste avstånd till denna axel. Proportionalitetskoefficienten är vinkelhastigheten. Punkternas hastigheter är riktade längs tangenterna till banorna och är därför vinkelräta mot rotationsradien. Hastigheter för kroppspunkter som ligger på ett rakt linjesegment OM, i enlighet med (9) fördelas enligt en linjär lag. De är ömsesidigt parallella, och deras ändar är belägna på samma räta linje som passerar genom rotationsaxeln. Vi delar upp en punkts acceleration i tangentiella och normala komponenter, dvs. a=a τ +a nτ Tangentiella och normala accelerationer beräknas med formler (10)
eftersom krökningsradien för en cirkel är p=h(Fig. 17 ). Således,
 Tangent-, normal- och totalaccelerationer av punkter, såväl som hastigheter, är också fördelade enligt en linjär lag. De beror linjärt på punkternas avstånd till rotationsaxeln. Normal acceleration riktas längs cirkelns radie mot rotationsaxeln. Riktningen för den tangentiella accelerationen beror på tecknet för den algebraiska vinkelaccelerationen. På φ’>0
Och φ’’>0
eller φ’<0
Och φ’<0
vi har accelererad rotation av kroppen och vektorernas riktningar a τ Och v passa ihop. Om φ’
Och φ’"
har olika tecken (långsam rotation), då a τ Och v riktade mitt emot varandra.
Tangent-, normal- och totalaccelerationer av punkter, såväl som hastigheter, är också fördelade enligt en linjär lag. De beror linjärt på punkternas avstånd till rotationsaxeln. Normal acceleration riktas längs cirkelns radie mot rotationsaxeln. Riktningen för den tangentiella accelerationen beror på tecknet för den algebraiska vinkelaccelerationen. På φ’>0
Och φ’’>0
eller φ’<0
Och φ’<0
vi har accelererad rotation av kroppen och vektorernas riktningar a τ Och v passa ihop. Om φ’
Och φ’"
har olika tecken (långsam rotation), då a τ Och v riktade mitt emot varandra.
Efter att ha utsett α vinkeln mellan en punkts totala acceleration och dess rotationsradie har vi
tgα = | a τ |/a n = ε/ω 2 (11)
sedan normal acceleration a sid alltid positiv. Hörn A samma för alla punkter på kroppen. Det bör skjutas upp från acceleration till rotationsradien i riktningen för bågpilen för vinkelacceleration, oavsett rotationsriktningen för den stela kroppen.
Vektorer av vinkelhastighet och vinkelacceleration
![]()
Låt oss introducera begreppen vektorer för en kropps vinkelhastighet och vinkelacceleration. Om TILLär enhetsvektorn för rotationsaxeln riktad i dess positiva riktning, sedan vinkelhastighetsvektorerna ώ och vinkelacceleration ε bestäms av uttryck (12)
Därför att kär en vektorkonstant i storlek och riktning, så av (12) följer att
ε=dώ/dt(13)

På φ’>0 Och φ’’>0 vektor riktningar ώ Och ε passa ihop. De är båda riktade mot den positiva sidan av rotationsaxeln Uns(Fig. 18.a) Om φ’>0 Och φ’’<0 , sedan riktas de i motsatta riktningar (Fig. 18.b ). Vinkelaccelerationsvektorn sammanfaller i riktning med vinkelhastighetsvektorn under accelererad rotation och är motsatt den under långsam rotation. Vektorer ώ Och ε kan avbildas när som helst på rotationsaxeln. De är rörliga vektorer. Denna egenskap följer av vektorformlerna för kroppspunkters hastigheter och accelerationer.
Komplex punktrörelse
Grundläggande koncept
För att studera några mer komplexa typer av rörelser hos en stel kropp, är det tillrådligt att överväga den enklaste komplexa rörelsen av en punkt. I många problem måste en punkts rörelse betraktas i förhållande till två (eller flera) referenssystem som rör sig i förhållande till varandra. Således måste rörelsen av en rymdfarkost som rör sig mot månen betraktas samtidigt både i förhållande till jorden och i förhållande till månen, som rör sig i förhållande till jorden. Varje rörelse av en punkt kan betraktas som komplex, bestående av flera rörelser. Till exempel kan ett fartygs rörelse längs en flod i förhållande till jorden betraktas som komplex, bestående av rörelse genom vattnet och tillsammans med det strömmande vattnet.
I det enklaste fallet består den komplexa rörelsen av en punkt av relativa och translationella rörelser. Låt oss definiera dessa rörelser. Låt oss ha två referenssystem som rör sig i förhållande till varandra. Om ett av dessa system O l x 1 y 1 z 1(Fig. 19 ) tas som den huvudsakliga eller stationära (dess rörelse i förhållande till andra referenssystem beaktas inte), sedan det andra referenssystemet Oxyz kommer att flyttas i förhållande till den första. Rörelse av en punkt i förhållande till en rörlig referensram Oxyz kallad relativ. Egenskaperna för denna rörelse, såsom bana, hastighet och acceleration, kallas relativ. De betecknas med indexet r; för hastighet och acceleration v r , a r . Rörelse av en punkt i förhållande till huvud- eller fast systemreferensramen O 1 x 1 y 1 z 1 kallad absolut(eller komplex ). Det kallas också ibland sammansatt rörelse. Banan, hastigheten och accelerationen för denna rörelse kallas absolut. Hastigheten och accelerationen för absolut rörelse indikeras med bokstäverna v, a inga index.
 |
Den bärbara rörelsen av en punkt är den rörelse som den gör tillsammans med en rörlig referensram, som en punkt som är stelt fäst vid detta system vid det aktuella ögonblicket. På grund av relativ rörelse sammanfaller en rörlig punkt vid olika tidpunkter med olika punkter på kroppen S, till vilket det rörliga referenssystemet är anslutet. Den bärbara hastigheten och den bärbara accelerationen är hastigheten och accelerationen för den punkten på kroppen S, med vilken rörelsepunkten för närvarande sammanfaller. Bärbar hastighet och acceleration anger v e, a e.
Om banorna för alla punkter i kroppen S, fäst vid det rörliga referenssystemet, avbildat i figuren (fig. 20), då får vi en familj av linjer - en familj av banor för den bärbara rörelsen av en punkt M. På grund av punktens relativa rörelse M vid varje tidpunkt är den på en av de bärbara rörelsernas banor. Punkt M kan sammanfalla med endast en punkt på var och en av banorna i denna familj av överföringsbanor. I detta avseende tror man ibland att det inte finns några banor för bärbar rörelse, eftersom det är nödvändigt att betrakta linjer som banor för bärbar rörelse, för vilka endast en punkt faktiskt är en punkt i banan.
I kinematiken för en punkt studerades en punkts rörelse i förhållande till vilket referenssystem som helst, oavsett om detta referenssystem rör sig i förhållande till andra system eller inte. Låt oss komplettera denna studie genom att betrakta komplex rörelse, i det enklaste fallet bestående av relativ och figurativ rörelse. En och samma absoluta rörelse, som väljer olika rörliga referensramar, kan anses bestå av olika bärbara och följaktligen relativa rörelser.
Hastighetstillägg
 Låt oss bestämma hastigheten för en punkts absoluta rörelse om hastigheterna för de relativa och bärbara rörelserna för denna punkt är kända. Låt punkten endast göra en, relativ rörelse med avseende på den rörliga referensramen Oxyz och vid tidpunkten t inta position M på den relativa rörelsens bana (fig. 20). Vid tidpunkten t+t, på grund av relativ rörelse, kommer punkten att vara i position Mi, efter att ha flyttats MM1 längs den relativa rörelsens bana. Låt oss anta att poängen är inblandad Oxyz och med en relativ bana kommer den att röra sig längs någon kurva vidare MM 2. Om en punkt deltar samtidigt i både relativa och bärbara rörelser, då i tid A; hon ska flytta till MM" längs den absoluta rörelsens bana och i tidens ögonblick t+At kommer att ta positionen M". Om tid På lite och sedan gå till gränsen kl På, tenderar mot noll, då kan små förskjutningar längs kurvor ersättas med segment av ackord och tas som förskjutningsvektorer. Lägger vi till vektorförskjutningarna får vi
Låt oss bestämma hastigheten för en punkts absoluta rörelse om hastigheterna för de relativa och bärbara rörelserna för denna punkt är kända. Låt punkten endast göra en, relativ rörelse med avseende på den rörliga referensramen Oxyz och vid tidpunkten t inta position M på den relativa rörelsens bana (fig. 20). Vid tidpunkten t+t, på grund av relativ rörelse, kommer punkten att vara i position Mi, efter att ha flyttats MM1 längs den relativa rörelsens bana. Låt oss anta att poängen är inblandad Oxyz och med en relativ bana kommer den att röra sig längs någon kurva vidare MM 2. Om en punkt deltar samtidigt i både relativa och bärbara rörelser, då i tid A; hon ska flytta till MM" längs den absoluta rörelsens bana och i tidens ögonblick t+At kommer att ta positionen M". Om tid På lite och sedan gå till gränsen kl På, tenderar mot noll, då kan små förskjutningar längs kurvor ersättas med segment av ackord och tas som förskjutningsvektorer. Lägger vi till vektorförskjutningarna får vi
![]() I detta avseende kasseras små kvantiteter av högre ordning, och tenderar till noll vid På, tenderar mot noll. När vi går till gränsen har vi (14)
I detta avseende kasseras små kvantiteter av högre ordning, och tenderar till noll vid På, tenderar mot noll. När vi går till gränsen har vi (14)
Därför kommer (14) att ha formen (15)
Den så kallade hastighetsadditionssatsen erhålls: hastigheten för en punkts absoluta rörelse är lika med vektorsumman av hastigheterna för den bärbara och relativa rörelsen för denna punkt. Eftersom i det allmänna fallet hastigheterna för de bärbara och relativa rörelserna inte är vinkelräta, då (15')
Relaterad information.
Roterande rörelse av en stel kropp. Rotationsrörelse är rörelsen hos en stel kropp där alla dess punkter som ligger på en viss rät linje, kallad rotationsaxeln, förblir orörliga.
Under rotationsrörelse rör sig alla andra punkter på kroppen i plan som är vinkelräta mot rotationsaxeln och beskriver cirklar vars centrum ligger på denna axel.
För att bestämma positionen för en roterande kropp ritar vi två halvplan genom z-axeln: halvplan I - stationär och halvplan II - kopplade till den stela kroppen och roterar med den (fig. 2.4). Då kommer kroppens position vid varje tidpunkt att bestämmas unikt av vinkeln j mellan dessa halvplan, tagna med motsvarande tecken, som kallas kroppens rotationsvinkel.
När en kropp roterar ändras rotationsvinkeln j beroende på tiden, dvs det är en funktion av tiden t:
Denna ekvation kallas ekvation rotationsrörelse hos en stel kropp.
De huvudsakliga kinematiska egenskaperna för rotationsrörelsen hos en stel kropp är dess vinkelhastighet w och vinkelacceleration e.
Om under tiden D t= t1 + t kroppen gör en sväng med Dj = j1 –j, då blir kroppens genomsnittliga vinkelhastighet under denna tidsperiod lika med
 (1.16)
(1.16)
Att bestämma värdet på en kropps vinkelhastighet vid en given tidpunkt t låt oss hitta gränsen för förhållandet mellan ökningen av rotationsvinkeln Dj och tidsintervallet D t eftersom den senare tenderar till noll:
 (2.17)
(2.17)
Således är kroppens vinkelhastighet vid en given tidpunkt numeriskt lika med den första derivatan av rotationsvinkeln i förhållande till tiden. Tecknet för vinkelhastigheten w sammanfaller med tecknet för kroppens rotationsvinkel j: w > 0 vid j > 0, och vice versa, om j < 0. sedan w < 0. Dimensionen på vinkelhastigheten är vanligtvis 1/s, så radianer är dimensionslösa.
Vinkelhastigheten kan representeras som en vektor w , vars numeriska värde är lika med dj/dt som är riktad längs kroppens rotationsaxel i den riktning från vilken rotationen kan ses ske moturs.
Förändringen i en kropps vinkelhastighet över tiden kännetecknas av vinkelacceleration t. I analogi med att hitta medelvärdet för vinkelhastigheten hittar vi ett uttryck för att bestämma värdet på medelaccelerationen:
 (2.18)
(2.18)
Sedan bestäms accelerationen av den stela kroppen vid en given tidpunkt från uttrycket
 (2.19)
(2.19)
dvs kroppens vinkelacceleration vid en given tidpunkt är lika med den första derivatan av vinkelhastigheten eller den andra derivatan av kroppens rotationsvinkel i förhållande till tiden. Dimensionen på vinkelaccelerationen är 1/s 2.
Vinkelaccelerationen hos en stel kropp, liksom vinkelhastigheten, kan representeras som en vektor. Vinkelaccelerationsvektorn sammanfaller i riktning med vinkelhastighetsvektorn under accelererad rörelse av en solid topp och är riktad i motsatt riktning under slow motion.
Efter att ha fastställt egenskaperna hos en stel kropps rörelse som helhet, låt oss gå vidare till att studera rörelsen hos dess individuella punkter. Låt oss överväga en punkt M fast kropp placerad på ett avstånd h från rotationsaxeln r (Fig. 2.3).
När kroppen roterar kommer punkt M att beskriva en cirkulär punkt med radie h centrerad på rotationsaxeln och som ligger i ett plan vinkelrätt mot denna axel. Om under tiden dt en elementär piskning av kroppen sker i vinkel dj , peka sedan M gör samtidigt en elementär rörelse längs dess bana dS = h*dj ,. Därefter bestämdes hastigheten för punkten M från uttrycket
![]() (2.20)
(2.20)
Hastigheten kallas den linjära eller periferiska hastigheten för punkt M.
Således är den linjära hastigheten för en punkt på en roterande stel kropp numeriskt lika med produkten av kroppens vinkelhastighet och avståndet från denna punkt till rotationsaxeln. Eftersom för alla punkter i kroppen vinkelhastigheten w; har samma värde, så följer av formeln för linjär hastighet att de linjära hastigheterna för punkterna i en roterande kropp är proportionella mot deras avstånd från rotationsaxeln. Den linjära hastigheten för en punkt i en stel kropp är en vektor n riktad tangentiellt mot cirkeln som beskrivs av punkten M.
Beli avståndet från rotationsaxeln för en solid pel till en viss punkt M betraktad som radievektorn h för punkt M, då kan den linjära hastighetsvektorn för punkt v representeras som vektorprodukten av vinkelhastighetsvektorn w radievektor h:
V = w * h (2/21)
Faktum är att resultatet av vektorprodukten (2.21) är en vektor lika i modul med produkten w*h och riktad (Fig. 2.5) vinkelrätt mot det plan i vilket de två faktorerna ligger, i den riktning från vilken den närmaste kombinationen av den första faktorn med den andra observeras att inträffa moturs, d.v.s. tangerar banan för punkt M.
Således motsvarar vektorn som resulterar från vektorprodukten (2.21) i storlek och riktning den linjära hastighetsvektorn för punkt M.

Ris. 2.5
För att hitta ett uttryck för acceleration A punkt M, differentierar vi med avseende på tid uttrycket (2.21) för punktens hastighet
 (2.22)
(2.22)
Med hänsyn till att dj/dt=e, och dh/dt = v, skriver vi uttryck (2.22) i formen
där аг och аn är tangent- respektive normalkomponenterna för den totala accelerationen av en punkt i en kropp under rotationsrörelse, bestämd från uttrycken
Den tangentiella komponenten av den totala accelerationen av en kroppspunkt (tangentiell acceleration) vid karakteriserar förändringen i hastighetsvektorns storlek och är riktad tangentiellt till kroppspunktens bana i riktning mot hastighetsvektorn under accelererad rörelse eller i motsatt riktning. riktning under slowmotion. Storleken på tangentiell accelerationsvektor för en punkt i en kropp under rotationsrörelse av en stel kropp bestäms av uttrycket
![]() (2,25)
(2,25)
Normal komponent av total acceleration (normal acceleration) A" uppstår på grund av en förändring i riktningen av hastighetsvektorn för en punkt när man målar en solid kropp. Som följer av uttryck (2.24) för normal acceleration riktas denna acceleration längs radien h till mitten av cirkeln längs vilken punkten rör sig. Modulen för den normala accelerationsvektorn för en punkt under rotationsrörelse hos en stel kropp bestäms med hänsyn till (2.20) av uttrycket
I naturen och tekniken möter vi ofta manifestationen av rotationsrörelse hos solida kroppar, till exempel axlar och kugghjul. Hur denna typ av rörelse beskrivs i fysiken, vilka formler och ekvationer som används för detta, dessa och andra frågor behandlas i den här artikeln.
Vad är rotation?
Var och en av oss vet intuitivt vilken typ av rörelse vi pratar om. Rotation är en process där en kropp eller materialpunkt rör sig i en cirkulär bana runt en viss axel. Ur geometrisk synvinkel är en stel kropp en rak linje, vars avstånd förblir oförändrat under rörelse. Detta avstånd kallas rotationsradien. I det följande kommer vi att beteckna det med bokstaven r. Om rotationsaxeln passerar genom kroppens masscentrum, kallas den för sin egen axel. Ett exempel på rotation runt sin egen axel är motsvarande rörelse hos solsystemets planeter.
För att rotation ska ske måste det finnas centripetalacceleration, som uppstår på grund av centripetalkraft. Denna kraft riktas från kroppens masscentrum till rotationsaxeln. Centripetalkraftens natur kan vara mycket olika. Så, på en kosmisk skala, spelas dess roll av gravitationen; om kroppen är säkrad med en tråd, kommer spänningskraften hos den senare att vara centripetal. När en kropp roterar runt sin egen axel, spelas rollen som centripetalkraft av den interna elektrokemiska interaktionen mellan de element som utgör kroppen (molekyler, atomer).
Det är nödvändigt att förstå att utan närvaron av en centripetalkraft kommer kroppen att röra sig i en rak linje.
Fysiska storheter som beskriver rotation

För det första är dessa dynamiska egenskaper. Dessa inkluderar:
- vinkelmoment L;
- tröghetsmoment I;
- kraftmoment M.
För det andra är dessa kinematiska egenskaper. Låt oss lista dem:
- rotationsvinkel θ;
- vinkelhastighet ω;
- vinkelacceleration α.
Låt oss kort beskriva var och en av dessa kvantiteter.
Vinkelmomentet bestäms av formeln:
Där p är linjärt rörelsemängd, m är massan av en materialpunkt, v är dess linjära hastighet.
Tröghetsmomentet för en materialpunkt beräknas med hjälp av uttrycket:
För varje kropp med komplex form beräknas värdet av I som integralsumman av materialpunkters tröghetsmoment.
Kraftmomentet M beräknas enligt följande:
Här är F den yttre kraften, d är avståndet från dess appliceringspunkt till rotationsaxeln.
Den fysiska betydelsen av alla kvantiteter vars namn innehåller ordet "ögonblick" liknar betydelsen av motsvarande linjära kvantiteter. Till exempel visar kraftmomentet förmågan hos den applicerade kraften att överföras till ett system av roterande kroppar.
Kinematiska egenskaper bestäms matematiskt av följande formler:
Som framgår av dessa uttryck liknar vinkelegenskaperna i betydelse de linjära (hastighet v och acceleration a), endast de är tillämpliga för en cirkulär bana.
Dynamik av rotation
Inom fysiken utförs studiet av rotationsrörelsen hos en stel kropp med hjälp av två grenar av mekanik: dynamik och kinematik. Låt oss börja med dynamik.
Dynamics studerar yttre krafter som verkar på ett system av roterande kroppar. Låt oss omedelbart skriva ner ekvationen för rotationsrörelse för en stel kropp och sedan analysera dess komponenter. Så denna ekvation ser ut så här:
Som verkar på ett system med ett tröghetsmoment I, vilket orsakar uppkomsten av vinkelacceleration α. Ju mindre värdet på I är, desto lättare är det, med hjälp av ett visst moment M, att snurra systemet till höga hastigheter under korta tidsperioder. Till exempel är det lättare att rotera en metallstav längs dess axel än vinkelrätt mot den. Det är dock lättare att rotera samma stång runt en axel som är vinkelrät mot den och passerar genom masscentrum än genom dess ände.
Lagen om bevarande av kvantitet L
Denna kvantitet introducerades ovan, den kallas vinkelmomentum. Ekvationen för rotationsrörelse för en stel kropp, presenterad i föregående stycke, är ofta skriven i en annan form:
Om momentet för externa krafter M verkar på systemet under tiden dt, så orsakar det en förändring i systemets vinkelmoment med mängden dL. Följaktligen, om kraftmomentet är noll, så är L = konst. Detta är lagen för bevarande av kvantiteten L. För den kan vi, med hjälp av förhållandet mellan linjär och vinkelhastighet, skriva:
L = m*v*r = m*ω*r2 = I*ω.
Sålunda, i frånvaro av vridmoment, är produkten av vinkelhastighet och tröghetsmoment ett konstant värde. Denna fysiska lag används av konståkare i sina framträdanden eller av konstgjorda satelliter som måste roteras runt sin egen axel i yttre rymden.

Centripetal acceleration
Ovan, när man studerar rotationsrörelsen hos en stel kropp, har denna mängd redan beskrivits. Arten av centripetalkrafter noterades också. Här kommer vi bara att komplettera denna information och tillhandahålla motsvarande formler för att beräkna denna acceleration. Låt oss beteckna det som ett c.
Eftersom centripetalkraften är riktad vinkelrätt mot axeln och passerar genom den, skapar den inte ett ögonblick. Det vill säga, denna kraft har absolut ingen effekt på de kinematiska egenskaperna hos rotationen. Det skapar dock centripetalacceleration. Här är två formler för att bestämma det:
Således, ju större vinkelhastighet och radie, desto större kraft måste anbringas för att hålla kroppen på en cirkulär bana. Ett slående exempel på denna fysiska process är sladd av en bil under en sväng. En sladd uppstår om centripetalkraften, vars roll spelas av friktionskraften, blir mindre än centrifugalkraften (tröghetskaraktäristik).

Tre huvudsakliga kinematiska egenskaper listades ovan i artikeln. fast kropp beskrivs med följande formler:
θ = ω*t => ω = konst., α = 0;
θ = ω 0 *t + α*t 2 /2 => ω = ω 0 + α*t, α = konst.
Den första raden innehåller formler för enhetlig rotation, som förutsätter frånvaron av ett yttre kraftmoment som verkar på systemet. Den andra raden innehåller formler för likformigt accelererad rörelse i en cirkel.

Observera att rotation inte bara kan ske med positiv acceleration, utan även med negativ. I det här fallet, i formlerna på den andra raden, bör du sätta ett minustecken före den andra termen.
Exempel på problemlösning
Ett kraftmoment på 1000 N*m verkade på metallaxeln i 10 sekunder. Genom att veta att axelns tröghetsmoment är lika med 50 kg * m 2 är det nödvändigt att bestämma vinkelhastigheten som det nämnda kraftmomentet gav axeln.

Med hjälp av den grundläggande rotationsekvationen beräknar vi axelns acceleration:
Eftersom denna vinkelacceleration verkade på axeln under en tid t = 10 sekunder, för att beräkna vinkelhastigheten använder vi formeln för likformigt accelererad rörelse:
ω = ω 0 + α*t = M/I*t.
Här ω 0 = 0 (axeln roterade inte förrän kraftmomentet M verkade).
Vi ersätter de numeriska värdena för kvantiteterna i likheten, och vi får:
ω = 1000/50*10 = 200 rad/s.
För att omvandla detta tal till vanliga varv per sekund måste du dividera det med 2*pi. Efter att ha utfört denna åtgärd finner vi att axeln kommer att rotera med en frekvens på 31,8 rpm.
DEFINITION: Roterande rörelse av en stel kropp vi kommer att kalla en sådan rörelse där alla punkter i kroppen rör sig i cirklar, vars centrum ligger på samma räta linje, kallad rotationsaxeln.
För att studera dynamiken hos den roterande, lägger vi till de kända kinematiska storheterna två kvantiteter: maktens ögonblick(M) och tröghetsmoment(J).
1. Det är känt av erfarenhet: accelerationen av rotationsrörelse beror inte bara på storleken av den kraft som verkar på kroppen, utan också på avståndet från rotationsaxeln till linjen längs vilken kraften verkar. För att karakterisera denna omständighet kallas en fysisk kvantitet kraftmoment.
Låt oss överväga det enklaste fallet.
DEFINITION: Momentet för en kraft kring en viss punkt "O" är en vektorkvantitet som definieras av uttrycket, där radievektorn dras från punkten "O" till punkten för kraftens applicering.
Av definitionen följer att det är en axiell vektor. Dess riktning är vald så att vektorns rotation runt punkten "O" i kraftens riktning och vektorn bildar ett högerhänt system. Modulen för kraftmomentet är lika med , där a är vinkeln mellan vektorernas riktningar och , och l= r synd a är längden på den vinkelräta som tappas från punkt "O" till den räta linje längs vilken kraften verkar (kallas axel av styrka relativt punkt "O") (Fig. 4.2).
2. Experimentella data indikerar att storleken på vinkelaccelerationen påverkas inte bara av den roterande kroppens massa, utan också av fördelningen av massan i förhållande till rotationsaxeln. Den kvantitet som tar hänsyn till denna omständighet kallas tröghetsmoment i förhållande till rotationsaxeln.
DEFINITION: Strängt taget, tröghetsmoment kropp i förhållande till en viss rotationsaxel kallas värdet J, lika med summan av produkterna av elementära massor med kvadraterna på deras avstånd från en given axel.
Summeringen utförs över alla elementära massor som kroppen delades in i. Man bör komma ihåg att denna kvantitet (J) existerar oavsett rotation (även om begreppet tröghetsmoment infördes när man övervägde rotationen av en stel kropp).
Varje kropp, oavsett om den är i vila eller roterar, har ett visst tröghetsmoment i förhållande till vilken axel som helst, precis som en kropp har massa oavsett om den rör sig eller i vila.
Med tanke på att , kan tröghetsmomentet representeras som: . Detta förhållande är ungefärligt och ju mindre elementära volymer och motsvarande masselement, desto mer exakt blir det. Följaktligen kommer uppgiften att hitta tröghetsmoment ner till integration: . Här utförs integration över hela kroppens volym.
Låt oss skriva ner tröghetsmomenten för några kroppar med regelbunden geometrisk form.
| 1. Enhetligt lång spö. | |
| Ris. 4.3 | Tröghetsmomentet kring axeln vinkelrät mot stången och som går genom dess mitt är lika med |
| 2. Solid cylinder eller skiva. | |
| Ris. 4.4 | Tröghetsmomentet kring axeln som sammanfaller med den geometriska axeln är lika med . |
| 3. Tunnväggig cylinder med radie R. | |
| Ris. 4.5 | |
| 4. Tröghetsmoment för en kula med radien R i förhållande till en axel som går genom dess centrum | |
| Ris. 4.6 | |
| 5. Tröghetsmoment för en tunn skiva (tjocklek b< | |
| Ris. 4.7 | |
| 6. Blockets tröghetsmoment | |
| Ris. 4.8 | |
| 7. Ringens tröghetsmoment | |
| Ris. 4.9 |
Beräkning av tröghetsmomentet här är ganska enkel, eftersom Kroppen antas vara homogen och symmetrisk, och tröghetsmomentet bestäms i förhållande till symmetriaxeln.
För att bestämma tröghetsmomentet för en kropp i förhållande till vilken axel som helst, är det nödvändigt att använda Steiners teorem.
DEFINITION: Tröghetsmoment J kring en godtycklig axelär lika med summan av tröghetsmomentet Jc i förhållande till en axel parallell med den givna och som går genom kroppens tröghetscentrum, och produkten av kroppsmassan med kvadraten på avståndet mellan axlarna (fig. 4.10).
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0

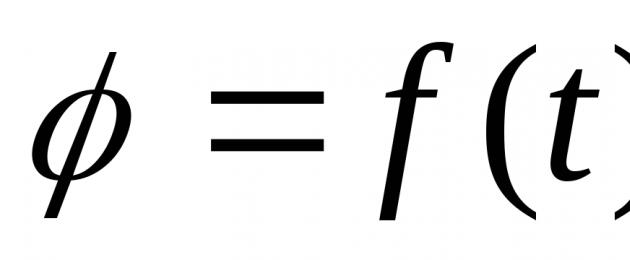
 .
. .
. .
.





